A High Sensitivity FBG Strain Sensor Based on Flexible Hinge
Abstract
:1. Introduction
2. Principle of the Sensors and Mathematical Model
2.1. Principle of FBG Sensing
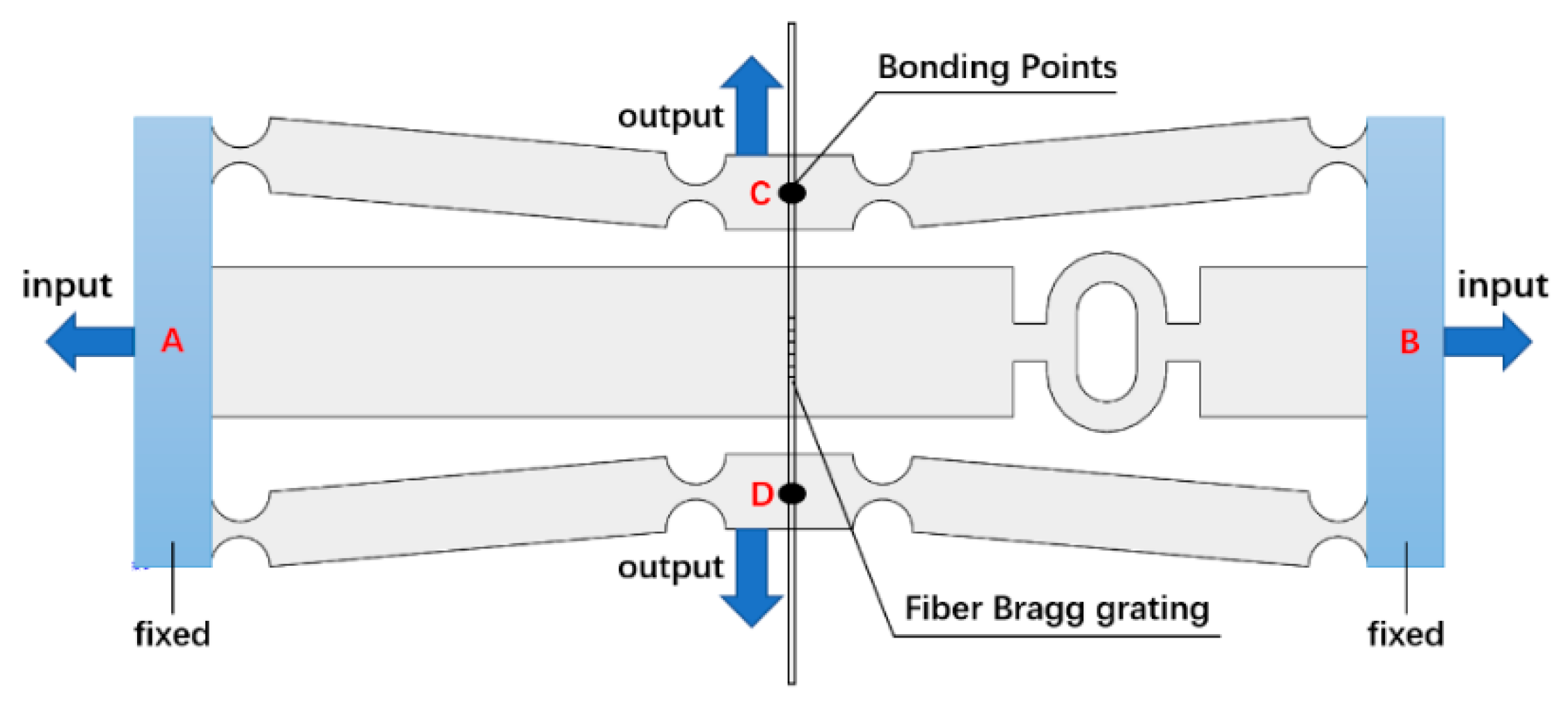
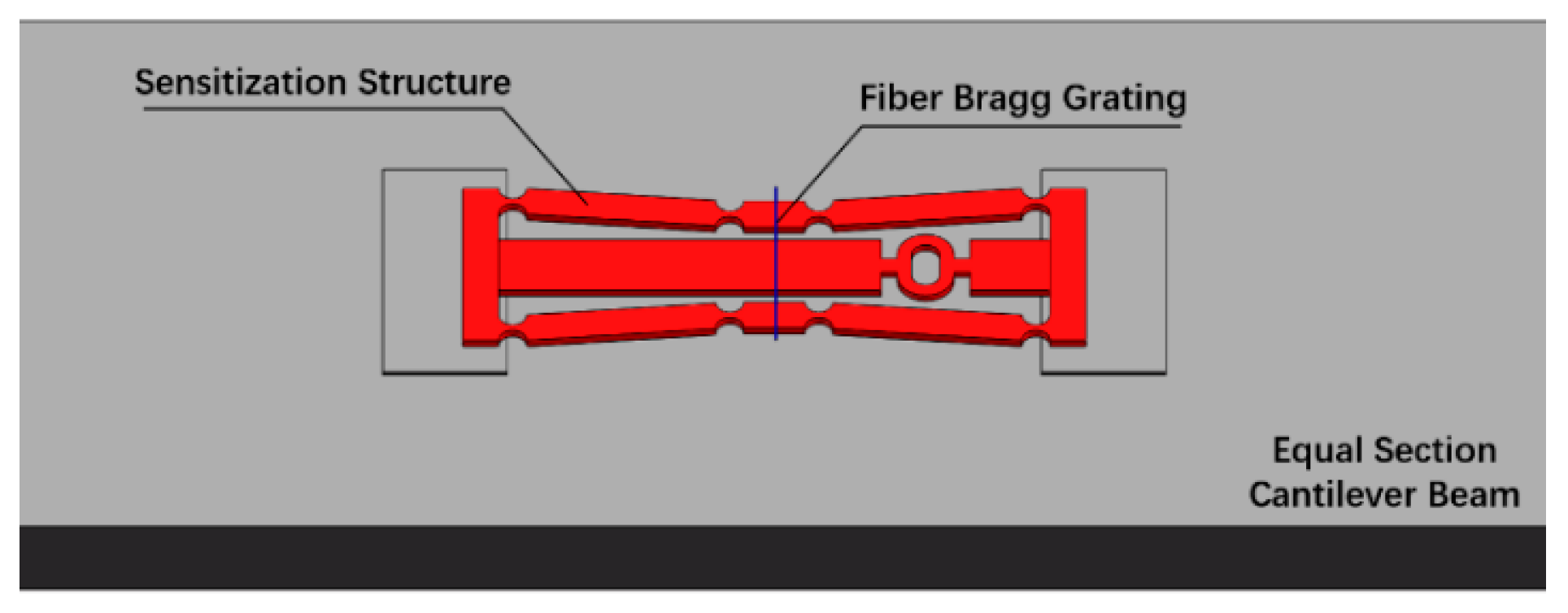
2.2. Measurement Principle of FBG Strain Sensor
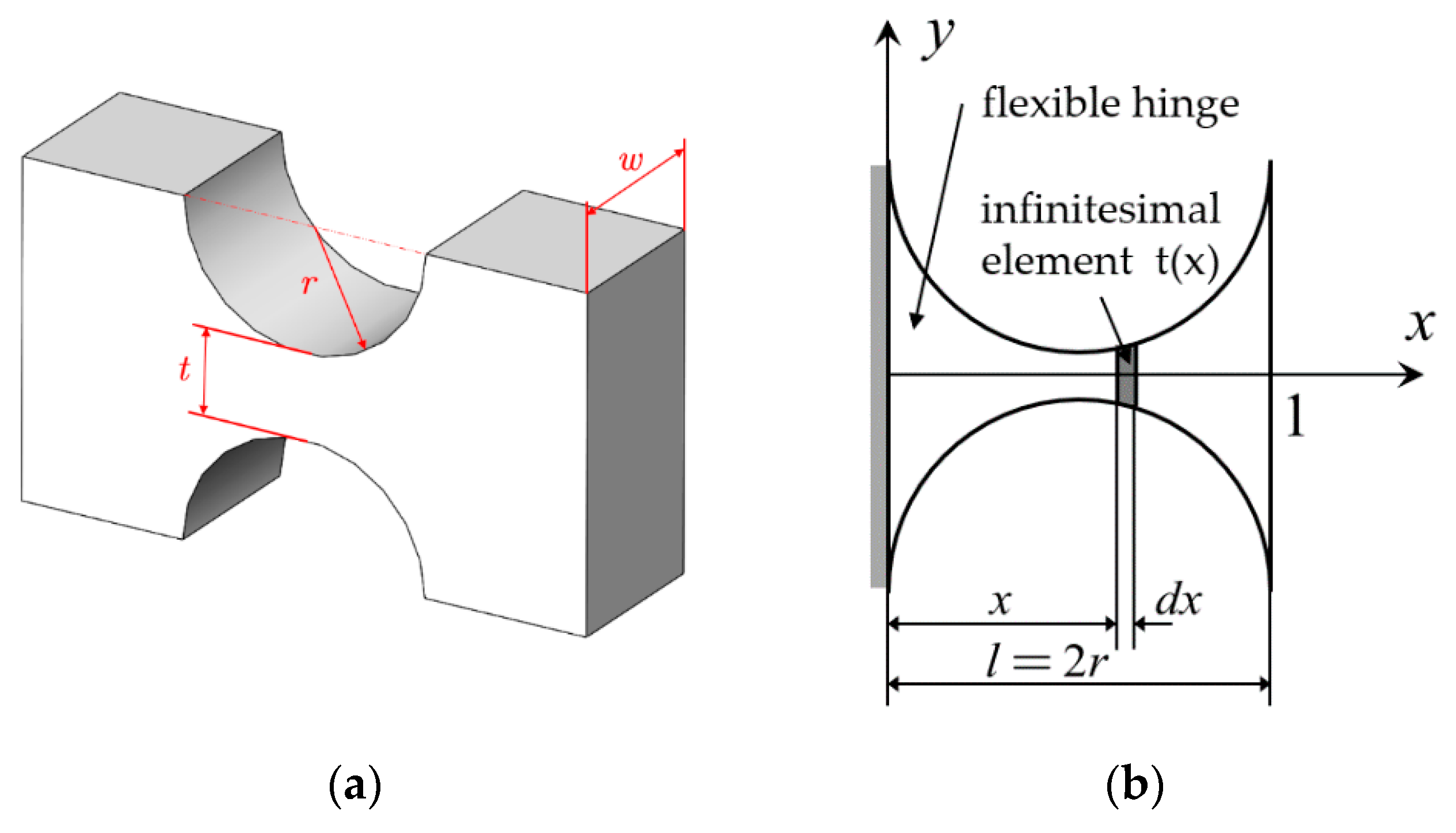
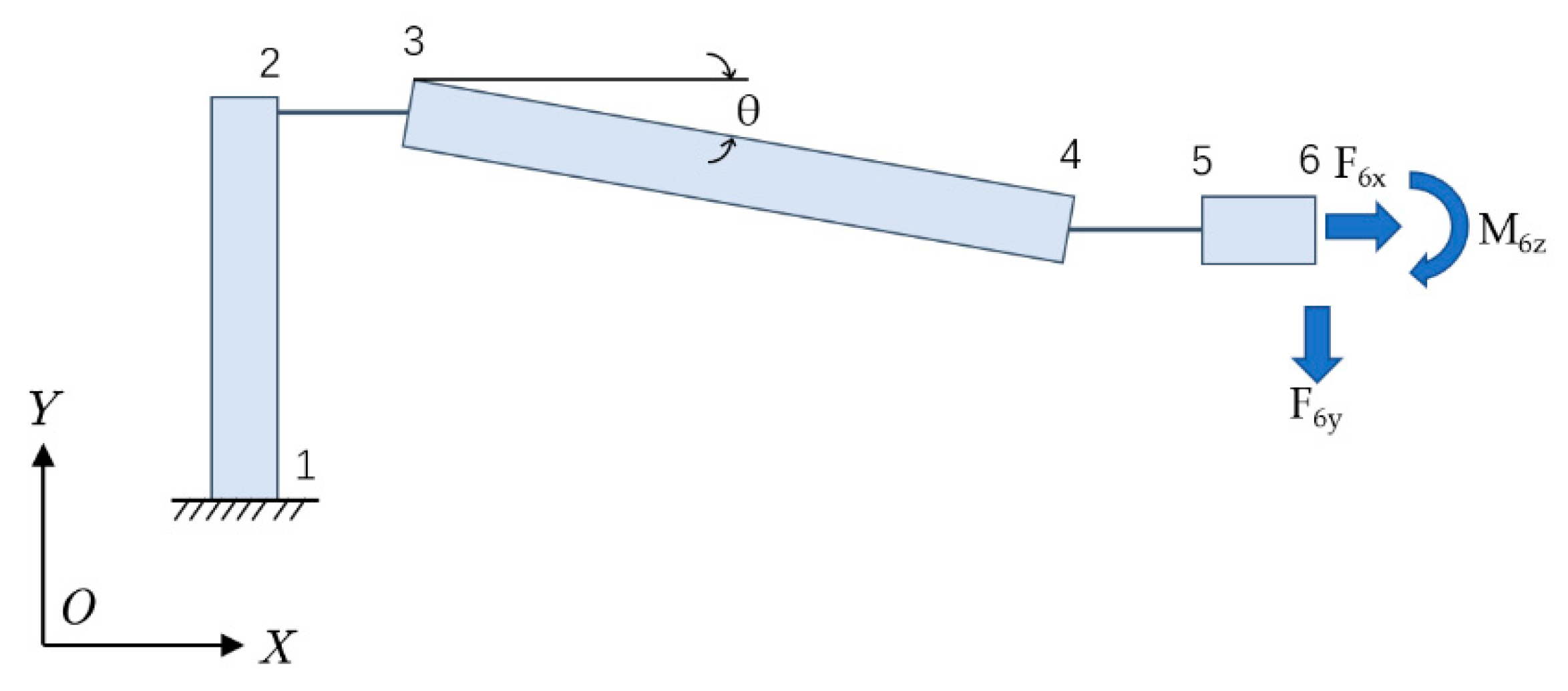
2.3. Mathematical Model of the Sensor
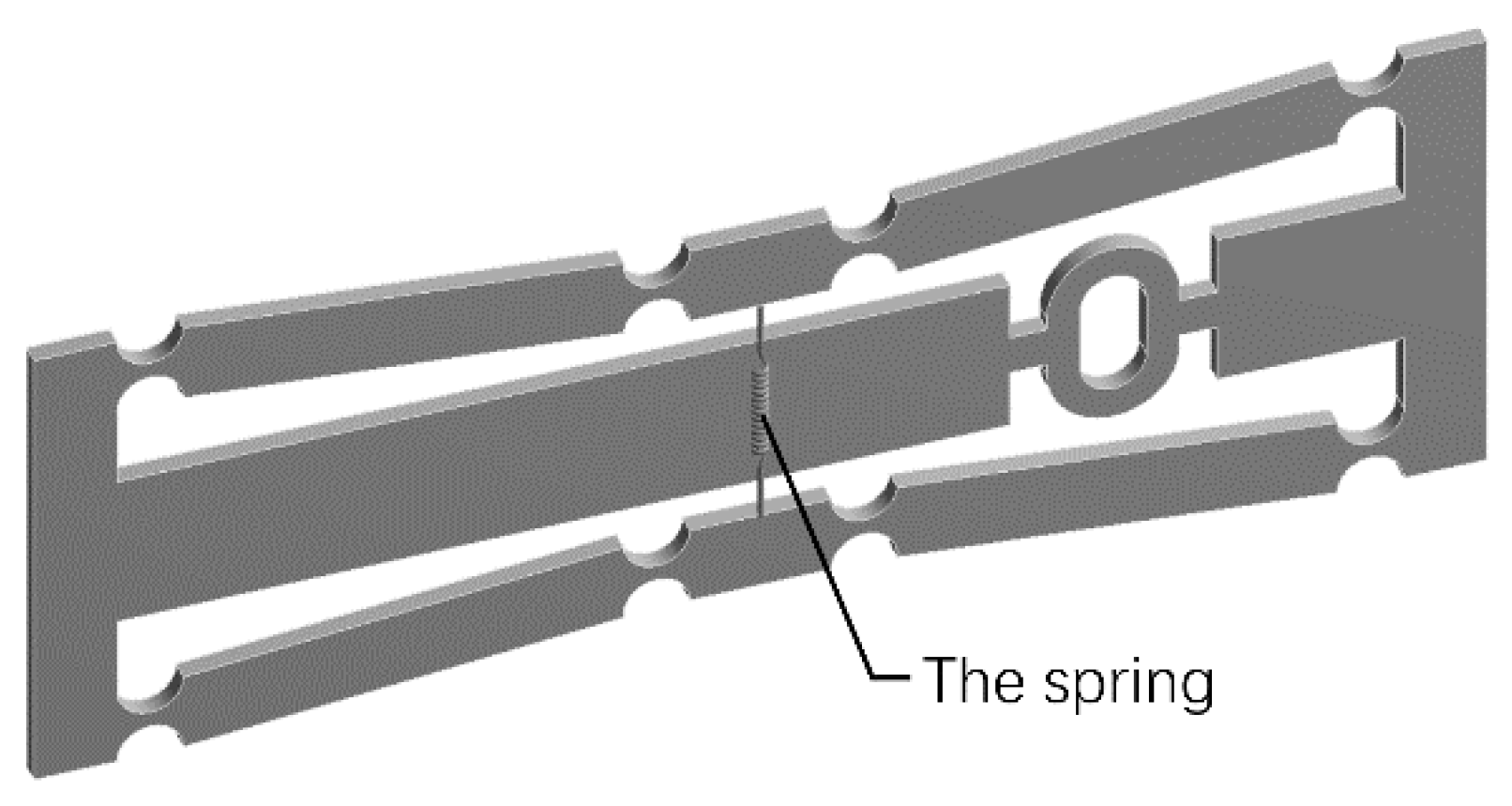
3. Simulation Analysis of Dynamic Properties of Sensors
3.1. Static Performance Simulation
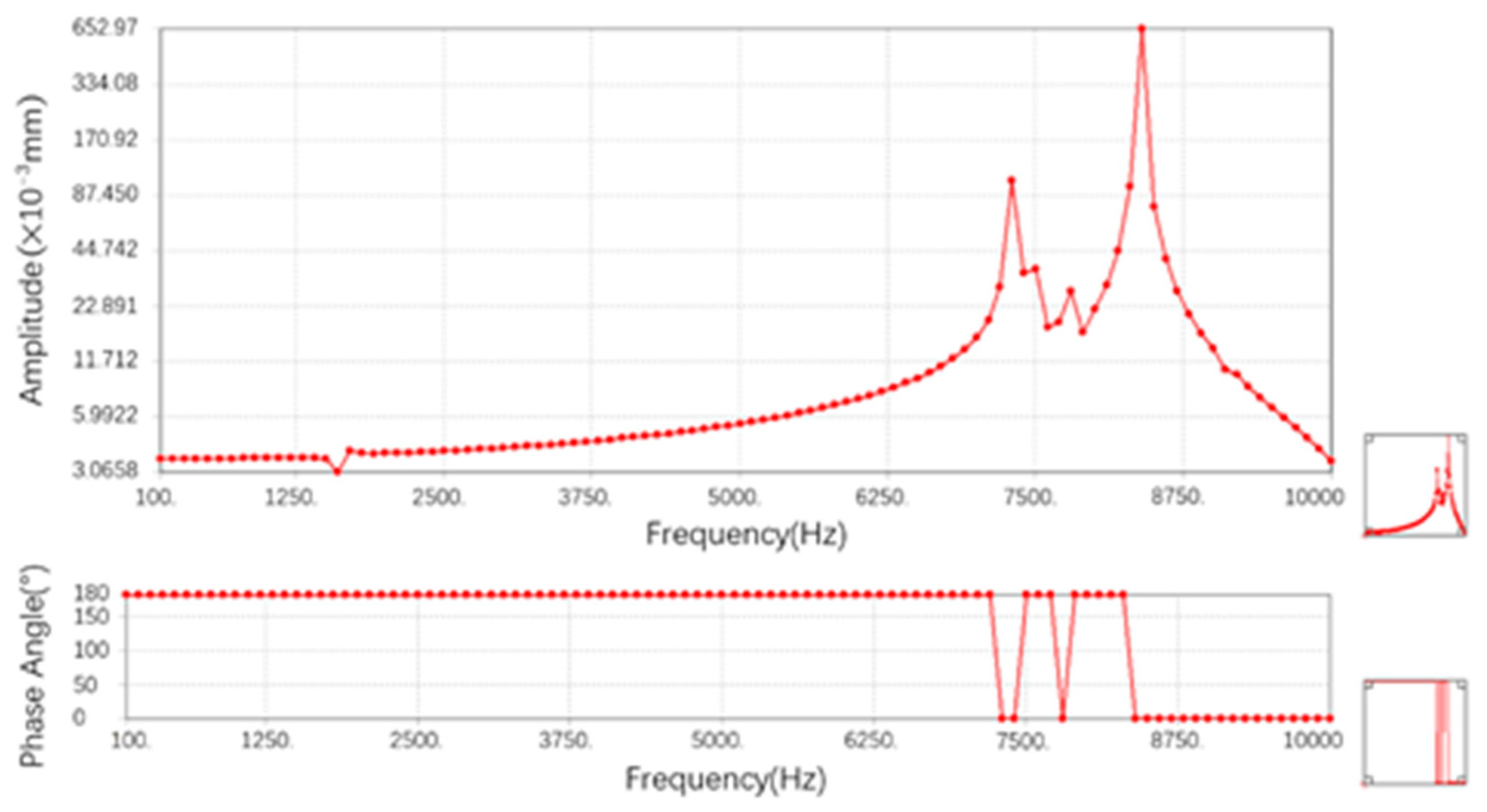
3.2. Dynamic Performance Simulation
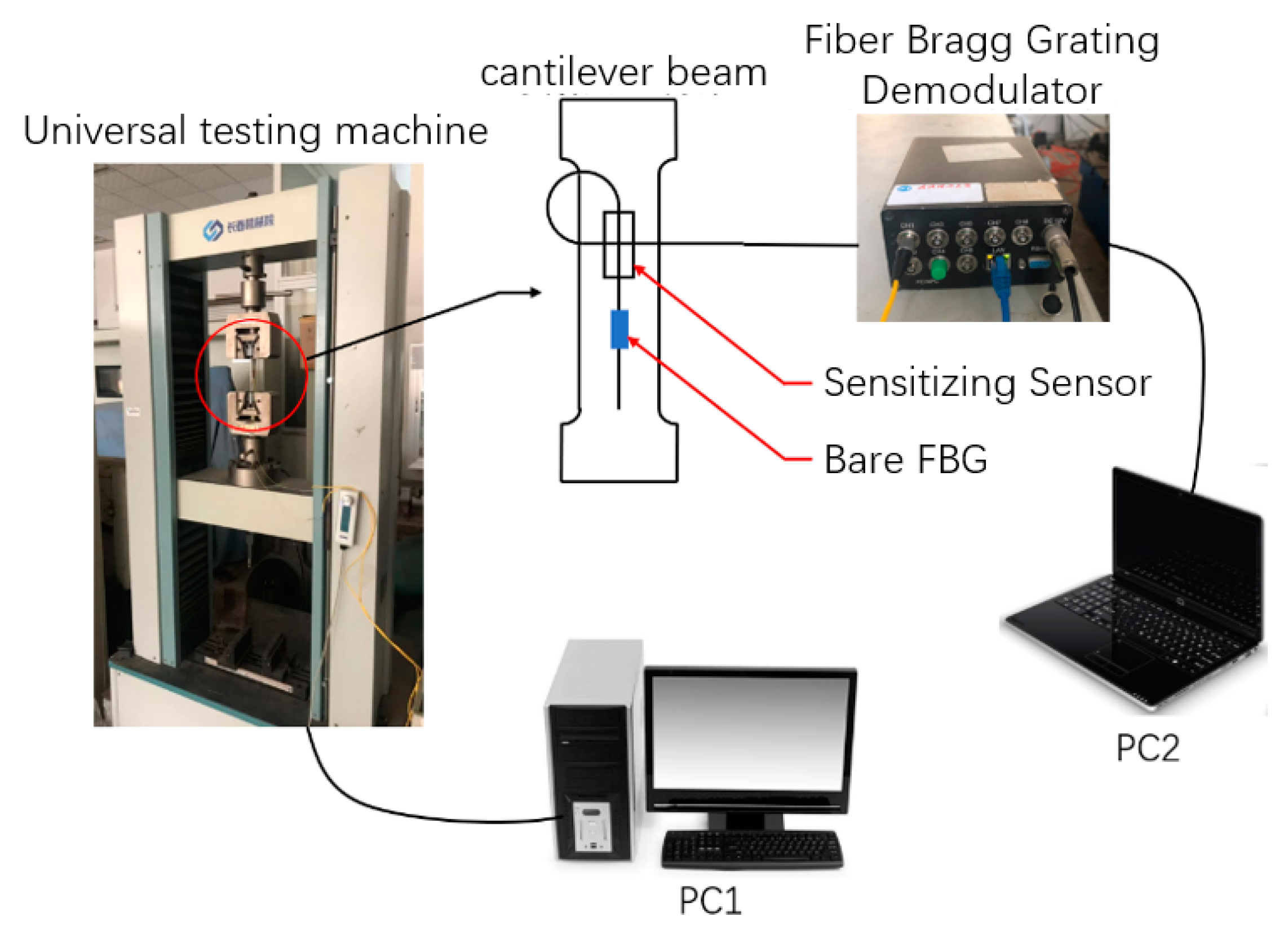
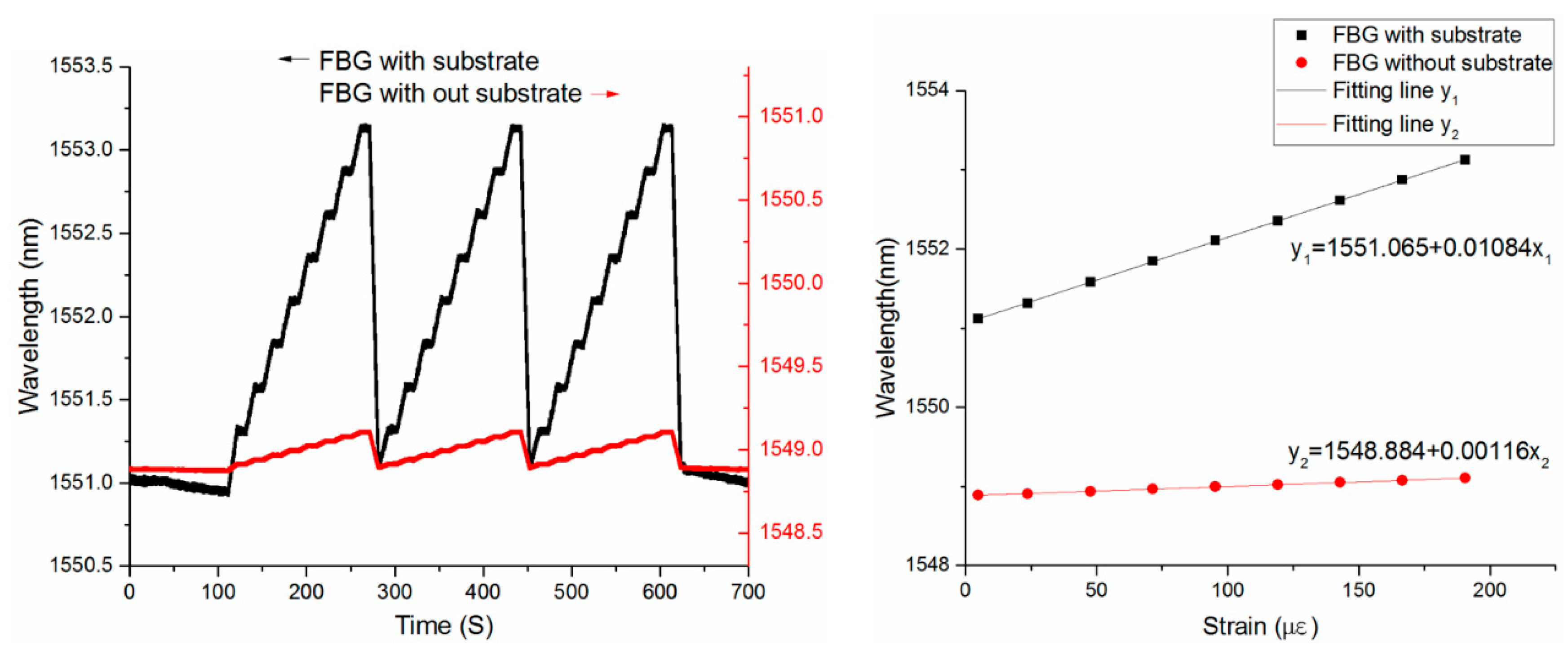
4. Experimental Analysis of Sensing Properties
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Lopez-Higuera, J.M.; Cobo, L.R.; Incera, A.Q.; Cobo, A. Fiber Optic Sensors in Structural Health Monitoring. J. Lightwave Technol. 2011, 29, 587–608. [Google Scholar] [CrossRef]
- Bakht, B.; Mufti, A. Structural Health Monitoring; Bridges; Springer: Cham, Switzerland, 2015; pp. 307–354. [Google Scholar]
- Campanella, C.; Cuccovillo, A.; Campanella, C.; Yurt, A.; Passaro, V. Fiber Bragg Grating Based Strain Sensors: Review of Technology and Applications. Sensors 2018, 18, 3115. [Google Scholar] [CrossRef]
- Worden, K.; Farrar, C.R.; Haywood, J.; Todd, M. A review of nonlinear dynamics applications to structural health monitoring. Struct. Control Health Monit. 2010, 15, 540–567. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [Green Version]
- Kesavan, K.; Ravisankar, K.; Senthil, R.; Sundaram, B.A.; Parivallal, S. Studies on Apparent Strain Using FBG Strain Sensors for Different Structural Materials. Exp. Tech. 2015, 38, 31–38. [Google Scholar] [CrossRef]
- Zhao, H.T.; Wang, Q.B.; Qiu, Y.; Chen, J.A.; Wang, Y.Y.; Fan, Z.M. Strain transfer of surface-bonded fiber Bragg grating sensors for airship envelope structural health monitoring. J. Zhejiang Univ. Sci. A 2012, 13, 538–545. [Google Scholar] [CrossRef]
- Bang, H.J.; Kim, H.I.; Lee, K.S. Measurement of strain and bending deflection of a wind turbine tower using arrayed FBG sensors. Int. J. Precis. Eng. Man. 2012, 13, 2121–2126. [Google Scholar] [CrossRef]
- Lau, K.T.; Yuan, L.; Zhou, L.M.; Wu, J.; Woo, C.H. Strain monitoring in FRP laminates and concrete beams using FBG sensors. Compos. Struct. 2001, 51, 9–20. [Google Scholar] [CrossRef] [Green Version]
- Ramly, R.; Kuntjoro, W.; Rahman, M.K.A. Using embedded fiber Bragg grating (FBG) sensors in smart aircraft structure materials. Procedia Eng. 2012, 41, 600–606. [Google Scholar] [CrossRef]
- You, R.; Ren, L.; Song, G. A Novel Fiber Bragg Grating (FBG) Soil Strain Sensor. Measurement 2019, 139, 85–91. [Google Scholar] [CrossRef]
- Kaur, G.; Kaler, R.S. Sensitivity enhancement of FBG sensor for portlandite monitoring. Opt. Fiber Technol. 2018, 46, 83–87. [Google Scholar] [CrossRef]
- Diaz, C.A.; Leal-Junior, A.G.; Andre, P.S.; da Costa Antunes, P.F.; Pontes, M.J.; Frizera-Neto, A.; Ribeiro, M.R. Liquid level measurement based on FBG-embedded diaphragms with temperature compensation. IEEE Sens. J. 2018, 18, 193–200. [Google Scholar] [CrossRef]
- Zhou, Z.D.; Liu, Q.; Ai, Q.S.; Xu, C. Intelligent monitoring and diagnosis for modern mechanical equipment based on the integration of embedded technology and FBGS technology. Measurement 2011, 44, 1499–1511. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Frizera, A.; Daz, C.R.; Ribeiro, M.R.; Pontes, M.J. FBG-embedded oblong diaphragms with extended dynamic range. IEEE Sens. Let. 2018, 2, 1–4. [Google Scholar] [CrossRef]
- Pachava, V.R.; Kamineni, S.; Madhuvarasu, S.S.; Putha, K. A high sensitive FBG pressure sensor using thin metal diaphragm. J. Opt. 2014, 43, 117–121. [Google Scholar] [CrossRef]
- Wen, Q.; Zhu, J.; Gong, S.; Huang, J.; Gu, H.; Zhao, P. Design and synthesis of a packaging polymer enhancing the sensitivity of fiber grating pressure sensor. Prog. Nat. Sci. 2008, 18, 197–200. [Google Scholar] [CrossRef]
- Li, L.; Zhang, D.; Liu, H.; Guo, Y.; Zhu, F. Design of an enhanced sensitivity FBG strain sensor and application in highway bridge engineering. Photonic Sens. 2014, 4, 162–167. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Kong, J.; Liu, H.; Hu, D.; Qin, L. Design and investigation of a reusable surface-mounted optical fiber Bragg grating strain sensor. IEEE Sens. J. 2016, 16, 8456–8462. [Google Scholar] [CrossRef]
- Li, R.; Chen, Y.; Tan, Y.; Zhou, Z.; Li, T.; Mao, J. Sensitivity enhancement of FBG-based strain sensor. Sensors 2018, 18, 1607. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Tan, Y.; Chen, Y.; Hong, L.; Zhou, Z. Investigation of sensitivity enhancing and temperature compensation for fiber Bragg grating (FBG)-based strain sensor. Opt. Fiber Technol. 2019, 48, 199–206. [Google Scholar] [CrossRef]
- Peng, J.; Jia, S.; Jin, Y.; Xu, S.; Xu, Z. Design and investigation of a sensitivity-enhanced fiber Bragg grating sensor for micro-strain measurement. Sens. Actuators A Phys. 2019, 285, 437–447. [Google Scholar] [CrossRef]
- Lobontiu, N. Compliant Mechanisms: Design of Flexure Hinges; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]


| Parameter | Parameter | ||
|---|---|---|---|
| U | 0.34 | R (m) | 0.8 × 10−3 |
| E (GPa) | 110 × 109 | W (m) | 0.5 × 10−3 |
| T (m) | 0.4 × 10−3 | L1 (m) | 5 × 10−3 |
| Θ (°) | 5 | L2 (m) | 1.6 × 10−3 |
| E1 (GPa) | 70 × 109 | L3 (m) | 10.64 × 10−3 |
| D (m) | 125 × 10−6 | L4 (m) | 1.6 × 10−3 |
| H (m) | 3 × 10−3 | L5 (m) | 1.7 × 10−3 |
| Component | Young Modulus (GPa) | Poisson Ratio |
|---|---|---|
| Substrate | 110 | 0.34 |
| FBG | 74 | 0.33 |
| Beam | 200 | 0.30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Wang, W.; Song, H.; Zhou, S.; Zhou, W. A High Sensitivity FBG Strain Sensor Based on Flexible Hinge. Sensors 2019, 19, 1931. https://doi.org/10.3390/s19081931
Liu M, Wang W, Song H, Zhou S, Zhou W. A High Sensitivity FBG Strain Sensor Based on Flexible Hinge. Sensors. 2019; 19(8):1931. https://doi.org/10.3390/s19081931
Chicago/Turabian StyleLiu, Mingyao, Wenzhi Wang, Han Song, Shiguang Zhou, and Weijian Zhou. 2019. "A High Sensitivity FBG Strain Sensor Based on Flexible Hinge" Sensors 19, no. 8: 1931. https://doi.org/10.3390/s19081931
APA StyleLiu, M., Wang, W., Song, H., Zhou, S., & Zhou, W. (2019). A High Sensitivity FBG Strain Sensor Based on Flexible Hinge. Sensors, 19(8), 1931. https://doi.org/10.3390/s19081931





