Modeling and Experimental Study for Online Measurement of Hydraulic Cylinder Micro Leakage Based on Convolutional Neural Network
Abstract
:1. Introduction
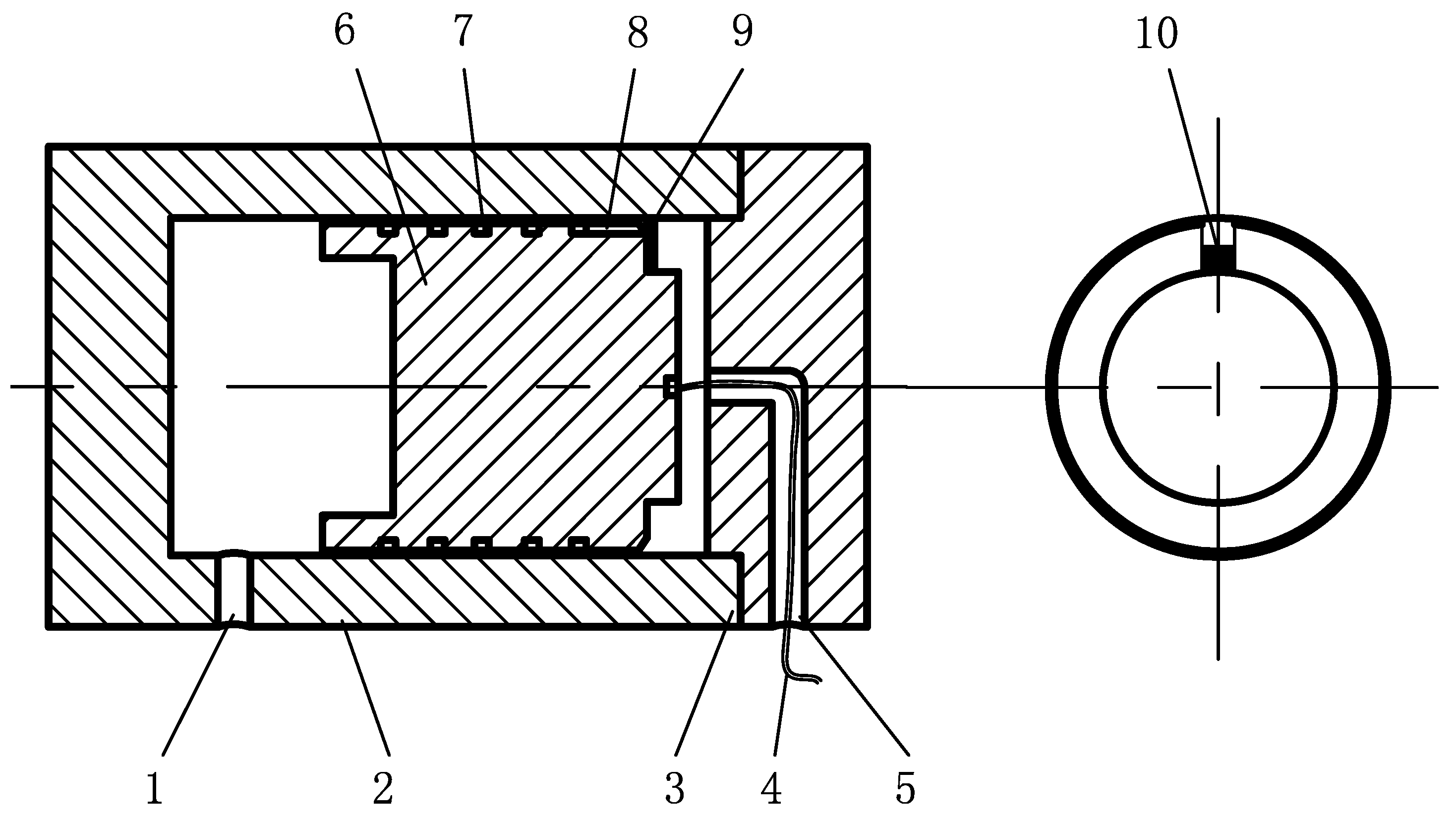
2. The Principle of Internal Leakage Online Measurement
2.1. Online Measurement System
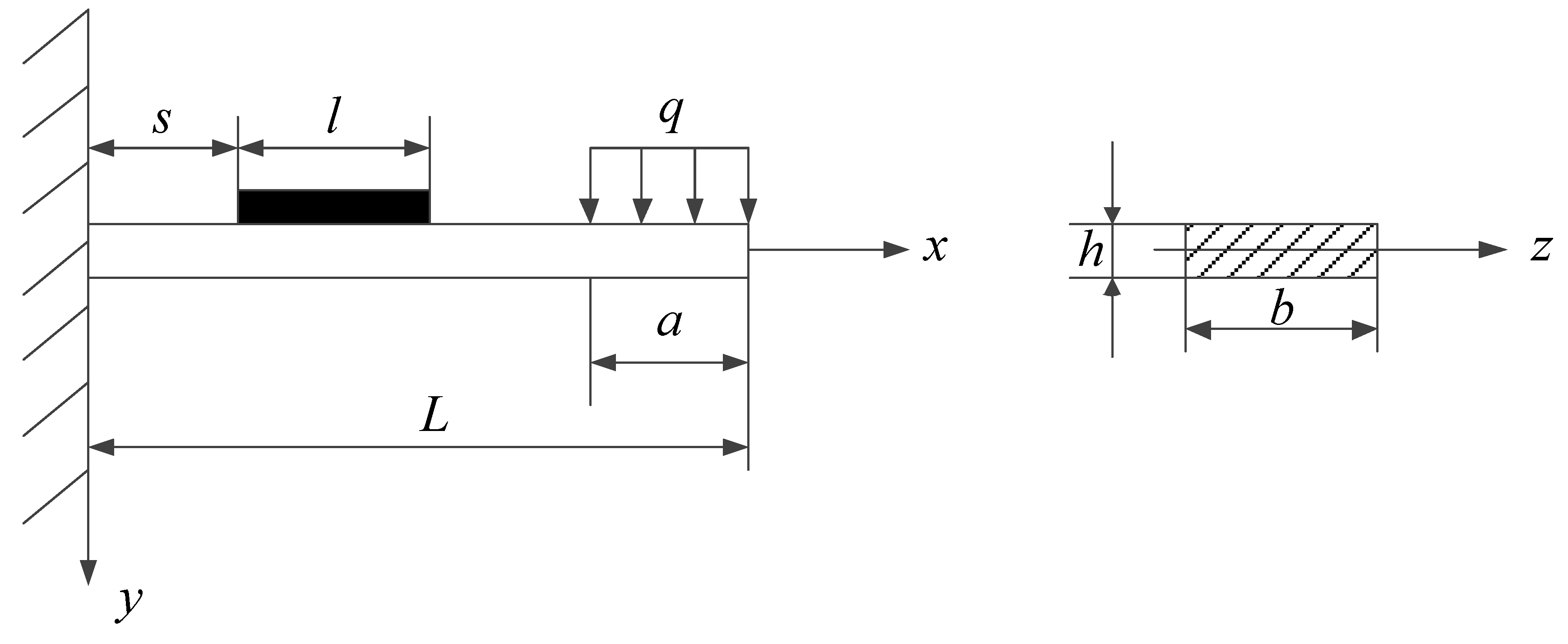
2.2. Flow-Strain Signal Conversion Mathematical Model
- increasing L, namely, reducing the fixed area of the strain gauge and the end face of piston.
- appropriately increasing a, namely, deepening the depth of oil collecting tank. Because Q is proportional to cube of annular gap interval, a should not be too large, otherwise strain gauge is not functioning.
3. Data Acquisition and Processing
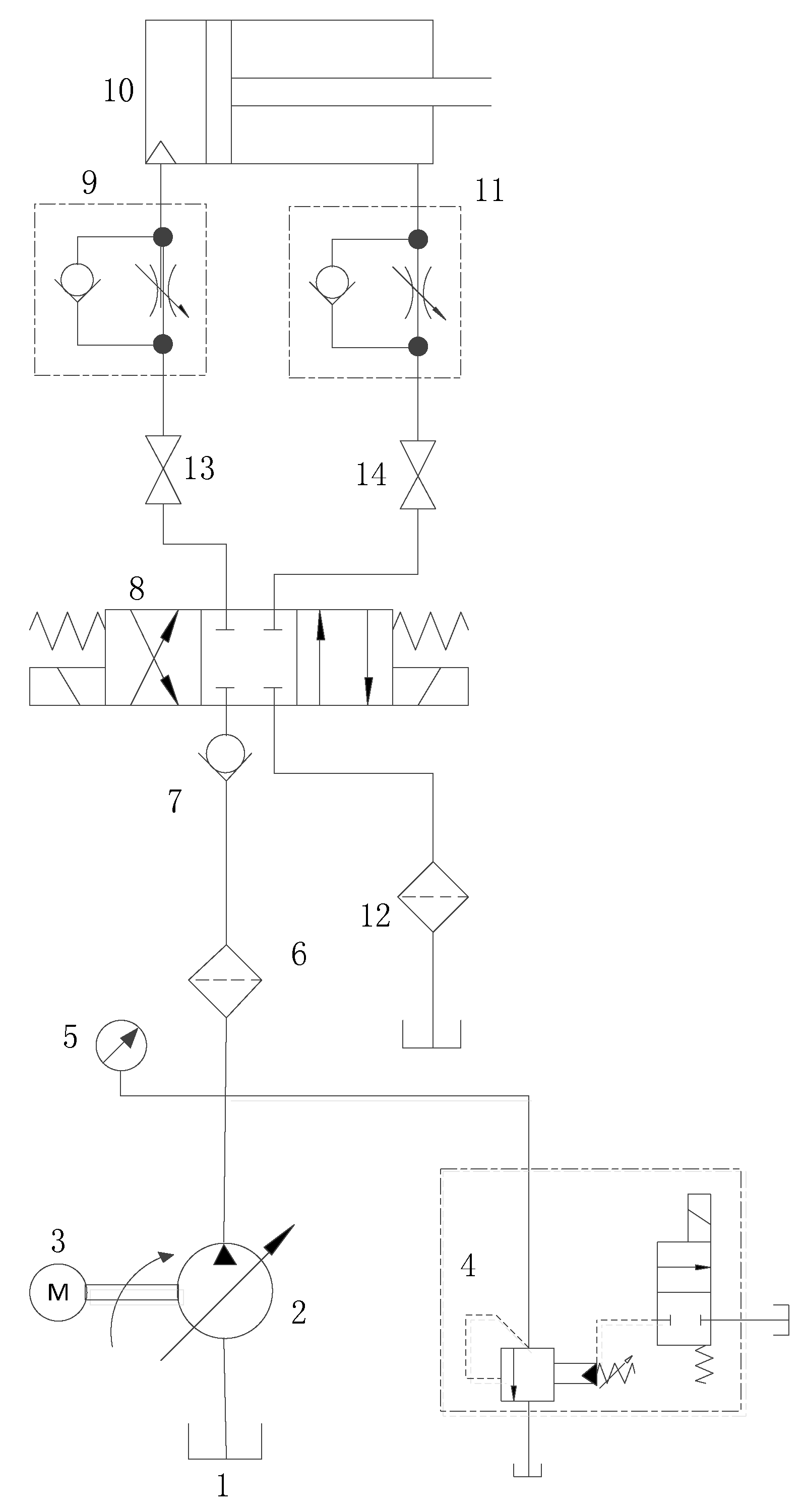
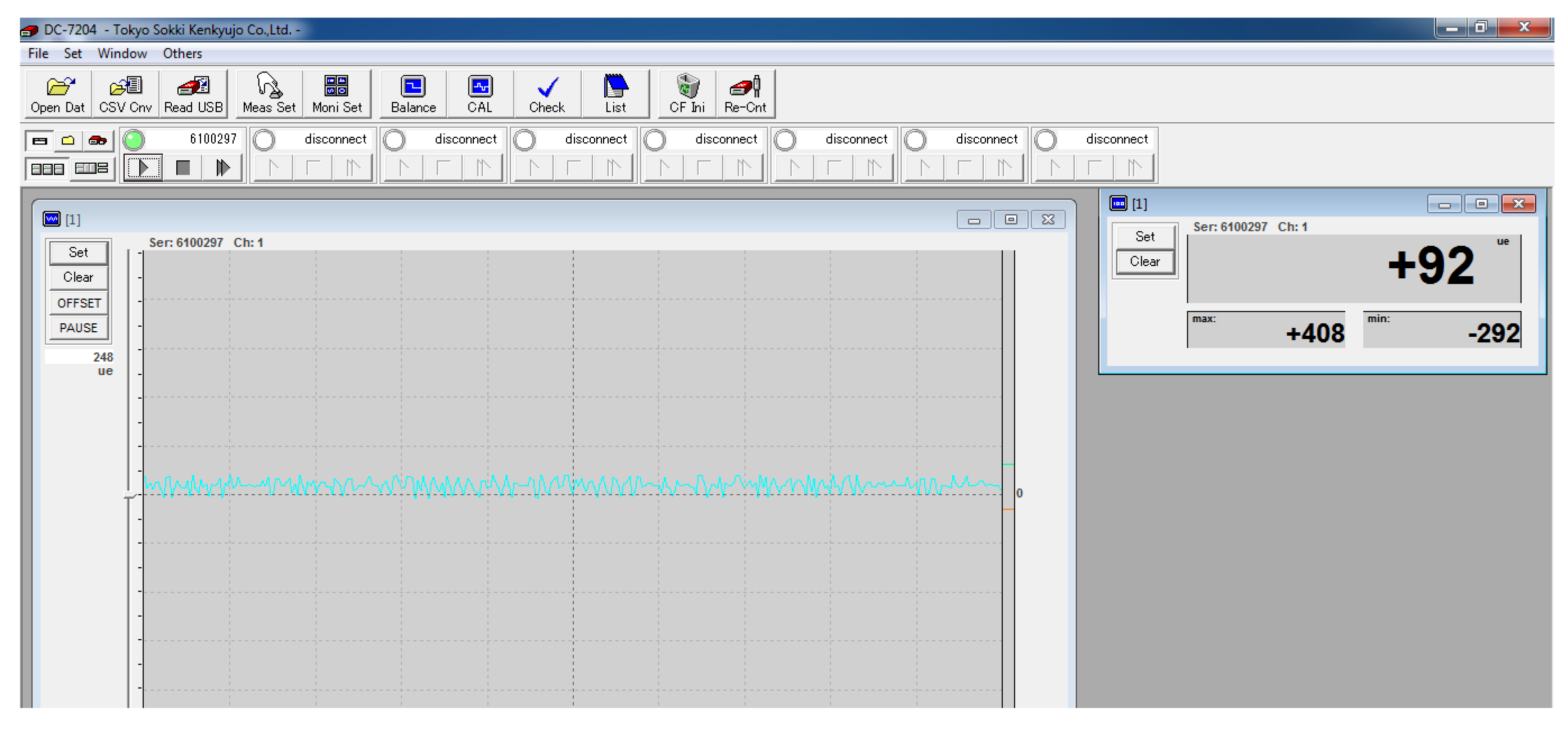
3.1. Data Acquisition System
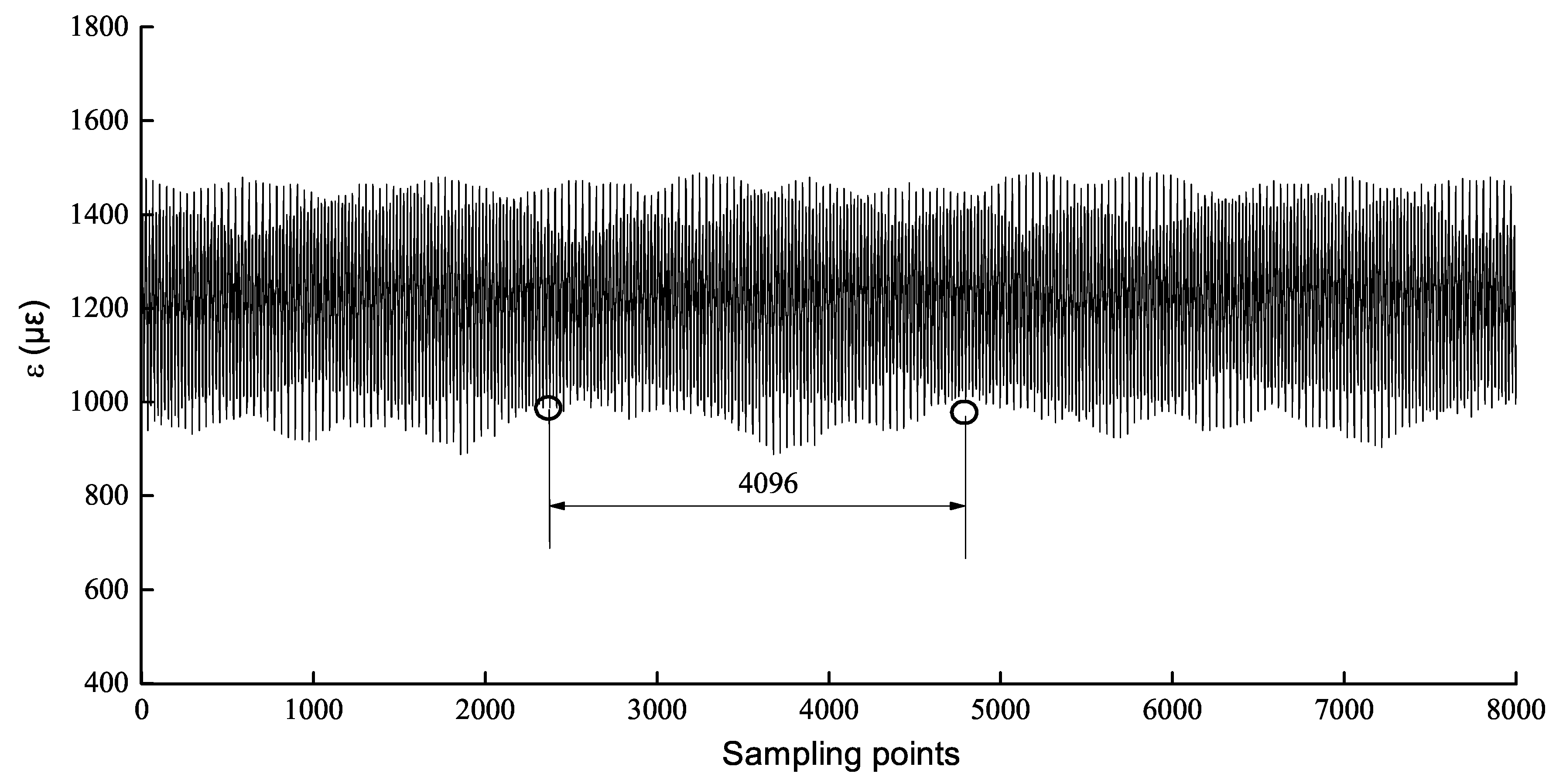
3.2. Process Testing Data
4. The Process of Micro Internal Leakage Prediction Based on CNN
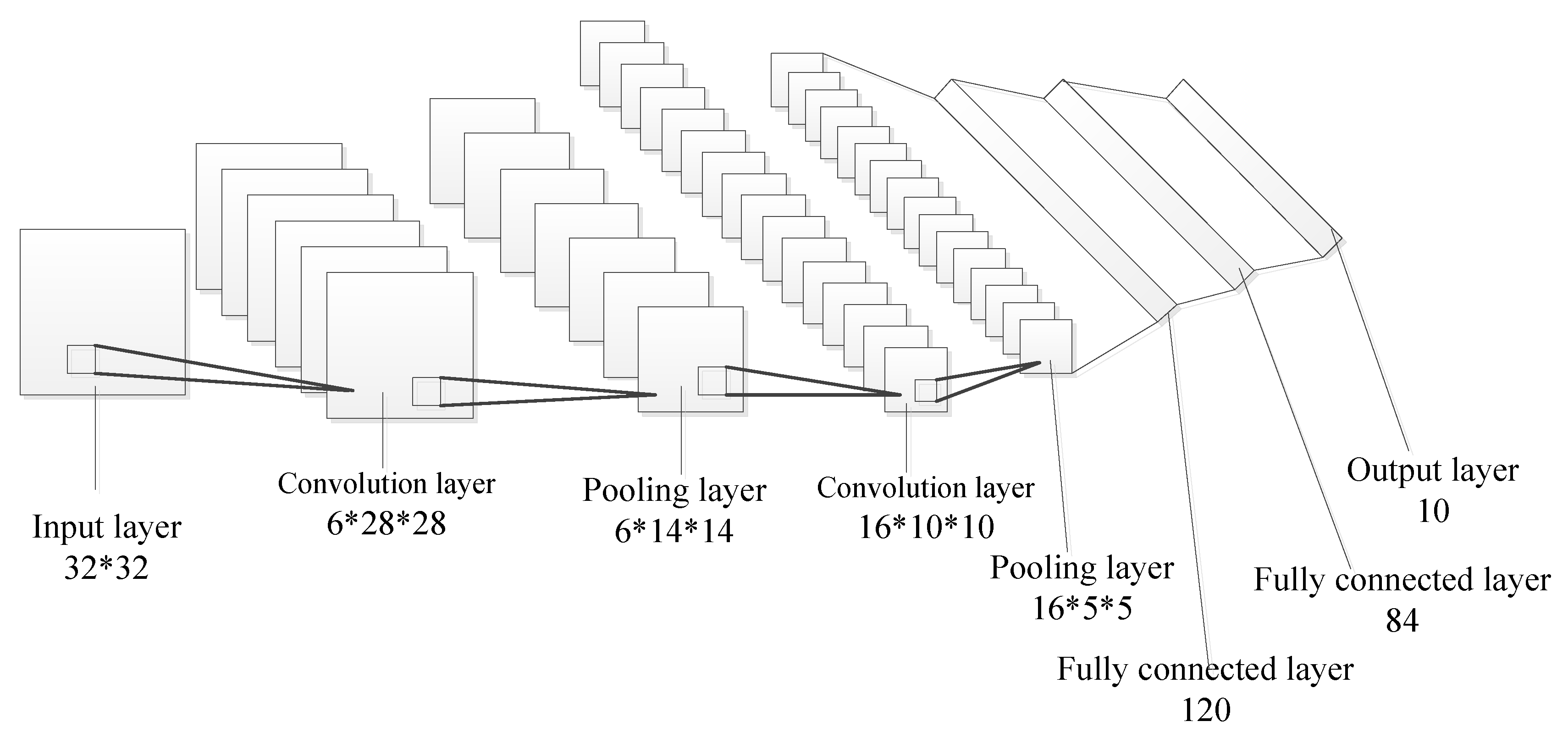
4.1. CNN Architecture
4.2. Prediction Process for Leakage in Hydraulic Cylinder
5. Materials and Methods
5.1. Create Dataset and Feature Extraction
5.1.1. Create Dataset
5.1.2. Feature Extraction
5.2. Parameters and Architecture of CNN
5.3. BPNN Architecture
5.4. Other Models for Regression about Leakage Prediction
5.4.1. Support Vector Regression
5.4.2. RBF Network for Regression
6. Results and Discussion
6.1. The Metric of Model Performance
6.2. Comparison and Discussion
7. Conclusions
- (1)
- A method for online measurement of leakage in hydraulic cylinder is proposed, which uses a strain gauge as a core sensor to convert flow signals into strain signals and takes the CNN as the internal leakage prediction module to output the internal leakage in real time.
- (2)
- Established a mathematical model for flow-strain signal conversion. Reducing the fixed area of the strain gauge and the end face of the piston and appropriately increasing the depth of the oil collecting tank can enhance the strain signal.
- (3)
- In the leakage prediction of hydraulic cylinder, CNN automatically extracts the features, avoiding the complexity brought by manually extracting features, saving time and enhancing the model performance.
- (4)
- This study can be applied to measure the small flow of other hydraulic components and related equipment online.
Author Contributions
Funding
Conflicts of Interest
References
- Gong, W.; Chen, H.; Zhang, Z.; Zhang, M.; Wang, R.; Guan, C.; Wang, Q. A Novel Deep Learning Method for Intelligent Fault Diagnosis of Rotating Machinery Based on Improved CNN-SVM and Multichannel Data Fusion. Sensors 2019, 19, 1693. [Google Scholar] [CrossRef] [PubMed]
- An, L.; Sepehri, N. Hydraulic Actuator Leakage Fault Detection using Extended Kalman Filter. Int. J. Fluid Power 2005, 6, 41–51. [Google Scholar] [CrossRef]
- Yang, S.S.; Mohamed, H.A.F.; Moghavvemi, M.; Goh, Y.H. Leakage detection via model based method. In Proceedings of the IEEE Conference on Robotics, Automation and Mechatronics, Chengdu, China, 21–24 September 2008; pp. 635–639. [Google Scholar]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Goharrizi, A.Y.; Sepehri, N. A wavelet-based approach for external leakage detection and isolation from internal leakage in valve-controlled hydraulic actuators. IEEE Trans. Ind. Electron. 2011, 58, 4374–4384. [Google Scholar] [CrossRef]
- Goharrizi, A.Y.; Sepehri, N. A wavelet-based approach to internal seal damage diagnosis in hydraulic actuators. IEEE Trans. Ind. Electron. 2010, 57, 1755–1763. [Google Scholar]
- Zhao, X.; Zhang, S.; Zhou, C.; Hu, Z.; Li, R.; Jiang, J. Experimental study of hydraulic cylinder leakage and fault feature extraction based on wavelet packet analysis. Comput. Fluids 2015, 106, 33–40. [Google Scholar] [CrossRef]
- Goharrizi, A.Y.; Sepehri, N.; Wu, Y. A Wavelet-Based Approach for Diagnosis of Internal Leakage in Hydraulic Actuators using On-Line Measurements. Int. J. Fluid Power 2010, 11, 61–69. [Google Scholar] [CrossRef]
- Goharrizi, A.Y.; Sepehri, N. Internal Leakage Detection in Hydraulic Actuators Using Empirical Mode Decomposition and Hilbert Spectrum. IEEE Trans. Ind. Electron. 2012, 61, 368–378. [Google Scholar] [CrossRef]
- Goharrizi, A.Y.; Sepehri, N. Application of Fast Fourier and Wavelet Transforms Towards Actuator Leakage Diagnosis: A Comparative Study. Int. J. Fluid Power 2013, 14, 39–51. [Google Scholar] [CrossRef]
- Tang, H.B.; Wu, Y.X.; Hua, G.J.; Ma, C.X. Internal leakage fault diagnosis of hydraulic cylinder using PCA and BP network. J. Cent. South Univ. (Sci. Technol.) 2011, 42, 3709–3714. [Google Scholar]
- Zang, R.H.; Wu, J. Internal leakage fault diagnosis approach of hydraulic cylinder using LMBP neural network. J. Tianjin Norm. Univ. (Nat. Sci. Ed.) 2013, 1, 38–44. [Google Scholar]
- Feng, L.; Zhang, Y.; Li, X.; Fu, Y. Independent component analysis based on data-driven reconstruction of multi-fault diagnosis. J. Chemom. 2017, 31, e2932. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Liu, L.; Xu, L.; Silva, C.W.D. An intelligent fault diagnosis approach with unsupervised feature learning by stacked denoising autoencoder. IET Sci. Meas. Technol. 2017, 11, 687–695. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Sigal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Wu, X.; Su, R.; Lu, C.; Rui, X. Internal leakage detection for wind turbine hydraulic pitching system with computationally efficient adaptive asymmetric SVM. In Proceedings of the 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 6126–6130. [Google Scholar]
- Yang, Q.; Guo, B.; Lin, M. Differential pressure prediction in air leak detection using RBF Neural Network. In Proceedings of the International Conference on Artificial Intelligence and Computational Intelligence, Sanya, China, 23–24 October 2010; pp. 211–213. [Google Scholar]
- Li, L.; Tao, J.F.; Huang, Y.X.; Liu, C.L. Internal Leakage Detection of Hydraulic Cylinder Based on BP Neural Network. Chin. Hydraul. Pneum. 2017, 7, 11–15. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.S.; Duan, J.H.; Tu, Y.Q. Convolution Neural Network Based Internal Leakage Fault Diagnosis for Hydraulic Cylinders. Mach. Tool Hydraul. 2017, 45, 182–185. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Deng, J.H.; Chen, X.Y.; Wu, L.; Guo, Y.; Huang, F.X.; Zhan, C.C. Hydraulic Cylinder Capable of Automatically Monitoring Internal Leakage. CN Patent 104963912 A, 7 October 2015. [Google Scholar]
- Liu, H. Material Mechanics, 5th ed.; Higher Education Press: Beijing, China, 2011; p. 141. [Google Scholar]
- Yang, N.; Jiang, Q.; Gao, F. Design of Intelligent Strain Target Flowmeter. Meas. Tech. 2004, 2, 8–9. [Google Scholar]
- Sha, Y. Fluid Mechanics; China University of Science and Technology Press: Anhui, China, 2016; pp. 284–285. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Boureau, Y.L.; Roux, N.L.; Bach, F.; Ponce, J.; Lecun, Y. Ask the Locals: Multi-way Local Pooling for Image Recognition. In Proceedings of the 13th International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2651–2658. [Google Scholar]
- Shan, J.H.; Lv, Q.; Zhang, S.L.; Meng, R.; Wang, X.Y. Multi-SoftMax Convolution Neural Network and Its Application in the Diagnosis of Planetary Gearbox Complicated Faults. Available online: http://chinaxiv.org/abs/201712.00240 (accessed on 26 December 2017).
- Ma, L.; Xie, W.; Zhang, Y. Blister Defect Detection Based on Convolutional Neural Network for Polymer Lithium-Ion Battery. Appl. Sci. 2019, 9, 1085. [Google Scholar] [CrossRef]
- Jia, J.L.; Yu, T.; Wu, Z.J.; Cheng, X.H. Fault Diagnosis Method of Transformer Based on Convolutional Neural Network. Electr. Meas. Instrum. 2017, 54, 62–67. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Neural Information Processing Systems Conference, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Rosasco, L.; De, V.E.; Caponnetto, A.; Piana, M.; Verri, A. Are Loss Functions All the Same? Neural Comput. 2004, 16, 1063–1076. [Google Scholar] [CrossRef] [PubMed]
- Qian, N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef]
- Kurbiel, T.; Khaleghian, S. Training of Deep Neural Networks based on Distance Measures using RMSProp. arXiv 2017, arXiv:1708.01911. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Nguyen, D.; Kang, M.; Kim, C.H.; Kim, J.M. Highly reliable state monitoring system for induction motors using dominant features in a two-dimension vibration signal. New Rev. Hypermedia Multimedia 2013, 19, 248–258. [Google Scholar] [CrossRef]
- Vapnik, V.; Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998; Volume 12, pp. 156–160. [Google Scholar]
- Cherkassky, V.; Mulier, F.M. Learning From Data: Concepts, Theory, and Methods; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]









| Features | Formulation |
|---|---|
| mean | |
| root mean square | |
| skewness | |
| kurtosis | |
| pulse factor | |
| crest factor | |
| waveform factor | |
| margin factor |
| Layer Index | Filter Size | Stride | Number of Feature Maps |
|---|---|---|---|
| I | - | - | 1 |
| C1 | 8 | ||
| P1 | 8 | ||
| C2 | 16 | ||
| P2 | 16 | ||
| C3 | 32 | ||
| P3 | 32 | ||
| F4 | - | - | 2048 |
| O | - | - | 1 |
| Model | RMSE | RAE | R Square | Training Time (s) | Prediction Time (s) |
|---|---|---|---|---|---|
| CNN | 0.4872 | 0.2791 | 1.0000 | 712.0029 | 0.2131 |
| BPNN | 37.8311 | 19.0778 | 0.9624 | 1383.0599 | 0.2251 |
| RBF | 23.7492 | 10.5905 | 0.9852 | - | - |
| SVR | 42.3979 | 23.3019 | 0.9528 | - | - |
| Optimization Algorithm | Learning Rate | Batch Size | Epochs |
|---|---|---|---|
| Adam | 0.0005 | 128 | 500 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Zeng, Y.; Fu, L.; Chen, X. Modeling and Experimental Study for Online Measurement of Hydraulic Cylinder Micro Leakage Based on Convolutional Neural Network. Sensors 2019, 19, 2159. https://doi.org/10.3390/s19092159
Guo Y, Zeng Y, Fu L, Chen X. Modeling and Experimental Study for Online Measurement of Hydraulic Cylinder Micro Leakage Based on Convolutional Neural Network. Sensors. 2019; 19(9):2159. https://doi.org/10.3390/s19092159
Chicago/Turabian StyleGuo, Yuan, Yinchuan Zeng, Liandong Fu, and Xinyuan Chen. 2019. "Modeling and Experimental Study for Online Measurement of Hydraulic Cylinder Micro Leakage Based on Convolutional Neural Network" Sensors 19, no. 9: 2159. https://doi.org/10.3390/s19092159
APA StyleGuo, Y., Zeng, Y., Fu, L., & Chen, X. (2019). Modeling and Experimental Study for Online Measurement of Hydraulic Cylinder Micro Leakage Based on Convolutional Neural Network. Sensors, 19(9), 2159. https://doi.org/10.3390/s19092159




