1. Introduction
Modern electronics applications often require accurate current measurements in a compact design, thus increasing the need for low power current sensing devices. Also, due to the extremely competitive market for power electronics devices, low cost for those current sensing devices is critical.
Contactless current measurement devices are based on detection of the magnetic field created by the current. When only the AC current component is measured, the most used devices are based on current transformers and Rogowski coils [
1,
2,
3]. However, to measure DC/AC currents, sensors able to detect DC magnetic fields with high accuracy must be used.
The (micro)fluxgate [
4,
5] sensors offer high performance and stability in detection of DC/AC currents. A Fluxgate current sensor uses a high permeability magnetic core to detect magnetic fields produced by a current flow. A system of coils such as the fluxgate coil, driven by a square wave current, compensation coil, and pick-up coil are used to determine the magnetization state of the magnetic core and, hence, the current to be measured. The electronics used to drive the currents, to demodulate the signal and to manage all the sensor’s functionality is quite complex and often power consuming. Now, new reported developments are ongoing, in which the fluxgate magnetometer is co-integrated along with circuitry on a die [
5]. Fluxgate sensors are much more sensitive than Hall sensors and have better temperature stability, and low noise and linearity. A main disadvantage is their relatively small full range of operation, of about 2 mT. In [
4] 16 integrated microfluxgate sensors TI DRV425 were used, which were placed around an Al conductor with the cross-section of 100 × 10 mm
2 able to support a current of 400 A. Using this complex system, composed from sensors, DAQ boards, and Mini-PC, a resolution of 1 mA and a temperature drift of 8 mA/°C were achieved for a maximum measured current of 400 A.
Magnetoresistive sensors (MR) made from magnetic layers and based on anisotropic magnetoresistance (AMR) [
6,
7,
8,
9], giant magnetoresistance (GMR) [
10,
11,
12,
13,
14,
15], and the tunneling magnetoresistance effect (TMR) [
16] are now extensively studied and used for detection of DC/AC currents.
The resistance behaviour of magnetic thin films (Fe, Co, Ni, or alloys like Permalloy—Ni
80Fe
20) is anisotropic (AMR effect) with respect to the applied field direction [
6]. The alloy’s resistance depends on the angle between the magnetization and the direction of current flow. In a magnetic field, magnetization rotates toward the direction of the magnetic field and the rotation angle depends on the external field’s magnitude. The resistance changes roughly as the square of the cosine of the angle between the magnetization and the direction of current flow. Based on this effect and on the planar Hall effect (PHE) which appears in such structures as a consequence of the AMR effect [
6], many sensing applications have been developed. Most of these sensors are obtained using integrated circuit technology [
7,
8,
9], where the resistive elements are connected in a Wheatstone bridge configuration to get high detection sensitivity around 0 field and a better thermal stability of the output signal. The resistive elements have a large aspect ratio (about 10 nm thin, a few μm wide, and tens of μm long), such that magnetization naturally aligns over the longitudinal axis (easy axis of magnetization). The Barber Pole biasing technique [
6,
8,
9] is used to linearize the transfer function.
To achieve a uniform rotation of the magnetization in the resistive elements, the magnetic field must be applied parallel with the sensor’s surface and perpendicular to the easy axis of magnetization. In [
7], eight AMR sensors (model KMZ51) were placed in a circular pattern around a conductor through which the current to be measured is flowing. A linearity error of ±0.05% in the current range of ±8 A, i.e., an absolute resolution of 4 mA was reported. In [
8], the AMR sensors are placed above a U-shaped current trace, the system being encapsulated in a SOIC16 package type.
Currents up to ±50 A can be measured with a zero offset current up to 120 mA. For a current range of ±5 A, the zero offset current can reach a maximum value of 60 mA; the sensitivity is 350 mV/A (with signal conditioning) with a non-linearity error up to 0.5% F.S. (full scale). In [
9], the AMR chip with a Wheatstone bridge was placed above the U-shaped conductor. As a common factor, these sensors contain, in their structure, a compensation conductor located above the MR elements [
8,
9]. Through this conductor a feedback current is driven to compensate the external magnetic field so that the sensor always works around a single point.
This feedback current is a measure of the detected current. Also, as the internal magnetization has no preferred direction along the longitudinal axis, a flipping of 180° can occur due to overcurrent spikes or due to exposure to certain external magnetic fields. This flipping of the magnetization results in a different sensitivity of the system. To overcome this problem, an internal coil (KMZ51) or external controlled magnetic field should be used to reset the magnetization to the initial orientation. Care should be taken to avoid a current passing directly underneath the device itself as the magnetic field generated by that current will be parallel to the printed circuit board (PCB) surface and will affect the functionality of the AMR sensors.
In 1988, the giant magnetoresistance (GMR) effect was discovered in a [Fe/Cr]
n magnetic multilayer. It was found that a change of relative magnetic moment orientation between adjacent magnetic layers results in a significant change of resistance. When the layers are magnetized in parallel, the resistance is at a minimum value,
Rp. When the magnetizations of the adjacent magnetic layers are antiparallel to each other, the resistance is at a maximum value, named
Rap. The physical mechanism of the GMR effect is the spin dependent electric transport in ferromagnetic transition metals. Thus, a new and dynamic field in science, named spintronics, has emerged from this discovery. In 2007, the importance of this discovery was awarded with a Nobel Prize in Physics. Many different applications have been developed subsequently, including low field sensors, position sensors, velocity sensors, Magnetic Random-Access Memory (MRAM) [
12], and hard disks read heads. GMR sensors offer high sensitivity, wide frequency range, small size, low power consumption, and they are compatible with many other state-of-the-art technologies [
13]. GMR sensors also have a number of drawbacks, from which we can note nonlinearity, hysteresis, offset, and a temperature dependent output that can reduce measurement accuracy [
14]. In addition, the output of some of GMR sensors is unipolar, which limits its application in AC measurements [
2].
In terms of theoretical considerations, several methods have been proven effective in improving the GMR sensor response. Using a bias field parallel to the sensitive axis can shift the operating point of the sensor to the linear region, thus reducing the hysteresis behavior and creating a bipolar signal. This field can be created either by using a permanent magnet or a coil system with DC, AC, or short pulse currents which can have either open or closed-loop control [
14]. Optimization in terms of signal measurement (such as using a differential measurement method) and acquisition can also be performed.
Regarding the application of GMR sensors as current sensors, a multitude of studies have been performed to improve their characteristics. In [
14], a closed-loop operation was used to improve the linearity of the GMR sensor. Hysteresis modelling compensation is used in [
11] to reduce hysteresis and temperature dependency. In [
15], low frequency capture is used to extend the sensor response up to ±800 A. Compared with AMR sensors, GMR sensors, offer a higher sensitivity and, in most cases, are more stable to overcurrent or magnetic field spikes.
3. Results and Discussion
The results presented in this section are a summary of many tests done for different input currents both in DC and AC. From
Figure 13a we can denoted that the sensors response is nonlinear in the −1.5 A to 1.5 A current region, which would not allow low currents measurement without biasing.
Figure 13b presents the output characteristic of the differential system obtained for unbiased sensors for a DC current between −3 A to 3 A. The response from each sensor is slightly different and presents a hysteretic behavior. The differential output is chaotic, and thus unusable.
In what follows, the results obtained with sensors biased at 8 Oe and using the setup from
Figure 10 and
Figure 11 will be presented.
Figure 14 presents the system response when measuring a variable DC current between −2 A to 2 A. The sensitivity for the differential output is
S = 0.0307 V/A. Due to inherent hysteresis effects (note
Figure 12b and
Figure 13a), a hysteresis effect of 0.04 A was observed in the range of ±2 A.
In
Figure 15a, the system’s output when measuring a variable DC current from −4 A to 4 A is presented, while
Figure 15b presents the signals variation over time. As expected, the sensitivity is almost the same but the hysteretic effects are lower. Above 4 A, the thermal stability of the setup is negatively impacted as heating occurs.
For the differential measurement system, the temperature drift of the offset can, theoretically, go to zero for sensors that perfectly matched and are subjected to the same biasing field. The temperature drift of the offset was measured with the sensors biased in order to place them in a linear operation regime and to have the same (almost) output voltage when no current is applied in the conductive band,
Figure 12b. The measured temperature drift of the offset is ΔU
0/ΔT ≈ −7.9 × 10
−6 V/°C which means about −2.59 × 10
−4 A/°C in terms of measured current, for a temperature variation of 20 °C. Thus, it can be noted that the temperature drift of the offset is affected mainly by the temperature dependence of the GMR effect. Also, we can note that any temperature drifts in the operating range of the bias magnet and FeSi plates lead to no significant changes to the bias magnetic field as we estimate that the temperature of these components is no larger than 37 °C during our tests. Moreover, we used a ferrite magnet from NVE to bias the sensors (which has a Curie temperature up to 300 °C).
The thermal drift of the sensor is defined by the TCoutput change with temperature using a constant current source) and TCOV (output change with temperature using a constant voltage source). According to the catalogue [
18], for a single sensor, TCIO is +0.03 %/°C, while TCOV is −0.1 %/°C. Since the sensors are supplied with 4.096 V constant voltage, TCOV is relevant in this case. An LM335AZ temperature sensor was mounted on the PCB for measuring temperature (
Figure 10a).
Figure 16a shows the time dependence of the temperature of the PCB in the sensors vicinity for I = 1 A, 2 A, and 3 A respectively. One can observe that for a current of 3A passing through the conductive band, the temperature reaches a plateau at about 36 °C after 2000 s.
Figure 16b shows the thermal drift of the differential output for I = 1 A, 2 A, and 3 A. The obtained values are: TCOV
1A = 0.07 %/°C, TCOV
2A = −0.0134 %/°C, and TCOV
3A = −0.12 %/°C.
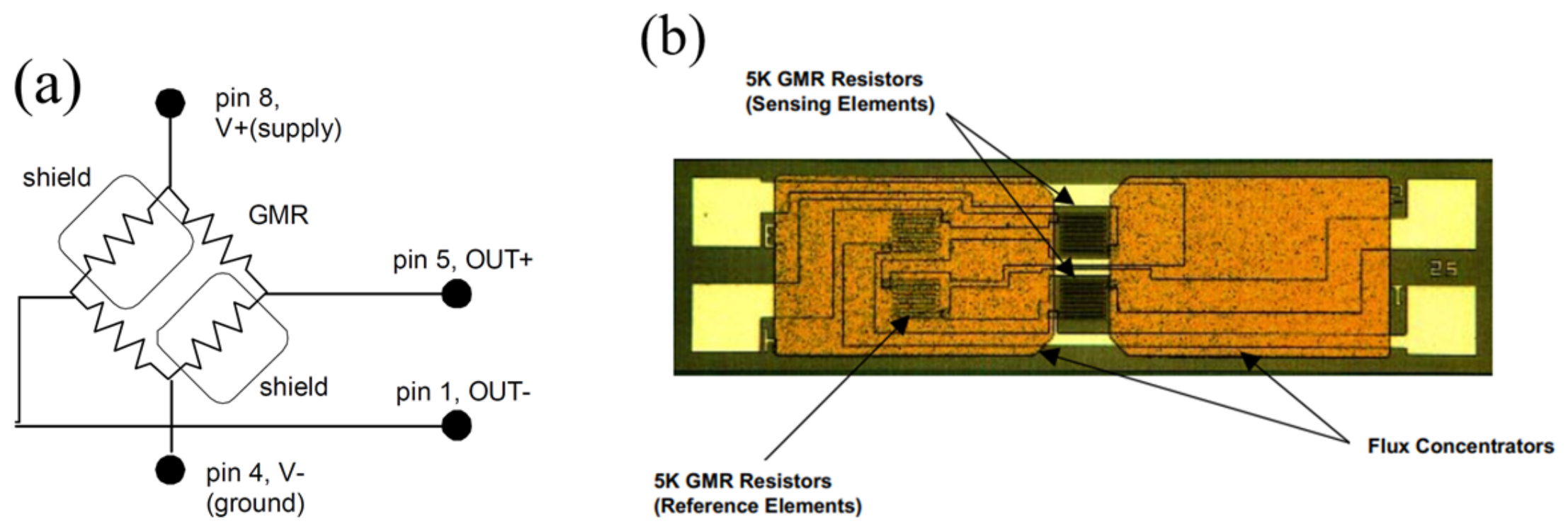
We can identify two possible effects responsible for the measured thermal drifts: (i) variation of the resistance of the metallic layers with temperature and (ii) temperature dependence of the GMR effect. The influence of the first effect is almost canceled by the Wheatstone bridge connection of the sensors inside the chip,
Figure 5a, and by the differential measurement setup,
Figure 11. This can be seen from data presented in
Figure 16b, when very low magnetic field is applied to sensors for I = 1 A and 2 A respectively. On the other hand, the effect of spin fluctuations is shown to play an important role in the temperature-dependency of the GMR amplitude. As a consequence, the GMR effect shows an almost linear decrease when temperature is raised [
28,
29].
From
Figure 16b we found a linear decrease of the output voltage, which is more important for I = 3 A where a larger amount of heat can be transferred to sensors and, hence, we expect a larger temperature variation of the GMR effect. This has an effect on the setup we used, but this can be compensated by applying a correction factor proportional with the measured temperature variation and using the calculated TCOV.
Figure 16b presents the compensated response for I = 3 A through the conductive band.
Thus, we can note that the system is thermally stable and can provide reliable data within a temperature interval between 20 to 37 °C.
In terms of low currents sensing capabilities, the limitation is due to some factors like: the sensor’s field sensitivity, electric noise of the detection setup, and the width of the current path. We found that the implemented differential system is effective with currents as low as 75 mA,
Figure 17a. For lower currents, the signal from the sensors is very weak and more precautions should be taken into account regarding electrical shielding, the noise of the signal amplifier, and the DAQ system. As we can see from Equation (3) and
Figure 8 and
Figure 9, a current line with a smaller width favours the measurement of low currents. However, a larger width of the conducting band is needed for measuring larger currents without excessive heating. For example, when I = 75 mA and w = 0.254 mm, H = 0.186 Oe, whereas H = 0.1344 Oe for I = 75 mA and w = 2 mm respectively.
In
Figure 17b, the response of the system when measuring a 200 mA, 50 Hz, alternative current is shown. In this case, a current of 150 mA is required in order for the output to be sufficiently linear. Below these thresholds, the nonlinearities in the sensor’s response provide an inaccurate differential output. That is due to the fact that at low currents, the sensors output no longer accurately follows the waveform of the magnetic field generated by said current. Thus, the output signal appears distorted and does not represent the actual sine waveform. This is also true when measuring DC currents, as the differential output can be scattered creating some nonlinearities in the response (
Figure 17a).
In
Figure 18a, the AC response of the system when measuring a 50 Hz sine waveform at 3 A is shown. The harmonic analysis for this measurement is shown in
Figure 18b. A THD (total harmonic distortion) of 0.176% was obtained in this case. We can notice that the signal integrity is very good with little to no distortion (the fundamental frequency is the major amplitude, while the effect of the 3rd, 5th, and 7th harmonics is negligible). Note that the frequency limits of the response in AC are mostly limited by the DAQ system, as the sensors have a theoretical maximum frequency response of 1 MHz [
18]. Further studies can be done to find the actual AC frequency limitations of the system.
Figure 19 shows the AC calibration curve for the device within the 0–3 A range. We used the adjusted R-squared term to show how well data is aligned over the fitting line. The adjusted. R-square is 0.99943. The calculated full-scale error is 0.66%. Note that there is a very good correlation between the measured current and the response of the system.
What is noteworthy for the implemented system’s output is that all the signal acquisition is done without implementing any filtering system. In this way, the system’s viability to measure both DC and AC currents was demonstrated. Thus, it can be noted that for a specific application (in DC or AC), further signal improvements can be made.
4. Conclusions
A high sensitivity non-contacting current measurement experimental setup based on giant magnetoresistance (GMR) sensors was implemented. The sensitivity of this detection setup is between 0.0272 to 0.0307 V/A with low (40 mA) hysteretic effects. A biasing magnetic field was used to linearize the field dependences of the sensors. Moreover, the implemented differential GMR system is very versatile, being able to measure both DC and AC currents. The current measurement system (
Figure 12a) was proven to be able to measure accurately and for extended periods of time in DC from 75 mA up to around 4 A, and in AC from 150 mA up to 4 A. This system has the following advantages: high sensitivity, galvanic isolation, thermal stability (when operating at specified parameters), immunity to low external magnetic fields, and preservation of signal integrity for the input current, as can be seen in
Figure 15 and
Figure 18. These results were obtained without EMF shielding or filtering systems. The custom PCB for the system was designed to measure currents up to 10 A (by taking into account the copper trace width [
17]), however, in practice, it was observed that significant heating occurs when measuring currents larger than 4 A for an extended period of time (
Figure 16).
Moreover, in terms of performance comparison of the implemented sensor setup with other solutions on the market, we can note the following: The novelty of our approach consists in using a double differential measurement system,
Figure 11, based on commercial GMR sensors, with an adjustable biasing system used to linearize the field response of the system. This approach was not seen in other works [
14,
30,
31,
32] or was implemented in commercial sensors like microfluxgate [
4,
5] or based on AMR effect [
7,
8,
9]. As we are using a movable permanent magnet to bias the sensors and there is no compensation coil, the power consumption of our detection system (DAQ card and PC is not included) is very small, of about 6.4 mW (as each sensor has a power consumption of 3.2 mW, as noted in [
18]).
To improve the measurement accuracy of a magnetometer using the same type of sensor like we used in this study, a closed-loop GMR–compensation coil is used in [
14,
30], the system operating similarly as in [
8,
9]. With this method, a sensitivity of about 0.03 V/A to 0.04 V/A (with signal conditioning) is reported in [
30] which is quite similar to our result obtained without a feedback coil. The power consumption was reported to be 1.6 W at low currents through the conductive band to 3.2 W for currents up to 45 A.
In [
9], for the MCA1101-xx-5 series current sensors, a sensitivity between 35 mV/A up to 350 mV/A for current sensors in the 5–50A range which is typical for AMR effect sensors, but lower than GMR based sensors. In [
31], a temperature coefficient TCOV of −0.17 %/°C of the sensor’s output voltage is obtained while for our system a TCOV between −0.0134 %/°C to −0.117 %/°C has been measured. Also, in [
8], typical CMS2000 series AMR sensors, have a typical offset voltage at room temperature of ±20 mV compared with our setup of −7.9 × 10
−6 V/°C. This result emphasizes the benefit of our double differential measurement system to lower the thermal drift of the output signal.
Furthermore, the present setup aims to serve as a novel proof concept of concept application, and with future development, the operation range and utility of the system can be improved greatly. The current implementation is a compromise between low current and high current measurement. For example, by taking into account, Equation (4), we can note that low currents sensing capabilities can be improved by using a narrower trace. Also, for high currents measurement, a setup utilizing a much thicker trace and thicker PCB can be used. Thus, by redesigning of the setup, a significant increase in the operation range can be achieved. Further improvements can also include a size reduction (by integrating the amplifiers on the same PCB), EMF shielding and implementing a filtering system.
Finally, the differential sensing method presented in this article can be used for other specific applications requiring a high degree of sensitivity. As measuring low currents implies accurate detection of magnetic fields smaller than 0.5 G, some of the results presented in this paper will be used to develop a high sensitivity detection setup of magnetic nanoparticles (MNPs) used to label biomolecules in lab-on-a-chip (LOC) applications [
33,
34,
35,
36,
37]. As we showed by micromagnetic simulations [
35,
36] and experiments [
34], to achieve a large signal from MNPs, they must be polarized in quite a large magnetic field that can saturate the spintronic sensors. To avoid this, we proposed a specific polarization setup for MNPs, where the field is applied perpendicular to the sensor’s surface [
35,
36,
37]. The MNPs will be localized on the surface of one GMR sensor whereas the second one will be used as reference sensor. The in-plane components of the magnetic fields locally generated by MNPs will be detected by GMR sensors using the differential setup described in
Figure 11. The current through the conductive band will be used to produce an AC excitation field for detection of the MNPs. To ensure a smaller distance between MNPs and GMR sensors, a package flip-chip package type will be used in this development, as in [
34].