Characteristics of Highly Sensitive Hydrogen Sensor Based on Pt-WO3/Si Microring Resonator
Abstract
:1. Introduction
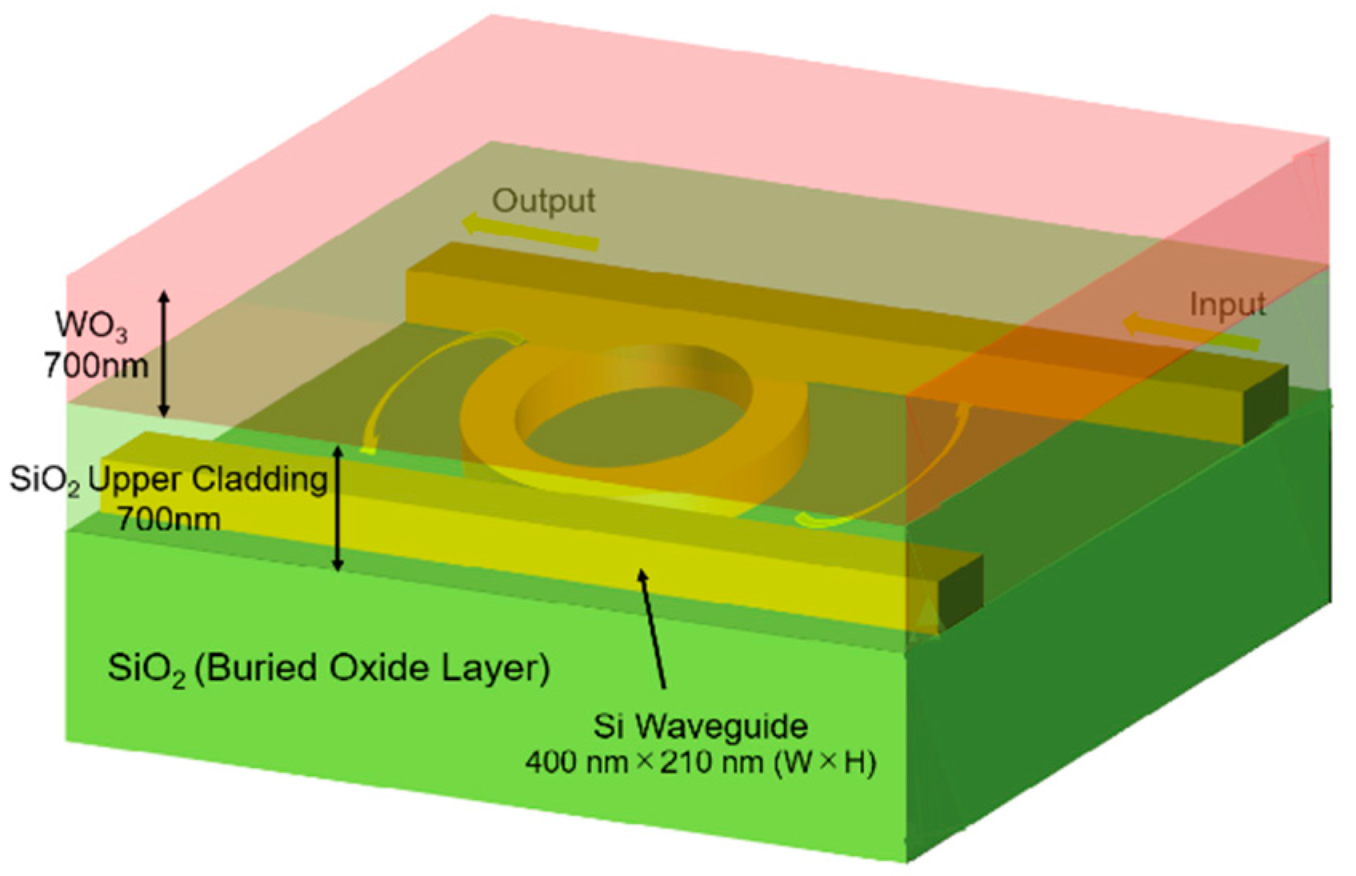
2. Structure and Operation Principle of Sensor
2.1. Structure
2.2. Principle of Sensing
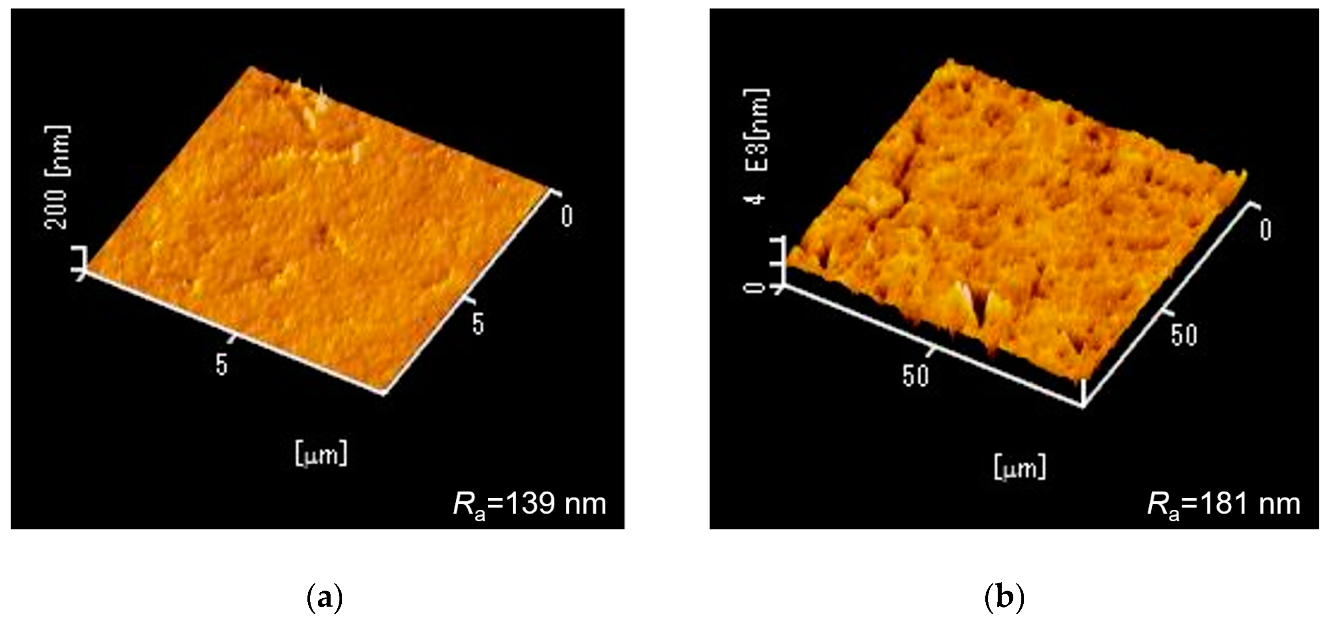
3. Fabrication
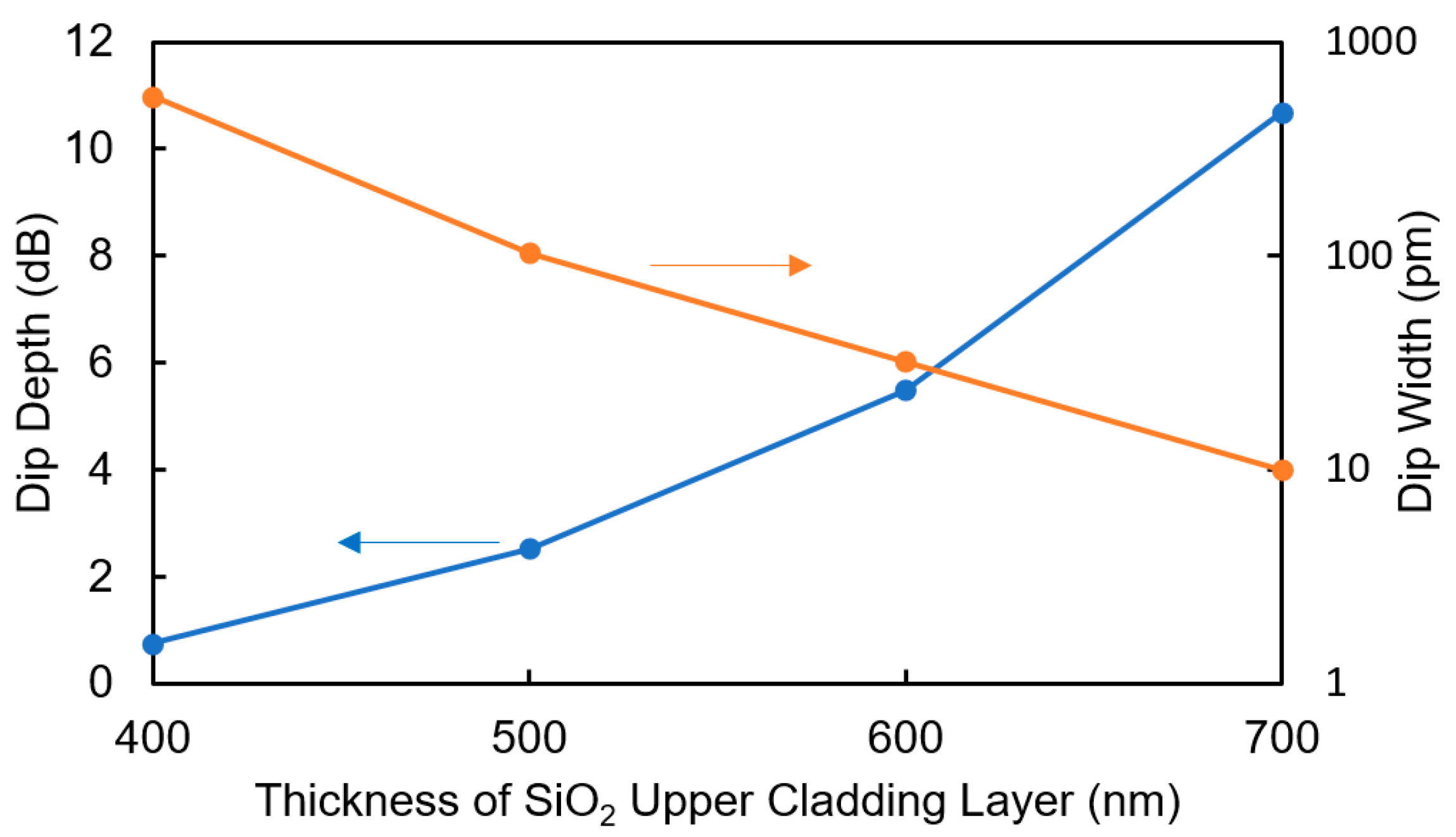
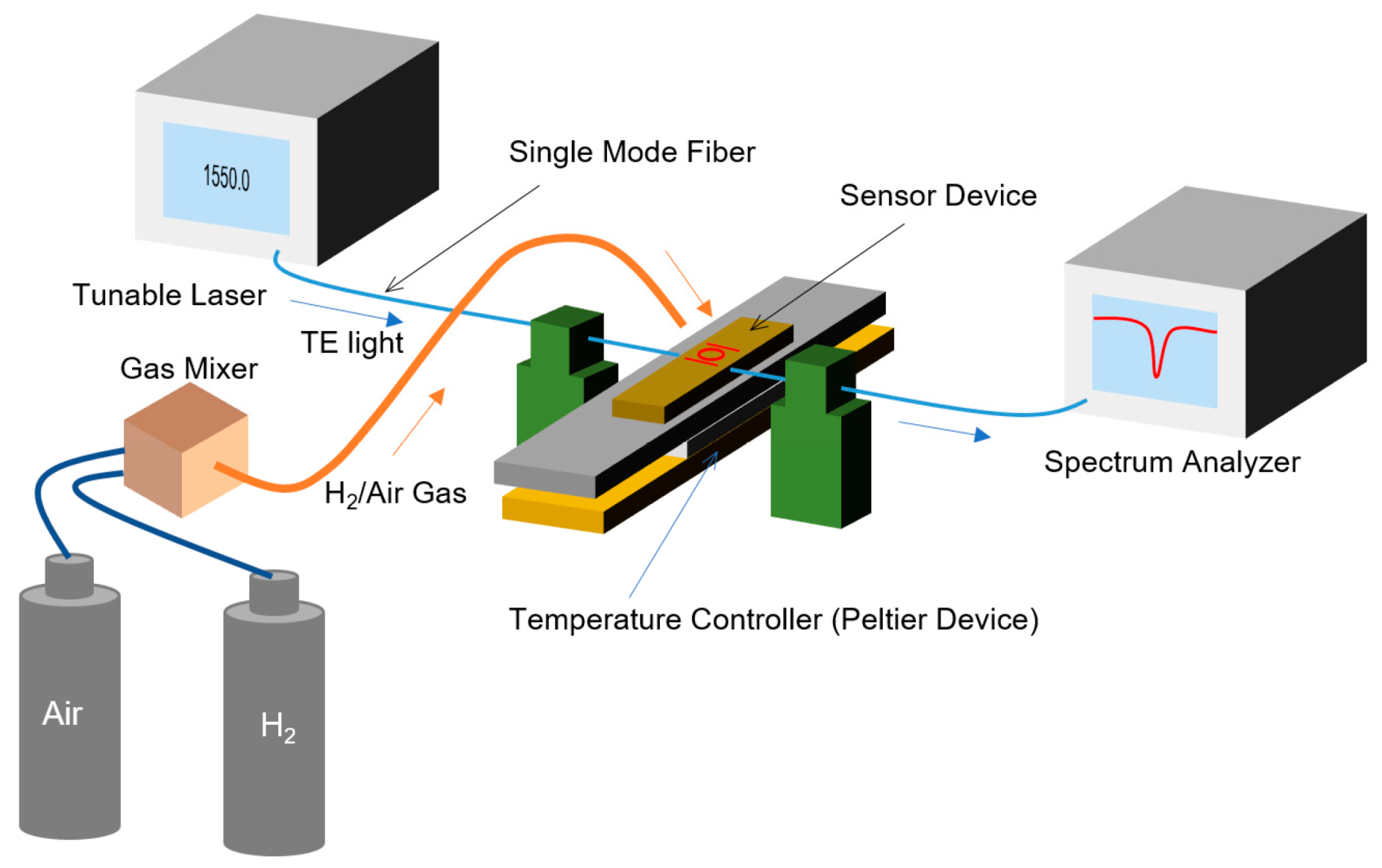
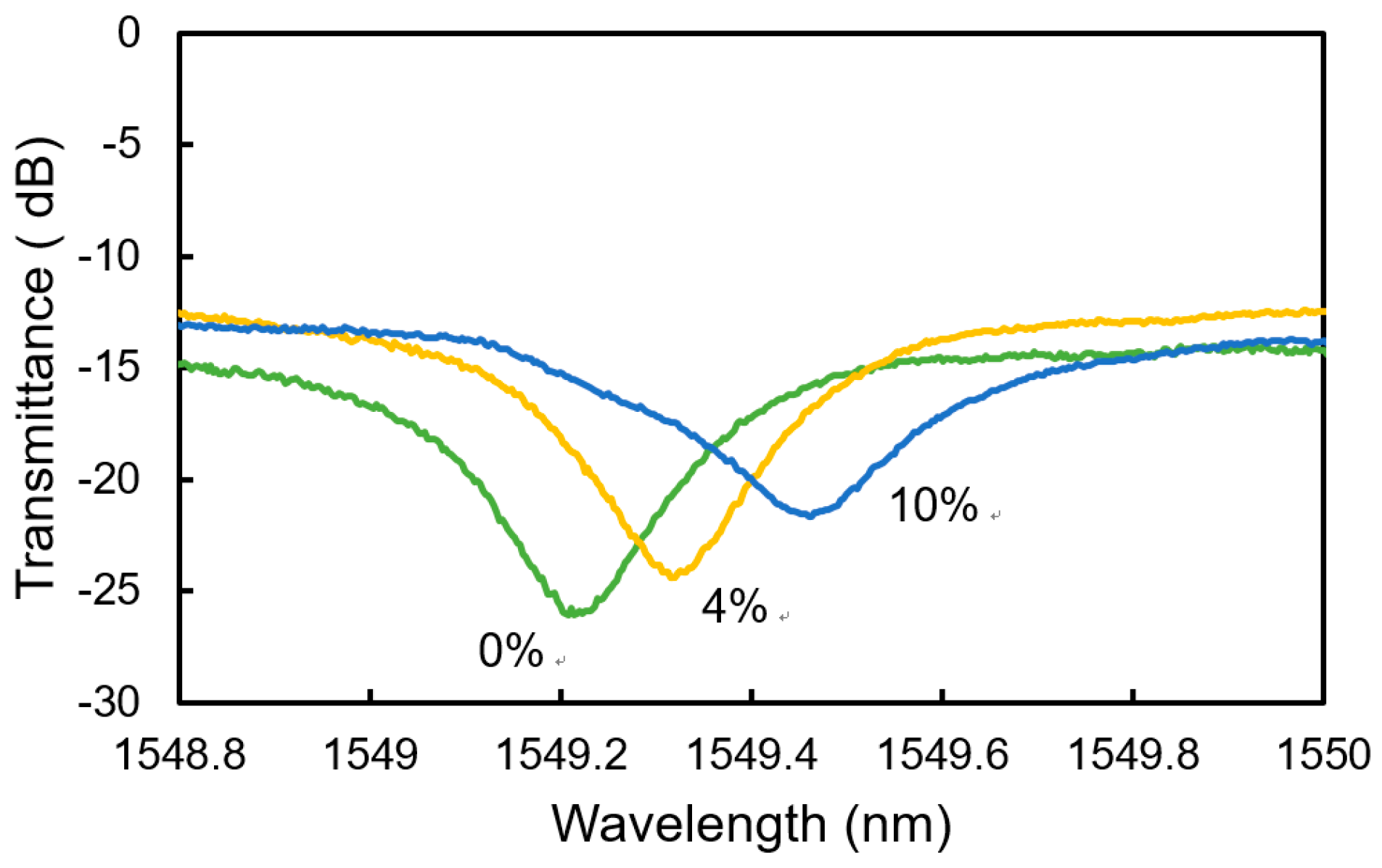
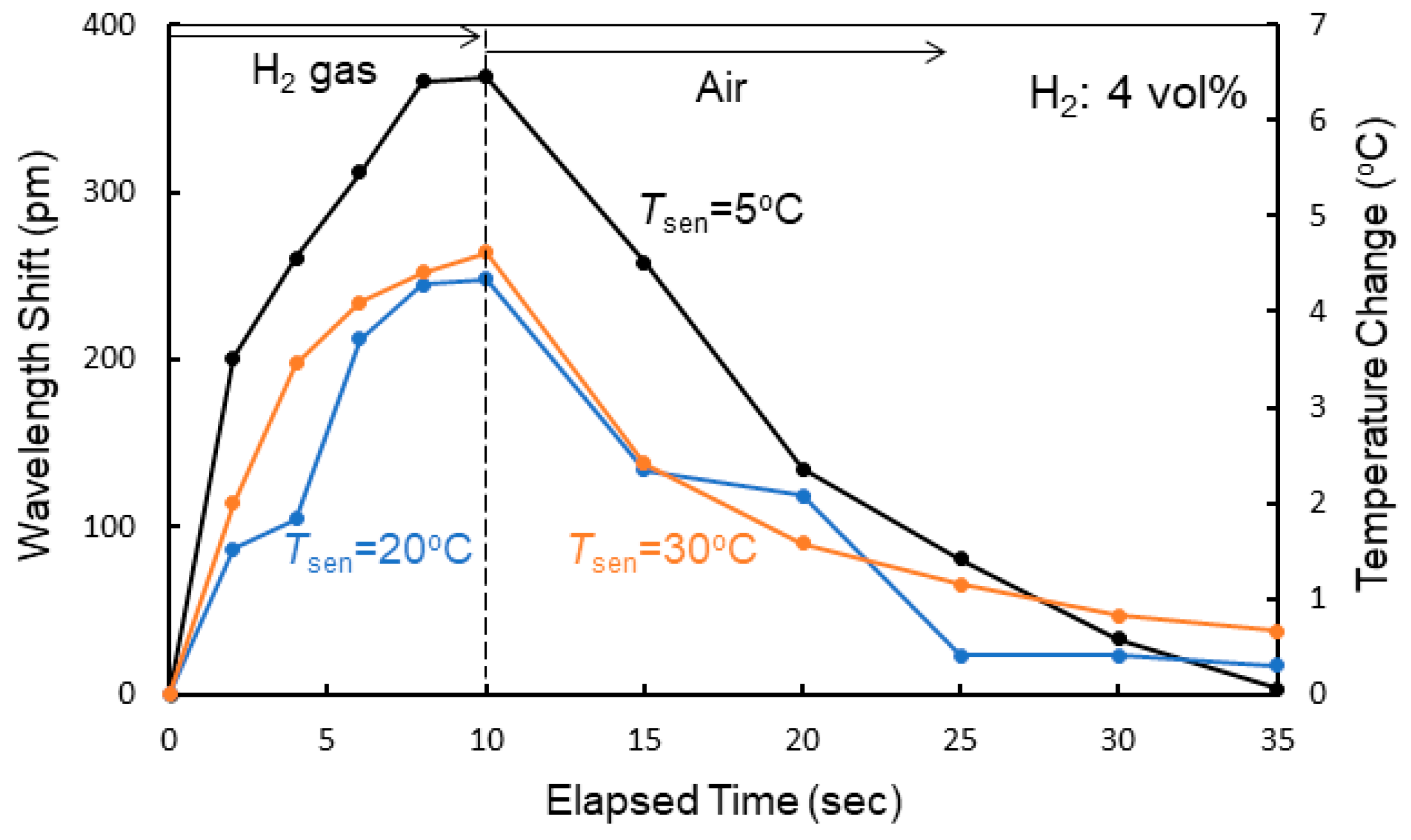
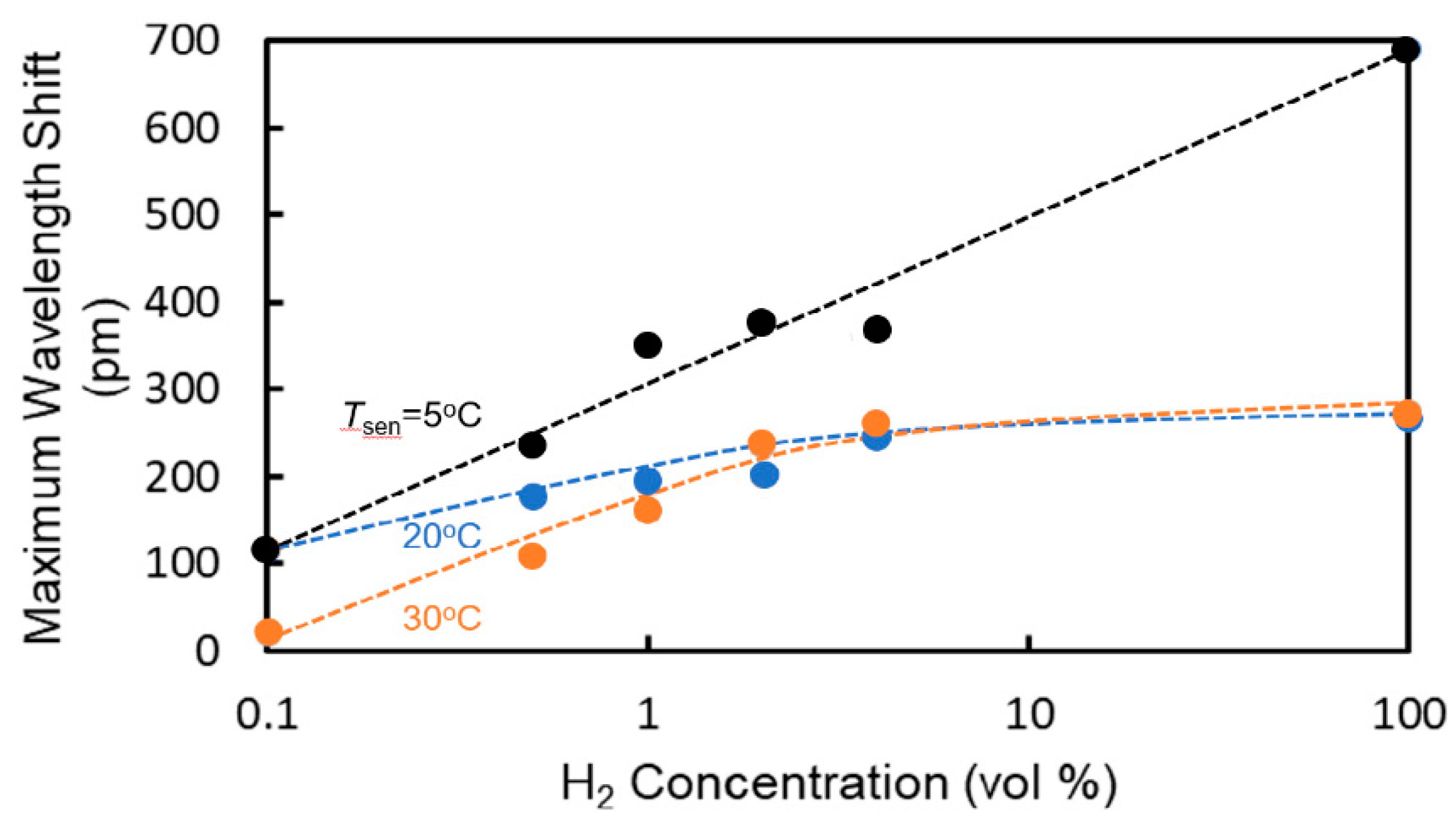
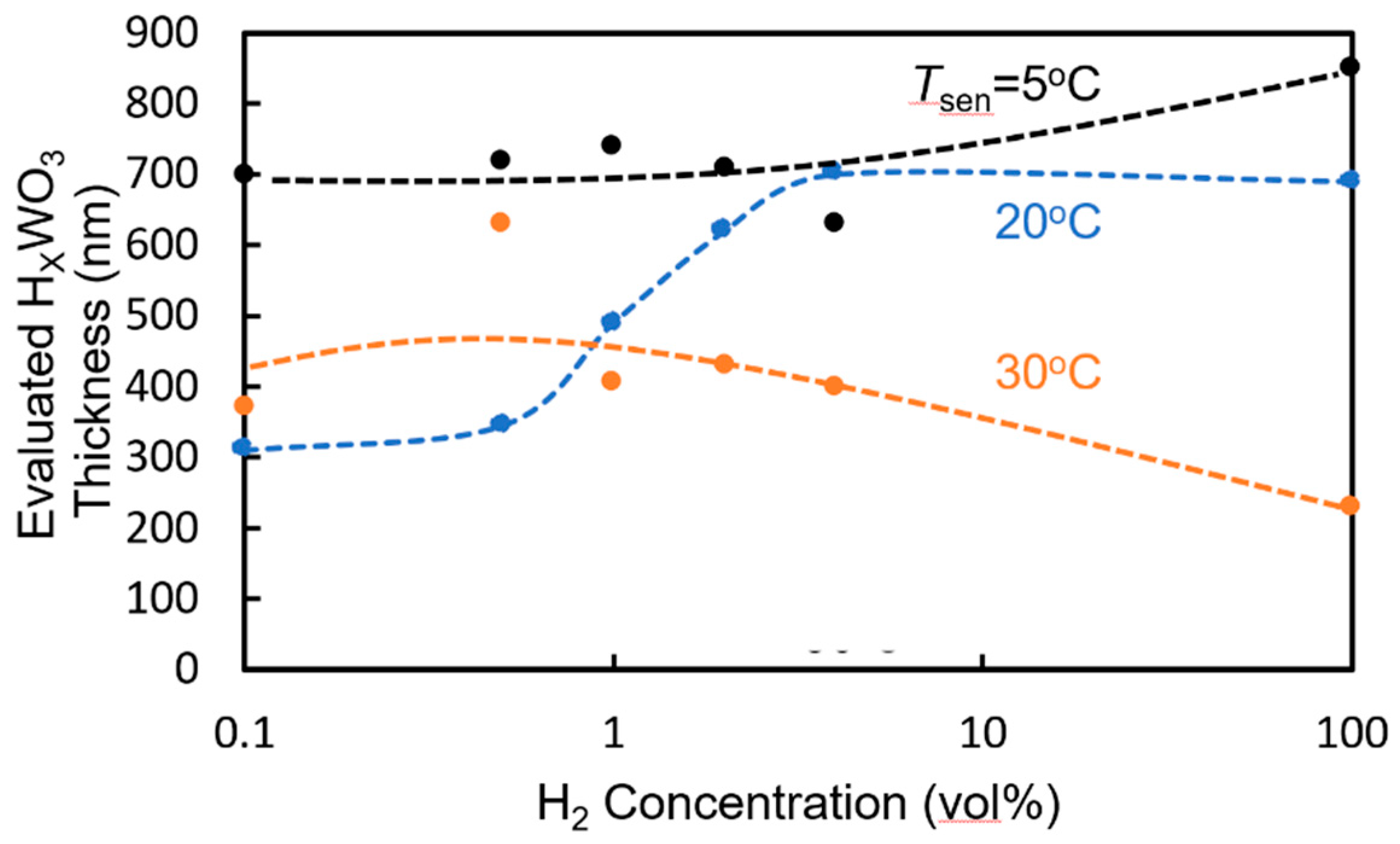
4. Sensing Characteristics of MRR Sensor
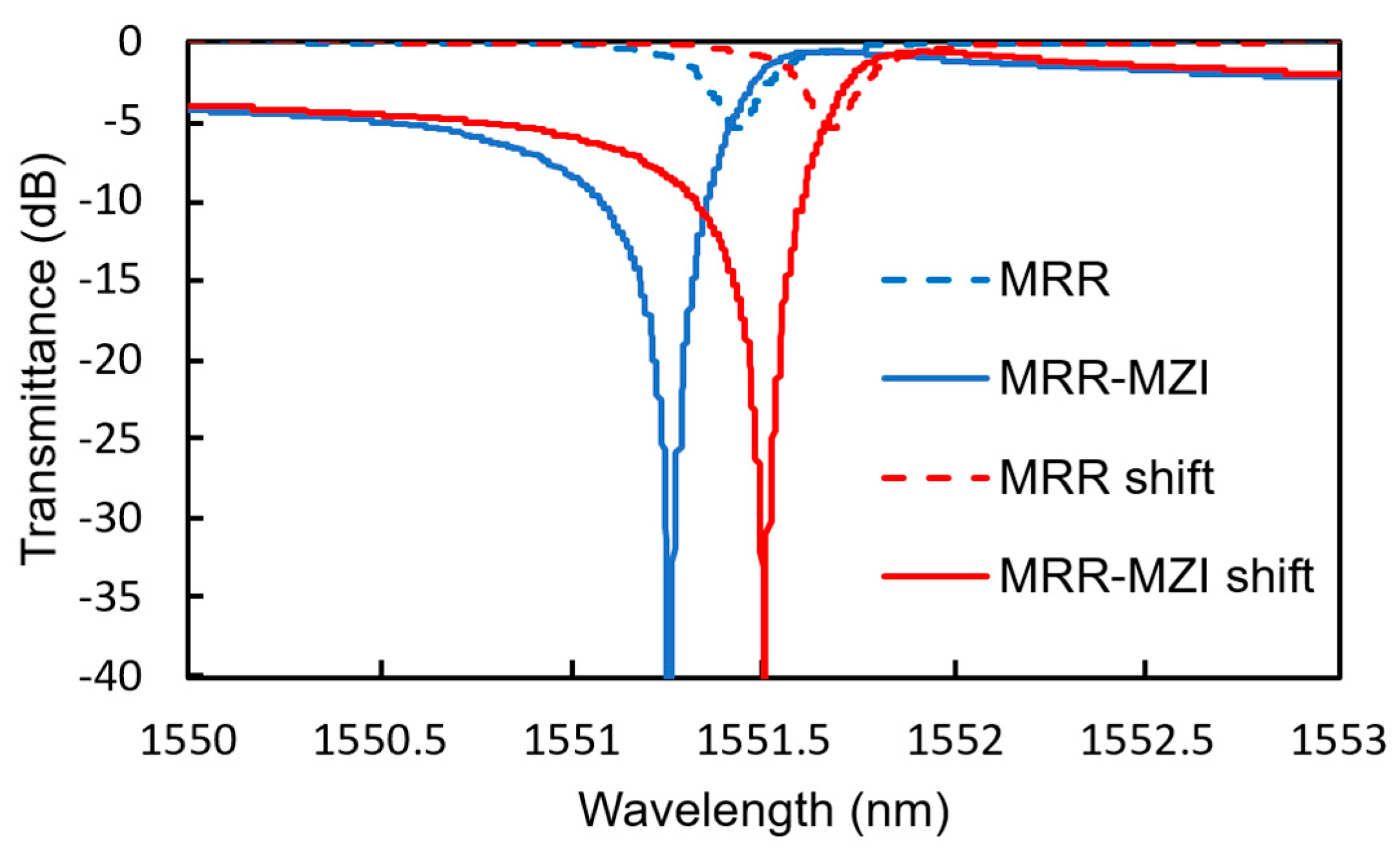
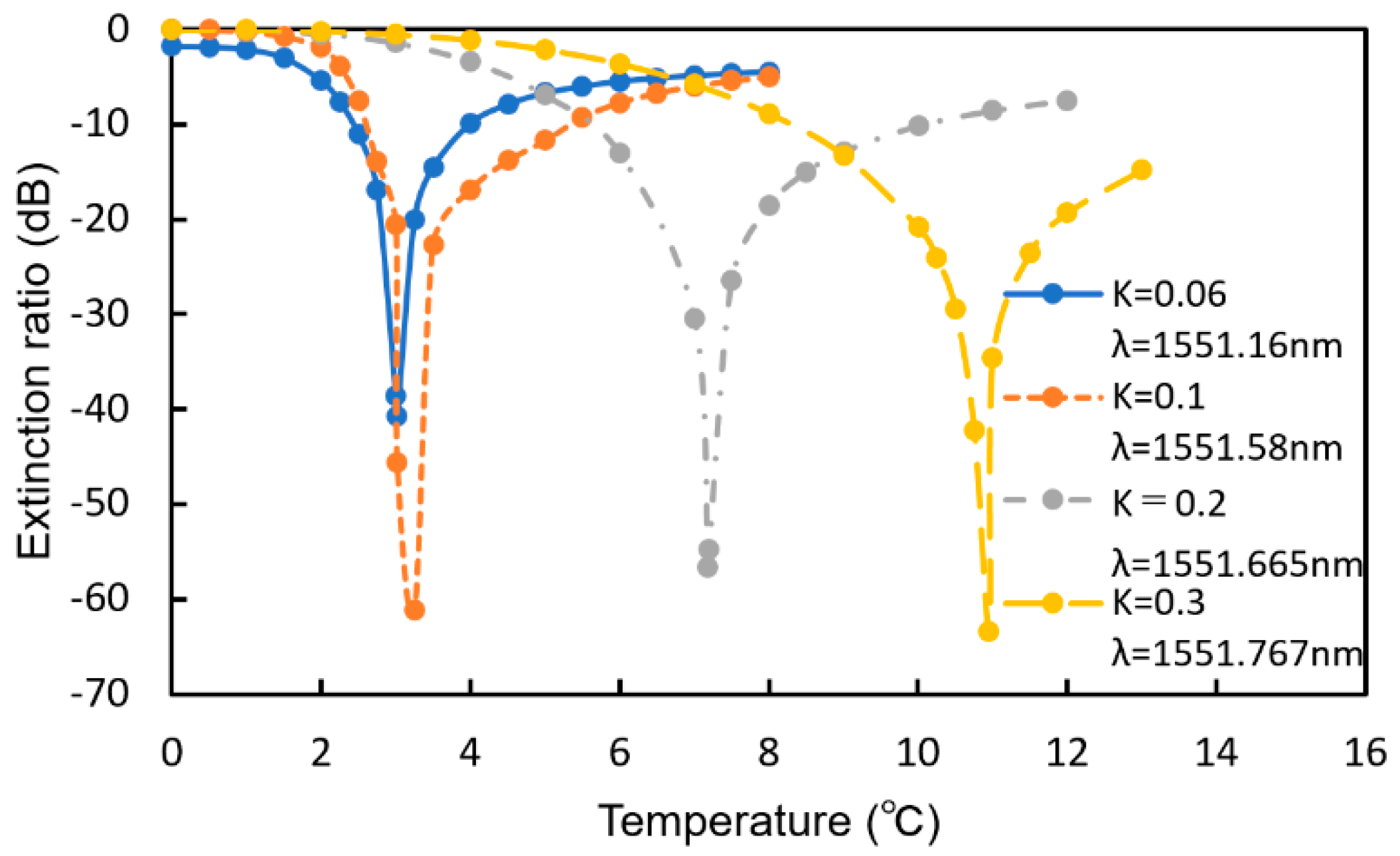
5. Design of MRR-Enhanced Mach–Zehnder Interferometer Sensor
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Crowl, D.A.; Jo, Y.D. The hazards and risks of hydrogen. J. Loss Prevent. Proc. 2007, 20, 158–164. [Google Scholar] [CrossRef]
- Hubert, T.; Boon-Brett, L.; Black, G.; Banach, U. Hydrogen sensors—A review. Sens. Actuators B 2011, 157, 329–352. [Google Scholar] [CrossRef]
- Buttner, W.J.; Post, M.B.; Burgess, R.; Rivkin, C. An overview of hydrogen safety sensors and requirements. Int. J. Hydrog. Energy 2011, 36, 2462–2470. [Google Scholar] [CrossRef]
- Katsuki, A.; Fukui, K. Improvement of humidity dependence in gas sensor based on SnO2. Sens. Actuators B 2000, 65, 316–318. [Google Scholar]
- Rosini, S.; Siebert, E. Electrochemical sensors for detection of hydrogen in air model of non-Nernstian potentiometric response of platinum gas diffusion electrodes. J. Electrochem. Acta. 2005, 50, 2942–2953. [Google Scholar] [CrossRef]
- Martin, L.P.; Pham, A.Q.; Glass, R.S. Electrochemical hydrogen sensor for safety monitoring. Solid State Ionics 2004, 175, 527–530. [Google Scholar] [CrossRef] [Green Version]
- Nakagawa, H.; Yamamoto, N.; Okazaki, S.; Chinzei, T.; Asakura, S. A room-temperature operated hydrogen leak sensor. Sens. Actuators B 2003, 93, 468–474. [Google Scholar] [CrossRef]
- Shukla, S.; Zhang, P.; Cho, H.J.; Seal, S.; Ludwig, L. Room temperature hydrogen response kinetics of nano-micro-integrated doped tin oxide sensor. Sens. Actuators B 2007, 120, 573–583. [Google Scholar] [CrossRef]
- Arya, S.K.; Krishman, S.; Silva, H.; Jean, S.; Bhansali, S. Advances in materials for room temperature hydrogen sensors. Analyst 2012, 137, 2743–2756. [Google Scholar] [CrossRef]
- Gu, H.; Wang, Z.; Hu, Y. Hydrogen Gas Sensors Based on Semiconductor Oxide Nanostructures. Sensors 2012, 12, 5517–5550. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Hu, Y.; Wang, W.; Zhang, X.; Wang, B.; Tian, H.; Wang, Y.; Guan, J.; Gu, H. Fast and highly-sensitive hydrogen sensing of Nb2O5 nanowires at room temperature. Int. J. Hydrog. Energy 2012, 37, 4526–4532. [Google Scholar] [CrossRef]
- Tokutake, K.; Okazaki, S. Development of an antenna coil type sensor device for hydrogen leakage detection. Sens. Actuators B 2014, 191, 165–170. [Google Scholar] [CrossRef] [Green Version]
- Sil, D.; Hines, J.; Udeoyo, U.; Borguet, E. Palladium nanoparticle-based surface acoustic wave hydrogen sensor. ACS Appl. Mater. Interfaces 2015, 7, 5709–5714. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.N.; Peng, H.; Qian, X.; Zhang, Y.; An, G.; Zhao, Y. Recent advancements in optical fiber hydrogen sensors. Sens. Actuators B 2017, 244, 393–416. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, T.; Okazaki, O.; Nakagawa, H.; Murata, K.; Fukuda, K. A fiber-optic hydrogen gas sensor with low propagation loss. Sens. Actuators B 2010, 145, 781–787. [Google Scholar] [CrossRef]
- Masuzawa, S.; Okazaki, S.; Yusuke, M.; Tadahiro, M. Catalyst-type-an optical fiber sensor for hydrogen leakage based on fiber Bragg gratings. Sens. Actuators B 2015, 217, 151–157. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, C.; Xu, B.; Wang, D.; Yang, M. Optical cascaded Fabry-Perot interferometer hydrogen sensor based on vernier effect. Opt. Commun. 2018, 414, 166–171. [Google Scholar] [CrossRef]
- Yan, M.; Tylczak, J.; Yu, Y.; Panagakos, G.; Ohodnicki, P. Multi-component optical sensing of high temperature gas streams using functional oxide integrated silica based optical fiber sensors. Sens. Actuators B 2018, 255, 357–365. [Google Scholar] [CrossRef]
- Mirzaei, A.; Kim, J.H.; Kim, H.W.; Kim, S.S. Gasochromic WO3 Nanostructures for the Detection of Hydrogen Gas: An Overview. Appl. Sci. 2019, 9, 1775. [Google Scholar] [CrossRef] [Green Version]
- Yebo, N.A.; Tailaert, D.; Roels, J.; Lahem, D.; Debliquy, M.; Thourhout, D.V.; Baets, R. Silicon-on-Insulator (SOI) Ring Resonator-Based Integrated Optical Hydrogen Sensor. IEEE Photonics Technol. Lett. 2009, 21, 960–962. [Google Scholar] [CrossRef] [Green Version]
- Olyaee, S.; Mohebzadeh-Bahabady, A. Designing a novel photonic crystal nano-ring resorator for biosensor application. Opt. Quantum Electron. 2015, 47, 1881–1888. [Google Scholar] [CrossRef]
- Eryurek, M.; Karadag, Y.; Tasaltin, N.; Kilibc, N.; Kiraz, A. Optical sensor for hydrogen gas based on a palladium-coated polymer mocroresonator. Sens. Actuators B 2015, 212, 78–83. [Google Scholar] [CrossRef]
- Meziane, F.; Raimbault, V.; Hallil, H.; Joly, S.; Conédéra, V.; Lachaud, J.L.; Béchou, L.; Rebière, D.; Dejous, C. Study of a polymer optical microring resonator for hexavalent chromium sensing. Sens. Actuators B 2015, 209, 1049–1056. [Google Scholar] [CrossRef]
- Donzella, V.; Sherwaili, A.; Flueckiger, J.; Grist, S.M.; Fard, S.T.; Chrostowski, L. Design and fabrication of SOI micro-ring resonators based on sub-wavelength grating waveguides. Opt. Express. 2015, 23, 4791–4803. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Ding, Y.; Wang, Y. Asymmetrical microring resonator based on whispering gallery modes for the detection of glucose concentration. Optik 2018, 171, 642–647. [Google Scholar] [CrossRef]
- Liu, Q.; Lim, B.K.L.; Lim, S.Y.; Tang, W.Y.; Gu, Z.; Chung, J.; Park, M.K.; Barkham, T. Label-free real-time and multiplex detection of Mycobacterium tuberculosis based on silicon photonic microring sensors and asymmetric isothermal amplification technique (SPMS-AIA). Sens. Actuators B 2018, 255, 1595–1603. [Google Scholar] [CrossRef]
- Fu, D.; Chung, J.; Liu, Q.; Raziq, R.; Kee, J.S.; Park, M.K.; Valiyaveettil, S.; Lee, P. Polymer coated silicon microring device for the detection of sub-ppm volatile organic compounds. Sens. Actuators B 2018, 257, 136–142. [Google Scholar] [CrossRef]
- Amrehn, S.; Wu, X.; Wagner, T. Tungsten Oxide Photonic Crystals as Optical Transducer for Gas Sensing. ACS Sens. 2018, 3, 191–199. [Google Scholar] [CrossRef] [Green Version]
- Kishikawa, H.; Sato, M.; Goto, N.; Yanagiya, S.; Kaito, T.; Liaw, S.K. An optical ammonia gas sensor with adjustable sensitivity using a silicon microring resonator covered with monolayer graphene. Jpn. J. Appl. Phys. 2019, 58, SDDJ05. [Google Scholar] [CrossRef]
- Yamasaku, N.; Matsuura, S.; Nishijima, Y.; Arakawa, T.; Okazaki, S. Response characteristics of silicon microring resonator. IEEJ Trans. Sens. Micromachines 2019, 139, 2–6. [Google Scholar] [CrossRef]
- Hussain, Z. Dopant-dependent reflectivity and refractive index of microcrystalline HxWO3 and LixWO3 bronze thin films. Appl. Opt. 2002, 41, 6708–6724. [Google Scholar] [CrossRef] [PubMed]
- Kaneshige, H.; Gautam, R.; Ueyama, Y.; Katouf, K.; Arakawa, T.; Kokubun, Y. Low-voltage quantum well microring-enhanced Mach-Zehnder modulator. Opt. Express. 2013, 21, 16888–16900. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, S.; Ishihara, S.; Arakawa, T.; Kokubun, Y. Highly sensitive optical biosensor based on silicon-microring-resonator-loaded Mach–Zehnder interferometer. Jpn. J. Appl. Phys. 2017, 56, 04CH08. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, S.; Ishihara, S.; Nishijima, Y.; Kokubun, Y.; Arakawa, T. Improved Sensitivity of Microring Resonator-Loaded Mach–Zehnder Interferometer Biosensor. Sens. Mater. 2017, 29, 1241–1246. [Google Scholar]






| Symbol | Description | Value |
|---|---|---|
| LMRR | Round-trip length of MRR | 69.3 μm |
| LC | Length of directional coupler | 5.4 μm |
| K | Power coupling efficiency of directional coupler | 0.2 |
| tWO3 | Thickness of WO3 upper cladding layer | 700 nm |
| tSiO2 | Thickness of SiO2 upper cladding layer | 700 nm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsuura, S.; Yamasaku, N.; Nishijima, Y.; Okazaki, S.; Arakawa, T. Characteristics of Highly Sensitive Hydrogen Sensor Based on Pt-WO3/Si Microring Resonator. Sensors 2020, 20, 96. https://doi.org/10.3390/s20010096
Matsuura S, Yamasaku N, Nishijima Y, Okazaki S, Arakawa T. Characteristics of Highly Sensitive Hydrogen Sensor Based on Pt-WO3/Si Microring Resonator. Sensors. 2020; 20(1):96. https://doi.org/10.3390/s20010096
Chicago/Turabian StyleMatsuura, Sosuke, Naoki Yamasaku, Yoshiaki Nishijima, Shinji Okazaki, and Taro Arakawa. 2020. "Characteristics of Highly Sensitive Hydrogen Sensor Based on Pt-WO3/Si Microring Resonator" Sensors 20, no. 1: 96. https://doi.org/10.3390/s20010096
APA StyleMatsuura, S., Yamasaku, N., Nishijima, Y., Okazaki, S., & Arakawa, T. (2020). Characteristics of Highly Sensitive Hydrogen Sensor Based on Pt-WO3/Si Microring Resonator. Sensors, 20(1), 96. https://doi.org/10.3390/s20010096





