Figure 1.
(a) Frontal view of the building; (b) Plant view of Structure A.
Figure 1.
(a) Frontal view of the building; (b) Plant view of Structure A.
Figure 2.
(a) North view of the City Hall building; (b) northwest view of the City Hall building; (c) southwest view of the City Hall building—Structure B.
Figure 2.
(a) North view of the City Hall building; (b) northwest view of the City Hall building; (c) southwest view of the City Hall building—Structure B.
Figure 3.
Plant type view of Structure B.
Figure 3.
Plant type view of Structure B.
Figure 4.
Identified monitoring points—Structure A.
Figure 4.
Identified monitoring points—Structure A.
Figure 5.
(a) Acquisition points A and C and the adopted reference system; (b) acquisition points B and D; (c) details of accelerometers positioned in point B by means of the cubic element; (d) details of accelerometers mounted on point C by means of the cubic element.
Figure 5.
(a) Acquisition points A and C and the adopted reference system; (b) acquisition points B and D; (c) details of accelerometers positioned in point B by means of the cubic element; (d) details of accelerometers mounted on point C by means of the cubic element.
Figure 6.
Geometry of Structure A for Operational Modal Analysis (OMA) along with accelerometers positions and directions.
Figure 6.
Geometry of Structure A for Operational Modal Analysis (OMA) along with accelerometers positions and directions.
Figure 7.
OMA identification with Enhanced Frequency Domain Decomposition (EFDD) method, Test 1.
Figure 7.
OMA identification with Enhanced Frequency Domain Decomposition (EFDD) method, Test 1.
Figure 8.
OMA identification with Stochastic Subspace Identification (SSI) method, Test 1.
Figure 8.
OMA identification with Stochastic Subspace Identification (SSI) method, Test 1.
Figure 9.
Mode shapes identified using SSI method – Structure A, Test 1.
Figure 9.
Mode shapes identified using SSI method – Structure A, Test 1.
Figure 10.
Identified monitoring points—Structure B.
Figure 10.
Identified monitoring points—Structure B.
Figure 11.
(a) Accelerometers in position A; (b) accelerometers in position E; (c) accelerometers in position M.
Figure 11.
(a) Accelerometers in position A; (b) accelerometers in position E; (c) accelerometers in position M.
Figure 12.
(a) Accelerometer time-history in point F, x direction; (b) accelerometer time-history in point F, y direction.
Figure 12.
(a) Accelerometer time-history in point F, x direction; (b) accelerometer time-history in point F, y direction.
Figure 13.
(a) Accelerometer time-history in point I, x direction; (b) accelerometer time-history in point F, y direction.
Figure 13.
(a) Accelerometer time-history in point I, x direction; (b) accelerometer time-history in point F, y direction.
Figure 14.
Geometry of Structure B for OMA along with accelerometers positions and directions.
Figure 14.
Geometry of Structure B for OMA along with accelerometers positions and directions.
Figure 15.
OMA identification with EFDD method, Test 3.
Figure 15.
OMA identification with EFDD method, Test 3.
Figure 16.
OMA identification with SSI method, Test 3.
Figure 16.
OMA identification with SSI method, Test 3.
Figure 17.
Mode shapes identified with SSI-UPC method—Structure B, Test 1.
Figure 17.
Mode shapes identified with SSI-UPC method—Structure B, Test 1.
Figure 18.
Three-dimensional (3D) Finite Element Model of the Structure A.
Figure 18.
Three-dimensional (3D) Finite Element Model of the Structure A.
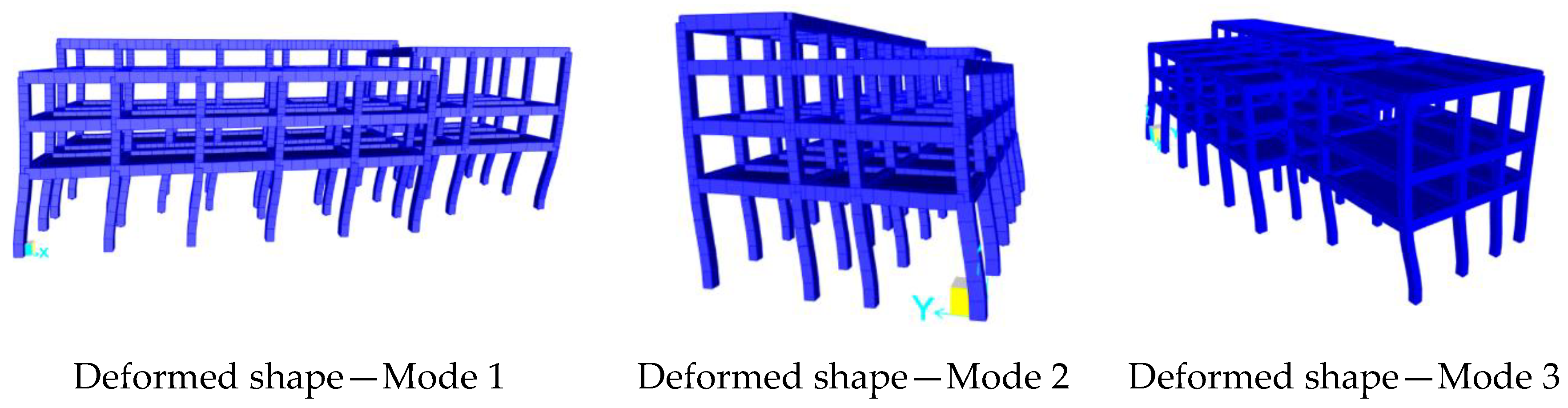
Figure 19.
Modes of vibration of the FE model of Structure A.
Figure 19.
Modes of vibration of the FE model of Structure A.
Figure 20.
3D Finite Element Model of Structure B.
Figure 20.
3D Finite Element Model of Structure B.
Figure 21.
Modes of vibration of the FE model of Structure B.
Figure 21.
Modes of vibration of the FE model of Structure B.
Figure 22.
(a) Acceleration spectrum for seismic action 1; (b) acceleration spectrum for seismic action 2.
Figure 22.
(a) Acceleration spectrum for seismic action 1; (b) acceleration spectrum for seismic action 2.
Figure 23.
Structure B, Test 2, seismic action 2: (a) maximum displacement; (b) maximum interstory drift %.
Figure 23.
Structure B, Test 2, seismic action 2: (a) maximum displacement; (b) maximum interstory drift %.
Table 1.
Experimental identified frequencies (Hz) by SSI and EFDD techniques and mode shape type.
Table 1.
Experimental identified frequencies (Hz) by SSI and EFDD techniques and mode shape type.
| STRUCTURE A. |
|---|
| | | TEST 1 | | TEST 2 | | TEST 3 |
|---|
| MODE | SSI | EFDD | Type | SSI | EFDD | Type | SSI | EFDD | Type |
|---|
| 1 | 8.06 | 8.04 | x_Flex | 8.04 | 8.07 | x_Flex | 8.05 | 8.06 | x_Flex |
| 2 | 9.70 | 9.72 | y_Flex | 9.55 | 9.82 | y_Flex | 9.64 | 9.73 | y_Flex |
| 3 | 11.31 | 11.25 | Tors | 11.40 | 11.39 | Tors | 11.37 | 11.40 | Tors |
Table 2.
Experimental identified frequencies [Hz] with SSI and EFDD techniques and mode shape type.
Table 2.
Experimental identified frequencies [Hz] with SSI and EFDD techniques and mode shape type.
| STRUCTURE B |
|---|
| | TEST 1 | TEST 2 | TEST 3 |
|---|
| MODE | SSI | EFDD | Type | SSI | EFDD | Type | SSI | EFDD | Type |
|---|
| 1 | 3.65 | 3.62 | x_Flex | 3.63 | 3.63 | x_Flex | 3.61 | 3.59 | x_Flex |
| 2 | 3.70 | - | y_Flex | 3.65 | - | y_Flex | 3.67 | 3.72 | y_Flex |
| 3 | 4.23 | 4.24 | Tors | 4.19 | 4.26 | Tors | 4.21 | 4.18 | Tors |
Table 3.
Material properties and elements type adopted in the Finite Element (FE) models—Structure A.
Table 3.
Material properties and elements type adopted in the Finite Element (FE) models—Structure A.
| | Material Properties | Element Type |
|---|
| | Modulus of Elasticity (N/mm2) | Poisson’s Ratio (-) | Density (kN/m3) | Number of Nodes | Number of Frames | Number of Shells |
|---|
| Reinforced Concrete | 31476 | 0.2 | 25 | 237 | 252 | 173 |
| Masonry | 1750 | 0.3 | 15.6 |
Table 4.
Numerical frequencies (f) and mode shape types obtained from the FE model—Structure A.
Table 4.
Numerical frequencies (f) and mode shape types obtained from the FE model—Structure A.
| | FEM | OMA | |
|---|
| MODE | f(Hz) | Type | f (Hz) | Type | Error (%) |
|---|
| 1 | 7.80 | x_Flex | 8.05 | x_Flex | 3.27 |
| 2 | 9.52 | y_Flex | 9.69 | y_Flex | 1.88 |
| 3 | 11.77 | Torsional | 11.35 | Torsional | 4.11 |
Table 5.
Material properties and elements type adopted in the FE models—Structure B.
Table 5.
Material properties and elements type adopted in the FE models—Structure B.
| Material Properties | Element Type |
|---|
| | Modulus of Elasticity (N/mm2) | Poisson’s Ratio (-) | Density (kN/m3) | Number of Nodes | Number of Frames | Number of Shells |
|---|
| Reinforced Concrete | 36416 | 0.2 | 24 | 180 | 322 | - |
Table 6.
Numerical frequencies (f) and mode shape types obtained from the FE model—Structure B.
Table 6.
Numerical frequencies (f) and mode shape types obtained from the FE model—Structure B.
| | FEM | OMA | |
|---|
| MODE | f (Hz) | Type | f(Hz) | Type | Error (%) |
|---|
| 1 | 3.53 | x_Flex | 3.62 | x_Flex | 2.82 |
| 2 | 3.62 | y_Flex | 3.69 | y_Flex | 0.35 |
| 3 | 3.85 | Torsional | 4.22 | Torsional | 8.57 |
Table 7.
Experimental modes residues with SSI technique.
Table 7.
Experimental modes residues with SSI technique.
| STRUCTURE A, TEST 1 |
|---|
| Point/Direction |
|---|
| MODE | Freq. [Hz] | A/x | A/y | C/x | C/y | B/x | B/y | D/x | D/y |
|---|
| 1 | 8.06 | 0.283 | −0.021 | 0.591 | −0.015 | 0.427 | 0.016 | 0.62 | 0.035 |
| 2 | 9.70 | 0.080 | 0.067 | 0.155 | 0.169 | −0.124 | 0.533 | −0.197 | 0.773 |
| 3 | 11.31 | −0.125 | 0.347 | −0.256 | 0.716 | 0.213 | −0.237 | 0.323 | −0.277 |
Table 8.
Maximum displacements [mm] for each point, seismic action 1, combination (100% x, 30% y).
Table 8.
Maximum displacements [mm] for each point, seismic action 1, combination (100% x, 30% y).
| STRUCTURE A, TEST 1 |
|---|
| Direction | Points Maximum Displacements [mm] |
|---|
| 11 | 12 | 13 | 14 | 15 | 16 | 21 | 22 | 23 | 24 | 25 | 26 |
|---|
| x | 1.57 | 1.53 | 1.53 | 1.56 | 1.56 | 1.58 | 2.60 | 2.69 | 2.69 | 2.62 | 2.62 | 2.60 |
| y | 0.34 | 0.24 | 0.34 | 0.24 | 0.20 | 0.20 | 0.55 | 0.46 | 0.55 | 0.46 | 0.40 | 0.40 |
Table 9.
Maximum Interstory Drift [%], seismic action 1, combination (100% x, 30% y).
Table 9.
Maximum Interstory Drift [%], seismic action 1, combination (100% x, 30% y).
| STRUCTURE A, TEST 1 |
|---|
| | | Interstory Drifts [%] |
|---|
| | Points | 22-12 | 23-13 | 24-14 | 25-15 | 26-16 | 21-11 | 16-6 | 11-1 | 14-4 | 15-5 | 13-3 | 12-2 |
|---|
| Direction | | | | | | | | | | | | | |
|---|
| x | 0.47 | 0.47 | 0.43 | 0.43 | 0.42 | 0.42 | 0.35 | 0.35 | 0.35 | 0.35 | 0.34 | 0.34 |
| y | 0.09 | 0.11 | 0.09 | 0.08 | 0.08 | 0.11 | 0.04 | 0.07 | 0.05 | 0.04 | 0.07 | 0.05 |
Table 10.
Maximum displacements [mm] for each point, seismic action 2, combination (100% x, 30% y).
Table 10.
Maximum displacements [mm] for each point, seismic action 2, combination (100% x, 30% y).
| STRUCTURE A, TEST 1 |
|---|
| Direction | Points Maximum Displacements [mm] |
|---|
| 11 | 12 | 13 | 14 | 15 | 16 | 21 | 22 | 23 | 24 | 25 | 26 |
|---|
| x | 0.62 | 0.60 | 0.6 | 0.61 | 0.61 | 0.62 | 1.02 | 1.06 | 1.06 | 1.03 | 1.03 | 1.02 |
| y | 0.13 | 0.09 | 0.13 | 0.09 | 0.08 | 0.08 | 0.21 | 0.18 | 0.21 | 0.18 | 0.16 | 0.16 |
Table 11.
Maximum interstory Drift [%], seismic action 2, combination (100% x, 30% y).
Table 11.
Maximum interstory Drift [%], seismic action 2, combination (100% x, 30% y).
| STRUCTURE A, TEST 1 |
|---|
| | | Interstory Drifts [%] |
|---|
| | Points | 22-12 | 23-13 | 24-14 | 25-15 | 26-16 | 21-11 | 16-6 | 11-1 | 14-4 | 15-5 | 13-3 | 12-2 |
|---|
| Direction | | | | | | | | | | | | | |
|---|
| x | 0.18 | 0.18 | 0.17 | 0.17 | 0.16 | 0.16 | 0.14 | 0.14 | 0.14 | 0.14 | 0.13 | 0.13 |
| y | 0.03 | 0.04 | 0.04 | 0.03 | 0.03 | 0.04 | 0.02 | 0.03 | 0.02 | 0.02 | 0.03 | 0.02 |
Table 12.
Maximum Interstory Drift (ISD) % and operativity indicators IOPS475 and IOPS100 for Operating Limit State (OLS) and Damage Limit State (DLS).
Table 12.
Maximum Interstory Drift (ISD) % and operativity indicators IOPS475 and IOPS100 for Operating Limit State (OLS) and Damage Limit State (DLS).
| STRUCTURE A |
|---|
| TEST 1 | TEST 2 | TEST 3 |
|---|
| OLS | DLS | OLS | DLS | OLS | DLS |
|---|
| ISD% | IOPS475 | ISD% | IOPS100 | ISD% | IOPS475 | ISD% | IOPS100 | ISD% | IOPS475 | ISD% | IOPS100 |
| 0.47 | 2.78 | 0.18 | 7.07 | 0.48 | 2.70 | 0.19 | 6.88 | 0.50 | 2.70 | 0.19 | 6.88 |
Table 13.
Maximum Interstory Drift (ISD) % and operativity indicators IOPS475 and IOPS100 for OLS and DLS, respectively.
Table 13.
Maximum Interstory Drift (ISD) % and operativity indicators IOPS475 and IOPS100 for OLS and DLS, respectively.
| STRUCTURE A—FE MODEL |
|---|
| OLS | DLS |
|---|
| ISD% | IOPS475 | ISD% | IOPS100 |
| 0.43 | 2.60 | 0.17 | 6.57 |
Table 14.
Maximum Interstory Drift (ISD) % and operativity indicators IOPS475 and IOPS100 for OLS and DLS.
Table 14.
Maximum Interstory Drift (ISD) % and operativity indicators IOPS475 and IOPS100 for OLS and DLS.
| STRUCTURE B |
|---|
| TEST 1 | TEST 2 | TEST 3 |
|---|
| OLS | DLS | OLS | DLS | OLS | DLS |
|---|
| ISD% | IOPS475 | ISD% | IOPS100 | ISD% | IOPS475 | ISD% | IOPS100 | ISD% | IOPS475 | ISD% | IOPS100 |
| 4.4 | 0.76 | 1.83 | 1.83 | 2.36 | 0.81 | 1.04 | 1.83 | 1.99 | 1.49 | 0.90 | 3.3 |
Table 15.
Maximum Interstory Drift (ISD) % and operativity indicators IOPS475 and IOPS100 for OLS and DLS.
Table 15.
Maximum Interstory Drift (ISD) % and operativity indicators IOPS475 and IOPS100 for OLS and DLS.
| STRUCTURE B—FE MODEL |
|---|
| OLS | DLS |
|---|
| ISD % | IOPS475 | ISD% | IOPS100 |
| 1.53 | 1.38 | 0.69 | 3.05 |