Multi-Field Interference Simultaneously Imaging on Single Image for Dynamic Surface Measurement
Abstract
1. Introduction
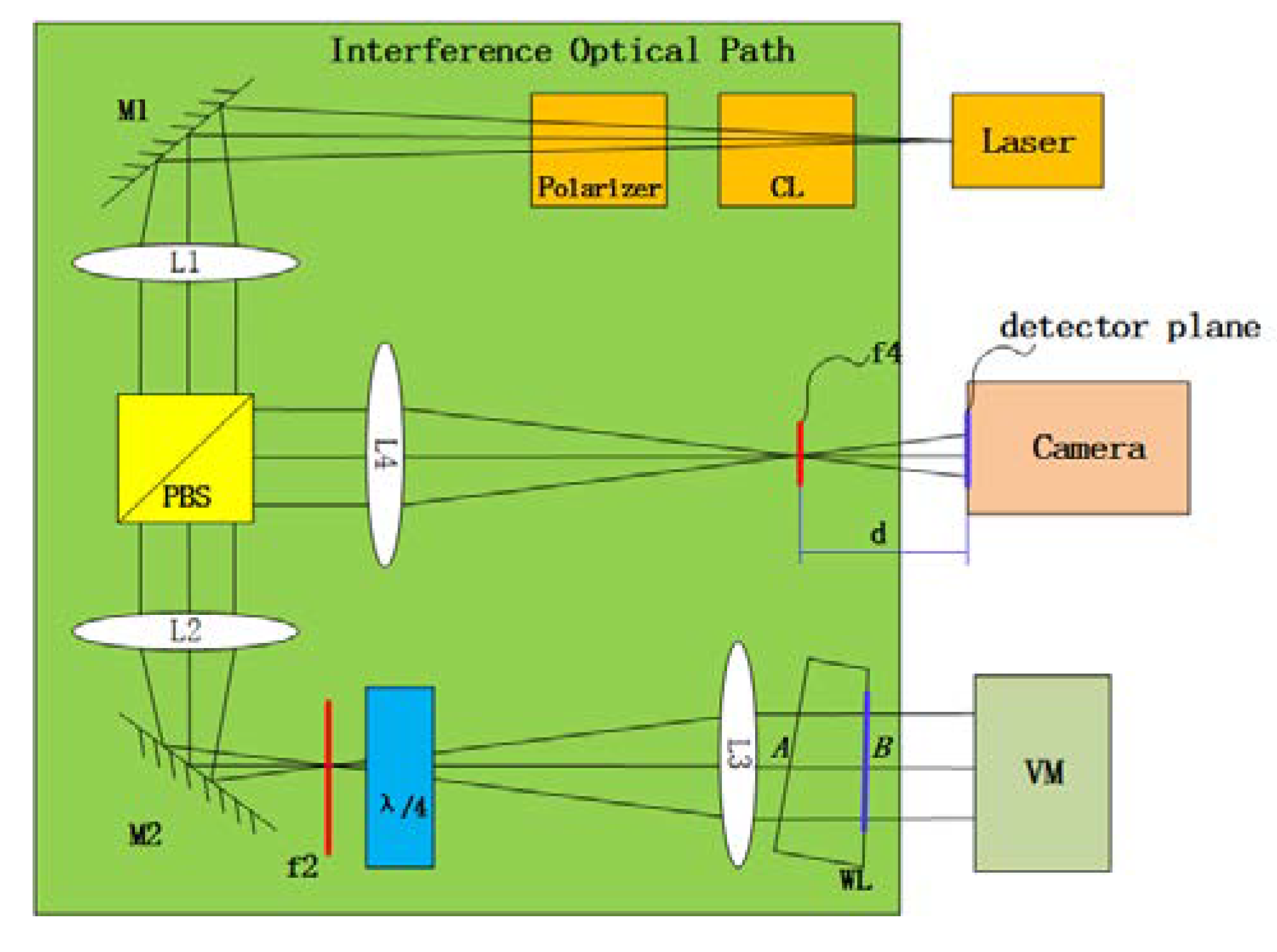
2. Multi-Field Interference Imaging Setup
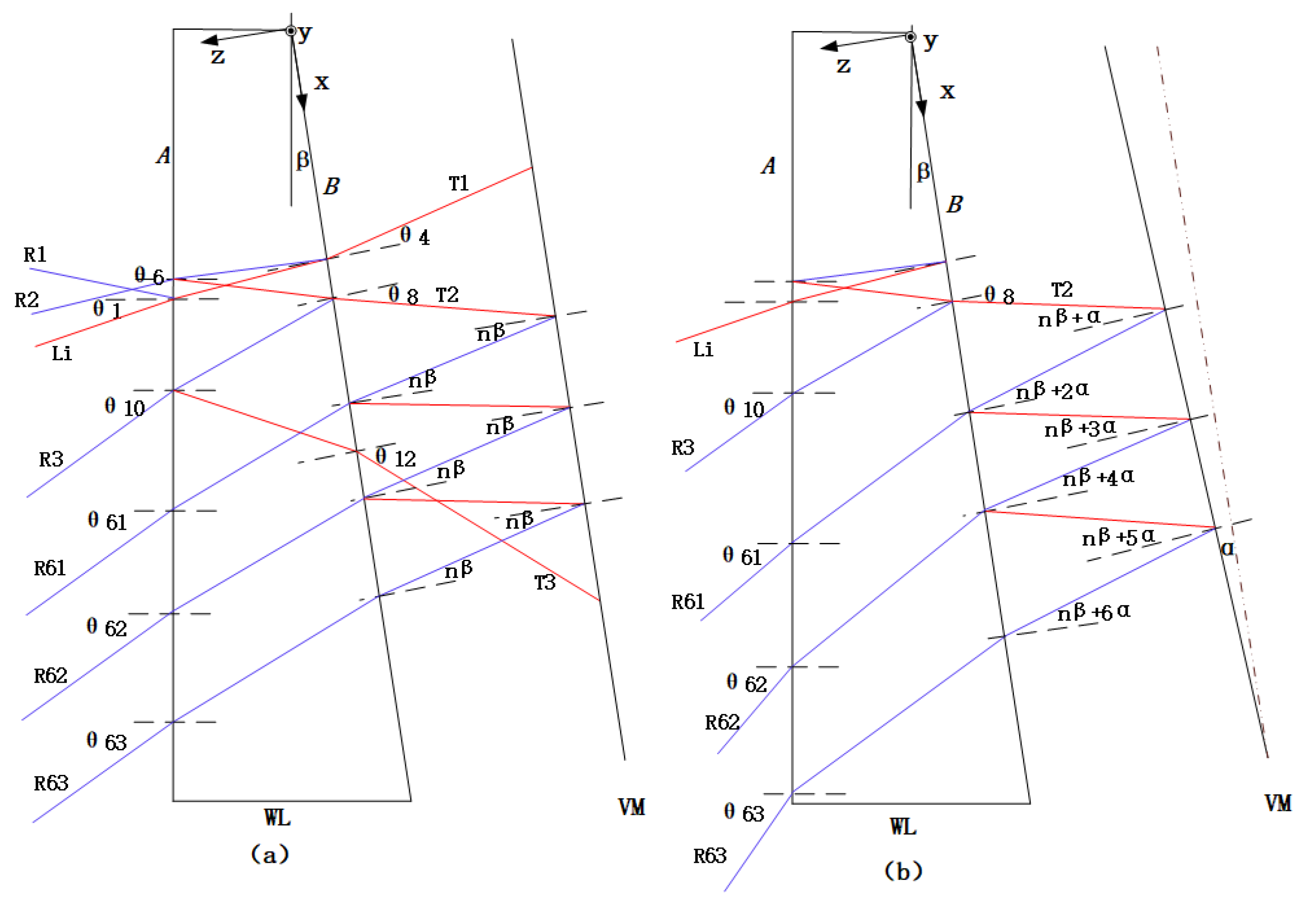
3. Principle of Multi-Field Interference
4. Results
4.1. Experimental Establishment
4.2. Results and Discussion
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
Appendix C
References
- Han, W.; Fan, Z.; Le, B.; Huang, T.; Zhao, R.; Liu, B.; Gao, X. A 3 kHz High-Frequency Vibration Mirror Based on Resonant Mode. Acta Microsc. 2020, 29, 1866–1879. [Google Scholar]
- Wang, X.; Liao, S.; Shen, M.; Huang, J. Real time background deduction with a scanning mirror. Opto-Electron. Eng. 2005, 32, 9–11. [Google Scholar]
- Antonin, M.; Jiri, N. Analysis of imaging properties of a vibrating thin flat mirror. J. Opt. Soc. Am. A 2004, 21, 1724–1729. [Google Scholar]
- Li, Q.; Feng, H.; Xu, Z.; Han, Y.; Huang, H. Review of computer stereo vision technique. Opt. Tech. 1999, 5, 71–73. [Google Scholar]
- Hsueh, W.J. 3D Surface Digitizing and Modeling Development at ITRI. Proc. SPIE 2000, 4080, 14–20. [Google Scholar]
- Addison, A.C. Virtualized Architectural Heritage: New Tools and Techniques. IEEE Multimedia 2000, 7, 26–31. [Google Scholar] [CrossRef]
- Hu, Z. Flexible Measuring Equipment 3 Coordinate Measuring Machine. Precise Manuf. Autom. 2006, 2, 57–58. [Google Scholar]
- Zhang, X.; Liu, J.; Xia, X. Design of Deep-sea Sonar Altimeter Based on PIC16C74. Microcomput. Inf. 2008, 24, 126–127. [Google Scholar]
- Chen, F.; Brown, G.M.; Song, M. Overview of Three-Dimensional Shape Measurement Using Optical Methods. Opt. Eng. 2000, 39, 10–22. [Google Scholar]
- Lu, Y. Progress on Laser Phase-shift Interferometry. Laser Infrared 1990, 20, 13–15. [Google Scholar]
- John, B.; Haubecker, H.; Geibler, P. Handbook of Computer Vision and Applications; Academic Press: Cardiff, UK, 1999. [Google Scholar]
- Gorthi, S.S.; Rastogi, P. Fringe projection techniques: Whither we are? Opt. Lasers Eng. 2010, 48, 133–140. [Google Scholar] [CrossRef]
- Salvi, J.; Pages, J.; Battle, J. Pattern codification strategies in structured light systems. Pattern Recognit. 2004, 37, 827–849. [Google Scholar] [CrossRef]
- Xian, T.; Su, X. Area modulation grating for sinusoidal structure illumination on phase-measuring profilometry. Appl. Opt. 2001, 40, 1201–1206. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Quan, C.; Tay, C.J.; Fu, Y. Shape measurement using one frame projected saw tooth fringe pattern. Opt. Commun. 2005, 246, 275–284. [Google Scholar] [CrossRef]
- Frank, O.C.; Ryan, P.; Wellesley, E.P.; John, K.; Jason, C. A passive optical technique to measure physical properties of a vibrating surface. Proc. SPIE 2014, 9219, 1–12. [Google Scholar]
- Massie, N.A.; Nelson, R.D.; Holly, S. High-performance real-time heterodyne interferometry. Appl. Opt. 1974, 18, 1797–1803. [Google Scholar] [CrossRef]
- John, E.G. Sub-Nyquist interferometry. Appl. Opt. 1987, 26, 5245–5258. [Google Scholar]
- John, E.G.; Andrew, E.L.; Russell, J.P. Sub-Nyquist interferometry: Implementation and measurement capability. Opt. Eng. 1996, 35, 2962–2969. [Google Scholar]
- Manuel, S.; Juan, A.Q.; Jose, M. General n-dimensional quadrature transform and its application to interferogram demodulation. J. Opt. Soc. Am. 2003, 20, 925–934. [Google Scholar]
- Marc, T.; Paul, D.; Greg, F. Sub-aperture approaches for asphere polishing and metrology. Proc. SPIE 2005, 5638, 284–299. [Google Scholar]
- Liu, H.; Hao, Q.; Zhu, Q.; Sha, D.; Zhang, C. A novel aspheric surface testing method using part-compensating lens. Proc. SPIE 2005, 5638, 324–329. [Google Scholar]
- Dumas, P.; Hall, C.; Hallock, B.; Tricard, M. Complete sub-aperture pre-polishing and finishing solution to improve speed and determinism in asphere manufacture. Proc. SPIE 2007, 6671, 667111. [Google Scholar]
- Liu, D.; Yang, Y.; Tian, C.; Luo, Y.; Wang, L. Practical methods for retrace error correction in nonnull aspheric testing. Opt. Express 2009, 17, 7025–7035. [Google Scholar] [CrossRef] [PubMed]
- Garbusi, E.; Baer, G.; Osten, W. Advanced studies on the measurement of aspheres and freeform surfaces with the tilted-wave interferometer. Proc. SPIE 2011, 8082, 80821F. [Google Scholar]
- Liu, D.; Shi, T.; Zhang, L.; Yang, Y.; Chong, S.; Shen, Y. Reverse optimization reconstruction of aspheric figure error in a non-null interferometer. Appl. Opt. 2014, 53, 5538–5546. [Google Scholar] [CrossRef]
- Saif, B.; Chaney, D.; Smith, W.; Greenfield, P.; Hack, W.; Bluth, J.; Feinberg, L. Nanometer level characterization of the James Webb Space Telescope optomechanical systems using high-speed interferometry. Appl. Opt. 2015, 54, 4285–4298. [Google Scholar] [CrossRef]
- Fortmeier, I.; Stavridis, M.; Wiegmann, A.; Schulz, M.; Osten, W.; Elster, C. Evaluation of absolute form measurements using a tilted-wave interferometer. Opt. Express 2016, 24, 3393–3404. [Google Scholar] [CrossRef]
- Hao, Q.; Wang, S.; Hu, Y.; Cheng, H.; Chen, M.; Li, T. Virtual interferometer calibration method of a non-null interferometer for freeform surface measurements. Appl. Opt. 2016, 55, 9992–10001. [Google Scholar] [CrossRef]
- Hao, Q.; Li, T.; Hu, Y.; Wang, S.; Ning, Y.; Tan, Y.; Zhang, X. Vertex radius of curvature error measurement of aspheric surface based on slope asphericity in partial compensation interferometry. Opt. Express 2017, 25, 18107–18121. [Google Scholar] [CrossRef]
- Hao, Q.; Wang, S.; Hu, Y.; Tan, Y.; Li, T.; Wang, S. Two-step carrier-wave stitching method for aspheric and freeform surface measurement with a standard spherical interferometer. Appl. Opt. 2018, 57, 4743–4750. [Google Scholar] [CrossRef]
- Chen, F.; Griffen, C.T.; Allen, T.E.; Brown, G.M. Measurement of shape and vibration using a single electronic speckle interferometry. Proc. SPIE 1996, 2860, 150–161. [Google Scholar]
- De Veuster, C.; Renotte, Y.L.; Berwart, L.; Lion, Y.F. Quantitative three-dimensional measurements of vibration amplitudes and phases as a function of frequency by Digital Speckle Pattern Interferometry. SPIE 1998, 3478, 322–333. [Google Scholar]
- Burning, J.H.; Herriott, D.R.; Gallagher, J.E.; Rosenfeld, D.P.; White, A.D.; Brangaccio, D.J. Digital Wave Front Measuring Interferometer for Testing Optical Surfaces and Lenses. Appl. Opt. 1974, 13, 2693–2703. [Google Scholar] [CrossRef] [PubMed]
- Dorband, B. Die 3-Interferogramm Method zur automatischen Streifenauswertung in rechnergesteuerten digitalten zweistrahlinterometern. Optik 1982, 60, 161–174. [Google Scholar]
- Wingerden, J.; Frankena, H.; Smorenburg, C. Linear approximation for measurement errors in phase shifting interferometry. Appl. Opt. 1991, 30, 2718–2729. [Google Scholar] [CrossRef]
- Baker, K.; Stappaerts, E. A single-shot pixellated phase-shifting interferometer utilizing a liquid-crystal spatial light modulator. Opt. Lett. 2006, 31, 733–735. [Google Scholar] [CrossRef]
- Styk, A.; Patorski, K. Analysis of systematic errors in spatial carrier phase shifting applied to interferogram intensity modulation determination. Appl. Opt. 2007, 46, 4613–4624. [Google Scholar] [CrossRef]
- Xu, J.; Xu, Q.; Chai, L. Tilt-shift determination and compensation in phase-shifting interferometry. J. Opt. A 2008, 10, 075011. [Google Scholar] [CrossRef]
- Abdelsalam, D.; Yao, B.; Gao, P.; Min, J.; Guo, R. Single-shot parallel four-step phase shifting using on-axis Fizeau interferometry. Appl. Opt. 2012, 51, 4891–4895. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Y.; Ji, F.; He, J. A three-step least-squares iterative method for tilt phase-shift interferometry. Opt. Express 2013, 21, 29505–29515. [Google Scholar] [CrossRef]
- Deck, L. Model-based phase shifting interferometry. Appl. Opt. 2014, 53, 4628–4636. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Wang, Y.; He, J.; Ji, F. Modified three-step iterative algorithm for phase-shifting interferometry in the presence of vibration. Appl. Opt. 2015, 54, 5833–5841. [Google Scholar] [CrossRef] [PubMed]
- Pramod, R.; Erwin, H. Phase Estimation in Optical Interferometry; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Jiri, N.; Pavel, N.; Antonin, M. Multi-step Phase-shifting Algorithms Insensitive to Linear Phase Shift Errors. Opt. Commun. 2008, 281, 5302–5309. [Google Scholar]
- Jiri, N. Five-Step Phase-Shifting Algorithms with Unknown Values of Phase Shift. Optik 2003, 114, 63–68. [Google Scholar]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Wang, W. Contemporary Optical Measurement Technology; China Machine Press: Beijing, China, 2013. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 1975. [Google Scholar]
- Hariharan, P.I. Basics of Interferometry; Academic Press: Boston, MA, USA, 1992. [Google Scholar]
- Han, W.; Gao, X.; Fan, Z.; Bai, L.; Liu, B. Long Exposure Short Pulse Synchronous Phase Lock Method for Capturing High Dynamic Surface Shape. Sensors 2020, 20, 2550. [Google Scholar] [CrossRef]







| Parameter | Value | Unit |
|---|---|---|
| Wavelength | 532 | nm |
| Repetition frequency | 10–200 | Hz |
| Pulse duration | 6–129 | ns |
| Pixel size | 5.5 | um |
| Resolution | 2048 × 2048 | pixels |
| Frame rate | 10 | fps |
| Integration Time | 100 | ms |
| Lens L1 focal length | 200 | mm |
| Lens L2 focal length | 200 | mm |
| Lens L3 focal length | 380 | mm |
| Lens L4 aperture | 40 | mm |
| Lens L4 focal length | 180 | mm |
| LRF | S1 | S2 | S3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SGmax | SGmin | SCR | SGmax | SGmin | SCR | SGmax | SGmin | SCR | |
| 200 | 4095 | 331 | 0.91 | 3743 | 587 | 0.78 | 686 | 210 | 0.80 |
| 100 | 2054 | 300 | 0.85 | 2026 | 387 | 0.78 | 307 | 166 | 0.82 |
| 50 | 990 | 190 | 0.91 | 991 | 257 | 0.77 | 246 | 155 | 0.90 |
| 20 | 492 | 160 | 0.94 | 481 | 176 | 0.85 | 166 | 153 | 0.68 |
| 10 | 317 | 155 | 0.94 | 307 | 160 | 0.88 | 158 | 153 | 0.55 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, W.; Gao, X.; Chen, Z.; Bai, L.; Liu, B.; Zhao, R. Multi-Field Interference Simultaneously Imaging on Single Image for Dynamic Surface Measurement. Sensors 2020, 20, 3372. https://doi.org/10.3390/s20123372
Han W, Gao X, Chen Z, Bai L, Liu B, Zhao R. Multi-Field Interference Simultaneously Imaging on Single Image for Dynamic Surface Measurement. Sensors. 2020; 20(12):3372. https://doi.org/10.3390/s20123372
Chicago/Turabian StyleHan, Weiqiang, Xiaodong Gao, Zhen Chen, Le Bai, Bo Liu, and Rujin Zhao. 2020. "Multi-Field Interference Simultaneously Imaging on Single Image for Dynamic Surface Measurement" Sensors 20, no. 12: 3372. https://doi.org/10.3390/s20123372
APA StyleHan, W., Gao, X., Chen, Z., Bai, L., Liu, B., & Zhao, R. (2020). Multi-Field Interference Simultaneously Imaging on Single Image for Dynamic Surface Measurement. Sensors, 20(12), 3372. https://doi.org/10.3390/s20123372







