Implementation and Performance of a Deeply-Coupled GNSS Receiver with Low-Cost MEMS Inertial Sensors for Vehicle Urban Navigation
Abstract
:1. Introduction
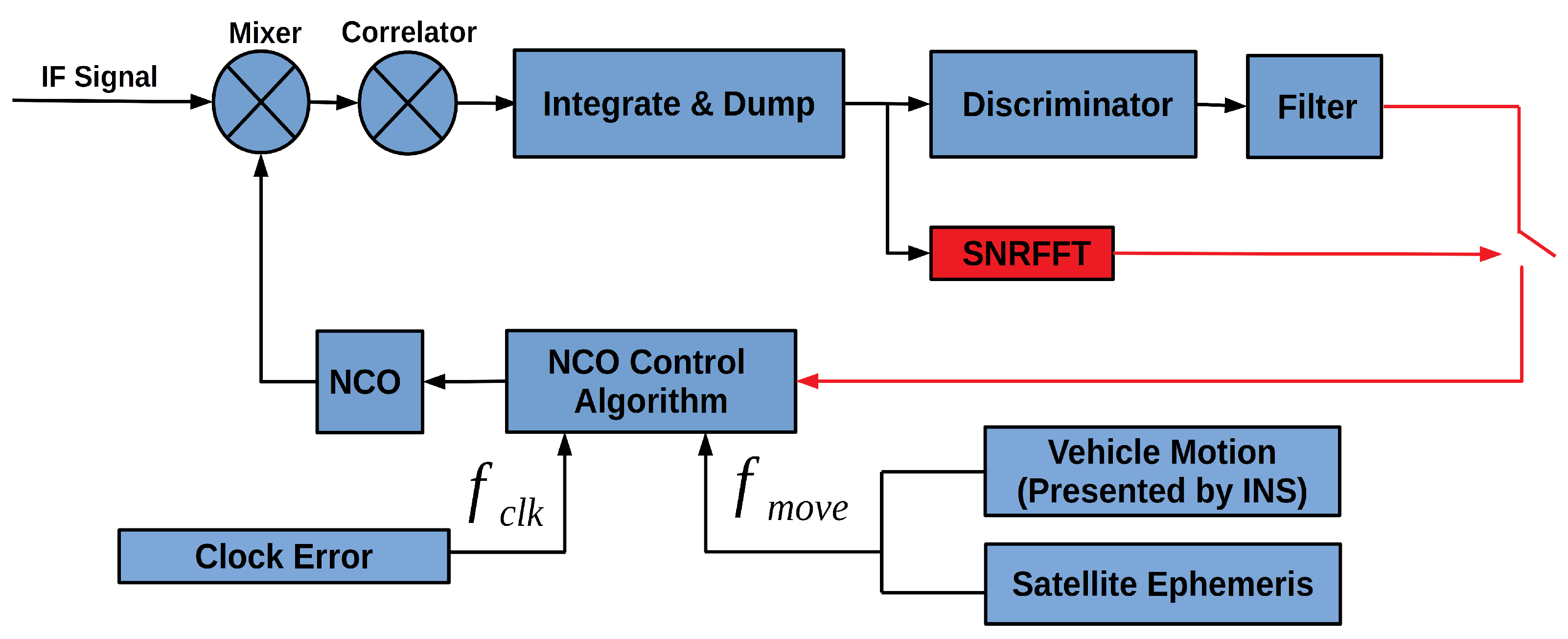
2. GNSS/INS Deeply-Coupled Software-Defined Receiver Implementation
2.1. Overview
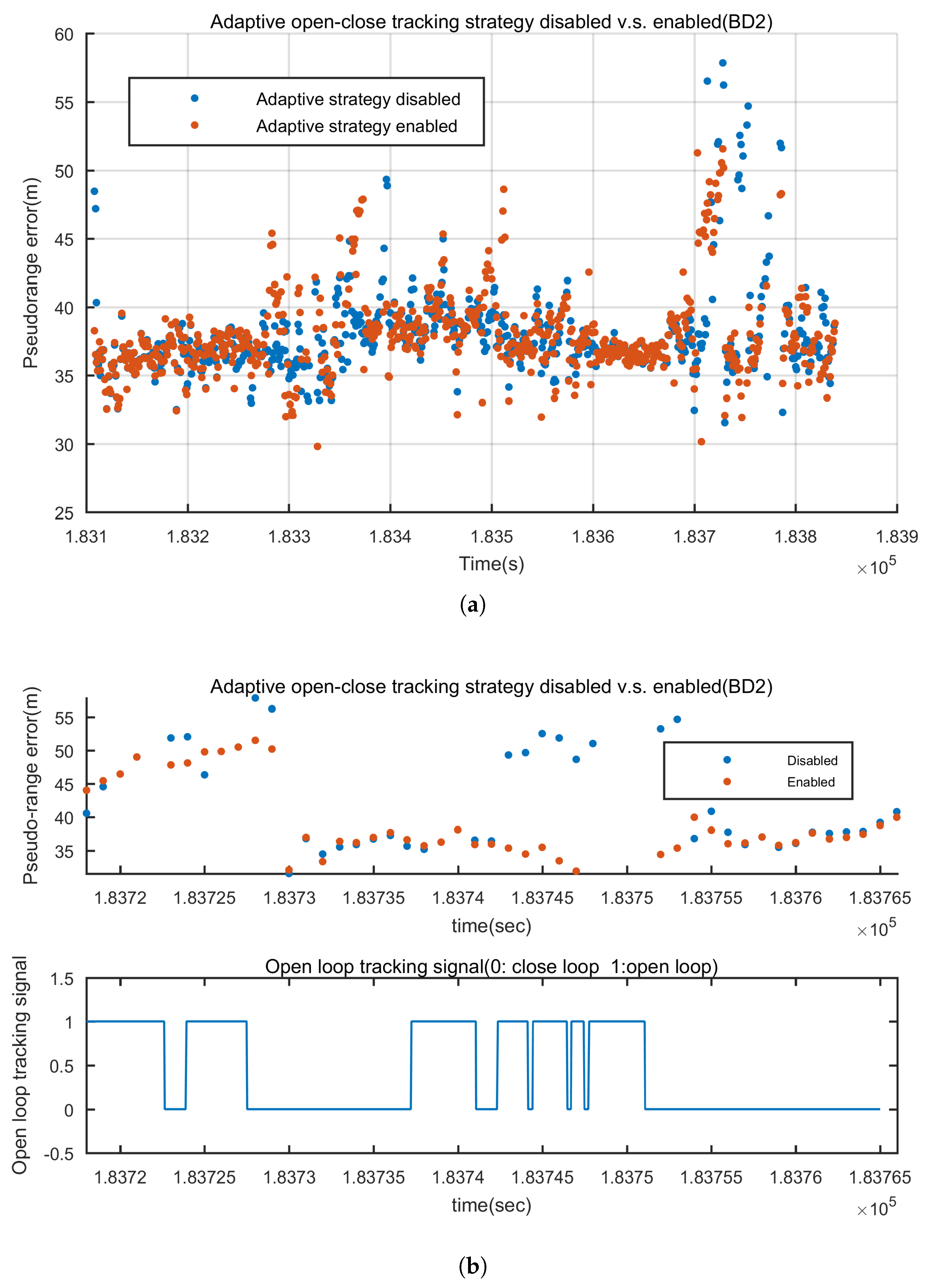
2.2. Adaptive Open-Close Loop Strategy
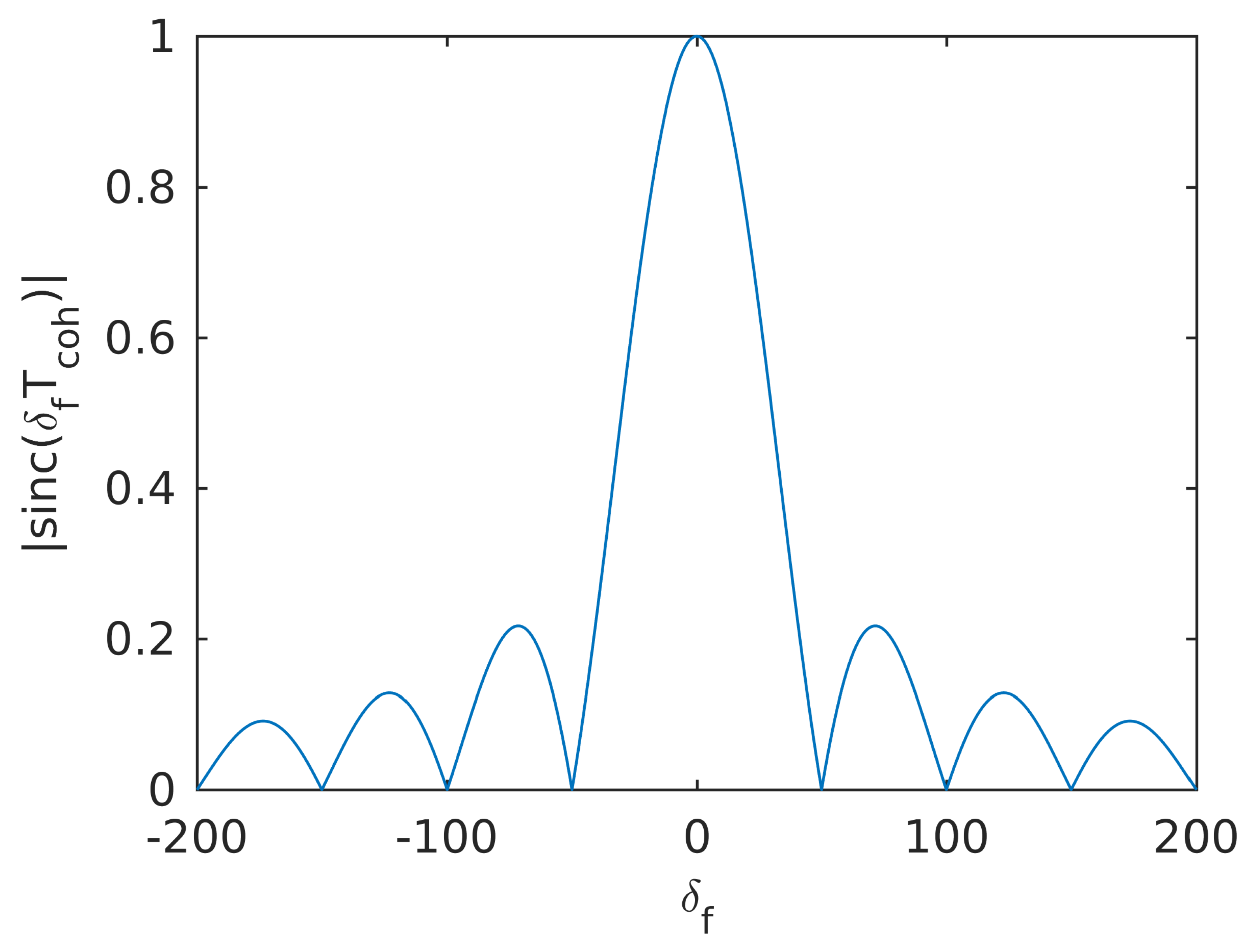
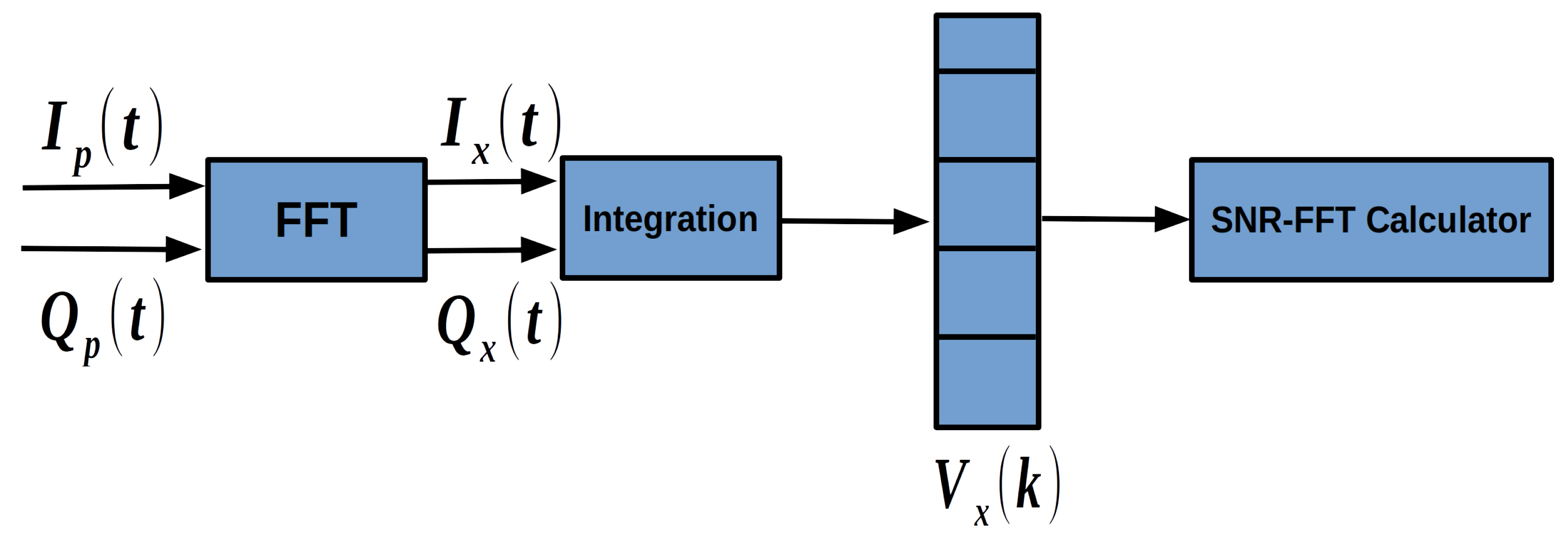
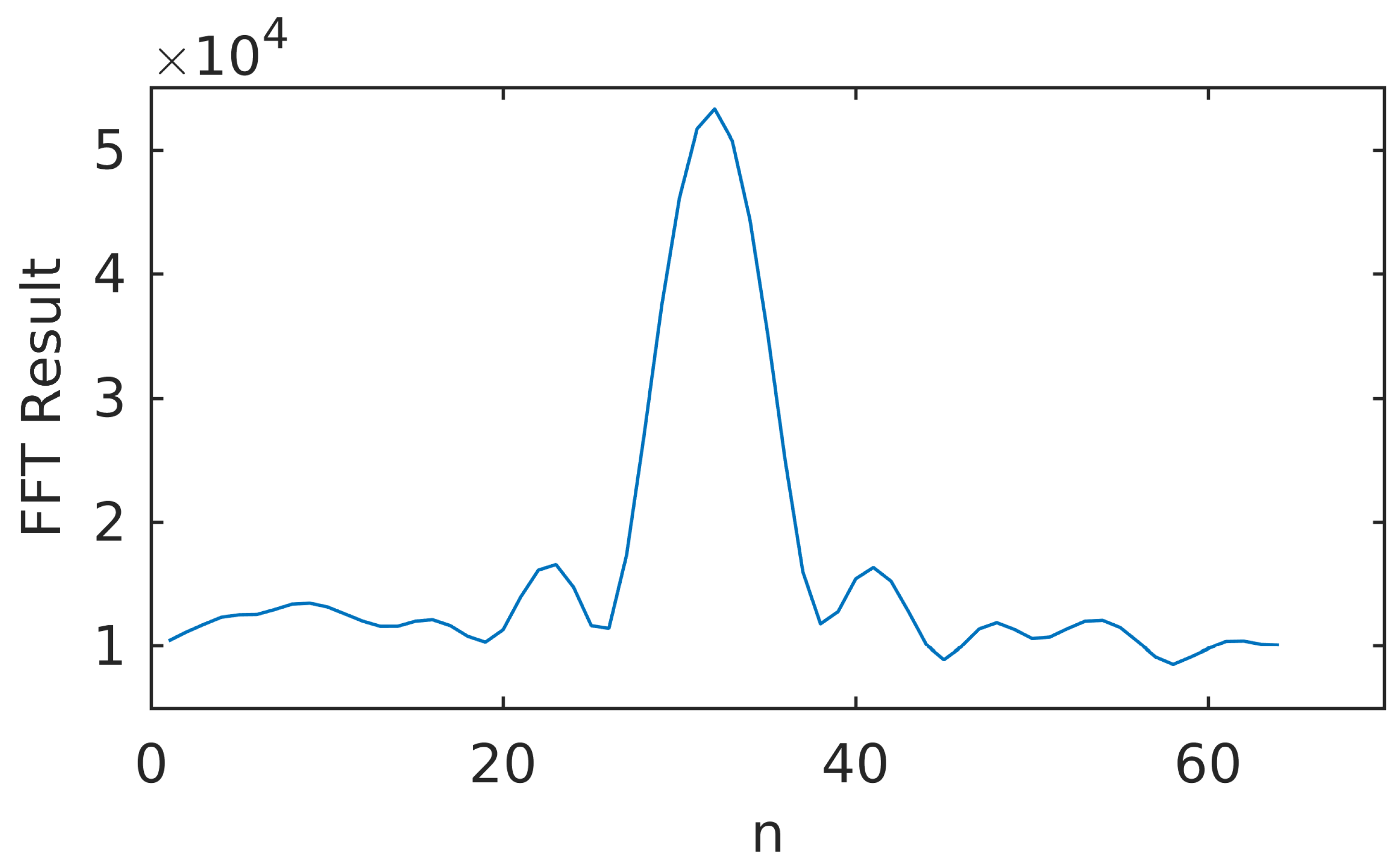
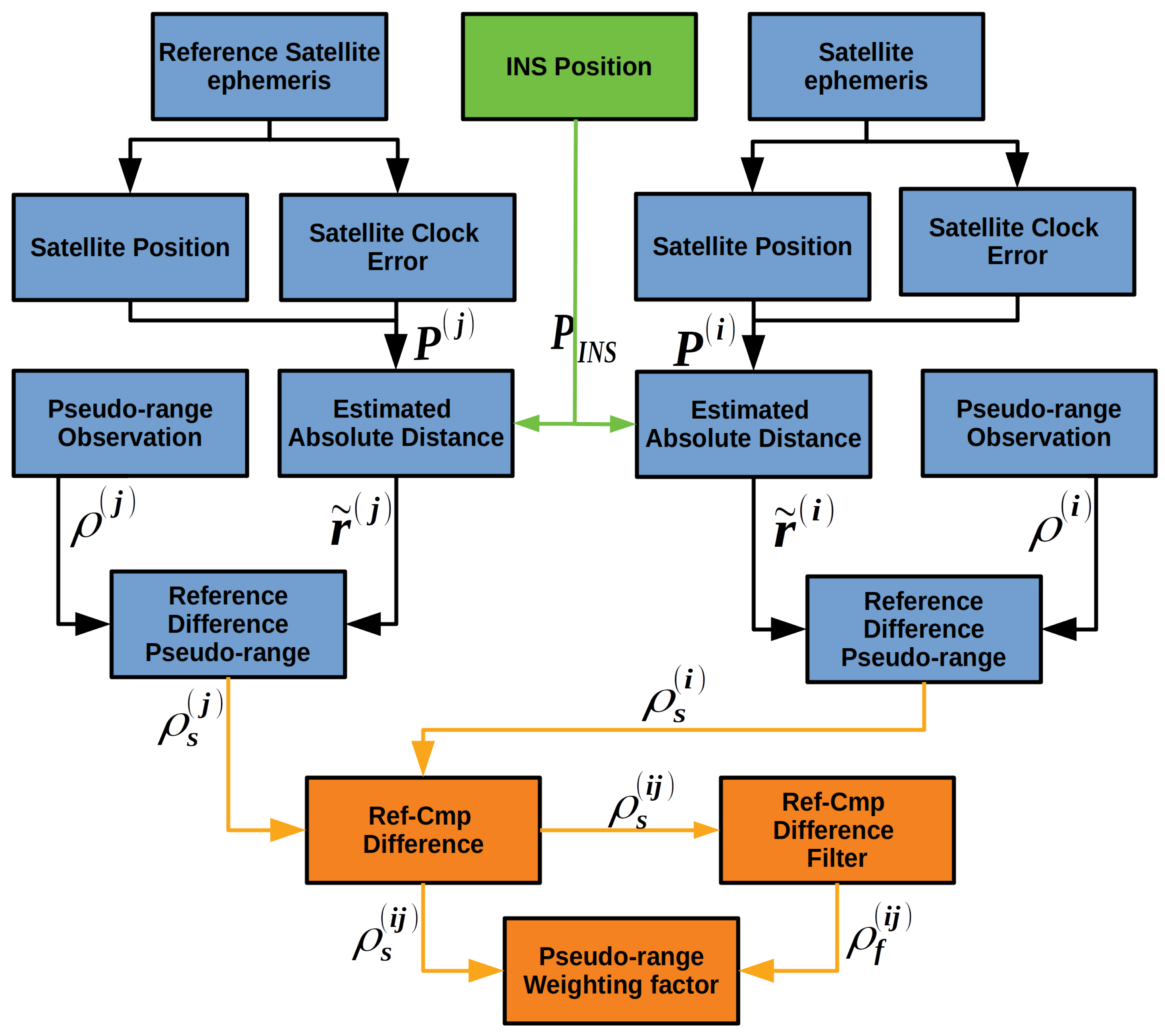
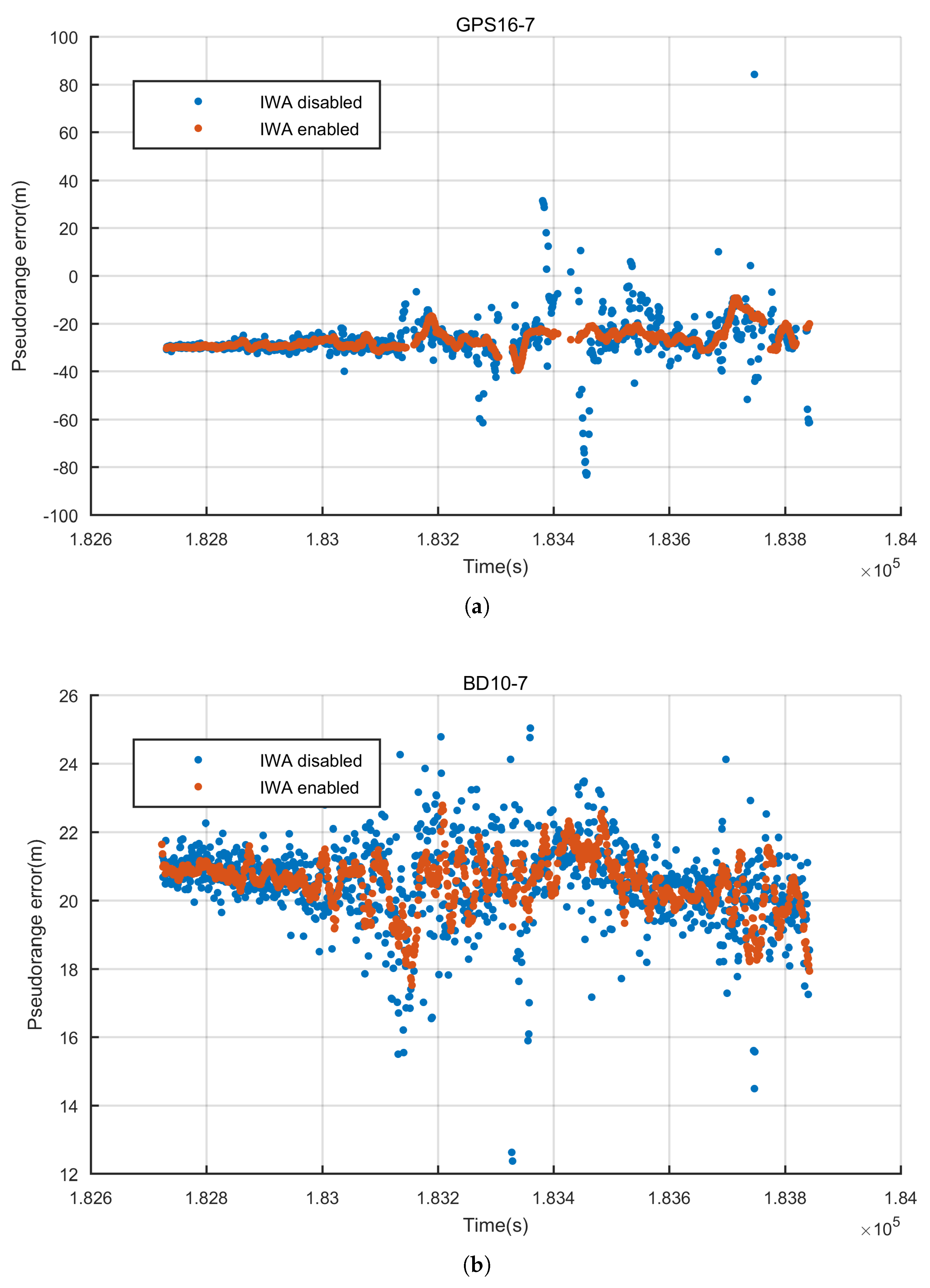
2.3. INS Aided Pseudo-Range Weight Control Algorithm
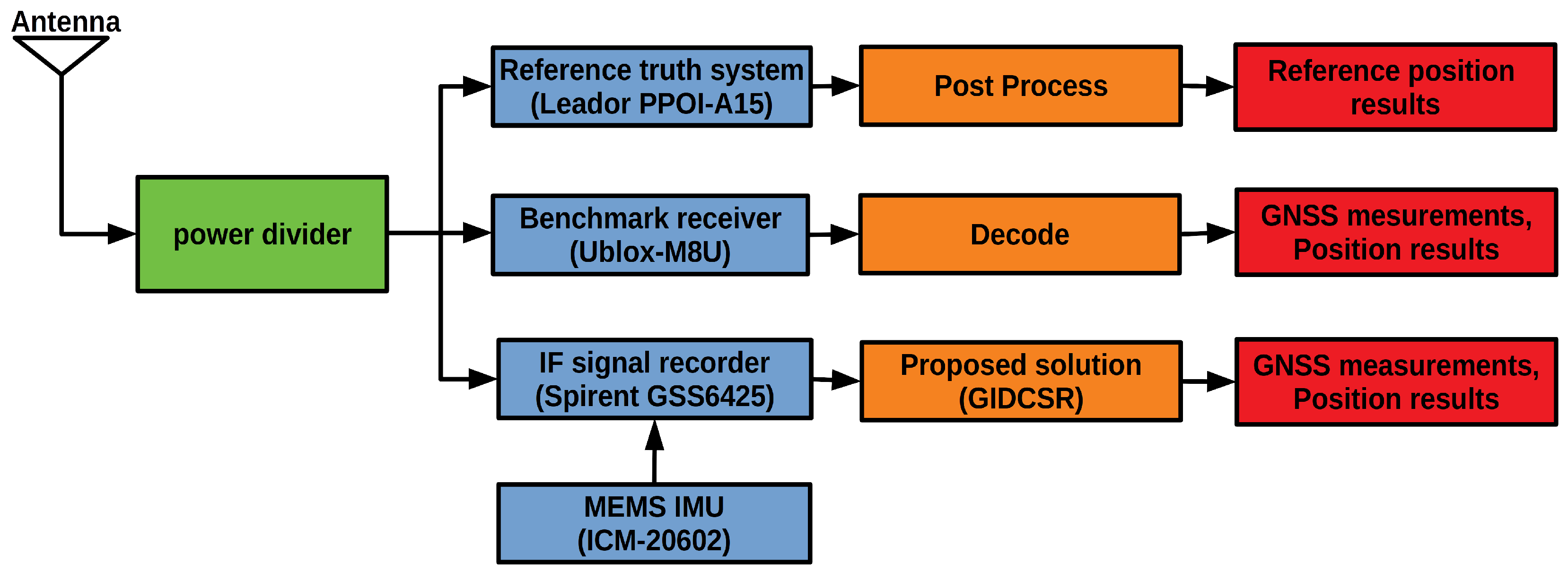
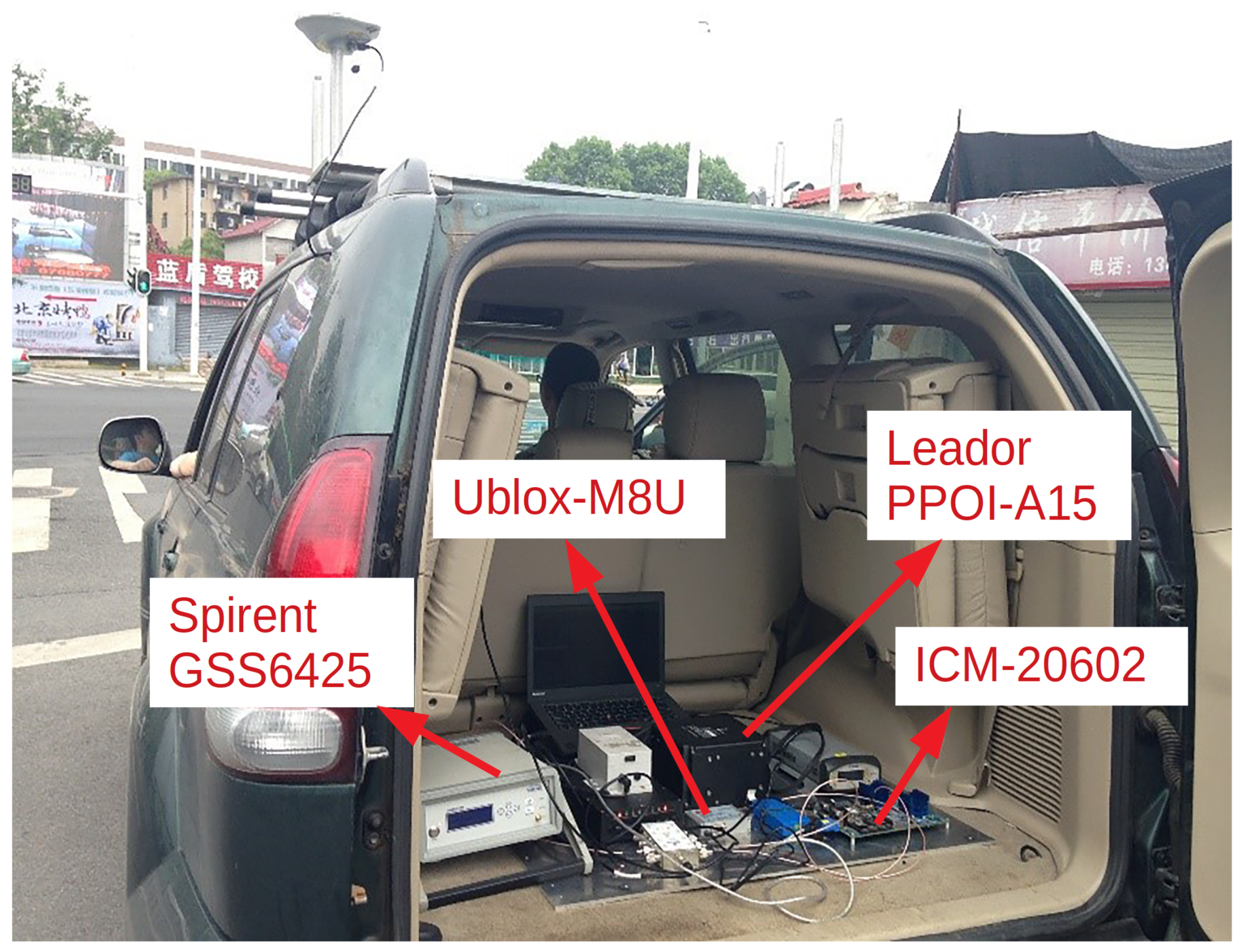
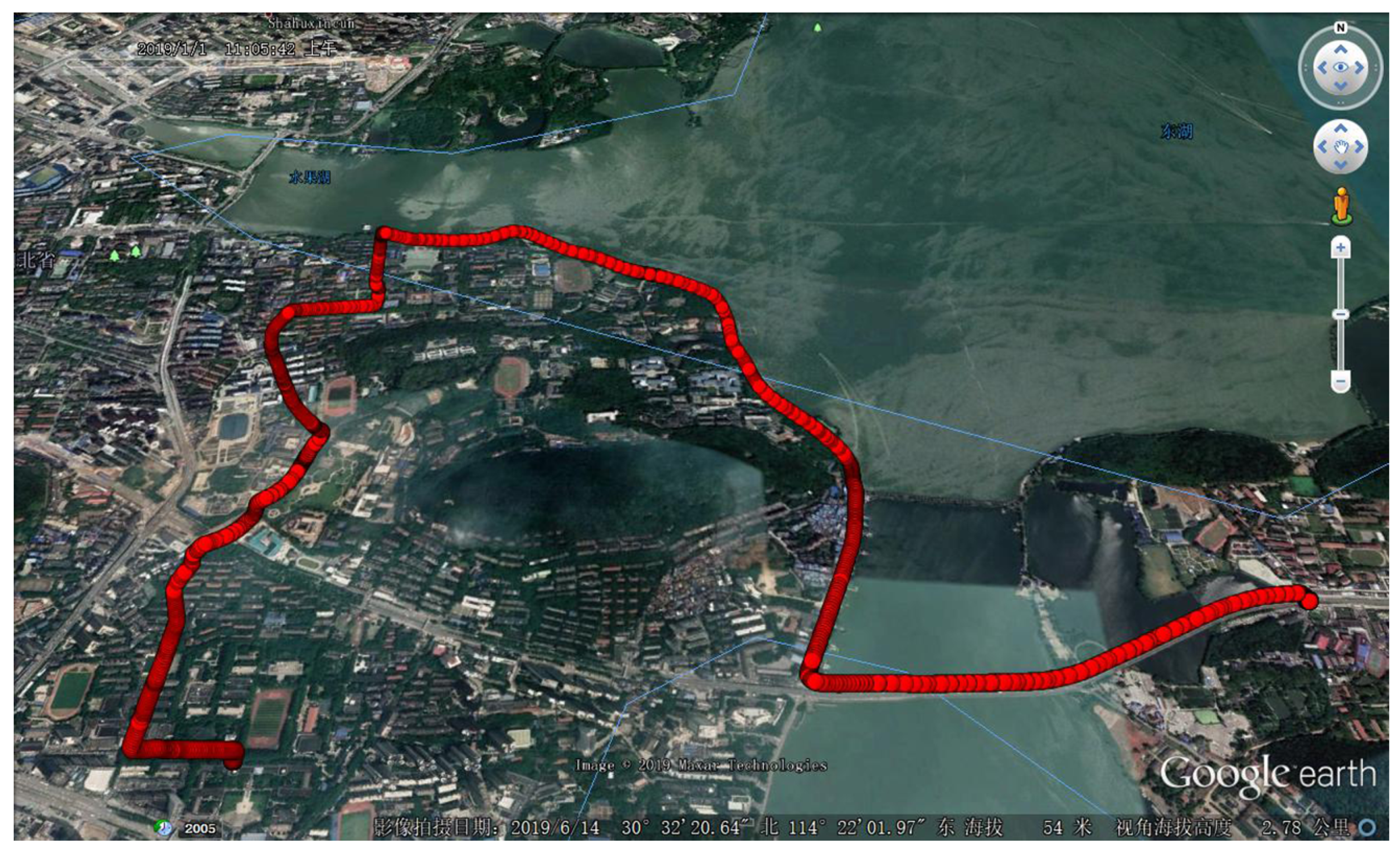
3. Experiment Setup
4. Experiment Results and Analysis
4.1. Deep Couple Performance Analysis
4.1.1. Adaptive Open-Close Tracking Loops Analysis
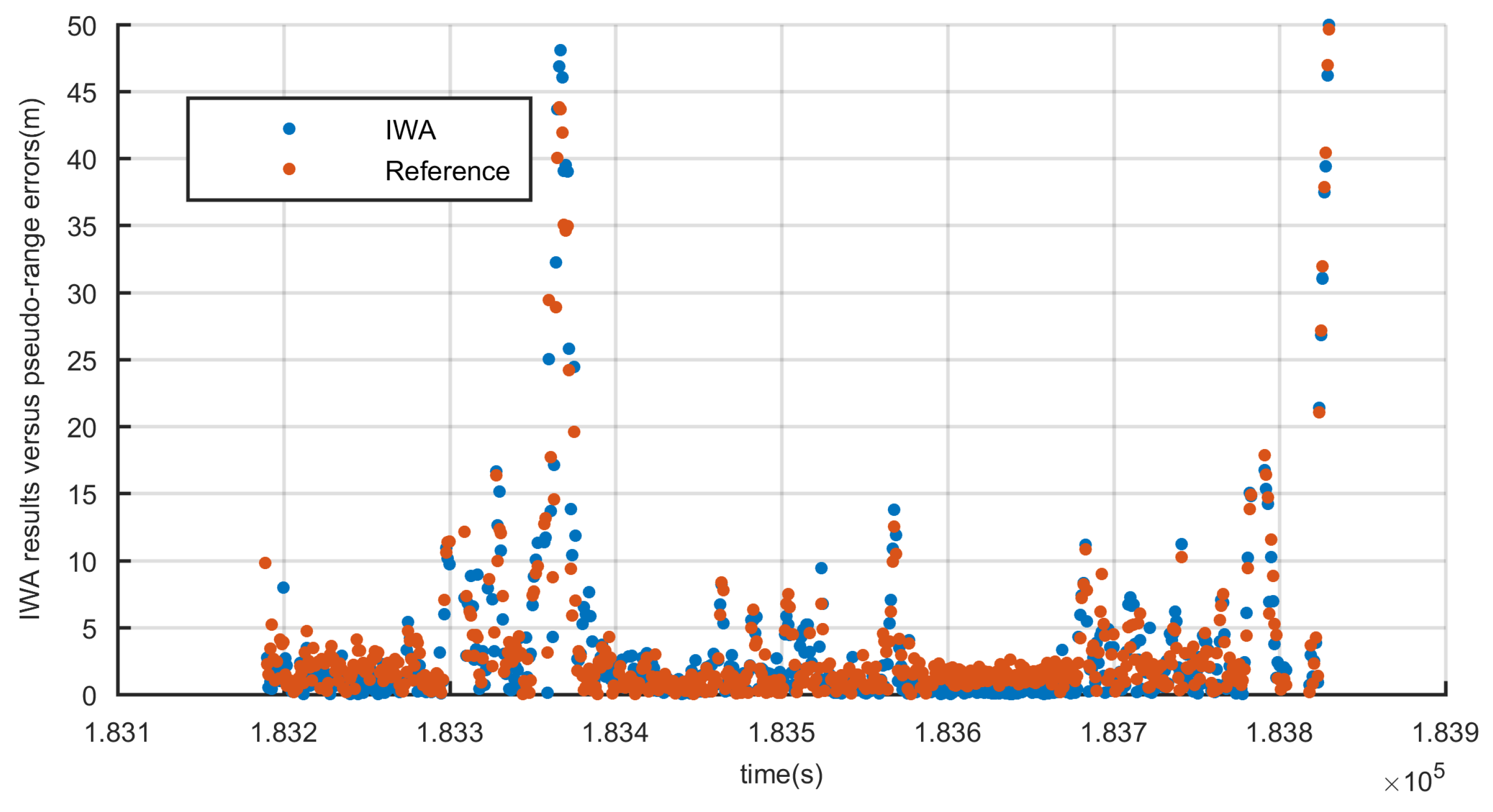
4.1.2. INS Aided Pseudo-Range Weight Control Algorithm Analysis
4.1.3. Deep Couple Positioning Analysis
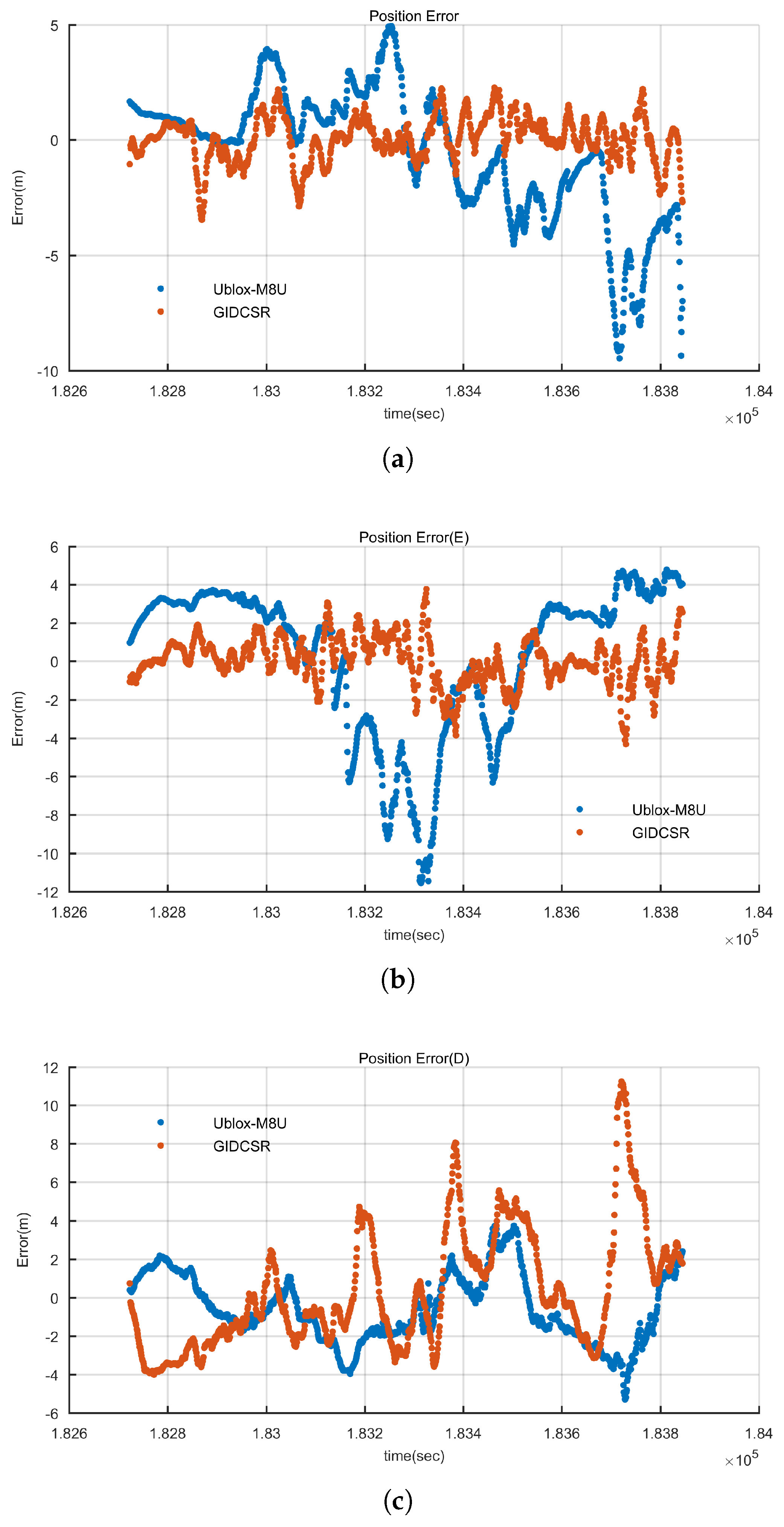
4.2. Experiment Results Comparison Between GIDCSR and M8U
4.2.1. Pseudo-Range Error Analysis
4.2.2. GNSS Positioning Analysis
4.2.3. GNSS/INS Integration Result Analysis
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Reid, T.G.R.; Houts, S.E.; Cammarata, R.; Mills, G.; Agarwal, S.; Vora, A.; Pandey, G. Localization requirements for autonomous vehicles. arXiv 2019, arXiv:1906.01061. [Google Scholar] [CrossRef] [Green Version]
- Gutierrez, P. u-blox ZED-F9K Offers Continuous Lane-Accurate Positioning in All Environments. Available online: https://insideunmannedsystems.com/u-blox-zed-f9k-offers-continuous-lane-accurate-positioning-in-all-environments/ (accessed on 2 May 2019).
- Humphreys, T.E.; Murrian, M.J.; Narula, L. Deep urban unaided precise gnss vehicle positioning. arXiv 2019, arXiv:1906.09539. [Google Scholar]
- Darbha, S.; Konduri, S.; Pagilla, P.R. Benefits of v2v communication for autonomous and connected vehicles. IEEE Trans. Intell. Trans. Syst. 2018, 20, 1954–1963. [Google Scholar] [CrossRef] [Green Version]
- Soloviev, A.; Veth, M.; Yang, C. Plug and play sensor fusion for lane-level positioning of connected cars in gnss-challenged environments. GPS World 2016, 27, 49. [Google Scholar]
- Grejner-Brzezinska, D.A.; Toth, C.K.; Moore, T.; Raquet, J.F.; Miller, M.M.; Kealy, A. Multisensor navigation systems: A remedy for gnss vulnerabilities? Proc. IEEE 2016, 104, 1339–1353. [Google Scholar] [CrossRef]
- Groves, P.D. The complexity problem in future multisensor navigation and positioning systems: A modular solution. J. Navig. 2014, 67, 311–326. [Google Scholar] [CrossRef] [Green Version]
- Parkinson, B. Assuredpntforourfuture: Pta. Available online: https://www.gpsworld.com/assured-pnt-for-our-future-pta/ (accessed on 20 February 2020).
- Yuanxi, Y. Concepts of comprehensive pnt and related key technologies. Acta Geodaetica et Cartographica Sinica 2016, 45, 505. [Google Scholar]
- Xie, P.; Petovello, M.G. Measuring gnss multipath distributions in urban canyon environments. IEEE Trans. Instrum. Meas. 2014, 64, 366–377. [Google Scholar]
- Williams, P.; Crump, M. All-source navigation for enhancing uav operations in gps-denied environments. In Proceedings of the 28th International Congress of the Aeronautical Sciences, Brisbane, Australia, 23–28 September 2012. [Google Scholar]
- Won, D.H.; Lee, E.; Heo, M.; Lee, S.-W.; Lee, J.; Kim, J.; Sung, S.; Lee, Y.J. Selective integration of gnss, vision sensor, and ins using weighted dop under gnss-challenged environments. IEEE Trans. Instrum. Meas. 2014, 63, 2288–2298. [Google Scholar] [CrossRef]
- Liang, X.; Huang, Z.; Qin, H.; Liu, Y. Gnss multi-frequency multi-system highly robust differential positioning based on an autonomous fault detection and exclusion method. IEEE Access 2017, 5, 26842–26851. [Google Scholar] [CrossRef]
- Chen, C.; Chang, G.; Zheng, N.; Xu, T. Gnss multipath error modeling and mitigation by using sparsity-promoting regularization. IEEE Access 2019, 7, 24096–24108. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, Y.; Farrell, J.A. High-precision vehicle navigation in urban environments using an mem’s imu and single-frequency gps receiver. IEEE Trans. Intell. Trans. Syst. 2016, 17, 2854–2867. [Google Scholar] [CrossRef]
- Niesen, U.; Jose, J.; Wu, X. Accurate positioning in gnss-challenged environments with consumer-grade sensors. In Proceedings of the 31st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 503–514. [Google Scholar]
- Yue, S.; Cong, L.; Qin, H.; Li, B.; Yao, J. A robust fusion methodology for mems-based land vehicle navigation in gnss-challenged environments. IEEE Access 2020, 8, 44087–44099. [Google Scholar] [CrossRef]
- Zhang, T.; Niu, X.; Ban, Y.; Zhang, H.; Shi, C.; Liu, J. Modeling and development of ins-aided plls in a gnss/ins deeply-coupled hardware prototype for dynamic applications. Sensors 2015, 15, 733–759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lachapelle, G. Performance comparison of difference correlator and co-op tracking architectures under receiver clock instability. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015; pp. 2887–2904. [Google Scholar]
- Alban, S.; Akos, D.M.; Rock, S.M.; Gebre-Egziabher, D. Performance analysis and architectures for ins-aided gps tracking loops. In Proceedings of the Institute of Navigation National Technical Meeting, San Diego, CA, USA, 22–24 January 2003; pp. 611–622. [Google Scholar]
- Gebre-Egziabher, D.; Razavi, A.; Enge, P.K.; Gautier, J.; Pullen, S.; Pervan, B.S.; Akos, D.M. Sensitivity and performance analysis of doppler-aided gps carrier-tracking loops. Navigation 2015, 52, 49–60. [Google Scholar] [CrossRef]
- Soloviev, S.; Gunawardena, S.; van Graas, F. Deeply integrated gps/low-cost imu for low cnr signal processing: Concept description and in-flight demonstration. Navigation 2008, 55, 1–138. [Google Scholar] [CrossRef]
- Li, T.; Petovello, M.G.; Lachapelle, G.; Basnayake, C. Performance evaluation of ultra-tight integration of gps/vehicle sensors for land vehicle navigation. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 1785–1796. [Google Scholar]
- O’Driscoll, C.; Petovello, M.G.; Lachapelle, G. Impact of extended coherent integration times on weak signal rtk in an ultra-tight receiver. In Proceedings of the NAV08 Conference, London, UK, 28–30 October 2008; pp. 1–11. [Google Scholar]
- Ye, P.; Zhan, X.; Fan, C. Novel optimal bandwidth design in ins-assisted gnss phase lock loop. IEICE Electr. Exp. 2011, 8, 650–656. [Google Scholar] [CrossRef] [Green Version]
- Chiou, T.Y.; Seo, J.; Walter, T.; Enge, P. Performance of a doppler-aided gps navigation system for aviation applications under ionospheric scintillation. In Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation, Savannah, GA, USA, 16–19 September 2008; pp. 1139–1147. [Google Scholar]
- Yan, L.; Zhang, T.; Niu, X.; Zhang, H.; Zhang, P.; Liu, J. Ins-aided tracking with fft frequency discriminator for weak gps signal under dynamic environments. GPS Solut. 2017, 21, 917–926. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, W.; Tang, K. A new inertial aid method for high dynamic compass signal tracking based on a nonlinear tracking differentiator. Sensors 2012, 12, 7634–7647. [Google Scholar] [CrossRef] [Green Version]
- Ohlmeyer, E.J. Analysis of an ultra-tightly coupled gps/ins system in jamming. In Proceedings of the 2006 IEEE/ION Position, Location, And Navigation Symposium, Coronado, CA, USA, 25–27 April 2006; IEEE: Piscataway, NJ, USA; pp. 44–53. [Google Scholar]
- Buck, T.M.; Wilmot, J.; Cook, M.J. A high g, mems based, deeply integrated, ins/gps, guidance, navigation and control flight management unit. In Proceedings of the 2006 IEEE/ION Position, Location, And Navigation Symposium, Coronado, CA, USA, 25–27 April 2006; IEEE: Piscataway, NJ, USA; pp. 772–794. [Google Scholar]
- Gustafson, D.; Dowdle, J. Deeply integrated code tracking: Comparative performance analysis. In Proceedings of the 16th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS/GNSS 2003), Portland, OR, USA, 9–12 September 2001; pp. 2553–2561. [Google Scholar]
- Schmidt, G.T.; Phillips, R.E. Ins/gps integration architecture performance comparisons. Low-Cost Navig. Sens. Integr. Technol. 2011, 1, 1–21. [Google Scholar]
- Pany, T.; Winkel, J.; Riedl, B.; Restle, M.; Wörz, T.; Schweikert, R.; Niedermeier, H.; Ameres, G.; Eissfeller, B.; Lagrasta, S.; et al. Performance of a partially coherent ultra-tightly coupled gnss/ins pedestrian navigation system enabling coherent integration times of several seconds to track gnss signals down to 1.5 db-hz. In Proceedings of the 22nd International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; Volume 2225. [Google Scholar]
- Soloviev, A.; Dickman, T.J. Deeply integrated gps for indoor navigation. indoor positioning and indoor navigation (ipin). In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Zurich, Switzerland, 15–17 September 2010. [Google Scholar]
- Kazemi, P.L.; O’Driscoll, C. Comparison of assisted and stand-alone methods for increasing coherent integration time for weak gps signal tracking. In Proceedings of the ION GNSS 2008, Savannah, GA, USA, 16–19 September 2008. [Google Scholar]
- Niu, X.J.; Ban, Y.L.; Zhang, T.S.; Liu, J.N. Research progress and prospects of gnss/ins deep integration. Acta Aeronaut. Astronaut. Sin. 2016, 37, 2895–2908. [Google Scholar]
- Karaim, M. Ultra-tight GPS/INS Integrated System for Land Vehicle Navigation in Challenging Environments. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2019. [Google Scholar]
- Kennedy, S.; Rossi, J. Performance of a deeply coupled commercial grade gps/ins system from kvh and novatel inc. In Proceedings of the 2008 IEEE/ION Position, Location and Navigation Symposium, Fort Worth, TX, USA, 5–8 May 2008; IEEE: Monterey, CA, USA; pp. 17–24. [Google Scholar]
- iMAR. iTranceRT-F402-E: Accurate Real-Time Surveying, Vehicle Trajectory and Dynamics Estimation with Deeply Coupled INS/GNSS Data Fusion. Available online: https://www.imar-navigation.de/downloads/TraceRT-F402-E_en.pdf (accessed on 20 February 2020).
- Tawk, Y.; Tomé, P.; Botteron, C.; Stebler, Y.; Farine, P.-A. Implementation and performance of a gps/ins tightly coupled assisted pll architecture using mems inertial sensors. Sensors 2014, 14, 3768–3796. [Google Scholar] [CrossRef] [PubMed]
- Cong, L.; Li, X.; Jin, T.; Yue, S.; Xue, R. An adaptive ins-aided pll tracking method for gnss receivers in harsh environments. Sensors 2016, 16, 146. [Google Scholar] [CrossRef] [PubMed]
- Ren, T.; Petovello, M.G. A stand-alone approach for high-sensitivity gnss receivers in signal-challenged environment. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2438–2448. [Google Scholar] [CrossRef]
- Groves, P.D.; Mather, C.J.; Macaulay, A.A. Demonstration of non-coherent deep ins/gps integration for optimised signal-to-noise performance. In Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 2627–2638. [Google Scholar]
- High Performance 6-Axis MEMS MotionTracking Device. Available online: https://invensense.tdk.com/wp-content/uploads/2016/10/DS-000176-ICM-20602-v1.0.pdf (accessed on 20 February 2020).
- Kaplan, E.; Hegarty, C. Understanding GPS: Principles and Applications; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements and Performance Second Edition. 2006. Available online: https://www.navtechgps.com/ (accessed on 20 February 2020).
- Gao, G. INS-Assisted High Sensitivity GPS Receivers for Degraded Signal Navigation. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2007. [Google Scholar]
- Kútik, O.; Orejas, M. Evaluation of c/n0 estimators performance for gnss receivers. In Proceedings of the 14th International Association of Institutes of Navigation, Cairo, Egypt, 1–3 October 2012. [Google Scholar]
- Groves, P.D.; Jiang, Z. Height aiding, c/n 0 weighting and consistency checking for gnss nlos and multipath mitigation in urban areas. J. Navig. 2013, 66, 653–669. [Google Scholar] [CrossRef] [Green Version]
- Leador. Positioning System PPOI-A Series. Available online: http://leador.com.cn/contents/64/14.html (accessed on 20 February 2020).
- S. GSS6425. Available online: https://www.spirent.com/Products (accessed on 6 July 2018).
- Lashley, M.; Bevly, D.M.; Hung, J.Y. Analysis of deeply integrated and tightly coupled architectures. In IEEE/ION Position, Location and Navigation Symposium; IEEE: Piscataway, NJ, USA, 2010; pp. 382–396. [Google Scholar]
- u-blox. EVK-M8U Evaluation Kit User Guide. Available online: https://www.u-blox.com/en/docs/UBX-15023994 (accessed on 20 February 2020).










| Parameter | M8U IMU | ICM-20602 |
|---|---|---|
| Gyroscope angularrandom walk (deg/sqrt(hr)) | 0.48 | 0.23 |
| Gyroscope bias instability (deg/hr) | 10.8 | 10.7 |
| Accelerometer velocityrandom walk (m/s/sqrt(hr)) | 0.06 | 0.042 |
| Accelerometer bias instability (mGal) | 50 | 16 |
| SD(m) | Max(m) | |||
|---|---|---|---|---|
| Satellite PRN | IWA Enabled | IWA Disabled | IWA Enabled | IWA Disabled |
| GPS 8 | 0.7793 | 1.3742 | 9.4010 | 15.3010 |
| GPS 9 | 4.5917 | 7.4000 | 42.1690 | 65.4270 |
| GPS 16 | 4.2423 | 10.1625 | 39.5030 | 84.2200 |
| GPS 18 | 1.1373 | 1.7913 | 16.8610 | 23.8980 |
| BD 10 | 0.7913 | 1.2251 | 22.7740 | 25.0350 |
| BD 1 | 0.9583 | 2.5315 | 12.1420 | 16.3540 |
| BD 29 | 0.8127 | 1.1714 | 19.4810 | 21.4100 |
| BD 2 | 2.8286 | 3.1086 | 49.9910 | 51.5310 |
| SD(m) | Max(m) | Valid Epochs Proportion(%) | ||||
|---|---|---|---|---|---|---|
| GPS PRN | GID CSR | M8U | GID CSR | M8U | GID CSR | M8U |
| 1 | 1.5972 | 2.355 | 10.176 | 13.634 | 98.93 % | 93.11 % |
| 8 | 0.7883 | 1.6264 | 9.527 | 15.792 | 100.00% | 99.55% |
| 9 | 4.3035 | 6.3829 | 42.269 | 64.313 | 86.31% | 71.20% |
| 11 | 0.8495 | 1.7414 | 8.892 | 14.208 | 100.00% | 99.64% |
| 16 | 3.9518 | 5.2928 | 40.428 | 35.55 | 85.15% | 76.48% |
| 18 | 1.1303 | 1.7902 | 16.94 | 21.105 | 100.00% | 99.28% |
| 27 | 1.8361 | 2.7757 | 23.151 | 27.899 | 99.11% | 91.50% |
| 30 | 1.5508 | 3.3141 | 22.371 | 60.433 | 97.32% | 92.93% |
| SD(m) | Max(m) | Valid Epochs Proportion(%) | ||||
|---|---|---|---|---|---|---|
| BD PRN | GID CSR | M8U | GID CSR | M8U | GID CSR | M8U |
| 1 | 0.9379 | 2.5351 | 12.149 | 23.299 | 99.11% | 97.14% |
| 2 | 2.6782 | 4.3748 | 49.553 | 62.227 | 78.80% | 83.18% |
| 3 | 1.098 | 1.5951 | 14.755 | 19.973 | 99.02% | 98.03% |
| 4 | 2.4376 | 4.1498 | 30.842 | 43.646 | 88.64% | 81.04% |
| 10 | 0.7915 | 1.592 | 22.765 | 27.779 | 99.46% | 100.00% |
| 29 | 0.804 | 1.586 | 19.457 | 26.105 | 99.73% | 99.91% |
| GIDCSR | u-blox M8U | ||
|---|---|---|---|
| N | SD(m) | 0.8878 | 1.1457 |
| Max(m) | 4.1221 | 6.9427 | |
| E | SD(m) | 1.3233 | 2.1456 |
| Max(m) | 6.4749 | 12.5989 | |
| D | SD(m) | 3.9818 | 6.4604 |
| Max(m) | 24.9116 | 40.4575 |
| GIDCSR | M8U | ||
|---|---|---|---|
| N | SD(m) | 0.9686 | 2.8252 |
| Max(m) | 3.4498 | 9.4681 | |
| E | SD(m) | 1.2232 | 3.9018 |
| Max(m) | 4.3111 | 11.5587 | |
| D | SD(m) | 3.1172 | 1.8053 |
| Max(m) | 11.2538 | 5.294 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, X.; Zhang, T.; Lin, T.; Tang, H.; Niu, X. Implementation and Performance of a Deeply-Coupled GNSS Receiver with Low-Cost MEMS Inertial Sensors for Vehicle Urban Navigation. Sensors 2020, 20, 3397. https://doi.org/10.3390/s20123397
Feng X, Zhang T, Lin T, Tang H, Niu X. Implementation and Performance of a Deeply-Coupled GNSS Receiver with Low-Cost MEMS Inertial Sensors for Vehicle Urban Navigation. Sensors. 2020; 20(12):3397. https://doi.org/10.3390/s20123397
Chicago/Turabian StyleFeng, Xin, Tisheng Zhang, Tao Lin, Hailiang Tang, and Xiaoji Niu. 2020. "Implementation and Performance of a Deeply-Coupled GNSS Receiver with Low-Cost MEMS Inertial Sensors for Vehicle Urban Navigation" Sensors 20, no. 12: 3397. https://doi.org/10.3390/s20123397
APA StyleFeng, X., Zhang, T., Lin, T., Tang, H., & Niu, X. (2020). Implementation and Performance of a Deeply-Coupled GNSS Receiver with Low-Cost MEMS Inertial Sensors for Vehicle Urban Navigation. Sensors, 20(12), 3397. https://doi.org/10.3390/s20123397





