Long-Term Evaluation and Calibration of Low-Cost Particulate Matter (PM) Sensor
Abstract
:1. Introduction
- Field evaluation of low-cost PM2.5 sensor in Seoul, Korea has been executed and analyzed. These were under several conditions, such as environmental explanatory variables (humidity/temperature/ambient light), sampling intervals (5 min/1 h/24 h), and calibration methods (linear/non-linear/SMART calibration).
- A novel combined calibration method has been introduced to increase low-cost sensor accuracy. The performance was compared to other calibration methods. This calibration method can also be applied to an upcoming future dataset with the previously generated models.
2. Methods
2.1. Data Collection
2.1.1. Multi-Sensor Platform—Low-Cost Light Scattering PM Sensor
2.1.2. Governmental BAM—High-End PM Monitoring Station
2.2. Data Preprocessing
2.3. Data Calibration
2.3.1. Linear Calibration
2.3.2. Nonlinear Calibration
2.3.3. SMART Calibration (Combined Calibration)
2.4. Metric Information
3. Results and Discussions
3.1. Preliminary Analysis
3.1.1. Performance Characteristics: Explanatory Variables
Performance Characteristics: Explanatory Variables, Short-Term Analysis (45 Days)
Performance Characteristics: Explanatory Variables, Long-Term Analysis (7.5 Months)
3.1.2. Performance Characteristics: Sampling Interval
3.2. Comparative Analysis: The Low-Sensor and Governmental BAM (Before Calibration)
3.3. Comparative Analysis: The Low-Cost Sensor and Governmental BAM (After Calibration)
3.4. Comparative Analysis: Other Calibration Methods
3.5. Comparative Analysis: Previous Similar Study
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Limitation on Linear/Nonlinear Approxiamation—Anscombe’s Quartet, Bias & Variance Trade-Off
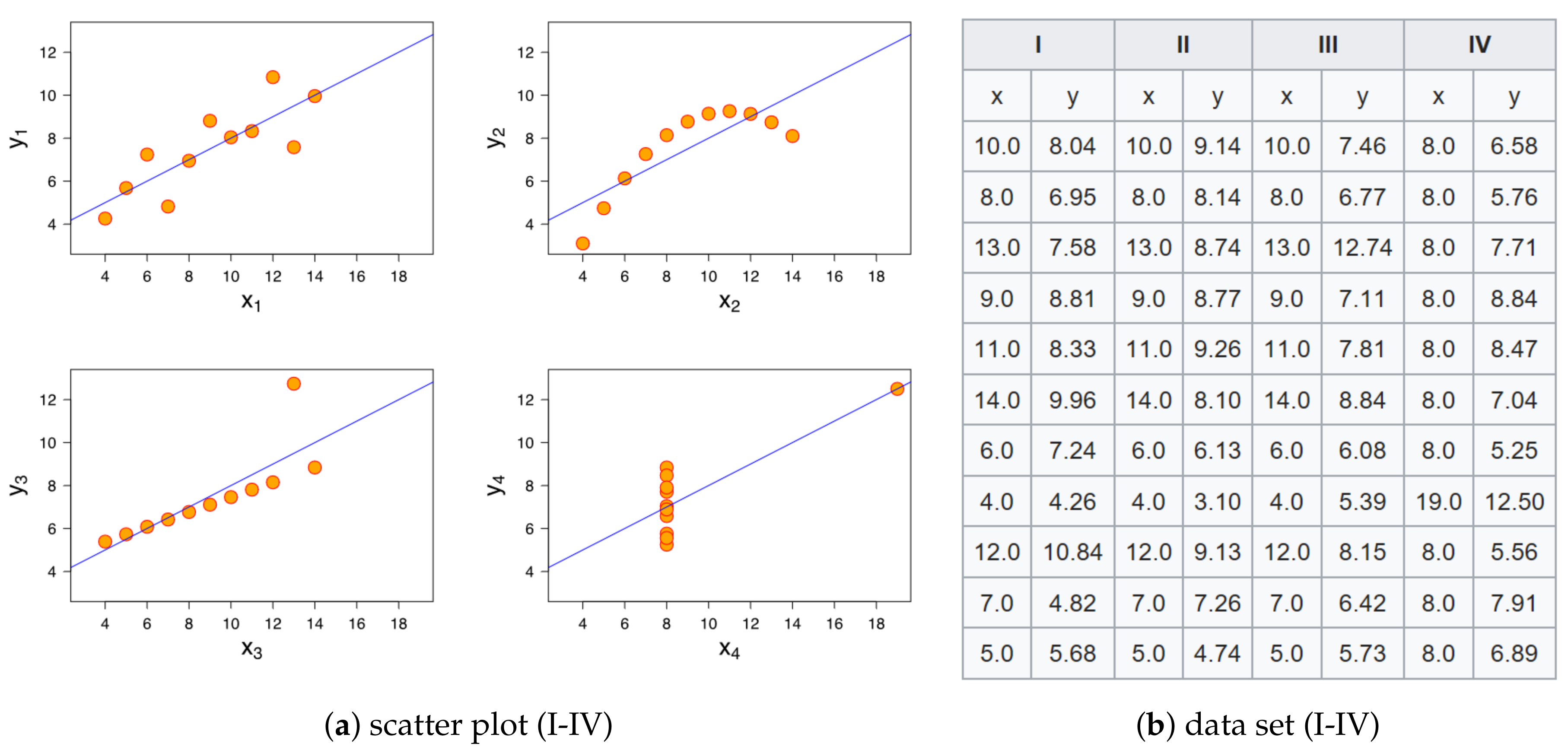
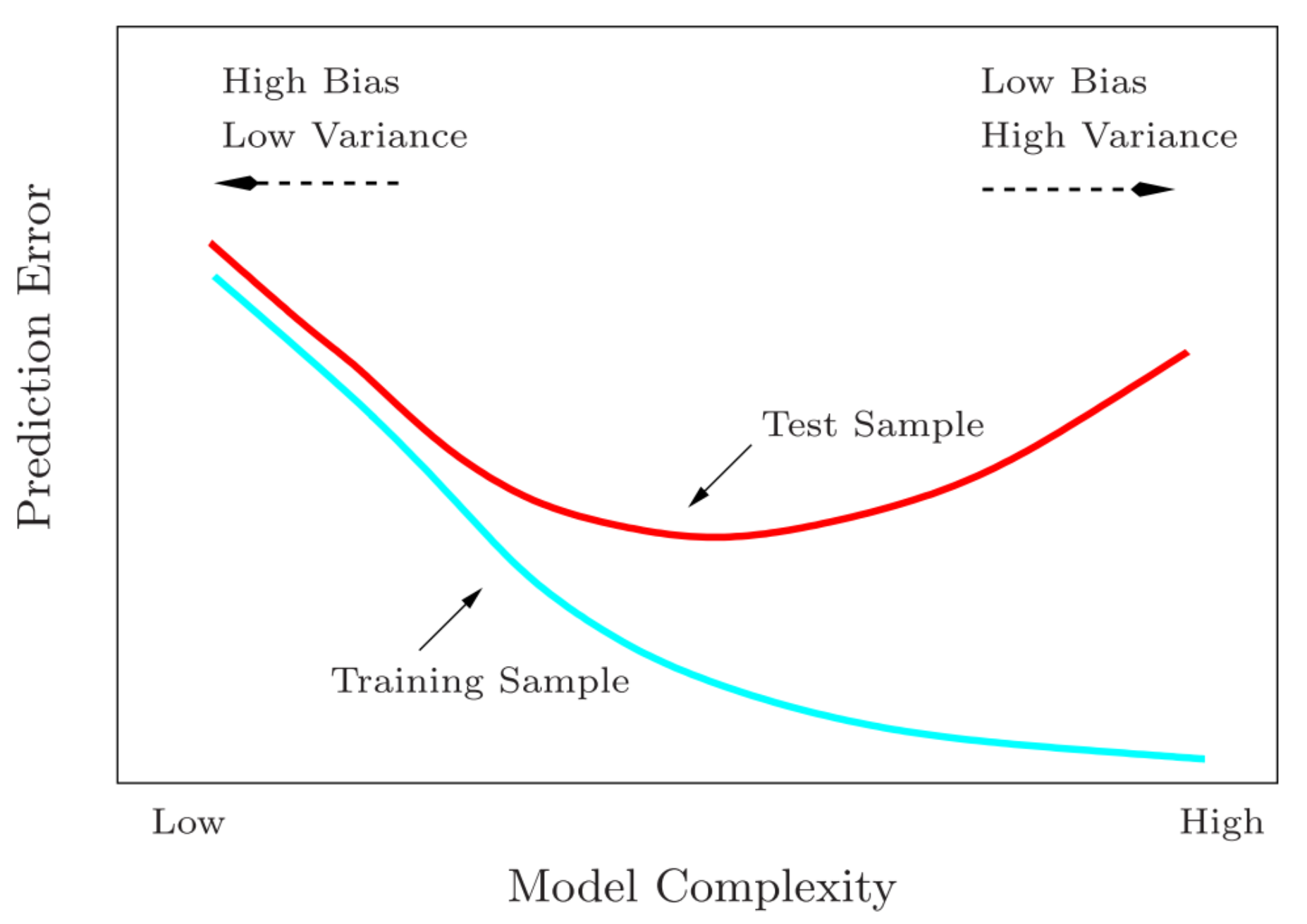
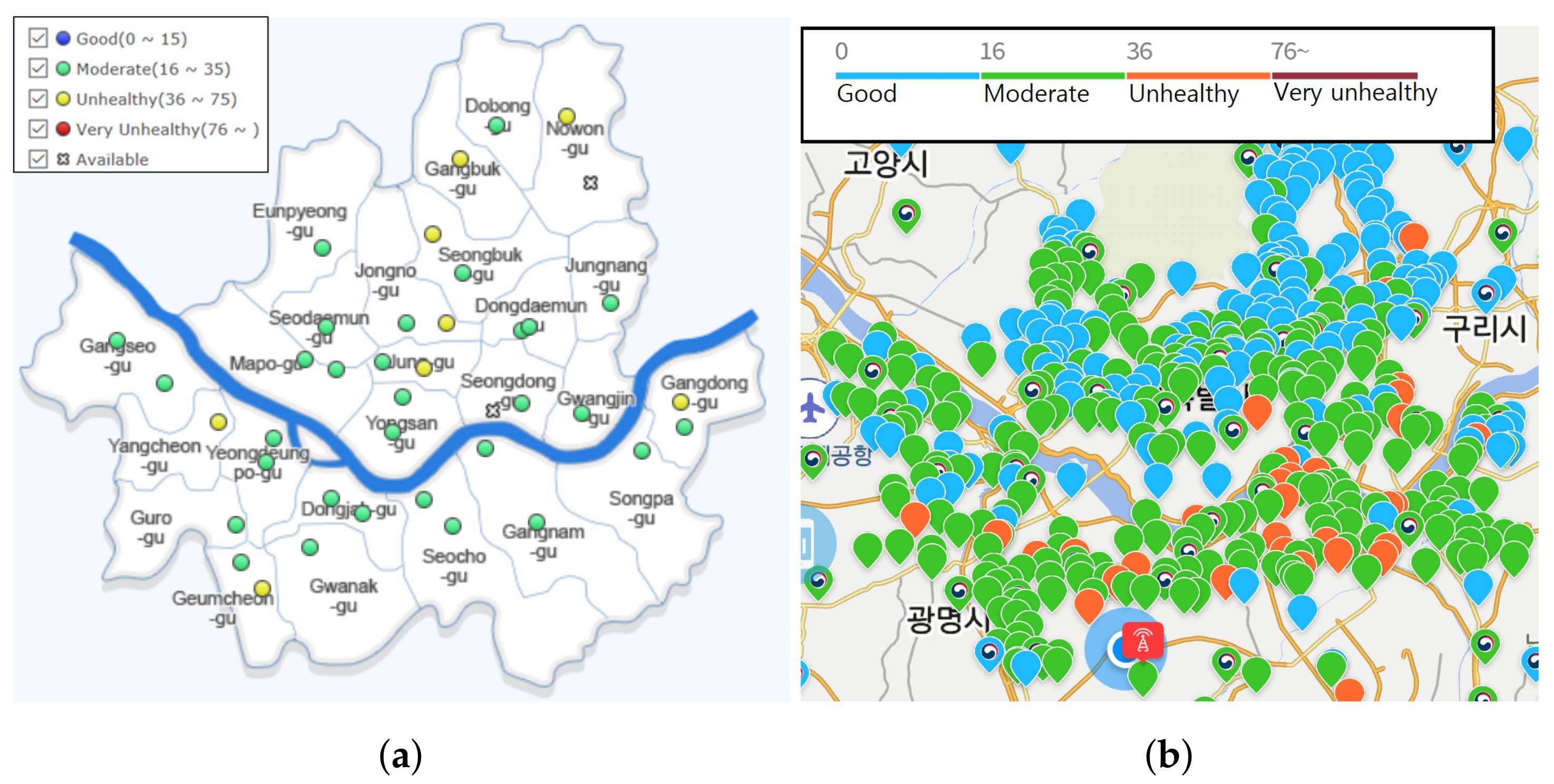
Appendix B. Additional Figures and Tables
| Raw(a) | Raw(b) | Raw(c) | BAM | |
|---|---|---|---|---|
| Raw(a) | 1.000 | slope = 0.837 intercept = 1.969 R = 0.937 MAE = 4.700 | slope = 0.998 intercept = 0.003 R = 0.994 MAE = 1.583 | slope = 0.436 intercept = 6.457 R = 0.416 MAE = 15.816 |
| Raw(b) | 0.987 | 1.000 | slope = 1.163 intercept = -1.335 R = 0.933 MAE = 4.737 | slope = 0.512 intercept = 5.732 R = 0.546 MAE = 11.952 |
| Raw(c) | 0.997 | 0.985 | 1.000 | slope = 0.435 intercept = 6.526 R = 0.417 MAE = 15.712 |
| BAM | 0.919 | 0.916 | 0.918 | 1.000 |
| Raw(a) | Raw(b) | Raw(c) | BAM | |
|---|---|---|---|---|
| No. of samples | 36911.00 | 36911.00 | 36911.00 | 36911.00 |
| Mean | 38.15 | 33.89 | 38.07 | 23.10 |
| STD | 31.29 | 26.52 | 31.32 | 14.84 |
| Min | 0.00 | 0.00 | 0.00 | 0.00 |
| 25% | 16.53 | 15.07 | 16.71 | 13.00 |
| 50% | 28.95 | 26.26 | 28.94 | 20.00 |
| 75% | 49.60 | 45.31 | 49.39 | 28.00 |
| Max | 215.42 | 179.73 | 225.46 | 115.00 |
| Raw | MLR | MLP | SMART | BAM | |
|---|---|---|---|---|---|
| Raw | 1.000 | - | - | - | slope = 0.434 intercept = 6.458 R = 0.41 MAE = 15.87 MSE = 573.23 |
| MLR | 0.989 | 1.000 | - | - | slope = 0.996 intercept = -0.028 R = 0.84 MAE = 4.00 MSE = 29.90 |
| MLP | 0.972 | 0.982 | 1.000 | - | slope = 1.062 intercept = -1.086 R = 0.86 MAE = 3.52 MSE = 23.88 |
| SMART | 0.954 | 0.964 | 0.979 | 1.000 | slope = 1.008 intercept = −0.258 R = 0.89 MAE = 3.32 MSE = 22.06 |
| BAM | 0.919 | 0.929 | 0.945 | 0.947 | 1.000 |
| Raw | MLR | MLP | SMART | BAM | |
|---|---|---|---|---|---|
| No. of samples | 7382.00 | 7382.00 | 7382.00 | 7382.00 | 7382.00 |
| Mean | 38.12 | 23.13 | 22.70 | 23.09 | 23.01 |
| STD | 31.18 | 13.74 | 13.12 | 13.85 | 14.74 |
| Min | 0.00 | 2.97 | 2.15 | −6.50 | 0.00 |
| 25% | 16.42 | 13.81 | 14.24 | 13.94 | 13.00 |
| 50% | 28.97 | 19.52 | 19.51 | 19.89 | 20.00 |
| 75% | 49.66 | 28.52 | 27.64 | 28.11 | 28.00 |
| Max | 210.93 | 100.82 | 104.48 | 98.55 | 115.00 |
Appendix C. Prototype Build/Validation

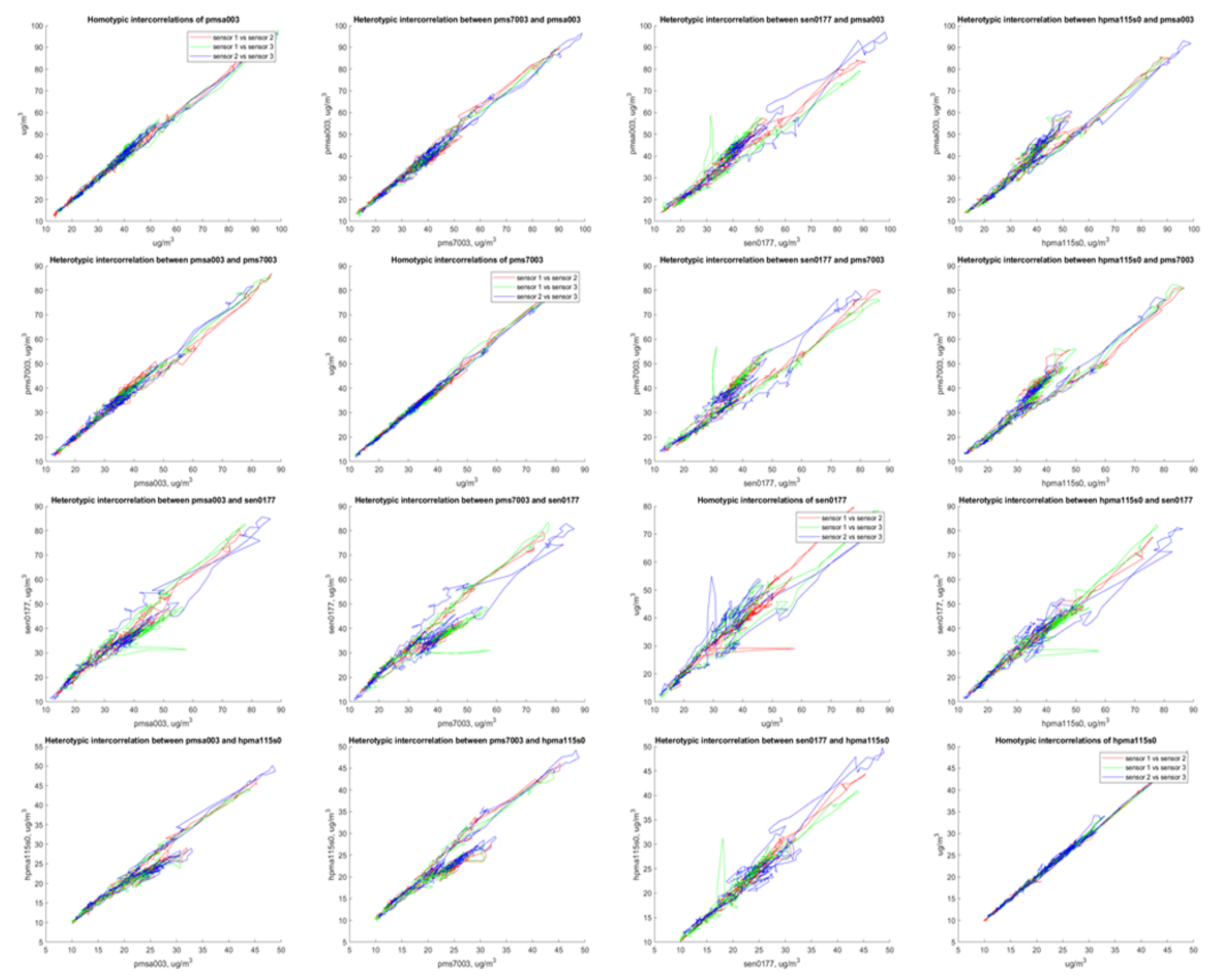
| Sensor | PMSA003 | PMS7003 | SEN0177 | HPMA115S0 |
|---|---|---|---|---|
| PMSA003 | 0.987 | - | - | - |
| PMS7003 | 0.983 | 0.994 | - | - |
| SEN0177 | 0.879 | 0.878 | 0.882 | - |
| HPMA115S0 | 0.918 | 0.910 | 0.921 | 0.994 |

Appendix D. Procedures of SMART Calibration
- Build a calibration model (a or b).
- MLR:
- MLP(ReLU activation):
- Segment each input space (i x j matrix)
- Calculate residuals of each cell (in i x j matrix) according to corresponding data and generate a residual map of the training dataset. (n calibration models)
- repeat 1–3 steps for the other model.
- Compare residual maps for each cell and build a prevailing model map.prevailing model: selected by
- 6.
- Infer test data from the prevailing model
- 7.
- Infer test data from residuals of the prevailing modelif <
Appendix E. Data Preprocessing Methods—More on Shuffled Methods
| Dataset Ratio | Metric | Shuffled - Hourly | Shuffled - Daily | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PM Only | PM+Humidity+Temp | PM Only | PM+Humidity+Temp | ||||||||
| Raw | LR | MLR | MLP | SMART | Raw | LR | MLR | MLP | SMART | ||
| 70%/30% | MAE | 14.71 | 4.33 | 3.99 | 3.65 | 3.57 | 15.64 | 4.38 | 4.01 | 3.56 | 3.68 |
| MSE | 527.41 | 36.04 | 30.72 | 26.82 | 26.09 | 580.05 | 34.34 | 29.20 | 23.94 | 28.73 | |
| R | 0.46 | 0.80 | 0.83 | 0.84 | 0.87 | 0.44 | 0.82 | 0.86 | 0.89 | 0.88 | |
| 80%/20% | MAE | 14.09 | 4.27 | 3.92 | 3.60 | 3.54 | 16.86 | 4.55 | 4.25 | 3.57 | 3.76 |
| MSE | 490.61 | 35.77 | 30.27 | 25.82 | 25.81 | 694.70 | 38.76 | 33.49 | 24.39 | 30.03 | |
| R | 0.46 | 0.79 | 0.83 | 0.85 | 0.87 | 0.41 | 0.83 | 0.86 | 0.89 | 0.88 | |
| 90%/10% | MAE | 14.14 | 3.92 | 3.75 | 3.45 | 3.41 | 18.99 | 4.85 | 4.48 | 3.85 | 3.77 |
| MSE | 535.50 | 29.96 | 26.73 | 25.21 | 25.09 | 842.96 | 44.03 | 36.97 | 26.19 | 26.88 | |
| R | 0.44 | 0.84 | 0.86 | 0.88 | 0.88 | 0.39 | 0.84 | 0.87 | 0.90 | 0.90 | |
| 95%/5% | MAE | 14.88 | 4.02 | 3.90 | 3.66 | 3.71 | 14.97 | 5.39 | 4.87 | 4.75 | 4.99 |
| MSE | 607.20 | 33.97 | 31.75 | 29.25 | 30.89 | 605.08 | 62.87 | 51.22 | 46.65 | 63.89 | |
| R | 0.39 | 0.82 | 0.83 | 0.84 | 0.85 | 0.51 | 0.73 | 0.79 | 0.79 | 0.69 | |

Appendix F. Grid Search CV Methods
- [Common params] = ‘cross validations’:[10], ‘random state’:[0], ‘scoring’:[MSE]
- Lasso params = ‘alpha’:[0.0001, 0.0005, 0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1, 5, 10, 20, 50, 100]
- Ridge params = ‘alpha’:[0.0001, 0.0005, 0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1, 5, 10, 20, 50, 100, 200]
- DT params = ‘max depth’:[4,6, 8,12,16], ‘min samples split’:[8, 16, 24, 32]
- RF params =‘n estimators’: [100, 200, 500], ‘max depth’: [6, 8,12], ‘min samples split’: [8, 16, 24], ‘min samples leaf’: [8,12,18]
- GB params = ‘n estimators’: [100, 200, 500], ‘learning rate’: [0.05, 0.1, 0.2]
- XGB params = ‘n estimators’: [100, 200, 500], ‘learning rate’: [0.05, 0.1, 0.2], ‘colsample bytree’: [0.3,0.5,0.7,1], ‘subsample’:[0.3,0.5,0.7,1], ‘n jobs’:[−1]
- LGB params = ‘n estimators’:[100, 200, 500], ‘learning rate’:[0.05, 0.1,0.2], ‘colsample bytree’: [0.5,0.7,1], ‘subsample’: [0.3,0.5,0.7,1], ‘num leaves’: [2,4,6], ‘reg lambda’: [10], ‘n jobs’: [−1]
References
- Lee, S.; Lee, W.; Kim, D.; Kim, E.; Myung, W.; Kim, S.Y.; Kim, H. Short-term PM 2.5 exposure and emergency hospital admissions for mental disease. Environ. Res. 2019, 171, 313–320. [Google Scholar] [CrossRef] [PubMed]
- Burnett, R.; Chen, H.; Szyszkowicz, M.; Fann, N.; Hubbell, B.; Pope, C.A.; Apte, J.S.; Brauer, M.; Cohen, A.; Weichenthal, S.; et al. Global estimates of mortality associated with longterm exposure to outdoor fine particulate matter. Proc. Natl. Acad. Sci. USA 2018, 115, 9592–9597. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- World Health Organization (WHO). RHN Workshop on Environment and Health (Air Pollution and Active Mobility), Ljubljana, Slovenia, 30 November 2018; p. 39. Available online: https://www.euro.who.int/en/about-us/networks/regions-for-health-network-rhn/activities/network-updates/rhn-workshop-on-environment-and-health-air-pollution-and-active-mobility-at-the-11th-european-public-health-conference (accessed on 26 June 2020).
- Motlagh, N.H.; Petaja, T.; Kulmala, M.; Trachoma, S.; Lagerspetz, E.; Nurmi, P.; Li, X.; Varjonen, S.; Mineraud, J.; Siekkinen, M.; et al. Toward Massive Scale Air Quality Monitoring. IEEE Commun. Mag. 2020, 58, 54–59. [Google Scholar] [CrossRef]
- Morawska, L.; Thai, P.K.; Liu, X.; Asumadu-Sakyi, A.; Ayoko, G.; Bartonova, A.; Bedini, A.; Chai, F.; Christensen, B.; Dunbabin, M.; et al. Applications of low-cost sensing technologies for air quality monitoring and exposure assessment: How far have they gone? Environ. Int. 2018, 116, 286–299. [Google Scholar] [CrossRef] [PubMed]
- Rai, A.C.; Kumar, P.; Pilla, F.; Skouloudis, A.N.; Di Sabatino, S.; Ratti, C.; Yasar, A.; Rickerby, D. End-user perspective of low-cost sensors for outdoor air pollution monitoring. Sci. Total Environ. 2017, 607–608, 691–705. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, Y.; Dong, W.; Guo, K.; Liu, X.; Chen, Y.; Liu, X.; Bu, J.; Chen, C. Mosaic: A low-cost mobile sensing system for urban air quality monitoring. In Proceedings of the IEEE INFOCOM 2016—The 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016. [Google Scholar] [CrossRef]
- BALZ MAAG. Air Quality Sensor Calibration and Its Peculiarities. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2019. [CrossRef]
- Maag, B.; Zhou, Z.; Saukh, O.; Thiele, L. SCAN: Multi-Hop Calibration for Mobile Sensor Arrays. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2017, 1, 1–21. [Google Scholar] [CrossRef]
- Air Korea from Goverment. Available online: https://www.airkorea.or.kr/eng/currentAirQuality?pMENU_NO=68 (accessed on 18 December 2019).
- Every Air from SK Telecom. Available online: https://www.onestore.co.kr/userpoc/apps/view?pid=0000745074 (accessed on 18 December 2019).
- Air map Korea from KT. Available online: https://iot.airmapkorea.kt.com/info/ (accessed on 18 December 2019).
- Bulot, F.M.; Johnston, S.J.; Basford, P.J.; Easton, N.H.; Apetroaie-Cristea, M.; Foster, G.L.; Morris, A.K.; Cox, S.J.; Loxham, M. Long-term field comparison of multiple low-cost particulate matter sensors in an outdoor urban environment. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, A.; Stanton, L.G.; Graham, A.R.; Roberts, P.T. Assessing the utility of low-cost particulate matter sensors over a 12-week period in the Cuyama valley of California. Sensors 2017, 17, 1805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, H.Y.; Schneider, P.; Haugen, R.; Vogt, M. Performance assessment of a low-cost PM 2.5 sensor for a near four-month period in Oslo, Norway. Atmosphere 2019, 10, 41. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Park, S.; Lee, J. Evaluation of performance of inexpensive laser based PM2.5 sensor monitors for typical indoor and outdoor hotspots of South Korea. Appl. Sci. 2019, 9, 1947. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, A.; Brown, S.G.; Mccarthy, M.C.; Pavlovic, N.R.; Stanton, L.G.; Snyder, J.L.; Andrea, S.D.; Hafner, H.R. Measuring Spatial and Temporal PM2.5 Variations in Sacramento, California, Communities Using a Network of Low-Cost Sensors. Sensors 2019, 19, 4701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plantower Inc. Available online: http://www.plantower.com/en/list/?118_1.html (accessed on 3 January 2020).
- DFRobot Inc. Available online: https://www.dfrobot.com/product-1272.html?search=sen0177&description=true (accessed on 3 January 2020).
- Honeywell Inc. Available online: https://sensing.honeywell.com/hpma115s0-xxx-particulate-matter-sensors (accessed on 3 January 2020).
- Karagulian, F.; Gerboles, M.; Barbiere, M.; Kotsev, A.; Lagler, F.; Borowiak, A. Review of Sensors for air Quality Monitoring; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar] [CrossRef]
- Crilley, L.R.; Shaw, M.; Pound, R.; Kramer, L.J.; Price, R.; Young, S.; Lewis, A.C.; Pope, F.D. Evaluation of a low-cost optical particle counter (Alphasense OPC-N2) for ambient air monitoring. Atmos. Meas. Tech. 2018, 11, 709–720. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Dong, W.; Chen, Y. Calibrating Low-Cost Sensors by a Two-Phase Learning Approach for Urban Air Quality Measurement. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2018, 2, 1–18. [Google Scholar] [CrossRef]
- Cordero, J.M.; Borge, R.; Narros, A. Using statistical methods to carry out in field calibrations of low cost air quality sensors. Sens. Actuators B 2018, 267, 245–254. [Google Scholar] [CrossRef]
- Magi, B.I.; Cupini, C.; Francis, J.; Green, M.; Hauser, C. Evaluation of PM2.5 measured in an urban setting using a low-cost optical particle counter and a Federal Equivalent Method Beta Attenuation Monitor. Aerosol Sci. Technol. 2019, 54, 1–13. [Google Scholar] [CrossRef]
- Kimoto Inc. Available online: https://www.kimoto-electric.co.jp/english/product/air/700.html#lineup (accessed on 3 January 2020).
- Matlab R2018b. Available online: https://www.mathworks.com/ (accessed on 3 January 2020).
- Pandas. Available online: https://pandas.pydata.org/ (accessed on 3 January 2020).
- Keras. Available online: https://keras.io/ (accessed on 3 January 2020).
- Scikit-Learn. Available online: https://scikit-learn.org/stable/index.html (accessed on 3 January 2020).
- Tensorflow. Available online: https://www.tensorflow.org/ (accessed on 3 January 2020).
- Zheng, T.; Bergin, M.H.; Johnson, K.K.; Tripathi, S.N.; Shirodkar, S.; Landis, M.S.; Sutaria, R.; Carlson, D.E. Field evaluation of low-cost particulate matter sensors in high-and low-concentration environments. Atmos. Meas. Tech. 2018, 11, 4823–4846. [Google Scholar] [CrossRef] [Green Version]
- Metone Inc. Available online: https://metone.com/products/bam-1020 (accessed on 3 January 2020).
- US EPA. Available online: https://www.epa.gov/ (accessed on 3 January 2020).
- Alexander, D.L.J.; Tropsha, A.; Winkler, D.A. Beware of R2: Simple, Unambiguous Assessment of the Prediction Accuracy of QSAR and QSPR Models. J. Chem. Inf. Model. 2015, 55, 1316–1322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Purple Air Inc. Available online: https://www2.purpleair.com/products/purpleair-pa-ii (accessed on 3 January 2020).
- Anscombe, F.J. Graphs in Statistical Analysis. Am. Stat. 1973, 27, 17–21. [Google Scholar]
- Anscombe’s Quartet. Available online: https://en.wikipedia.org/wiki/Anscombe%27s_quartet (accessed on 26 June 2020).
- Nordhausen, K. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition by Trevor Hastie, Robert Tibshirani, Jerome Friedman; Springer: New York, NY, USA, 2009; pp. 37–38. [Google Scholar] [CrossRef]














| Raw(a) | Humidity | Temperature | Intercept |
|---|---|---|---|
| Hidden Layer | Neurons/Layer | Epoch | Batch | Activation | Dropout Rate | Learning Rate | Optimizer |
|---|---|---|---|---|---|---|---|
| 2 | 24 | 200 | 32 | ReLU | 0.2 | 0.005 | Adam |
| MAE | MSE | RMSE | R |
|---|---|---|---|
| Input Variables | Linear - ULR/MLR | Nonlinear - MLP | ||||
|---|---|---|---|---|---|---|
| MAE | MSE | R | MAE | MSE | R | |
| [uncalibrated] Raw PM | 9.78 | 216.89 | 0.52 | 9.78 | 216.89 | 0.52 |
| [ calibrated] Raw PM | 3.69 | 24.44 | 0.78 | 3.55 | 23.12 | 0.80 |
| [ calibrated] Raw PM + Humidity | 3.11 | 18.72 | 0.84 | 2.99 | 16.69 | 0.84 |
| [ calibrated] Raw PM + Temp | 3.22 | 19.56 | 0.83 | 3.11 | 18.39 | 0.83 |
| [ calibrated] Raw PM + Light | 3.39 | 21.40 | 0.81 | 3.23 | 18.97 | 0.84 |
| [ calibrated] Raw PM + Humidity + Temp | 3.11 | 18.70 | 0.84 | 2.95 | 16.91 | 0.83 |
| [ calibrated] Raw PM + Humidity + Light | 3.09 | 18.61 | 0.84 | 2.99 | 17.01 | 0.83 |
| [ calibrated] Raw PM + Temp + Light | 3.19 | 19.25 | 0.83 | 3.10 | 18.15 | 0.83 |
| [ calibrated] Raw PM + Humidity + Temp + Light | 3.08 | 18.41 | 0.84 | 2.93 | 16.76 | 0.83 |
| Input Variables | Linear - ULR/MLR | Nonlinear - MLP | ||||
|---|---|---|---|---|---|---|
| MAE | MSE | R | MAE | MSE | R | |
| [uncalibrated] Raw PM | 15.87 | 573.23 | 0.41 | 15.87 | 573.23 | 0.41 |
| [ calibrated] Raw PM | 4.28 | 33.79 | 0.82 | 4.21 | 33.79 | 0.79 |
| [ calibrated] Raw PM + Humidity | 4.01 | 30.13 | 0.84 | 4.04 | 32.15 | 0.77 |
| [ calibrated] Raw PM + Humidity + Temp. | 4.00 | 29.90 | 0.84 | 3.52 | 23.88 | 0.86 |
| Sampling Interval | Metric | Raw | LR | MLP | SMART |
|---|---|---|---|---|---|
| 5 min | MAE | 15.87 | 4.00 | 3.52 | 3.32 |
| MSE | 573.23 | 29.90 | 23.88 | 22.06 | |
| R | 0.41 | 0.84 | 0.86 | 0.89 | |
| 1 h | MAE | 14.72 | 3.68 | 3.29 | 3.51 |
| MSE | 486.26 | 25.22 | 21.29 | 25.75 | |
| R | 0.41 | 0.85 | 0.88 | 0.86 | |
| 24 h | MAE | 12.33 | 2.71 | 2.92 | 2.68 |
| MSE | 299.55 | 21.72 | 29.62 | 21.99 | |
| R | 0.37 | 0.77 | 0.75 | 0.77 |
| Dataset Ratio | Metric | Shuffled | Sequential | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PM Only | PM+Humidity+Temp | PM Only | PM+Humidity+Temp | ||||||||
| Raw | LR | MLR | MLP | SMART | Raw | LR | MLR | MLP | SMART | ||
| 70%/30% | MAE | 15.68 | 4.25 | 3.98 | 3.65 | 3.29 | 8.92 | 3.54 | 3.60 | 3.60 | 3.32 |
| MSE | 563.90 | 33.45 | 29.61 | 25.27 | 21.80 | 182.31 | 21.99 | 22.49 | 23.70 | 21.56 | |
| R | 0.41 | 0.82 | 0.84 | 0.83 | 0.89 | 0.47 | 0.66 | 0.66 | 0.58 | 0.61 | |
| 80%/20% | MAE | 15.87 | 4.28 | 4.00 | 3.52 | 3.32 | 9.06 | 3.36 | 2.91 | 2.97 | 2.79 |
| MSE | 573.23 | 33.79 | 29.90 | 23.88 | 22.06 | 196.35 | 18.70 | 14.84 | 15.20 | 14.02 | |
| R | 0.41 | 0.82 | 0.84 | 0.86 | 0.89 | 0.41 | 0.71 | 0.76 | 0.66 | 0.76 | |
| 90%/10% | MAE | 15.8 | 4.34 | 4.06 | 3.47 | 3.23 | 11.67 | 3.62 | 2.86 | 2.84 | 2.80 |
| MSE | 570.1 | 34.80 | 30.76 | 22.70 | 20.85 | 311.90 | 21.31 | 14.73 | 15.06 | 14.05 | |
| R | 0.42 | 0.81 | 0.84 | 0.87 | 0.90 | 0.33 | 0.76 | 0.83 | 0.82 | 0.82 | |
| 95%/5% | MAE | 15.44 | 4.40 | 4.09 | 3.64 | 3.35 | 10.07 | 3.63 | 2.83 | 3.19 | 2.74 |
| MSE | 549.64 | 36.53 | 31.96 | 24.63 | 22.48 | 194.54 | 19.44 | 13.34 | 15.92 | 12.75 | |
| R | 0.42 | 0.80 | 0.83 | 0.86 | 0.88 | 0.18 | 0.57 | 0.72 | 0.60 | 0.74 | |
| Data Set Ratio | Metric | Raw | LR | MLR | MLP | SMART | PLR | Lasso | Ridge | DT | RF | GB | XGB | LGB |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 70%/ 30% | MAE | 8.92 | 3.54 | 3.60 | 3.60 | 3.32 | 3.31 | 3.40 | 3.60 | 4.00 | 3.00 | 3.00 | 2.98 | 3.15 |
| MSE | 182.31 | 21.99 | 22.49 | 23.70 | 21.56 | 19.21 | 20.71 | 22.49 | 30.18 | 16.69 | 16.45 | 16.26 | 17.82 | |
| R | 0.47 | 0.66 | 0.66 | 0.58 | 0.61 | 0.65 | 0.68 | 0.66 | 0.69 | 0.78 | 0.77 | 0.77 | 0.74 | |
| 80%/ 20% | MAE | 9.06 | 3.36 | 2.91 | 2.97 | 2.79 | 2.94 | 2.92 | 2.91 | 3.39 | 2.85 | 2.88 | 2.79 | 2.84 |
| MSE | 196.35 | 18.70 | 14.84 | 15.20 | 14.02 | 14.80 | 14.98 | 14.84 | 21.24 | 14.43 | 14.58 | 13.80 | 14.26 | |
| R | 0.41 | 0.71 | 0.76 | 0.66 | 0.76 | 0.75 | 0.75 | 0.76 | 0.71 | 0.77 | 0.78 | 0.78 | 0.79 | |
| 90%/ 10% | MAE | 11.67 | 3.62 | 2.86 | 2.84 | 2.80 | 2.87 | 2.85 | 2.86 | 3.81 | 2.95 | 2.85 | 2.85 | 2.95 |
| MSE | 311.90 | 21.31 | 14.73 | 15.06 | 14.05 | 14.67 | 14.61 | 14.73 | 26.74 | 15.11 | 14.78 | 14.71 | 15.54 | |
| R | 0.33 | 0.76 | 0.83 | 0.82 | 0.82 | 0.83 | 0.83 | 0.83 | 0.72 | 0.81 | 0.83 | 0.84 | 0.83 | |
| 95%/ 5% | MAE | 10.07 | 3.63 | 2.83 | 3.19 | 2.74 | 2.81 | 2.80 | 2.83 | 3.33 | 2.86 | 2.84 | 2.86 | 2.89 |
| MSE | 194.54 | 19.44 | 13.34 | 15.92 | 12.75 | 13.21 | 13.01 | 13.34 | 19.20 | 13.37 | 13.88 | 14.07 | 14.14 | |
| R | 0.17 | 0.57 | 0.72 | 0.60 | 0.74 | 0.72 | 0.71 | 0.72 | 0.67 | 0.71 | 0.75 | 0.74 | 0.74 |
| Category | Metric | Other Group – Shuffled (MLR) | Our Group – Shuffled (SMART) | Our Group – Sequential (SMART) |
|---|---|---|---|---|
| Before calibration | MAE | 5.8 | 15.1 | 11.4 |
| RMSE | 7.5 | 23.1 | 17.3 | |
After calibration | MAE | 3.2 | 3.4 | 2.8 |
| RMSE | 4.1 | 4.8 | 3.7 | |
| R | 0.57 | 0.89 | 0.81 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Kang, J.; Kim, S.; Im, Y.; Yoo, S.; Lee, D. Long-Term Evaluation and Calibration of Low-Cost Particulate Matter (PM) Sensor. Sensors 2020, 20, 3617. https://doi.org/10.3390/s20133617
Lee H, Kang J, Kim S, Im Y, Yoo S, Lee D. Long-Term Evaluation and Calibration of Low-Cost Particulate Matter (PM) Sensor. Sensors. 2020; 20(13):3617. https://doi.org/10.3390/s20133617
Chicago/Turabian StyleLee, Hoochang, Jiseock Kang, Sungjung Kim, Yunseok Im, Seungsung Yoo, and Dongjun Lee. 2020. "Long-Term Evaluation and Calibration of Low-Cost Particulate Matter (PM) Sensor" Sensors 20, no. 13: 3617. https://doi.org/10.3390/s20133617
APA StyleLee, H., Kang, J., Kim, S., Im, Y., Yoo, S., & Lee, D. (2020). Long-Term Evaluation and Calibration of Low-Cost Particulate Matter (PM) Sensor. Sensors, 20(13), 3617. https://doi.org/10.3390/s20133617





