Performance Degradation Prediction Based on a Gaussian Mixture Model and Optimized Support Vector Regression for an Aviation Piston Pump
Abstract
1. Introduction
2. The Performance Degradation Prediction Method
2.1. Degradation Feature Extraction and Selection
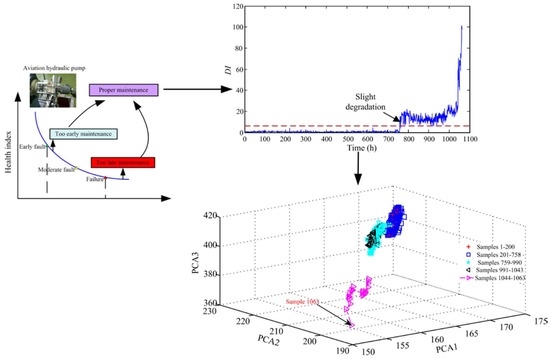
2.2. DI Sequences Acquisition Based on GMM
2.2.1. Brief Description of GMM
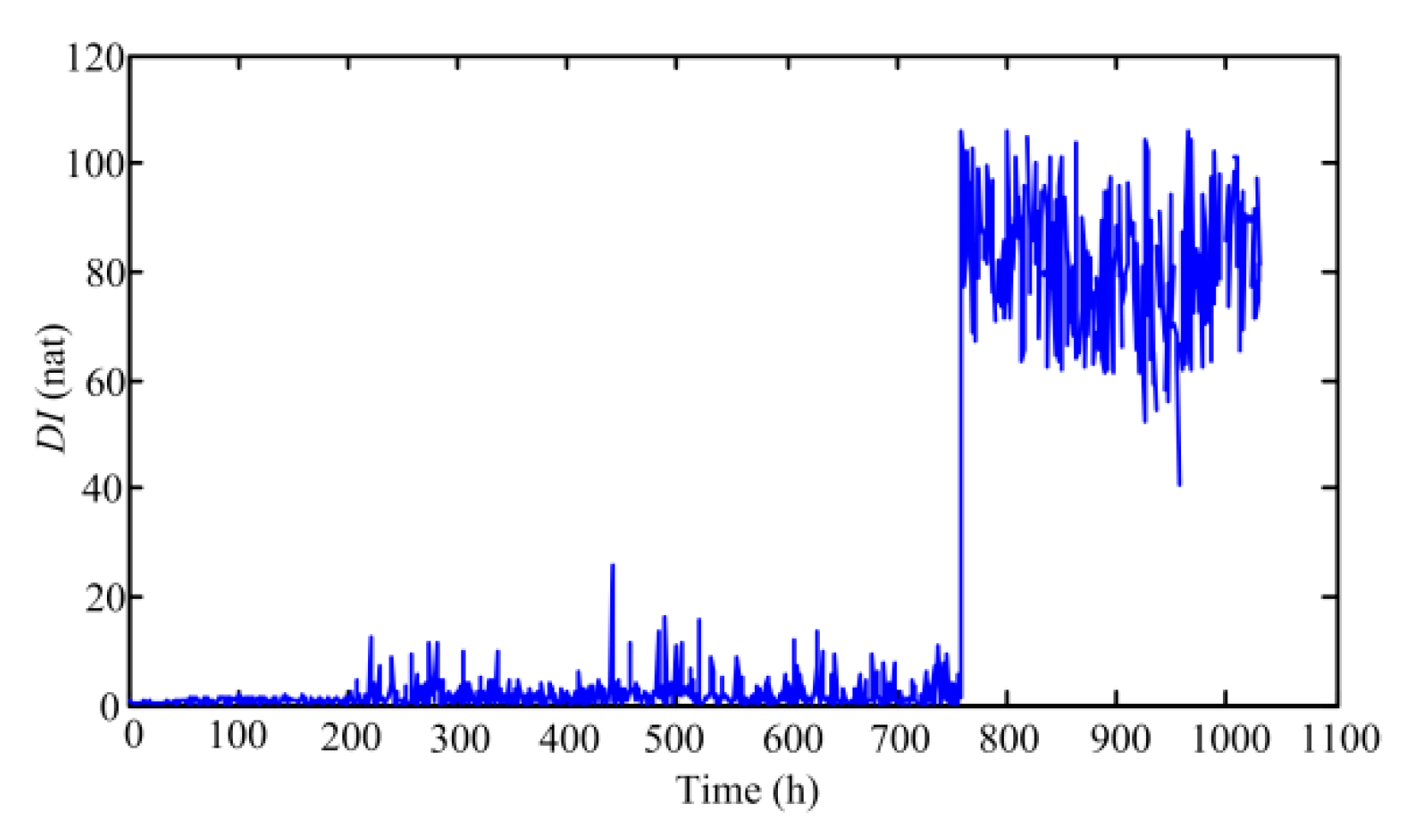
2.2.2. DI Obtained from GMM
2.3. Degradation Prediction Based on Optimized SVR Model
2.3.1. The Basic Theory of SVR
2.3.2. Optimization of SVR Prediction Model
Determination of Inputs of SVR Model
Internal Parameters Optimization of SVR Model
Utilization of On-Line Data and Historical Data
3. Results and Experimental Validation
3.1. Experimental Platform
3.2. Experimental Results and Analysis
4. Comparisons and Discussion
5. Conclusions
- (1)
- The multi-domain features extracted from EEMD paving based on pump outlet pressure signals can successfully characterize the degradation degree of the pump than traditional features, such as RMS and WI.
- (2)
- The DI derived from GMM can effectively identify and track the current deterioration stage, which enables the determination of the critical fault occurrence accurately and the realization of condition-based maintenance.
- (3)
- The proposed method provides a useful tool for multi-step ahead prediction of the DI and has higher accuracy compared to some previously published methods, including BP, GA-SVR, and so on.
- (4)
- As full life cycle experiment of the aviation pump is expensive and very time-consuming, there is only few life samples, which will affect the further verification of the method. Meanwhile, the weights of the models are given according to the experience. In the future, some research will be explored on how to determine the weights more reasonably.
Author Contributions
Funding
Conflicts of Interest
References
- Ma, Z.H.; Wang, S.P.; Shi, J.; Li, T.Y.; Wang, X.J. Fault diagnosis of an intelligent hydraulic pump based on a nonlinear unknown input observer. Chin. J. Aeronaut. 2018, 31, 385–394. [Google Scholar] [CrossRef]
- Lu, C.Q.; Wang, S.P.; Wang, X.J. A multi-source information fusion fault diagnosis for aviation hydraulic pump based on the new evidence similarity distance. Aerosp. Sci. Technol. 2017, 71, 392–401. [Google Scholar] [CrossRef]
- Wang, X.J.; Lin, S.R.; Wang, S.P.; He, Z.M.; Zhang, C. Remaining useful life prediction based on the Wiener process for an aviation axial piston pump. Chin. J. Aeronaut. 2016, 29, 779–788. [Google Scholar] [CrossRef]
- Du, J.; Wang, S.P.; Zhang, H.Y. Layered clustering multi-fault diagnosis for hydraulic piston pump. Mech. Syst. Signal Process. 2013, 36, 487–504. [Google Scholar] [CrossRef]
- Lu, C.Q.; Wang, S.P.; Wang, X.J. Fault severity recognition of aviation piston pump based on feature extraction of EEMD paving and optimized support vector regression model. Aerosp. Sci. Technol. 2017, 67, 105–117. [Google Scholar] [CrossRef]
- Pan, Y.N.; Chen, J.; Li, X.L. Bearing performance degradation assessment based on lifting wavelet packet decomposition and fuzzy c-means. Mech. Syst. Signal Process. 2010, 24, 559–566. [Google Scholar] [CrossRef]
- Tong, Q.J.; Hu, J.Z. Bearing performance degradation assessment based on information-theoretic metric learning and fuzzy C-means clustering. Meas. Sci. Technol. 2020, 31, 075001. [Google Scholar]
- Wang, B.; Hu, X.; Li, H.R. Rolling bearing performance degradation condition recognition based on mathematical morphological fractal dimension and fuzzy C-means. Measurement 2017, 109, 1–8. [Google Scholar] [CrossRef]
- Hong, S.; Zhou, Z.; Zio, E.; Hong, K. Condition assessment for the performance degradation of bearing based on a combinatorial feature extraction method. Digit. Signal Process. 2014, 27, 159–166. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, B.P.; Han, Y.; Deng, L. Bearing performance degradation assessment based on time-frequency code features and SOM network. Meas. Sci. Technol. 2017, 28, 045601. [Google Scholar] [CrossRef]
- Yu, J.B. Bearing performance degradation assessment using locality preserving projections and Gaussian mixture models. Mech. Syst. Signal Process. 2011, 7, 2573–2588. [Google Scholar] [CrossRef]
- Liu, H.M.; Zhang, J.C.; Lu, C. Performance degradation prediction for a hydraulic servo system based on Elman network observer and GMM-SVR. Appl. Math. Model. 2015, 39, 5882–5895. [Google Scholar] [CrossRef]
- Pham, H.T.; Yang, B.S. Estimation and forecasting of machine health condition using ARMA/GARCH model. Mech. Syst. Signal Process. 2010, 24, 546–558. [Google Scholar] [CrossRef]
- Wang, Y.R.; Wang, D.C.; Tang, Y. Clustered hybrid wind power prediction model based on ARMA, PSO-SVM, and clustering Methods. IEEE Access 2020, 8, 17071–17079. [Google Scholar] [CrossRef]
- Baptista, M.; Sankararaman, S.; de Medeiros, I.P.; Nascimento, C., Jr.; Prendinger, H.; Henriques, E.M.P. Forecasting fault events for predictive maintenance using data-driven techniques and ARMA modeling. Comput. Ind. Eng. 2018, 115, 41–53. [Google Scholar] [CrossRef]
- Yan, W.Z.; Zhang, B.; Zhao, G.Q.; Tang, S.J.; Niu, G.X.; Wang, X.F. A battery management system with a lebesgue-sampling-based extended Kalman filter. IEEE Trans. Ind. Electron. 2019, 66, 3227–3236. [Google Scholar] [CrossRef]
- Zuluaga, C.D.; Alvarez, M.A.; Giraldo, E. Short-term wind speed prediction based on robust Kalman filtering: An experimental comparison. Appl. Energy 2015, 156, 321–330. [Google Scholar] [CrossRef]
- Mahamad, A.K.; Saon, S.; Hiyama, T. Predicting remaining useful life of rotating machinery based artificial neural network. Comput. Math. Appl. 2010, 60, 1078–1087. [Google Scholar] [CrossRef]
- Ali, J.B.; Chebel-Morello, B.; Saidi, L.; Malinowski, S.; Fnaiech, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56, 150–172. [Google Scholar]
- Pan, Y.B.; Hong, R.J.; Chen, J.; Wu, W.W. A hybrid DBN-SOM-PF-based prognostic approach of remaining useful life for wind turbine gearbox. Renew. Energy 2020, 152, 138–154. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, S.H.; Li, W.H. Bearing performance degradation assessment using long short-term memory recurrent network. Comput. Ind. 2019, 106, 14–29. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.P.; Jia, F.; Lei, Y.G.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Smola, A.J.; Scholkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Dong, S.J.; Luo, T.H. Bearing degradation process prediction based on PCA and optimized LS-SVM model. Measurement 2013, 46, 3143–3152. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, S.B.; Lee, J.H. Data-Driven Prediction of Vessel Propulsion Power Using Support Vector Regression with Onboard Measurement and Ocean Data. Sensors 2020, 20, 1588. [Google Scholar] [CrossRef]
- Shen, C.Q.; Wang, D.; Liu, Y.B.; Kong, F.R.; Tse, P.W. Recognition of rolling bearing fault patterns and sizes based on two-layer support vector regression model. Smart Struct. Syst. 2014, 13, 453–471. [Google Scholar] [CrossRef]
- Soualhi, A.; Medjaher, K.; Zerhouni, N. Bearing health monitoring based on hilbert-huang transform, support vector machine, and regression. IEEE Trans. Instrum. Meas. 2015, 64, 52–62. [Google Scholar] [CrossRef]
- Gao, Y.J.; Zhang, Q. A wavelet packet and residual analysis based method for hydraulic pump health diagnosis. J. Automob. Eng. 2006, 220, 735–745. [Google Scholar] [CrossRef]
- Grasso, M.; Pennacchi, P.; Colosimo, B.M. Empirical mode decomposition of pressure signal for health condition monitoring in waterjet cutting. Int. J. Adv. Manuf. Technol. 2014, 72, 347–364. [Google Scholar] [CrossRef][Green Version]
- Lu, C.Q.; Wang, S.P.; Tomvic, M. Fault severity recognition of hydraulic piston pumps based on EMD and feature energy entropy. In Proceedings of the 2015 IEEE 10th Conference on Industrial Electronics and Applications (ICIEA), Auckland, New Zealand, 15–17 June 2015; pp. 489–494. [Google Scholar]
- Kembe, G.; Fowler, A.C. A correlation function for choosing time delays in phase portrait reconstructions. Phys. Lett. A 1993, 179, 72–80. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. Reconstruction expansion as a geometry-based framework for choosing proper delay times. Phys. D Nonlinear Phenom. 1994, 73, 82–98. [Google Scholar] [CrossRef]
- Albano, A.M.; Passamante, A.; Farrell, M.E. Using higher-order correlations to define an embedding window. Phys.-Sect. D 1991, 54, 85–97. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.Y. Practical method for determining the minimum embedding dimension of a scalar time series. Phys. D Nonlinear Phenom. 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Sarosh, A.; Dong, Y.F. The GA-ANN expert system for mass-model classification of TSTO surrogates. Aerosp. Sci. Technol. 2016, 48, 146–157. [Google Scholar] [CrossRef]
- Jaffel, I.; Taouali, O.; Harkat, M.F.; Messaoud, H. Kernel principal component analysis with reduced complexity for nonlinear dynamic process monitoring. Int. J. Adv. Manuf. Technol. 2017, 88, 3265–3279. [Google Scholar] [CrossRef]













| Square root amplitude value: | Impulsive index: |
| Shape index: | Clearance index: |
| Crest index: | Root mean square frequency: |
| Skewness index: | Centroid frequency: |
| Kurtosis index: | Frequency variation: |
| Hilbert marginal spectrum-based energy entropy: | |
| Parameter | The Value |
|---|---|
| The maximum number of generations | 200 |
| The number of the particles | 20 |
| Learn factors | 1.5,1.7 |
| Inertia weight | 1 |
| The initial range of C | [0,1000] |
| The initial range of σ | [0,100] |
| The initial range of ε | [0.001,1] |
| H | MRE | ARE | RMSE |
|---|---|---|---|
| 29 | 0.1079 | 0.0323 | 0.85 |
| 50 | 0.1188 | 0.0363 | 2.82 |
| Methods | H | MRE | ARE | RMSE |
|---|---|---|---|---|
| GS-SVR | 29 | 0.3605 | 0.1422 | 3.66 |
| 50 | 0.4889 | 0.1464 | 9.02 | |
| GA-SVR | 29 | 0.3605 | 0.1434 | 3.74 |
| 50 | 0.3605 | 0.1256 | 5.29 | |
| PSO-SVR | 29 | 0.3110 | 0.0615 | 1.92 |
| 50 | 0.3110 | 0.0779 | 7.32 | |
| BP | 29 | 0.3250 | 0.078 | 2.13 |
| 50 | 0.3887 | 0.0719 | 5.27 | |
| LSTM | 29 | 0.1686 | 0.0537 | 1.68 |
| 50 | 0.3087 | 0.0874 | 7.28 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Wang, S. Performance Degradation Prediction Based on a Gaussian Mixture Model and Optimized Support Vector Regression for an Aviation Piston Pump. Sensors 2020, 20, 3854. https://doi.org/10.3390/s20143854
Lu C, Wang S. Performance Degradation Prediction Based on a Gaussian Mixture Model and Optimized Support Vector Regression for an Aviation Piston Pump. Sensors. 2020; 20(14):3854. https://doi.org/10.3390/s20143854
Chicago/Turabian StyleLu, Chuanqi, and Shaoping Wang. 2020. "Performance Degradation Prediction Based on a Gaussian Mixture Model and Optimized Support Vector Regression for an Aviation Piston Pump" Sensors 20, no. 14: 3854. https://doi.org/10.3390/s20143854
APA StyleLu, C., & Wang, S. (2020). Performance Degradation Prediction Based on a Gaussian Mixture Model and Optimized Support Vector Regression for an Aviation Piston Pump. Sensors, 20(14), 3854. https://doi.org/10.3390/s20143854