Antenna Combining for Interference Limited MIMO Cellular Networks
Abstract
:1. Introduction
- Conventional antenna combining methods are investigated in an interference limited MIMO cellular network. In this network, it is found that the gain of the QBC method is limited because the inter-cell interference is more dominant than the intra-cell multiuser interference induced by a quantization error. Therefore, the QBC method has a lower performance than the maximum-ratio combining (MRC) method despite the small number of feedback bits.
- The QBC method is proposed for interference limited MIMO cellular networks. Conventional analysis framework described in [18,23,32] using random vector quantization (RVQ) is not applicable in interference limited MIMO cellular networks. Thus, the SCVQ model is approximated on the assumption of many feedback bits. From this approximation, it is shown that the QBC method reduces the dimension of the effective single antenna channel to where the numbers of transmit and receive antennas are and respectively. Accordingly, the ergodic spectral efficiency and the optimal number of feedback bits for the QBC method are reduced compared to that of the MRC method where the number of feedback bits increases.
- A selective antenna combining solution is proposed to overcome the reduction. The optimization problem is first introduced that enables selection of the antenna combining solution to maximize the ergodic spectral efficiency. Because the inter-cell interference is important in selecting the antenna combining, especially for cellular networks, the inter-cell interference is only averaged over beamforming vectors of other cells and the distance information in the cell interference is conserved. The required number of other cells to measure the inter-cell interference is derived from the simulation.
2. System Model
2.1. Signal Model
2.2. Quantization-Based Combining
2.3. Finite Rate Feedback Model
2.4. Performance Metric
3. Spherical-Cap Approximation of Vector Quantization-Based Analysis
4. Proposed Antenna Combining Method
4.1. Problem Formulation
4.2. Proposed Algorithm
| Algorithm 1: Proposed algorithm |
| 1 Initialization: |
| 2 Obtain the channel information |
| 3 fordo |
| 4 |
| 5 Calculate the antenna combining |
| 6 Compute the effective channel |
| 7 Obtain the distance and , |
| 8 Calculate the expected SINR in [28] |
| 9 end |
| 10 |
| 11 Determine the antenna combining vector . |
| 12 Select the codebook index from the effective channel |
| 13 Obtain the quantized CDI and its index |
| 13 Feedback the quantized index to the BS. |
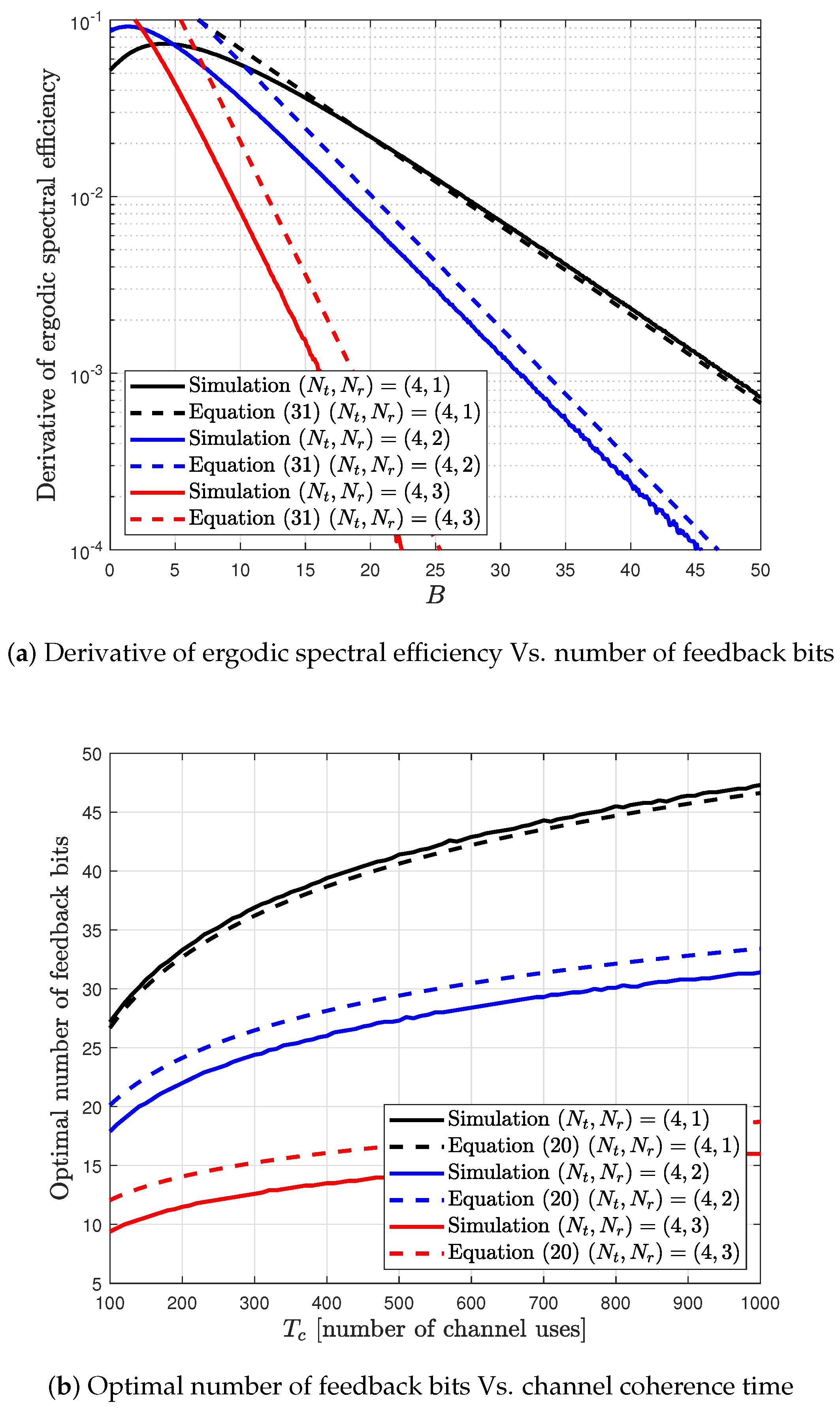
5. Simulation Results
6. Conclusions
Funding
Conflicts of Interest
Appendix A. Proof of Lemma 1
References
- Tse, D.N.C.; Viswanath, P. Fundamentals of Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Biglieri, E.; Calderbank, R.; Constantinides, A.; Goldsmith, A.; Paulraj, A.; Poor, H.V. MIMO Wireless Communications; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Hassan, N.; Fernando, X. Massive MIMO Wireless Networks: An overview. Electronics 2017, 6, 63. [Google Scholar] [CrossRef] [Green Version]
- Caire, G.; Shamai, S. On the achievable throughput of a multiantenna Gaussian broadcast channel. IEEE Trans. Inf. Theory 2003, 49, 1691–1706. [Google Scholar] [CrossRef]
- Jindal, N.; Goldsmith, A. Dirty-paper coding versus TDMA for MIMO Broadcast channels. IEEE Trans. Inf. Theory 2005, 51, 1783–1794. [Google Scholar] [CrossRef]
- Yoo, T.; Goldsmith, A. On the optimality of multiantenna broadcast scheduling using zero-forcing beamforming. IEEE J. Sel. Areas Commun. 2006, 24, 528–541. [Google Scholar]
- Yoo, T.; Jindal, N.; Goldsmith, A. Multi-antenna downlink channels with limited feedback and user selection. IEEE J. Sel. Areas Commun. 2007, 25, 1478–1491. [Google Scholar] [CrossRef]
- Love, D.J.; Heath, R.W. Limited feedback unitary precoding for spatial multiplexing systems. IEEE J. Sel. Areas Commun. 2005, 51, 2967–2976. [Google Scholar] [CrossRef]
- Au-Yeung, C.K.; Love, D. On the performance of random vector quantization limited feedback beamforming in a MISO system. IEEE Trans. Wirel. Commun. 2007, 6, 458–462. [Google Scholar] [CrossRef]
- Caire, G.; Jindal, N.; Kobayashi, M.; Ravindran, N. Multiuser MIMO achievable rates with downlink training and channel state feedback. IEEE Trans. Inf. Theory 2010, 56, 2845–2866. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.K.; Min, M. On the accuracy of quantization cell approximation in MIMO broadcast systems based on limited feedback. IEEE Access 2020, 8, 73432–73450. [Google Scholar] [CrossRef]
- Love, D.J. Duplex distortion models for limited feedback MIMO communication. IEEE Trans. Signal Process. 2006, 54, 766–774. [Google Scholar] [CrossRef]
- Kobayashi, M.; Jindal, N.; Caire, G. Training and feedback optimization for multiuser MIMO downlink. IEEE Trans. Commun. 2011, 59, 2228–2240. [Google Scholar] [CrossRef]
- Rajanna, A.; Jindal, N. Multiuser diversity in downlink channels: When does the feedback cost outweigh the spectral efficiency benefit? IEEE Trans. Wirel. Commun. 2012, 11, 408–418. [Google Scholar] [CrossRef]
- Min, M.; Jeon, Y.S.; Im, G.H. On achievable multiplexing gain of BD in MIMO broadcast channels with limited feedback. IEEE Trans. Wirel. Commun. 2016, 15, 871–885. [Google Scholar] [CrossRef]
- Min, M.; Jeon, Y.S.; Im, G.H. On achievable rate of user selection for MIMO broadcast channels with limited feedback. IEEE Trans. Commun. 2017, 65, 122–135. [Google Scholar] [CrossRef]
- Jindal, N. MIMO broadcast channels with finite-rate feedback. IEEE Trans. Inf. Theory 2006, 52, 5045–5060. [Google Scholar] [CrossRef] [Green Version]
- Jindal, N. Antenna combining for the MIMO downlink channel. IEEE Trans. Wirel. Commun. 2008, 7, 3834–3844. [Google Scholar] [CrossRef] [Green Version]
- Bjornson, E.; Kountouris, M.; Bengtsson, M.; Ottersten, B. Receive Combining vs. Multi-stream multiplexing in downlink systems with multi-antenna users. IEEE Trans. Signal Process. 2013, 61, 3431–3446. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.S.; Min, M. Grouped channel quantization and antenna combining for multiuser MIMO OFDM systems. IEEE Commun. Lett. 2014, 18, 2217–2220. [Google Scholar] [CrossRef]
- Schwarz, S.; Rupp, M. Subspace quantization based combining for limited feedback block-diagonalization. IEEE Trans. Wirel. Commun. 2013, 12, 5868–5879. [Google Scholar] [CrossRef]
- Sanchez-Garcia, J.; Soriano-Equigua, L.; Heath, R.W. Quantized antenna combining for multiuser MIMO-OFDM with limited feedback. IEEE Signal Process. Lett. 2009, 16, 1027–1030. [Google Scholar] [CrossRef]
- Song, J.; Lee, B.; Noh, S.; Lee, J.H. Limited feedback designs for machine-type communications exploiting user cooperation. IEEE Access 2019, 7, 95154–95169. [Google Scholar] [CrossRef]
- Dhillon, H.S.; Kountouris, M.; Andrews, J.G. Downlink MIMO HetNets: Modeling ordering results and performance analysis. IEEE Trans. Wirel. Commun. 2013, 12, 5208–5222. [Google Scholar] [CrossRef] [Green Version]
- Renzo, M.D.; Guan, P. A mathematical framework to the computation of the error probability of downlink MIMO cellular networks by using stochastic geometry. IEEE Trans. Commun. 2014, 62, 2860–2879. [Google Scholar] [CrossRef]
- Li, C.; Zhang, J.; Andrews, J.G.; Letaief, K.B. Success probability and area spectral efficiency in multiuser MIMO HetNets. IEEE Trans. Commun. 2016, 64, 1544–1556. [Google Scholar] [CrossRef]
- ElSawy, H.; Sultan-Salem, A.; Alouini, M.S.; Win, M.Z. Modeling and analysis of cellular networks using stochastic geometry: A tutorial. IEEE Commun. Surv. Tutorials 2017, 19, 167–203. [Google Scholar] [CrossRef] [Green Version]
- Renzo, M.; Lu, W. Stochastic geometry modeling and performance evaluation of MIMO cellular networks using the equivalent-indistribution (EiD)-based approach. IEEE Trans. Commun. 2015, 63, 977–996. [Google Scholar] [CrossRef]
- Park, J.; Lee, N.; Andrews, J.G.; Heath, R.W. On the optimal feedback rate in interference-limited multi-antenna cellular systems. IEEE Trans. Wirel. Commun. 2016, 15, 5748–5762. [Google Scholar] [CrossRef]
- Min, M. Bounds on the optimal feedback rate for multi-antenna systems in interference-limited cellular networks. IEEE Trans. Wirel. Commun. 2018, 17, 4845–4860. [Google Scholar] [CrossRef]
- Kang, Y.S.; Min, M. Unified derivation of optimal feedback rate in multiple antenna cellular networks. IEEE Access 2019, 7, 161871–161884. [Google Scholar] [CrossRef]
- Son, H.; Kim, S.; Lee, S. A multi-user MIMO downlink receiver and quantizer design based on SINR optimization. IEEE Trans. Commun. 2012, 60, 559–568. [Google Scholar] [CrossRef]
- Baccelli, F.; Blaszczyszyn, B. Stochastic Geometry and Wireless Networks, Volume I—Theory; ser. Foundations and Trends in Networking; NOW Publishers: Paris, France, 2009. [Google Scholar]
- Mukkavilli, K.K.; Sabharwal, A.; Erkip, E.; Aazhang, B. On beamforming with finite rate feedback in multiple-antenna systems. IEEE Trans. Inf. Theory 2003, 49, 2562–2579. [Google Scholar] [CrossRef] [Green Version]
- Lee, N.; Baccelli, F.; Heath, R.W. Spectral efficiency scaling laws in dense random wireless networks with multiple receive antennas. IEEE Trans. Inf. Theory 2016, 62, 1344–1359. [Google Scholar] [CrossRef]







© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.-K. Antenna Combining for Interference Limited MIMO Cellular Networks. Sensors 2020, 20, 4210. https://doi.org/10.3390/s20154210
Kim T-K. Antenna Combining for Interference Limited MIMO Cellular Networks. Sensors. 2020; 20(15):4210. https://doi.org/10.3390/s20154210
Chicago/Turabian StyleKim, Tae-Kyoung. 2020. "Antenna Combining for Interference Limited MIMO Cellular Networks" Sensors 20, no. 15: 4210. https://doi.org/10.3390/s20154210




