Prediction of Soil Organic Carbon in a New Target Area by Near-Infrared Spectroscopy: Comparison of the Effects of Spiking in Different Scale Soil Spectral Libraries
Abstract
1. Introduction
2. Materials and Methods
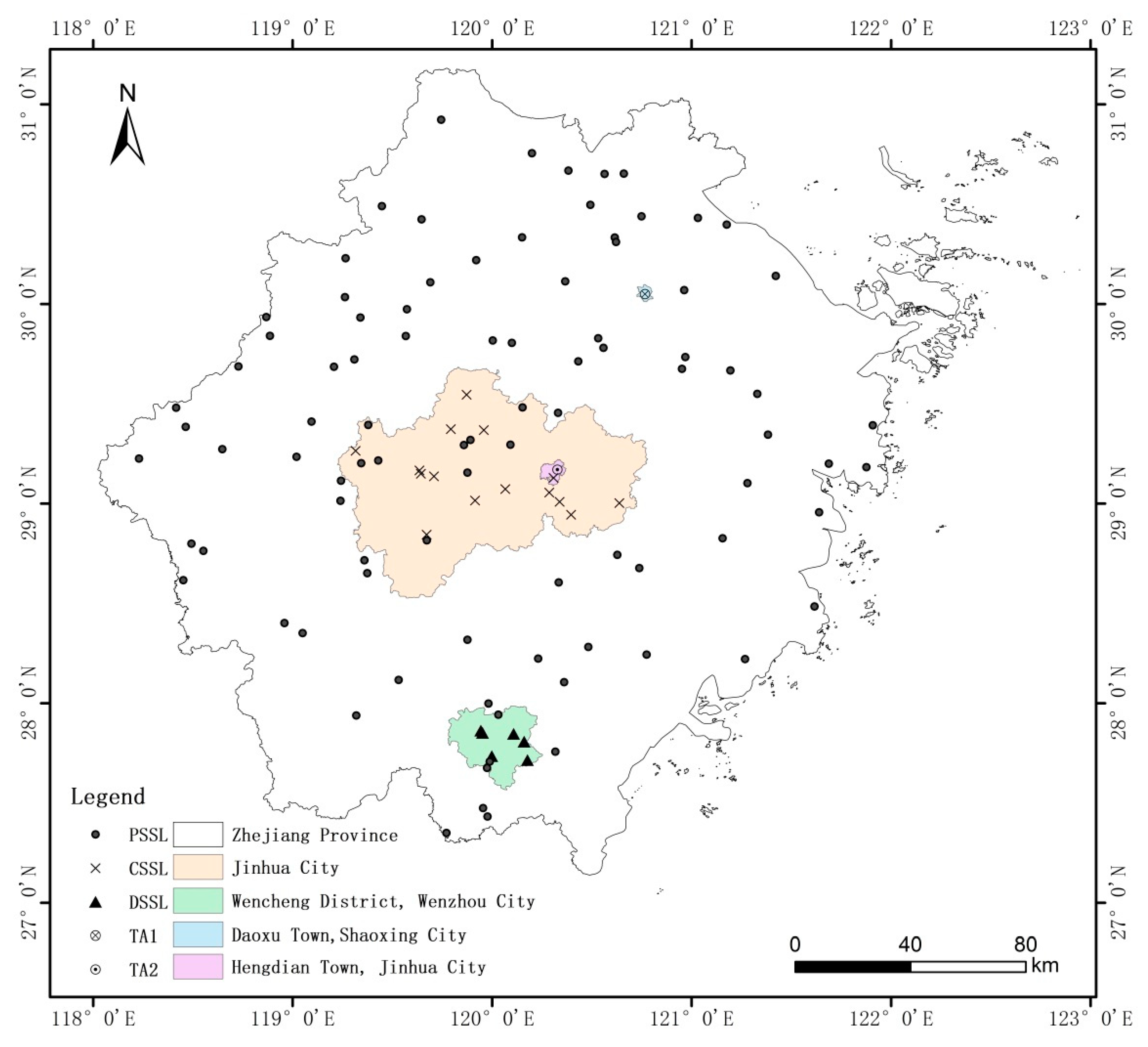
2.1. Soil Samples
2.2. NIR Spectral Data Measurement
2.3. Modeling Methods
2.4. Model Evaluation
2.5. Stastical Analysis
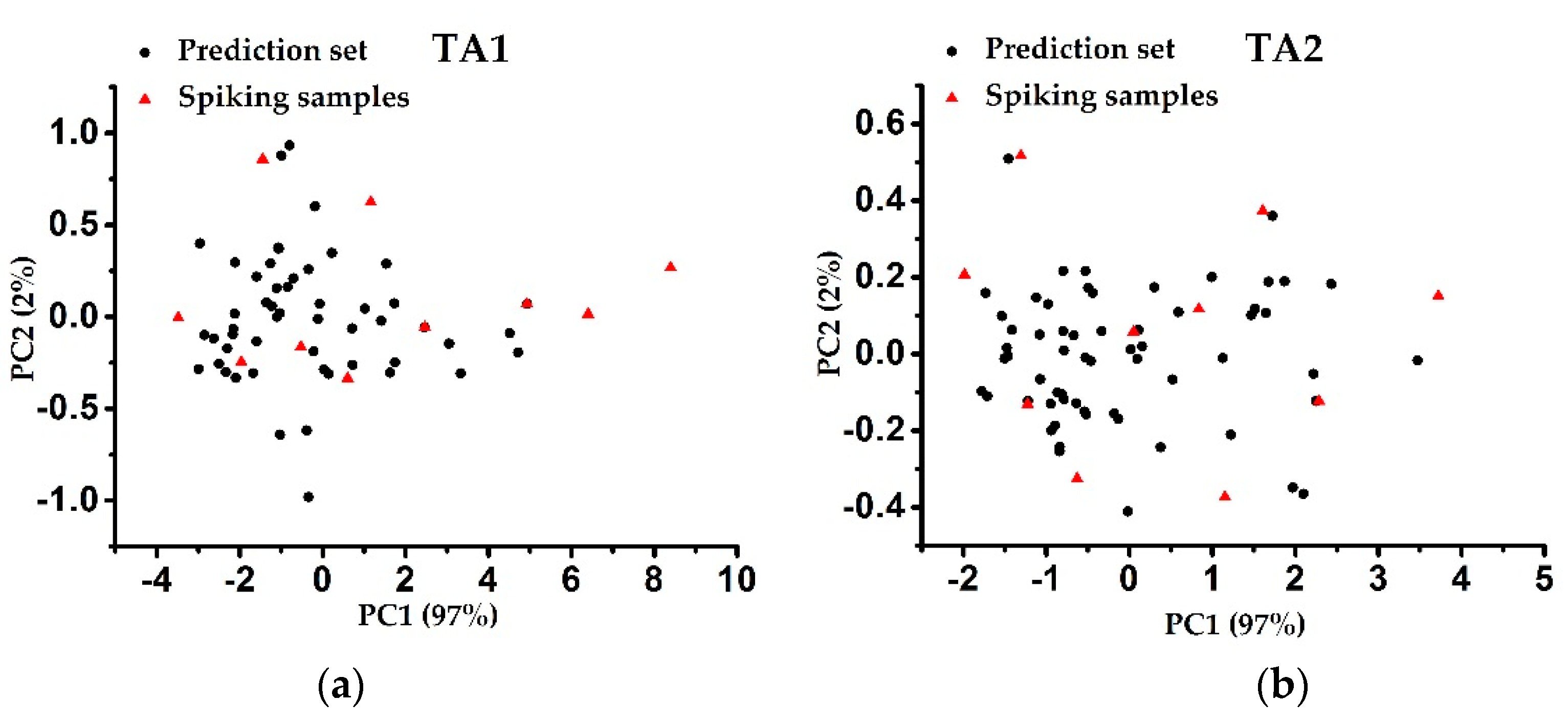
3. Results and Discussion
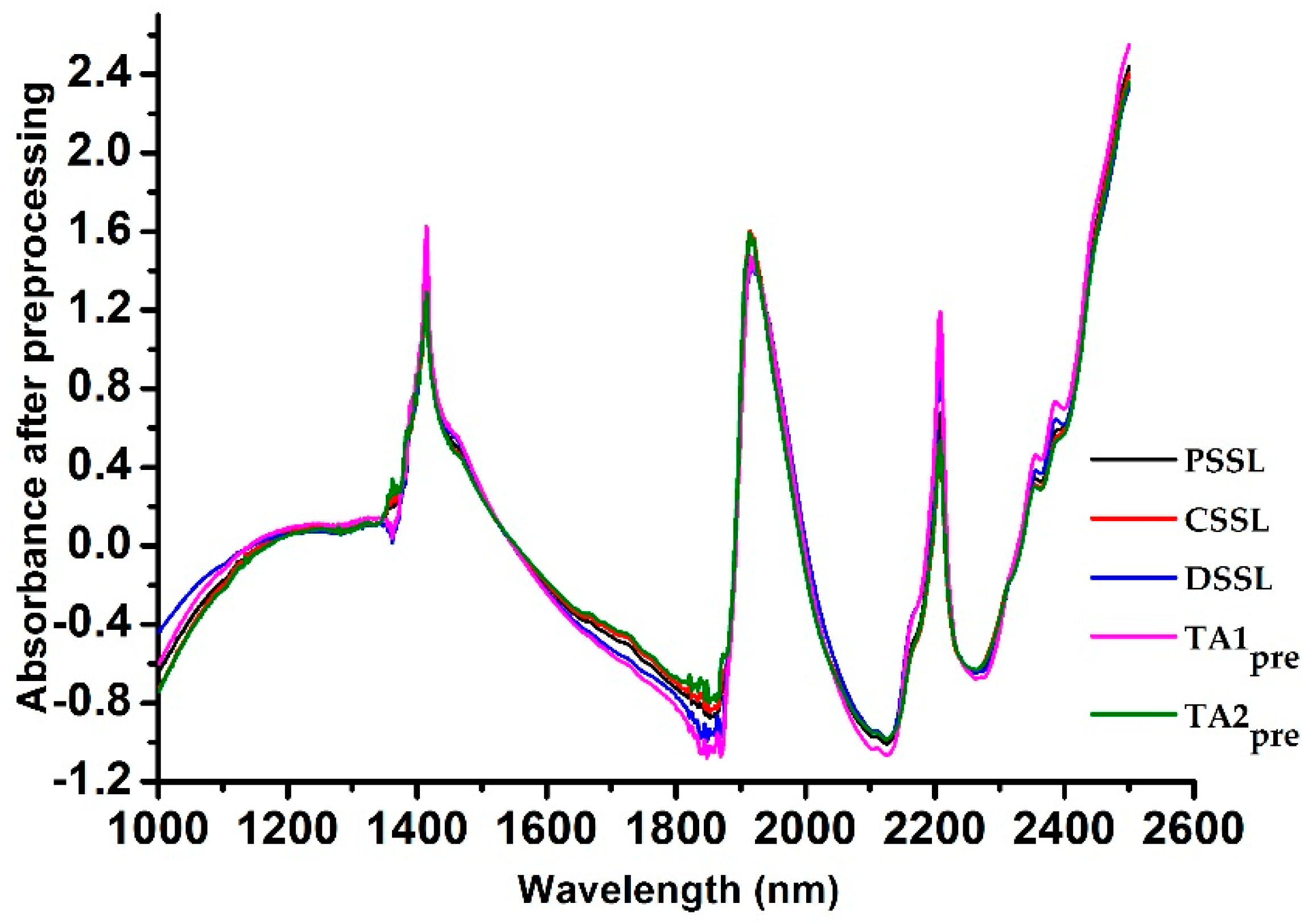
3.1. Soil Spectrum
3.2. ANOVA Test
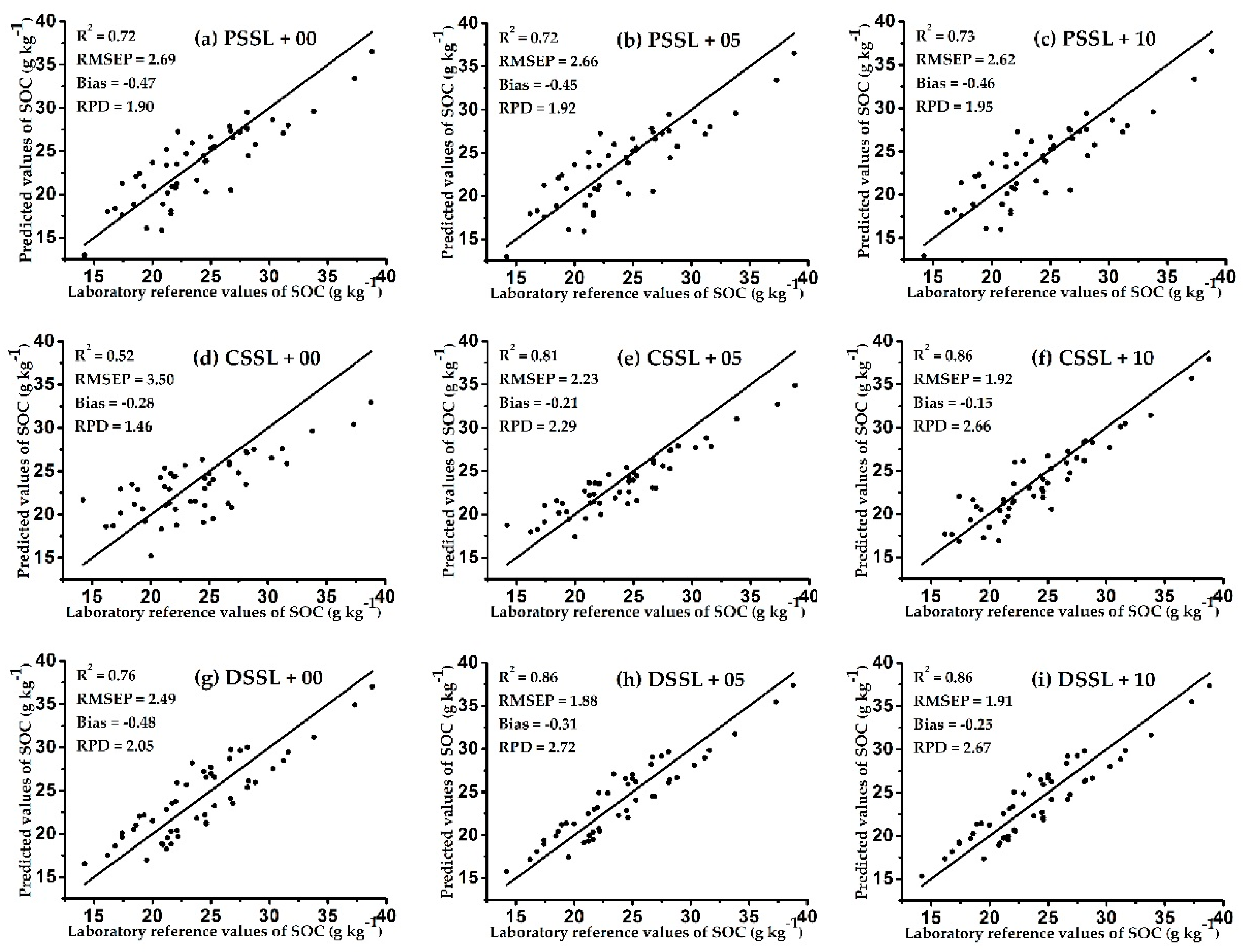
3.3. Unspiked Models
3.4. Spiked Models
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, T. Effects Of Different Fertilisation Technologies And Cultivation Technology on Soil Organic Carbon Content. Appl. Ecol. Environ. Res. 2019, 17, 10491–10507. [Google Scholar] [CrossRef]
- Pei, X.; Sudduth, K.A.; Veum, K.S.; Li, M. Improving In-Situ Estimation of Soil Profile Properties Using a Multi-Sensor Probe. Sensors (Basel) 2019, 19, 1011. [Google Scholar] [CrossRef]
- Mikhailova, E.A.; Groshans, G.R.; Post, C.J.; Schlautman, M.A.; Post, G.C. Valuation of Soil Organic Carbon Stocks in the Contiguous United States Based on the Avoided Social Cost of Carbon Emissions. Resources 2019, 8, 153. [Google Scholar] [CrossRef]
- Tamburini, E.; Vincenzi, F.; Costa, S.; Mantovi, P.; Pedrini, P.; Castaldelli, G. Effects of Moisture and Particle Size on Quantitative Determination of Total Organic Carbon (TOC) in Soils Using Near-Infrared Spectroscopy. Sensors (Basel) 2017, 17, 2366. [Google Scholar] [CrossRef]
- He, Y.; Huang, M.; García, A.; Hernández, A.; Song, H. Prediction of soil macronutrients content using near-infrared spectroscopy. Comput. Electron. Agric. 2007, 58, 144–153. [Google Scholar] [CrossRef]
- Reda, R.; Saffaj, T.; Ilham, B.; Saidi, O.; Issam, K.; Brahim, L.; El Hadrami, E.M. A comparative study between a new method and other machine learning algorithms for soil organic carbon and total nitrogen prediction using near infrared spectroscopy. Chemom. Intell. Lab. Syst. 2019, 195, 103873. [Google Scholar] [CrossRef]
- Stevens, A.; Nocita, M.; Toth, G.; Montanarella, L.; van Wesemael, B. Prediction of Soil Organic Carbon at the European Scale by Visible and Near InfraRed Reflectance Spectroscopy. PLoS ONE 2013, 8, e66409. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, Z.; Zhang, G.; Chen, Y.; Li, S.; Hong, Y.; Shi, T.; Wang, J.; Liu, Y. Application of Spectrally Derived Soil Type as Ancillary Data to Improve the Estimation of Soil Organic Carbon by Using the Chinese Soil Vis-NIR Spectral Library. Remote Sens. 2018, 10, 1747. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V.; et al. A global spectral library to characterize the world’s soil. Earth-Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef]
- Nocita, M.; Stevens, A.; Toth, G.; Panagos, P.; van Wesemael, B.; Montanarella, L. Prediction of soil organic carbon content by diffuse reflectance spectroscopy using a local partial least square regression approach. Soil Biol. Biochem. 2014, 68, 337–347. [Google Scholar] [CrossRef]
- Wetterlind, J.; Stenberg, B. Near-infrared spectroscopy for within-field soil characterization small local calibrations compared with national libraries spiked with local samples. Eur. J. Soil Sci. 2010, 61, 823–843. [Google Scholar] [CrossRef]
- Brown, D.J. Using a global VNIR soil-spectral library for local soil characterization and landscape modeling in a 2nd-order Uganda watershed. Geoderma 2007, 140, 444–453. [Google Scholar] [CrossRef]
- Guerrero, C.; Zornoza, R.; Gómez, I.; Mataix-Beneyto, J. Spiking of NIR regional models using samples from target sites: Effect of model size on prediction accuracy. Geoderma 2010, 158, 66–77. [Google Scholar] [CrossRef]
- Guy, A.L.; Siciliano, S.D.; Lamb, E.G. Spiking regional vis-NIR calibration models with local samples to predict soil organic carbon in two High Arctic polar deserts using a vis-NIR probe. Can. J. Soil Sci. 2015, 95, 237–249. [Google Scholar] [CrossRef]
- Gogé, F.; Gomez, C.; Jolivet, C.; Joffre, R. Which strategy is best to predict soil properties of a local site from a national Vis–NIR database? Geoderma 2014, 213, 1–9. [Google Scholar] [CrossRef]
- Jia, S.; Li, H.; Wang, Y.; Tong, R.; Li, Q. Hyperspectral Imaging Analysis for the Classification of Soil Types and the Determination of Soil Total Nitrogen. Sensors 2017, 17, 2252. [Google Scholar] [CrossRef]
- Jia, S.; Li, H.; Wu, X.; Li, Q. Laboratory-based hyperspectral image analysis for the classification of soil texture. J. Appl. Remote Sens. 2019, 13, 1. [Google Scholar] [CrossRef]
- Jia, S.; Yang, X.; Zhang, J.; Li, G. Quantitative Analysis of Soil Nitrogen, Organic Carbon, Available Phosphorous, and Available Potassium Using Near-Infrared Spectroscopy Combined With Variable Selection. Soil Sci. 2014, 179, 211–219. [Google Scholar] [CrossRef]
- Carra, J.B.; Fabris, M.; Dieckow, J.; Brito, O.R.; Vendrame, P.R.S.; Macedo Dos Santos Tonial, L. Near-Infrared Spectroscopy Coupled with Chemometrics Tools: A Rapid and Non-Destructive Alternative on Soil Evaluation. Commun. Soil Sci. Plant. Anal. 2019, 50, 421–434. [Google Scholar] [CrossRef]
- Nie, P.; Dong, T.; He, Y.; Qu, F. Detection of Soil Nitrogen Using Near Infrared Sensors Based on Soil Pretreatment and Algorithms. Sensors (Basel) 2017, 17, 1102. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, R.; Qi, T.; Qi, L.; Zhang, C. Constructing Representative Calibration Dataset Based on Spectral Transformation and Kennard-Stone Algorithm for VNIR Modeling of Soil Total Nitrogen in Paddy Soil. Spectrosc. Spectr. Anal. 2017, 37, 2133–2139. [Google Scholar]
- Jia, S.; Zhang, J.; Li, G.; Yang, X. Predicting Soil Nitrogen and Organic Carbon Using Near Infrared SpectroscopyCoupled with Variable Selection. Appl. Eng. Agric. 2014, 30, 641–647. [Google Scholar]
- Jaconi, A.; Don, A.; Freibauer, A. Prediction of soil organic carbon at the country scale: Stratification strategies for near-infrared data. Eur. J. Soil Sci. 2017, 68, 919–929. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, F.; Kong, W.; He, Y. Application of Visible and Near-Infrared Hyperspectral Imaging to Determine Soluble Protein Content in Oilseed Rape Leaves. Sensors (Basel) 2015, 15, 16576–16588. [Google Scholar] [CrossRef] [PubMed]
- Guerrero, C.; Stenberg, B.; Wetterlind, J.; Viscarra Rossel, R.A.; Maestre, F.T.; Mouazen, A.M.; Zornoza, R.; Ruiz-Sinoga, J.D.; Kuang, B. Assessment of soil organic carbon at local scale with spiked NIR calibrations: Effects of selection and extra-weighting on the spiking subset. Eur. J. Soil Sci. 2014, 65, 248–263. [Google Scholar] [CrossRef]
- Zeng, R.; Zhao, Y.-G.; Li, D.-C.; Wu, D.-W.; Wei, C.-L.; Zhang, G.-L. Selection of “Local” Models for Prediction of Soil Organic Matter Using a Regional Soil Vis-NIR Spectral Library. Soil Sci. 2016, 181, 13–19. [Google Scholar] [CrossRef]
- Liu, S.; Shen, H.; Chen, S.; Zhao, X.; Biswas, A.; Jia, X.; Shi, Z.; Fang, J. Estimating forest soil organic carbon content using vis-NIR spectroscopy: Implications for large-scale soil carbon spectroscopic assessment. Geoderma 2019, 348, 37–44. [Google Scholar] [CrossRef]
- Araújo, S.R.; Wetterlind, J.; Demattê, J.A.M.; Stenberg, B. Improving the prediction performance of a large tropical vis-NIR spectroscopic soil library from Brazil by clustering into smaller subsets or use of data mining calibration techniques. Eur. J. Soil Sci. 2014, 65, 718–729. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, Y.; Zhang, Y.; Liu, Y.; Liu, Y.; Yu, L.; Liu, Y.; Cheng, H. Transferability of Vis-NIR models for Soil Organic Carbon Estimation between Two Study Areas by using Spiking. Soil Sci. Soc. Am. J. 2018, 82, 1231–1242. [Google Scholar] [CrossRef]
- Guerrero, C.; Wetterlind, J.; Stenberg, B.; Mouazen, A.M.; Gabarrón-Galeote, M.A.; Ruiz-Sinoga, J.D.; Zornoza, R.; Viscarra Rossel, R.A. Do we really need large spectral libraries for local scale SOC assessment with NIR spectroscopy? Soil Tillage Res. 2016, 155, 501–509. [Google Scholar] [CrossRef]
- Seidel, M.; Hutengs, C.; Ludwig, B.; Thiele-Bruhn, S.; Vohland, M. Strategies for the efficient estimation of soil organic carbon at the field scale with vis-NIR spectroscopy: Spectral libraries and spiking vs. local calibrations. Geoderma 2019, 354, 113856. [Google Scholar] [CrossRef]
- Nawar, S.; Mouazen, A.M. Comparison between Random Forests, Artificial Neural Networks and Gradient Boosted Machines Methods of On-Line Vis-NIR Spectroscopy Measurements of Soil Total Nitrogen and Total Carbon. Sensors (Basel) 2017, 17, 2428. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Q.; Li, Q.; Wang, X.; Wu, Y.; Yang, X.; Liu, F. Estimation of soil organic carbon and total nitrogen in different soil layers using VNIR spectroscopy: Effects of spiking on model applicability. Geoderma 2017, 293, 54–63. [Google Scholar] [CrossRef]
- Castaldi, F.; Chabrillat, S.; Chartin, C.; Genot, V.; Jones, A.R.; van Wesemael, B. Estimation of soil organic carbon in arable soil in Belgium and Luxembourg with the LUCAS topsoil database. Eur. J. Soil Sci. 2018, 69, 592–603. [Google Scholar] [CrossRef]
| Sample Set | Soil Type | Number | Range (g kg−1) | Mean (g kg−1) | SD (g kg−1) | Skew |
|---|---|---|---|---|---|---|
| PSSL | Red, yellow, paddy, and saline soil | 714 | 6.6–46.3 | 24.9 | 7.28 | 0.14 |
| CSSL | Red, yellow, and paddy soil | 167 | 9.8–42.0 | 25.2 | 5.91 | −0.20 |
| DSSL | Paddy soil | 102 | 7.5–40.0 | 22.2 | 6.07 | 0.50 |
| TA1 | Paddy soil | 60 | 14.2–38.8 | 23.4 | 4.98 | 0.83 |
| TA2 | Red, yellow, and paddy soil | 66 | 12.6–39.9 | 24.7 | 6.65 | 0.32 |
| Prediction Set | Soil Type | Number | Range (g kg−1) | Mean (g kg−1) | SD (g kg−1) | Skew |
|---|---|---|---|---|---|---|
| TA1pre | Paddy soil | 50 | 14.2–38.8 | 24.0 | 5.11 | 0.74 |
| TA2pre | Red, yellow, and paddy soil | 56 | 14.0–39.9 | 24.7 | 6.63 | 0.37 |
| Model | TA1pre | TA2pre | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSEP (g kg−1) | RPD | R2 | RMSEP (g kg−1) | RPD | |||||||
| Mean | SD | Mean (g kg−1) | SD (g kg−1) | Mean | SD | Mean | SD | Mean (g kg−1) | SD (g kg−1) | Mean | SD | |
| PSSL | 0.67 | 0.066 | 2.83 | 0.478 | 1.83 | 0.274 | 0.77 | 0.041 | 3.26 | 0.487 | 2.08 | 0.302 |
| CSSL | 0.51 | 0.048 | 3.52 | 0.504 | 1.45 | 0.198 | 0.81 | 0.032 | 2.88 | 0.301 | 2.32 | 0.233 |
| DSSL | 0.71 | 0.038 | 2.66 | 0.216 | 1.95 | 0.158 | 0.71 | 0.027 | 3.76 | 0.446 | 1.78 | 0.202 |
| Prediction Set | Source | Sum of Squares | Degrees of Freedom | Mean Square | F | P |
|---|---|---|---|---|---|---|
| TA1pre | SSL | 5.333 | 2 | 2.666 | 57.41 | 0.000 |
| Error | 6.828 | 147 | 0.046 | |||
| TA2pre | SSL | 7.272 | 2 | 3.363 | 58.47 | 0.000 |
| Error | 9.142 | 147 | 0.062 |
| Model | TA1pre | TA2pre | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSEP (g kg−1) | Bias | RPD | R2 | RMSEP (g kg−1) | Bias | RPD | |
| PSSL-UM | 0.72 | 2.69 | −0.47 | 1.90 | 0.78 | 3.06 | 0.45 | 2.17 |
| CSSL-UM | 0.52 | 3.50 | −0.28 | 1.46 | 0.82 | 2.81 | 0.18 | 2.36 |
| DSSL-UM | 0.76 | 2.49 | −0.48 | 2.05 | 0.70 | 3.62 | −0.11 | 1.83 |
| Model | No. | TA1pre | TA2pre | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSEP (g kg−1) | Bias | RPD | R2 | RMSEP (g kg−1) | Bias | RPD | ||
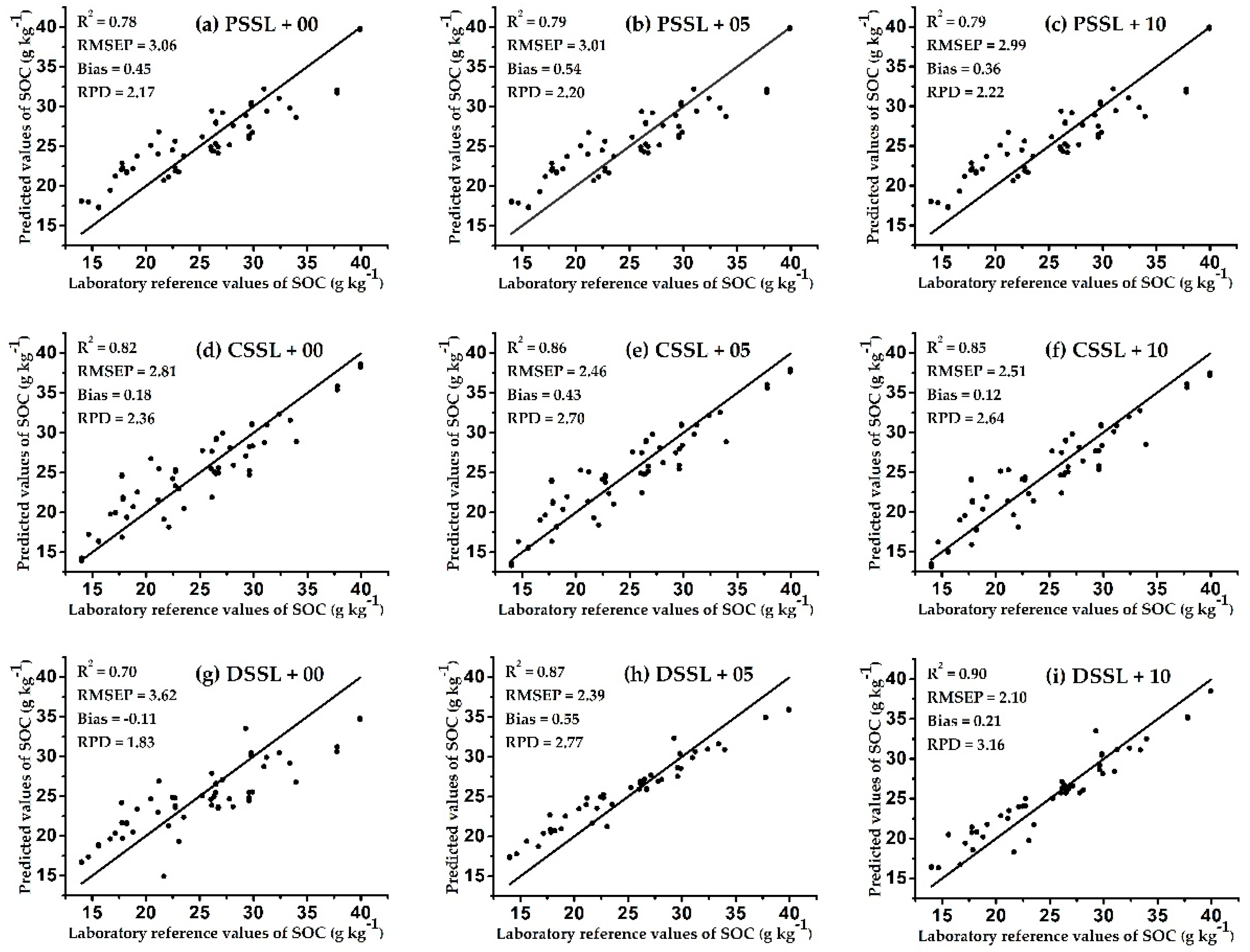
| PSSL-SM | 5 | 0.72 | 2.66 | −0.45 | 1.92 | 0.79 | 3.01 | 0.54 | 2.20 |
| 10 | 0.73 | 2.62 | −0.46 | 1.95 | 0.79 | 2.99 | 0.36 | 2.22 | |
| CSSL-SM | 5 | 0.81 | 2.23 | −0.21 | 2.29 | 0.86 | 2.46 | 0.43 | 2.70 |
| 10 | 0.86 | 1.92 | −0.15 | 2.66 | 0.85 | 2.51 | 0.12 | 2.64 | |
| DSSL-SM | 5 | 0.86 | 1.88 | −0.31 | 2.72 | 0.87 | 2.39 | 0.55 | 2.77 |
| 10 | 0.86 | 1.91 | −0.25 | 2.67 | 0.90 | 2.10 | 0.21 | 3.16 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Jia, S.; Le, Z. Prediction of Soil Organic Carbon in a New Target Area by Near-Infrared Spectroscopy: Comparison of the Effects of Spiking in Different Scale Soil Spectral Libraries. Sensors 2020, 20, 4357. https://doi.org/10.3390/s20164357
Li H, Jia S, Le Z. Prediction of Soil Organic Carbon in a New Target Area by Near-Infrared Spectroscopy: Comparison of the Effects of Spiking in Different Scale Soil Spectral Libraries. Sensors. 2020; 20(16):4357. https://doi.org/10.3390/s20164357
Chicago/Turabian StyleLi, Hongyang, Shengyao Jia, and Zichun Le. 2020. "Prediction of Soil Organic Carbon in a New Target Area by Near-Infrared Spectroscopy: Comparison of the Effects of Spiking in Different Scale Soil Spectral Libraries" Sensors 20, no. 16: 4357. https://doi.org/10.3390/s20164357
APA StyleLi, H., Jia, S., & Le, Z. (2020). Prediction of Soil Organic Carbon in a New Target Area by Near-Infrared Spectroscopy: Comparison of the Effects of Spiking in Different Scale Soil Spectral Libraries. Sensors, 20(16), 4357. https://doi.org/10.3390/s20164357





