Characterization and Monitoring of Titanium Bone Implants with Impedance Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Porous Samples Preparation
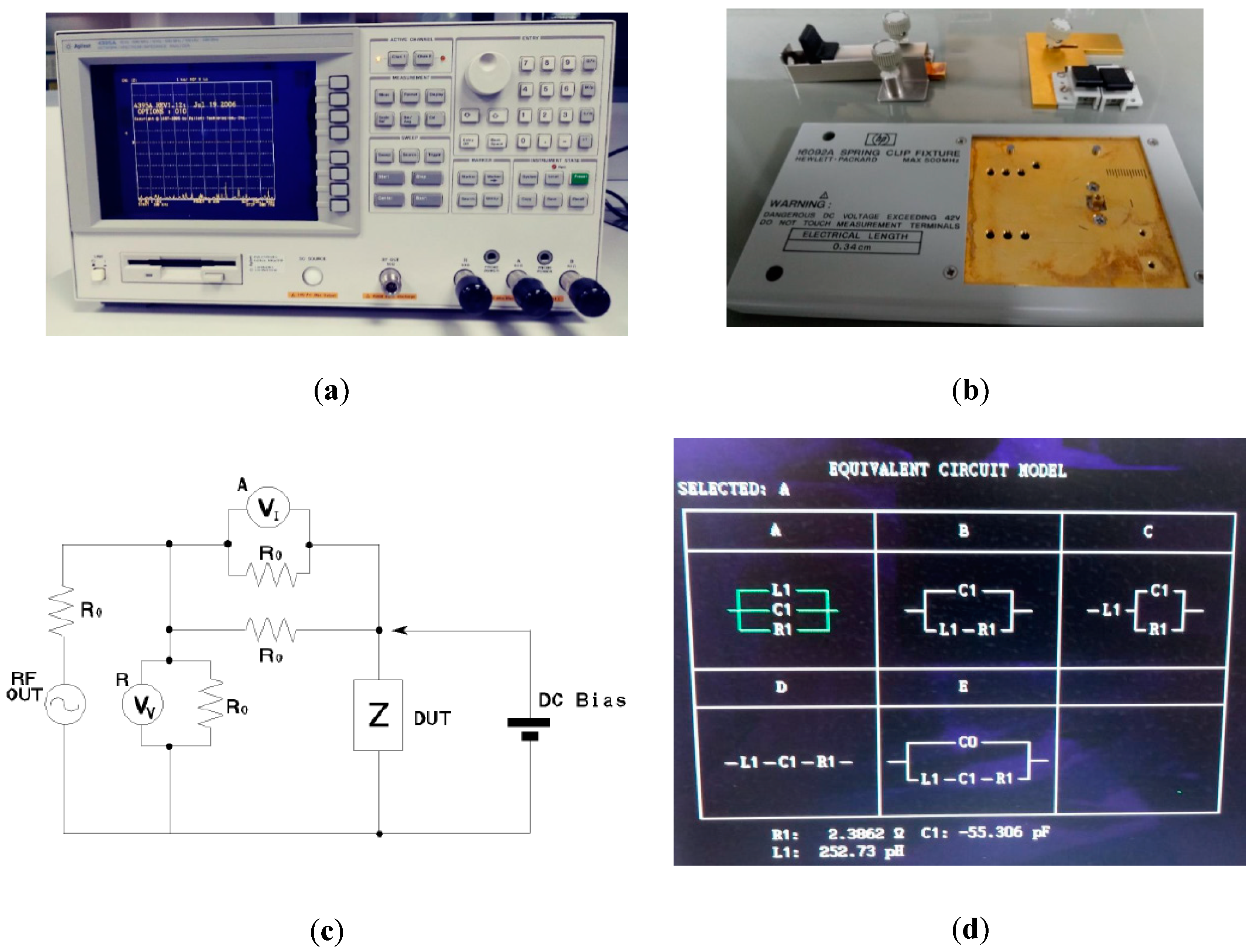
2.2. Electrical Impedance Spectroscopy and Porosity Characterization
3. Results
3.1. Porous Samples Fabrication
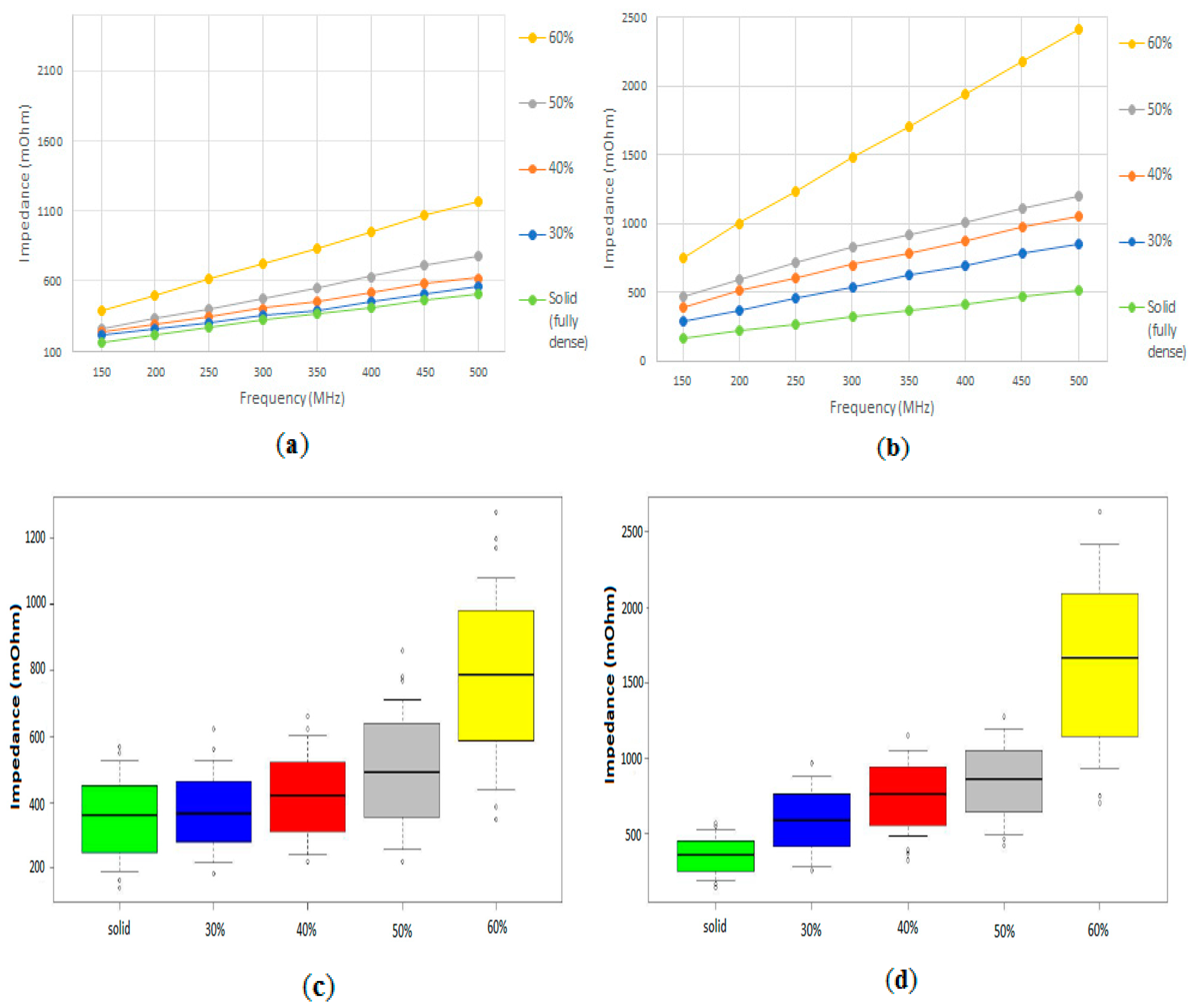
3.2. Electrical Impedance Measurements
4. Discussion
4.1. Characterization of Volumetric Porosity and Pore Size
4.2. Real Time Monitoring of Biological Osseointegration and Potential Use in Medical Sensors
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Holder, D. Electrical Impedance Tomography: Methods, History and Applications; Institute of Physics Pub.: Bristol, UK, 2005. [Google Scholar]
- Marchena, D.R.; Olmo, A.; Miguel, J.A.; Martinez, M.; Huertas, G.; Yúfera, A. Real-Time Electrical Bioimpedance Characterization of Neointimal Tissue for Stent Applications. Sensors 2017, 17, 1737. [Google Scholar] [CrossRef] [PubMed]
- Arpaia, P.; Clemente, F.; Zanesco, A. Low-Invasive Diagnosis of Metallic Prosthesis Osseointegration by Electrical Impedance Spectroscopy. IEEE Trans. Instrum. Meas. 2007, 56, 784–789. [Google Scholar] [CrossRef]
- Taji, B.; Chan, A.D.C.; Shirmohammadi, S. Effect of Pressure on Skin-Electrode Impedance in Wearable Biomedical Measurement Devices. IEEE Trans. Instrum. Meas. 2018, 67, 1900–1912. [Google Scholar] [CrossRef]
- Sapuan, I.; Yasin, M.; Ain, K.; Apsari, R. Anomaly Detection Using Electric Impedance Tomography Based on Real and Imaginary Images. Sensors 2020, 20, 1907. [Google Scholar] [CrossRef]
- Guerado-Parra, E.; Caso, E. Challenges of bone tissue engineering in orthopaedic patients. World J. Orthop. 2017, 8, 87–98. [Google Scholar] [CrossRef]
- Palka, K.; Pokrowiecki, R. Porous Titanium Implants: A Review. Adv. Eng. Mater. 2018, 20, 1700648. [Google Scholar] [CrossRef]
- Torres, Y.; Lascano, S.; Bris, J.; Pavón-Palacio, J.-J.; Rodríguez-Ortiz, J.A. Development of porous titanium for biomedical applications: A comparison between loose sintering and space-holder techniques. Mater. Sci. Eng. C 2014, 37, 148–155. [Google Scholar] [CrossRef]
- Vanderesse, N.; Ky, I.; González, F.Q.; Nuño, N.; Bocher, P. Image analysis characterization of periodic porous materials produced by additive manufacturing. Mater. Des. 2016, 92, 767–778. [Google Scholar] [CrossRef]
- Ke, Z.; Cheng-Feng, L.; Zhen-Gang, Z. Measurement of Electrical Conductivity of Porous Titanium and Ti6Al4V Prepared by the Powder Metallurgy Method. Chin. Phys. Lett. 2007, 24, 187–190. [Google Scholar] [CrossRef]
- Pan, J.; Thierry, D.; Leygraf, C. Electrochemical impedance spectroscopy study of the passive oxide film on titanium for implant application. Electrochim. Acta 1996, 41, 1143–1153. [Google Scholar] [CrossRef]
- Menini, R.; Dion, M.-J.; So, S.K.V.; Gauthier, M.; Lefebvre, L.-P. Surface and Corrosion Electrochemical Characterization of Titanium Foams for Implant Applications. J. Electrochem. Soc. 2006, 153, B13. [Google Scholar] [CrossRef]
- Seah, K.; Thampuran, R.; Teoh, S. The influence of pore morphology on corrosion. Corros. Sci. 1998, 40, 547–556. [Google Scholar] [CrossRef]
- Chen, X.; Fu, Q.; Jin, Y.; Li, M.; Yang, R.; Cui, X.; Gong, M. In vitro studying corrosion behavior of porous titanium coating in dynamic electrolyte. Mater. Sci. Eng. C 2017, 70, 1071–1075. [Google Scholar] [CrossRef] [PubMed]
- Grewal, P.K.; Golnaraghi, F. Pilot study: Electrical impedance based tissue classification using support vector machine classifier. IET Sci. Meas. Technol. 2014, 8, 579–587. [Google Scholar] [CrossRef]
- Arpaia, P.; Clemente, F.; Romanucci, C. An instrument for prosthesis osseointegration assessment by electrochemical impedance spectrum measurement. Measurement 2008, 41, 1040–1044. [Google Scholar] [CrossRef]
- Beltrán, A.M.; Civantos, A.; Dominguez-Trujillo, C.; Moriche, R.; Rodríguez-Ortiz, J.A.; Garcia-Moreno, F.; Webster, T.J.; Kamm, P.; Restrepo, A.M.; Torres, Y. Porous Titanium Surfaces to Control Bacteria Growth: Mechanical Properties and Sulfonated Polyetheretherketone Coatings as Antibiofouling Approaches. Metals 2019, 9, 995. [Google Scholar] [CrossRef]
- Domínguez-Trujillo, C.; Ternero, F.; Rodríguez-Ortiz, J.A.; Heise, S.; Boccaccini, A.R.; Lebrato, J.; Torres, Y. Bioactive coatings on porous titanium for biomedical applications. Surf. Coat. Technol. 2018, 349, 584–592. [Google Scholar] [CrossRef]
- Civantos, A.; Domínguez, C.; Pino, R.J.; Setti, G.; Pavon, J.J.; Martínez-Campos, E.; Garcia, F.J.G.; Rodriguez, J.A.; Allain, J.P.; Torres, Y. Designing bioactive porous titanium interfaces to balance mechanical properties and in vitro cells behavior towards increased osseointegration. Surf. Coat. Technol. 2019, 368, 162–174. [Google Scholar] [CrossRef]
- Torres, Y.; Pavón-Palacio, J.-J.; Nieto, I.; Rodríguez-Ortiz, J.A. Conventional Powder Metallurgy Process and Characterization of Porous Titanium for Biomedical Applications. Metall. Mater. Trans. B Process. Metall. Mater. Process. Sci. 2011, 42, 891–900. [Google Scholar] [CrossRef]
- Torres, Y.; Pavón-Palacio, J.-J.; Rodríguez, J.; Rodríguez-Ortiz, J.A. Processing and characterization of porous titanium for implants by using NaCl as space holder. J. Mater. Process. Technol. 2012, 212, 1061–1069. [Google Scholar] [CrossRef]
- Trueba, P.; Chicardi, E.; Rodríguez-Ortiz, J.A.; Pavón, J.J.; Torres, Y.; Cobos, J. Design, Processing and Characterization of Materials with Controlled Radial Porosity for Biomedical and Nuclear Applications. Key Eng. Mater. 2016, 704, 325–333. [Google Scholar] [CrossRef]
- Trueba, P.; Beltrán, A.M.; Bayo, J.M.; Rodríguez-Ortiz, J.A.; Larios, D.F.; Alonso, E.; Dunand, D.C.; Torres, Y. Porous Titanium Cylinders Obtained by the Freeze-Casting Technique: Influence of Process Parameters on Porosity and Mechanical Behavior. Metals 2020, 10, 188. [Google Scholar] [CrossRef]
- Lascano, S.; Arevalo, C.; Montealegre_Meléndez, I.; Muñoz, S.; Rodríguez-Ortiz, J.A.; Trueba, P.; Torres, Y. Porous Titanium for Biomedical Applications: Evaluation of the Conventional Powder Metallurgy Frontier and Space-Holder Technique. Appl. Sci. 2019, 9, 982. [Google Scholar] [CrossRef]
- Pavón-Palacio, J.-J.; Trueba, P.; Rodríguez-Ortiz, J.A.; Torres, Y. Development of new titanium implants with longitudinal gradient porosity by space-holder technique. J. Mater. Sci. 2015, 50, 6103–6112. [Google Scholar] [CrossRef]
- Miao, X.; Sun, D. Graded/Gradient Porous Biomaterials. Materials 2009, 3, 26–47. [Google Scholar] [CrossRef]
- Giaever, I.; Keese, C.R. Use of Electric Fields to Monitor the Dynamical Aspect of Cell Behavior in Tissue Culture. IEEE Trans. Biomed. Eng. 1986, 242–247. [Google Scholar] [CrossRef]
- Serrano, J.A.; Huertas, G.; Maldonado-Jacobi, A.; Olmo, A.; Pérez, P.; Martin, M.E.; Daza, P.; Yufera, A. An Empirical-Mathematical Approach for Calibration and Fitting Cell-Electrode Electrical Models in Bioimpedance Tests. Sensors 2018, 18, 2354. [Google Scholar] [CrossRef]
- Pérez, P.; Huertas, G.; Olmo, A.; Maldonado-Jacobi, A.; Serrano, J.A.; Martin, M.E.; Daza, P.; Yufera, A. Remote Cell Growth Sensing Using Self-Sustained Bio-Oscillations. Sensors 2018, 18, 2550. [Google Scholar] [CrossRef]
- Daza, P.; Olmo, A.; Canete, D.; Yúfera, A. Monitoring living cell assays with bio-impedance sensors. Sens. Actuators B Chem. 2013, 176, 605–610. [Google Scholar] [CrossRef]
- Olmo, A.; Yuste, Y.; Serrano, J.A.; Maldonado-Jacobi, A.; Pérez, P.; Huertas, G.; Pereira, S.; Yúfera, A.; De La Portilla, F. Electrical Modeling of the Growth and Differentiation of Skeletal Myoblasts Cell Cultures for Tissue Engineering. Sensors 2020, 20, 3152. [Google Scholar] [CrossRef]
- Lee, E.J.; Wi, H.; McEwan, A.; Farooq, A.; Sohal, H.; Woo, E.J.; Seo, J.K.; Oh, T.I. Design of a microscopic electrical impedance tomography system for 3D continuous non-destructive monitoring of tissue culture. Biomed. Eng. Online 2014, 13, 142. [Google Scholar] [CrossRef] [PubMed]
- Domínguez-Trujillo, C.; Beltrán, A.M.; Garvi, D.; Salazar-Moya, A.; Lebrato, J.; Hickey, D.; Rodríguez-Ortiz, J.A.; Kamm, P.H.; Lebrato, C.; García-Moreno, F.; et al. Bacterial behavior on coated porous titanium substrates for biomedical applications. Surf. Coat. Technol. 2019, 357, 896–902. [Google Scholar] [CrossRef]




| Spacer | Archimedes Method | Image Analysis | ||||
|---|---|---|---|---|---|---|
| Density (g/cm3) | Porosity (%) | PT (%) | Size Range (µm) | |||
| Volumetric Porosity (%) | Size Range (µm) | Total | Interconnected | |||
| 30 | 100–200 | 3.14 ± 0.02 | 30.2 ± 0.2 | 18.0 ± 0.1 | 31.2 ± 0.6 | 192 ± 117 |
| 355–500 | 3.15 ± 0.01 | 30.0 ± 0.19 | 19.0 ± 0.1 | 24.6 ± 2.5 | 435 ± 401 | |
| 40 | 100–200 | 2.69 ± 0.02 | 40.2 ± 0.6 | 32.9 ± 0.8 | 42.1 ± 3.3 | 226 ± 178 |
| 355–500 | 2.67 ± 0.02 | 40.8 ± 0.5 | 27.9 ± 0.7 | 43.7 ± 7.8 | 359 ± 223 | |
| 50 | 100–200 | 2.37 ± 0.01 | 47.4 ± 0.1 | 46.7 ± 0.1 | 58.4 ± 4.2 | 217 ± 154 |
| 355–500 | 2.14 ± 0.01 | 52.5 ± 0.3 | 50.8 ± 0.3 | 56.6 ± 6.9 | 278 ± 322 | |
| 60 | 100–200 | 1.97 ± 0.02 | 56.4 ± 0.5 | 51.8 ± 1.3 | 61.0 ± 2.4 | 295 ± 287 |
| 355–500 | 1.90 ± 0.04 | 57.8 ± 0.5 | 53.0 ± 0.9 | 55.5 ± 10.3 | 302 ± 332 | |
| Range of Pore | |||||||
|---|---|---|---|---|---|---|---|
| Porosity volume | 100–200 µm | 355–500 µm | |||||
| R1(mΩ) | L1(pH) | C1(pF) | R1(mΩ) | L1(pH) | C1(pF) | ||
| 30% | 2386.2 ± 0.1 | 252.73 ± 0.01 | 55.31 ± 0.01 | 3795.2 ± 0.1 | 283.27 ± 0.01 | 34.29 ± 0.01 | |
| 40% | 3853.2 ± 0.1 | 307.34 ± 0.01 | 36.29 ± 0.01 | 14578.6 ± 0.1 | 443.12 ± 0.01 | 26.34 ± 0.01 | |
| 50% | 5298.1 ± 0.1 | 375.29 ± 0.01 | 27.27 ± 0.01 | 27817 ± 0.1 | 603.70 ± 0.01 | 17.39 ± 0.01 | |
| 60% | 6646.2 ± 0.1 | 421.88 ± 0.01 | 20.68 ± 0.01 | 36963 ± 0.1 | 768.41 ± 0.01 | 4.18 ± 0.01 | |
| Fully dense | R1 = 1095.5 ± 0.01 mΩ L1 = 169.88 ± 0.01 pH C1 = 53.528 ± 0.01 pF | ||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olmo, A.; Hernández, M.; Chicardi, E.; Torres, Y. Characterization and Monitoring of Titanium Bone Implants with Impedance Spectroscopy. Sensors 2020, 20, 4358. https://doi.org/10.3390/s20164358
Olmo A, Hernández M, Chicardi E, Torres Y. Characterization and Monitoring of Titanium Bone Implants with Impedance Spectroscopy. Sensors. 2020; 20(16):4358. https://doi.org/10.3390/s20164358
Chicago/Turabian StyleOlmo, Alberto, Miguel Hernández, Ernesto Chicardi, and Yadir Torres. 2020. "Characterization and Monitoring of Titanium Bone Implants with Impedance Spectroscopy" Sensors 20, no. 16: 4358. https://doi.org/10.3390/s20164358
APA StyleOlmo, A., Hernández, M., Chicardi, E., & Torres, Y. (2020). Characterization and Monitoring of Titanium Bone Implants with Impedance Spectroscopy. Sensors, 20(16), 4358. https://doi.org/10.3390/s20164358






