A High-Performance Transmitarray Antenna with Thin Metasurface for 5G Communication Based on PSO (Particle Swarm Optimization)
Abstract
:1. Introduction
2. Transmitarray Antenna Design
2.1. Feed Antenna Design
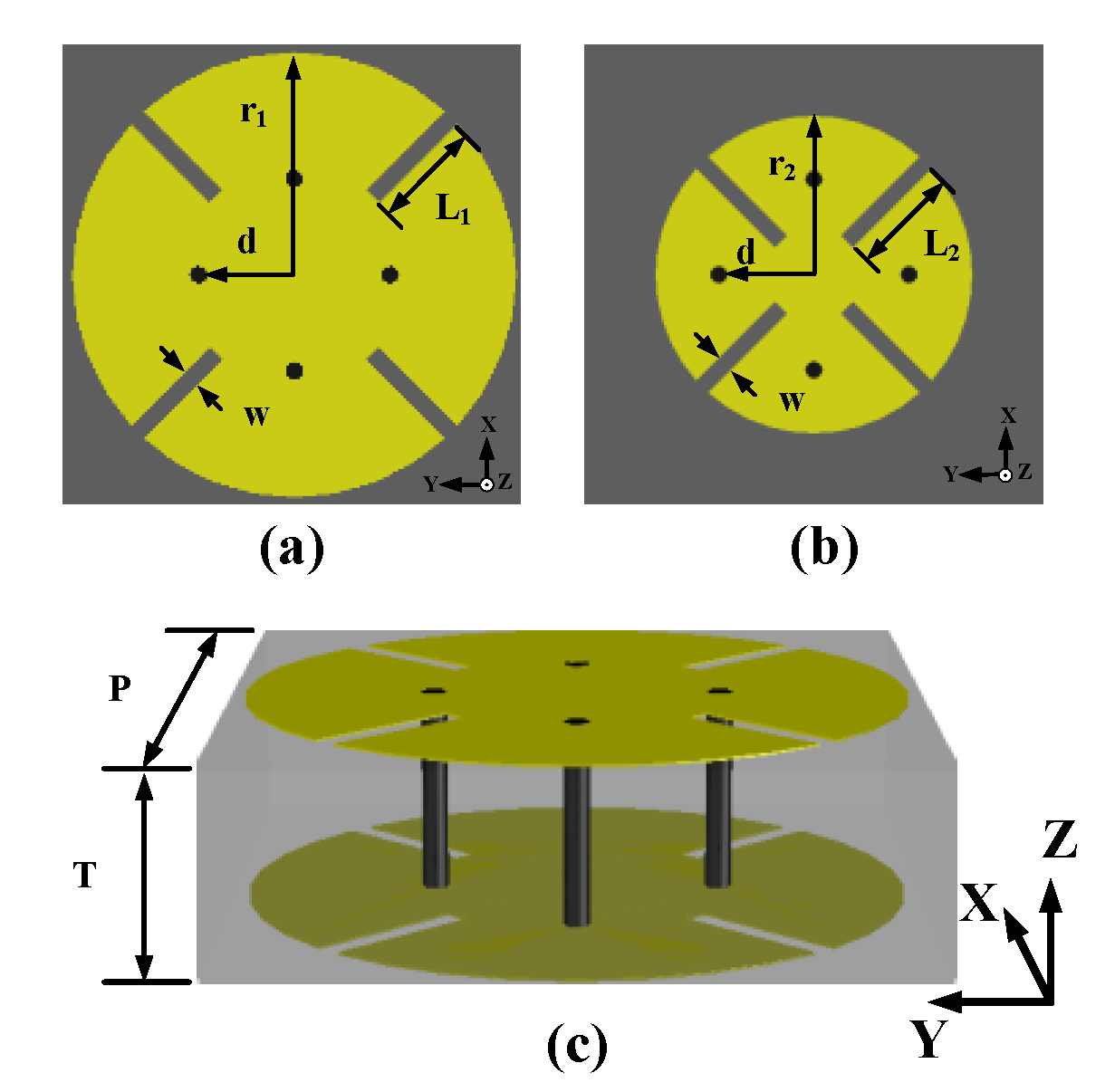
2.2. Design of Unit Cell of MS
2.3. Array of MS
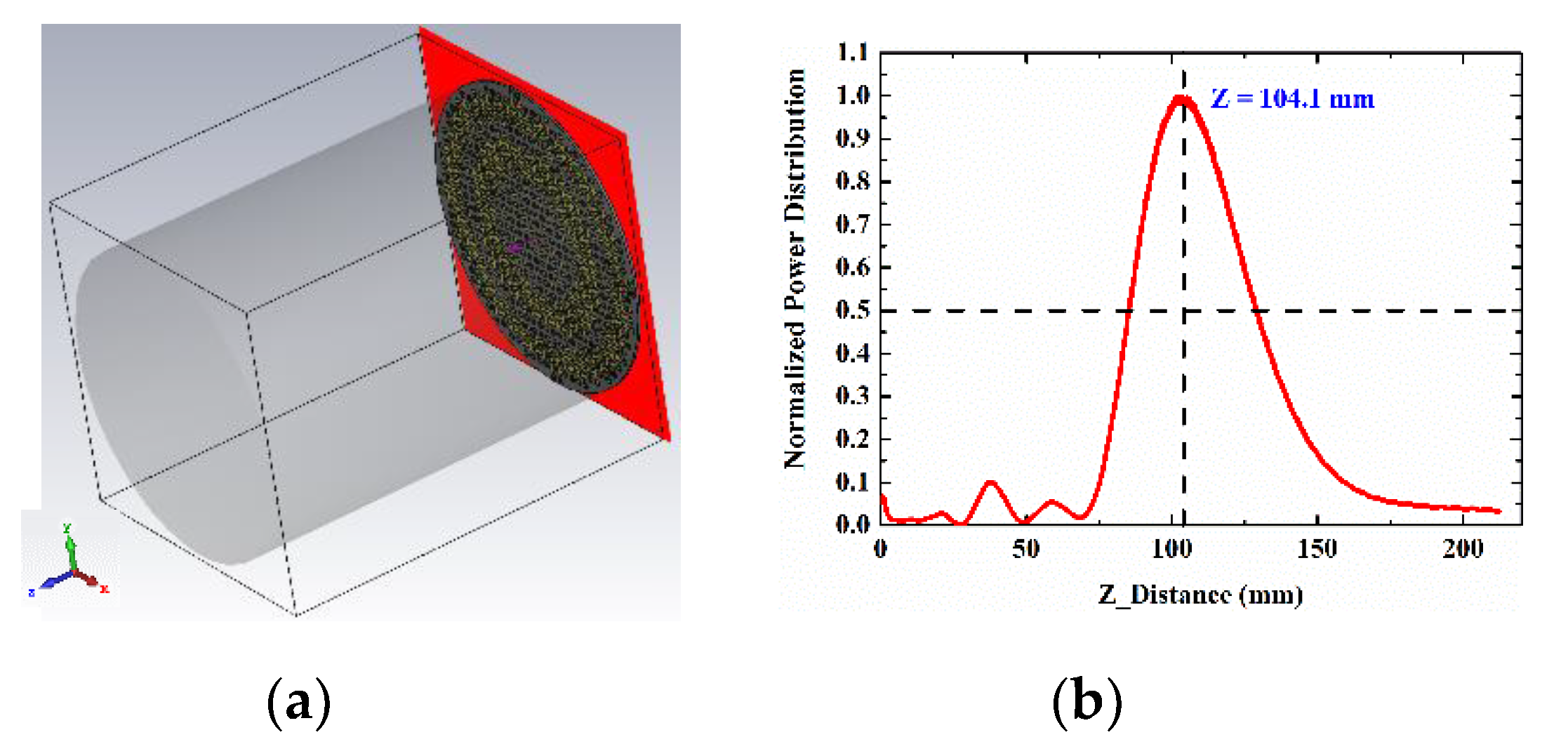
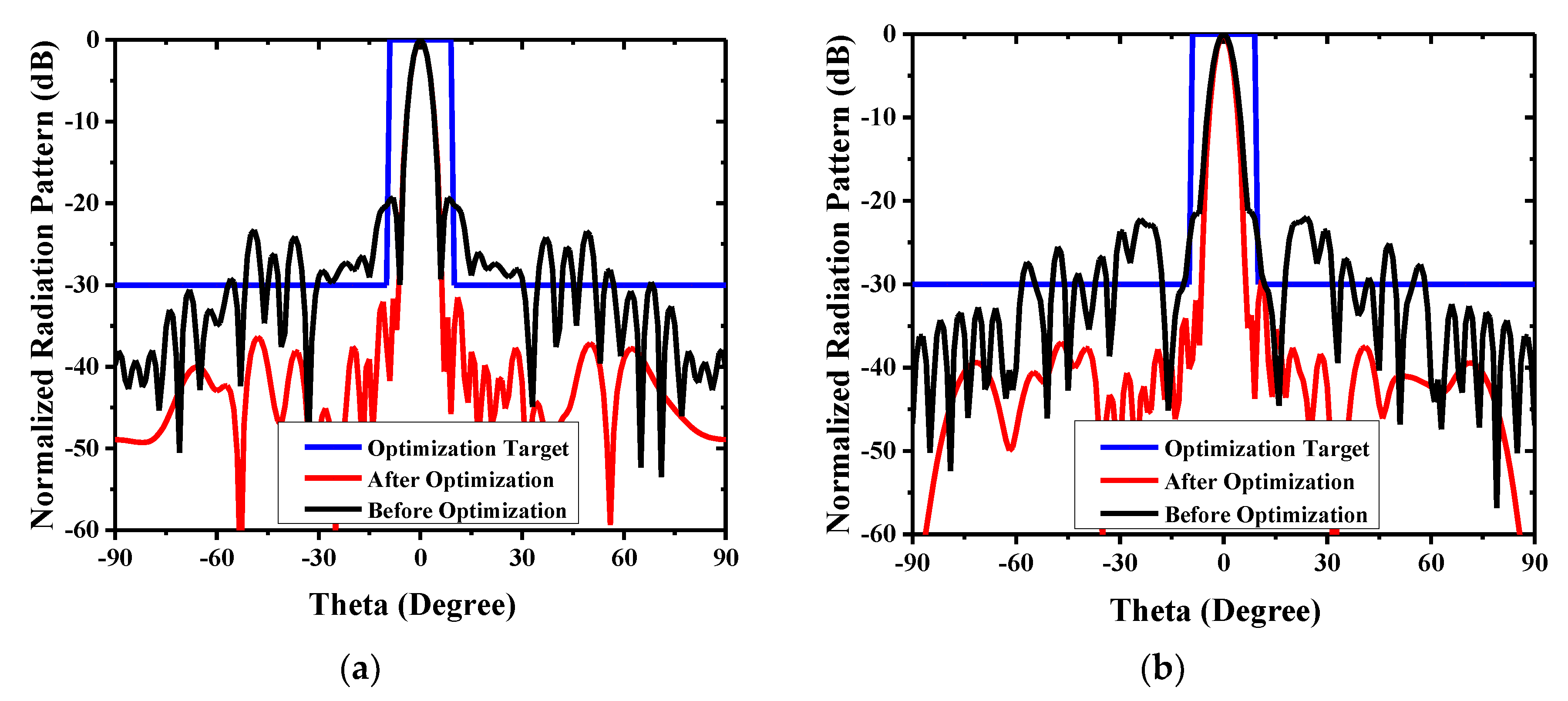
2.4. Optimization Result
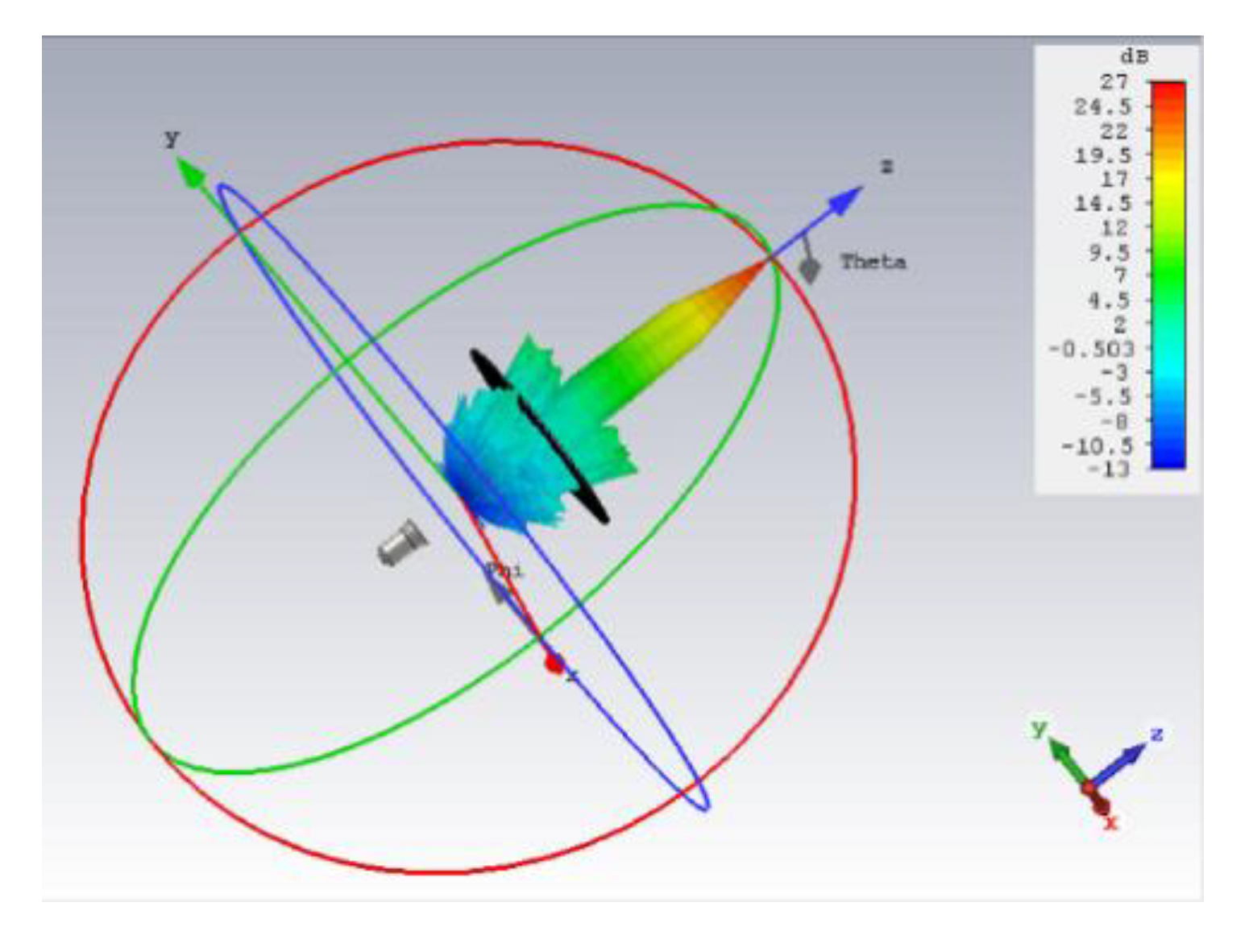
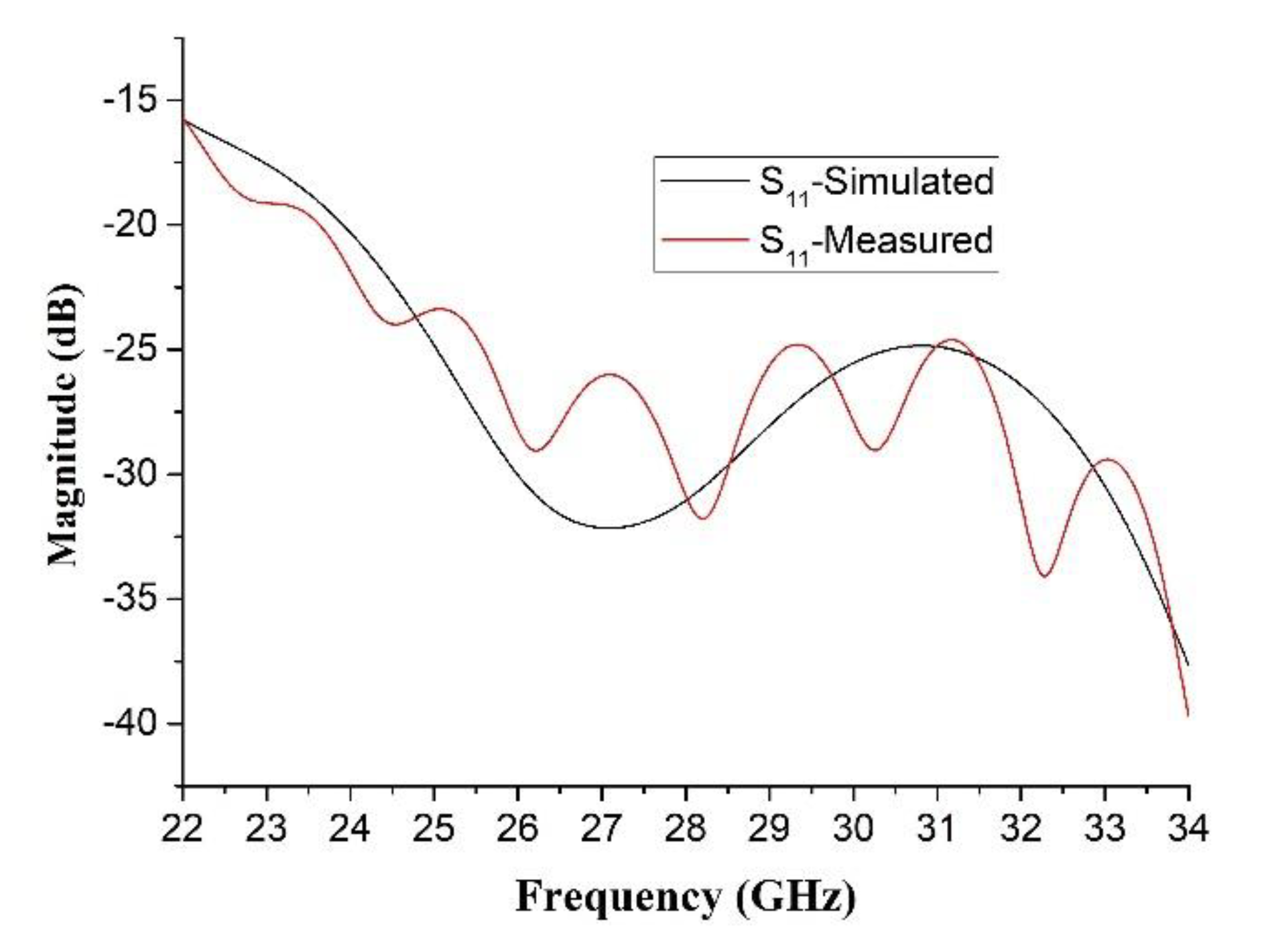
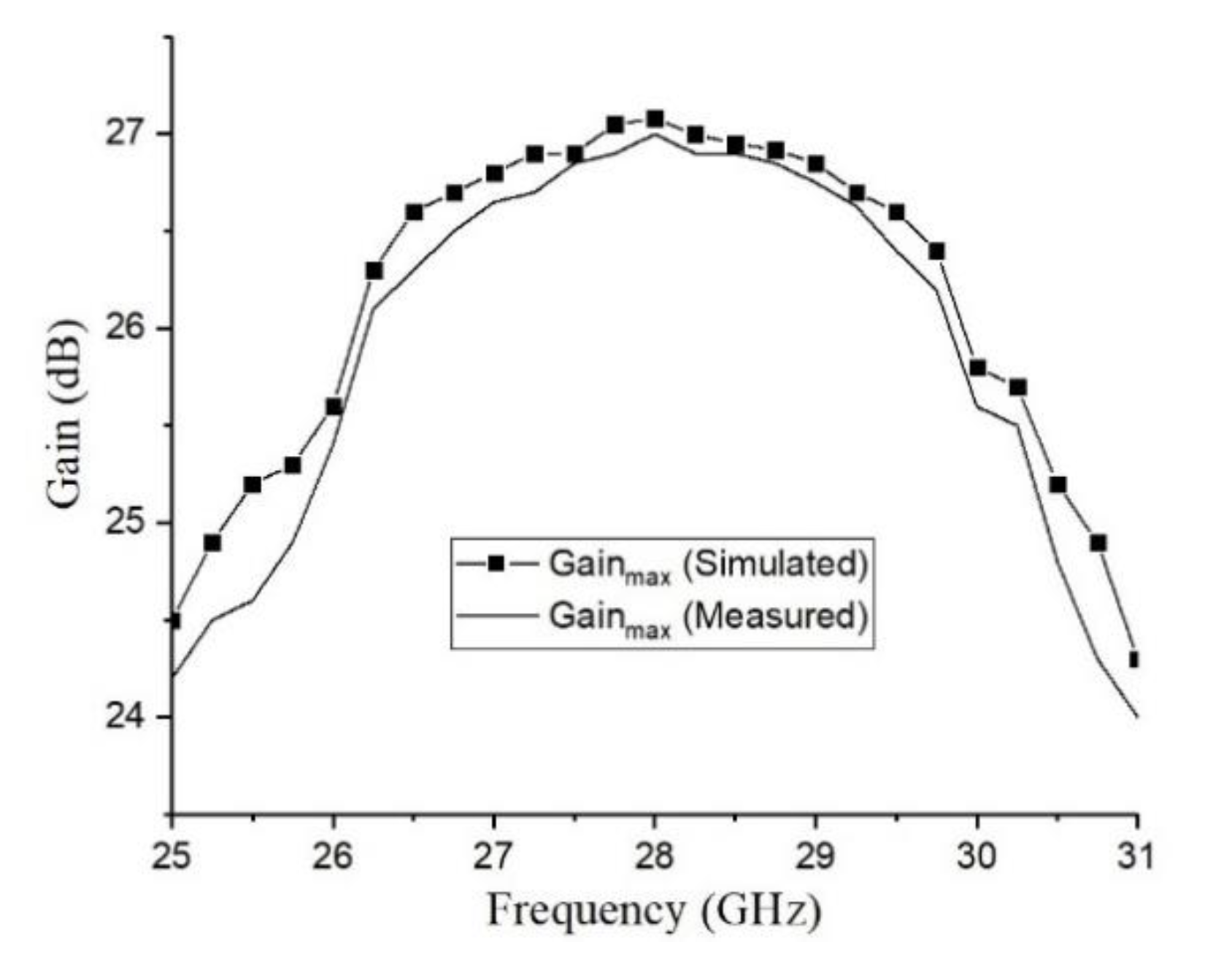
3. Result and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter wave mobile communications for 5G cellular: It will work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Akpakwu, G.A.; Silva, B.J.; Hancke, G.P.; Abu-Mahfouz, A.M. A survey on 5G networks for the Internet of Things: Communication technologies and challenges. IEEE Access 2017, 6, 3619–3647. [Google Scholar] [CrossRef]
- Azar, Y.; Wong, G.N.; Wang, K.; Mayzus, R.; Schulz, J.K.; Zhao, H.; Gutierrez, F.; Hwang, D.; Rappaport, T.S. 28 GHz propagation measurements for outdoor cellular communications using steerable beam antennas in New York city. ICC Int. Conf. Commun. 2013, 5143–5147. [Google Scholar] [CrossRef]
- Roh, W.; Seol, J.Y.; Park, J.; Lee, B.; Lee, J.; Kim, Y.; Cho, J.; Cheun, K.; Aryanfar, F. Millimeter-wave beamforming as an enabling technology for 5G cellular communications: Theoretical feasibility and prototype results. IEEE Commun. Mag. 2014, 52, 106–113. [Google Scholar] [CrossRef]
- Syrytsin, I.; Zhang, S.; Pedersen, G.F.; Morris, A.S. Compact quad-mode planar phased array with wideband for 5G mobile terminals. IEEE Trans. Antennas Propag. 2018, 66, 4648–4657. [Google Scholar] [CrossRef] [Green Version]
- Khalily, M.; Tafazolli, R.; Rahman, T.A.; Kamarudin, M.R. Design of phased arrays of series-fed patch antennas with reduced number of the controllers for 28-GHz mm-wave applications. IEEE Antennas Wirel. Propag. Lett. 2015, 15, 1305–1308. [Google Scholar] [CrossRef] [Green Version]
- Pal, A.; Mehta, A.; Mirshekar-Syahkal, D.; Nakano, H. $2\times2 $ Phased Array Consisting of Square Loop Antennas for High Gain Wide Angle Scanning with Low Grating Lobes. IEEE Trans. Antennas Propag. 2016, 65, 576–583. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, L.; Wang, H.; Luo, Y.; Yang, G. A compact, scanning tightly coupled dipole array with parasitic strips for next-generation wireless applications. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 534–537. [Google Scholar] [CrossRef]
- Anguera, J.; Andújar, A.; Jayasinghe, J. High Directivity Microstrip Patch Antennas Perturbing TModd-0 modes. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 439–443. [Google Scholar] [CrossRef]
- Rajagopalan, H.; Xu, S.; Rahmat-Samii, Y. On understanding the radiation mechanism of reflectarray antennas: An insightful and illustrative approach. IEEE Antennas Propag. Mag. 2012, 54, 14–38. [Google Scholar] [CrossRef]
- Huang, J.; Pogorzelski, R.J. A Ka-band microstrip reflectarray with elements having variable rotation angles. IEEE Trans. Antennas Propag. 1998, 46, 650–656. [Google Scholar] [CrossRef]
- Yao, W.; Yang, H.; Huang, X.; Tian, Y.; Guo, L. An X-band parabolic antenna based on gradient metasurface. AIP Adv. 2016, 6, 75–83. [Google Scholar] [CrossRef] [Green Version]
- Shafiee, M.A.S.M.; Yusoff, M.F.M.; Johari, Z.; Ismail, M.K.H.; Rahim, M.K.A. Reflectarray antenna performances using combination of rectangular and Jerusalem unit cells at 5.2 GHz. In Proceedings of the 2016 IEEE Asia-Pacific Conference on Applied Electromagnetics (APACE), Kedah, Malaysia, 11 December 2016; pp. 163–166. [Google Scholar]
- An, W.; Xu, S.; Yang, F. A metal-only reflectarray antenna using slot-type elements. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1553–1556. [Google Scholar] [CrossRef]
- Ryan, C.G.; Chaharmir, M.R.; Shaker, J.R.B.J.; Bray, J.R.; Antar, Y.M.; Ittipiboon, A. A wideband transmitarray using dual-resonant double square rings. IEEE Trans. Antennas Propag. 2010, 58, 1486–1493. [Google Scholar] [CrossRef]
- De la Torre, P.P.; Sierra-Castaner, M. Design of a 12 GHz transmit-array. IEEE Antennas Propag. Soc. Int. Symp. 2007, 2007, 2152–2155. [Google Scholar]
- Feng, P.Y.; Qu, S.W.; Yang, S. Ultrawideband Low-Profile Transmitarray with Vivaldi Array Feed. IEEE Trans. Antennas Propag. 2020, 55, 3265–3270. [Google Scholar] [CrossRef]
- Plaza, E.; Leon, G.; Loredo, S.; Las-Heras, F. A simple model for analyzing transmitarray lenses. IEEE Antennas Propag. Mag. 2015, 57, 131–144. [Google Scholar] [CrossRef]
- Nematollahi, H.; Laurin, J.J.; Page, J.E.; Encinar, J.A. Design of broadband transmitarray unit cells with comparative study of different numbers of layers. IEEE Trans. Antennas Propag. 2015, 63, 1473–1481. [Google Scholar] [CrossRef] [Green Version]
- Abdelrahman, A.H.; Elsherbeni, A.Z.; Yang, F. Transmitarray antenna design using cross-slot elements with no dielectric substrate. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 177–180. [Google Scholar] [CrossRef]
- Li, H.; Wang, G.; Xu, H.X.; Cai, T.; Liang, J. X-band phase-gradient metasurface for high-gain lens antenna application. IEEE Trans. Antennas Propag. 2015, 63, 5144–5149. [Google Scholar] [CrossRef]
- Tuloti, S.H.R.; Rezaei, P.; Hamedani, F.T. High-efficient wideband transmitarray antenna. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 817–820. [Google Scholar] [CrossRef]
- Li, Z.; Su, J.; Li, Z. Design of high-gain lens antenna based on phase-gradient metasurface. In Proceedings of the 2016 11th International Symposium on Antennas, Propagation and EM Theory (ISAPE), Guilin, China, 18–21 October 2016; pp. 135–138. [Google Scholar]
- Abdelrahman, A.H.; Yang, F.; Elsherbeni, A.Z.; Nayeri, P. Analysis and design of transmitarray antennas. Synth. Lect. Antennas 2017, 6, 1–175. [Google Scholar] [CrossRef]
- Jiang, M.; Chen, Z.N.; Zhang, Y.; Hong, W.; Xuan, X. Metamaterial-based thin planar lens antenna for spatial beamforming and multibeam massive MIMO. IEEE Trans. Antennas Propag. 2016, 65, 464–472. [Google Scholar] [CrossRef]
- Li, H.; Wang, G.; Liang, J.; Gao, X.; Hou, H.; Jia, X. Single-layer focusing gradient metasurface for ultrathin planar lens antenna application. IEEE Trans. Antennas Propag. 2016, 65, 1452–1457. [Google Scholar]
- Luo, Q.; Gao, S.; Sobhy, M.; Yang, X. Wideband transmitarray with reduced profile. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 450–453. [Google Scholar] [CrossRef] [Green Version]
- An, W.; Xu, S.; Yang, F.; Li, M. A double-layer transmitarray antenna using malta crosses with vias. IEEE Trans. Antennas Propag. 2015, 64, 1120–1125. [Google Scholar] [CrossRef]
- Pozar, D. Flat lens antenna concept using aperture coupled microstrip patches. Electron. Lett. 1996, 32, 2109–2111. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Horst, R.; Pardalos, P.M.; van Thoai, N. Introduction to Global Optimization; Springer Science & Business Media: Berlin, Germany, 2000. [Google Scholar]
- Haupt, R.L. Thinned arrays using genetic algorithms. IEEE Trans. Antennas Propag. 1994, 42, 993–999. [Google Scholar] [CrossRef]
- Boeringer, D.W.; Werner, D.H. Particleswarm optimization versus genetic algorithms for phased array synthesis. IEEE Trans. Antennas Propag. 2004, 52, 771–779. [Google Scholar] [CrossRef]
- Robinson, J.; Rahmat-Samii, Y. Particle swarm optimization in electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 397–407. [Google Scholar] [CrossRef]
- Xu, S.; Rahmat-Samii, Y. Boundary conditions in particle swarm optimization revisited. IEEE Trans. Antennas Propag. 2007, 55, 760–765. [Google Scholar] [CrossRef]
- Nayeri, P.; Yang, F.; Elsherbeni, A.Z. Design of single-feed reflectarray antennas with asymmetric multiple beams using the particle swarm optimization method. IEEE Trans. Antennas Propag. 2013, 61, 4598–4605. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design; John Wiley & Sons: Berlin, Germany, 2016. [Google Scholar]
- Abdelrahman, A.H.; Nayeri, P.; Elsherbeni, A.Z.; Yang, F. Bandwidth improvement methods of transmitarray antennas. IEEE Trans. Antennas Propag. 2015, 63, 2946–2954. [Google Scholar] [CrossRef]
- Cai, T.; Wang, G.M.; Fu, X.L.; Liang, J.G.; Zhuang, Y.Q. High-efficiency metasurface with polarization-dependent transmission and reflection properties for both reflectarray and transmitarray. IEEE Trans. Antennas Propag. 2018, 66, 3219–3224. [Google Scholar] [CrossRef]
- Abbas-Azimi, M.; Mazlumi, F.; Behnia, F. Design of broadband constant-beamwidth conical corrugated-horn antennas [Antenna designer’s notebook]. IEEE Antennas Propag. Mag. 2009, 51, 109–114. [Google Scholar] [CrossRef]









| Ref. | Freq. (GHz) | TA Thickness | Array Size | SLL (dB) | Number of Elements | Bandwidth | Gainmax | Aperture Efficiency (%) |
|---|---|---|---|---|---|---|---|---|
| [25] | 28 | 0.18 | 89.5 | −18 | 484 | 11.% | 24.2 | 24.5 |
| [28] | 20 | 10.5 | 368.5 | −22.5 | 2032 | 10.2% | 33.0 | 40 |
| [38] | 13.5 | 0.76 | 164.7 | −22 | 621 | 9.8% | 29.95 | 50 |
| This paper | 28 | 0.14 | 173.3 | −30 | 660 | 11.2% | 27 | 28 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.; Pan, L.; Jiao, Y.; Jia, J. A High-Performance Transmitarray Antenna with Thin Metasurface for 5G Communication Based on PSO (Particle Swarm Optimization). Sensors 2020, 20, 4460. https://doi.org/10.3390/s20164460
Song C, Pan L, Jiao Y, Jia J. A High-Performance Transmitarray Antenna with Thin Metasurface for 5G Communication Based on PSO (Particle Swarm Optimization). Sensors. 2020; 20(16):4460. https://doi.org/10.3390/s20164460
Chicago/Turabian StyleSong, Chengtian, Lizhi Pan, Yonghui Jiao, and Jianguang Jia. 2020. "A High-Performance Transmitarray Antenna with Thin Metasurface for 5G Communication Based on PSO (Particle Swarm Optimization)" Sensors 20, no. 16: 4460. https://doi.org/10.3390/s20164460
APA StyleSong, C., Pan, L., Jiao, Y., & Jia, J. (2020). A High-Performance Transmitarray Antenna with Thin Metasurface for 5G Communication Based on PSO (Particle Swarm Optimization). Sensors, 20(16), 4460. https://doi.org/10.3390/s20164460





