Origin–Destination Flow Estimation from Link Count Data Only
Abstract
:1. Introduction
- We estimated OD flows in a road network using link count data only, thereby overcoming the requirement for historical trip data and dependency on prior beliefs of any unobserved events. We also provide the necessary constraints and conditions of time geography for existing OD flow models for transportation network.
- We integrated a microscopic simulator to incorporate physical movement of traffic into a road-network. Further, this enables us to evaluate travel times for individual vehicles in the estimated OD flow.
- The traditional validation techniques are necessary but not sufficient, as there are multiple solutions [10]. We provide an additional validation technique for the estimated OD flows. We compared the estimated travel times with observed travel times from real-world data to evaluate the quality of our estimated OD flow.
2. Literature Review
- There are limitations in other MLE estimation methods, as discussed by Vardi [26], Hazelton [11], and Tebaldi and West [12]. Hence, ref. [26] proposed to derive the first and second-order moments of Y to solve Equation (10). However, derivation of the first and second-order moments of Y is not theoretically proven for the Markovian routing.
- Vardi’s [26] network tomography assumes that the values of route choice probabilities are known in a computer network, and does not provide any derivation for a transport network.
- Poisson assumptions might be true at the origins, but are definitely not true at the destinations with the same parameter values, due to road traffic. Hence, estimated solutions, i.e., estimated inter-arrival rates between all OD pairs (), need to be modified at the destinations.
3. Theory
3.1. Network Tomography
3.2. Transport Network Tomography
- Derivation of the first and second-order moments of Y is not theoretically proven for the Markovian routing.
- Derivation of the Markovian routing matrix is not provided for a transport network.
- Independent Poisson assumptions need to be modified at the destinations due to space-time constraints.
3.2.1. Estimation Using First and Second-Order Moments
3.2.2. Derivation of the Markovian Routing Matrix
3.2.3. Space-Time Constraints
- In an urban road network, we assume that each road intersection can be an origin or destination for a vehicle that has been counted at least once by any traffic counting sensor installed in the same road network [31].(This assumption was adopted from Internet traffic, and a sufficient approximation that a vehicle is at least counted once to be observable at the link count data).
- The traffic generation rate at the origins of the vehicles can be assumed to be constant over a small interval of time. This assumption stems from a continuous traffic flow function over the course of a day that can be approximated as constant over small periods of time.(In contrast to the network tomography, this assumption only assumes a Poisson distribution at the origins and not at the destination).
- Within this time interval, a vehicle must stay inside the space-time cone [39] formed by its origin and physical constraints of space and speed of travel, guaranteeing that its current location is reachable within the time budget.(Physical travel constraints do not apply for Internet traffic).
- All vehicles may travel along any of the possible routes available from origin to destinations with different probabilities. These probabilities are calculated based on minimum travel time required to travel between two adjacent nodes. In our model, we have assumed higher travel time leads to lower probability of travel. We have calculated the minimum travel time of an origin to a destination using the distances between the OD pair and speed-limit in that shortest route of the graph for that OD pair. The initial routing matrix is built first based on minimum travel time between two adjacent nodes. Then the Markovian routing matrix has been calculated from the initial routing matrix.(Distance and travel time do not matter in Internet traffic).
- The vehicles’ travel distances can be safely assumed to be larger than the distances between neighbouring urban road intersections, i.e., at least one full link long.(Internet traffic has no minimal distances between OD for existence).
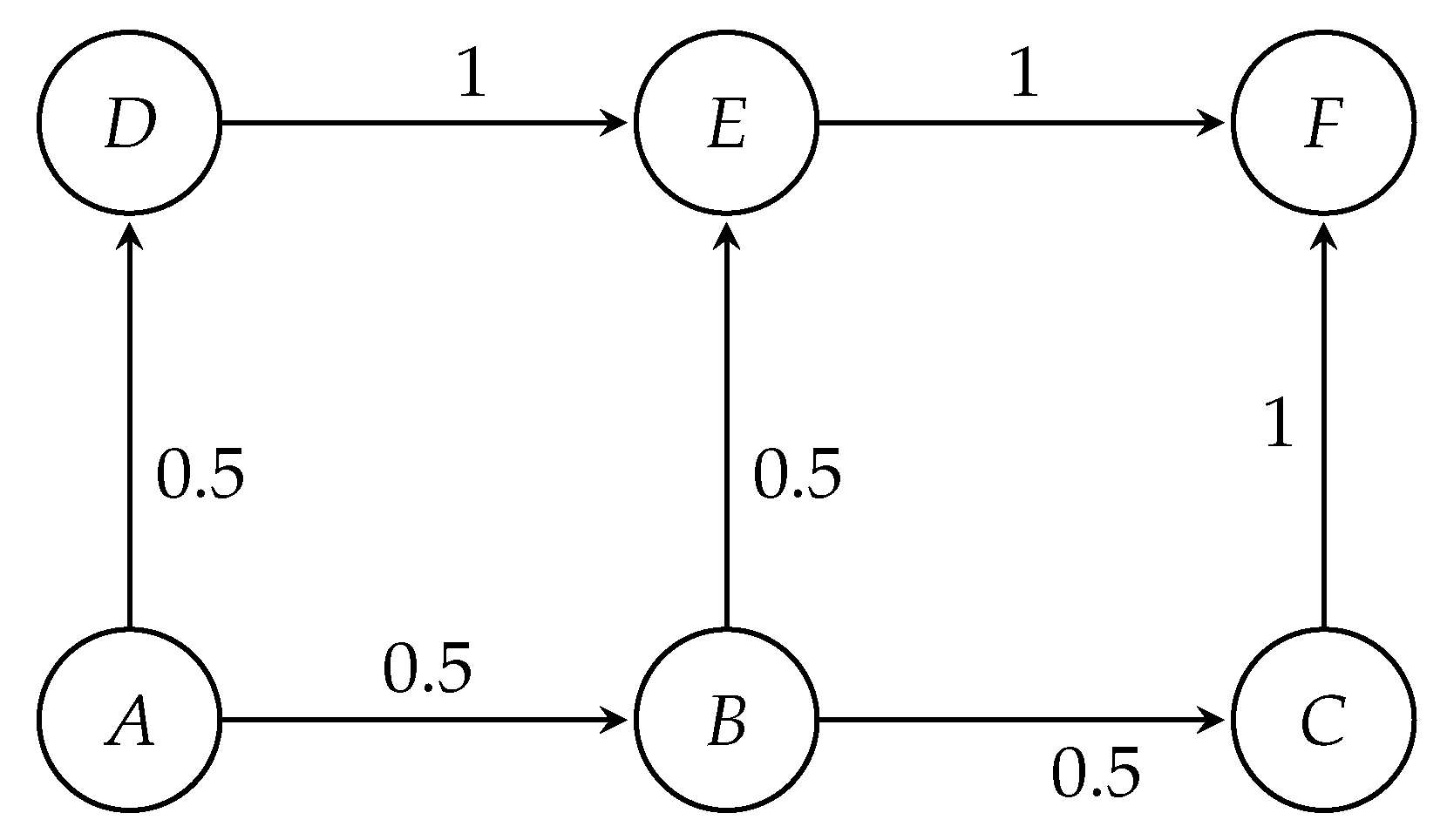
3.3. Transport Network Tomography: An Illustrative Example
4. Implementation
4.1. Data Requirements
4.2. Data Pre-Processing
4.2.1. Microscopic Simulation
4.2.2. Route Generation and Scheduling:
4.2.3. Road Network Graph:
4.2.4. Traffic Generation Rate at Origins:
5. Validation
5.1. Validation with Simulated Data
5.2. Validation with Real World Data
5.2.1. Sygic Data
5.2.2. Uber Movement Data
5.2.3. Error Measures
6. Results
6.1. Validation Using Simulated Data
6.2. Validation Using Real World Travel Time Data
6.2.1. Cross Validation of Observed Data
6.2.2. Estimated Travel Time Validation with Uber Movement Data
6.2.3. Estimated Travel Time Validation with Sygic Data
6.2.4. Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| G | Road network graph |
| n | Number of nodes in G |
| J | Maximum possible OD pair in G |
| I | number of links/edges in G |
| T | A constant time interval of a day |
| Number of cars travelling between OD pair j at time interval | |
| Number of cars observed at a link i at time interval | |
| Rate of cars originating between OD pair j | |
| Probability of a car observed at a link i belongs to OD pair j without the knowledge of previous link | |
| Probability of a car observed at a link i belongs to OD pair j with the knowledge of previous link | |
| First order moment of a random variable X | |
| A | Initial routing matrix with memory less Marokvian assumption |
| P | Route choice matrix with finite memory Marokvian assumption |
| order state transition matrix | |
| Co-variance matrices |
References
- Bauer, D.; Richter, G.; Asamer, J.; Heilmann, B.; Lenz, G.; Kölbl, R. Quasi-Dynamic Estimation of OD Flows From Traffic Counts Without Prior OD Matrix. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2025–2034. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Bierlaire, M.; Koutsopoulos, H.; Mishalani, R. DynaMIT: A simulation-based system for traffic prediction. In Proceedings of the DACCORD Short Term Forecasting Work shop, Delft, The Netherlands, February 1998; pp. 1–12. Available online: http://www.es.lancs.ac.uk/cres/daccord/workshop.html (accessed on 11 July 2020).
- Benenson, I.; Martens, K.; Rofé, Y.; Kwartler, A. Public transport versus private car GIS-based estimation of accessibility applied to the Tel Aviv metropolitan area. Ann. Reg. Sci. 2011, 47, 499–515. [Google Scholar] [CrossRef] [Green Version]
- Horni, A.; Nagel, K.; Axhausen, K.W. The Multi-Agent Transport Simulation MATSim; Ubiquity Press: London, UK, 2016. [Google Scholar]
- Van Zuylen, H.J.; Willumsen, L.G. The most likely trip matrix estimated from traffic counts. Transp. Res. Part Methodol. 1980, 14, 281–293. [Google Scholar] [CrossRef]
- Bera, S.; Rao, K. Estimation of origin-destination matrix from traffic counts: The state of the art. Eur. Transp. 2011, 49, 3–23. [Google Scholar]
- Cascetta, E.; Papola, A.; Marzano, V.; Simonelli, F.; Vitiello, I. Quasi-dynamic estimation of O-D flows from traffic counts: Formulation, statistical validation and performance analysis on real data. Transp. Res. Part Methodol. 2013, 55, 171–187. [Google Scholar] [CrossRef]
- Antoniou, C.; Barceló, J.; Breen, M.; Bullejos, M.; Casas, J.; Cipriani, E.; Ciuffo, B.; Djukic, T.; Hoogendoorn, S.; Marzano, V.; et al. Towards a generic benchmarking platform for origin–destination flows estimation/updating algorithms: Design, demonstration and validation. Transp. Res. Part Emerg. Technol. 2016, 66, 79–98. [Google Scholar] [CrossRef]
- Marzano, V.; Papola, A.; Simonelli, F.; Papageorgiou, M. A Kalman filter for quasi-dynamic od flow estimation/updating. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3604–3612. [Google Scholar] [CrossRef]
- Maher, M. Inferences on trip matrices from observations on link volumes: A Bayesian statistical approach. Transp. Res. Part Methodol. 1983, 17, 435–447. [Google Scholar] [CrossRef]
- Hazelton, M.L. Estimation of origin–destination matrices from link flows on uncongested networks. Transp. Res. Part Methodol.l 2000, 34, 549–566. [Google Scholar] [CrossRef]
- Tebaldi, C.; West, M. Bayesian inference on network traffic using link count data. J. Am. Stat. Assoc. 1998, 93, 557–573. [Google Scholar] [CrossRef]
- Antoniou, C.; Balakrishna, R.; Koutsopoulos, H.N. A synthesis of emerging data collection technologies and their impact on traffic management applications. Eur. Transp. Res. Rev. 2011, 3, 139–148. [Google Scholar] [CrossRef] [Green Version]
- Xia, J.; Dai, W.; Polak, J.; Bierlaire, M. Dimension Reduction for Origin-Destination Flow Estimation: Blind Estimation Made Possible. arXiv 2020, arXiv:1810.06077. [Google Scholar]
- Robinson, S. The development and application of an urban link travel time model using data derived from inductive loop detectors. Ph.D. Thesis, Imperial College London, Londen, UK, August 2005. [Google Scholar]
- Shan, D.; Sun, X.; Liu, J.; Sun, M. Optimization of Scanning and Counting Sensor Layout for Full Route Observability with a Bi-Level Programming Model. Sensors 2018, 18, 2286. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- NSW Transport Road Maritime Services. SCATS: THE BENCHMARK IN URBAN TRAFFIC CONTROL. Available online: http://www.scats.com.au/ (accessed on 11 July 2020).
- Bauer, D.; Tulic, M. Travel time predictions: Should one model speeds or travel times? Eur. Transp. Res. Rev. 2018, 10, 46. [Google Scholar] [CrossRef] [Green Version]
- Bell, M.G. The estimation of origin-destination matrices by constrained generalised least squares. Transp. Res. Part Methodol.l 1991, 25, 13–22. [Google Scholar] [CrossRef]
- Cascetta, E.; Nguyen, S. A unified framework for estimating or updating origin/destination matrices from traffic counts. Transp. Res. Part Methodol.l 1988, 22, 437–455. [Google Scholar] [CrossRef]
- Djukic, T. Dynamic OD Demand Estimation and Prediction for Dynamic Traffic Management. Ph.D. Thesis, Delft University of Technology, Tu Delft, Netherlands, November 2014. [Google Scholar]
- Marzano, V.; Papola, A.; Simonelli, F. Limits and perspectives of effective O–D matrix correction using traffic counts. Transp. Res. Part Emerg. Technol. 2009, 17, 120–132. [Google Scholar] [CrossRef]
- Lo, H.; Zhang, N.; Lam, W.H. Estimation of an origin-destination matrix with random link choice proportions: A statistical approach. Transp. Res. Part Methodol. 1996, 30, 309–324. [Google Scholar] [CrossRef]
- Hazelton, M.L. Estimation of origin–destination trip rates in Leicester. J. R. Stat. Soc. Ser. 2001, 50, 423–433. [Google Scholar] [CrossRef]
- Uber lTechnologies Inc. Uber Movement. Available online: https://movement.uber.com/?lang=en-US (accessed on 11 July 2020).
- Vardi, Y. Network Tomography : Estimating Source-Destination Traffic Intensities From Link Data. J. Am. Stat. Assoc. 1996, 1459, 37–41. [Google Scholar] [CrossRef]
- Miller, H.J. Time Geography. In Encyclopedia of GIS; Springer: Boston, MA, USA, 2008; pp. 1151–1156. [Google Scholar]
- Bell, M.G. The estimation of an origin-destination matrix from traffic counts. Transp. Sci. 1983, 17, 198–217. [Google Scholar] [CrossRef]
- Cascetta, E. Estimation of trip matrices from traffic counts and survey data: A generalized least squares estimator. Transp. Res. Part Methodol. 1984, 18, 289–299. [Google Scholar] [CrossRef]
- McNeil, S.; Hendrickson, C. A regression formulation of the matrix estimation problem. Transp. Sci. 1985, 19, 278–292. [Google Scholar] [CrossRef]
- Cascetta, E. Transportation Systems Analysis: Models and Applications; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Ashok, K.; Ben-Akiva, M.E. Alternative approaches for real-time estimation and prediction of time-dependent origin–destination flows. Transp. Sci. 2000, 34, 21–36. [Google Scholar] [CrossRef]
- Cipriani, E.; Nigro, M.; Fusco, G.; Colombaroni, C. Effectiveness of link and path information on simultaneous adjustment of dynamic OD demand matrix. Eur. Transp. Res. Rev. 2014, 6, 139. [Google Scholar] [CrossRef] [Green Version]
- Barcelö, J.; Montero, L.; Marqués, L.; Carmona, C. Travel time forecasting and dynamic origin-destination estimation for freeways based on bluetooth traffic monitoring. Transp. Res. Rec. 2010, 2175, 19–27. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.H.; Tseng, S.S.; Tsai, S.H. A knowledge based real-time travel time prediction system for urban network. Expert Syst. Appl. 2009, 36, 4239–4247. [Google Scholar] [CrossRef]
- Yang, H.; Sasaki, T.; Iida, Y.; Asakura, Y. Estimation of origin-destination matrices from link traffic counts on congested networks. Transp. Res. Part Methodol. 1992, 26, 417–434. [Google Scholar] [CrossRef]
- Tulic, M.; Bauer, D.; Scherrer, W. Link and route travel time prediction including the corresponding reliability in an urban network based on taxi floating car data. Transp. Res. Rec. 2014, 2442, 140–149. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. (Methodol.) 1977, 39, 1–22. [Google Scholar]
- Winter, S.; Yin, Z.C. The elements of probabilistic time geography. GeoInformatica 2011, 15, 417–434. [Google Scholar] [CrossRef]
- Ramamohanarao, K.; Xie, H.; Kulik, L.; Karunasekera, S.; Tanin, E.; Zhang, R.; Bin Khunayn, E.; Khunayn, E.B. SMARTS: Scalable Microscopic Adaptive Road Traffic Simulator. ACM Trans. Intell. Syst. Technol. Artic. 2016, 8, 1–22. [Google Scholar] [CrossRef]
- State Government of Victoria. VicRoads: Victoria’s Open Data Directory. Available online: https://www.data.vic.gov.au/ (accessed on 11 July 2020).
- SYGIC. Sygic: The Most Advanced Navigation. Available online: https://www.sygic.com/gps-navigation (accessed on 11 July 2020).
- Scherrer, L.; Tomko, M.; Ranacher, P.; Weibel, R. Travelers or locals? Identifying meaningful sub-populations from human movement data in the absence of ground truth. EPJ Data Sci. 2018, 7, 19. [Google Scholar] [CrossRef]
- Newson, P.; Krumm, J. Hidden Markov map matching through noise and sparseness. In Proceedings of the 17th ACM SIGSPATIAL international conference on advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009; pp. 336–343. [Google Scholar]
- Nitti, M.; Pinna, F.; Pintor, L.; Pilloni, V.; Barabino, B. iABACUS: A Wi-Fi-Based Automatic Bus Passenger Counting System. Energies 2020, 13, 1446. [Google Scholar] [CrossRef] [Green Version]
- Olivo, A.; Maternini, G.; Barabino, B. Empirical Study on the Accuracy and Precision of Automatic Passenger Counting in European Bus Services. Open Transp. J. 2019, 13, 250–260. [Google Scholar] [CrossRef]
















| Confidence Bound Percentage Error (CBPE) | |
| Root Mean Squared Error (RMSE) from the Observed Mean | |
| Mean Absolute Percentage Error (MAPE) from the Mbserved Mean |
| MAPE | CBPE | RMSE | Hod | |
|---|---|---|---|---|
| 1 | 17.669511 | 15.517241 | 2.645850 | 1.0 |
| 2 | 0.202307 | 15.740741 | 2.445008 | 2.0 |
| 3 | 0.718313 | 14.432990 | 2.393097 | 3.0 |
| 4 | 22.953926 | 19.767442 | 2.329059 | 4.0 |
| 5 | 26.719827 | 20.535714 | 3.328379 | 5.0 |
| 6 | 12.443983 | 11.538462 | 2.206808 | 6.0 |
| 7 | 14.955032 | 13.445378 | 2.081354 | 7.0 |
| 8 | 27.649186 | 13.157895 | 2.963124 | 8.0 |
| 9 | 32.979581 | 24.299065 | 3.858327 | 9.0 |
| 10 | 1.480969 | 12.222222 | 3.080802 | 10.0 |
| 11 | 2.016291 | 19.642857 | 2.882764 | 11.0 |
| 12 | 1.424106 | 24.637681 | 3.278605 | 12.0 |
| 13 | 1.534412 | 25.000000 | 3.168098 | 13.0 |
| 14 | 16.658874 | 23.404255 | 2.993369 | 14.0 |
| 15 | 22.793953 | 12.121212 | 2.591443 | 15.0 |
| 16 | 9.032345 | 6.666667 | 2.953414 | 16.0 |
| 17 | 30.181544 | 13.043478 | 2.855195 | 17.0 |
| 18 | 1.401953 | 46.666667 | 3.206350 | 18.0 |
| 19 | 28.902722 | 5.555556 | 1.326432 | 19.0 |
| 20 | 10.646802 | 16.129032 | 2.375741 | 20.0 |
| 21 | 31.177547 | 8.000000 | 1.634604 | 21.0 |
| 22 | 16.119596 | 23.376623 | 2.923352 | 22.0 |
| 23 | 4.494027 | 15.476190 | 2.502182 | 23.0 |
| 24 | 4.236363 | 12.359551 | 2.608609 | 24.0 |
| MAPE | CBPE | RMSE | Hod | |
|---|---|---|---|---|
| 0 | 18.456364 | 2.212389 | 1.086122 | 0.0 |
| 1 | 28.449028 | 0.641026 | 1.071584 | 1.0 |
| 2 | 37.291042 | 0.000000 | 1.142930 | 2.0 |
| 3 | 41.875131 | 2.105263 | 1.234366 | 3.0 |
| 4 | 41.253799 | 2.061856 | 1.149237 | 4.0 |
| 5 | 23.741862 | 1.036269 | 1.096324 | 5.0 |
| 6 | 15.789029 | 14.418605 | 1.864147 | 6.0 |
| 7 | 2.361422 | 7.490637 | 1.570877 | 7.0 |
| 8 | 1.162064 | 5.769231 | 2.244866 | 8.0 |
| 9 | 13.253511 | 9.717868 | 2.024412 | 9.0 |
| 10 | 23.498247 | 21.806854 | 2.083335 | 10.0 |
| 11 | 18.150688 | 12.852665 | 2.046035 | 11.0 |
| 12 | 10.440517 | 14.375000 | 2.049898 | 12.0 |
| 13 | 11.458377 | 16.455696 | 2.454868 | 13.0 |
| 14 | 18.620275 | 13.354037 | 2.210899 | 14.0 |
| 15 | 24.994183 | 17.378049 | 2.663201 | 15.0 |
| 16 | 22.769228 | 17.538462 | 2.538258 | 16.0 |
| 17 | 14.798218 | 13.213213 | 2.722560 | 17.0 |
| 18 | 22.258559 | 20.783133 | 2.602251 | 18.0 |
| 19 | 11.269477 | 17.177914 | 1.846150 | 19.0 |
| 20 | 11.470420 | 13.931889 | 1.753256 | 20.0 |
| 21 | 0.246007 | 8.598726 | 1.601560 | 21.0 |
| 22 | 2.320536 | 9.615385 | 1.837532 | 22.0 |
| 23 | 16.737412 | 2.090592 | 1.323046 | 23.0 |
| CBPE | MAPE | RMSE | Hod | |
|---|---|---|---|---|
| 0 | 9.090909 | 23.380651 | 1.568953 | 1.0 |
| 1 | 14.285714 | 32.053831 | 2.062144 | 2.0 |
| 2 | 0.000000 | 30.691456 | 1.983764 | 3.0 |
| 3 | 0.000000 | 8.316054 | 0.779859 | 4.0 |
| 4 | 0.000000 | 23.730673 | 1.332108 | 5.0 |
| 5 | 8.333333 | 19.952337 | 1.948909 | 6.0 |
| 6 | 4.761905 | 2.174713 | 1.738910 | 7.0 |
| 7 | 33.333333 | 47.974776 | 2.624935 | 8.0 |
| 8 | 44.827586 | 61.672828 | 3.215480 | 9.0 |
| 9 | 18.750000 | 28.348935 | 1.984638 | 10.0 |
| 10 | 33.333333 | 26.419977 | 2.746909 | 11.0 |
| 11 | 26.666667 | 40.617233 | 2.151389 | 12.0 |
| 12 | 27.586207 | 38.360967 | 2.357824 | 13.0 |
| 13 | 22.222222 | 30.253156 | 2.071730 | 14.0 |
| 14 | 46.666667 | 69.130894 | 3.357464 | 15.0 |
| 15 | 37.037037 | 58.616123 | 2.701654 | 16.0 |
| 16 | 50.000000 | 78.787198 | 3.434253 | 17.0 |
| 17 | 41.379310 | 78.718194 | 3.540826 | 18.0 |
| 18 | 42.857143 | 50.967232 | 2.666515 | 19.0 |
| 19 | 14.814815 | 8.287783 | 1.671548 | 20.0 |
| 20 | 4.166667 | 4.728311 | 1.502707 | 21.0 |
| 21 | 4.000000 | 12.711000 | 1.491700 | 22.0 |
| 22 | 0.000000 | 16.183482 | 1.363504 | 23.0 |
| 23 | 0.000000 | 19.018031 | 1.418765 | 24.0 |
| Error | MAPE | CBPE | RMSE | ||||
|---|---|---|---|---|---|---|---|
| Data | |||||||
| Mean | Standard deviation | Mean | Standard deviation | Mean | Standard deviation | ||
| Sygic vs Uber | 14.1 | 11.48 | 17.19 | 8.43 | 2.6 | 0.55 | |
| Estimated vs Uber | 18.02 | 11.54 | 10.2 | 6.87 | 1.84 | 0.54 | |
| Estimated vs Syic | 33 | 22.7 | 20.1 | 17.4 | 2.1 | 0.7 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, S.; Winter, S.; Tomko, M. Origin–Destination Flow Estimation from Link Count Data Only. Sensors 2020, 20, 5226. https://doi.org/10.3390/s20185226
Dey S, Winter S, Tomko M. Origin–Destination Flow Estimation from Link Count Data Only. Sensors. 2020; 20(18):5226. https://doi.org/10.3390/s20185226
Chicago/Turabian StyleDey, Subhrasankha, Stephan Winter, and Martin Tomko. 2020. "Origin–Destination Flow Estimation from Link Count Data Only" Sensors 20, no. 18: 5226. https://doi.org/10.3390/s20185226
APA StyleDey, S., Winter, S., & Tomko, M. (2020). Origin–Destination Flow Estimation from Link Count Data Only. Sensors, 20(18), 5226. https://doi.org/10.3390/s20185226






