Electrically Elicited Force Response Characteristics of Forearm Extensor Muscles for Electrical Muscle Stimulation-Based Haptic Rendering
Abstract
:1. Introduction
- The simplified force response model developed for lower limb muscles in the field of rehabilitation was introduced for EMS-based haptic rendering, and its feasibility for the forearm extensor muscles was experimentally verified. Thus, the model can be utilized for EMS-based haptic rendering given its feasibility for upper limb muscles.
- The force response characteristics, including the peak force and response time, were identified through the experiment based on a quantitative evaluation using the force response model. The peak force–amplitude relationship was assumed as an exponential function and verified by comparing the estimated peak force with the experimentally measured peak force. The response time characteristics were also identified by performing a quantitative evaluation using the force response model fitted to the experimental data. The presented results are expected to contribute to our understanding of the transient and steady-state features of the muscle contraction force response.
2. Materials and Methods
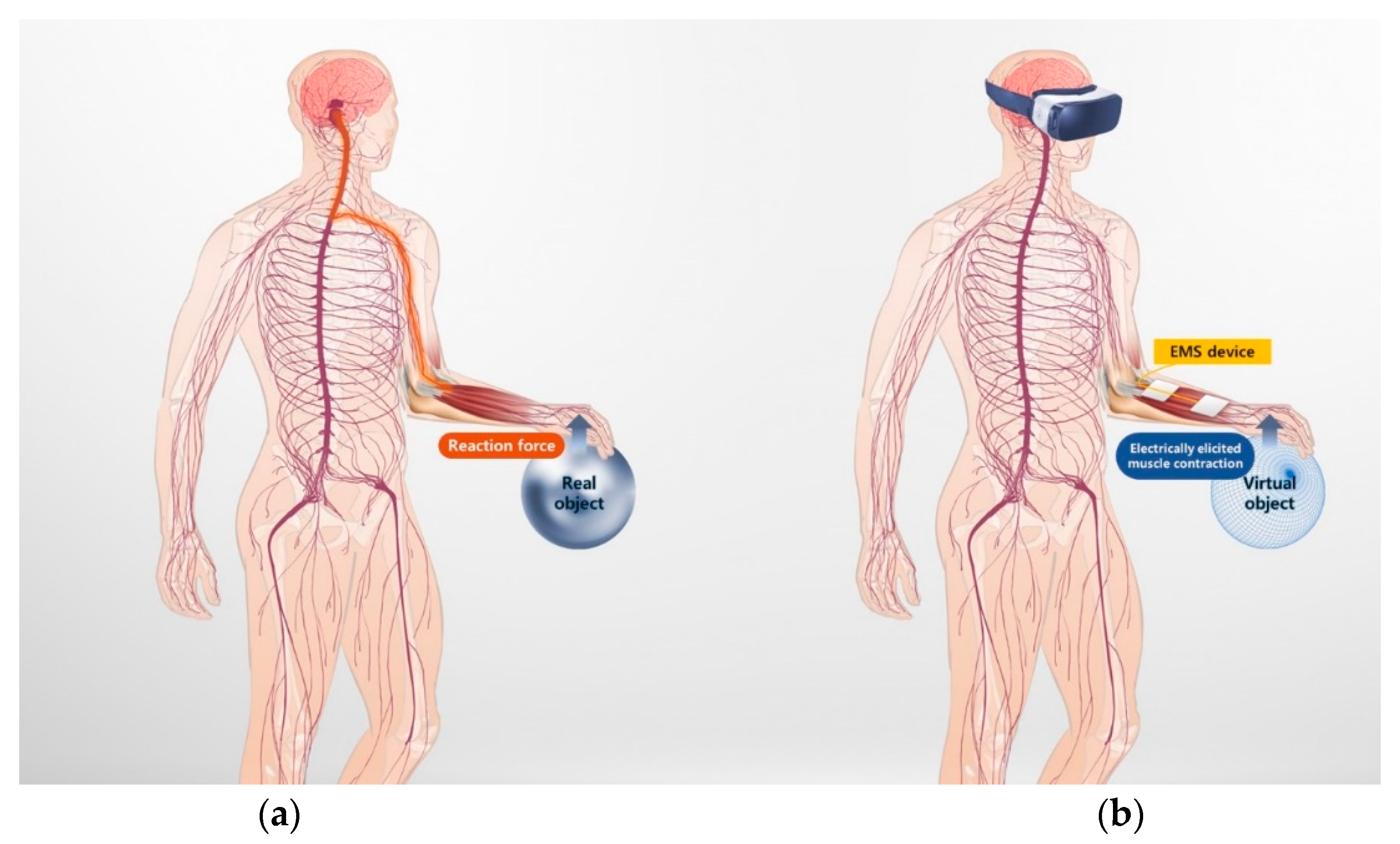
2.1. Principles of EMS-Based Haptic Rendering
2.2. Simplified Force Response Model of Muscle Contraction Elicited by Electrical Stimulation
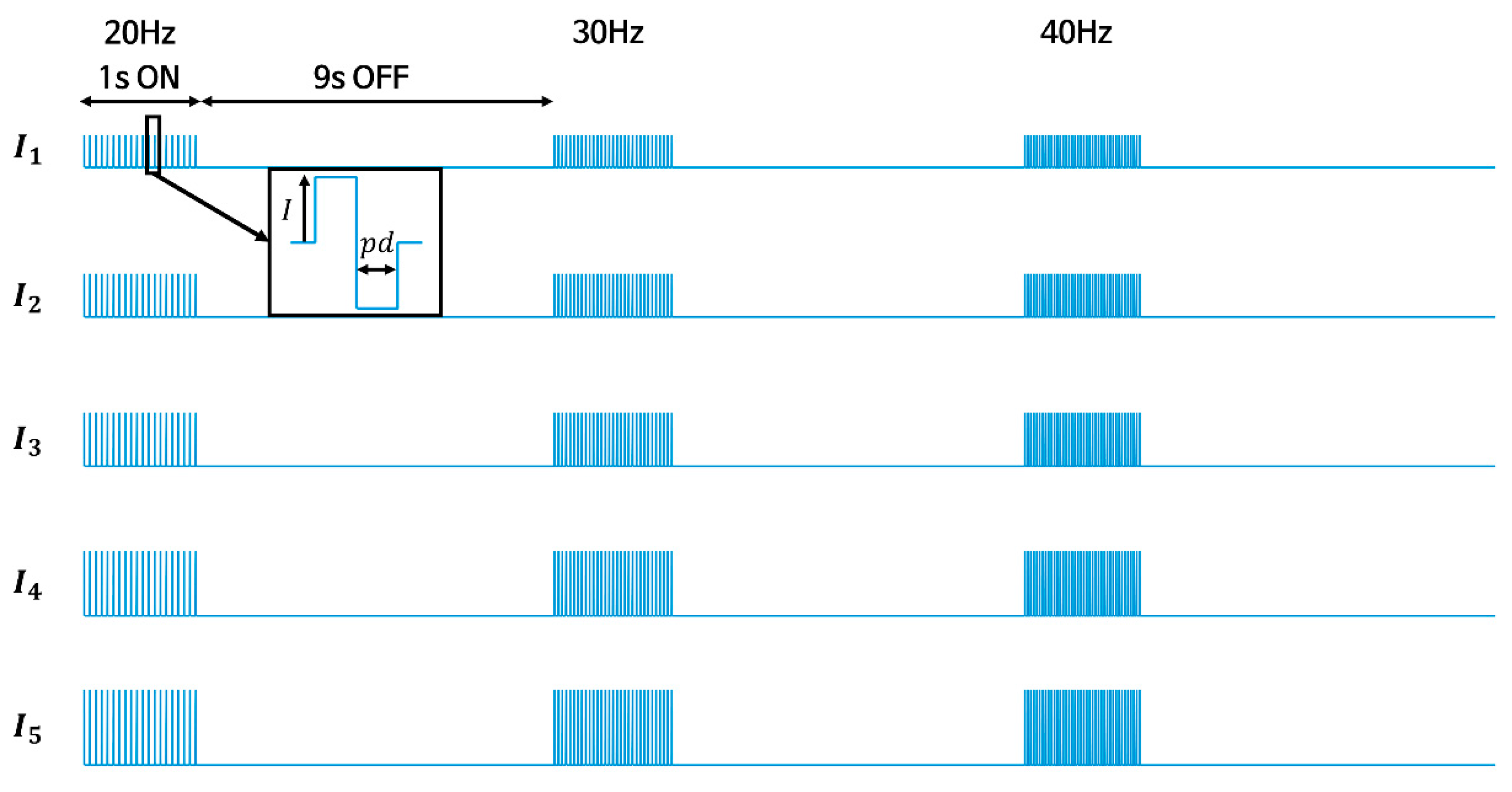
2.2.1. EMS Parameters
2.2.2. Force Response Model for Biphasic Pulse Input
2.2.3. Amplitude Modulation
2.3. Experimental Evaluation of the Force Response
2.3.1. Participants
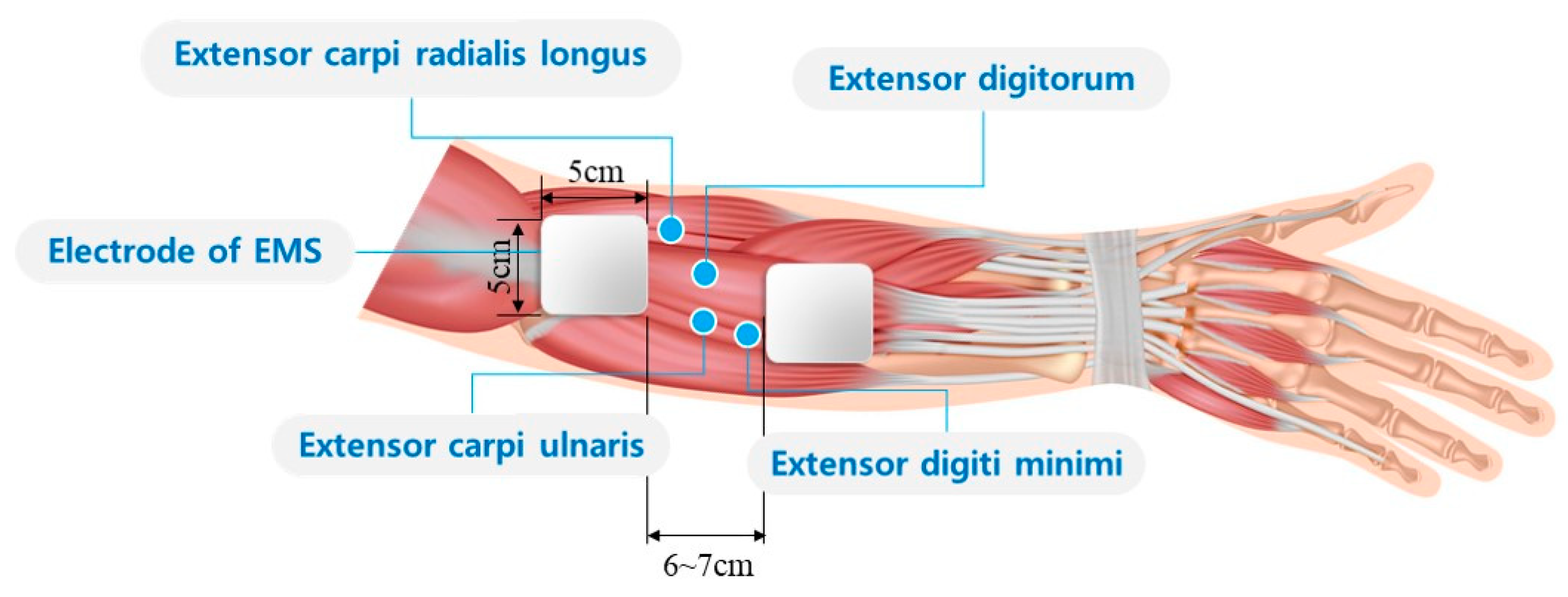
2.3.2. Experimental Setup
2.3.3. Experimental Procedures
2.4. Parameter Identification
3. Results
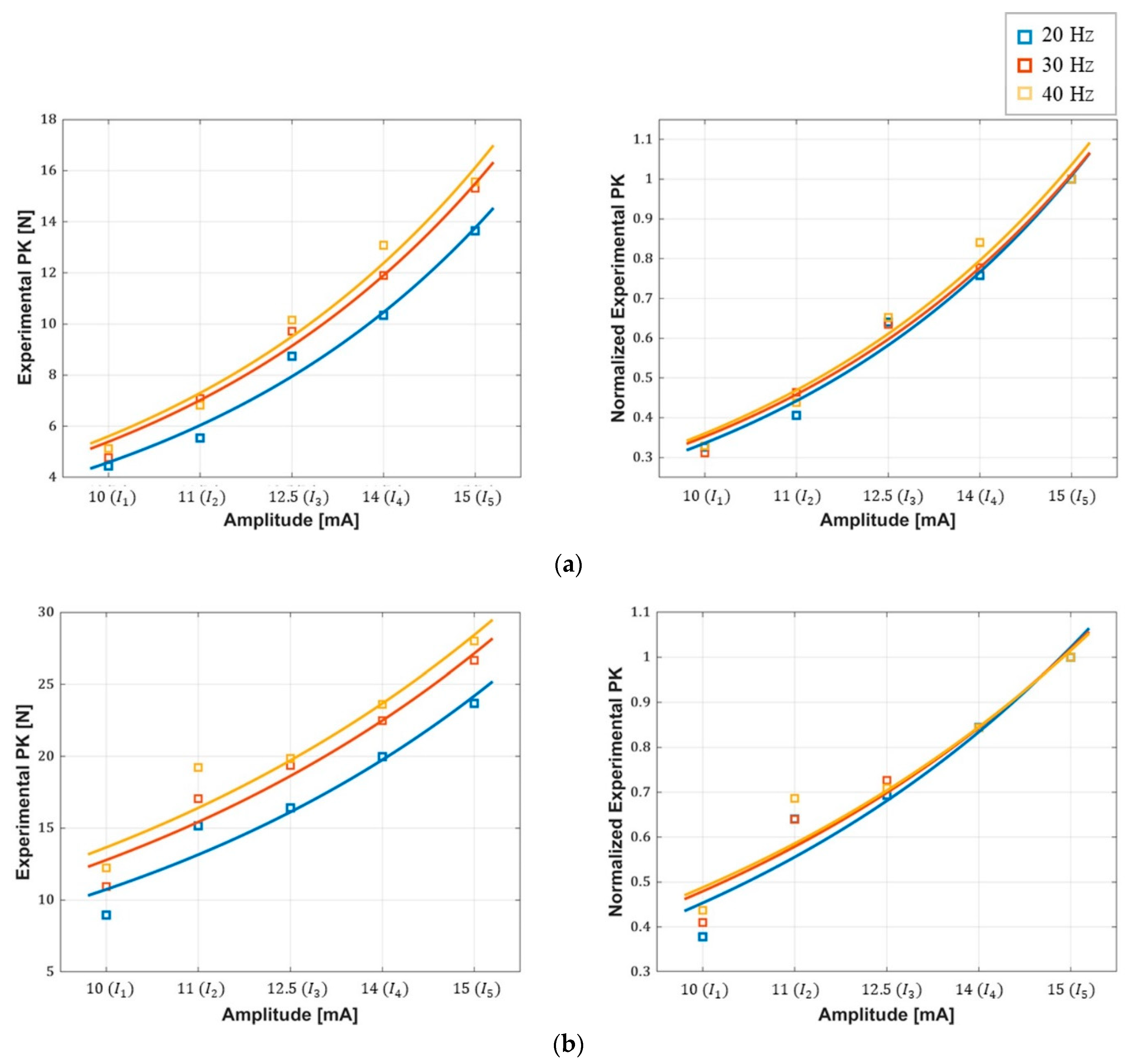
3.1. Peak Force–Amplitude Relationship
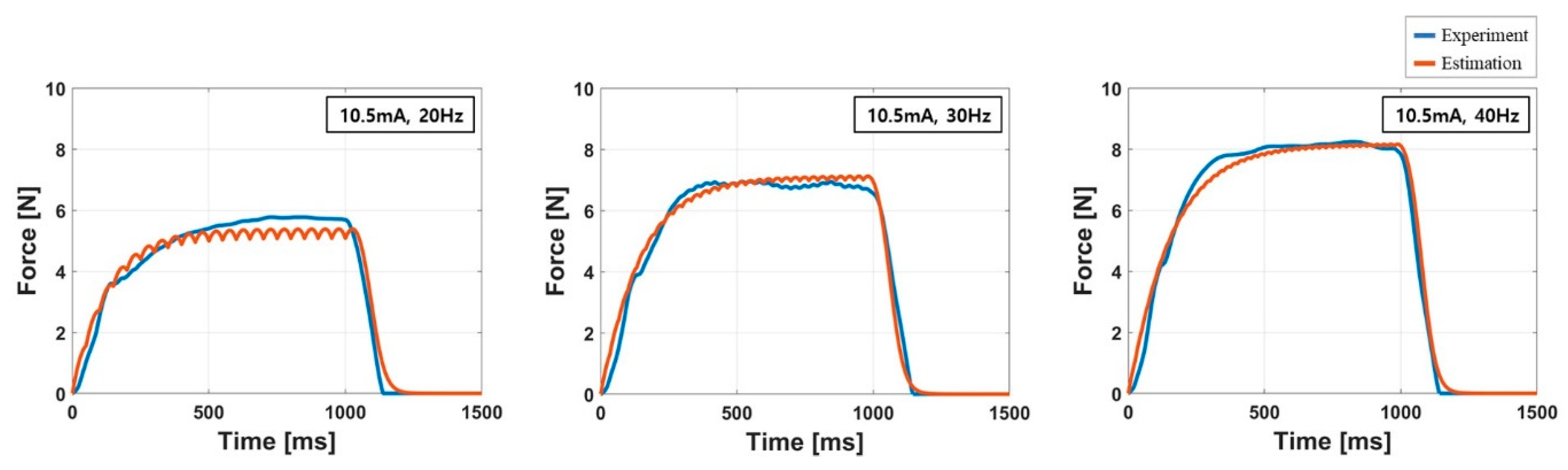
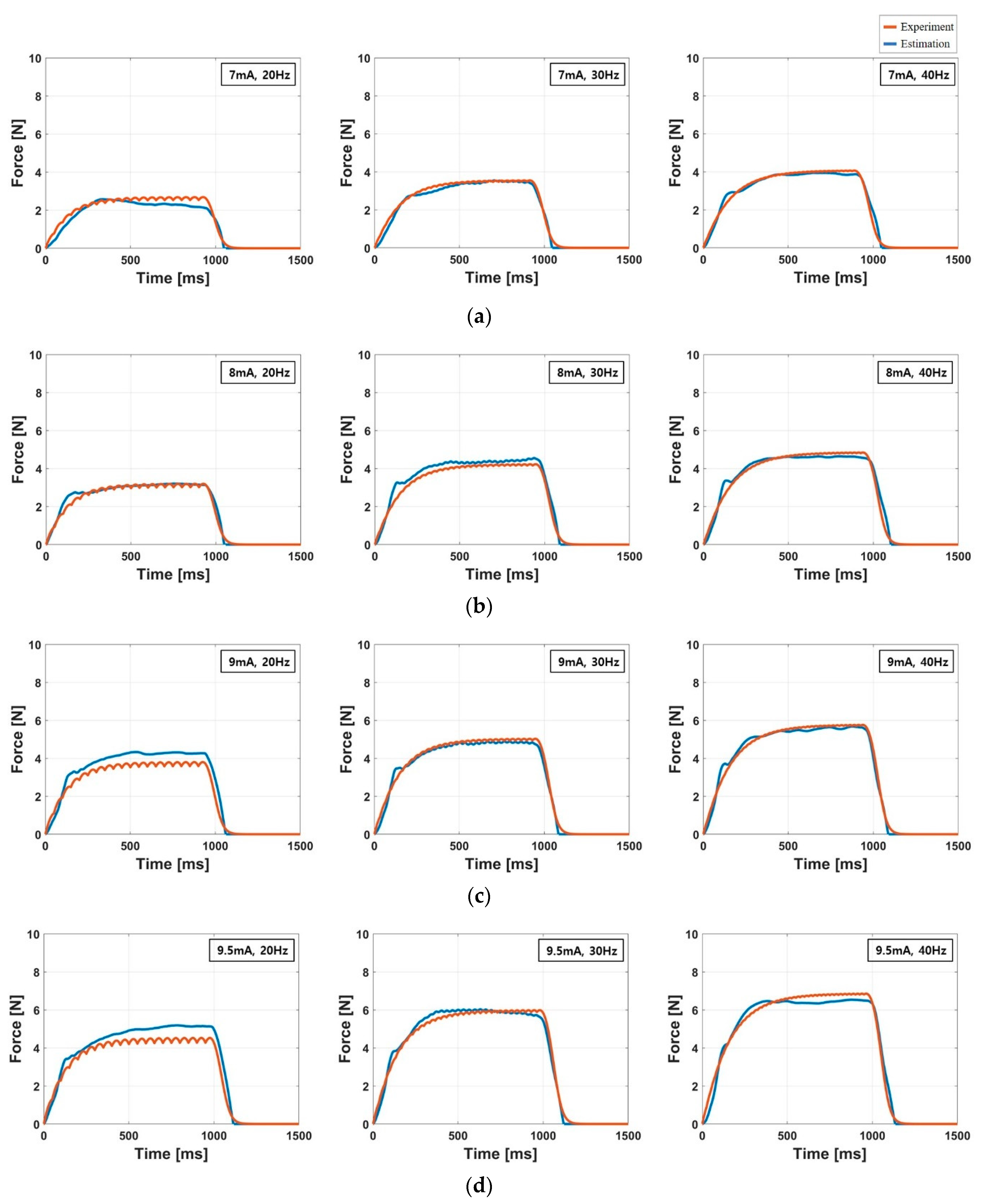
3.2. Accuracy of the Force Response Model
3.3. Characteristics of the Response Time
4. Discussion
4.1. Peak Force–Amplitude Relationship
4.2. Accuracy of the Force Response Model
4.3. Response Time
4.4. Limitation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sherman, W.R.; Craig, A.B. Understanding Virtual Reality: Interface, Application, and Design; Morgan Kaufmann: Cambridge, MA, USA, 2018; ISBN 978-0-12-801038-9. [Google Scholar]
- Bernardo, A. Virtual Reality and Simulation in Neurosurgical Training. World Neurosurgery 2017, 106, 1015–1029. [Google Scholar] [CrossRef]
- Pacchierotti, C.; Prattichizzo, D.; Kuchenbecker, K.J. Cutaneous Feedback of Fingertip Deformation and Vibration for Palpation in Robotic Surgery. IEEE Trans. Biomed. Eng. 2016, 63, 278–287. [Google Scholar] [CrossRef]
- Salisbury, K.; Conti, F.; Barbagli, F. Haptic rendering: Introductory concepts. IEEE Comput. Graph. Appl. 2004, 24, 24–32. [Google Scholar] [CrossRef] [Green Version]
- Salisbury, K.; Brock, D.; Massie, T.; Swarup, N.; Zilles, C. Haptic rendering: Programming touch interaction with virtual objects. In Proceedings of the 1995 Symposium on Interactive 3D Graphics—SI3D ’95, Monterey, CA, USA, 9–12 April 1995; pp. 123–130. [Google Scholar]
- Diolaiti, N.; Niemeyer, G.; Barbagli, F.; Salisbury, J.K. Stability of Haptic Rendering: Discretization, Quantization, Time Delay, and Coulomb Effects. IEEE Trans. Robot. 2006, 22, 256–268. [Google Scholar] [CrossRef]
- Berg, L.P.; Vance, J.M. Industry use of virtual reality in product design and manufacturing: A survey. Virtual Real. 2017, 21, 1–17. [Google Scholar] [CrossRef]
- Pacchierotti, C.; Meli, L.; Chinello, F.; Malvezzi, M.; Prattichizzo, D. Cutaneous haptic feedback to ensure the stability of robotic teleoperation systems. Int. J. Rob. Res. 2015, 34, 1773–1787. [Google Scholar] [CrossRef]
- Okamura, A.M. Methods for haptic feedback in teleoperated robot-assisted surgery. Ind. Robot 2004, 31, 499–508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Son, H.I.; Bhattacharjee, T.; Lee, D.Y. Estimation of environmental force for the haptic interface of robotic surgery. Int. J. Med. Robot. 2010, 6, 221–230. [Google Scholar] [CrossRef] [PubMed]
- Choi, C.; Kim, J.; Han, H.; Ahn, B.; Kim, J. Graphic and haptic modelling of the oesophagus for VR-based medical simulation. Int. J. Med. Robot. 2009, 5, 257–266. [Google Scholar] [CrossRef]
- Ullrich, S.; Kuhlen, T. Haptic Palpation for Medical Simulation in Virtual Environments. IEEE Trans. Visual. Comput. Graphics 2012, 18, 617–625. [Google Scholar] [CrossRef] [PubMed]
- Coles, T.R.; John, N.W.; Gould, D.; Caldwell, D.G. Integrating Haptics with Augmented Reality in a Femoral Palpation and Needle Insertion Training Simulation. IEEE Trans. Haptics 2011, 4, 199–209. [Google Scholar] [CrossRef] [PubMed]
- Lopes, P.; You, S.; Ion, A.; Baudisch, P. Adding Force Feedback to Mixed Reality Experiences and Games using Electrical Muscle Stimulation. In Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems—CHI ’18, Montreal, QC, Canada, 21–26 April 2018; pp. 1–13. [Google Scholar]
- Gu, X.; Zhang, Y.; Sun, W.; Bian, Y.; Zhou, D.; Kristensson, P.O. Dexmo: An Inexpensive and Lightweight Mechanical Exoskeleton for Motion Capture and Force Feedback in VR. In Proceedings of the 2016 CHI Conference on Human Factors in Computing Systems, San Jose, CA, USA, 7–12 May 2016; pp. 1991–1995. [Google Scholar]
- Lopes, P.; You, S.; Cheng, L.-P.; Marwecki, S.; Baudisch, P. Providing Haptics to Walls & Heavy Objects in Virtual Reality by Means of Electrical Muscle Stimulation. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, Denver, CO, USA, 6–11 May 2017; pp. 1471–1482. [Google Scholar]
- TESLASUIT—Haptic Feedback VR Suit for Motion Capture and VR Training. Available online: https://teslasuit.io/the-suit/ (accessed on 24 July 2020).
- Massie, T.H.; Salisbury, J.K. The PHANTOM Haptic Interface: A Device for Probing Virtual Objects. Available online: https://alliance.seas.upenn.edu/~medesign/wiki/uploads/Courses/Massie94-DSC-Phantom.pdf (accessed on 23 July 2020).
- Force Dimension - Products - omega.7 - Overview. Available online: https://www.forcedimension.com/products/omega-7/overview (accessed on 23 July 2020).
- Frisoli, A.; Rocchi, F.; Marcheschi, S.; Dettori, A.; Salsedo, F.; Bergamasco, M. A New Force-Feedback Arm Exoskeleton for Haptic Interaction in Virtual Environments. In Proceedings of the First Joint Eurohaptics Conference and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, Pisa, Italy, 18–20 March 2005; pp. 195–201. [Google Scholar]
- Aiple, M.; Schiele, A. Pushing the limits of the CyberGrasp for haptic rendering. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3541–3546. [Google Scholar]
- Yem, V.; Vu, K.; Kon, Y.; Kajimoto, H. Effect of Electrical Stimulation Haptic Feedback on Perceptions of Softness-Hardness and Stickiness While Touching a Virtual Object. In Proceedings of the 2018 IEEE Conference on Virtual Reality and 3D User Interfaces (VR), Reutlingen, Germany, 18–22 March 2018; pp. 89–96. [Google Scholar]
- Kurita, Y.; Ishikawa, T.; Tsuji, T. Stiffness Display by Muscle Contraction Via Electric Muscle Stimulation. IEEE Robot. Autom. Lett. 2016, 1, 1014–1019. [Google Scholar] [CrossRef]
- Pfeiffer, M.; Duente, T.; Rohs, M. A Wearable Force Feedback Toolkit with Electrical Muscle Stimulation. In Proceedings of the 2016 CHI Conference Extended Abstracts on Human Factors in Computing Systems—CHI EA ’16, San Jose, CA, USA, 7–12 May 2016; pp. 3758–3761. [Google Scholar]
- Lynch, C.L.; Popovic, M.R. Functional Electrical Stimulation. IEEE Control Syst. 2008, 28, 40–50. [Google Scholar] [CrossRef] [Green Version]
- Kitamura, T.; Hasegawa, Y.; Sakaino, S.; Tsuji, T. Estimation of Relationship between Stimulation Current and Force Exerted during Isometric Contraction. arXiv 2018, arXiv:1811.02795 [cs, q-bio]. [Google Scholar]
- Ding, J.; Lee, S.C.K.; Johnston, T.E.; Wexler, A.S.; Scott, W.B.; Binder-Macleod, S.A. Mathematical model that predicts isometric muscle forces for individuals with spinal cord injuries. Muscle Nerve 2005, 31, 702–712. [Google Scholar] [CrossRef]
- Ben Hmed, A.; Bakir, T.; Garnier, Y.M.; Sakly, A.; Lepers, R.; Binczak, S. An approach to a muscle force model with force-pulse amplitude relationship of human quadriceps muscles. Comput. Biol. Med. 2018, 101, 218–228. [Google Scholar] [CrossRef]
- Wilson, E.; Rustighi, E.; Newland, P.L.; Mace, B.R. A comparison of models of the isometric force of locust skeletal muscle in response to pulse train inputs. Biomech. Model. Mechanobiol. 2012, 11, 519–532. [Google Scholar] [CrossRef]
- Ding, J.; Chou, L.-W.; Kesar, T.M.; Lee, S.C.K.; Johnston, T.E.; Wexler, A.S.; Binder-Macleod, S.A. Mathematical model that predicts the force–intensity and force–frequency relationships after spinal cord injuries. Muscle Nerve 2007, 36, 214–222. [Google Scholar] [CrossRef] [Green Version]
- Hashemi, J.; Morin, E.; Mousavi, P.; Mountjoy, K.; Hashtrudi-Zaad, K. EMG–force modeling using parallel cascade identification. J. Electromyogr. Kinesiol. 2012, 22, 469–477. [Google Scholar] [CrossRef]
- Bobet, J.; Gossen, E.R.; Stein, R.B. A comparison of models of force production during stimulated isometric ankle dorsiflexion in humans. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 444–451. [Google Scholar] [CrossRef]
- Youn, W.; Kim, J. Estimation of elbow flexion force during isometric muscle contraction from mechanomyography and electromyography. Med. Biol. Eng. Comput. 2010, 48, 1149–1157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohamad, N.Z.; Hamzaid, N.A.; Davis, G.M.; Abdul Wahab, A.K.; Hasnan, N. Mechanomyography and Torque during FES-Evoked Muscle Contractions to Fatigue in Individuals with Spinal Cord Injury. Sensors 2017, 17, 1627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meglič, A.; Uršič, M.; Škorjanc, A.; Đorđević, S.; Belušič, G. The Piezo-resistive MC Sensor is a Fast and Accurate Sensor for the Measurement of Mechanical Muscle Activity. Sensors 2019, 19, 2108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Esposito, D.; Andreozzi, E.; Fratini, A.; Gargiulo, G.; Savino, S.; Niola, V.; Bifulco, P. A Piezoresistive Sensor to Measure Muscle Contraction and Mechanomyography. Sensors 2018, 18, 2553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Đorđević, S.; Tomažič, S.; Narici, M.; Pišot, R.; Meglič, A. In-Vivo Measurement of Muscle Tension: Dynamic Properties of the MC Sensor during Isometric Muscle Contraction. Sensors 2014, 14, 17848–17863. [Google Scholar] [CrossRef] [Green Version]
- Esposito, D.; Andreozzi, E.; Gargiulo, G.D.; Fratini, A.; D’Addio, G.; Naik, G.R.; Bifulco, P. A Piezoresistive Array Armband with Reduced Number of Sensors for Hand Gesture Recognition. Front. Neurorobot. 2020, 13. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Z.G.; Menon, C. A Review of Force Myography Research and Development. Sensors 2019, 19, 4557. [Google Scholar] [CrossRef] [Green Version]
- Laufer, Y.; Ries, J.D.; Leininger, P.M.; Alon, G. Quadriceps Femoris Muscle Torques and Fatigue Generated by Neuromuscular Electrical Stimulation with Three Different Waveforms. Phys. Ther. 2001, 81, 1307–1316. [Google Scholar] [CrossRef]
- Bowman, B.R.; Baker, L.L. Effects of waveform parameters on comfort during transcutaneous neuromuscular electrical stimulation. Ann. Biomed. Eng. 1985, 13, 59–74. [Google Scholar] [CrossRef]
- Miller, J.P.; Eldabe, S.; Buchser, E.; Johanek, L.M.; Guan, Y.; Linderoth, B. Parameters of Spinal Cord Stimulation and Their Role in Electrical Charge Delivery: A Review. Neuromodulation Technol. Neural Interface 2016, 19, 373–384. [Google Scholar] [CrossRef]
- Chou, L.-W.; Binder-Macleod, S.A. The effects of stimulation frequency and fatigue on the force–intensity relationship for human skeletal muscle. Clin. Neurophysiol. 2007, 118, 1387–1396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matsunaga, T.; Shimada, Y.; Sato, K. Muscle fatigue from intermittent stimulation with low and high frequency electrical pulses. Arch. Phys. Med. Rehabil. 1999, 80, 48–53. [Google Scholar] [CrossRef]
- Glaviano, N.R.; Saliba, S. Can the Use of Neuromuscular Electrical Stimulation Be Improved to Optimize Quadriceps Strengthening? Sports Health 2016, 8, 79–85. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.K.; Trew, M.L.; Pullan, A.J.; Röhrle, O. Simulating a dual-array electrode configuration to investigate the influence of skeletal muscle fatigue following functional electrical stimulation. Comput. Biol. Med. 2012, 42, 915–924. [Google Scholar] [CrossRef]
- Jailani, R.; Tokhi, M.O. The effect of functional electrical stimulation (FES) on paraplegic muscle fatigue. In Proceedings of the 2012 IEEE 8th International Colloquium on Signal Processing and its Applications, Malacca, Malaysia, 23–25 March 2012; pp. 500–504. [Google Scholar]
- Mellor, R.; Stokes, M.J. Detection and severity of low frequency fatigue in the human adductor pollicis muscle. J. Neurol. Sci. 1992, 108, 196–201. [Google Scholar] [CrossRef]
- Doucet, B.M.; Lam, A.; Griffin, L. Neuromuscular electrical stimulation for skeletal muscle function. Yale J. Biol. Med. 2012, 85, 201–215. [Google Scholar]
- Maffiuletti, N.A.; Morelli, A.; Martin, A.; Duclay, J.; Billot, M.; Jubeau, M.; Agosti, F.; Sartorio, A. Effect of gender and obesity on electrical current thresholds. Muscle Nerve 2011, 44, 202–207. [Google Scholar] [CrossRef]
- Ding, J.; Binder-Macleod, S.A.; Wexler, A.S. Two-step, predictive, isometric force model tested on data from human and rat muscles. J. Appl. Physiol. 1998, 85, 2176–2189. [Google Scholar] [CrossRef] [Green Version]
- Huxley, H.E. Fifty years of muscle and the sliding filament hypothesis. Eur. J. Biochem. 2004, 271, 1403–1415. [Google Scholar] [CrossRef]
- Levy, M.; Mizrahi, J.; Susak, Z. Recruitment, force and fatigue characteristics of quadriceps muscles of paraplegics isometrically activated by surface functional electrical stimulation. J. Biomed. Eng. 1990, 12, 150–156. [Google Scholar] [CrossRef]
- Buckmire, A.J.; Lockwood, D.R.; Doane, C.J.; Fuglevand, A.J. Distributed stimulation increases force elicited with functional electrical stimulation. J. Neural Eng. 2018, 15, 026001. [Google Scholar] [CrossRef] [PubMed]
- Bajd, T.; Munih, M. Basic functional electrical stimulation (FES) of extremities: An engineer’s view. Technol. Health Care off. J. Eur. Soc. Eng. Med. 2010, 18, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Alon, G.; Allin, J.; Inbar, G.F. Optimization of Pulse Duration and Pulse Charge During Transcutaneous Electrical Nerve Stimulation. Aust. J. Physiotherapy 1983, 29, 195–201. [Google Scholar] [CrossRef] [Green Version]
- Allin, S.; Matsuoka, Y.; Klatzky, R. Measuring just noticeable differences for haptic force feedback: Implications for rehabilitation. In Proceedings of the 10th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, HAPTICS 2002, Orlando, FL, USA, 24–25 March 2002; pp. 299–302. [Google Scholar]
- Zeng, J.; Zhou, Y.; Yang, Y.; Liu, H. Hand Grip Force Enhancer Based on sEMG- Triggered Functional Electrical Stimulation. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Suzhou, China, 29 July–2 August 2019; pp. 231–236. [Google Scholar]





| Type | Parameter | Value |
|---|---|---|
| Static | Waveform | Biphasic rectangular |
| Pulse Width (pd) | 400 | |
| Control | Frequency | 20, 30, 40 Hz |
| Pulse Amplitude | [ ~ ] 1 |
| Subject | 20 Hz | 30 Hz | 40 Hz | |||
|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | |
| K01 | 1.47(8) * | 8.95(12) | 1.68(8) | 12.8(12) | 2.16(8) | 15.6(12) |
| K02 | 1.69(12) | 5.31(18) | 2.10(12) | 6.61(18) | 2.48(12) | 7.66(18) |
| K03 | 8.57(10) | 23.7(15) | 10.8(10) | 26.7(15) | 11.0(10) | 28.0(15) |
| K04 | 3.77(9) | 16.9(13.5) | 5.21(9) | 21.7(13.5) | 5.82(9) | 25.3(13.5) |
| K05 | 4.45(10) | 13.6(15) | 4.77(10) | 15.3(15) | 5.13(10) | 15.6(15) |
| K06 | 2.80(8) | 14.9(12) | 4.13(8) | 18.3(12) | 4.69(8) | 19.9(12) |
| K07 | 2.45(10) | 7.67(15) | 2.80(10) | 11.6(15) | 2.94(10) | 11.7(15) |
| K08 | 3.69(8) | 13.5(12) | 5.81(8) | 16.1(12) | 6.93(8) | 17.0(12) |
| K09 | 4.03(7) | 8.69(10.5) | 5.79(7) | 11.8(10.5) | 5.42(7) | 12.8(10.5) |
| K10 | 2.45(7) | 5.61(10.5) | 3.43(7) | 6.92(10.5) | 3.88(7) | 8.24(10.5) |
| Frequency (Hz) | (N) | RMSE (N) | NRMSE (%) | ||
|---|---|---|---|---|---|
| 20 | 0.497(0.457) * | 0.275(0.076) | 0.96(0.029) | 0.72(0.53) | 8.35(3.37) |
| 30 | 0.715(0.718) | 0.278(0.099) | 0.97(0.019) | 0.73(0.47) | 7.27(2.01) |
| 40 | 0.734(0.730) | 0.288(0.118) | 0.97(0.025) | 0.90(0.62) | 7.76(3.05) |
| Subject | (N/s) | RMSE (N) | NRMSE (%) | |||||
|---|---|---|---|---|---|---|---|---|
| K01 | 121.9 | 0.300 | 20.8 | 33.1 | 194.4 | 0.97 | 0.64 | 5.97 |
| K02 | 75.9 | 0.128 | 15.6 | 76.2 | 52.0 | 0.96 | 0.43 | 7.22 |
| K03 | 438.9 | 0.326 | 31.1 | 40.5 | 51.8 | 0.93 | 2.13 | 9.07 |
| K04 | 183.1 | 0.094 | 15.9 | 50.2 | 117.9 | 0.97 | 1.20 | 6.28 |
| K05 | 130.8 | 0.012 | 11.5 | 5.0 | 124.1 | 0.89 | 1.47 | 10.3 |
| K06 | 148.7 | 0.162 | 22.5 | 14.4 | 17.6 | 0.95 | 1.15 | 7.22 |
| K07 | 85.0 | 0.113 | 17.0 | 11.8 | 189.8 | 0.91 | 0.91 | 9.41 |
| K08 | 218.0 | 0.190 | 26.3 | 10.0 | 98.4 | 0.90 | 1.41 | 9.74 |
| K09 | 122.2 | 0.215 | 21.9 | 24.1 | 137.4 | 0.89 | 0.93 | 9.30 |
| K10 | 68.5 | 0.293 | 29.3 | 20.7 | 163.6 | 0.94 | 0.40 | 6.06 |
| Ave. (SD) | 159.3 (121) | 0.180 (0.110) | 21.2 (6.36) | 28.6 (23.0) | 130.5 (55.2) | 0.93 (0.032) | 1.07 (0.53) | 8.06 (1.67) |
| Subject | |||||
|---|---|---|---|---|---|
| K01 | 0.86(14.7) | 0.77(16.4) | 0.76(19.8) | 0.85(14.4) | 0.97(5.97) |
| K02 | 0.89(10.0) | 0.87(8.67) | 0.91(11.9) | 0.87(13.6) | 0.96(7.22) |
| K03 | 0.78(17.2) | 0.88(14.3) | 0.91(8.99) | 0.94(8.82) | 0.93(9.07) |
| K04 | 0.79(13.8) | 0.92(10.9) | 0.89(11.0) | 0.96(6.65) | 0.97(6.28) |
| K05 | 0.79(12.3) | 0.84(11.0) | 0.80(16.0) | 0.90(11.9) | 0.89(10.3) |
| K06 | 0.77(14.0) | 0.95(7.22) | 0.86(16.2) | 0.82(18.4) | 0.95(7.22) |
| K07 | 0.83(13.5) | 0.78(16.6) | 0.81(15.3) | 0.85(13.8) | 0.91(9.41) |
| K08 | 0.72(11.9) | 0.94(8.32) | 0.88(12.2) | 0.82(14.1) | 0.90(9.74) |
| K09 | 0.89(11.5) | 0.91(8.51) | 0.85(11.9) | 0.85(11.4) | 0.89(9.30) |
| K10 | 0.92(6.92) | 0.94(6.32) | 0.91(7.44) | 0.92(7.44) | 0.94(6.06) |
| Average | 0.82(12.6) | 0.88(10.8) | 0.86(13.1) | 0.88(12.0) | 0.93(8.06) |
| Subject | ||||||
|---|---|---|---|---|---|---|
| K01 | 15.3(4.15) * | 113.0(9.78) | 364.3(38.3) | 97.6(5.77) | 251.3(29.1) | 349.0(34.2) |
| K02 | 10.6(1.72) | 77.3(6.12) | 261.5(4.16) | 66.7(4.41) | 194.9(0.87) | 250.9(4.86) |
| K03 | 8.67(1.19) | 61.5(2.43) | 193.0(13.8) | 52.8(1.32) | 131.5(11.4) | 184.3(12.7) |
| K04 | 13.6(2.32) | 97.4(10.0) | 335.6(16.9) | 83.8(7.78) | 238.2(7.39) | 322.0(14.6) |
| K05 | 12.0(1.34) | 80.8(6.39) | 277.3(8.87) | 68.8(5.05) | 196.5(2.75) | 265.3(7.54) |
| K06 | 15.3(2.75) | 108.0(5.58) | 347.7(26.5) | 92.6(2.89) | 239.7(20.9) | 332.4(23.8) |
| K07 | 15.1(3.34) | 106.2(13.4) | 359.7(32.5) | 91.1(10.1) | 253.5(19.1) | 344.6(29.2) |
| K08 | 8.87(1.46) | 64.1(4.16) | 195.3(17.1) | 55.2(2.79) | 131.3(13.0) | 186.4(15.7) |
| K09 | 12.3(2.47) | 85.3(10.7) | 292.4(20.9) | 73(8.25) | 207.1(10.6) | 280.1(18.5) |
| K10 | 15.2(2.87) | 102.6(7.90) | 334.7(18.6) | 87.4(5.06) | 232.1(10.8) | 319.5(15.8) |
| Ave. (SD) | 12.7 (2.63) | 98.6 (37.6) | 296.2 (63.9) | 71.7 (27.9) | 207.6 (45.3) | 283.5 (61.3) |
| Subject | |||
|---|---|---|---|
| 20 Hz | 30 Hz | 40 Hz | |
| K01 | 304.8 * | 357.8 | 384.2 |
| K02 | 255.4 | 262.4 | 266.8 |
| K03 | 167.0 | 193.6 | 192.4 |
| K04 | 303.2 | 325.6 | 337.2 |
| K05 | 255.6 | 267.0 | 273.2 |
| K06 | 303.6 | 333.6 | 359.8 |
| K07 | 305.4 | 357.8 | 370.6 |
| K08 | 165.0 | 196.0 | 198.4 |
| K09 | 254.8 | 291.0 | 294.4 |
| K10 | 299.4 | 322.9 | 336.28 |
| Ave. (SD) | 261.4 (54.9) | 290.8 (60.4) | 301.3 (68.4) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Kim, Y.; Jung, H. Electrically Elicited Force Response Characteristics of Forearm Extensor Muscles for Electrical Muscle Stimulation-Based Haptic Rendering. Sensors 2020, 20, 5669. https://doi.org/10.3390/s20195669
Lee J, Kim Y, Jung H. Electrically Elicited Force Response Characteristics of Forearm Extensor Muscles for Electrical Muscle Stimulation-Based Haptic Rendering. Sensors. 2020; 20(19):5669. https://doi.org/10.3390/s20195669
Chicago/Turabian StyleLee, Jungeun, Yeongjin Kim, and Hoeryong Jung. 2020. "Electrically Elicited Force Response Characteristics of Forearm Extensor Muscles for Electrical Muscle Stimulation-Based Haptic Rendering" Sensors 20, no. 19: 5669. https://doi.org/10.3390/s20195669
APA StyleLee, J., Kim, Y., & Jung, H. (2020). Electrically Elicited Force Response Characteristics of Forearm Extensor Muscles for Electrical Muscle Stimulation-Based Haptic Rendering. Sensors, 20(19), 5669. https://doi.org/10.3390/s20195669







