Refinement of TOA Localization with Sensor Position Uncertainty in Closed-Form
Abstract
:1. Introduction
- The weighted spherical-interpolation is derived, which solves the source position and redundant variable successively;
- An approximate expression of the theoretical covariance analysis is presented for the weighted spherical-interpolation;
- Eliminating the redundant variable, a refinement for the solution is proposed to improve the MSE and bias further;
- The simulation shows the proposed method performs better than the state-of-the-art methods when using fewer sensors.
- Introducing a weighting matrix for spherical-interpolation resulting in the weighted spherical-interpolation;
- Analyzing the covariance in the small noise region;
- Refining the solution to improve the MSE and lower the bias further when using only 4 sensors.
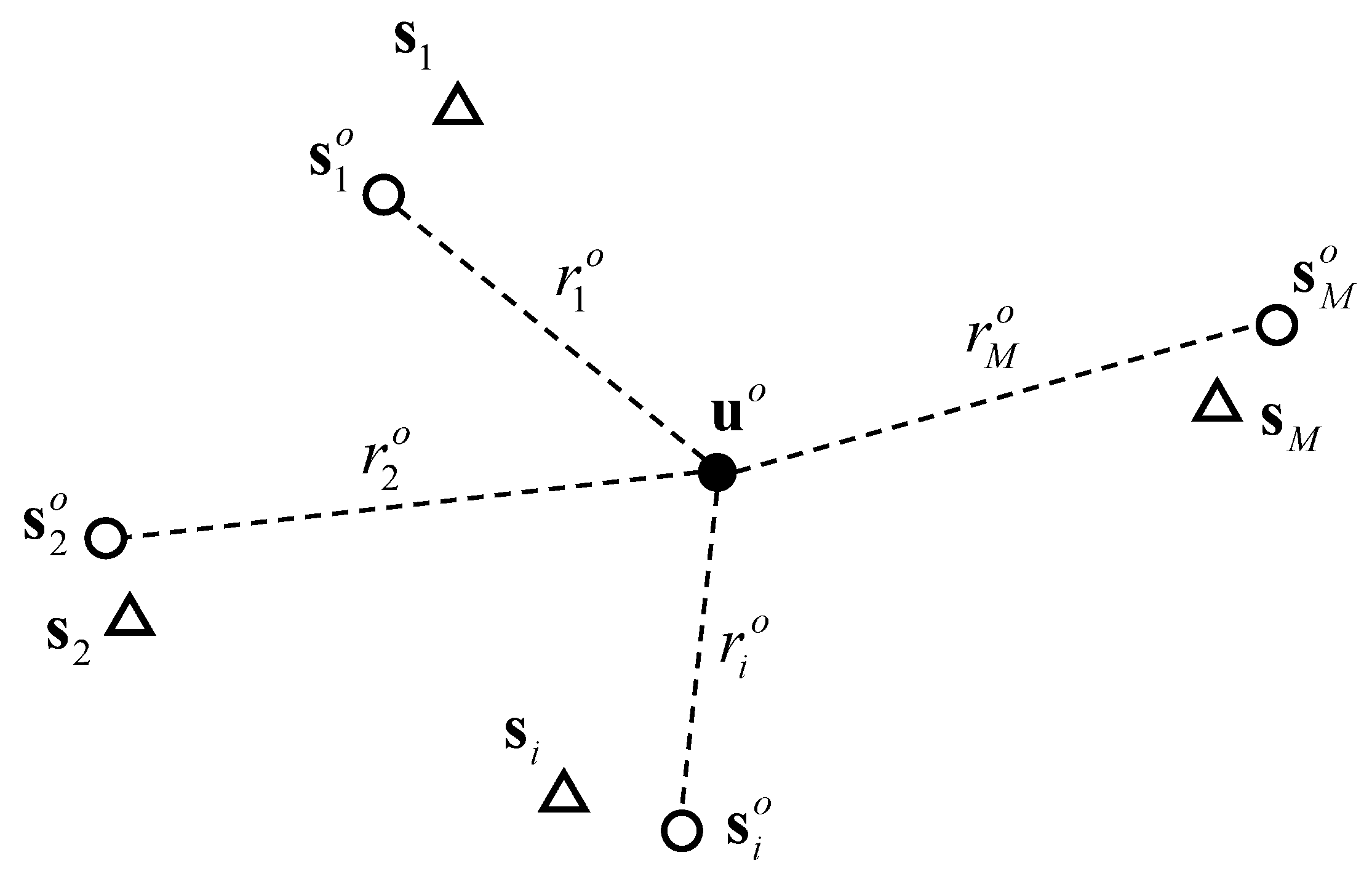
2. Problem Formulation
3. Refined Estimator
3.1. Coarse Solution
3.2. Error Reduction
3.3. Refinement
4. Analysis
4.1. CRLB
4.2. Covariance
4.3. Comparison
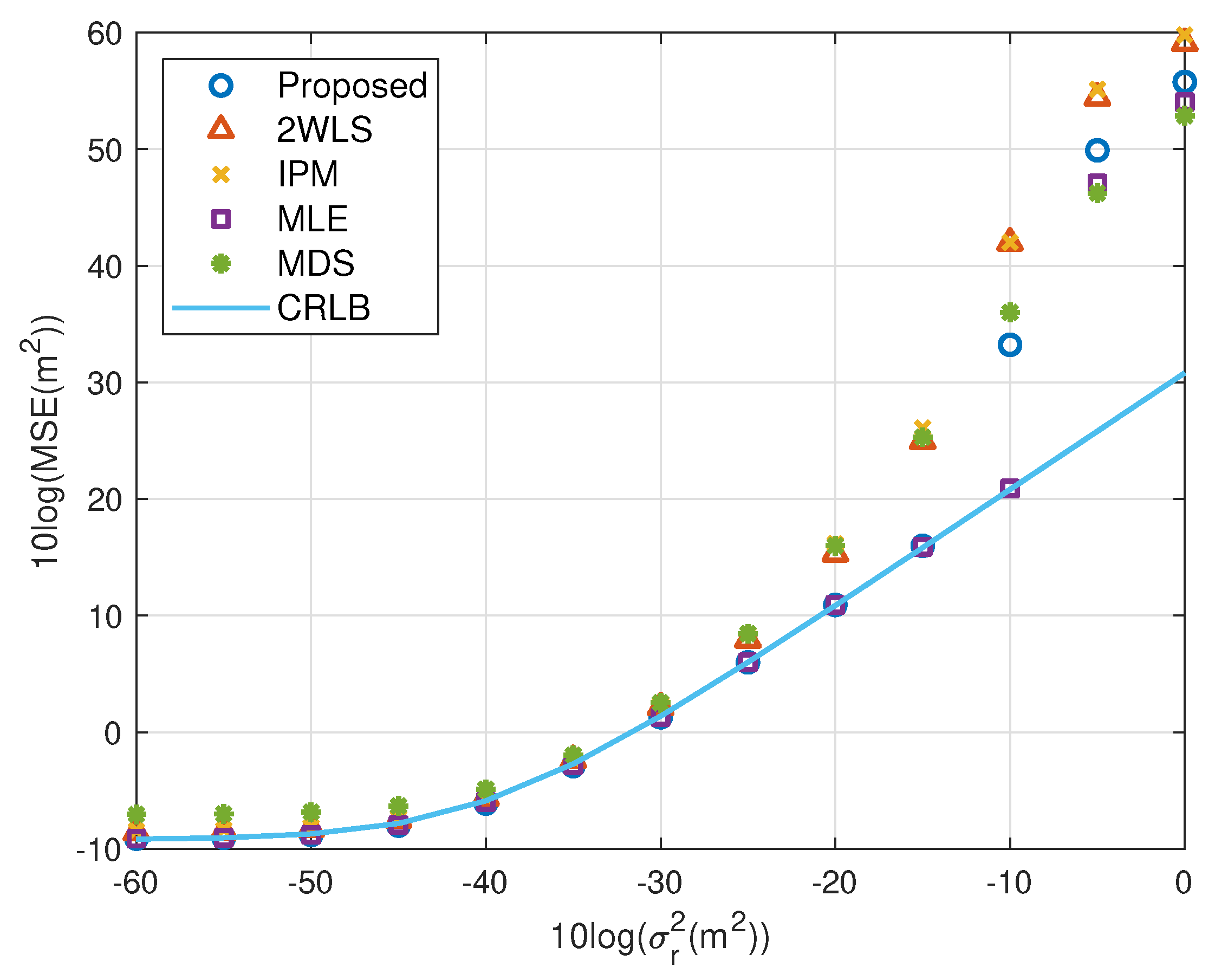
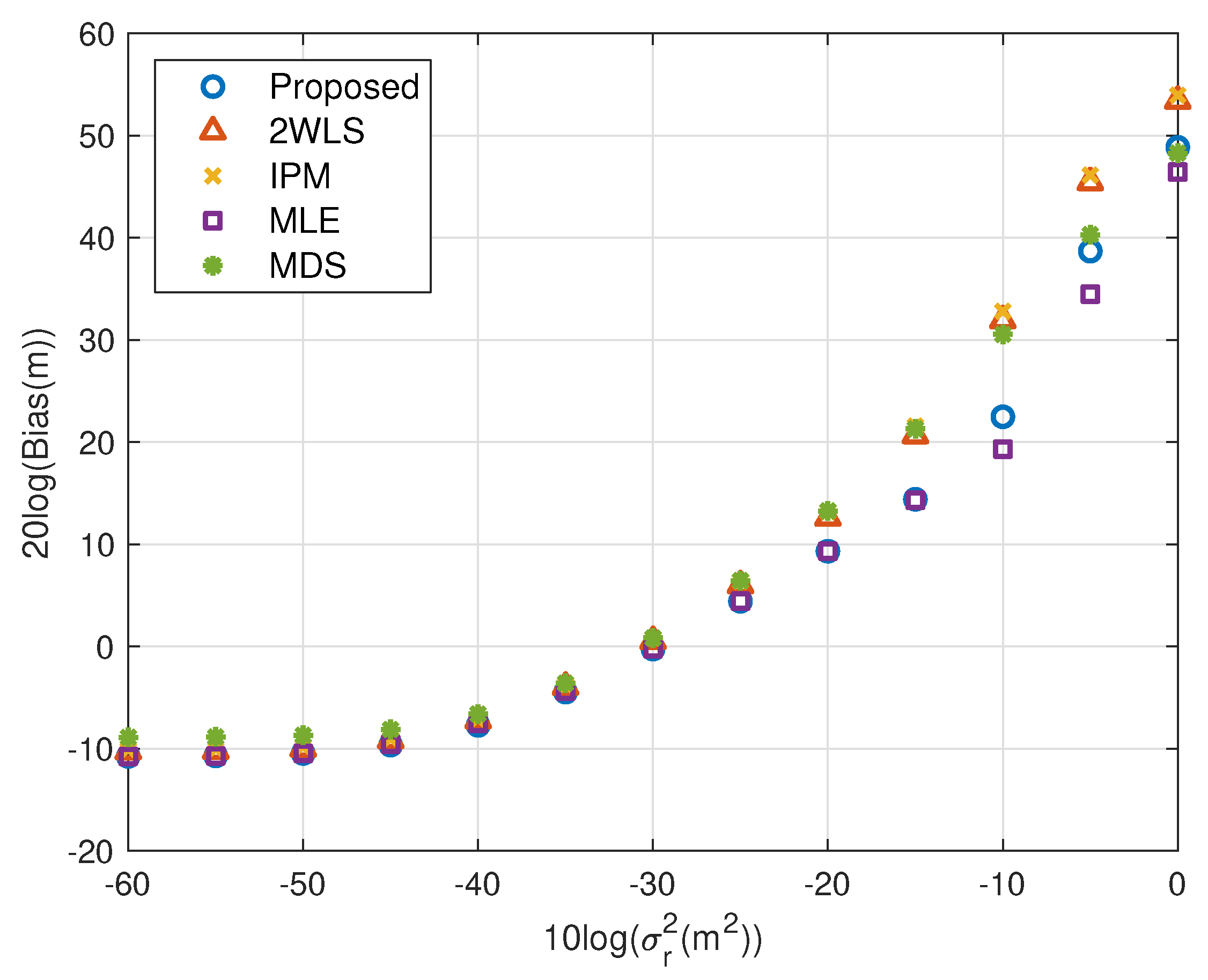
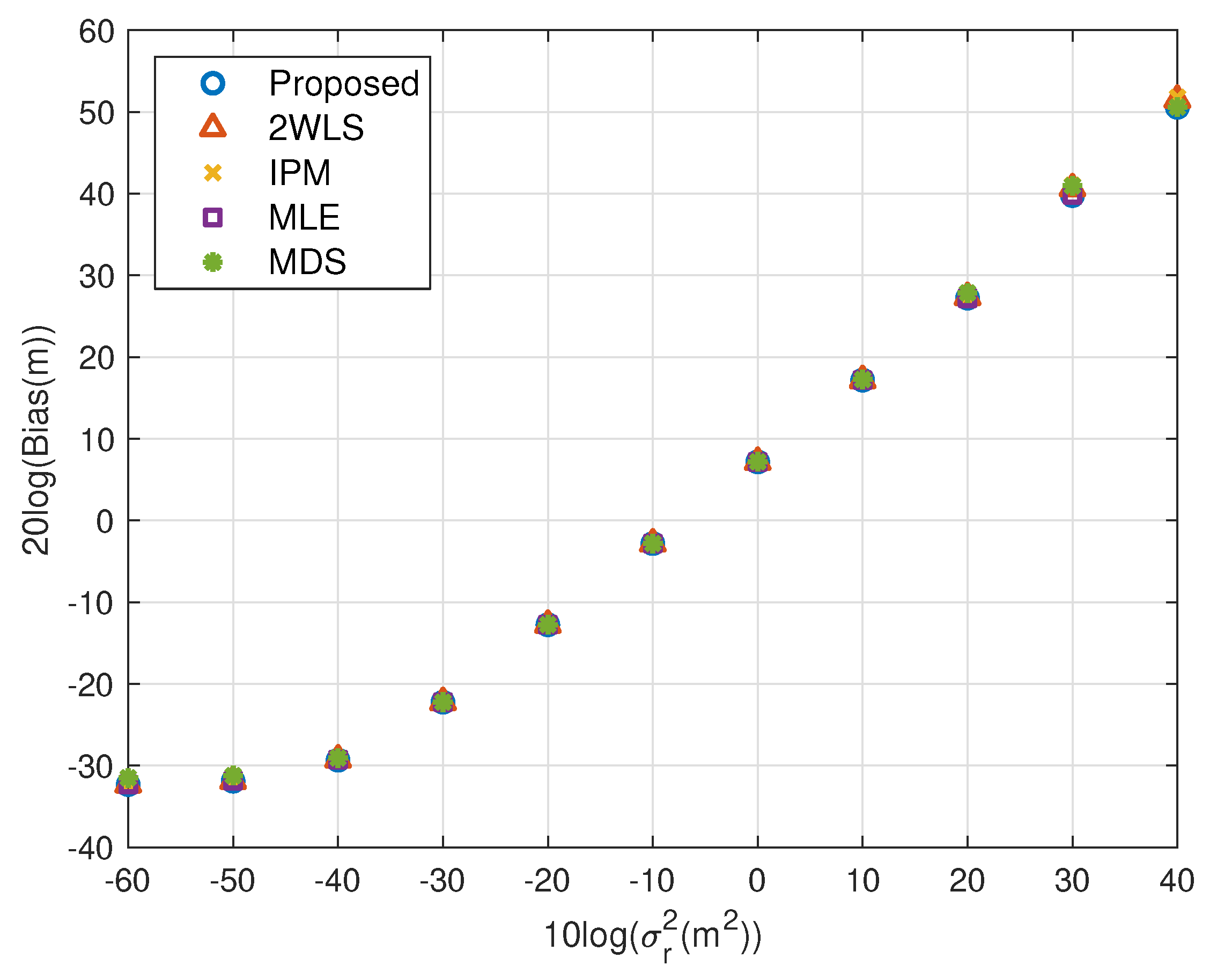
5. Simulations
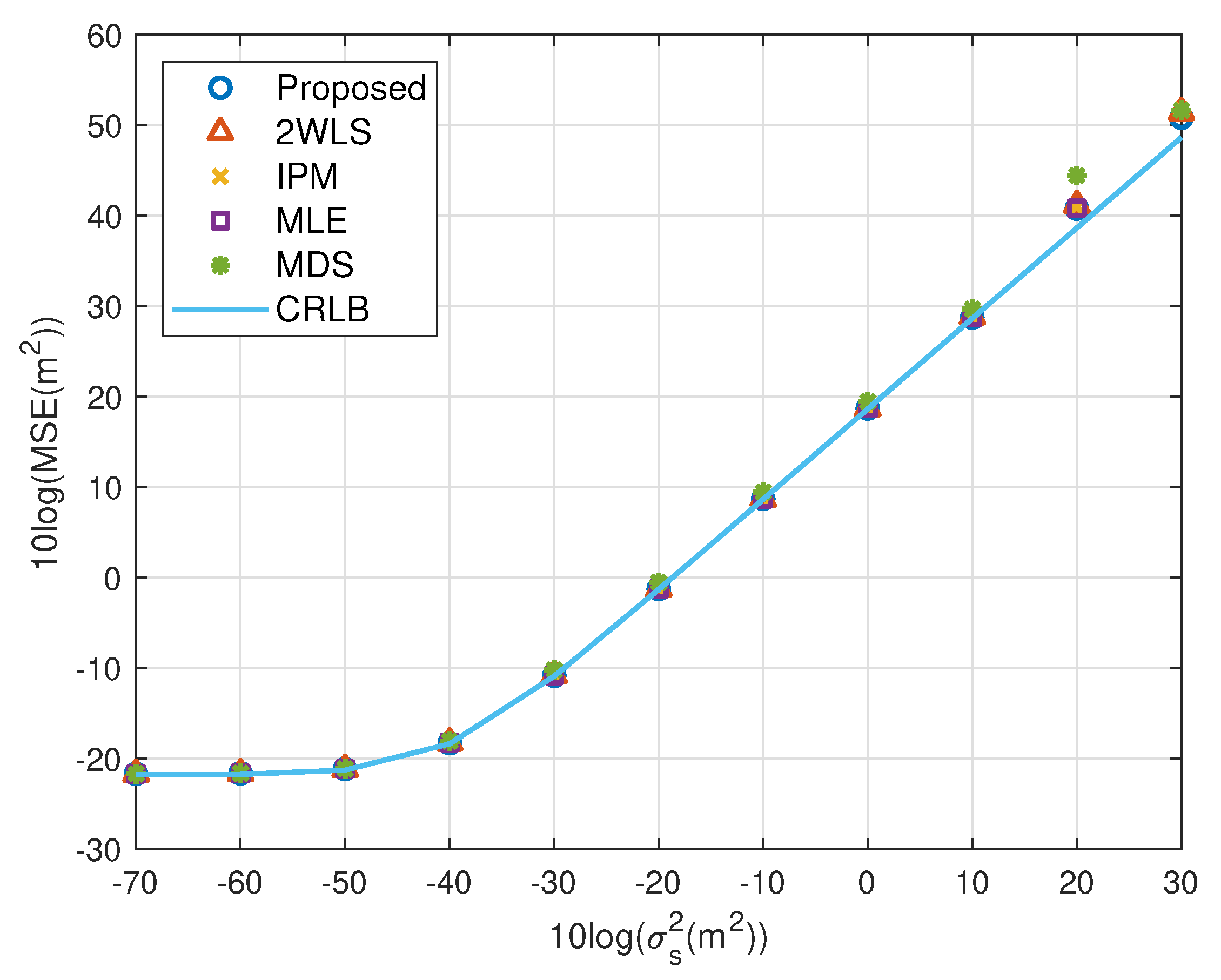
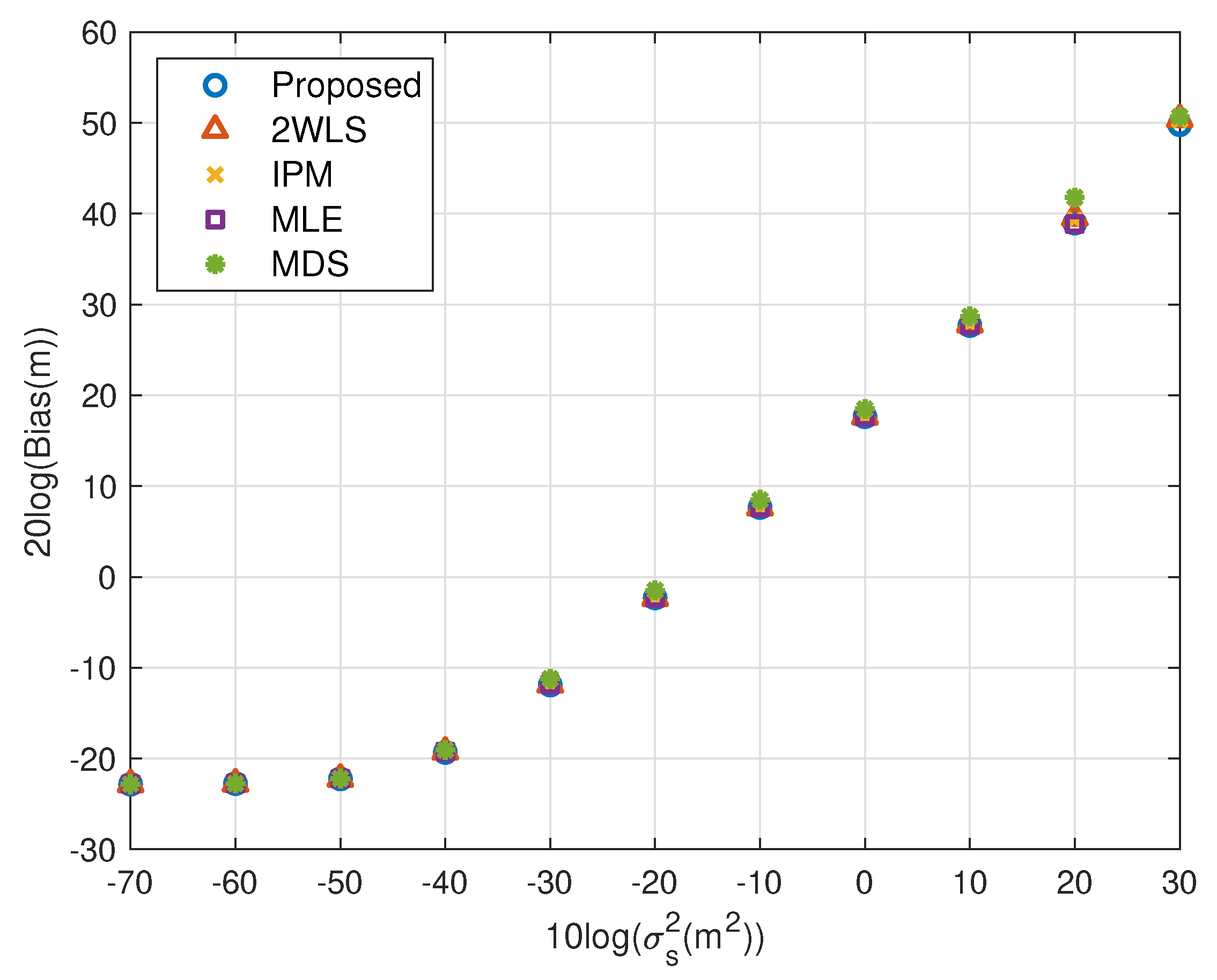
5.1. Fewer Sensors
5.2. More Sensors
5.3. Computation Time
5.4. Summary of Simulations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Witrisal, K.; Meissner, P.; Leitinger, E.; Shen, Y.; Gustafson, C.; Tufvesson, F.; Haneda, K.; Dardari, D.; Molisch, A.F.; Conti, A.; et al. High-Accuracy Localization for Assisted Living: 5G systems will turn multipath channels from foe to friend. IEEE Signal Process. Mag. 2016, 33, 59–70. [Google Scholar] [CrossRef]
- Buehrer, R.M.; Wymeersch, H.; Vaghefi, R.M. Collaborative Sensor Network Localization: Algorithms and Practical Issues. Proc. IEEE 2018, 106, 1089–1114. [Google Scholar] [CrossRef] [Green Version]
- Aditya, S.; Molisch, A.F.; Behairy, H.M. A Survey on the Impact of Multipath on Wideband Time-of-Arrival Based Localization. Proc. IEEE 2018, 106, 1183–1203. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, Y.; Wan, Q. Calibrating the error from sensor position uncertainty in TDOA-AOA localization. Signal Process. 2019, 166, 107213. [Google Scholar] [CrossRef]
- Díez-González, J.; Álvarez, R.; Sánchez-González, L.; Fernández-Robles, L.; Pérez, H.; Castejón-Limas, M. 3D TDOA Problem Solution with Four Receiving Nodes. Sensors 2019, 19, 2892. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Lv, J.; Tian, S.; Zhu, J.; Lu, W. Robust Least-Square Localization Based on Relative Angular Matrix in Wireless Sensor Networks. Sensors 2019, 19, 2627. [Google Scholar] [CrossRef] [Green Version]
- Wen, F. Computationally Efficient DOA Estimation Algorithm for MIMO Radar with Imperfect Waveforms. IEEE Commun. Lett. 2019, 23, 1037–1040. [Google Scholar] [CrossRef]
- Wen, F.; Mao, C.; Zhang, G. Direction finding in MIMO radar with large antenna arrays and nonorthogonal waveforms. Digital Signal Process. 2019, 94, 75–83. [Google Scholar] [CrossRef]
- Wu, P.; Su, S.; Zuo, Z.; Guo, X.; Sun, B.; Wen, X. Time Difference of Arrival (TDoA) Localization Combining Weighted Least Squares and Firefly Algorithm. Sensors 2019, 19, 2554. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Ho, K.C.; Wan, Q. Solution and Analysis of TDOA Localization of a Near or Distant Source in Closed-Form. IEEE Trans. Signal Process. 2019, 67, 320–335. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, F.; Wan, Q. Wireless Sensor Network Based Localization Method Using TDOA Measurements in MPR. IEEE Sensors J. 2019, 19, 3741–3750. [Google Scholar] [CrossRef]
- Yin, J.; Wang, D.; Wu, Y. An Efficient Direct Position Determination Method for Multiple Strictly Noncircular Sources. Sensors 2018, 18, 324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Du, J.; Wang, D.; Yu, W.; Yu, H. Direct Position Determination of Unknown Signals in the Presence of Multipath Propagation. Sensors 2018, 18, 892. [Google Scholar]
- Malanowski, M.; Kulpa, K. Two Methods for Target Localization in Multistatic Passive Radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 572–580. [Google Scholar] [CrossRef]
- Amiot, N.; Pedersen, T.; Laaraiedh, M.; Uguen, B. A Hybrid Positioning Method Based on Hypothesis Testing. IEEE Wirel. Commun. Lett. 2012, 1, 348–351. [Google Scholar] [CrossRef] [Green Version]
- Coluccia, A.; Fascista, A. On the Hybrid TOA/RSS Range Estimation in Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2018, 17, 361–371. [Google Scholar] [CrossRef]
- Shen, J.; Molisch, A.F.; Salmi, J. Accurate Passive Location Estimation Using TOA Measurements. IEEE Trans. Wirel. Commun. 2012, 11, 2182–2192. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Dogancay, K. Optimal Geometry Analysis for Multistatic TOA Localization. IEEE Trans. Signal Process. 2016, 64, 4180–4193. [Google Scholar] [CrossRef]
- Beck, A.; Stoica, P.; Li, J. Exact and Approximate Solutions of Source Localization Problems. IEEE Trans. Signal Process. 2008, 56, 1770–1778. [Google Scholar] [CrossRef]
- Chen, S.; Ho, K.C. Achieving asymptotic efficient performance for squared range and squared range difference localizations. IEEE Trans. Signal Process. 2013, 61, 2836–2849. [Google Scholar] [CrossRef]
- Rui, L.; Ho, K.C. Elliptic Localization: Performance Study and Optimum Receiver Placement. IEEE Trans. Signal Process. 2014, 62, 4673–4688. [Google Scholar] [CrossRef]
- Coluccia, A.; Ricciato, F.; Ricci, G. Positioning Based on Signals of Opportunity. IEEE Commun. Lett. 2014, 18, 356–359. [Google Scholar] [CrossRef]
- Wang, G.; Cai, S.; Li, Y.; Jin, M. Second-Order Cone Relaxation for TOA-Based Source Localization with Unknown Start Transmission Time. IEEE Trans. Veh. Technol. 2014, 63, 2973–2977. [Google Scholar] [CrossRef]
- Vaghefi, R.M.; Buehrer, R.M. Cooperative Joint Synchronization and Localization in Wireless Sensor Networks. IEEE Trans. Signal Process. 2015, 63, 3615–3627. [Google Scholar] [CrossRef]
- Zou, Y.; Wan, Q. Asynchronous Time-of-Arrival-Based Source Localization with Sensor Positio Uncertainties. IEEE Commun. Lett. 2016, 20, 1860–1863. [Google Scholar] [CrossRef]
- Wang, G.; Ansari, N.; Li, Y. A Fractional Programming Method for Target Localization in Asynchronous Networks. IEEE Access 2018, 6, 56727–56736. [Google Scholar] [CrossRef]
- Kang, Y.; Wang, Q.; Wang, J.; Chen, R. A High-Accuracy TOA-Based Localization Method without Time Synchronization in a Three-Dimensional Space. IEEE Trans. Ind. Informat. 2019, 15, 173–182. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M. Exact Robust Solution to TW-ToA-Based Target Localization Problem with Clock Imperfections. IEEE Signal Process. Lett. 2018, 25, 531–535. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Zhang, S.; Xu, K.; Huang, D. Neural Network Localization with TOA Measurements Based on Error Learning and Matching. IEEE Access 2019, 7, 19089–19099. [Google Scholar] [CrossRef]
- Wei, H.; Wan, Q.; Chen, Z.; Ye, S. A Novel Weighted Multidimensional Scaling Analysis for Time-of-Arrival-Based Mobile Location. IEEE Trans. Signal Process. 2008, 56, 3018–3022. [Google Scholar] [CrossRef]
- Ma, Z.; Ho, K.C. A study on the effects of sensor position error and the placement of calibration emitter for source localization. IEEE Trans. Wirel. Commun. 2014, 13, 5440–5452. [Google Scholar] [CrossRef]
- Yang, L.; Ho, K.C. An Approximately Efficient TDOA Localization Algorithm in Closed-Form for Locating Multiple Disjoint Sources with Erroneous Sensor Positions. IEEE Trans. Signal Process. 2009, 57, 4598–4615. [Google Scholar] [CrossRef]
- Ho, K.C.; Lu, X.; Kovavisaruch, L. Source Localization Using TDOA and FDOA Measurements in the Presence of Receiver Location Errors: Analysis and Solution. IEEE Trans. Signal Process. 2007, 55, 684–696. [Google Scholar] [CrossRef]
- Ma, Z.; Ho, K.C. TOA localization in the presence of random sensor position errors. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 2468–2471. [Google Scholar]
- Wang, Y.; Ho, K.C. An Asymptotically Efficient Estimator in Closed-Form for 3-D AOA Localization Using a Sensor Network. IEEE Trans. Wirel. Commun. 2015, 14, 6524–6535. [Google Scholar] [CrossRef]
- Amar, A.; Leus, G.; Friedlander, B. Emitter Localization Given Time Delay and Frequency Shift Measurements. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1826–1837. [Google Scholar] [CrossRef]
- Jinzhou, L.; Ho, K.C.; Fucheng, G.; Wenli, J. Improving the projection method for TOA source localization in the presence of sensor position errors. In Proceedings of the 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), A Coruna, Spain, 22–25 June 2014; pp. 45–48. [Google Scholar]
- Cao, J.-M.; Deng, B.; Ouyang, X.-X.; Wan, Q.; Ibrahim Ahmed, H.; Zou, Y. Multidimensional scaling-based passive emitter localization from TOA measurements with sensor position uncertainties. In Proceedings of the 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 1692–1696. [Google Scholar]
- Amiri, R.; Behnia, F.; Noroozi, A. An Efficient Estimator for TDOA-Based Source Localization with Minimum Number of Sensors. IEEE Commun. Lett. 2018, 22, 2499–2502. [Google Scholar] [CrossRef]
- Ho, K.C. Bias Reduction for an Explicit Solution of Source Localization Using TDOA. IEEE Trans. Signal Process. 2012, 60, 2101–2114. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Chan, Y.T.; Ho, K.C. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef] [Green Version]
- Cheung, K.W.; So, H.C.; Ma, W.K.; Chan, Y.T. A Constrained Least Squares Approach to Mobile Positioning: Algorithms and Optimality. Eurasip J. Adv. Signal Process. 2006, 2006, 020858. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; An, J.; Bu, X.; Sun, G. Constrained Total Least-Squares Location Algorithm Using Time-Difference-of-Arrival Measurements. IEEE Trans. Veh. Technol. 2010, 59, 1558–1562. [Google Scholar] [CrossRef]
- Yu, H.; Huang, G.; Gao, J.; Liu, B. An Efficient Constrained Weighted Least Squares Algorithm for Moving Source Location Using TDOA and FDOA Measurements. IEEE Trans. Wirel. Commun. 2012, 11, 44–47. [Google Scholar] [CrossRef]
- Lin, L.; So, H.C.; Chan, F.K.; Chan, Y.T.; Ho, K.C. A new constrained weighted least squares algorithm for TDOA-based localization. Signal Process. 2013, 93, 2872–2878. [Google Scholar] [CrossRef]







| Sensor | ||||||
|---|---|---|---|---|---|---|
| x (m) | −100 | 200 | 400 | 350 | 300 | 300 |
| y (m) | 100 | −300 | 150 | 200 | 500 | 100 |
| z (m) | −100 | −200 | 100 | 100 | 200 | 150 |
| Noise Power (dB) | −60 | −50 | −40 | −30 | −20 | −10 | 0 | 10 | 20 |
|---|---|---|---|---|---|---|---|---|---|
| Proposed (%) | 0.42 | −1.42 | −0.57 | −1.62 | 0.34 | 1.10 | 3.04 × 103 | 4.55 × 104 | 9.61 × 104 |
| 2WLS (%) | 3.54 | 1.74 | 1.38 | 3.37 | 34.15 | 367.12 | 2.96 × 104 | 7.55 × 104 | 1.52 × 104 |
| IPM (%) | 5.59 | 4.36 | 1.31 | 5.48 | 50.56 | 538.84 | 5.78 × 104 | 2.23 × 105 | 2.62 × 104 |
| MLE (%) | 0.40 | −1.22 | −0.94 | −1.38 | 0.34 | 1.05 | 1.27 | 3.60 × 104 | 8.39 × 103 |
| MDS (%) | 54.86 | 44.10 | 12.83 | 5.44 | 49.05 | 508.94 | 8.24 × 103 | 2.89 × 104 | 6.79 × 103 |
| Noise Power (dB) | −60 | −50 | −40 | −30 | −20 | −10 | 0 |
|---|---|---|---|---|---|---|---|
| Proposed (%) | 0.92 | −1.84 | −1.27 | −1.06 | 0.93 | 1.64 × 103 | 3.12 × 103 |
| 2WLS (%) | 14.34 | 10.58 | 6.43 | 19.37 | 178.63 | 1.30 × 104 | 6.73 × 104 |
| IPM (%) | 18.34 | 14.94 | 8.85 | 27.36 | 237.50 | 1.31 × 104 | 7.90 × 104 |
| MLE (%) | 0.86 | −0.88 | −1.32 | −1.68 | 0.88 | 1.98 | 2.09 × 104 |
| MDS (%) | 62.80 | 53.94 | 25.53 | 30.20 | 225.49 | 3.20 × 103 | 1.59 × 104 |
| Method | Proposed | 2WLS | MLE | IPM | MDS |
|---|---|---|---|---|---|
| Time (s) | 29.90 | 21.69 | 142.07 | 72.80 | 112.15 |
| Rel. Time | 1 | 0.73 | 4.75 | 2.43 | 3.75 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, Y.; Cong, X.; Sun, Y. Refinement of TOA Localization with Sensor Position Uncertainty in Closed-Form. Sensors 2020, 20, 390. https://doi.org/10.3390/s20020390
Gan Y, Cong X, Sun Y. Refinement of TOA Localization with Sensor Position Uncertainty in Closed-Form. Sensors. 2020; 20(2):390. https://doi.org/10.3390/s20020390
Chicago/Turabian StyleGan, Yi, Xunchao Cong, and Yimao Sun. 2020. "Refinement of TOA Localization with Sensor Position Uncertainty in Closed-Form" Sensors 20, no. 2: 390. https://doi.org/10.3390/s20020390





