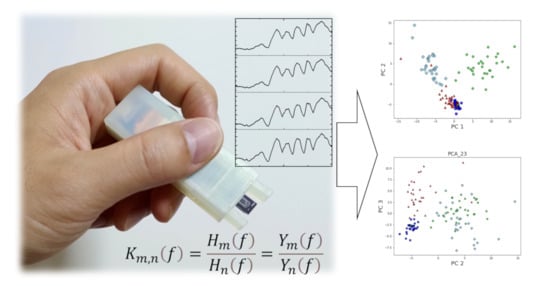
Development of a Mobile Device for Odor Identification and Optimization of Its Measurement Protocol Based on the Free-Hand Measurement
Abstract
1. Introduction
2. Materials and Methods
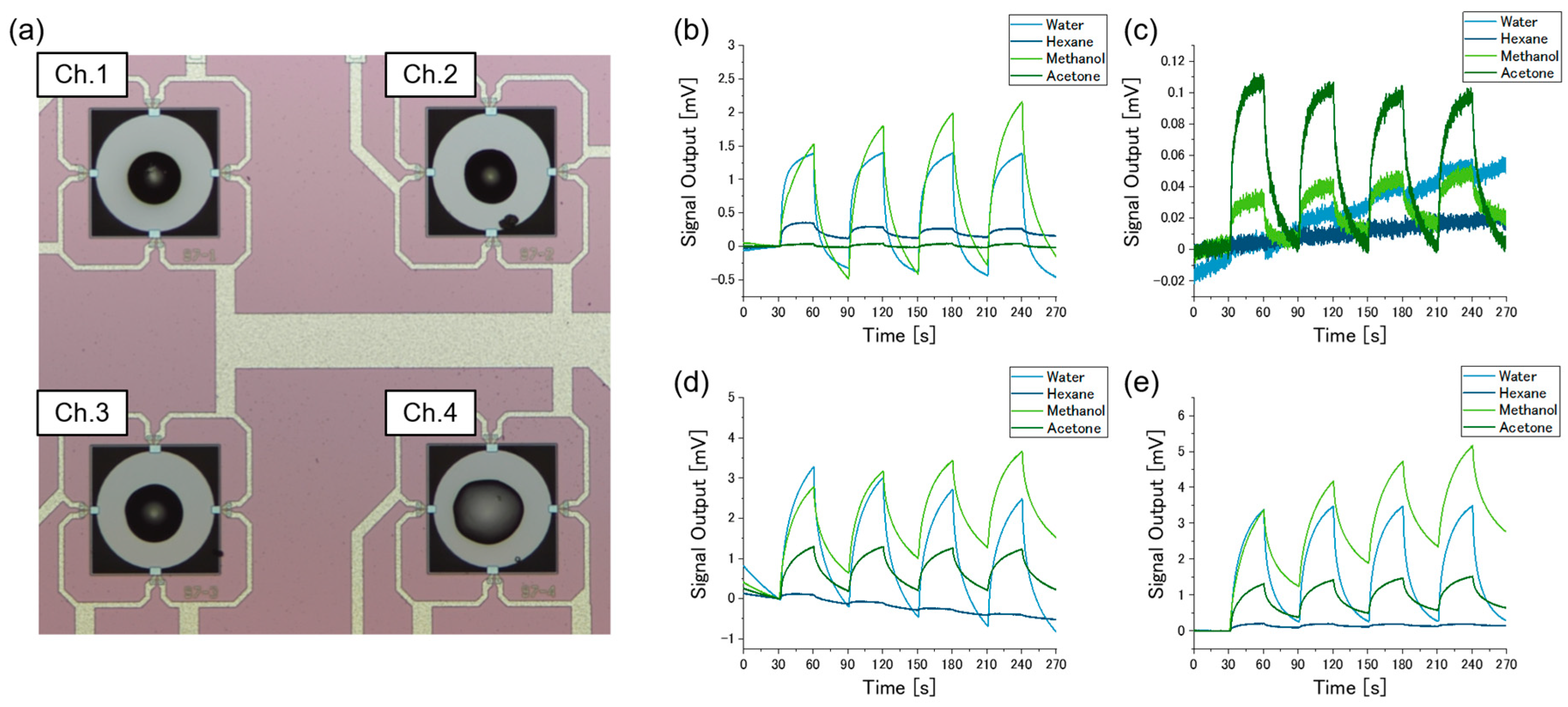
2.1. MSS
2.2. Free-Hand Measurements
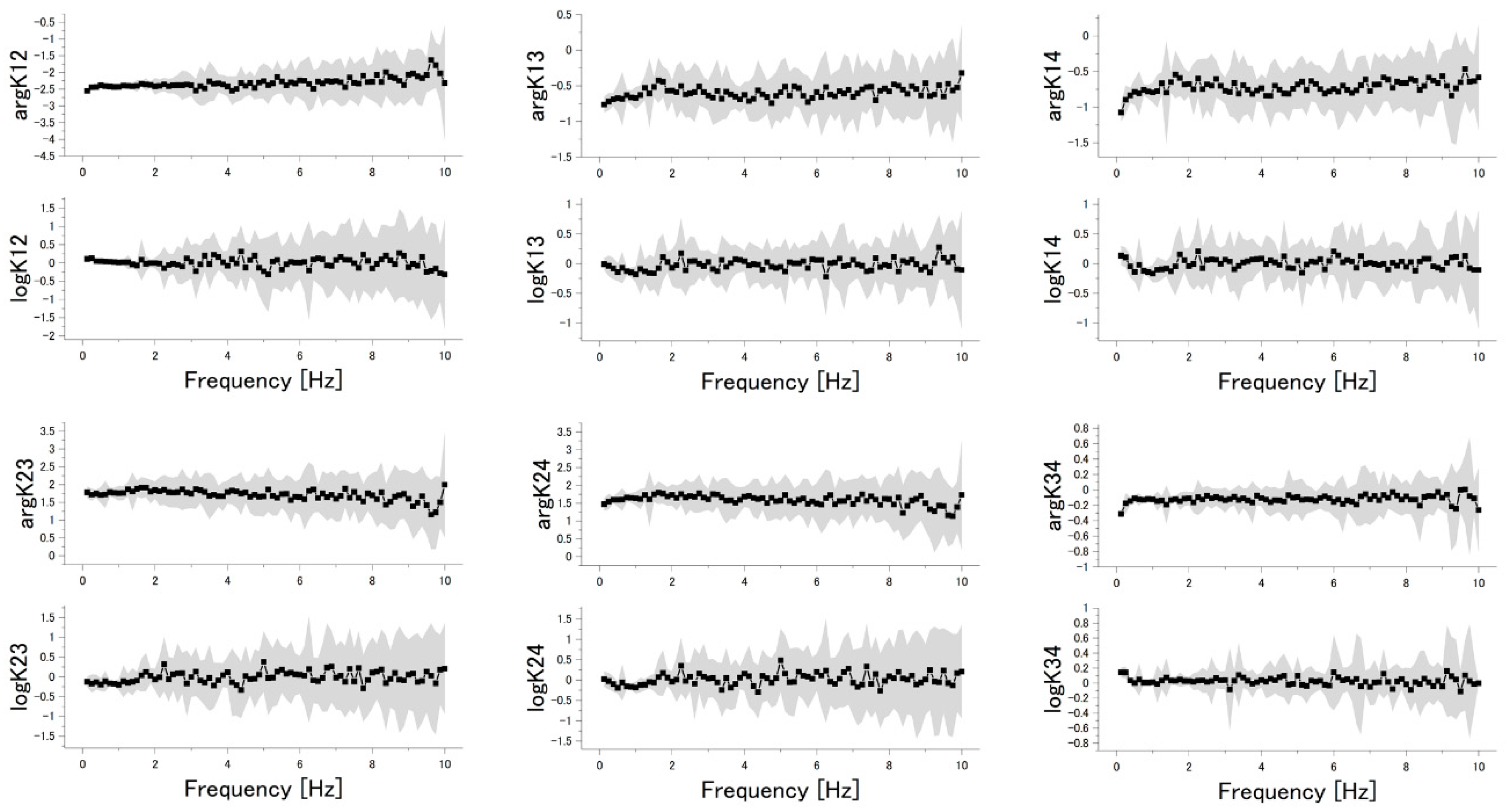
2.3. TFRs
2.4. Cluster Analysis
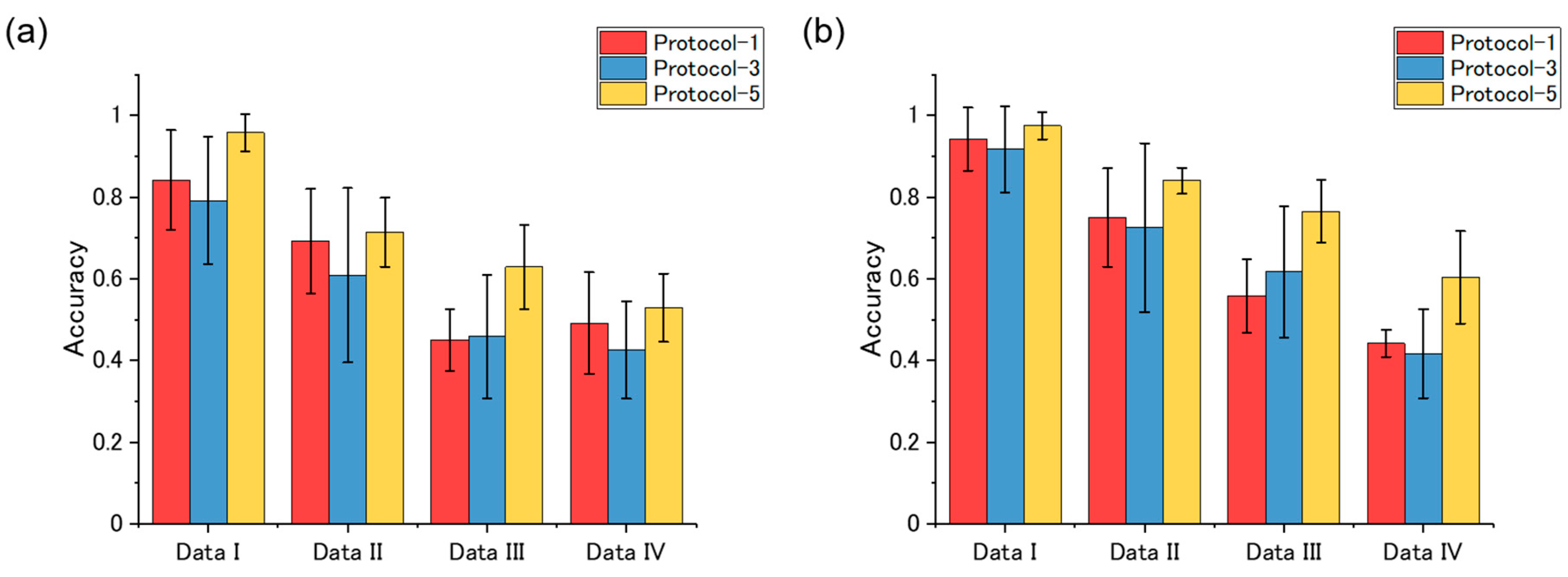
2.5. Machine Learning Classification
3. Results
3.1. Basic Properties of the MSS
3.2. Cluster Analysis and Machine Learning Classification
3.3. Dependence on Frequency Range
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chandrashekar, J.; Hoon, M.A.; Ryba, N.J.P.; Zuker, C.S. The receptors and cells for mammalian taste. Nature 2006, 444, 288–294. [Google Scholar] [CrossRef]
- Tahara, Y.; Toko, K. Electronic Tongues–A Review. IEEE Sens. J. 2013, 13, 3001–3011. [Google Scholar] [CrossRef]
- Persaud, K.; Dodd, G. Analysis of discrimination mechanisms in the mammalian olfactory system using a model nose. Nature 1982, 299, 352–355. [Google Scholar] [CrossRef] [PubMed]
- Persaud, K.C. Biomimetic Olfactory Sensors. IEEE Sens. J. 2012, 12, 3108–3112. [Google Scholar] [CrossRef]
- Dam, R.; Sarkar, S.; Sarbadhikary, R.; Ghosh, A.; Ghosh, S. Evolution of nanomechanical olfactory sensor as an artificial nose. In Proceedings of the 2016 IEEE 7th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 13–15 October 2016; pp. 1–6. [Google Scholar]
- Potyrailo, R.A. Multivariable Sensors for Ubiquitous Monitoring of Gases in the Era of Internet of Things and Industrial Internet. Chem. Rev. 2016, 116, 11877–11923. [Google Scholar] [CrossRef]
- Bhattacharyya, P. Technological Journey Towards Reliable Microheater Development for MEMS Gas Sensors: A Review. IEEE Trans. Device Mater. Reliab. 2014, 14, 589–599. [Google Scholar] [CrossRef]
- Robert, B. Recent developments in MEMS sensors: A review of applications, markets and technologiesnull. Sens. Rev. 2013, 33, 300–304. [Google Scholar]
- Yan, J.; Guo, X.; Duan, S.; Jia, P.; Wang, L.; Peng, C.; Zhang, S. Electronic Nose Feature Extraction Methods: A Review. Sensors 2015, 15, 27804. [Google Scholar] [CrossRef]
- Nimsuk, N.; Nakamoto, T. Improvement of Robustness of Odor Classification in Dynamically Changing Concentration Against Environmental Change. IEEJ Trans. Sens. Micromach. 2008, 128, 214–218. [Google Scholar] [CrossRef]
- Nimsuk, N.; Nakamoto, T. Improvement of capability for classifying odors in dynamically changing concentration using QCM sensor array and short-time Fourier transform. Sens. Actuators B Chem. 2007, 127, 491–496. [Google Scholar] [CrossRef]
- Trincavelli, M. Gas Discrimination for Mobile Robots. Ki-Künstliche Intell. 2011, 25, 351–354. [Google Scholar] [CrossRef]
- Trincavelli, M.; Coradeschi, S.; Loutfi, A. Odour classification system for continuous monitoring applications. Sens. Actuators B Chem. 2009, 139, 265–273. [Google Scholar] [CrossRef]
- Vergara, A.; Fonollosa, J.; Mahiques, J.; Trincavelli, M.; Rulkov, N.; Huerta, R. On the performance of gas sensor arrays in open sampling systems using Inhibitory Support Vector Machines. Sens. Actuators B Chem. 2013, 185, 462–477. [Google Scholar] [CrossRef]
- Imamura, G.; Shiba, K.; Yoshikawa, G.; Washio, T. Free-hand gas identification based on transfer function ratios without gas flow control. Sci. Rep. 2019, 9, 9768. [Google Scholar] [CrossRef]
- Yoshikawa, G.; Akiyama, T.; Gautsch, S.; Vettiger, P.; Rohrer, H. Nanomechanical Membrane-type Surface Stress Sensor. Nano Lett. 2011, 11, 1044–1048. [Google Scholar] [CrossRef]
- Loizeau, F.; Akiyama, T.; Gautsch, S.; Vettiger, P.; Yoshikawa, G.; de Rooij, N. Membrane-Type Surface Stress Sensor with Piezoresistive Readout. Procedia Eng. 2012, 47, 1085–1088. [Google Scholar] [CrossRef]
- Yoshikawa, G.; Akiyama, T.; Loizeau, F.; Shiba, K.; Gautsch, S.; Nakayama, T.; Vettiger, P.; Rooij, N.; Aono, M. Two Dimensional Array of Piezoresistive Nanomechanical Membrane-Type Surface Stress Sensor (MSS) with Improved Sensitivity. Sensors 2012, 12, 15873. [Google Scholar] [CrossRef]
- Vashist, S.K.; Vashist, P. Recent Advances in Quartz Crystal Microbalance-Based Sensors. J. Sens. 2011, 2011, 571405. [Google Scholar] [CrossRef]
- Sunil, T.T.; Chaudhuri, S.; Mishra, V. Optimal selection of SAW sensors for E-Nose applications. Sens. Actuators B Chem. 2015, 219, 238–244. [Google Scholar] [CrossRef]
- Yoo, Y.K.; Chae, M.-S.; Kang, J.Y.; Kim, T.S.; Hwang, K.S.; Lee, J.H. Multifunctionalized Cantilever Systems for Electronic Nose Applications. Anal. Chem. 2012, 84, 8240–8245. [Google Scholar] [CrossRef]
- Imamura, G.; Minami, K.; Shiba, K.; Mistry, K.; Musselman, K.P.; Yavuz, M.; Yoshikawa, G.; Saiki, K.; Obata, S. Graphene Oxide as a Sensing Material for Gas Detection Based on Nanomechanical Sensors in the Static Mode. Chemosensors 2020, 8, 82. [Google Scholar] [CrossRef]
- Ngo, H.; Minami, K.; Imamura, G.; Shiba, K.; Yoshikawa, G. Effects of Center Metals in Porphines on Nanomechanical Gas Sensing. Sensors 2018, 18, 1640. [Google Scholar] [CrossRef]
- Imamura, G.; Shiba, K.; Yoshikawa, G. Smell identification of spices using nanomechanical membrane-type surface stress sensors. Jpn. J. Appl. Phys. 2016, 55, 1102B3. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Heinrich, S.M.; Wenzel, M.J.; Josse, F.; Dufour, I. An analytical model for transient deformation of viscoelastically coated beams: Applications to static-mode microcantilever chemical sensors. J. Appl. Phys. 2009, 105, 124903. [Google Scholar] [CrossRef]
- Wenzel, M.J.; Josse, F.; Heinrich, S.M.; Yaz, E.; Datskos, P.G. Sorption-induced static bending of microcantilevers coated with viscoelastic material. J. Appl. Phys. 2008, 103, 064913. [Google Scholar] [CrossRef]
- Imamura, G.; Shiba, K.; Yoshikawa, G.; Washio, T. Analysis of nanomechanical sensing signals; physical parameter estimation for gas identification. AIP Adv. 2018, 8, 075007. [Google Scholar] [CrossRef]
- Trunk, G.V. A Problem of Dimensionality: A Simple Example. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 306–307. [Google Scholar] [CrossRef] [PubMed]







| Classification Models Based on Logistic Regression | Classification Models Based on Random Forests | |
|---|---|---|
| Hyperparameters (Name of the parameter in the scikit-learn library) |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imamura, G.; Yoshikawa, G. Development of a Mobile Device for Odor Identification and Optimization of Its Measurement Protocol Based on the Free-Hand Measurement. Sensors 2020, 20, 6190. https://doi.org/10.3390/s20216190
Imamura G, Yoshikawa G. Development of a Mobile Device for Odor Identification and Optimization of Its Measurement Protocol Based on the Free-Hand Measurement. Sensors. 2020; 20(21):6190. https://doi.org/10.3390/s20216190
Chicago/Turabian StyleImamura, Gaku, and Genki Yoshikawa. 2020. "Development of a Mobile Device for Odor Identification and Optimization of Its Measurement Protocol Based on the Free-Hand Measurement" Sensors 20, no. 21: 6190. https://doi.org/10.3390/s20216190
APA StyleImamura, G., & Yoshikawa, G. (2020). Development of a Mobile Device for Odor Identification and Optimization of Its Measurement Protocol Based on the Free-Hand Measurement. Sensors, 20(21), 6190. https://doi.org/10.3390/s20216190