Structural Health Monitoring Using Fibre Optic Acoustic Emission Sensors
Abstract
:1. Introduction
2. Fundamentals of FOAES
2.1. Principles of FOAES
2.2. Acoustic Emission
3. Fused Tapered Couplers
3.1. Principle of Operation
3.2. Development and Applications
4. Mach-Zehnder Interferometers for AE Sensing
4.1. Principle of Operation
4.2. Development and Applications
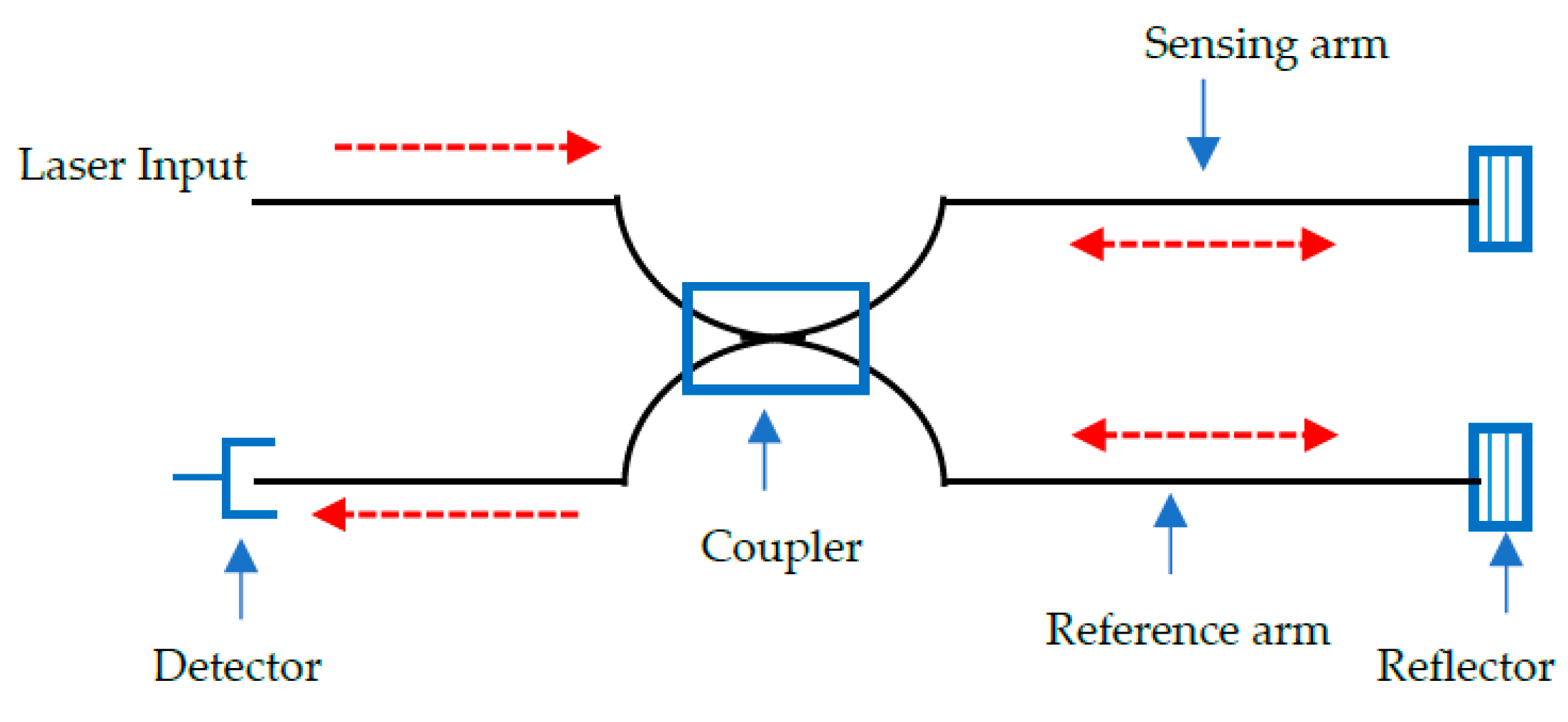
5. Michaelson Interferometer for AE Sensing
5.1. Principle of Operation
5.2. Development and Applications
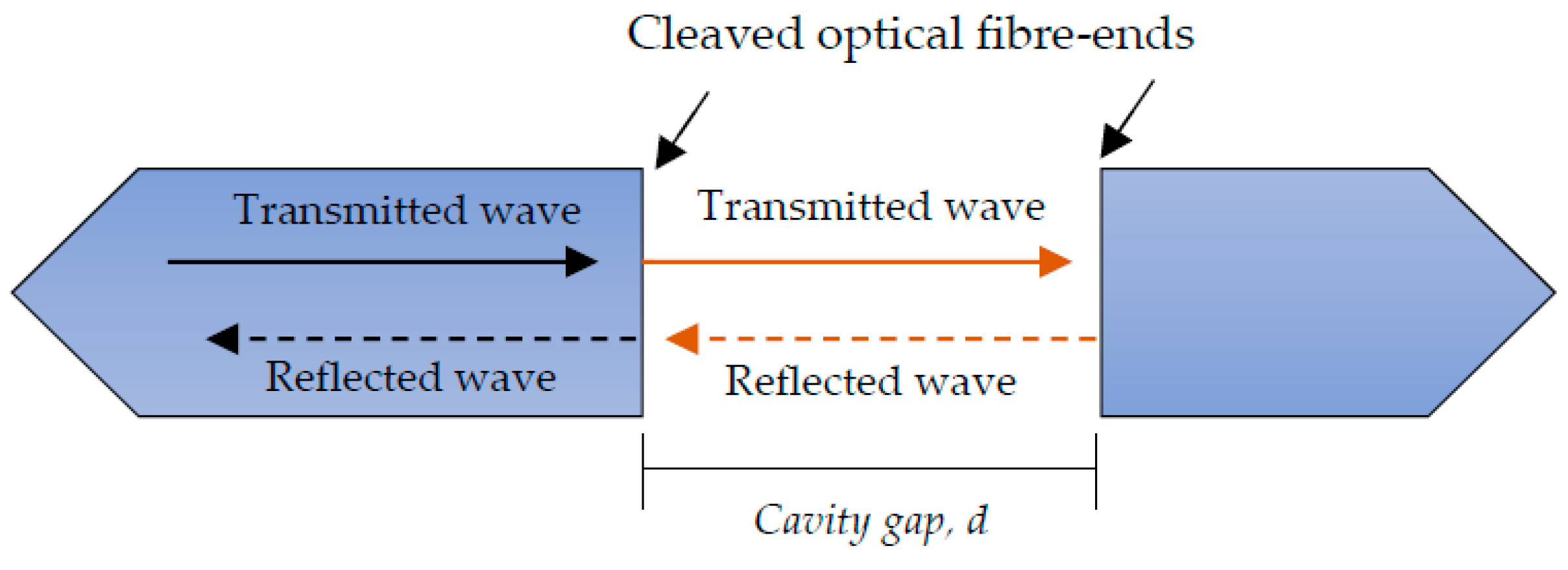
6. Fabry-Perot Interferometers for AE Sensing
6.1. Principle of Operation
6.2. Development and Applications
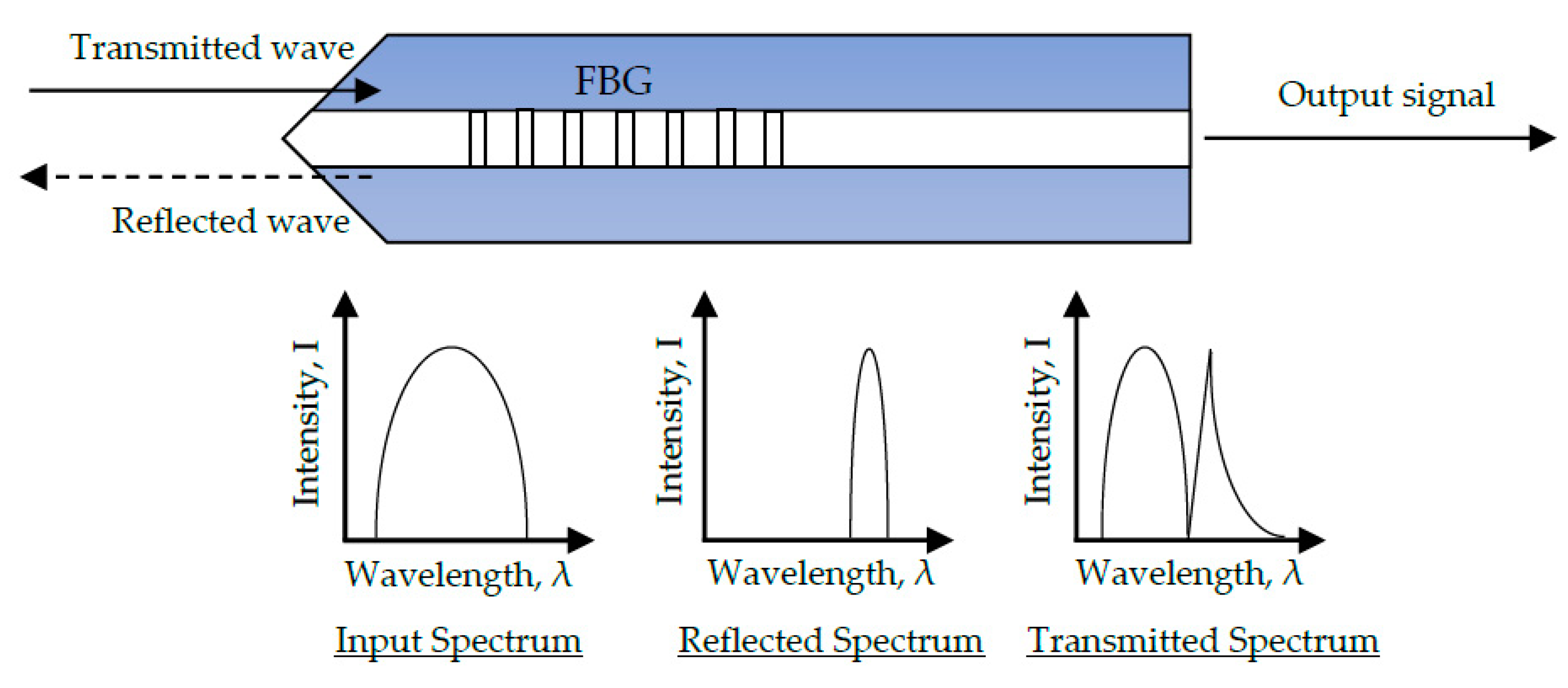
7. AE Fibre Bragg Gratings
7.1. Principle of Operation
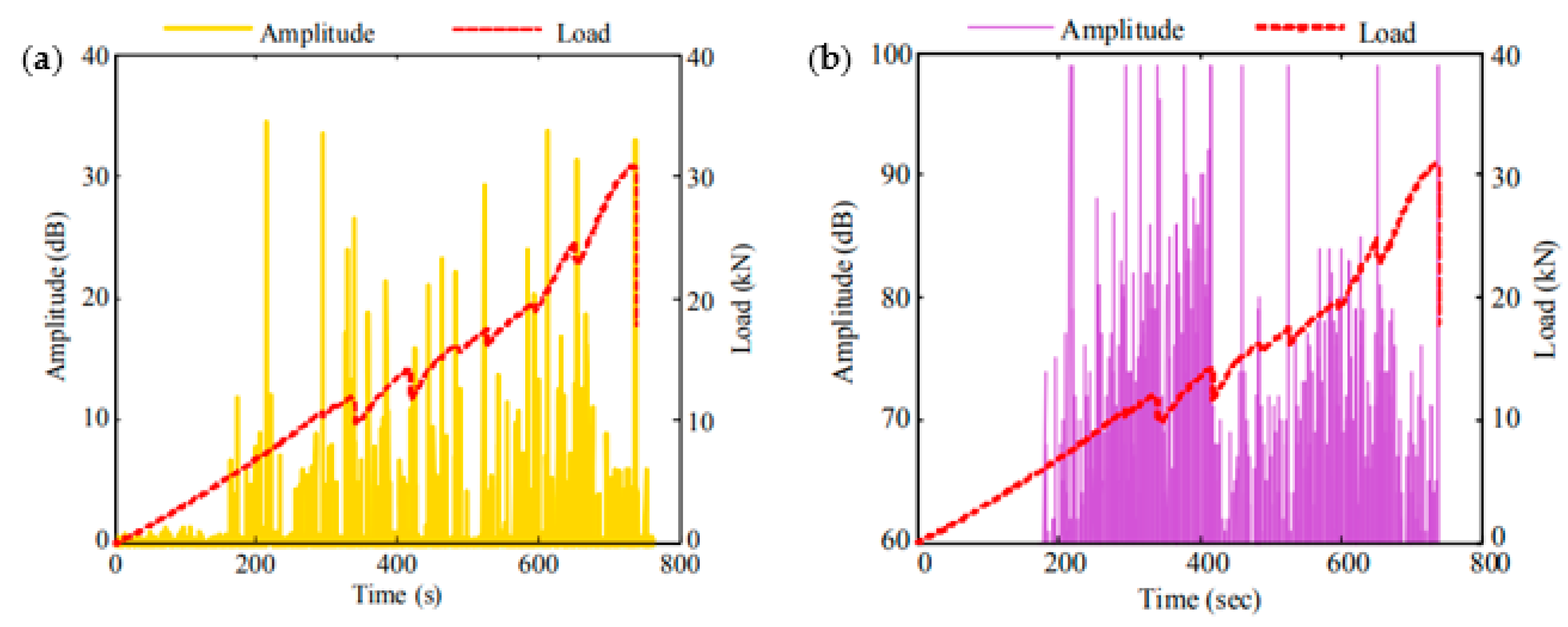
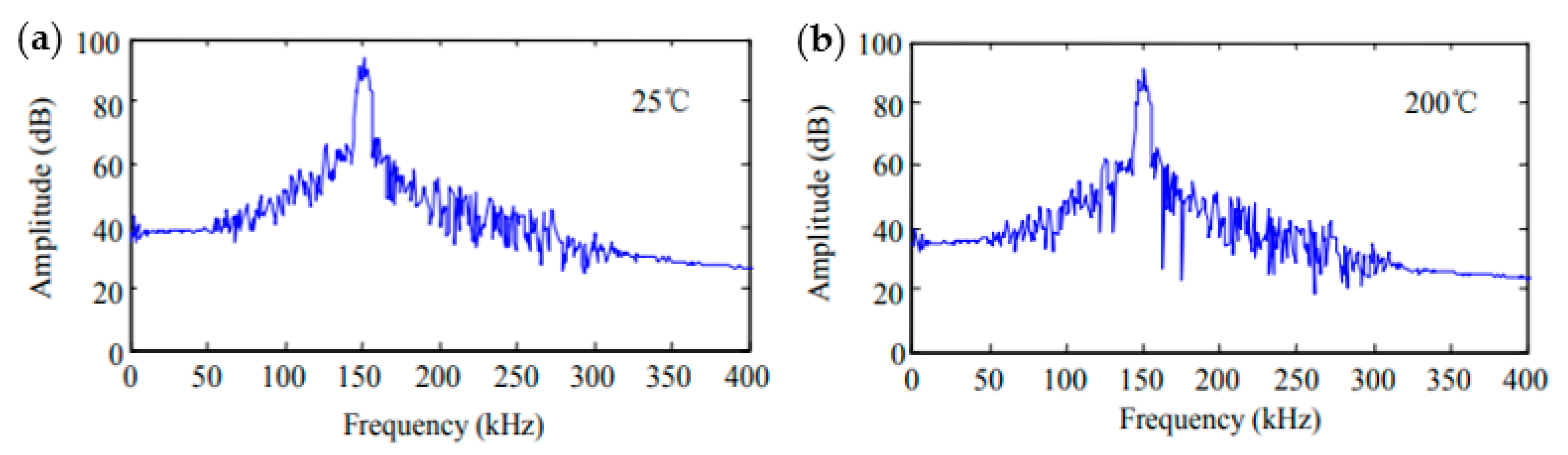
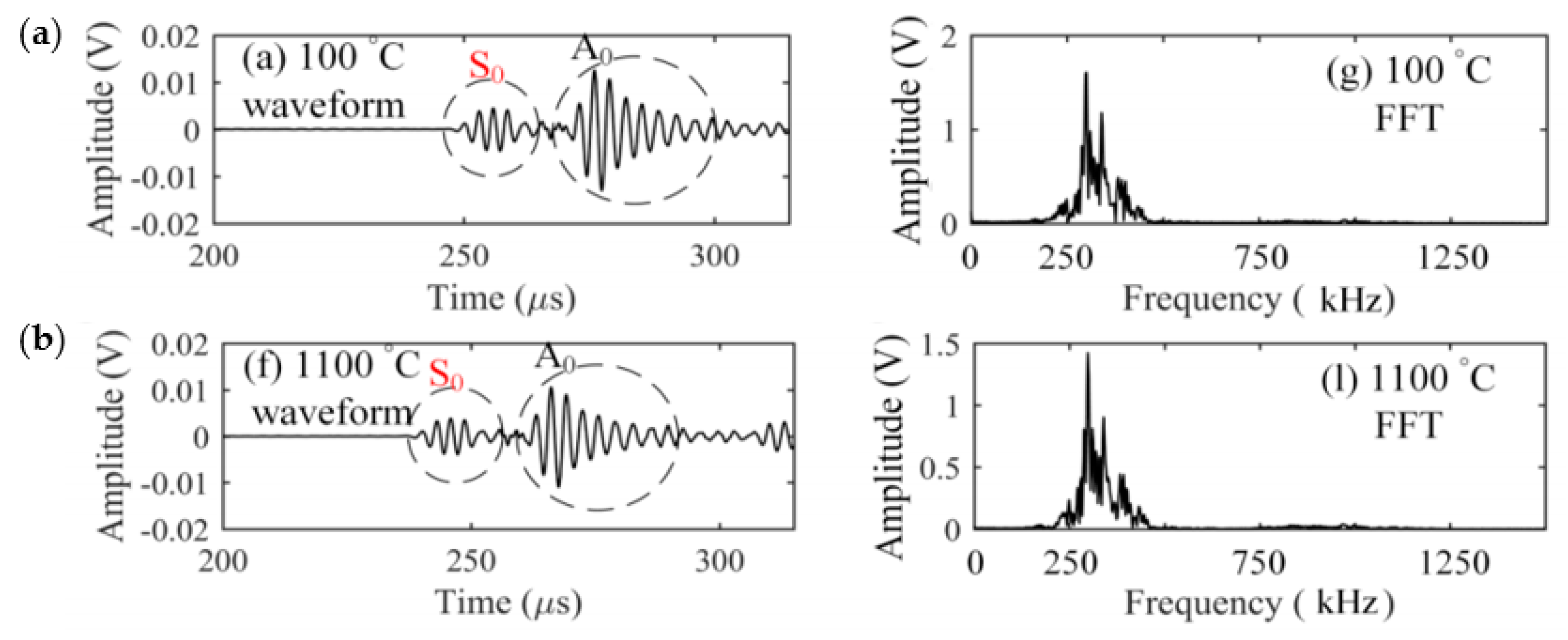
7.2. Development and Applications
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Uprety, B.; Kim, S.; Mathews, V.J.; Adams, D.O. A comparative evaluation of piezoelectric sensors for acoustic emission-based impact location estimation and damage classification in composite structures. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2015; Volume 1650, pp. 1146–1154. [Google Scholar]
- Cai, J.; Qiu, L.; Yuan, S.; Shi, L.; Liu, P.; Liang, D. Structural Health Monitoring for Composite Materials. In Composites and Their Applications; Hu, N., Ed.; InTechOpen: Rijeka, Croatia, 2012. [Google Scholar]
- Bockenheimer, C.; Speckmann, H.; Team, I. Validation, verification and implementation of SHM at Airbus. In Proceedings of the 9th International Workshop on Structural Health Monitoring (IWSHM 2013), Stanford University, Stanford, CA, USA, 10–12 September 2013. [Google Scholar]
- Di Sante, R. Fibre Optic Sensors for Structural Health Monitoring of Aircraft Composite Structures: Recent Advances and Applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef]
- Kister, G.; Winter, D.; Badcock, R.A.; Gebremichael, Y.M.; Boyle, W.J.O.; Meggitt, B.T.; Grattan, K.T.V.; Fernando, G.F. Structural health monitoring of a composite bridge using Bragg grating sensors. Part. 1: Evaluation of adhesives and protection systems for the optical sensors. Eng. Struct. 2007, 29, 440–448. [Google Scholar] [CrossRef]
- Alani, A.M.; Aboutalebi, M.; Kilic, G. Integrated health assessment strategy using NDT for reinforced concrete bridges. NDT E Int. 2014, 61, 80–94. [Google Scholar] [CrossRef]
- Maria, M. Advanced composite materials of the future in aerospace industry. INCAS Bull. 2013, 5, 139–150. [Google Scholar] [CrossRef]
- Drewry, M.; Georgiou, G. A review of NDT techniques for wind turbines. Insight 2007, 49, 137–141. [Google Scholar] [CrossRef] [Green Version]
- Galappaththi, U.I.K.; de Silva, A.K.M.; Macdonald, M.; Adewale, O.R. Review of inspection and quality control techniques for composite wind turbine blades. Insight Non Destr. Test. Cond. Monit. 2012, 54, 82–85. [Google Scholar] [CrossRef]
- Camacho, J.; Atehortua, D.; Cruza, J.F.; Brizuela, J.; Ealo, J. Ultrasonic crack evaluation by phase coherence processing and TFM and its application to online monitoring in fatigue tests. NDT E Int. 2018, 93, 164–174. [Google Scholar] [CrossRef]
- Ciampa, F.; Mahmoodi, P.; Pinto, F.; Meo, M. Recent advances in active infrared thermography for non-destructive testing of aerospace components. Sensors 2018, 18, 609. [Google Scholar] [CrossRef] [Green Version]
- Hung, Y.Y. Shearography: A novel and practical approach for nondestructive inspection. J. Nondestr. Eval. 1989, 8, 55–67. [Google Scholar] [CrossRef]
- Hellier, C. Radiographic Testing. In Handbook of Nondestructive Evaluation, 2nd ed.; Hellier, C., Ed.; McGraw-Hill Education: New York, NY, USA, 2012; pp. 6.1–6.10. [Google Scholar]
- Munoz, V.; Vales, B.; Perrin, M.; Pastor, M.; Welemane, H.; Cantarel, A.; Karama, M. Damage detection in CFRP by coupling acoustic emission and infrared thermography. Compos. Part B Eng. 2016, 85, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Sagaidak, A.; Bardakov, V.; Elizarov, S.; Terentyev, D. The Use of Acoustic Emission Method in the Modern Construction; JSC SIC Construction; Research Dept. Interunis-IT LLC: Moscow, Russia, 2015. [Google Scholar]
- Hellier, C. Acoustic Emission Testing. In Handbook of Nondestructive Evaluation, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2012; pp. 10.1–10.39. [Google Scholar]
- Sachse, W.; Yamaguchi, K.; Roget, J. Acoustic Emission: Current Practice and Future Directions; STM International: West Conshohocken, PA, USA, 1991. [Google Scholar]
- Chandarana, N.; Sanchez, D.M.; Soutis, C.; Gresil, M. Early Damage Detection in Composites during Fabrication and Mechanical Testing. Materials 2017, 10, 685. [Google Scholar] [CrossRef] [PubMed]
- Crawford, A.; Droubi, M.G.; Faisal, N.H. Analysis of acoustic emission propagation in metal-to-metal adhesively bonded joints. J. Nondestr. Eval. 2018, 37, 33. [Google Scholar] [CrossRef] [Green Version]
- Diakhate, M.; Angellier, N.; Pitti, R.M.; Dubois, F. On the crack tip propagation monitoring within wood material: Cluster analysis of acoustic emission data compared with numerical modelling. Constr. Build. Mater. 2017, 156, 911–920. [Google Scholar] [CrossRef]
- Fedele, R.; Pratico, F.G.; Carotenuto, R.; della Corte, F.G. Damage detection into road pavement through acoustic signature analysis: First results. In Proceedings of the 24th International Congress on Sound and Vibration (ICSV 24), London, UK, 23–27 July 2017. [Google Scholar]
- Mujica, L.; Rodellar, J.; Vehí, J. A review of impact damage detection in structures using strain data. Int. J. COMADEM 2013, 13, 3–18. [Google Scholar]
- Doyle, C.T.M.; Chen, R.; Liu, T.; Zheng, G.; Fernando, G.F. Fiber optic acoustic emission sensor based on a fused tapered coupler. In Proceedings of the SPIE’s 9th Annual International Symposium on Smart Structures and Materials, San Diego, CA, USA, 17–21 March 2002; Volume 4694. [Google Scholar]
- Chen, R.; Liao, Y.; Zheng, G.; Fernando, G.F. A novel ultrasound fibre optic sensor based on a fused-tapered optical fibre coupler. Meas. Sci. Technol. 2004, 15, 1490. [Google Scholar] [CrossRef]
- Fornel, F.d.; Ragdale, C.M.; Mears, R.J. Analysis of Single-Mode Fused Tapered Fibre Couplers. Microwaves Opt. Antennas IEE Proc. H 1984, 131, 221–227. [Google Scholar] [CrossRef] [Green Version]
- Pierce, S.G.; Philp, W.R.; Gachagan, A.; McNab, A.; Hayward, G.; Culshaw, B. Surface-bonded and embedded optical fibers as ultrasonic sensors. Appl. Opt. 1996, 35, 5191–5197. [Google Scholar] [CrossRef] [PubMed]
- Lan, C.; Zhou, W.; Xie, Y. Detection of Ultrasonic Stress Waves in Structures Using 3D Shaped Optic Fiber Based on a Mach.-Zehnder Interferometer. Sensors 2018, 18, 1218. [Google Scholar] [CrossRef] [Green Version]
- Tada, K.; Yuki, H. detection of acoustic emission signals with the fabry-perot interferometer type optical fiber sensor. J. Acoust. Emiss. 2017, 34, S38. [Google Scholar]
- Islam, M.; Ali, M.M.; Lai, M.; Lim, K.; Ahmad, H. Chronology of Fabry-Perot Interferometer Fiber-Optic Sensors and Their Applications: A Review. Sensors 2014, 14, 7451–7488. [Google Scholar] [CrossRef] [Green Version]
- Grouve, W.J.B.; Warnet, L.; de Boer, A.; Akkerman, R.; Vlekken, J. Delamination detection with fibre Bragg gratings based on dynamic behaviour. Compos. Sci. Technol. 2008, 68, 2418–2424. [Google Scholar] [CrossRef]
- Wild, G.; Hinckley, S. Fiber Bragg Grating Sensors for Acoustic Emission and Transmission Detection Applied to Robotic NDE in Structural Health Monitoring. In Proceedings of the 2007 IEEE Sensors Applications Symposium, San Diego, CA, USA, 6–8 February 2007. [Google Scholar]
- Guo, N.; Cawley, P. Lamb wave propagation in composite laminates and its relationship with acousto-ultrasonics. NDT E Int. 1993, 26, 75–84. [Google Scholar] [CrossRef]
- Wang, D.; Ye, L.; Tang, Y.; Lu, Y. Monitoring of delamination onset and growth during Mode I and Mode II interlaminar fracture tests using guided waves. Compos. Sci. Technol. 2012, 72, 145–151. [Google Scholar] [CrossRef]
- Sohn, H.; Park, G.; Wait, J.R.; Limback, N.P.; Farrar, C.R. Wavelet-based active sensing for delamination detection in composite structures. Smart Mater. Struct. 2003, 13, 153–160. [Google Scholar] [CrossRef]
- Gangadharan, R.; Prasanna, G.; Bhat, M.R.; Murthy, C.R.L.; Gopalakrishnan, S. Acoustic emission source location and damage detection in a metallic structure using a graph-theory-based geodesic approach. Smart Mater. Struct. 2009, 18, 115022. [Google Scholar] [CrossRef]
- Sherafat, M.H.; Quaegebeur, N.; Hubert, P.; Lessard, L.; Masson, P. Finite element modeling of Lamb wave propagation in composite stepped joints. J. Reinf. Plast. Compos. 2016, 35, 796–806. [Google Scholar] [CrossRef]
- Tsuda, H.; Lee, J.-R.; Guan, Y. Fatigue crack propagation monitoring of stainless steel using fiber Bragg grating ultrasound sensors. Smart Mater. Struct. 2006, 15, 1429–1437. [Google Scholar] [CrossRef]
- Cawley, P.; Alleyne, D. The use of Lamb waves for the long range inspection of large structures. Ultrasonics 1996, 34, 287–290. [Google Scholar] [CrossRef]
- Eckert, E.G.; Maresca, J.W.; Hillger, R.W.; Yezzi, J.J. Location of Leaks in Pressurized Petroleum Pipelines by Means of Passive-Acoustic Sensing Methods. In Leak Detection for Underground Storage Tanks; Durgin, P., Young, T., Eds.; ASTM International: West Conshohocken, PA, USA, 1992; pp. 53–69. [Google Scholar]
- Mukhopadhyay, C.K.; Haneef, T.K.; Rao, B.P.C.; Jayakumar, T. On-line Monitoring of Engineering Components Using Acoustic Emission Technique. Procedia Eng. 2014, 86, 496–502. [Google Scholar] [CrossRef] [Green Version]
- Lacidogna, G.; Manuello, A.; Niccolini, G.; Accornero, F.; Carpinteri, A. Acoustic emission wireless monitoring of structures. In Acoustic Emission and Related Non-Destructive Evaluation Techniques in the Fracture Mechanics of Concrete; Ohtsu, M., Ed.; Woodhead Publishing: Oxford, UK, 2015; pp. 15–40. [Google Scholar]
- Masmoudi, S.; el Mahi, A.; Turki, S. Use of piezoelectric as acoustic emission sensor for in situ monitoring of composite structures. Compos. Part B Eng. 2015, 80, 307–320. [Google Scholar] [CrossRef]
- Yu, F.; Okabe, Y.; Wu, Q.; Shigeta, N. Fiber-optic sensor-based remote acoustic emission measurement of composites. Smart Mater. Struct. 2016, 25, 105033. [Google Scholar] [CrossRef]
- Shiotani, T.; Yuyama, S.; Carlos, M.; Vahaviolos, S.J. Continuous monitoring of rock failure by a remote AE system. J. Acoust. Emiss. 2000, 18, 248–257. [Google Scholar]
- Pang, D.; Sui, Q.; Wang, M.; Guo, D.; Sai, Y. Development of high temperature acoustic emission sensing system using fiber Bragg grating. Photonic Sens. 2018, 8, 56–62. [Google Scholar] [CrossRef] [Green Version]
- Yu, F.; Okabe, Y. Fiber-optic sensor-based remote acoustic emission measurement in a 1000 °C environment. Sensors 2017, 17, 2908. [Google Scholar]
- Leal-Junior, A.; Frizera-Neto, A.; Marques, C.; Pontes, M.J. A polymer optical fiber temperature sensor based on material features. Sensors 2018, 18, 301. [Google Scholar] [CrossRef] [Green Version]
- Broadway, C.; Kalli, K.; Theodosiou, A.; Zubel, M.; Sugden, K.; Megret, P.; Caucheteur, C. L-band CYTOP Bragg gratings for ultrasound sensing. In Proceedings of the Micro-Structured and Specialty Optical Fibres V, Strasbourg, France, 22–26 April 2018; Volume 10681. [Google Scholar]
- Bucaro, J.A.; Dardy, H.D.; Carome, E.F. Fiber-optic hydrophone. J. Acoust. Soc. Am. 1977, 62, 1302–1304. [Google Scholar] [CrossRef]
- Kawasaki, B.S.; Hill, K.O.; Lamont, R.G. Biconical-taper single-mode fiber coupler. Opt. Lett. 1981, 6, 327–328. [Google Scholar] [CrossRef]
- Sorazu, B.; Thursby, G.; Culshaw, B.; Dong, F.; Pierce, S.G.; Yang, Y.; Betz, D. Optical generation and detection of ultrasound. Strain 2003, 39, 111–114. [Google Scholar] [CrossRef]
- Dewhurst, R.J.; Edwards, C.E.; McKie, A.D.W.; Palmer, S.B. Comparative study of wide-band ultrasonic transducers. Ultrasonics 1987, 25, 315–321. [Google Scholar] [CrossRef]
- Mistras. WD Sensor (Wideband Differential Sensor). Product Data Sheet 2011. Available online: http://www.physicalacoustics.com/content/literature/sensors/Model_WD.pdf (accessed on 29 October 2020).
- Wild, G.; Hinckley, S. Acousto-Ultrasonic Optical Fiber Sensors: Overview and State-of-the-Art. IEEE Sens. J. 2008, 8, 1184–1193. [Google Scholar] [CrossRef] [Green Version]
- Hromadka, J.; Korposh, S.; Partridge, M.C.; James, S.W.; Davis, F.; Crump, D.; Tatam, R.P. Multi-parameter measurements using optical fibre long period gratings for indoor air quality monitoring. Sens. Actuators B Chem. 2017, 244, 217–225. [Google Scholar] [CrossRef]
- Nair, A.K.; Machavaram, V.R.; Mahendran, R.S.; Pandita, S.D.; Paget, C.; Barrow, C.; Fernando, G.F. Process. monitoring of fibre reinforced composites using a multi-measurand fibre-optic sensor. Sens. Actuators B Chem. 2015, 212, 93–106. [Google Scholar] [CrossRef] [Green Version]
- Thursby, G.; Culshaw, B.; Betz, D.C. Multifunctional fibre optic sensors monitoring strain and ultrasound. Fatigue Fract. Eng. Mater. Struct. 2008, 31, 660–673. [Google Scholar] [CrossRef]
- Rao, Y.J.; Henderson, P.J.; Jackson, D.A.; Zhang, L.; Bennion, I. Simultaneous strain, temperature and vibration measurement using a multiplexed in-fibre-Bragg-grating/fibre-Fabry-Perot sensor system. Electron. Lett. 1997, 33, 2063–2064. [Google Scholar] [CrossRef]
- Oliveira, R.; Osório, J.H.; Aristilde, S.; Bilro, L.; Nogueira, R.N.; Cordeiro, C.M.B. Simultaneous measurement of strain, temperature and refractive index based on multimode interference, fiber tapering and fiber Bragg gratings. Meas. Sci. Technol. 2016, 27, 075107. [Google Scholar] [CrossRef] [Green Version]
- Jones, M. Structural-health monitoring: A sensitive issue. Nat. Photonics 2008, 2, 153. [Google Scholar] [CrossRef]
- Wevers, M.; Rippert, L.; Papy, J.M.; van Huffel, S. Damage in CFRP composite materials monitored with intensity modulated fiber optic sensors. In Emerging Technologies in NDT, Proceedings of the 3rd International Conference on Emerging Technologies in Non-Destructive Testing, Thessaloniki, Greece, 26–28 May 2003; Hemelrijck, D., Anastaopoulos, A., Melanitis, N.E., Eds.; Taylor & Francis: Oxfordshire, UK; p. 6.
- Wei, P.; Han, X.; Xia, D.; Liu, T.; Lang, H. Novel fiber-optic ring acoustic emission sensor. Sensors 2018, 18, 215. [Google Scholar]
- Cole, J.H.; Danver, B.A.; Bucaro, J.A. Synthetic-Heterodyne Interferometric Demodulation. IEEE Trans. Microwav. Theory Tech. 1982, 30, 540–543. [Google Scholar] [CrossRef] [Green Version]
- Paschotta, R. Cladding Modes. Encyclopedia of Laser Physics and Technology October 2008. Available online: https://www.rp-photonics.com/cladding_modes.html (accessed on 29 October 2020).
- Ivanov, O.V.; Nikitov, S.A.; Gulyaev, Y.V. Cladding modes of optical fibers: Properties and applications. Physics-Uspekhi 2006, 49, 167. [Google Scholar] [CrossRef]
- Haggans, C.W.; Singh, H.; Varner, W.F.; Wang, J. Narrow-depressed cladding fiber design for minimization of cladding mode losses in azimuthally asymmetric fiber Bragg gratings. J. Lightwave Technol. 1998, 16, 902–909. [Google Scholar] [CrossRef]
- Berendt, M.O.; Gruner-Nielsen, L.; Bjarklev, A.; Soccorich, C.E. Reduction of cladding mode coupling losses in fiber Bragg gratings. In 1999 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference; IEEE: Piscataway, NJ, USA, 1999. [Google Scholar]
- Weik, M. Communications Standard Dictionary; Springer: New York, NY, USA, 2012. [Google Scholar]
- Leon-Saval, S.G.; Fontaine, N.K.; Amezcua-Correa, R. The photonic lantern. In Proceedings of the 2014 Conference on Lasers and Electro-Optics (CLEO)—Laser Science to Photonic Applications, San Jose, CA, USA, 8–13 June 2014. [Google Scholar]
- 630HP—Single Mode Optical Fiber, 600–770 nm, Ø125 µm Cladding. 2020. Available online: https://www.thorlabs.com/thorproduct.cfm?partnumber=630HP (accessed on 29 October 2020).
- Hollow Round Glass Capillaries ID 0.60 mm OD 0.84 mm (75 capillaries per pack). 2020. Available online: https://www.cmscientific.com/proddetail.php?prod=Hollow+Round+Glass+Capillaries+ID+0.60mm+OD+0.84mm+%2875+capillaries+per+pack%29 (accessed on 29 October 2020).
- Grosse, C.U. Wireless Sensing and Acoustic Emission Array Techniques. In Acoustic Emission Testing: Basics for Research—Applications in Civil. Engineering; Grosse, C., Ohtsu, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 367–381. [Google Scholar]
- Wang, L.; Liu, Y.; Fu, W.; Li, F.; Zhao, Z.; Yu, K. Source location using an optimized microfiber coupler sensor based on modal acoustic emission method. Struct. Control Health Monit. 2017, 24, e2011. [Google Scholar] [CrossRef]
- Rosiek, M.; Martowicz, A.; Uhl, T. An Overview of Electromechanical Impedance Method for Damage Detection in Mechanical Structures. In Proceedings of the 6th European Workshop on Structural Health Monitoring, Dresden, Germany, 3–6 July 2012. [Google Scholar]
- Hellier, C. Introduction to Nondestructive Testing. In Handbook of Nondestructive Evaluation, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2012; pp. 1.1–1.27. [Google Scholar]
- Williams, R.V. Acoustic Emission; Adam Hilger Ltd: Bristol, UK, 1980; p. 118. [Google Scholar]
- Zhou, C.; Zhang, Y. Particle filter based noise removal method for acoustic emission signals. Mech. Syst. Signal Process. 2012, 28, 63–77. [Google Scholar] [CrossRef]
- Corporation, P.A. PCI-2 Based AE System User’s Manual Rev 3. April 2007. Available online: https://material.karlov.mff.cuni.cz/people/mathis/Navody/PCI2.pdf (accessed on 29 October 2020).
- Sun, L.; Li, Y. Acoustic emission sound source localization for crack in the pipeline. In Proceedings of the 2010 Chinese Control and Decision Conference, Xuzhou, China, 26–28 May 2010. [Google Scholar]
- Fasana, A.; Garibaldi, L. Measurement of Acoustic Emission Signals: Influence of the Couplant; Trans Tech Publications Ltd, Scientific.net: Bäch SZ, Switzerland, 2007; Volume 347, pp. 375–380. [Google Scholar]
- Hamstad, M.A. Some observations on rayleigh waves and acoustic emission in thick steel plates. J. Acoust. Emiss. 2009, 27, 23. [Google Scholar]
- Fu, T.; Li, Q.; Liu, Y.; Leng, J. A novel embedded fiber optic acoustic emission sensor and its applications for monitoring failures of composite laminates. In Smart Sensor Phenomena, Technology, Networks, and Systems 2009; SPIE: Bellingham, WA, USA, 2009; Volume 7293. [Google Scholar]
- Hughes, J.M.; Vidler, J.; Ng, C.; Khanna, A.; Mohabuth, M.; Rose, L.R.F.; Kotousov, A. Comparative evaluation of in situ stress monitoring with Rayleigh waves. Struct. Health Monit. 2018, 18, 205–215. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Bradshaw, T.; Burns, J.; Cole, P.; Jarman, P.; Pedder, D.; Theobald, R.; Fernando, G.F. Linear location of acoustic emission using a pair of novel fibre optic sensors. Meas. Sci. Technol. 2006, 17, 2313. [Google Scholar] [CrossRef]
- Unnþórsson, R.N. Hit Detection and Determination in AE Bursts. In Acoustic Emission—Research and Applications; Sikorski, D.W., Ed.; InTechOpen: London, UK, 2013; p. 20. [Google Scholar]
- Ogura, G. Laser stripping of optical fibers opens up new applications. Laser Focus World 2001, 37, 169–176. [Google Scholar]
- Zlatanov, N. Introduction to Fiber Optics Theory. Available online: https://www.academia.edu/28851433/Introduction_to_Fiber_Optics_Theory (accessed on 29 October 2020).
- Son, G.; Jung, Y.; Yu, K. Tapered Optical Fiber Couplers Fabricated by Droplet-Based Chemical Etching. IEEE Photonics J. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Zhang, H.; Healy, N.; Dasgupta, S.; Hayes, J.R.; Petrovich, M.N.; Richardson, D.J.; Peacock, A.C. A Tuneable Multi-Core to Single Mode Fiber Coupler. IEEE Photonics Technol. Lett. 2017, 29, 591–594. [Google Scholar] [CrossRef] [Green Version]
- Pal, B. Fabrication and modeling of fused biconical tapered fiber couplers. Fiber Integr. Opt. 2003, 22, 97–117. [Google Scholar] [CrossRef]
- Zhang, J.-L.; Mao, Z.-M.; Lin, Z.-Q. Measurements and analyses of fields in fused tapered single-mode fiber couplers. Appl. Opt. 1989, 28, 2026–2030. [Google Scholar] [CrossRef]
- Lee, B.H.; Eom, J.B.; Kim, J.; Moon, D.S.; Paek, U.C.; Yang, G.H. Photonic crystal fiber coupler. Opt. Lett. 2002, 27, 812–814. [Google Scholar] [CrossRef]
- Bogonez, F.D.N. Manufacturing and Characterisation of a Fibre Optic Acoustic Emission Sensor. In School of Metallurgy and Materials; University of Birmingham: Birmingham, UK, 2017; p. 240. [Google Scholar]
- Burns, J.M. Development and Characterisation of a Fibre-Optic Acoustic Emission Sensor. In School of Metallurgy and Materials; University of Birmingham: Birmingham, UK, 2011; p. 302. [Google Scholar]
- Snyder, A.W. Coupled-Mode Theory for Optical Fibers. J. Opt. Soc. Am. 1972, 62, 1267–1277. [Google Scholar] [CrossRef]
- Shuai, C.-j.; Duan, J.-A.; Zhong, J. Novel manufacturing method of optical fiber coupler. J. Cent. South Univ. Technol. 2006, 13, 242–245. [Google Scholar] [CrossRef]
- Eisenmann, M.; Weidel, E. Single-mode fused biconical couplers for wavelength division multiplexing with channel spacing between 100 and 300 nm. J. Lightwave Technol. 1988, 6, 113–119. [Google Scholar] [CrossRef]
- Birks, T.A.; Russell, P.S.J.; Culverhouse, D.O. The acousto-optic effect in single-mode fiber tapers and couplers. J. Lightwave Technol. 1996, 14, 2519–2529. [Google Scholar] [CrossRef]
- Pidishety, S. Fused Fiber Couplers: Basic Theory and Automated Fabrication. Available online: https://www.semanticscholar.org/paper/Fused-Fiber-Couplers%3A-Basic-Theory-and-Automated/ccd28657365d8e9f66a6e008b677938760999dc1 (accessed on 29 October 2020).
- Matthews, A.L.; Murphy, K.A.; Rogers, R.E.; Claus, R.O. Acoustic Fiber Waveguide Coupler. In Proceedings of the IEEE 1987 Ultrasonics Symposium, Denver, CO, USA, 14–16 October 1987. [Google Scholar]
- Ghatak, A.; Thyagarajan, K. An. Introduction to Fiber Optics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Ghatak, A.; Thyagarajan, K. Single-mode fiber optic components. In An Introduction to Fiber Optics; Ghatak, A., Thyagarajan, K., Eds.; Cambridge University Press: Cambridge, UK, 1998; pp. 360–396. [Google Scholar]
- Li, Y.; Wang, X.; Bao, X. Sensitive acoustic vibration sensor using single-mode fiber tapers. Appl. Opt. 2011, 50, 1873–1878. [Google Scholar] [CrossRef] [PubMed]
- Musa, B.; Kamil, Y.M.; Bakar, M.H.; Noor, A.S.M.; Ismail, A.; Mahdi, M. Investigating the effect of taper length on sensitivity of the tapered-fiber based temperature sensor. Mater. Sci. 2016, 78. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Zheng, G.; Liu, T.; Fernando, G.F.; Liao, Y.B. A Novel Acoustic Emission Fiber Optic Sensor Based on a Single Mode Optical Fiber Coupler. Chin. J. Lasers 2000, 10, 4. [Google Scholar]
- Li, F.; Liu, Y.; Wang, L.; Zhao, Z. Investigation on the response of fused taper couplers to ultrasonic wave. Appl. Opt. 2015, 54, 6986–6993. [Google Scholar] [CrossRef]
- Wang, S.; Lu, P.; Zhang, L.; Liu, D.; Zhang, J. Optical fiber acoustic sensor based on nonstandard fused coupler and aluminum foil. IEEE Sens. J. 2014, 14, 2293–2298. [Google Scholar] [CrossRef]
- Xu, J.; Ma, B.; Zhou, X. Theoretical analysis and experimental investigation of fiber-optic coupler’s strain characteristic. In Proceedings of the 2009 IEEE International Conference on Automation and Logistics, Shenyang, China, 5–7 August 2009. [Google Scholar]
- Butler., T.; Krishnamurthy, S.; Badcock, R.; Chen, R. A Low-Cost Fiber Optic Acoustic Emission Sensor for Damage Detection in Engineering Composite Materials and Structures. In Structural Health Monitoring 2003: From Diagnostics & Prognostics to Structural Health Management, Proceedings of the 4th International Workshop on Structural Health Monitoring, Stanford University Stanford, CA, USA, 15–17 September 2003; Chang, F., Ed.; DEStech Publications, Inc: Lancaster, PA, USA, 2003; p. 1552. [Google Scholar]
- Badcock, R.; Krishnamurthy, S.; Fernando, G.F.; Butler, T.; Chen, R.; Tetlow, J. Health monitoring of composite structures using a novel fibre optic acoustic emission sensors. In Proceedings of the 11th European Conference on Composite Materials; Elsevier: Amsterdam, The Netherlands, 2004; ISBN 978-0-12-409605-9. [Google Scholar]
- Birks, T.A. Practical tuning mechanism for fused-tapered couplers. Opt. Lett. 1988, 13, 1126–1128. [Google Scholar] [CrossRef]
- Fu, T.; Liu, Y.; Li, Q.; Leng, J. Fiber optic acoustic emission sensor and its applications in the structural health monitoring of CFRP materials. Opt. Lasers Eng. 2009, 47, 1056–1062. [Google Scholar] [CrossRef]
- Fu, T.; Liu, Y.; Lau, K.; Leng, J. Impact source identification in a carbon fiber reinforced polymer plate by using embedded fiber optic acoustic emission sensors. Compos. Part B Eng. 2014, 66, 420–429. [Google Scholar] [CrossRef]
- Thursby, G.; Culshaw, B. Evaluation of the internal strains and stresses produced in a plate by propagating Lamb waves through the use of fibre optic sensors. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 6–10 March 2011; Volume 7982. [Google Scholar]
- Papasalouros, D.; Tsopelas, N.; Anastasopoulos, A.; Kourousis, D.; Lekou, D.J.; Mouzakis, F. Acoustic emission monitoring of composite blade of NM48/750 NEG-MICON wind turbine. J. Acoust. Emiss. 2013, 31, 36–49. [Google Scholar]
- Beattie, A.G. Acoustic Emission Monitoring of a Wind Turbine Blade during a Fatigue Test; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1997. [Google Scholar]
- Sutherland, H.; Beattie, A.; Hansche, B.; Musial, W.; Allread, J.; Johnson, J.; Summers, M. The Application of Non-Destructive Techniques to the Testing of a Wind Turbine Blade; Sandia National Labs: Albuquerque, NM, USA, 1994; p. 61. [Google Scholar]
- Joosse, P.A.; Blanch, M.J.; Dutton, A.G.; Kouroussis, D.A.; Philippidis, T.P.; Vionis, P.S. Acoustic Emission Monitoring of Small Wind Turbine Blades. J. Sol. Energy Eng. 2002, 124, 446–454. [Google Scholar] [CrossRef]
- Doyle, C.; Tuck, C.; Chen, R.; Fernando, G.F.; Zheng, G.; Liu, T.; Joosse, P.; Van Delft, V.; Dutton, A.; Blanch, M.; et al. Application of a fibre-optic acoustic emission sensor to the fatigue testing of wind turbine blades. 2003. Available online: https://www.researchgate.net/publication/333517246_Application_of_a_fibre-optic_acoustic_emission_sensor_to_the_fatigue_testing_of_wind_turbine_blades (accessed on 29 October 2020).
- Her, S.-C.; Yang, C.-M. Dynamic strain measured by mach.-zehnder interferometric optical fiber sensors. Sensors 2012, 12, 3314–3326. [Google Scholar] [CrossRef] [PubMed]
- Heijmans, J.A.C.; Cheng, L.K.; Wieringa, F.P. Optical Fiber Sensors for Medical Applications—Practical Engineering Considerations; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ahsani, V.; Ahmed, F.; Jun, M.B.G.; Bradley, C. Tapered fiber-optic mach-zehnder interferometer for ultra-high. sensitivity measurement of refractive index. Sensors 2019, 19, 1652. [Google Scholar]
- Gao, S.; Ji, C.; Ning, Q.; Chen, W.; Li, J. High-sensitive Mach.-Zehnder interferometric temperature fiber-optic sensor based on core-offset splicing technique. Opt. Fiber Technol. 2020, 56, 102202. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, H.; Dai, Y.; Zhou, A.; Yuan, L. Fiber In-Line Mach–Zehnder Interferometer for Gas. Pressure Sensing. IEEE Sens. J. 2018, 18, 8012–8016. [Google Scholar]
- Shen, C.; Wang, Y.; Chu, J.; Lu, Y.; Li, Y.; Dong, X. Optical fiber axial micro-displacement sensor based on Mach.-Zehnder interferometer. Opt. Express 2014, 22, 31984–31992. [Google Scholar] [CrossRef]
- Bucaro, J.A.; Dardy, H.D.; Carome, E.F. Optical fiber acoustic sensor. Appl. Opt. 1977, 16, 1761–1762. [Google Scholar] [CrossRef]
- Xu, Y. Delamination detection at web/flange junction of I-section composite beam with fiber optical interferometer sensor. Compos. Part B Eng. 2014, 58, 140–146. [Google Scholar] [CrossRef]
- Hocker, G.B. Fiber optic acoustic sensors with composite structure: An analysis. Appl. Opt. 1979, 18, 3679–3683. [Google Scholar] [CrossRef] [PubMed]
- Hocker, G.B. Fiber-optic acoustic sensors with increased sensitivity by use of composite structures. Opt. Lett. 1979, 4, 320–321. [Google Scholar] [CrossRef]
- Lagakos, N.; Hickman, T.R.; Ehrenfeuchter, P.; Bucaro, J.A.; Dandridge, A. Planar flexible fiber-optic acoustic sensors. J. Lightwave Technol. 1990, 8, 1298–1303. [Google Scholar] [CrossRef]
- Liang, S.; Zhang, C.; Lin, W.; Li, L.; Li, C.; Feng, X.; Lin, B. Fiber-optic intrinsic distributed acoustic emission sensor for large structure health monitoring. Opt. Lett. 2009, 34, 1858–1860. [Google Scholar] [CrossRef]
- Gong, J.; MacAlpine, J.M.K.; Jin, W.; Liao, Y. Locating acoustic emission with an amplitude-multiplexed acoustic sensor array based on a modified Mach–Zehnder interferometer. Appl. Opt. 2001, 40, 6199–6202. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Li, D.; Liu, J.; Wang, R. Membrane-free acoustic sensing based on an optical fiber Mach–Zehnder interferometer. Appl. Opt. 2020, 59, 1775–1779. [Google Scholar] [CrossRef]
- Teixeira, J.G.V.; Leite, I.T.; Silva, S.; Frazão, O. Advanced fiber-optic acoustic sensors. Photonic Sens. 2014, 4, 198–208. [Google Scholar] [CrossRef] [Green Version]
- Brandenburg., A.; Hinkov, V.; Konz., W. Integrated Optic Sensors. In Sensors, A Comprehensive Survey; Wagner, E., Dandliker, R., Spenner, K., Eds.; Wiley–VCH: Hoboken, NJ, USA, 1992; pp. 405–417. [Google Scholar]
- Tsuda, H.; Ikeguchi, T.; Takahashi, J.; Kemmochi, K. Damage monitoring of carbon-fibre-reinforced plastics using Michelson interferometric fibre-optic sensors. J. Mater. Sci. Lett. 1998, 17, 503–506. [Google Scholar] [CrossRef]
- Liu, K.; Ferguson, S.M.; Measures, R.M. Fiber-optic interferometric sensor for the detection of acoustic emission within composite materials. Opt. Lett. 1990, 15, 1255–1257. [Google Scholar] [CrossRef]
- Pierce, S.G.; Culshaw, B.; Philp, W.R.; Lecuyer, F.; Farlow, R. Broadband Lamb wave measurements in aluminium and carbon/glass fibre reinforced composite materials using non-contacting laser generation and detection. Ultrasonics 1997, 35, 105–114. [Google Scholar] [CrossRef]
- Zhang, T.; Pang, F.; Liu, H.; Cheng, J.; Lv, L.; Zhang, X.; Chen, N.; Wang, T. A fiber-optic sensor for acoustic emission detection in a high. voltage cable system. Sensors 2016, 16, 2026. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lű, T.; Li, Z.; Xia, D.; He, K.; Zhang, G. Asymmetric Fabry–Pérot fiber-optic pressure sensor for liquid-level measurement. Rev. Sci. Instrum. 2009, 80, 033104. [Google Scholar] [CrossRef]
- Zhao, J.H.; Shi, Y.K.; Shan, N.; Yuan, X.Q. Stabilized fiber-optic extrinsic Fabry–Perot sensor system for acoustic emission measurement. Opt. Laser Technol. 2008, 40, 874–880. [Google Scholar] [CrossRef]
- Yu, B.; Kim, D.W.; Deng, J.; Xiao, H.; Wang, A. Fiber Fabry-Perot sensors for detection of partial discharges in power transformers. Appl. Opt. 2003, 42, 3241–3250. [Google Scholar] [CrossRef]
- Dong, Y. Non-destructive evaluation (NDE) of composites: Using fiber optic sensors. In Non-Destructive Evaluation (NDE) of Polymer Matrix Composites; Karbhari, V.M., Ed.; Woodhead Publishing: Cambridge, UK, 2013; pp. 617–633. [Google Scholar]
- Wang, Z.; Shen, F.; Song, L.; Wang, X.; Wang, A. Multiplexed fiber fabry-perot interferometer sensors based on ultrashort bragg gratings. IEEE Photonics Technol. Lett. 2007, 19, 622–624. [Google Scholar] [CrossRef]
- Kbashi, H.J. Fabrication of Submicron-Diameter and Taper Fibers Using Chemical Etching. J. Mater. Sci. Technol. 2012, 28, 308–312. [Google Scholar] [CrossRef]
- Read, I.; Foote, P.; Murray, S. Optical fibre acoustic emission sensor for damage detection in carbon fibre composite structures. Meas. Sci. Technol. 2001, 13, N5–N9. [Google Scholar] [CrossRef]
- Bucaro, J.A.; Carome, E.F. Single fiber interferometric acoustic sensor. Appl. Opt. 1978, 17, 330–331. [Google Scholar] [CrossRef]
- Tran, T.A.; Miller, W.V.; Murphy, K.A.; Vengsarkar, A.M.; Claus, R.O. Stabilized extrinsic fiber-optic Fizeau sensor for surface acoustic wave detection. J. Lightwave Technol. 1992, 10, 1499–1506. [Google Scholar] [CrossRef]
- Beard, P.C.; Mills, T.N. Extrinsic optical-fiber ultrasound sensor using a thin polymer film as a low-finesse Fabry–Perot interferometer. Appl. Opt. 1996, 35, 663–675. [Google Scholar] [CrossRef]
- Kim, D.-H.; Koo, B.Y.; Kim, C.G.; Hong, C.S. Damage detection of composite structures using a stabilized extrinsic Fabry–Perot interferometric sensor system. Smart Mater. Struct. 2004, 13, 593–598. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, Y.; Luo, X.; Liu, G.; Han, M. Acoustic emission sensor system using a chirped fiber-Bragg-grating Fabry–Perot interferometer and smart feedback control. Opt. Lett. 2017, 42, 631–634. [Google Scholar] [CrossRef]
- Pappu, R.P. Acoustic Emission Detection Using Optical Fibre Sensors for Aerospace Applications. Ph.D. Thesis, Aston University, Birmingham, UK, 2012; p. 177. [Google Scholar]
- Campanella, C.E.; Cuccovillo, A.; Campanella, C.; Yurt, A.; Passaro, V. Fibre Bragg Grating Based Strain Sensors: Review of Technology and Applications. Sensors 2018, 18, 3115. [Google Scholar] [CrossRef] [Green Version]
- Majumder, M.; Gangopadhyay, T.K.; Chakraborty, A.K.; Dasgupta, K.; Bhattacharya, D. K Fibre Bragg gratings in structural health monitoring—Present status and applications. Sens. Actuators A Phys. 2008, 147, 150–164. [Google Scholar] [CrossRef]
- Kashyap, R. Chapter 10—Principles of Optical Fiber Grating Sensors. In Fiber Bragg Gratings, 2nd ed.; Kashyap, R., Ed.; Academic Press: Boston, MA, USA, 2010; pp. 441–502. [Google Scholar]
- Huang, D.W.; Liu, W.F.; Wu, C.W.; Yang, C.C. Reflectivity-tunable fiber Bragg grating reflectors. IEEE Photonics Technol. Lett. 2000, 12, 176–178. [Google Scholar] [CrossRef]
- Liu, W.F.; Russell, P.S.J.; Dong, L. 100% efficient narrow-band acoustooptic tunable reflector using fiber Bragg grating. J. Lightwave Technol. 1998, 16, 2006–2009. [Google Scholar] [CrossRef]
- Il, D.Y.; Su, P.H.; Yoon, K.B. Tunable narrow-bandwidth optical filter based on acoustically modulated fiber Bragg grating. IEEE Photonics Technol. Lett. 2004, 16, 1313–1315. [Google Scholar]
- Guo, H.; Xiao, G.; Mrad, N.; Yao, J. Fiber optic sensors for structural health monitoring of air platforms. Sensors 2011, 11, 3689–3705. [Google Scholar] [CrossRef] [PubMed]
- Minardo, A.; Cusano, A.; Bernini, R.; Zeni, L.; Giordano, M. Response of fiber Bragg gratings to longitudinal ultrasonic waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 304–312. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Ye, C.; Cai, Z.; Dai, X.; Kang, Y.; Xu, H. Numerical analysis and optimization of optical spectral characteristics of fiber Bragg gratings modulated by a transverse acoustic wave. Appl. Opt. 2007, 46, 6959–6965. [Google Scholar] [CrossRef]
- Erdogan, T. Cladding-mode resonances in short- and long-period fiber grating filters. J. Opt. Soc. Am. 1997, 14, 1760–1773. [Google Scholar] [CrossRef]
- Lee, R.J.; Tsuda, H.; Koo, B.-Y. Single-mode fibre optic Bragg grating sensing on the base of birefringence in surface-mounting and embedding applications. Opt. Laser Technol. 2007, 39, 157–164. [Google Scholar] [CrossRef]
- Rao, Y.J. Recent progress in applications of in-fibre Bragg grating sensors. Opt. Lasers Eng. 1999, 31, 297–324. [Google Scholar] [CrossRef]
- James, S.W.; Korposh, S.; Lee, S.W.; Tatam, R.P. A long period grating-based chemical sensor insensitive to the influence of interfering parameters. Opt. Express 2014, 22, 8012–8023. [Google Scholar] [CrossRef] [Green Version]
- Giurgiutiu, V. Chapter 7—Fiber-Optic Sensors. In Structural Health Monitoring of Aerospace Composites; Giurgiutiu, V., Ed.; Academic Press: Oxford, UK, 2016; pp. 249–296. [Google Scholar]
- Kawasaki, B.S.; Hill, K.O.; Johnson, D.C.; Fujii, Y.J.O.L. Narrow-band Bragg reflectors in optical fibers. Opt. Lett. 1978, 3, 66–68. [Google Scholar] [CrossRef]
- Beukema, R.P. Embedding technologies of FBG sensors in composites: Technologies, applications and practical use. In Proceedings of the 6th European Workshop—Structural Health Monitoring 2012, EWSHM 2012, Dresden, Germany, 3–6 July 2012. [Google Scholar]
- Kister, G.; Winter, D.; Gebremichael, Y.M.; Leighton, J.; Badcock, R.A.; Tester, P.D.; Krishnamurthy, S.; Boyle, W.J.O.; Grattan, K.T.V.; Fernando, G.F. Methodology and integrity monitoring of foundation concrete piles using Bragg grating optical fibre sensors. Eng. Struct. 2007, 29, 2048–2055. [Google Scholar] [CrossRef]
- Čápová, K.; Velebil, L.; Včelák, J. Laboratory and In-Situ Testing of Integrated FBG Sensors for SHM for Concrete and Timber Structures. Sensors 2020, 20, 1661. [Google Scholar] [CrossRef] [Green Version]
- Ngoi, B.K.A.; Paul, J.; Zhao, L.P.; Fang, Z.P. Enhanced lateral pressure tuning of fiber Bragg gratings by polymer packaging. Opt. Commun. 2004, 242, 425–430. [Google Scholar] [CrossRef]
- Yu, F.M.; Okabe, Y.; Wu, Q.; Shigeta, N. A novel method of identifying damage types in carbon fiber-reinforced plastic cross-ply laminates based on acoustic emission detection using a fiber-optic sensor. Compos. Sci. Technol. 2016, 135, 116–122. [Google Scholar] [CrossRef]
- Azmi, A.I.; Peng, G.D. Failure monitoring of E-glass/vinylester composites using fiber grating acoustic sensor. Photonic Sens. 2013, 3, 184–192. [Google Scholar] [CrossRef] [Green Version]
- Tsuda, H. Ultrasound and damage detection in CFRP using fiber Bragg grating sensors. Compos. Sci. Technol. 2006, 66, 676–683. [Google Scholar] [CrossRef]
- Tsuda, H.; Toyama, N.; Takatsubo, J. Damage detection of CFRP using fiber Bragg gratings. J. Mater. Sci. 2004, 39, 2211–2214. [Google Scholar] [CrossRef]
- Takeda, N.; Okabe, Y.; Kuwahara, J.; Kojima, S.; Ogisu, T. Development of smart composite structures with small-diameter fiber Bragg grating sensors for damage detection: Quantitative evaluation of delamination length in CFRP laminates using Lamb wave sensing. Compos. Sci. Technol. 2005, 65, 2575–2587. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, W.; Huang, Y.; Wang, H.; Jianping, H.; Huang, M.; Jinping, O. Optical fiber Bragg grating sensor assembly for 3D strain monitoring and its case study in highway pavement. Mech. Syst. Signal Process. 2012, 28, 36–49. [Google Scholar] [CrossRef]
- Betz, D.C.; Thursby, G.; Culshaw, B.; Staszewski, W.J. Identification of structural damage using multifunctional Bragg grating sensors: I. Theory and implementation. Smart Mater. Struct. 2006, 15, 1305–1312. [Google Scholar] [CrossRef]
- Tsuda, H.; Sato, E.; Nakajima, T.; Nakamura, H.; Arakawa, T.; Shiono, H.; Minato, M.; Kurabayashi, H.; Sato, A. Acoustic emission measurement using a strain-insensitive fiber Bragg grating sensor under varying load conditions. Opt. Lett. 2009, 34, 2942–2944. [Google Scholar] [CrossRef]
- Lee, J.-R.; Tsuda, H. Acousto-ultrasonic sensing using capsular fibre Bragg gratings for temperature compensation. Meas. Sci. Technol. 2006, 17, 2920–2926. [Google Scholar] [CrossRef]
- Betz, D.C.; Thursby, G.; Culshaw, B.; Staszewski, W.J. Acousto-ultrasonic sensing using fiber Bragg gratings. Smart Mater. Struct. 2003, 12, 122. [Google Scholar] [CrossRef]
- Tsuda, H.; Lee, J.R.; Guan, Y.; Takatsubo, J. Investigation of fatigue crack in stainless steel using a mobile fiber Bragg grating ultrasonic sensor. Opt. Fiber Technol. 2007, 13, 209–214. [Google Scholar] [CrossRef]
- Takahashi, N.; Yoshimura, K.; Takahashi, S.; Imamura, K. Development of an optical fiber hydrophone with fiber Bragg grating. Ultrasonics 2000, 38, 581–585. [Google Scholar] [CrossRef]
- Abdullah, M.; Bidin, N.; Yasin, M. Fiber optic vibration sensor using bifurcated plastic optical fiber. AIP Conf. Proc. 2016, 1787, 070004. [Google Scholar]
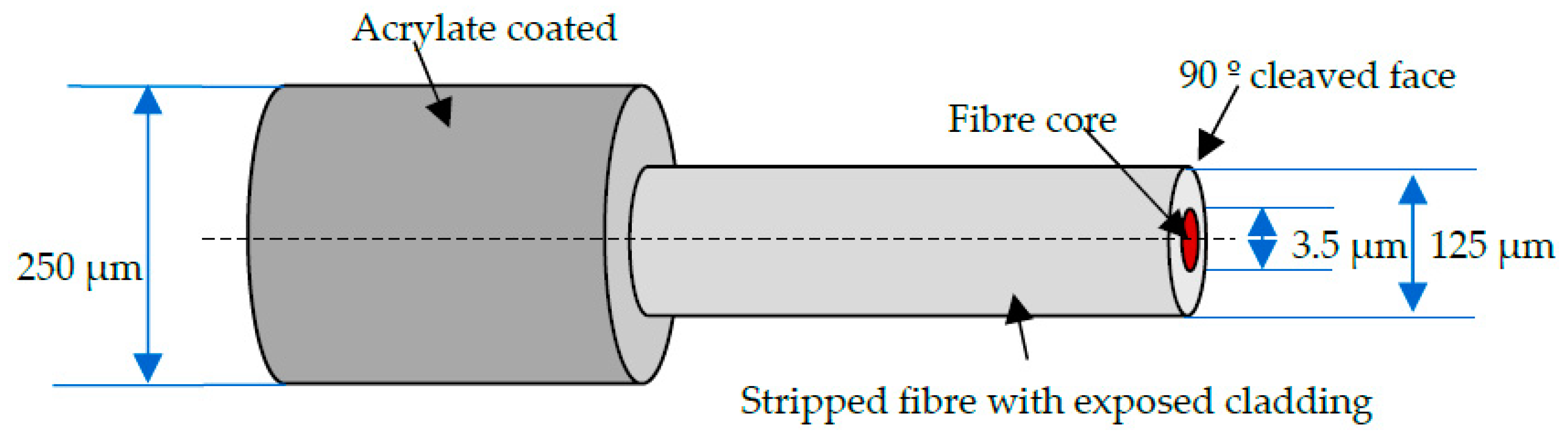
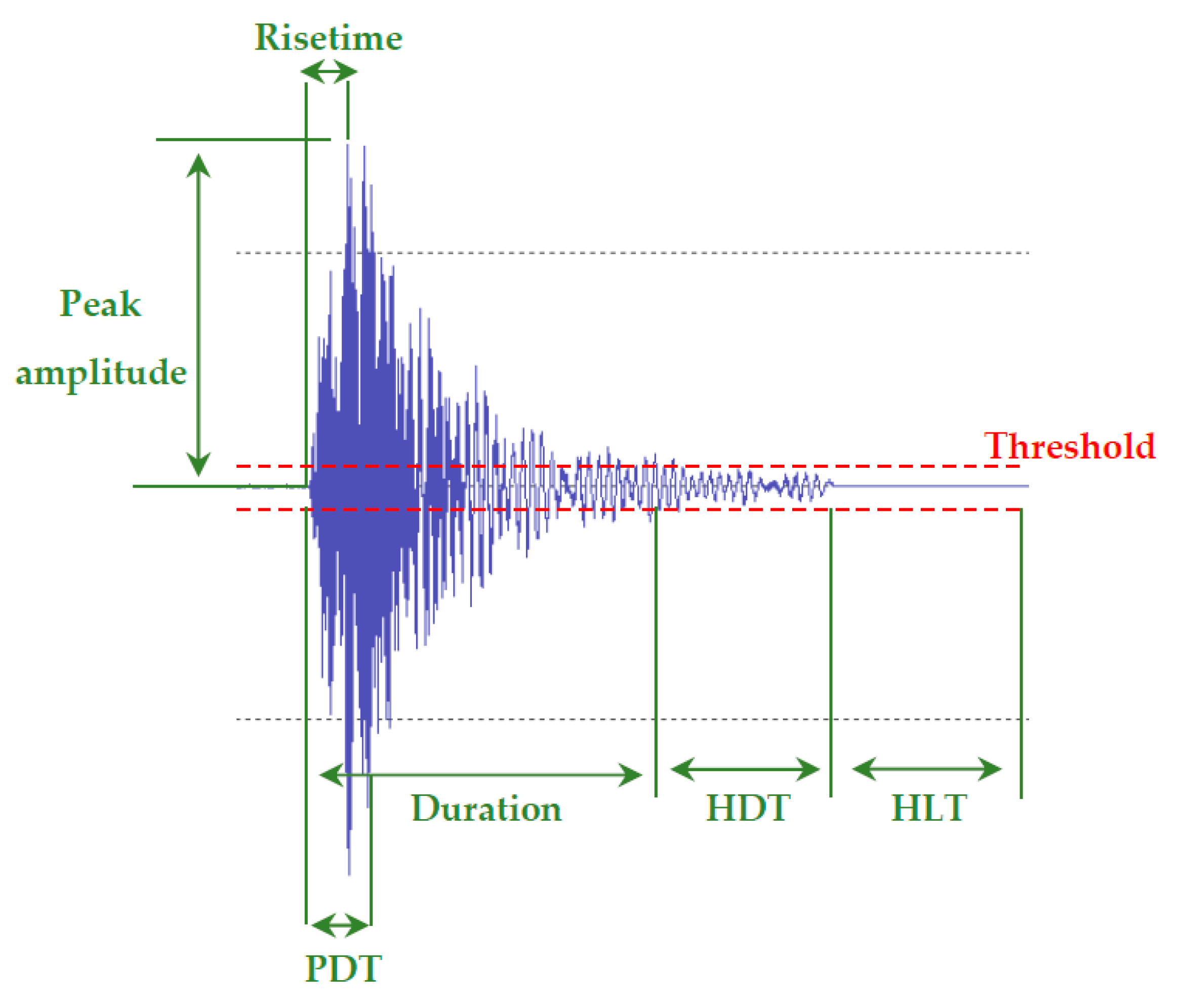
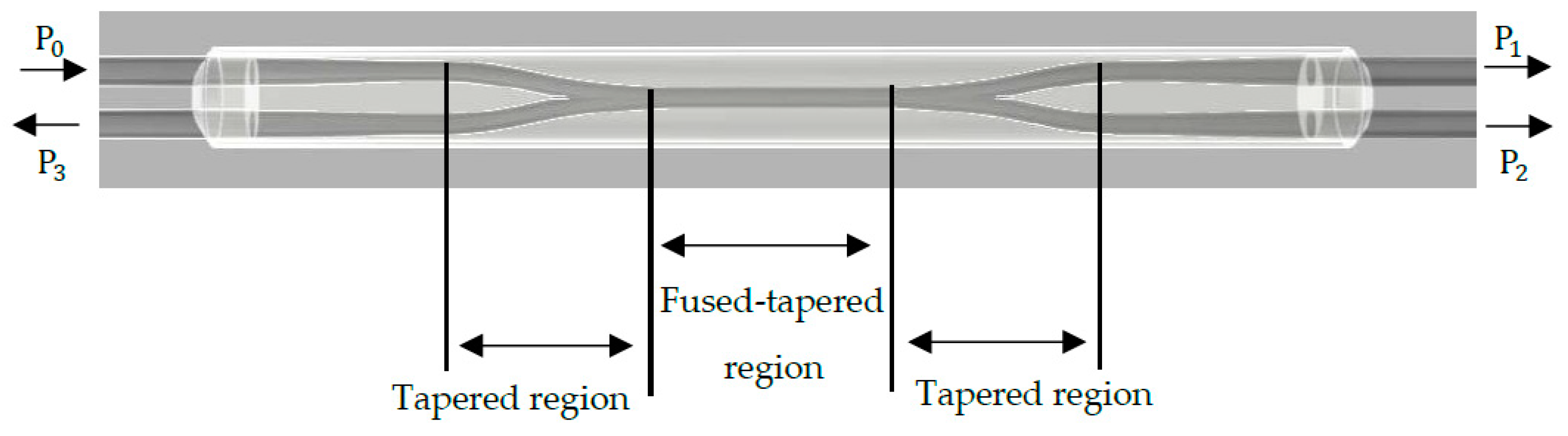
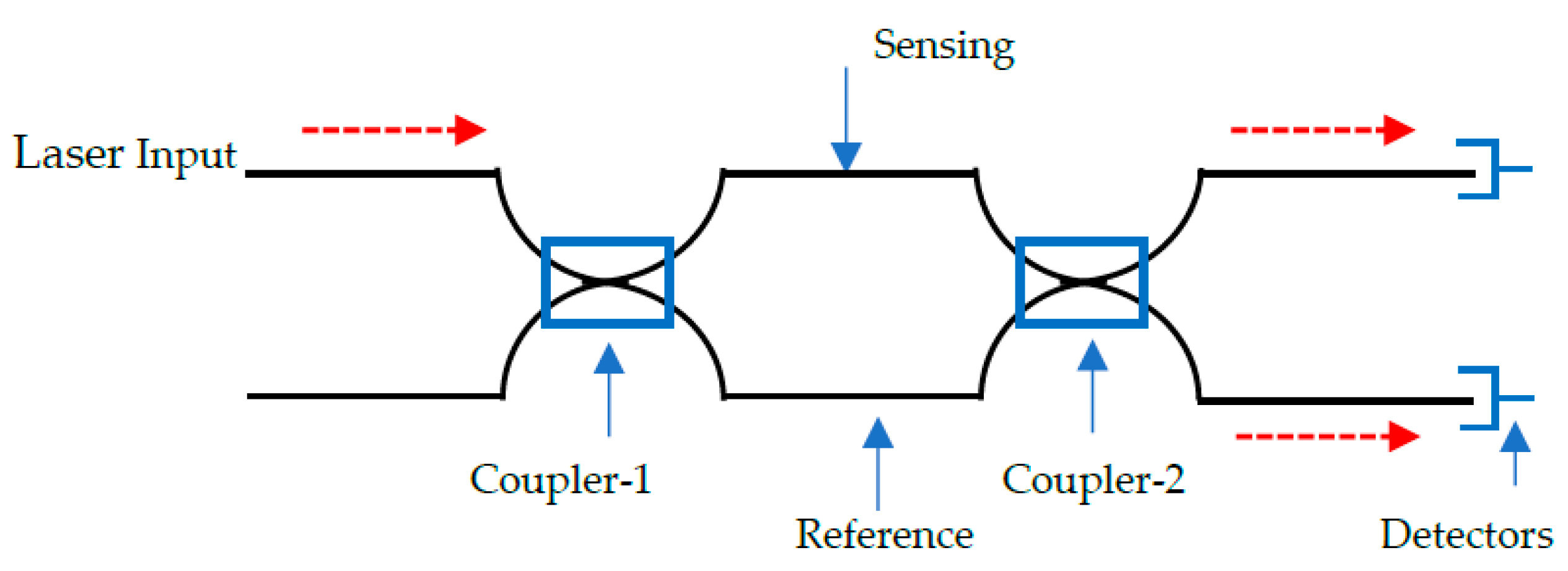

| Sensor | Monitoring Methods and Techniques | Typical Uses |
|---|---|---|
| Fused Tapered Coupler | Merging of two optical fibres via etching, polishing or fibre fusion. An AE stress wave interacts with the fibres causing a change in the effective strain field, thus altering the coupling ratio output of the two fibres. | Acoustic emission, temperature, refractive index |
| Mach-Zehnder interferometer | A beam splitter separates incoming light into two components to a sensing and reference fibre. The sensing fibre is usually coated with a material that is sensitive to the parameter of interest. The phase of the light propagating through the sensing fibre alters with the influence of an external parameter. | Acoustic emission, strain, refractive index, temperature, pressure, displacement |
| Michelson interferometer | Like the Mach-Zehnder interferometer, a beam splitter separates incoming light into two components. The sensitivity of the interferometer can be dependent on the length of the exposed fibre. | Acoustic emission, strain, refractive index, temperature, pressure, displacement |
| Fabry-Perot interferometer | Insertion of two cleaved fibres into a capillary housing. Analysis of the transmitted and reflected waves between the two fibre-ends creates a multiple peak wavelength trace on an optical spectrum analyser. | Acoustic emission, strain, refractive index |
| Fibre Bragg grating | Manufactured by inscribing a grating into the fibre core with a high-powered UV laser. The reflection of a low-power laser captured by an optical spectrum analyser determines the wavelength peak from the grating. | Acoustic emission, strain, temperature, displacement, and pressure |
| Strengths | Weaknesses | Opportunities | Threats |
|---|---|---|---|
| Inherent small size and versatility | Reproducibility difficulties during manufacture | Multiplexing of different sensors attached to one fibre | Piezoelectric sensors offer established and reliable sensing systems |
| Reduced weight | Limited durability when mounting | Available development of automated fabrication process | Limited automated manufacturing available |
| Immunity to electromagnetic interference | Lower tensile and compressive strength compared with piezoelectric AE sensors | Remote condition monitoring | Some FOS configurations cease to operate in the presence of static strain |
| Higher operational temperature than piezoelectric sensors | The material cost can often exceed that of some piezoelectric sensors in the long term | Compatibility with telemetry and optical communications | Multiple-use piezoelectric sensors are often preferred over single-use FOAES |
| Can be embedded into composite structures | High sensitivity limited to along the fibre sensor axis | Collaboration with multiple industries available including aerospace, rail, energy and marine | The increased contact area of piezoelectric sensors to the substrate generally offer increased SNR |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Willberry, J.O.; Papaelias, M.; Franklyn Fernando, G. Structural Health Monitoring Using Fibre Optic Acoustic Emission Sensors. Sensors 2020, 20, 6369. https://doi.org/10.3390/s20216369
Willberry JO, Papaelias M, Franklyn Fernando G. Structural Health Monitoring Using Fibre Optic Acoustic Emission Sensors. Sensors. 2020; 20(21):6369. https://doi.org/10.3390/s20216369
Chicago/Turabian StyleWillberry, James Owen, Mayorkinos Papaelias, and Gerard Franklyn Fernando. 2020. "Structural Health Monitoring Using Fibre Optic Acoustic Emission Sensors" Sensors 20, no. 21: 6369. https://doi.org/10.3390/s20216369
APA StyleWillberry, J. O., Papaelias, M., & Franklyn Fernando, G. (2020). Structural Health Monitoring Using Fibre Optic Acoustic Emission Sensors. Sensors, 20(21), 6369. https://doi.org/10.3390/s20216369






