Powered Two-Wheeler Riding Profile Clustering for an In-Depth Study of Bend-Taking Practices
Abstract
1. Introduction
- We propose an easy-to-use methodology for providing data analysis tools to road safety researchers to help them in their study of the motorcyclists’ behavior during bend negotiation maneuver.
- We successfully apply the proposed framework to a real dataset of sensor data collected during experimentation that involves eight subjects with different profiles.
- We present a multi-sensors architecture to capture the rider’s actions during the bend taking maneuver, and we analyze with a certain level of detail the collected data, which makes this manuscript a valuable reference for practitioners interested in such topic of research.
2. Experimental Protocol: Data Collection And Description
2.1. Experimental Protocol
2.2. Data Collection
2.3. Data Representation
3. Clustering Methodology
3.1. Dimensionality Reduction Using the Piecewise Aggregate Approximation (PAA) Algorithm
3.2. Homogeneity Study for the Three Attempts of Each Instruction Using the Anderson–Darling Test
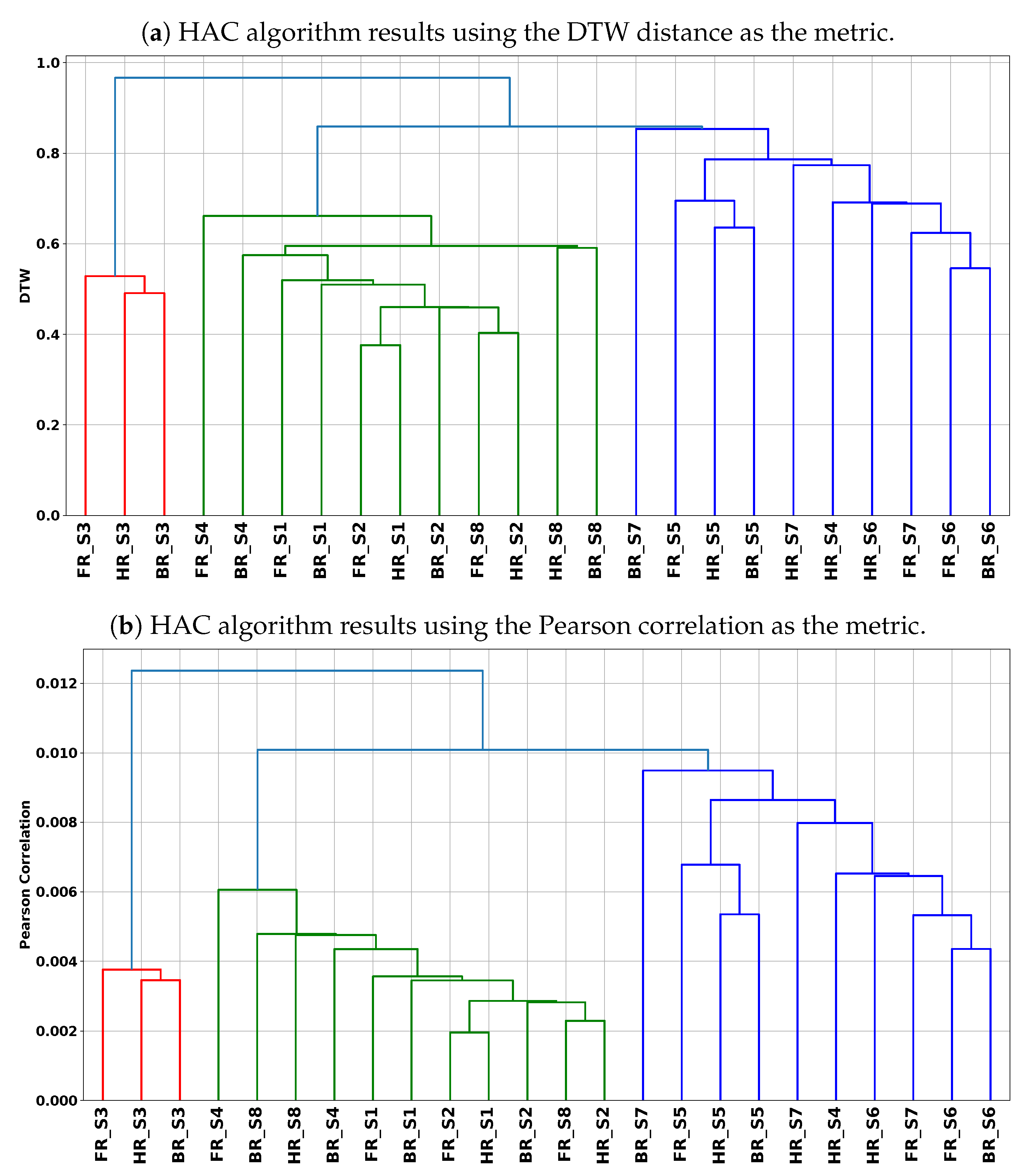
3.3. Clustering of Subjects Using Hierarchical Agglomerative Clustering (HAC)
| Algorithm 1 The hierarchical agglomerative clustering (HAC) algorithm applied on the data matrix. |
| Require: data matrix. |
| 1: Calculate the similarity: using the Pearson correlation and DTW metrics between each row pair of the data matrix . |
| 2: Compute the proximity matrix. |
| 3: Merge the closest clusters according to the proximity matrix. |
| 4: Update the proximity between new and original clusters. |
| 5: Repeat steps 3 and 4 until a single cluster is obtained. |
4. Results and Discussion
4.1. Clusters Analysis
- Cluster 1 analysis: This cluster is essentially composed of three riding instructions of subject S3. An in-depth analysis of the dendrograms shows that in this cluster, the similarity is more observed between HR and BR instructions. Therefore, subject S3 has difficulty in differentiating between HR and BR instructions. Thus, for this subject, contradictions can be observed in terms of his riding preference (BR) and compliance with the HR and BR instructions.
- Cluster 2 analysis: Subjects S2, S4, and S8 have their riding instructions in this cluster, whereas subject S4 has only FR and BR instructions. Therefore, subjects S2, S4, and S8 did not respect the HR and BR riding instructions. Subject S4, who declared a preference for BR instruction, is consistent with his declaration of preference while respecting the riding instructions.
- Cluster 3 analysis: For the same reasons mentioned in the analysis of Cluster 2, subjects S5, S6, and S7 did not respect the HR and BR riding instructions. Subject S4, who has his HR instruction in this cluster, appears to respect this riding instruction.
4.2. Interpretation of the Clustering Results
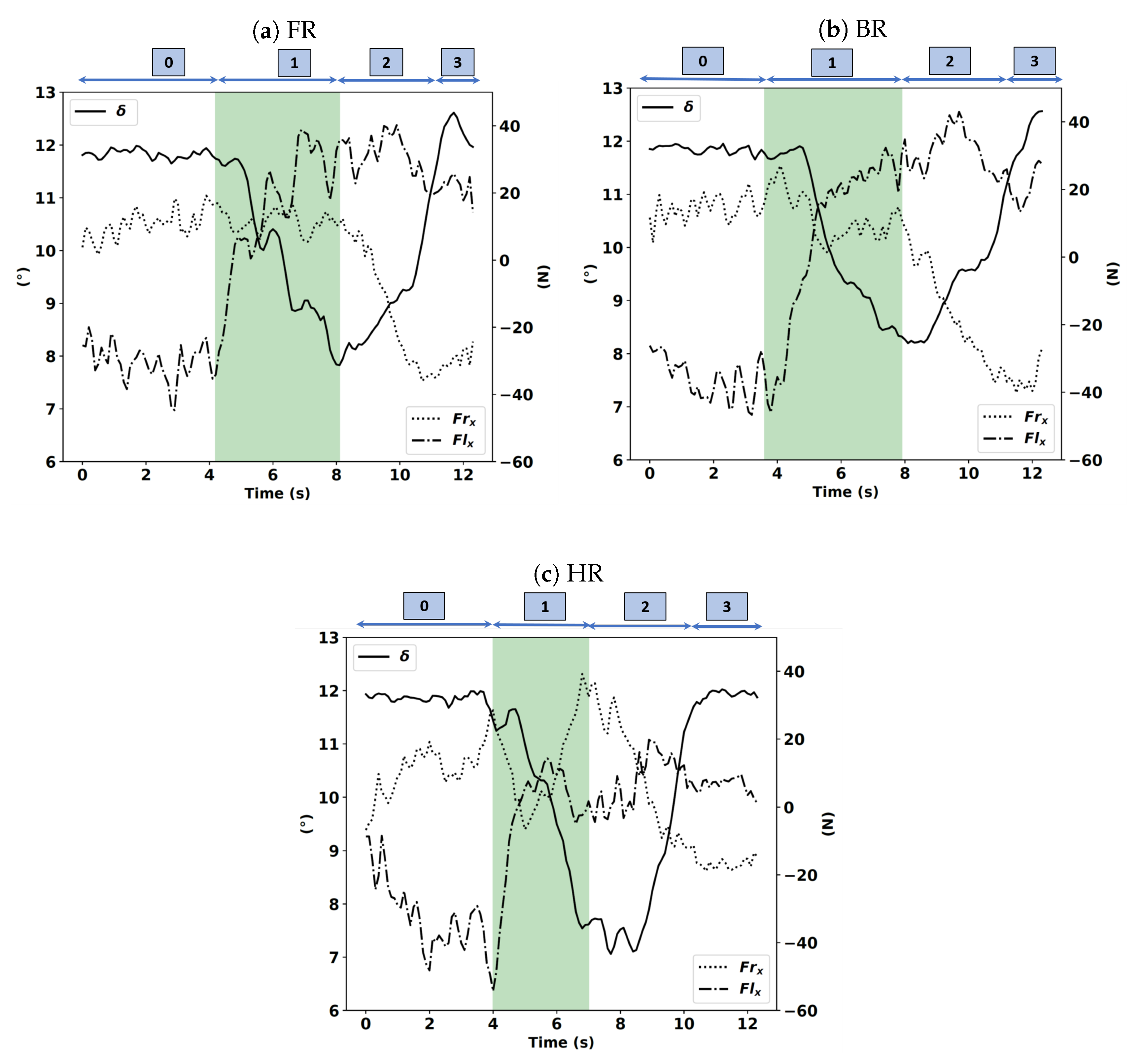
5. In-Depth Analysis of the Behavior of Subject S4
- Phase 0 corresponds to when the rider travels in a straight line before entering the curve.
- Phase 1 corresponds to the time when the rider initiates the curve and reaches the middle of the curve. In the following figures, the time interval corresponding to phase 1 is represented by a shaded area.
- Phase 2 corresponds to the elapsed time from the moment that the rider reaches the middle of the curve and that when he/she exits the turn.
- Phase 3 corresponds to when the rider is traveling in a straight line after exiting the curve.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- 2018 Road Safety Annual Report. 2019. Available online: https://www.onisr.securite-routiere.gouv.fr/en/road-safety-performance/annual-road-safety-reports/2018-road-safety-annual-report (accessed on 22 November 2020).
- Popov, A.; Rowell, S.; Meijaard, J. A review on motorcycle and rider modelling for steering control. Veh. Syst. Dyn. 2010, 48, 775–792. [Google Scholar]
- Kooijman, J.; Schwab, A. A review on bicycle and motorcycle rider control with a perspective on handling qualities. Veh. Syst. Dyn. 2013, 51, 1722–1764. [Google Scholar]
- Rice, R.S. Rider Skill Influences on Motorcycle Maneuvering. In SAE Technical Paper; SAE International: Detroit, MI, USA, 1978. [Google Scholar]
- Bocciolone, M.; Cheli, F.; Leo, E.; Pezzola, M. Experimental identification of kinematic coupled effects between driver–motorcycle. In Proceedings of the IMAC–XXV: A Conference & Exposition on Structural Dynamics, Orlando, FL, USA, 19–22 February 2007; pp. 19–22. [Google Scholar]
- Evertse, M.V.C. Rider Analysis Using a Fully Instrumented Motorcycle. Master’s Thesis, Faculty of Aerospace Engineering-Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Loiseau, P.; Boultifat, C.N.E.; Chevrel, P.; Claveau, F.; Espie, S.; Mars, F. Rider model identification using dynamic neural networks. In Proceedings of the IFAC World Congress, Berlin, Germany, 11–17 July 2020. [Google Scholar]
- Loiseau, P.; Boultifat, C.N.E.; Chevrel, P.; Claveau, F.; Espie, S.; Mars, F. Rider model identification: Neural networks and quasi-LPV models. IET Intell. Transp. Syst. 2020, 14, 1259–1264. [Google Scholar]
- Spiegel, B. The Upper Half of the Motorcycle: On the Unity of Rider and Machine; Meredith, H., Translator; Whitehorse Press: Center Conway, NH, USA, 2010. [Google Scholar]
- Kalsoom, R.; Halim, Z. Clustering the driving features based on data streams. In Proceedings of the INMIC, Lahore, Parkistan, 19–20 December 2013; pp. 89–94. [Google Scholar] [CrossRef]
- Higgs, B.; Abbas, M. A two-step segmentation algorithm for behavioral clustering of naturalistic driving styles. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 857–862. [Google Scholar]
- Wu, C.; Sun, C.; Chu, D.; Huang, Z.; Ma, J.; Li, H. Clustering of Several Typical Behavioral Characteristics of Commercial Vehicle Drivers Based on GPS Data Mining: Case Study of Highways in China. Transp. Res. Rec. 2016, 2581, 154–163. [Google Scholar]
- Xu, J.; Luo, X.; Shao, Y.M. Vehicle trajectory at curved sections of two-lane mountain roads: A field study under natural driving conditions. ETRR 2018, 10, 12. [Google Scholar]
- Zardosht, M.; Beauchemin, S.; Bauer, M. Identifying Driver Behavior in Preturning Maneuvers Using In-Vehicle CANbus Signals. J. Adv. Transp. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Crundall, E.; Crundall, D.; Stedmon, A. Negotiating Left-Hand and Right-Hand Bends: A Motorcycle Simulator Study to Investigate Experiential and Behaviour Differences Across Rider Groups. PLoS ONE 2012, 7, e29978. [Google Scholar] [CrossRef]
- Lobjois, R.; Mars, F. Effects of motorcycle simulator configurations on steering control and gaze behavior in bends. J. Exp. Psychol. Appl. 2019. [Google Scholar] [CrossRef]
- Smaiah, S.; Sadoun, R.; Elouardi, A.; Larnaudie, B.; Bouaziz, S.; Boubezoul, A.; Vincke, B.; Espié, S. A Practical Approach for High Precision Reconstruction of a Motorcycle Trajectory Using a Low-Cost Multi-Sensor System. Sensors 2018, 18, 2282. [Google Scholar] [CrossRef]
- Available online: https://www.sick.com/fr/fr/capteurs-de-distance/capteurs-de-distance-a-moyenne-portee/dx35/dt35-b15251/p/p295353 (accessed on 22 November 2020).
- Available online: https://ams.com/AS5047P (accessed on 22 November 2020).
- Available online: https://www.xsens.com/products/mti-100-series (accessed on 22 November 2020).
- Available online: https://www.mesurex.fr/en/ (accessed on 22 November 2020).
- Available online: https://www.xsensor.com/body-pressure-sensors (accessed on 22 November 2020).
- Available online: https://www.teaergo.com/products/tea-captiv-t-sens-motion-imu/ (accessed on 22 November 2020).
- Available online: https://www.septentrio.com/en/products/gnss-receivers/rover-base-receivers/smart-antennas/aps3g (accessed on 22 November 2020).
- Lemonakis, P.V.; Eliou, N.E.; Karakasidis, T.; Botzoris, G. A new methodology for approaching motorcycle riders’ behavior at curved road sections. Eur. Transp. Res. Rev. 2014, 6, 303–314. [Google Scholar]
- Nayak, A.; Murigendrappa, S.; Suresh, A. Stability enhancement of a powered two wheeler vehicle under curve negotiation. Veh. Syst. Dyn. 2016, 7, 85–95. [Google Scholar]
- Keogh, E.; Chakrabarti, K.; Pazzani, M.; Mehrotra, S. Dimensionality Reduction for Fast Similarity Search in Large Time Series Databases. Knowl. Inf. Syst. 2002, 3. [Google Scholar] [CrossRef]
- Senin, P.; Lin, J.; Wang, X.; Oates, T.; Gandhi, S.; Boedihardjo, A.P.; Chen, C.; Frankenstein, S. GrammarViz 3.0: Interactive Discovery of Variable-Length Time Series Patterns. ACM Trans. Knowl. Discov. Data 2018, 12, 10:1–10:28. [Google Scholar] [CrossRef]
- Massey, F.J.M., Jr. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar]
- Scholz, F.W.; Stephens, M.A. K-Sample Anderson–Darling Tests. J. Am. Stat. Assoc. 1987, 82, 918–924. [Google Scholar]
- Mohd Razali, N.; Yap, B. Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling Tests. J. Stat. Model. Analytics 2011, 2, 21–33. [Google Scholar]
- Engmann, S.; Cousineau, D. Comparing distributions: The two-sample Anderson–Darling test as an alternative to the Kolmogorov–Smirnov test. J. Appl. Quant. Methods 2011, 6, 1–17. [Google Scholar]
- Zhang, Z.; Murtagh, F.; Van Poucke, S.; Lin, S.; Lan, P. Hierarchical cluster analysis in clinical research with heterogeneous study population: Highlighting its visualization with R. Ann. Transl. Med. 2017, 5, 75. [Google Scholar] [CrossRef]
- Freedman, D.; Pisani, R.; Purves, R. Purves, 4th ed.; Statistics (international student edition); Pisani, R., Ed.; WW Norton & Company: New York, NY, USA, 2007. [Google Scholar]
- Senin, P. Dynamic time warping algorithm review. Inf. Comput. Sci. Dep. Univ. Hawaii Manoa Honolulu USA 2008, 855, 40. [Google Scholar]
- Weakliem, D.L. A Critique of the Bayesian Information Criterion for Model Selection. Sociol. Methods Res. 1999, 27, 359–397. [Google Scholar]
- Zambelli, A. A Data-Driven Approach to Estimating the Number of Clusters in Hierarchical Clustering. F1000Research 2016, 5. [Google Scholar] [CrossRef]
- Cossalter, V.; Doria, A.; Lot, R. Steady turning of two-wheeled vehicles. Veh. Syst. Dyn. 1999, 31, 157–181. [Google Scholar]
- Chamroukhi, F.; Samé, A.; Govaert, G.; Aknin, P. Time series modeling by a regression approach based on a latent process. Neural Netw. 2009, 22, 593–602. [Google Scholar] [PubMed]
- Chamroukhi, F.; Trabelsi, D.; Mohammed, S.; Oukhellou, L.; Amirat, Y. Joint segmentation of multivariate time series with hidden process regression for human activity recognition. Neurocomputing 2013, 120, 633–644. [Google Scholar]













| PTW Dynamic Measurements | ||||
|---|---|---|---|---|
| Sensor | Measurement | Symbol | Description | |
| 1 | Two Hall effect sensors | Wheel Speed | v | Velocity along the longitudinal axis |
| 2 | SICK DT35 Laser [18] | Roll angle measurement | Two laser sensors are placed on both sides (right and left) of the motorbike to measure the roll angle of the motorcycle | |
| 3 | Magnetic sensor AS5047P of AMS [19] | Steering angle | To acquire the handlebar steering angle | |
| 4 | MTi Xsens [20] | Three-dimensional (accelerometers, magnetometers, and gyroscopes) | − | To acquire inertial movements: longitudinal, lateral, vertical accelerations, and rotational velocities and angles (pitch, yaw, and roll) |
| Rider Action Measurements | ||||
| 5 | Strain gauges [21] | Applied forces on the handlebar | FrX and FlX | Strain gauges are placed on the half-handlebars (right and left) of the motorbike to measure the forces applied by the rider on each half-handlebar (right and left) |
| 6 | Mesurex D2 piezoelectric force button [21] | Applied forces on the foot-pegs | and | Strain gauges are placed on the (right and left) foot-pegs of the motorbike to measure the forces applied by the rider on each foot-peg |
| 7 | XSENSOR LX100 and PX100 pressure matrix pads [22] | Left and right pressure of the buttock | LbP and RbP | To acquire pressure forces of the rider’s buttocks |
| Rider Motion Measurements | ||||
| 8 | Tea Ergo CAPTIV Motion IMU [23] | Roll angle measurement | LbRa | To measure a lower-body roll angle |
| 9 | Tea Ergo CAPTIV Motion IMU [23] | Roll angle measurement. | HbRa | To measure a higher-body roll angle. |
| 10 | Tea Ergo CAPTIV Motion IMU [23] | Roll angle measurement | To Mmeasure a head roll angle. | |
| Context Information | ||||
| 11 | RTK-GPS Septentrio Altus APS3G [24] | Latitude and longitude positions | GPS | To acquire a precise real-time kinematic positioning of the motorcycle. |
| 12 | Video camera | Context videos | − | Action camera on the top case, looking to the front (field of view including the back of the rider). |
| Subjects | LA | km | Preference | Instruction Order |
|---|---|---|---|---|
| S1 | 2 | 8000 | handlebar | FR, HR, BR |
| S2 | 7 | 3000 | handlebar | FR, BR, HR |
| S3 | 0 | 0 | body | FR, HR, BR |
| S4 | 11 | 0 | body | FR, HR, BR |
| S5 | 2 | 20,000 | handlebar | FR, BR, HR |
| S6 | 16 | 0 | handlebar | FR, HR, BR |
| S7 | 18 | 2000 | handlebar | FR, BR, HR |
| S8 | 12 | 3000 | handlebar | FR, HR, BR |
| Subjects | v | an | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FR | HR | BR | FR | HR | BR | FR | HR | BR | FR | HR | BR | FR | HR | BR | |
| S1 | 0.69 | 0.51 | 0.96 | 0.99 | 0.99 | 0.91 | 0.99 | 0.99 | 0.99 | 0.70 | 0.30 | 0.74 | 0.99 | 0.99 | 0.99 |
| S2 | 0.97 | 0.90 | 0.95 | 0.99 | 0.99 | 0.99 | 0.99 | 1 | 1 | 0.24 | 0.87 | 0.99 | 1 | 1 | 0.99 |
| S3 | 0.96 | 0.66 | 0.70 | 0.99 | 0.99 | 0.99 | 1 | 0.99 | 0.99 | 0.84 | 0.90 | 0.92 | 1 | 0.99 | 0.99 |
| S4 | 0.99 | 0.98 | 0.99 | 01 | 0.99 | 0.91 | 0.99 | 1 | 0.99 | 0.85 | 0.94 | 0.99 | 0.99 | 0.99 | 0.99 |
| S5 | 0.74 | 0.92 | 0.99 | 0.90 | 0.99 | 0.99 | 1 | 0.99 | 0.99 | 0.76 | 0.92 | 0.77 | 1 | 0.99 | 1 |
| S6 | 0.55 | 0.74 | 0.81 | 0.88 | 0.99 | 0.99 | 0.99 | 0.99 | 1 | 0.99 | 0.64 | 0.98 | 0.99 | 0.99 | 1 |
| S7 | 0.99 | 0.97 | 0.92 | 0.99 | 0.99 | 0.99 | 1 | 01 | 0.99 | 0.96 | 0.85 | 0.88 | 0.99 | 0 1 | 0.99 |
| S8 | 0.95 | 0.98 | 0.90 | 0.99 | 0.94 | 0.99 | 1 | 0.99 | 0.99 | 0.48 | 0.26 | 0.99 | 0.99 | 0.99 | 0.93 |
| Clusters | Metrics | |
|---|---|---|
| DTW | Pearson Correlation | |
| Cluster 1 (Red) | S3 (FR, HR, BR) | S3 (FR, HR, BR) |
| Cluster 2 (Green) | S1 (FR, HR, BR) | S1 (FR, HR, BR) |
| S2 (FR, HR, BR) | S2 (FR, HR, BR) | |
| S4 (FR, BR) | S4 (FR, BR) | |
| S8 (FR, HR, BR) | S8 (FR, HR, BR) | |
| Cluster 3 (Blue) | S4 (HR) | S4 (HR) |
| S5 (FR, HR, BR) | S5 (FR, HR, BR) | |
| S6 (FR, HR, BR) | S6 (FR, HR, BR) | |
| S7 (FR, HR, BR) | S7 (FR, HR, BR) | |
| Riding Variables | p-Value |
|---|---|
| Handlebar steering angle | 0.001 |
| Velocity | 0.25 |
| Normal acceleration | 0.25 |
| Jerk | 0.25 |
| Curvature | 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diop, M.; Boubezoul, A.; Oukhellou, L.; Espié, S. Powered Two-Wheeler Riding Profile Clustering for an In-Depth Study of Bend-Taking Practices. Sensors 2020, 20, 6696. https://doi.org/10.3390/s20226696
Diop M, Boubezoul A, Oukhellou L, Espié S. Powered Two-Wheeler Riding Profile Clustering for an In-Depth Study of Bend-Taking Practices. Sensors. 2020; 20(22):6696. https://doi.org/10.3390/s20226696
Chicago/Turabian StyleDiop, Mohamed, Abderrahmane Boubezoul, Latifa Oukhellou, and Stéphane Espié. 2020. "Powered Two-Wheeler Riding Profile Clustering for an In-Depth Study of Bend-Taking Practices" Sensors 20, no. 22: 6696. https://doi.org/10.3390/s20226696
APA StyleDiop, M., Boubezoul, A., Oukhellou, L., & Espié, S. (2020). Powered Two-Wheeler Riding Profile Clustering for an In-Depth Study of Bend-Taking Practices. Sensors, 20(22), 6696. https://doi.org/10.3390/s20226696






