Statistical Distribution Analysis of Navigation Positioning System Errors—Issue of the Empirical Sample Size
Abstract
:1. Introduction
- The iterative method used to determine coordinates, where the next position is calculated from the previous one.
- Widespread use of Kalman filtering in positioning system receivers for filtering out movement (course and speed) parameters.
- Normally navigation positioning system errors are correlated over time.
- To develop a method for calculating the length of a representative sample of any positioning system, the results of which would be considered to be close to the actual accuracy values of the positioning system.
- To propose a method for assessing the consistency of navigation system position errors with theoretical statistical distributions (normal distribution), based on empirical measurement data, which will ensure high reliability assessment with a high statistical test power.
2. Materials and Methods
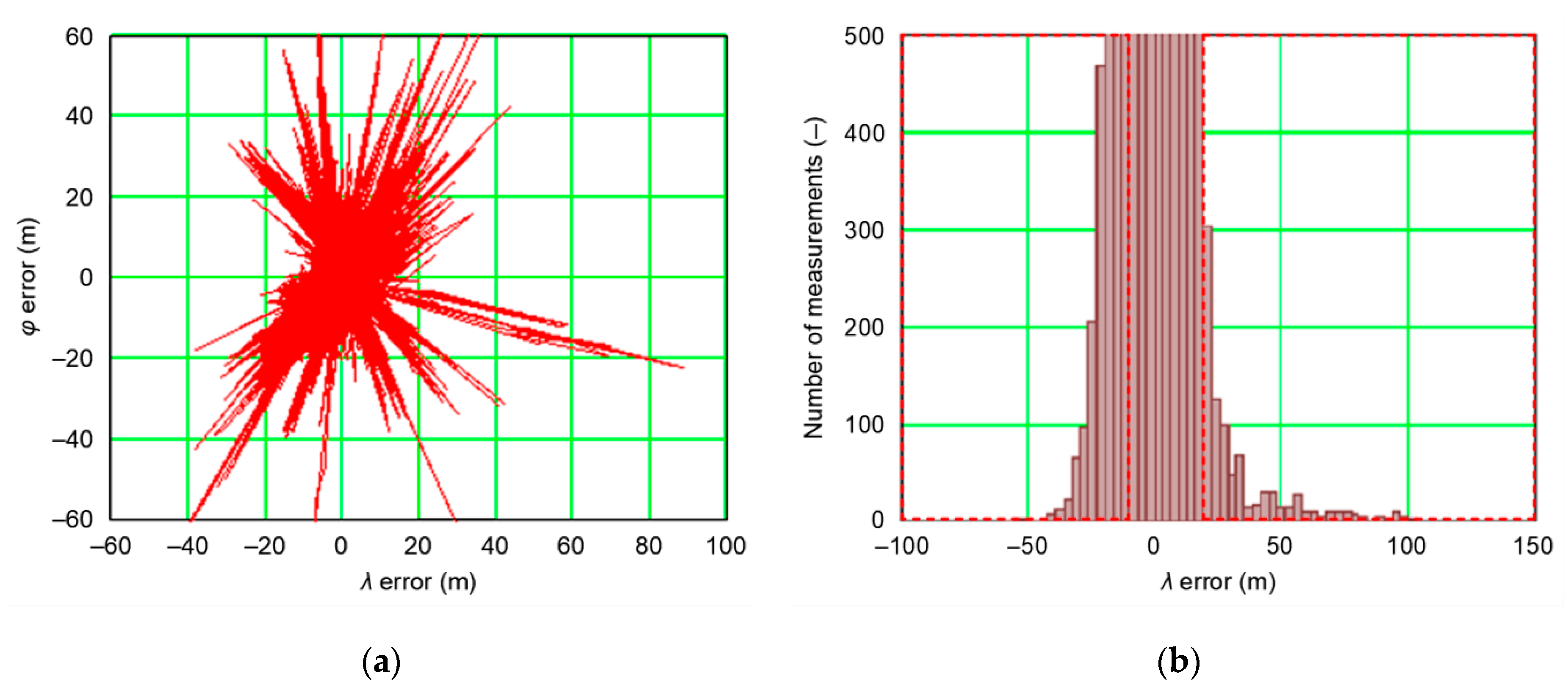
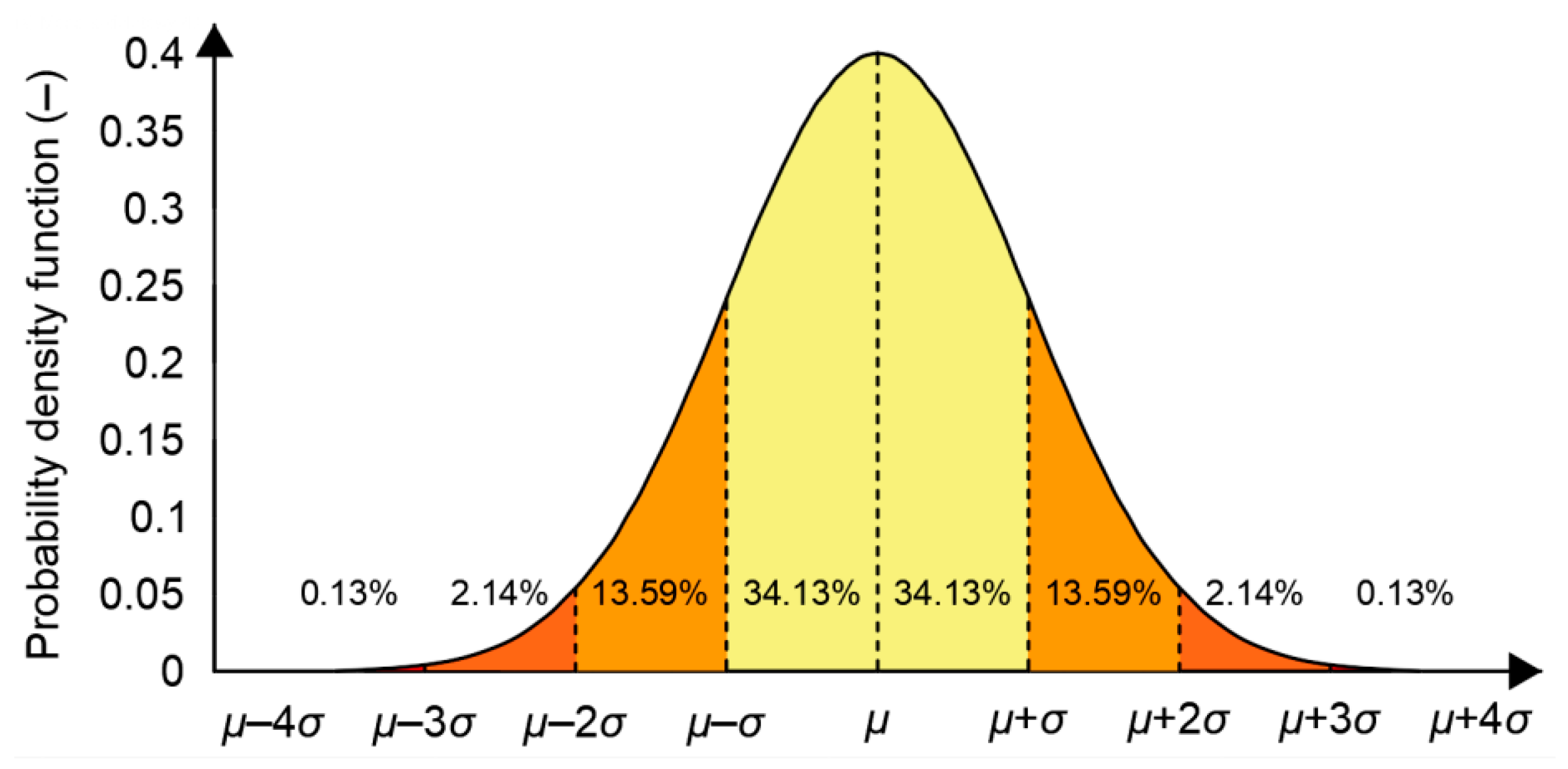
2.1. Normal Distribution in Positioning
- To correctly determine the accuracy of position determination (described by RMS and 2DRMS measures) using the navigation system, can any number of measurements be taken, followed by determination of the standard deviation and the mean values of φ and λ (which are most often assumed to be real), or is there any minimum number of measurements (referred to in statistics as representative sample) that is necessary to ensure that its RMS and mean values of φ and λ are identical or very close to the true accuracy of the positioning system?
- Do the statistical distributions of empirical φ and λ errors of the positioning system conform with the normal distribution for any sample size (100, 1000, or 10′000 measurements, etc.)?
- Are the answers to questions 1 and 2 different depending on the type of positioning system (GPS, GLONASS (GLObal NAvigation Satellite System), DGPS, EGNOS, etc.)?
- Are there any special statistical features of the distributions of navigation system position errors that distinguish them from other, typical studies of empirical distributions in technical or other sciences?
2.2. Statistical Testing of the Empirical Distribution of Position Errors
- Tests based on the chi-square goodness of fit test: Pearson’s chi-squared test [32].
- H0—the empirical distribution of φ or λ errors of the X positioning system fits the normal distribution.
- H1—the empirical distribution of φ or λ errors of the X positioning system does not fit the normal distribution.
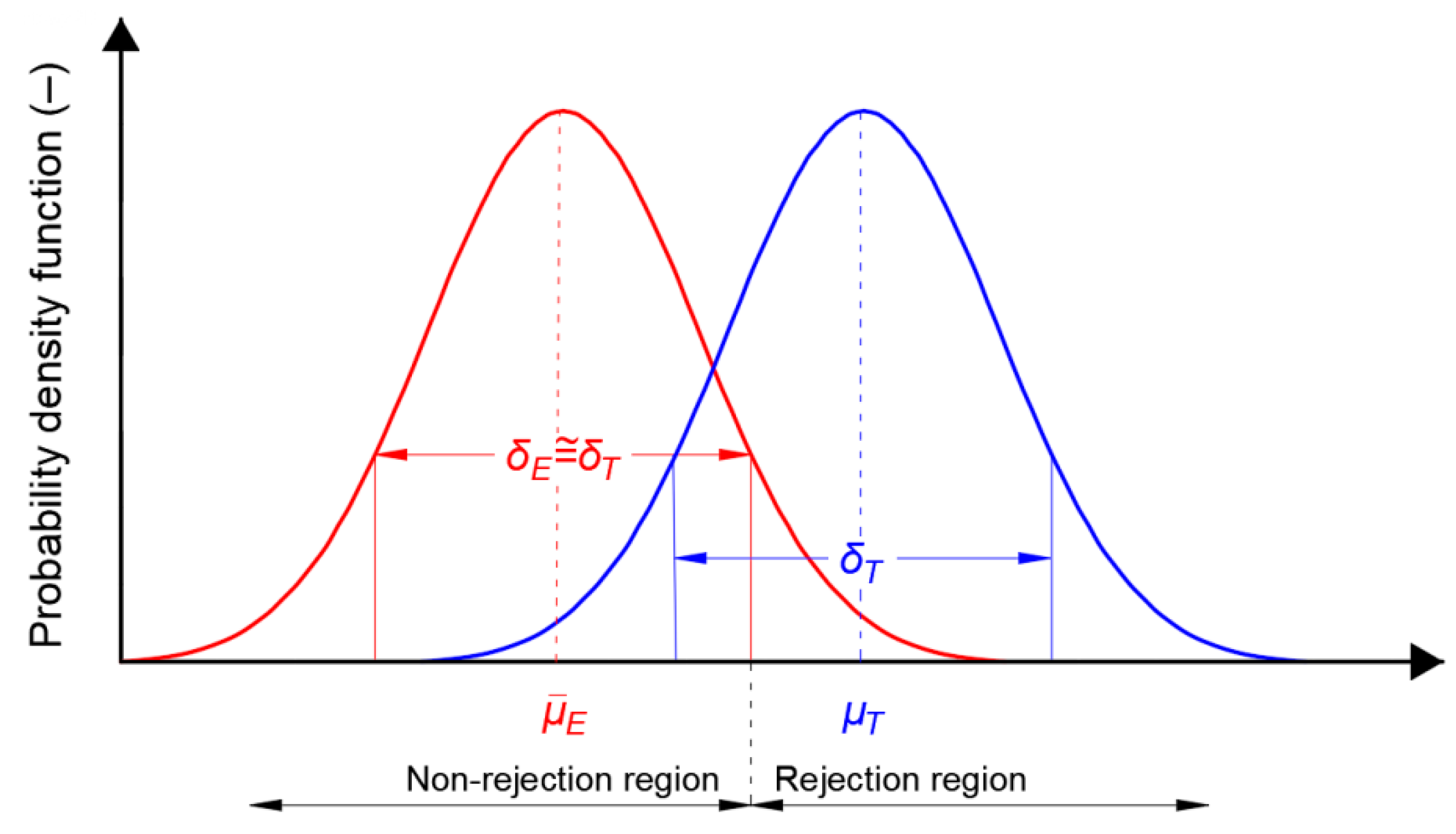
2.3. Effect Size as a Function of Measurement Errors
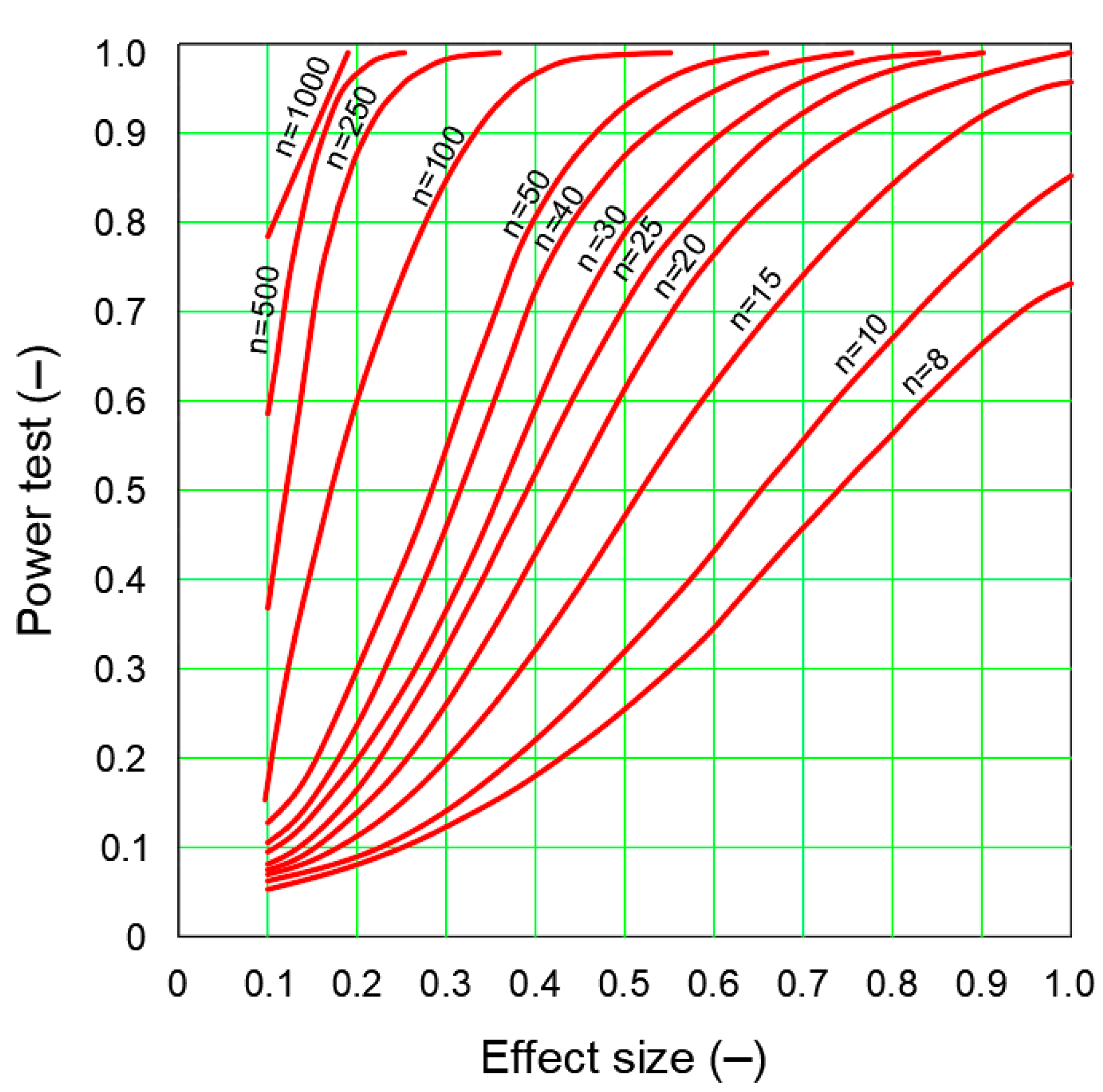
2.4. Power Test and Sample Size
- Actual effect size against the background of random variation in the population.
- Assumed significance level α (usually 0.05).
- Sample size n used in the test.
3. Results
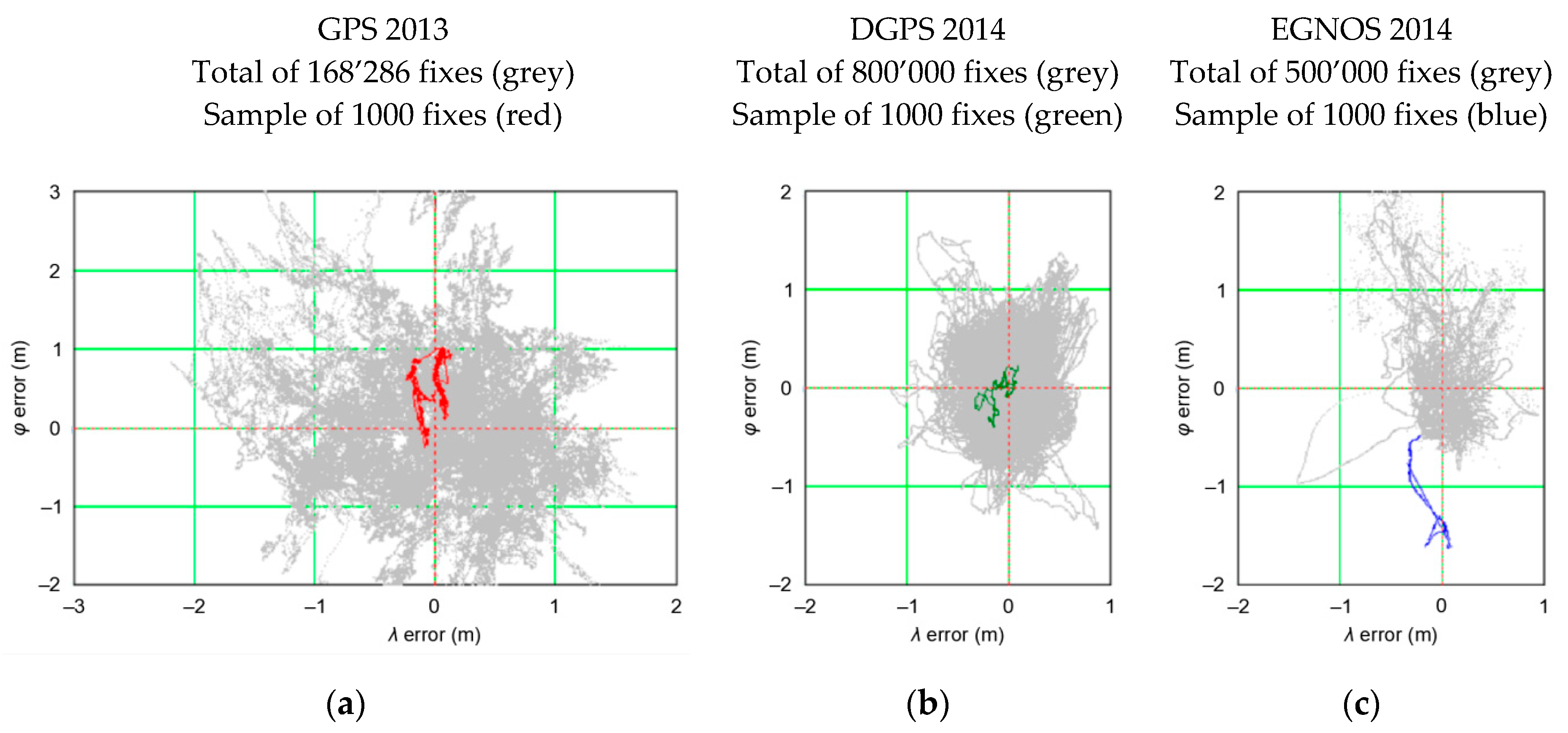
3.1. Position Random Walk Analysis
- How fast (in terms of changes in coordinates between successive measurements) is the PRW process?
- Does the Position Random Walk process depend on the nominal (typical) navigation system position error?
- — calculated from empirical GPS data for the session S number N, for N = 1, 2, 3, 4, 5. Each session consists of 1000 measurements. The session is part of the entire campaign of 168′286 measurements.
- μT(φGPS)—nominal (assumed to be real) value of φ of the measuring receiver typical for the GPS system. In the analyses, it is determined as an arithmetic mean of φ from empirical measurements from a very long measurement campaign. Its results should be very close to the real values, so they were considered to be true (reference) for the GPS system.
- — calculated from empirical GPS data for the session S number N, for N = 1, 2, 3, 4, 5. Each session consists of 1000 measurements. The session is part of the entire campaign of 168′286 measurements.
- μT(λGPS)—nominal (assumed to be real) value of λ of the measuring receiver typical for the GPS system. In the analyses, it is determined as an arithmetic mean of λ from empirical measurements from a very long measurement campaign. Its results should be very close to the real values, so they were considered to be true (reference) for the GPS system.
- —mean 2D position calculated from empirical GPS data for the session S number N, for N = 1,2,3,4,5, with the following values: and Each session consists of 1000 measurements. The session is part of the entire campaign of 168′286 measurements.
- δE(φGPS,SN)—RMS with respect to calculated from empirical GPS data for the session S number N, for N = 1, 2, 3, 4, 5.
- δT(φGPS)—nominal (assumed to be real) value of RMS with respect to . It was calculated based on GPS empirical data from a very long measurement campaign (168′286 measurements) and was therefore considered true (reference) for the GPS system.
- δE(λGPS,SN)—RMS with respect to calculated from empirical GPS data for the session S number N, for N = 1, 2, 3, 4, 5.
- δT(λGPS)—nominal (assumed to be real) value of RMS with respect to . It was calculated based on GPS empirical data from a very long measurement campaign (168′286 measurements) and was therefore considered true (reference) for the GPS system.
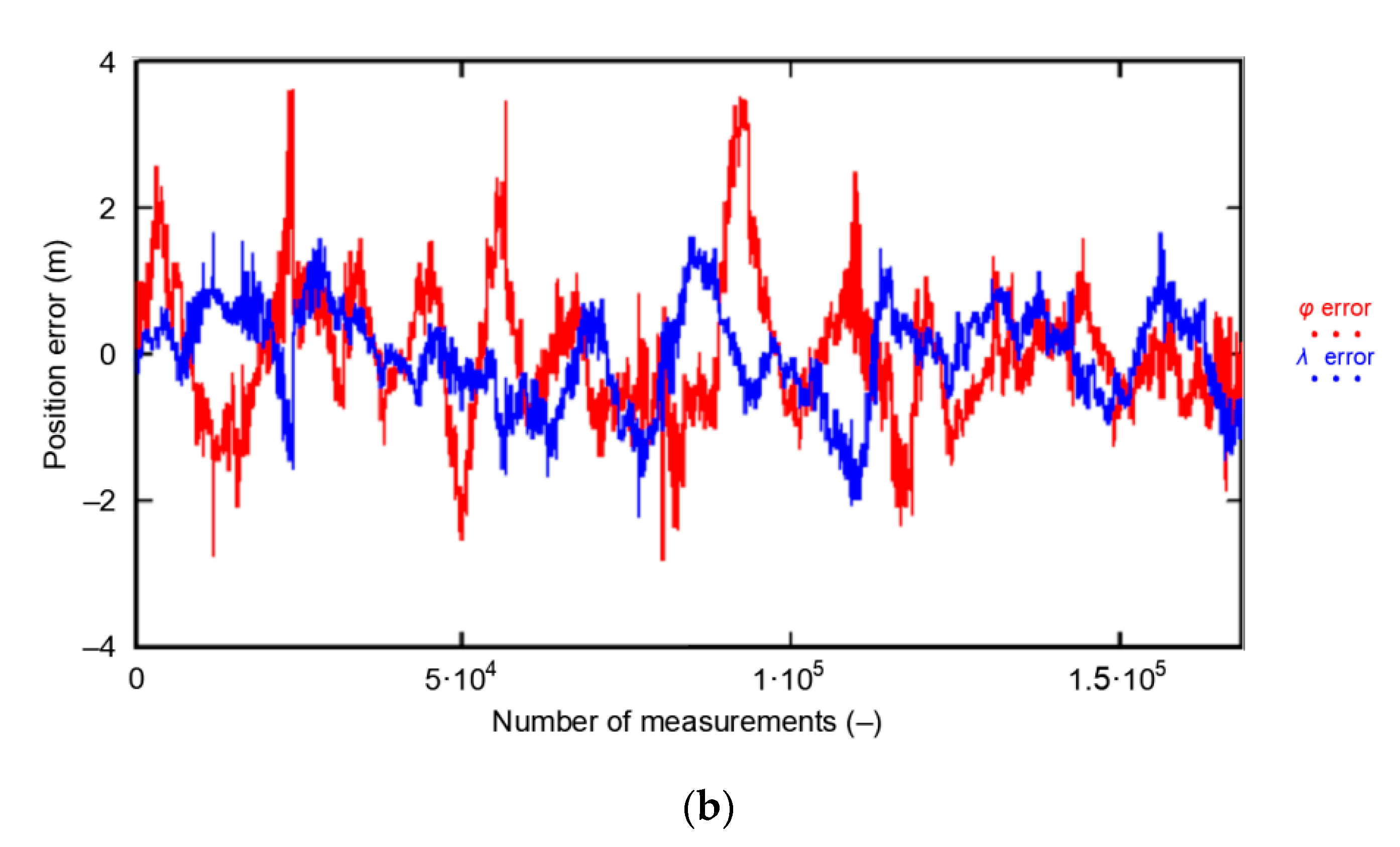
3.2. Influence of Position Random Walk on Determining the Navigation System Positioning Accuracy
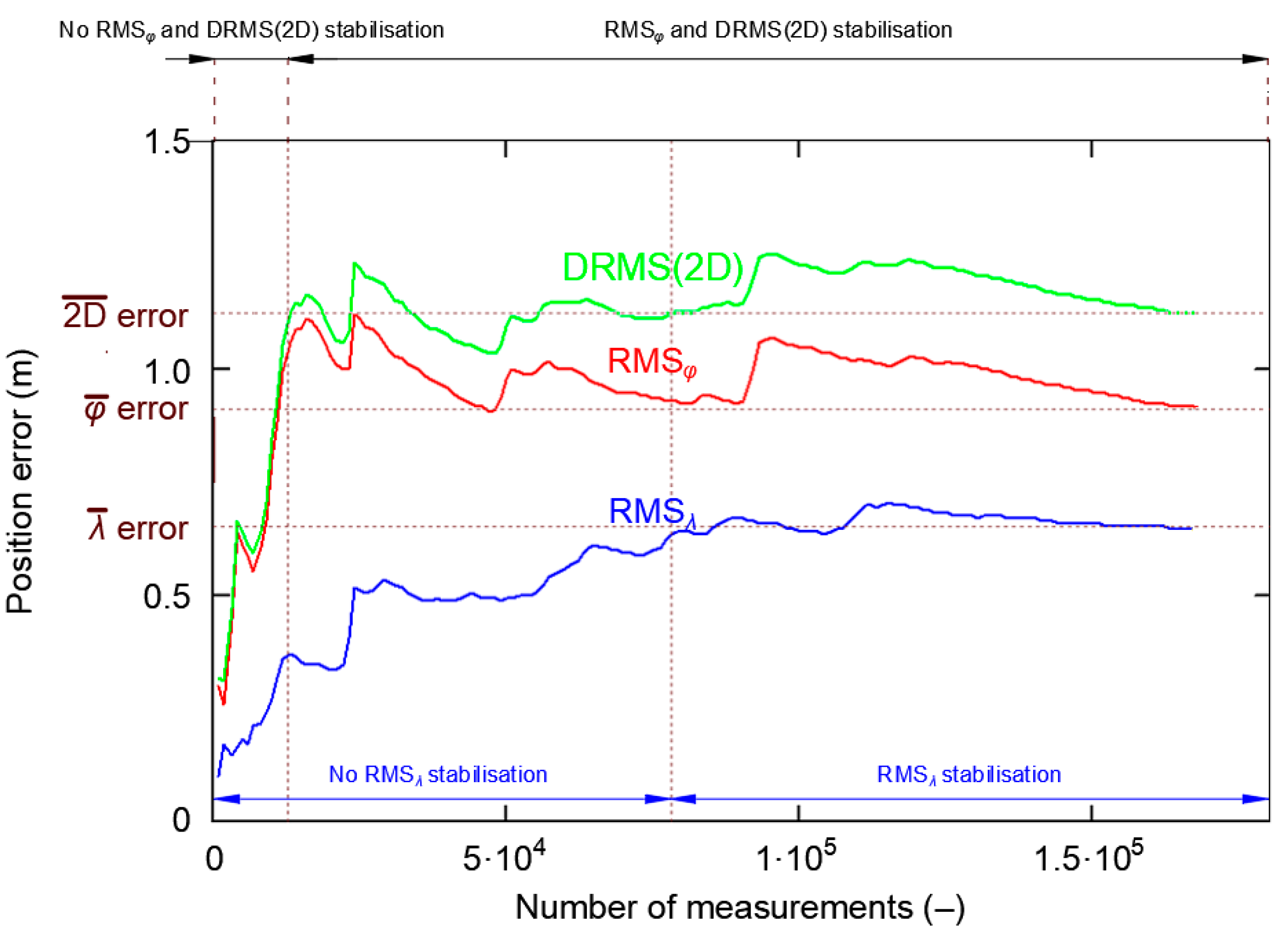
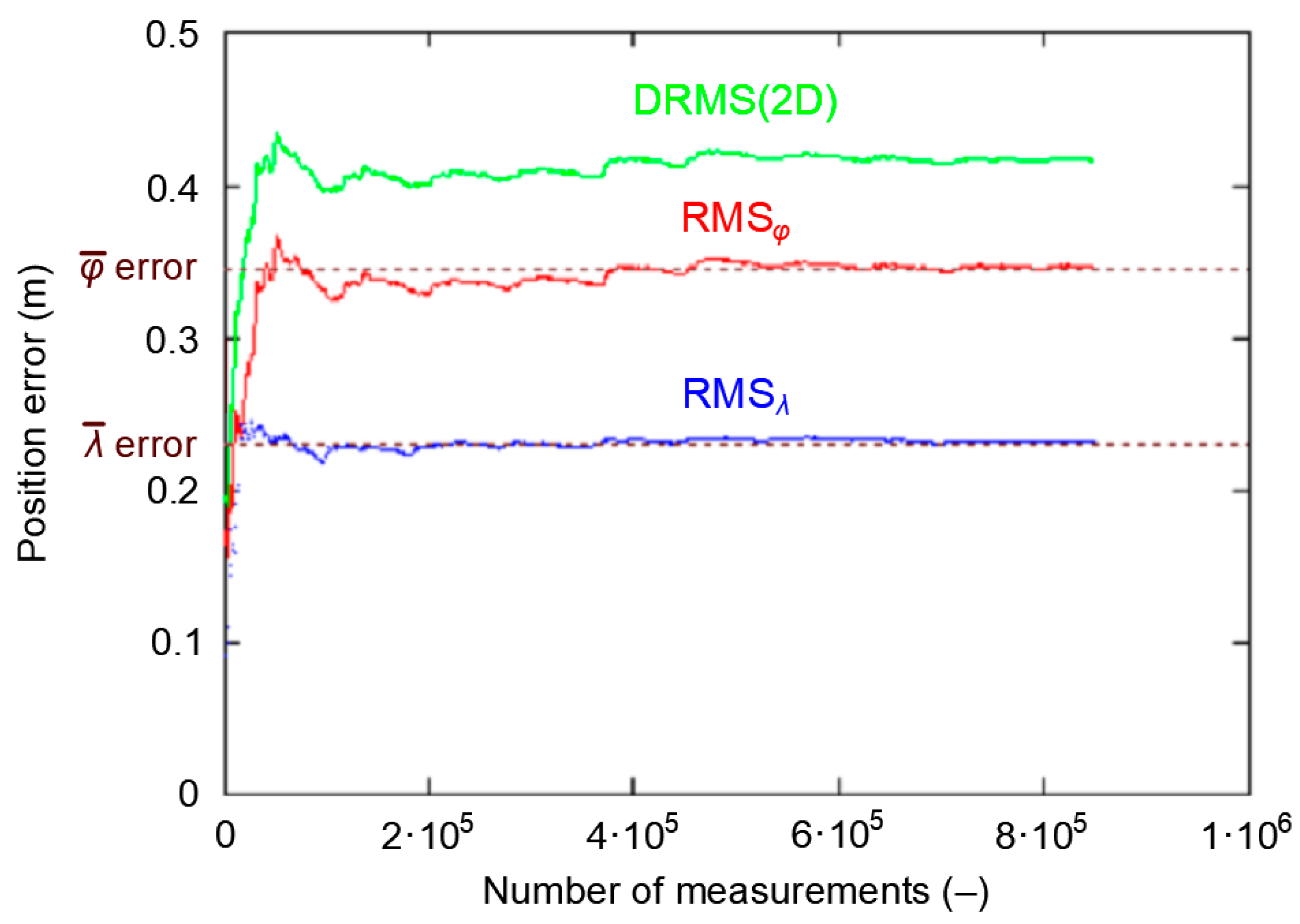
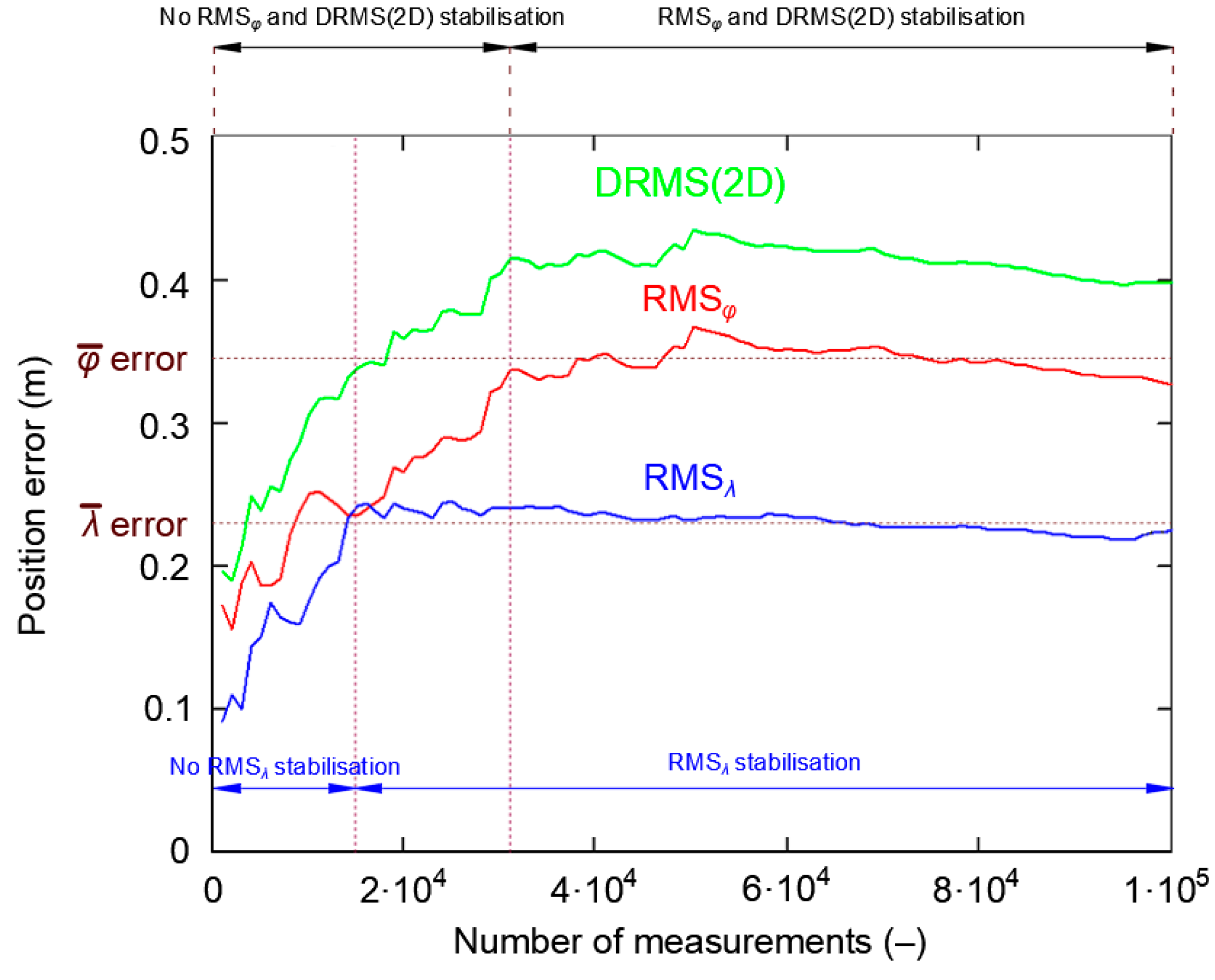
3.3. Representative Sample Size
- The whole population of 2D position errors (168′286 measurements) was divided into 168 sessions with the number of measurements increasing by a fixed value (1000 measurements). This means that the length of the first session was 1000 measurements, the subsequent session consisted of 2000 measurements, then 3000 measurements up to a session of 168′000 measurements.
- For each of the sessions, the and δE values were determined, followed by the DRMS(2D) value on their basis.
- Such a session (of minimum length) will be considered representative if the δE values is close to the standard deviation from the whole campaign.
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Bowditch, N. American Practical Navigator; Paradise Cay Publications: Blue Lake, CA, USA, 2019; Volume 1–2. [Google Scholar]
- Hofmann-Wellenhof, B.; Legat, K.; Wieser, M. Navigation—Principles of Positioning and Guidance; Springer: Wien, Austria, 2003. [Google Scholar]
- Specht, C. System GPS; Bernardinum Publishing House: Pelplin, Poland, 2007. (In Polish) [Google Scholar]
- IALA AISM. Navigation. Available online: https://www.iala-aism.org/wiki/dictionary/index.php/Navigation (accessed on 12 December 2020).
- Cutler, T.J. Dutton’s Nautical Navigation, 15th ed.; Naval Institute Press: Annapolis, MD, USA, 2003. [Google Scholar]
- Krasuski, K.; Ćwiklak, J.; Jafernik, H. Aircraft Positioning Using PPP Method in GLONASS System. Aircr. Eng. Aerosp. Technol. 2018, 90, 1413–1420. [Google Scholar] [CrossRef]
- Marais, J.; Beugin, J.; Berbineau, M. A Survey of GNSS-based Research and Developments for the European Railway Signaling. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2602–2618. [Google Scholar] [CrossRef] [Green Version]
- Ambroziak, S.J.; Katulski, R.J.; Sadowski, J.; Siwicki, W.; Stefański, J. Ground-based, Hyperbolic Radiolocation System with Spread Spectrum Signal—AEGIR. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2011, 5, 233–238. [Google Scholar]
- Chen, Q.; Niu, X.; Zuo, L.; Zhang, T.; Xiao, F.; Liu, Y.; Liu, J. A Railway Track Geometry Measuring Trolley System Based on Aided INS. Sensors 2018, 18, 538. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paziewski, J.; Sieradzki, R.; Baryla, R. Multi-GNSS High-rate RTK, PPP and Novel Direct Phase Observation Processing Method: Application to Precise Dynamic Displacement Detection. Meas. Sci. Technol. 2018, 29, 091001. [Google Scholar] [CrossRef]
- Sánchez, A.; Bravo, J.L.; González, A. Estimating the Accuracy of Track-surveying Trolley Measurements for Railway Maintenance Planning. J. Surv. Eng. 2017, 143, 05016008. [Google Scholar] [CrossRef]
- Dziewicki, M.; Specht, C. Position Accuracy Evaluation of the Modernized Polish DGPS. Pol. Marit. Res. 2009, 16, 57–61. [Google Scholar] [CrossRef]
- Specht, C.; Pawelski, J.; Smolarek, L.; Specht, M.; Dąbrowski, P. Assessment of the Positioning Accuracy of DGPS and EGNOS Systems in the Bay of Gdansk Using Maritime Dynamic Measurements. J. Navig. 2019, 72, 575–587. [Google Scholar] [CrossRef] [Green Version]
- Bowditch, N. American Practical Navigator: An Epitome of Navigation; DMA: Washington, DC, USA, 1984. [Google Scholar]
- Langley, R.B. The Mathematics of GPS. GPS World 1991, 2, 45–50. [Google Scholar]
- van Diggelen, F. GPS Accuracy: Lies, Damn Lies, and Statistics. GPS World 1998, 9, 1–6. [Google Scholar]
- U.S. DoD. Global Positioning System Standard Positioning Service Signal Specification, 1st ed.; U.S. DoD: Arlington County, VA, USA, 1993. [Google Scholar]
- Specht, C. Preliminary Accuracy Results of EGNOS After the Implementation of Operational Status. In Proceedings of the 5th International Conference & Exhibition (MELAHA 2010), Cairo, Egypt, 3–5 May 2010. [Google Scholar]
- Pearson, K. The Problem of the Random Walk. Nature 1905, 72, 294. [Google Scholar] [CrossRef]
- Mertikas, S.P. Error Distributions and Accuracy Measures in Navigation: An Overview. Available online: https://unbscholar.lib.unb.ca/islandora/object/unbscholar%3A8708 (accessed on 12 December 2020).
- Kendall, M.G.; Buckland, W.R. A Dictionary of Statistical Terms, 4th ed.; Longman: Harlow, UK, 1982. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications, 3rd ed.; John Wiley & Sons, Inc: Hoboken, NJ, USA, 1968; Volume 1. [Google Scholar]
- Biecek, P. Wybrane Testy Normalności. Available online: http://tofesi.mimuw.edu.pl/~cogito/smarterpoland/samouczki/testyNormalnosci/testyNormalnosci.pdf (accessed on 12 December 2020).
- Anderson, T.W.; Darling, D.A. A Test of Goodness of Fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Cramér, H. On the Composition of Elementary Errors. Scand. Actuar. J. 1928, 1928, 13–74. [Google Scholar] [CrossRef]
- von Mises, R.E. Wahrscheinlichkeit, Statistik und Wahrheit; Springer: Berlin/Heidelberg, Germany, 1928. (In German) [Google Scholar]
- Kolmogorov, A. Sulla Determinazione Empirica di una Legge di Distribuzione. G. dell’Istituto Ital. degli Attuari 1933, 4, 83–91. (In Italian) [Google Scholar]
- Smirnov, N. Table for Estimating the Goodness of Fit of Empirical Distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Francia, R. An Approximate Analysis of Variance Test for Normality. J. Am. Stat. Assoc. 1972, 67, 215–216. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Pearson, K. On the Criterion that a Given System of Deviations from the Probable in the Case of a Correlated System of Variables is Such that it Can be Reasonably Supposed to have Arisen from Random Sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef] [Green Version]
- Anscombe, F.J.; Glynn, W.J. Distribution of the Kurtosis Statistic b2 for Normal Samples. Biometrika 1983, 70, 227–234. [Google Scholar] [CrossRef]
- D’Agostino, R.B. Transformation to Normality of the Null Distribution of g1. Biometrika 1970, 57, 679–681. [Google Scholar] [CrossRef]
- D’Agostino, R.; Pearson, E.S. Tests for Departure from Normality. Empirical Results for the Distributions of b2 and √b1. Biometrika 1973, 60, 613–622. [Google Scholar] [CrossRef]
- Masereka, E.M.; Otieno, F.A.O.; Ochieng, G.M.; Snyman, J. Best Fit and Selection of Probability Distribution Models for Frequency Analysis of Extreme Mean Annual Rainfall Events. Int. J. Eng. Res. Dev. 2015, 11, 34–53. [Google Scholar]
- Das, S.; Mitra, K.; Mandal, M. Sample Size Calculation: Basic Principles. Indian J. Anaesth. 2016, 60, 652–656. [Google Scholar] [CrossRef] [PubMed]
- Górecki, T. Podstawy Statystyki z Przykładami w R; BTC Publishing House: Legionowo, Poland, 2011. (In Polish) [Google Scholar]
- Kelley, K.; Preacher, K.J. On Effect Size. Psychol. Methods 2012, 17, 137–152. [Google Scholar] [CrossRef]
- Hedges, L.V.; Pigott, T.D. The Power of Statistical Tests in Meta-analysis. Psychol. Methods 2001, 6, 203–217. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1988. [Google Scholar]
- Cohen, J. A Power Primer. Psychol. Bull. 1992, 112, 155–159. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The Probability Distribution of the GPS Baseline for a Class of Integer Ambiguity Estimators. J. Geod. 1999, 73, 275–284. [Google Scholar] [CrossRef]
- Cohen, J. The Statistical Power of Abnormal-social Psychological Research: A Review. J. Abnorm. Soc. Psychol. 1962, 65, 145–153. [Google Scholar] [CrossRef]
- Rossi, J.S. Statistical Power of Psychological Research: What Have We Gained in 20 Years? J. Consult. Clin. Psychol. 1990, 58, 646–656. [Google Scholar] [CrossRef]
- Sedlmeier, R.; Gigerenzer, G. Do Studies of Statistical Power Have an Effect on the Power of Studies? Psychol. Bull. 1989, 105, 309–316. [Google Scholar] [CrossRef]
- Moher, D.; Dulberg, C.S.; Wells, G.A. Statistical Power, Sample Size, and Their Reporting in Randomized Controlled Trials. JAMA J. Am. Med Assoc. 1994, 272, 122–124. [Google Scholar] [CrossRef]
- King, B.M.; Minium, E.W. Statystyka dla Psychologów i Pedagogów; Polish Scientific Publishers PWN: Warsaw, Poland, 2009. (In Polish) [Google Scholar]
- Cohen, J. Some Statistical Issues in Psychological Research. In Handbook of Clinical Psychology; Wolmann, B.B., Ed.; McGraw-Hill: New York City, NY, USA, 1965; pp. 95–121. [Google Scholar]
- Wilkinson, L.; Task Force on Statistical Inference. Statistical Methods in Psychology Journals. Guidelines and Explanations. Am. Psychol. 1999, 54, 594–604. [Google Scholar] [CrossRef]




| Normal Distribution | Chi-Squared Distribution | ||||
|---|---|---|---|---|---|
| α | Probability (%) | Notation | Probability (%) | Notation | |
| 0.67 | 50.0 | LEP | 1.00 | 39.4 | level or standard ellipse |
| 1.00 | 68.3 | level or RMS | 1.18 | 50.0 | CEP |
| 1.96 | 95.0 | 95% confidence level | 63.2 | DRMS | |
| 2.00 | 95.4 | level | 2.00 | 86.5 | ellipse |
| 3.00 | 99.7 | level | 2.45 | 95.0 | 95% confidence level |
| 98.2 | 2DRMS | ||||
| 3.00 | 98.9 | ellipse | |||
| Reality | |||
|---|---|---|---|
| H0 | H1 | ||
| Decision | H0 | Correctly accepted H0 (1−β) | Type II error (β) |
| H1 | Type I error (α) | Correctly rejected H0 (1−α) | |
| Measure | All Fixes (168′286) | S1—Red Session (1–1000) | S2—Blue Session (1001–2000) | S3—Green Session (2001–3000) | S4—Purple Session (3001–4000) | S5—Sky-Blue Session (4001–5000) | Mean from S1–S5 |
|---|---|---|---|---|---|---|---|
| shift | 0.000 m | 0.572 m | 0.633 m | 1.268 m | 1.956 m | 1.463 m | 1.178 m |
| shift | 0.000 m | −0.047 m | 0.251 m | 0.157 m | 0.326 m | 0.427 m | 0.223 m |
| Distance of point from the real coordinates (0, 0) | 0.000 m | 0.574 m | 0.681 m | 1.278 m | 1.983 m | 1.524 m | 1.208 m |
| 0.910 m | 0.299 m | 0.201 m | 0.414 m | 0.275 m | 0.358 m | 0.309 m | |
| Session RMSφ vs all measurements RMSφ (%) | 100.00% | 32.86% | 22.12% | 45.54% | 30.26% | 39.37% | 34.03% |
| 0.653 m | 0.098 m | 0.066 m | 0.059 m | 0.120 m | 0.085 m | 0.086 m | |
| Session RMSλ vs all measurements RMSλ (%) | 100.00% | 15.07% | 10.09% | 9.01% | 18.36% | 13.01% | 13.11% |
| Positioning System | Empirical Accuracy of All Fixes (R95) | P1(1–1000) vs. P2(1001–2000) | P2(1001–2000) vs. P3(2001–3000) | P3(2001–3000) vs. P4(3001–4000) | P4(3001–4000) vs. P5(4001–5000) | Mean Shift between Sessions |
|---|---|---|---|---|---|---|
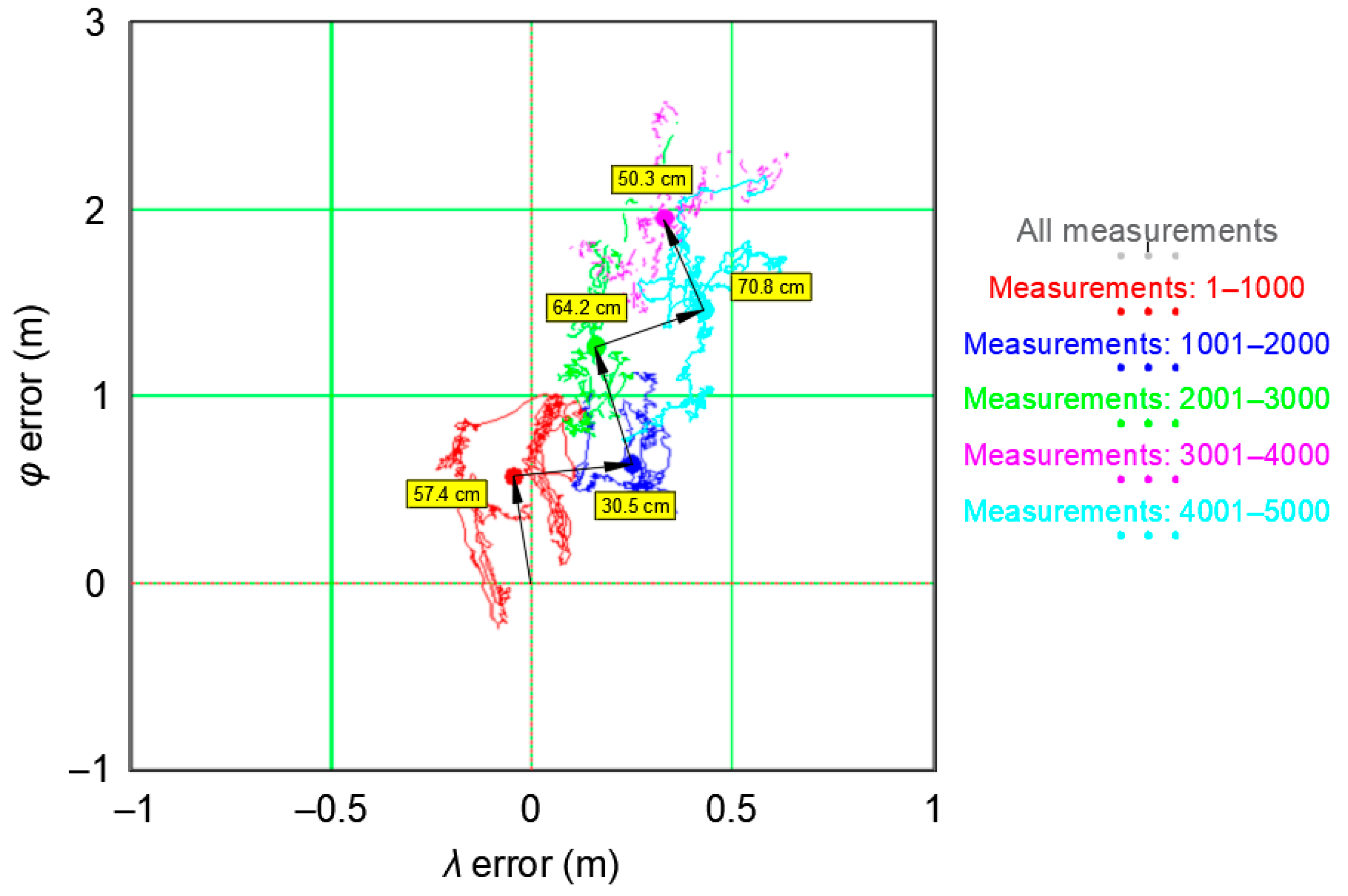
| GPS | 2.039 m | 30.5 cm | 64.2 cm | 70.8 cm | 50.3 cm | 54.0 cm |
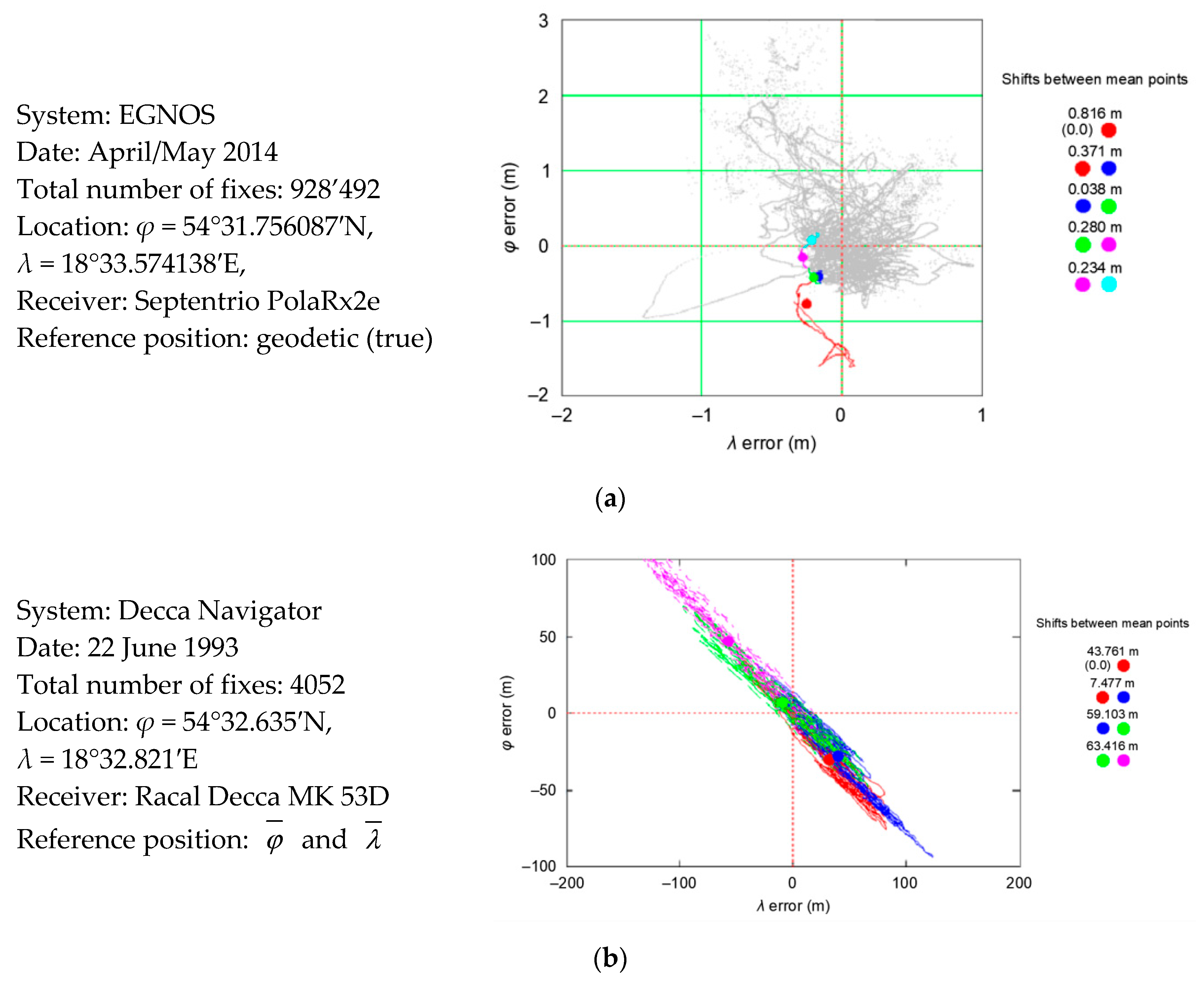
| EGNOS | 0.871 m | 37.1 cm | 3.8 cm | 28.0 cm | 23.4 cm | 23.1 cm |
| Decca Navigator | 131.719 m | 7.477 m | 59.103 m | 63.416 m | No data | 43.332 m |
| Probability density function for φ error | |
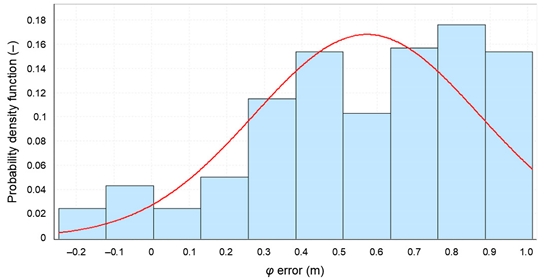 | |
| Probability density function for λ error | |
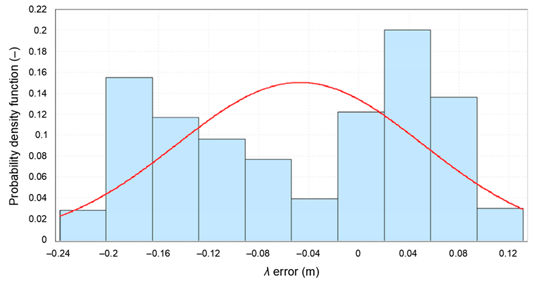 | |
| Probability difference for φ error | |
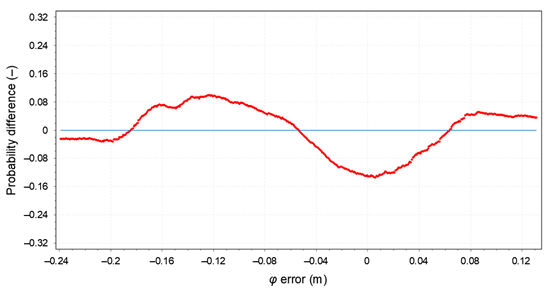 | |
| Probability difference for λ error | |
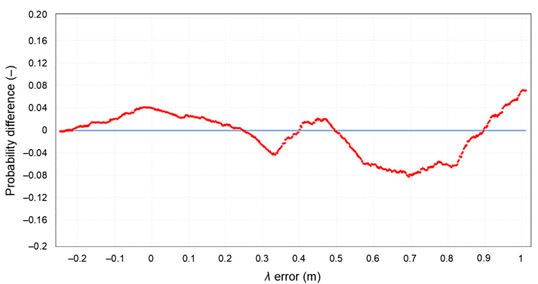 | |
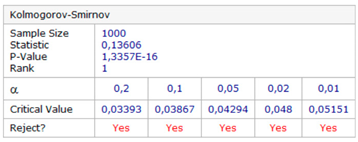
| Kolmogorov–Smirnov test | |
| φ error | λ error |
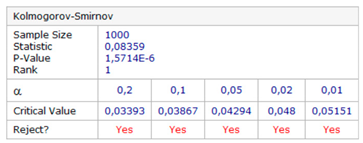 |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Specht, M. Statistical Distribution Analysis of Navigation Positioning System Errors—Issue of the Empirical Sample Size. Sensors 2020, 20, 7144. https://doi.org/10.3390/s20247144
Specht M. Statistical Distribution Analysis of Navigation Positioning System Errors—Issue of the Empirical Sample Size. Sensors. 2020; 20(24):7144. https://doi.org/10.3390/s20247144
Chicago/Turabian StyleSpecht, Mariusz. 2020. "Statistical Distribution Analysis of Navigation Positioning System Errors—Issue of the Empirical Sample Size" Sensors 20, no. 24: 7144. https://doi.org/10.3390/s20247144
APA StyleSpecht, M. (2020). Statistical Distribution Analysis of Navigation Positioning System Errors—Issue of the Empirical Sample Size. Sensors, 20(24), 7144. https://doi.org/10.3390/s20247144





