Achieving 3D Beamforming by Non-Synchronous Microphone Array Measurements
Abstract
:1. Introduction
2. Forward Model of Acoustic Imaging and Acoustic Measurement
2.1. Conventional Beamforming
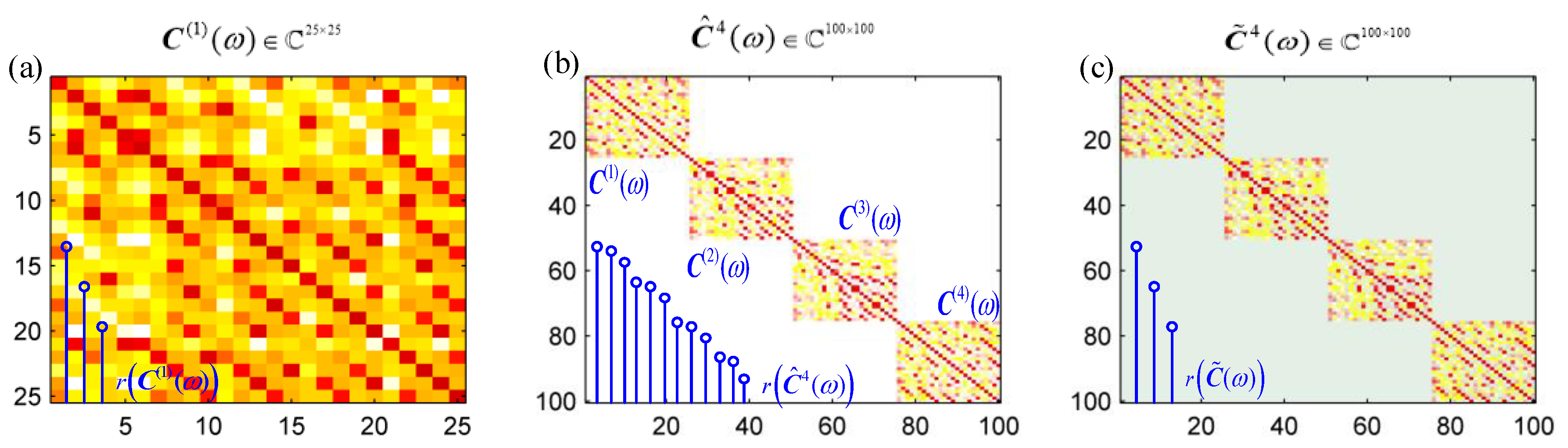
2.2. Non-Synchronous Measurements Theory
- The 1st constraint: ensures that the rank of the reconstructed cross-spectral matrix is still equal to the number of the sources .
- The 2nd constraint: denotes the sampling operator that gets the elements in the diagonal block of a matrix, and the size is , which is identical to . ensures that the difference between and in the Frobenius norm is less than a given tolerance .
- The 3rd constraint: is a projection matrix. is the cross-spectral matrix of , where the projected matrix can be the smooth pressure [40] of the non-synchronous measured pressure . To ensure the acoustic field’s spatial continuity, is added here, and the difference in the cross-spectral matrix between and is required to be smaller than a given tolerance . The detailed discussion on this constraint is addressed in Section 2.2.
- The 4th constraint: ensures that both and are positive semi-definite matrixes.
2.3. Spatial Basis and Spatial Continuity of the Acoustic Field
3. Simulation Results
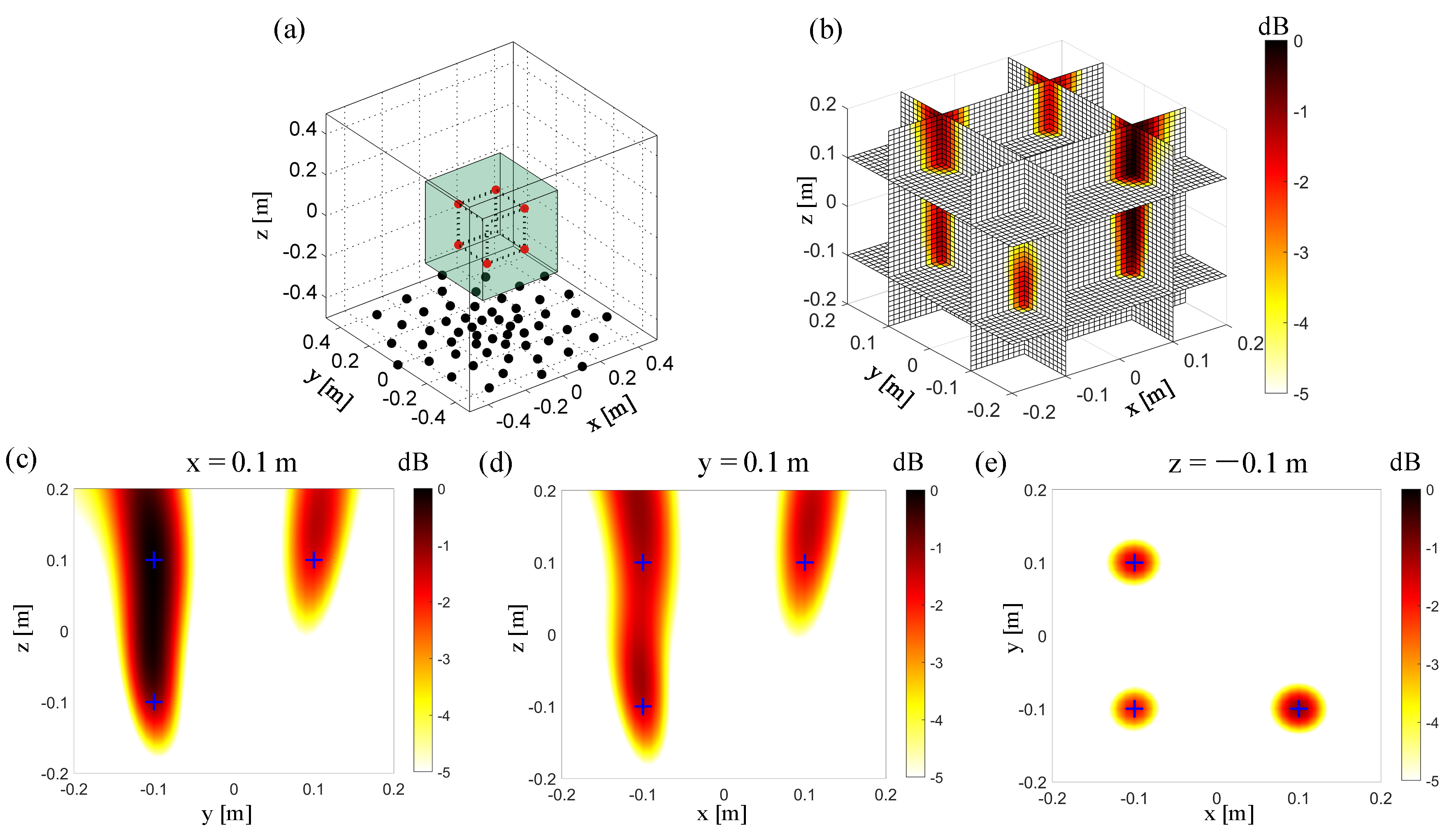
3.1. 3D Imaging by the Conventional Beamforming with a Planar Array
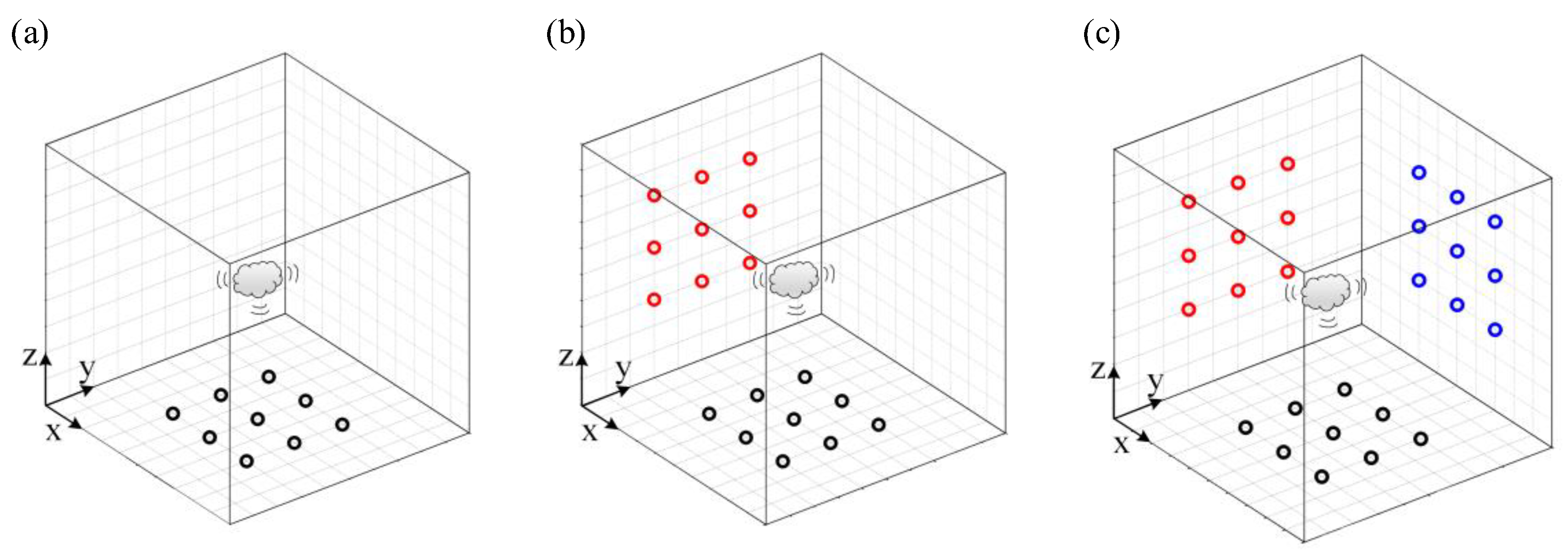
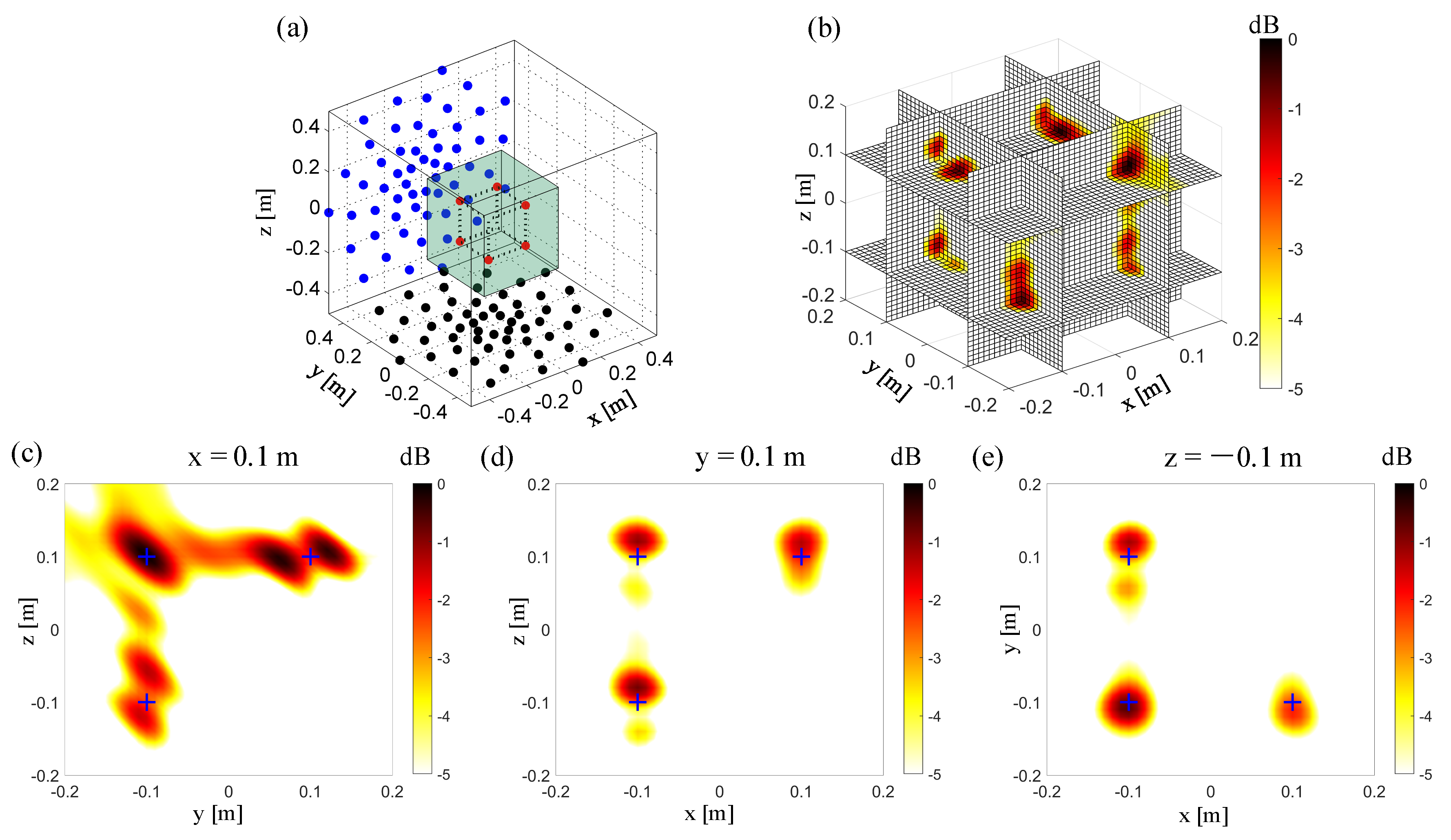
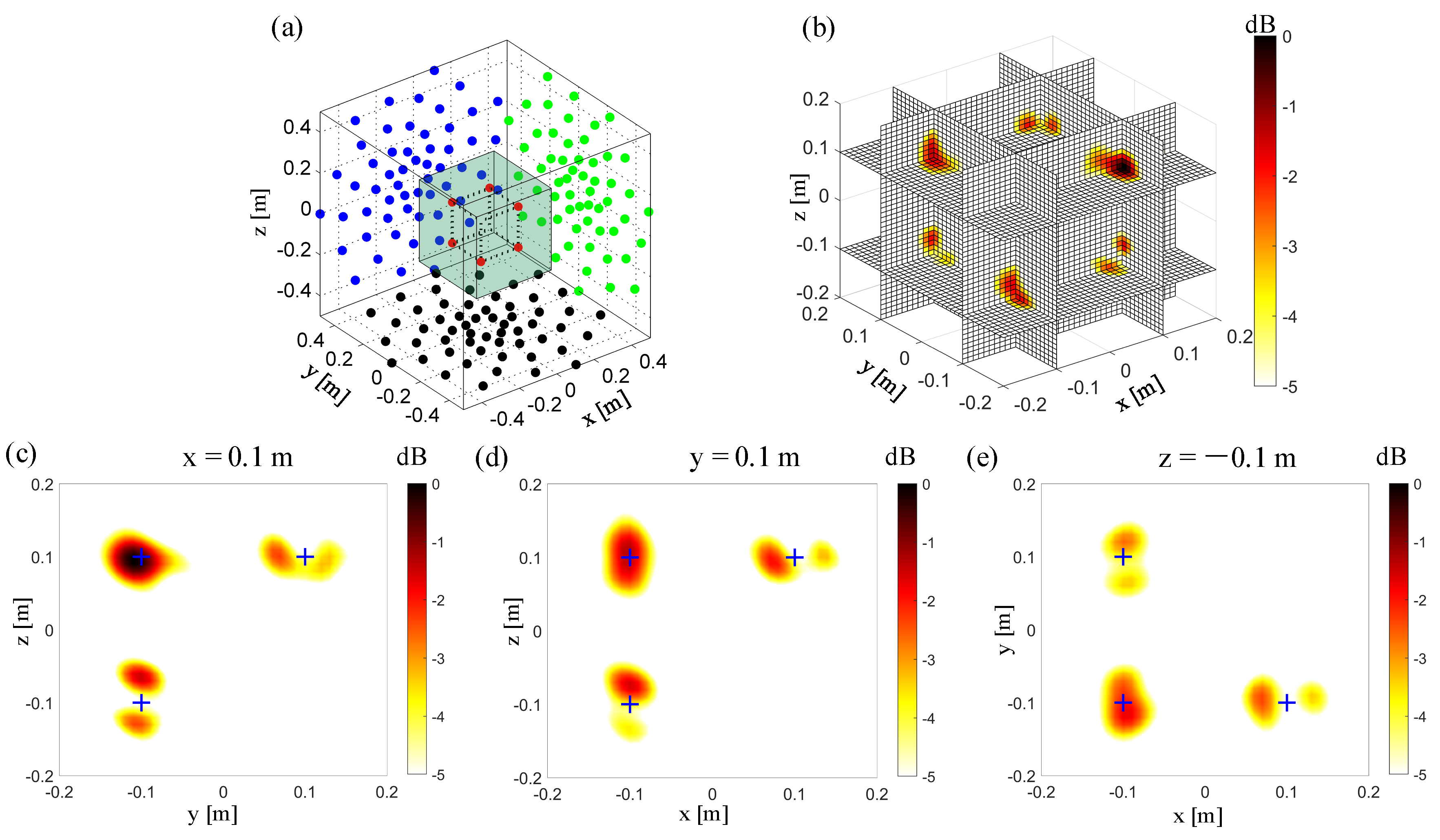
3.2. 3D Imaging by the Non-Synchronous Measurements with Orthogonal Moving Arrays
3.3. 3D Imaging by the Non-Synchronous Measurements with Non-Orthogonal Moving Arrays
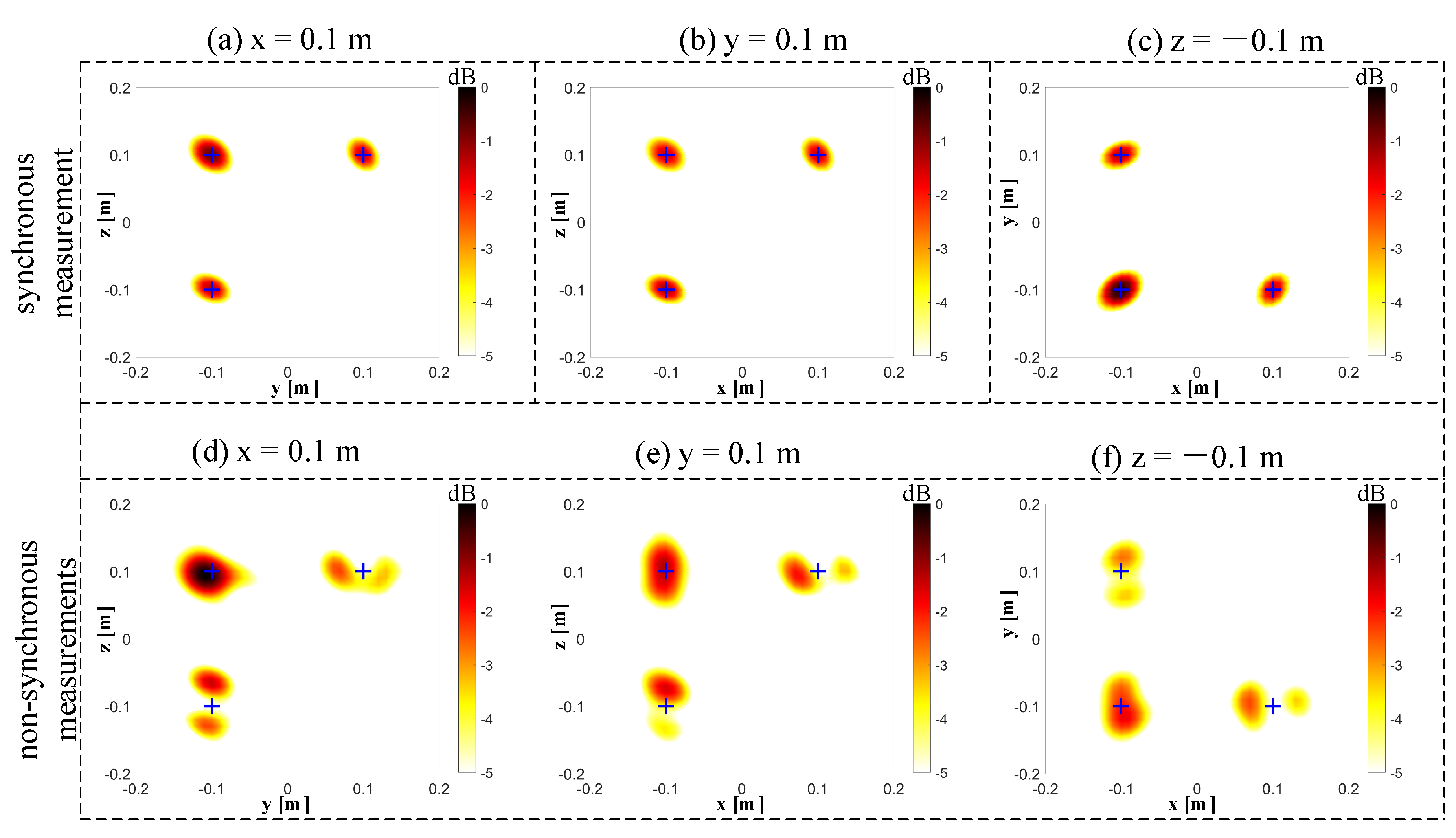
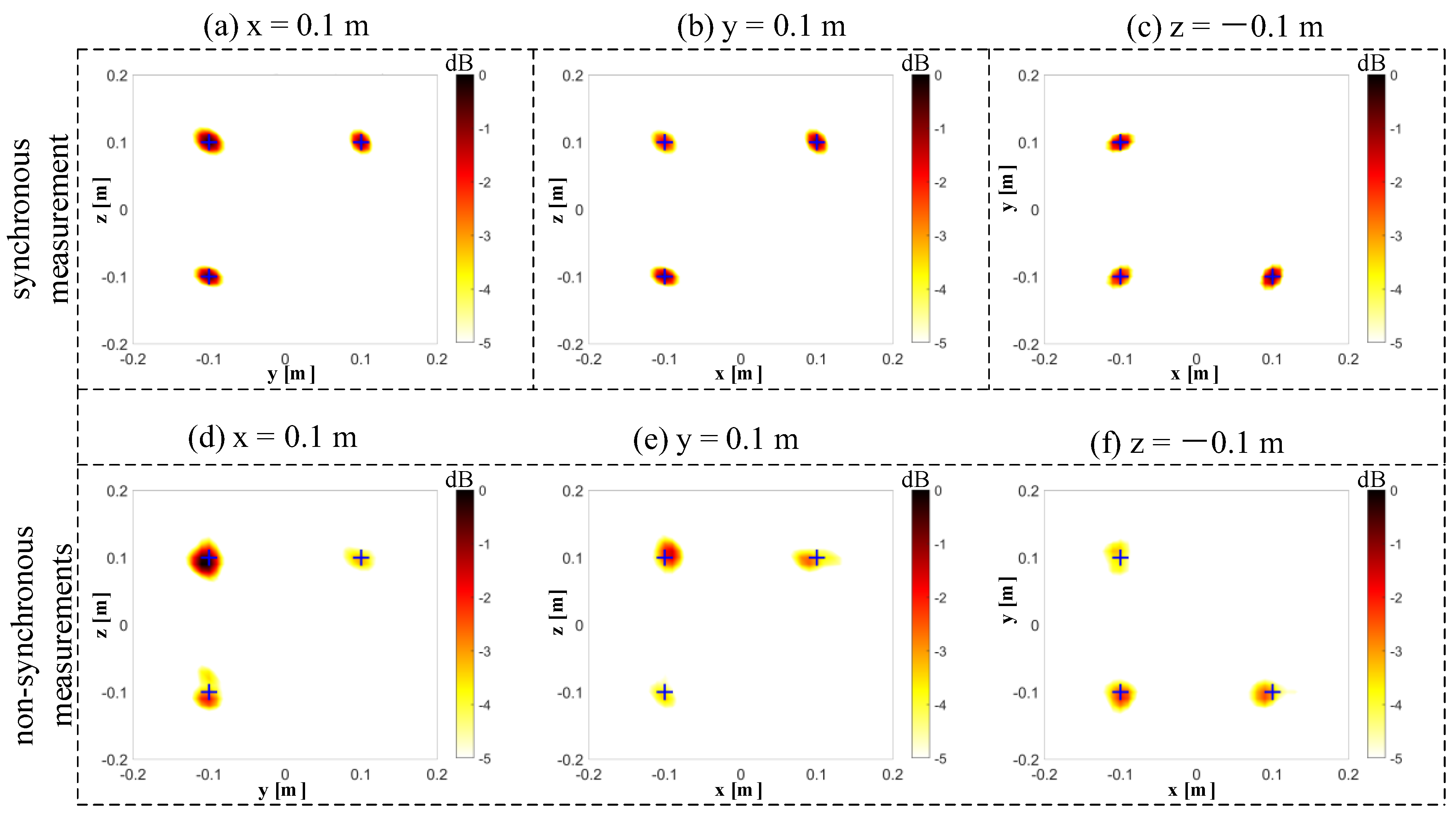
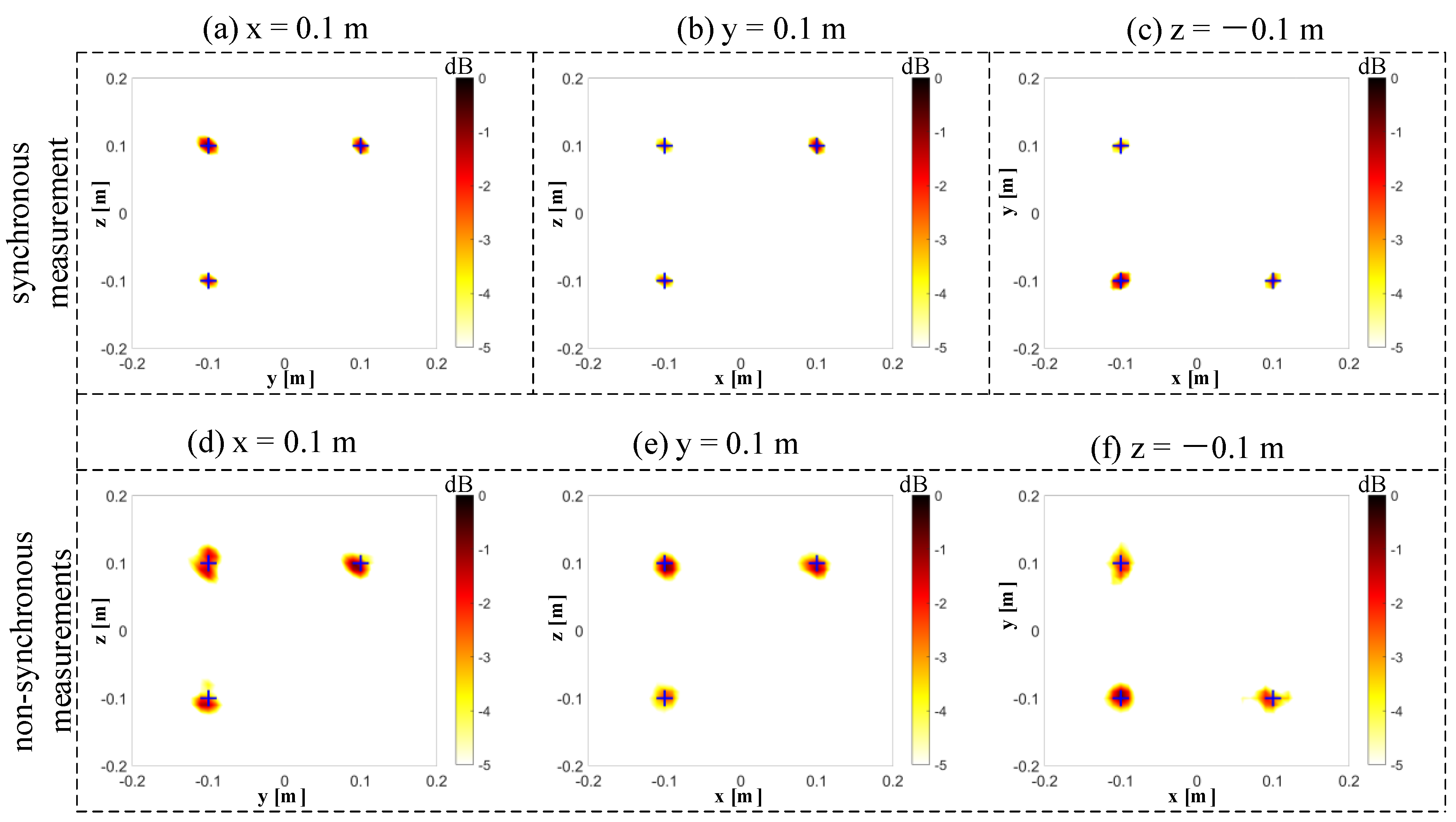
4. Comparison between the Synchronous Measurements and Non-Synchronous Measurements
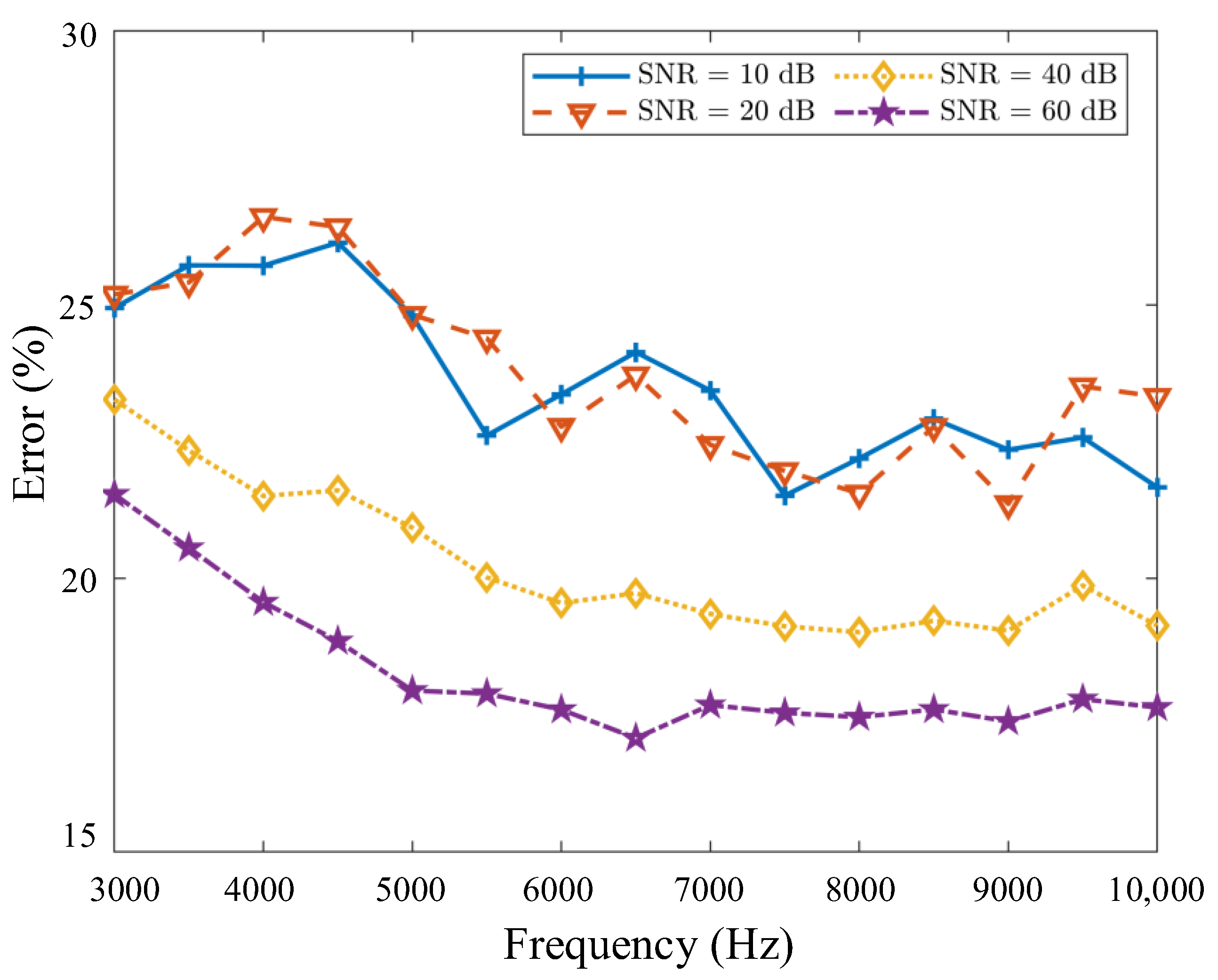
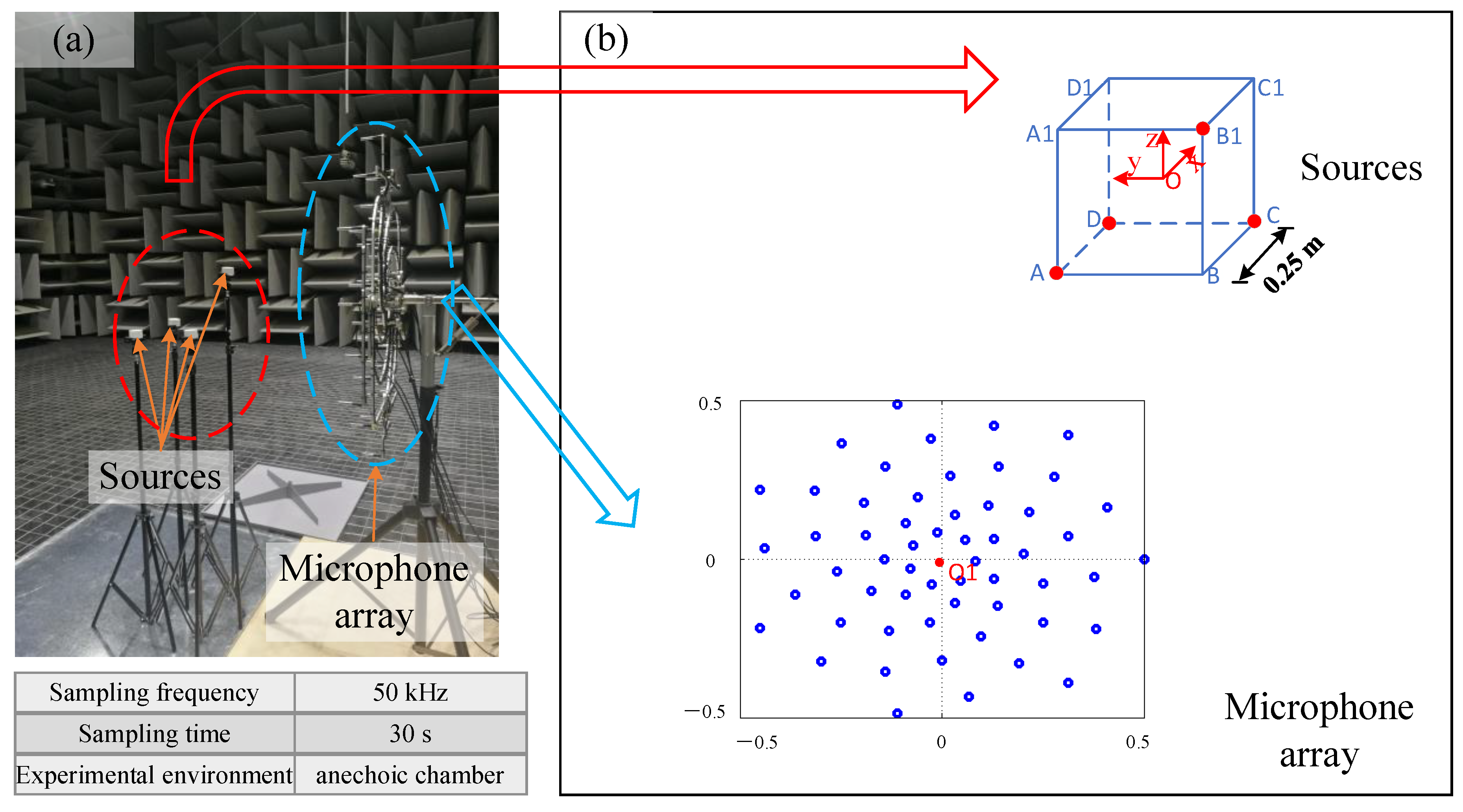
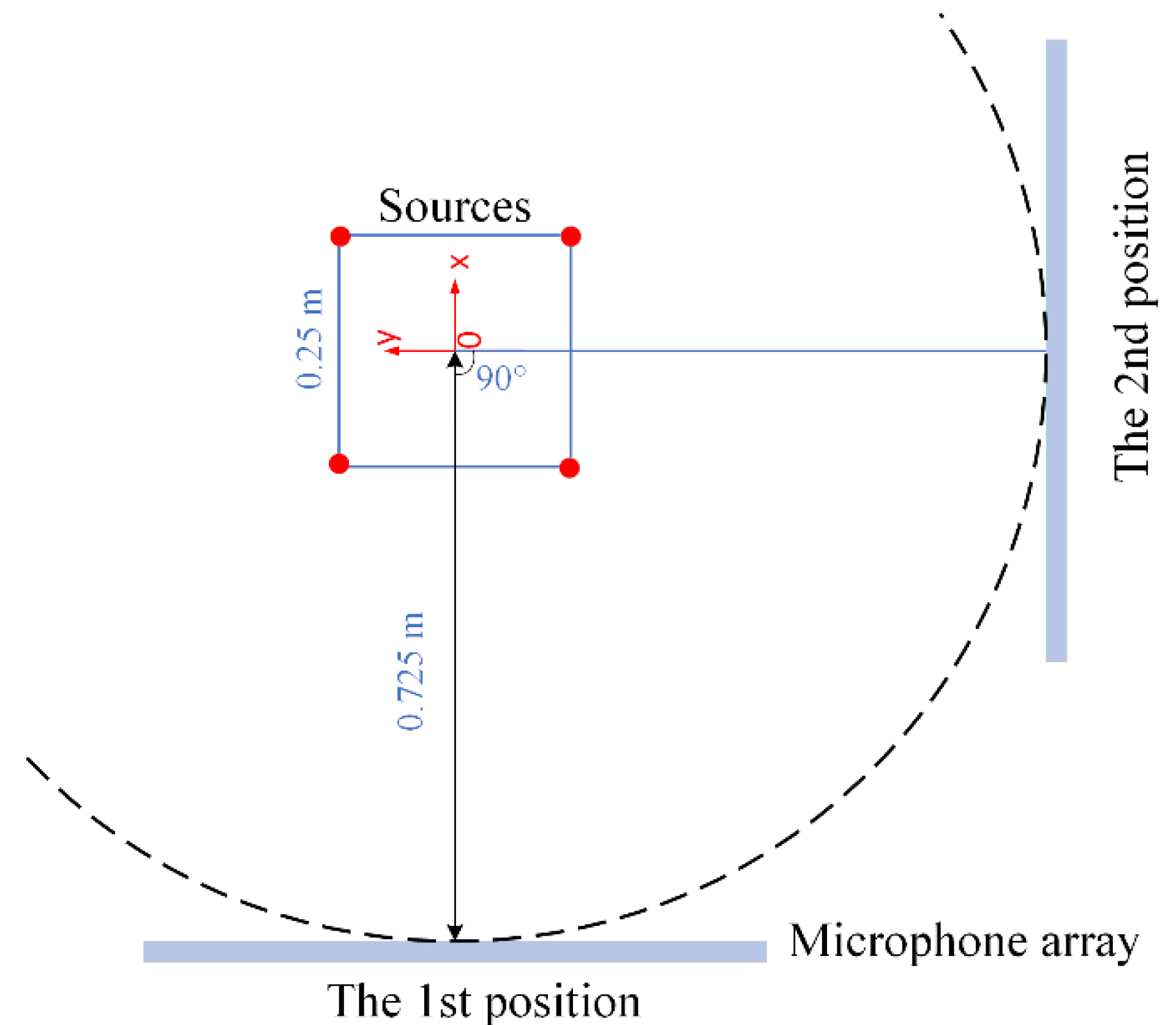
5. Experimental Verification
5.1. Experimental Setup
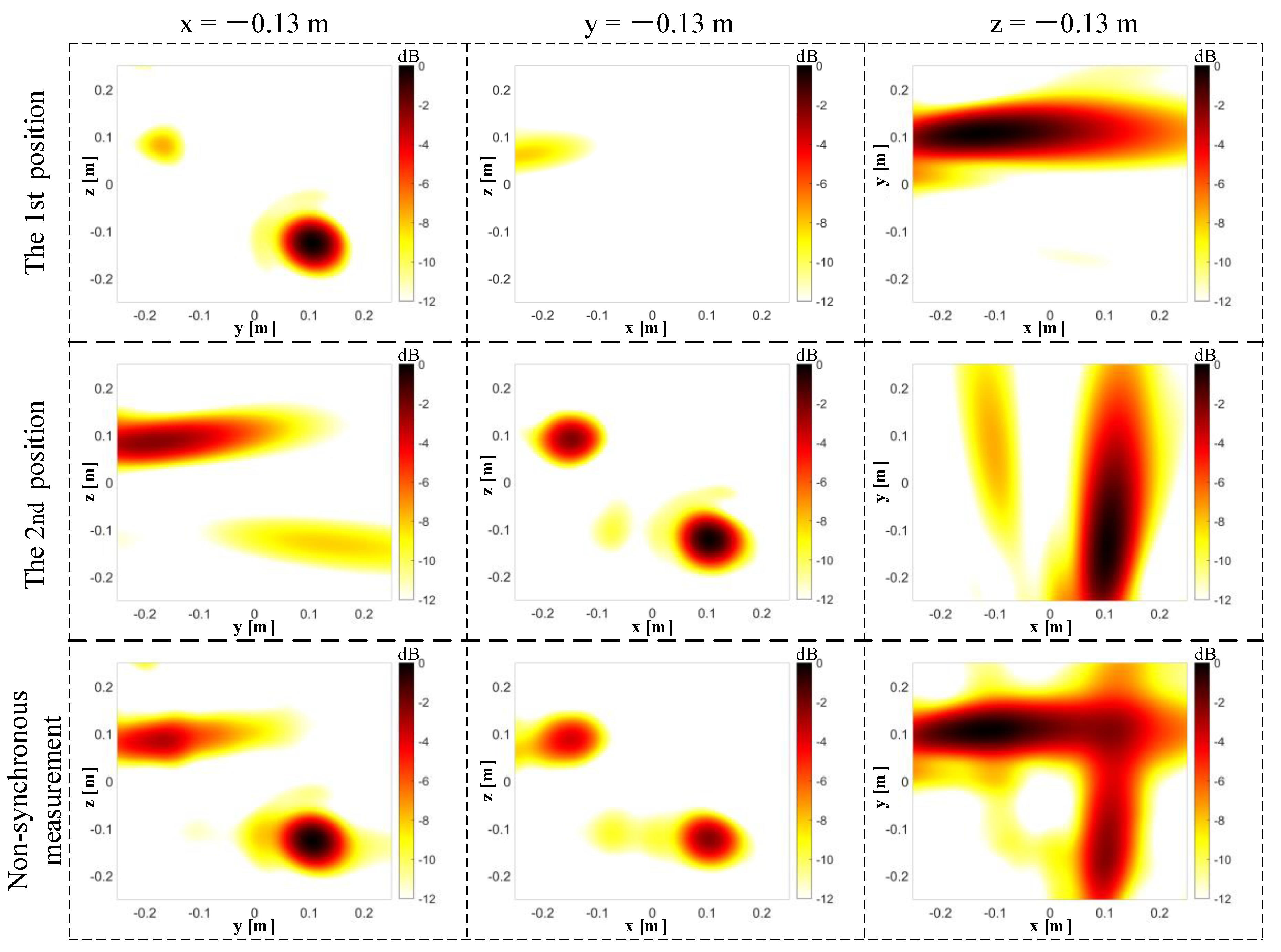
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Park, Y.; Choi, A.; Kim, K. Parametric Estimations Based on Homomorphic Deconvolution for Time of Flight in Sound Source Localization System. Sensors 2020, 20, 925. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, R.; Yang, K.; Yang, Q.; Chen, P.; Sun, Q.; Xue, R. Localization of Two Sound Sources Based on Compressed Matched Field Processing with a Short Hydrophone Array in the Deep Ocean. Sensors 2019, 19, 3810. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Siller, H.; Drescher, M.; Saueressig, G.; Lange, R. Fly-over Source Localisation on a Boeing 747-400. In Proceedings of the Berlin Beamforming Conference, Berlin, Germany, 24–25 February 2010; pp. 1–11. [Google Scholar]
- Dinsenmeyer, A.; Antoni, J.; Leclere, Q.; Pereira, A. On the Denoising of Cross-Spectral Matrices for (aero) Acoustic Applications. In Proceedings of the Berlin Beamforming Conference, Berlin, Germany, 5–6 March 2018. [Google Scholar]
- Leclère, Q.; Pereira, A.; Bailly, C.; Antoni, J.; Picard, C. A unified formalism for acoustic imaging based on microphone array measurements. Int. J. Aeroacoustics 2017, 16, 431–456. [Google Scholar] [CrossRef] [Green Version]
- Chu, Z.G.; Yang, Y.; Wang, W.D.; Xiao, X.B.; He, Y.S. Identification of truck noise sources under passby condition based on wave beamforming method. J. Vib. Shock 2012, 31, 66–70. [Google Scholar]
- Maynard, J.D.; Williams, E.G.; Lee, Y. Nearfield acoustic holography: I. Theory of generalized holography and the development of NAH. JASA 1985, 78, 1395. [Google Scholar] [CrossRef]
- Tan, D.; Chu, Z.; Wu, G. Robust reconstruction of equivalent source method based near-field acoustic holography using an alternative regularization parameter determination approach. J. Acoust. Soc. Am. 2019, 146, EL34–EL38. [Google Scholar] [CrossRef]
- Luo, Z.-W.; Fernandez Comesana, D.; Zheng, C.-J.; Bi, C.-X. Near-field acoustic holography with three-dimensional scanning measurements. J. Sound Vibration. 2019, 439, 43–55. [Google Scholar] [CrossRef]
- Bai, M.R. Application of BEM (boundary element metliod)-based acoustic holography to radiation analysis of sound sources with arbitrarily shaped geometries. J. Acoust. Soc. Am. 1992, 92, 199–209. [Google Scholar] [CrossRef] [Green Version]
- Schuhmacher, A.; Hald, J.R.; Rasmussen, K.B.; Hansen, P.C. Sound source reconstruction using inverse boundary element calculations. J. Acoust. Soc. Am. 2003, 113, 114–127. [Google Scholar] [CrossRef]
- Bi, C.X.; Liu, Y.; Xu, L.; Zhang, Y.B. Sound field reconstruction using compressed modal equivalent point source method. J. Acoust. Soc. Am. 2017, 141, 73–79. [Google Scholar] [CrossRef]
- Ping, G.; Chu, Z.; Yang, Y.; Xu, Z. Wideband holography based spherical equivalent source method with rigid spherical arrays. Mech. Syst. Signal Process. 2018, 111, 303–313. [Google Scholar] [CrossRef]
- Bi, C.X.; Hu, D.Y.; Zhang, Y.B.; Jing, W.Q. Identification of active sources inside cavities using the equivalent source method-based free-field recovery technique. J. Sound Vib. 2015, 346, 153–164. [Google Scholar] [CrossRef]
- Yu, L.; Antoni, J.; Zhao, H.; Guo, Q.; Wang, R.; Jiang, W. The acoustic inverse problem in the framework of alternating direction method of multipliers. Mech. Syst. Signal Process. 2020, 49, 107220. [Google Scholar] [CrossRef]
- Steiner, R.; Hald, J. Near-field acoustical holography without the errors and limitations caused by the use of spatial DFT. Int. J. Acoust. Vib. 2001, 6, 83–89. [Google Scholar] [CrossRef]
- Hald, J. Basic theory and properties of statistically optimized near-field acoustical holography. J. Acoust. Soc. Am. 2009, 125, 2105. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wu, S.F. Helmholtz equation-least-squares method for reconstructing acoustic pressure fields. J. Acoust. Soc. Am. 1997, 102, 2020–2032. [Google Scholar] [CrossRef]
- Sarradj, E. Three-dimensional acoustic source mapping with different beamforming steering vector formulations. Adv. Acoust. Vib. 2012, 2012. [Google Scholar] [CrossRef] [Green Version]
- Brooks, T.; Humphreys, W. Three-dimensional applications of DAMAS methodology for aeroacoustic noise source definition. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005; p. 2960. [Google Scholar]
- Legg, M.; Bradley, S. Comparison of CLEAN-SC for 2D and 3D scanning surfaces. In Proceedings of the 4th Berlin Beamforming Conference., Berlin, Germany, 22–23 February 2012. [Google Scholar]
- Ding, H.; Lu, H.; Li, C.; Jing, J.; Chai, G. Localization and identification of three-dimensional sound source with beamforming based acoustic tomography. Proc. Mtgs. Acoust. 2013, 19, 1–8. [Google Scholar]
- Xenaki, A.; Jacobsen, F.; Fernandez-Grande, E. Improving the resolution of three-dimensional acoustic imaging with planar phased arrays. J. Sound Vib. 2012, 331, 1939–1950. [Google Scholar] [CrossRef] [Green Version]
- Chu, Z.; Yang, Y.; He, Y. Deconvolution for three-dimensional acoustic source identification based on spherical harmonics beamforming. J. Sound Vib. 2015, 344, 484–502. [Google Scholar] [CrossRef]
- Ning, F.; Wei, J.; Qiu, L.; Shi, H.; Li, X. Three-dimensional acoustic imaging with planar microphone arrays and compressive sensing. J. Sound Vib. 2016, 380, 112–128. [Google Scholar] [CrossRef]
- Battista, G.; Chiariotti, P.; Herold, G.; Sarradj, E.; Castellini, P. Inverse methods for three-dimensional acoustic mapping with a single planar array. In Proceedings of the 7th Berlin Beamforming Conference, Berlin, Germany, 5–6 March 2018. [Google Scholar]
- Padois, T.; Robin, O.; Berry, A. 3D Source localization in a closed wind-tunnel using microphone arrays. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, 27–29 May 2013; p. 2213. [Google Scholar]
- Padois, T.; Berry, A. Two and Three-Dimensional Sound Source Localization with Beamforming and Several Deconvolution Techniques. Acta Acust. United Acust. 2017, 103, 392–400. [Google Scholar] [CrossRef]
- Porteous, R.; Prime, Z.; Doolan, C.J.; Moreau, D.J.; Valeau, V. Three-dimensional beamforming of dipolar aeroacoustic sources. J. Sound Vib. 2015, 355, 117–134. [Google Scholar] [CrossRef]
- Ping, G.; Fernandez-Grande, E.; Gerstoft, P.; Chu, Z. Three-dimensional source localization using sparse Bayesian learning on a spherical microphone array. J. Acoust. Soc. Am. 2020, 147, 3895–3904. [Google Scholar] [CrossRef] [PubMed]
- Chu, N.; Ning, Y.; Yu, L.; Huang, Q.; Wu, D. A High-resolution and Low-frequency Acoustic Beamforming based on Bayesian Inference and Non-synchronous Measurements. IEEE Access 2020, 8, 82500–82513. [Google Scholar] [CrossRef]
- Yu, L.; Antoni, J.; Leclere, Q.; Jiang, W. Acoustical source reconstruction from non-synchronous sequential measurements by Fast Iterative Shrinkage Thresholding Algorithm. J. Sound Vib. 2017, 408, 351–367. [Google Scholar]
- Antoni, J.; Liang, Y.; Leclère, Q. Reconstruction of sound quadratic properties from non-synchronous measurements with insufficient or without references: Proof of concept. J. Sound Vib. 2015, 349, 123–149. [Google Scholar] [CrossRef]
- Yu, L.; Antoni, J.; Wu, H.; Leclere, Q.; Jiang, W. Fast iteration algorithms for implementing the acoustic beamforming of non-synchronous measurements. Mech. Syst. Signal Process. 2019, 134, 106309. [Google Scholar]
- Chu, N. Bayesian Approach in Acoustic Source Localization and Imaging. Ph.D. Thesis, Université Paris Sud-Paris XI, Orsay, France, 22 November 2013. [Google Scholar]
- Schmidt, R. Multiple emitter location and signal parameter estimation. Ieee Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Antoni, J.; Le Magueresse, T.; Leclère, Q.; Simard, P. Sparse acoustical holography from iterated Bayesian focusing. J. Sound Vib. 2019, 446, 289–325. [Google Scholar] [CrossRef]
- Brillinger, D.R. Time Series: Data Analysis and Theory; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
- Kim, Y.; Nelson, P. Optimal regularisation for acoustic source reconstruction by inverse methods. J. Sound Vib. 2004, 275, 463–487. [Google Scholar] [CrossRef]
- Yu, L.; Antoni, J.; Leclere, Q. Spectral matrix completion by Cyclic Projection and application to sound source reconstruction from non-synchronous measurements. J. Sound Vib. 2016, 372, 31–49. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Guo, Q.; Chu, N.; Wang, R. Achieving 3D Beamforming by Non-Synchronous Microphone Array Measurements. Sensors 2020, 20, 7308. https://doi.org/10.3390/s20247308
Yu L, Guo Q, Chu N, Wang R. Achieving 3D Beamforming by Non-Synchronous Microphone Array Measurements. Sensors. 2020; 20(24):7308. https://doi.org/10.3390/s20247308
Chicago/Turabian StyleYu, Liang, Qixin Guo, Ning Chu, and Rui Wang. 2020. "Achieving 3D Beamforming by Non-Synchronous Microphone Array Measurements" Sensors 20, no. 24: 7308. https://doi.org/10.3390/s20247308
APA StyleYu, L., Guo, Q., Chu, N., & Wang, R. (2020). Achieving 3D Beamforming by Non-Synchronous Microphone Array Measurements. Sensors, 20(24), 7308. https://doi.org/10.3390/s20247308




