Multi-under-Actuated Unmanned Surface Vessel Coordinated Path Tracking
Abstract
:1. Introduction
1.1. USV Control
1.2. Main Contributions
2. Under-Actuated USV Model and Problem Description
2.1. Under-Actuated USV Model
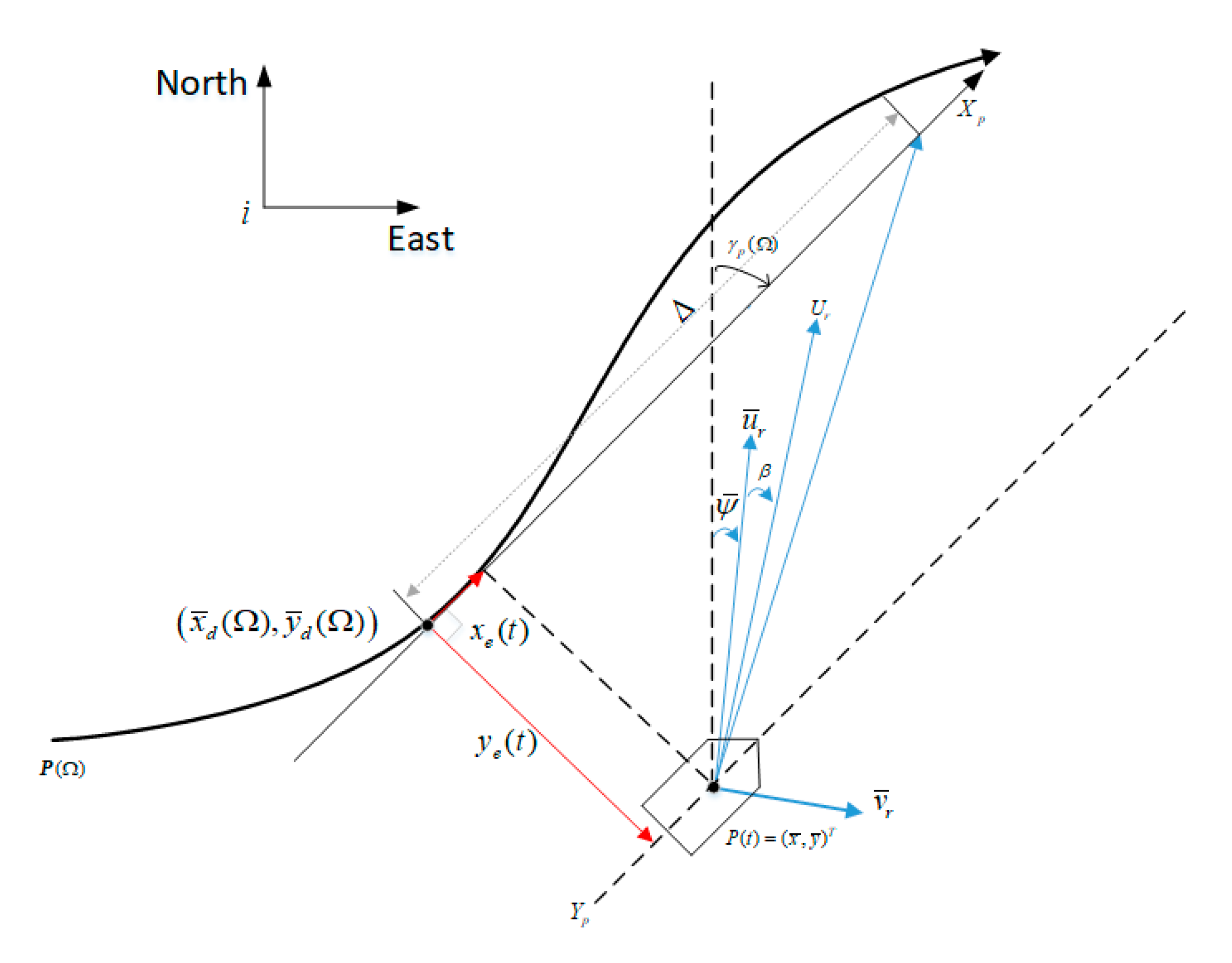
2.2. Coordinate Transformation
2.3. Problem Description of Path Tracking
3. Control Objectives
3.1. Single USV Path Tracking Control Objective
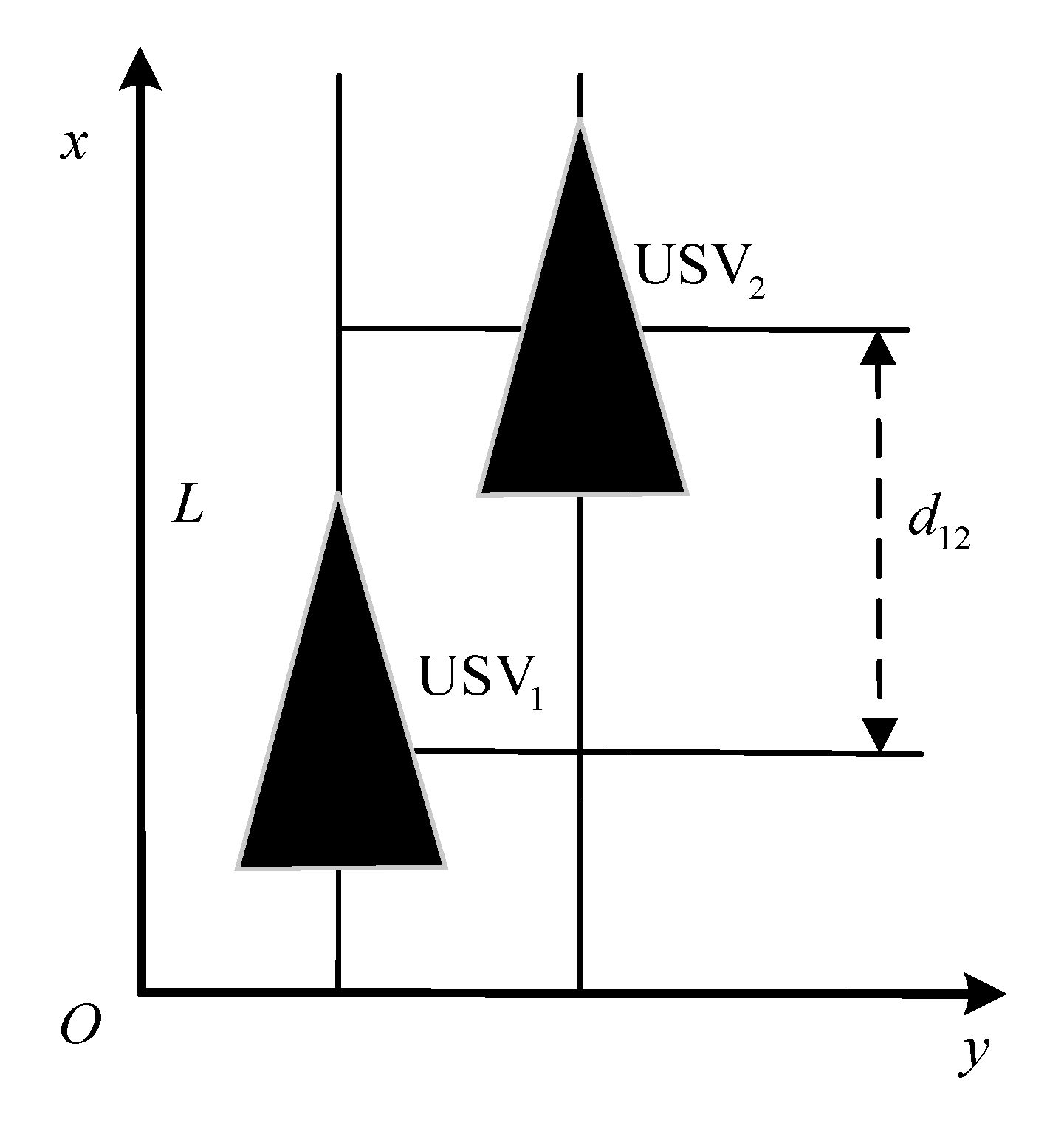
3.2. Coordinated Formation Control Objective
- Designing a single USV path tracking controller for USV control to realize the control objective Equations (24) and (25), of position and heading, and move along the axis at the given velocity ;
- Designing a controller for to coordinate USVs for the expected distance on the axis, so as to meet the coordinated control objective Equation (26) and control the formation velocity tracking to the expected velocity .
4. Controller Design
4.1. Design of Path Tracking Controller Based on Adaptive Integral Line-of-Sight Guidance Algorithm
4.2. Design of Heading and Velocity Controller
4.3. Design of Coordinated Formation Controller
5. Stability Verification
5.1. Stability of Guidance System
5.2. Stability of Heading and Velocity Controller
5.3. Stability of Path Tracking System
5.4. Stability of Coordinated Formation Controller
6. Simulation and Experiment
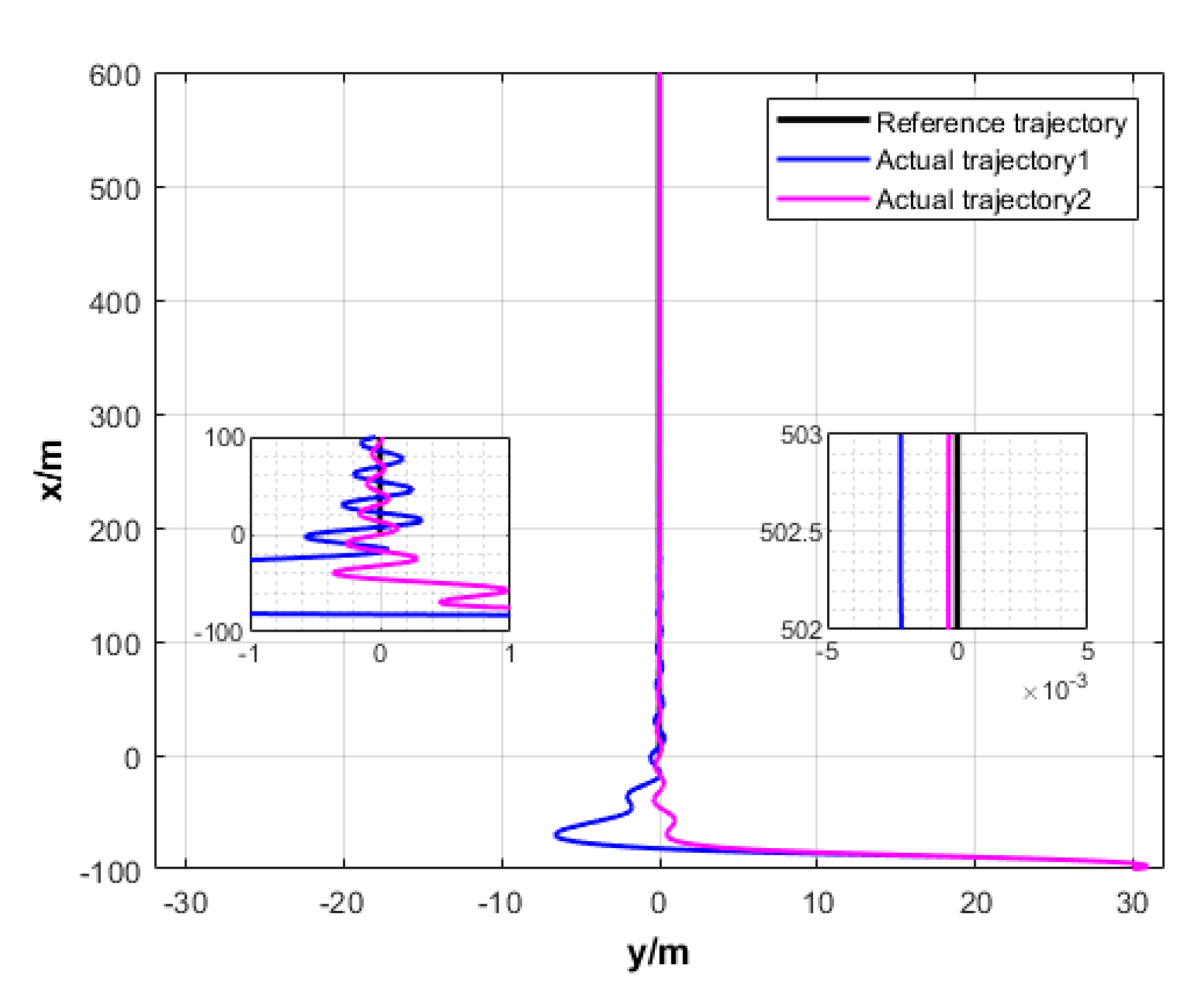
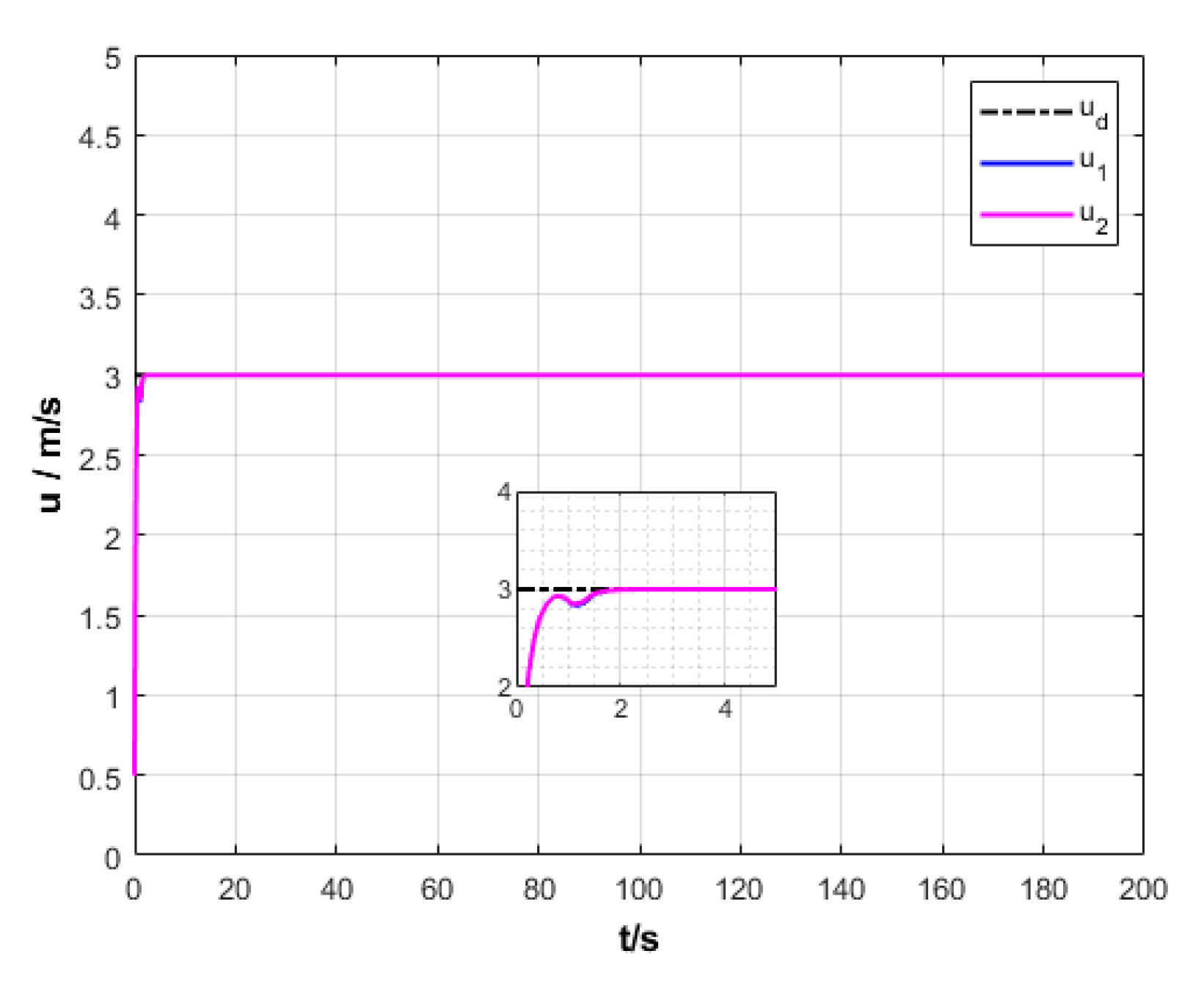
6.1. Single USV Simulation Experiment
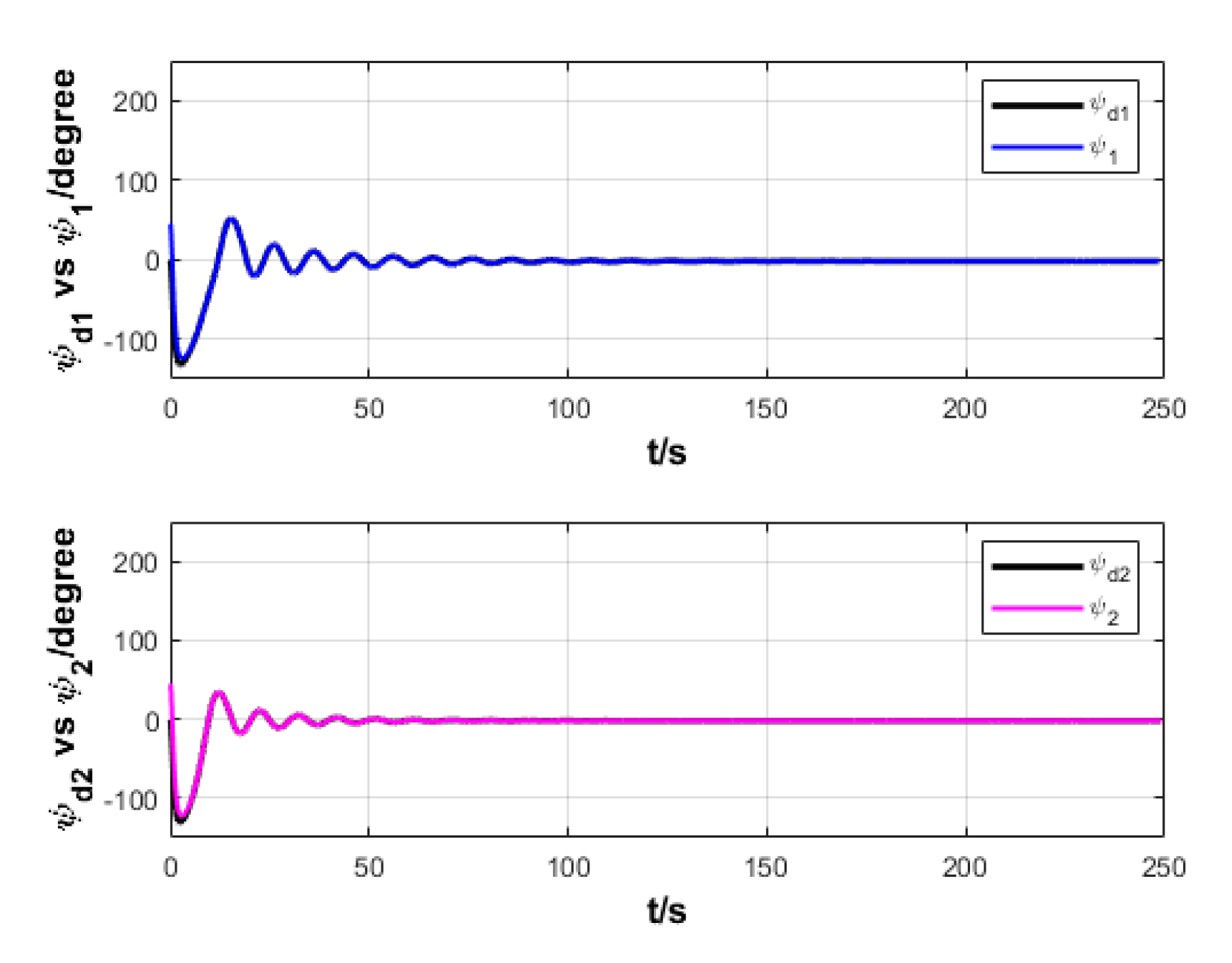
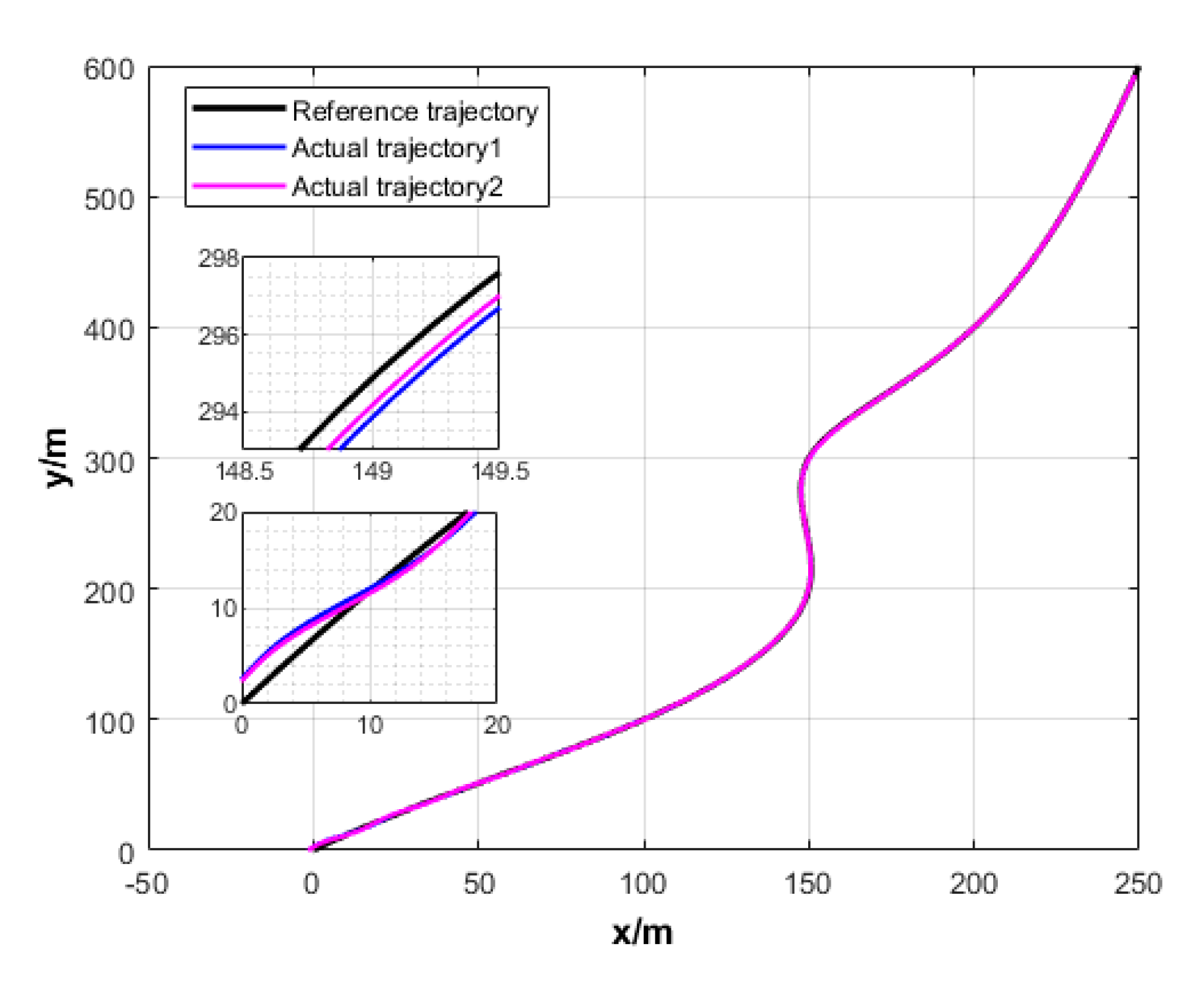
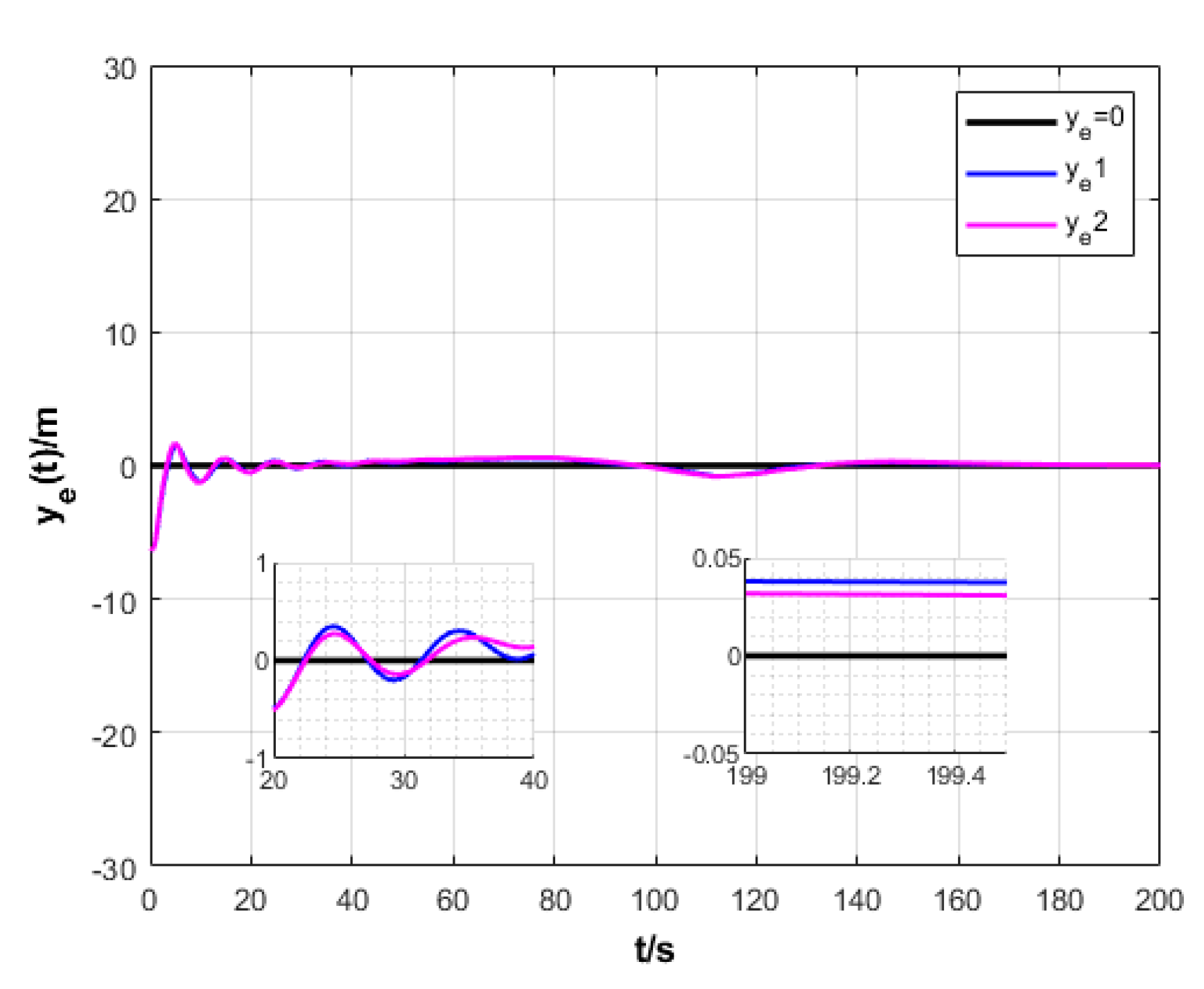
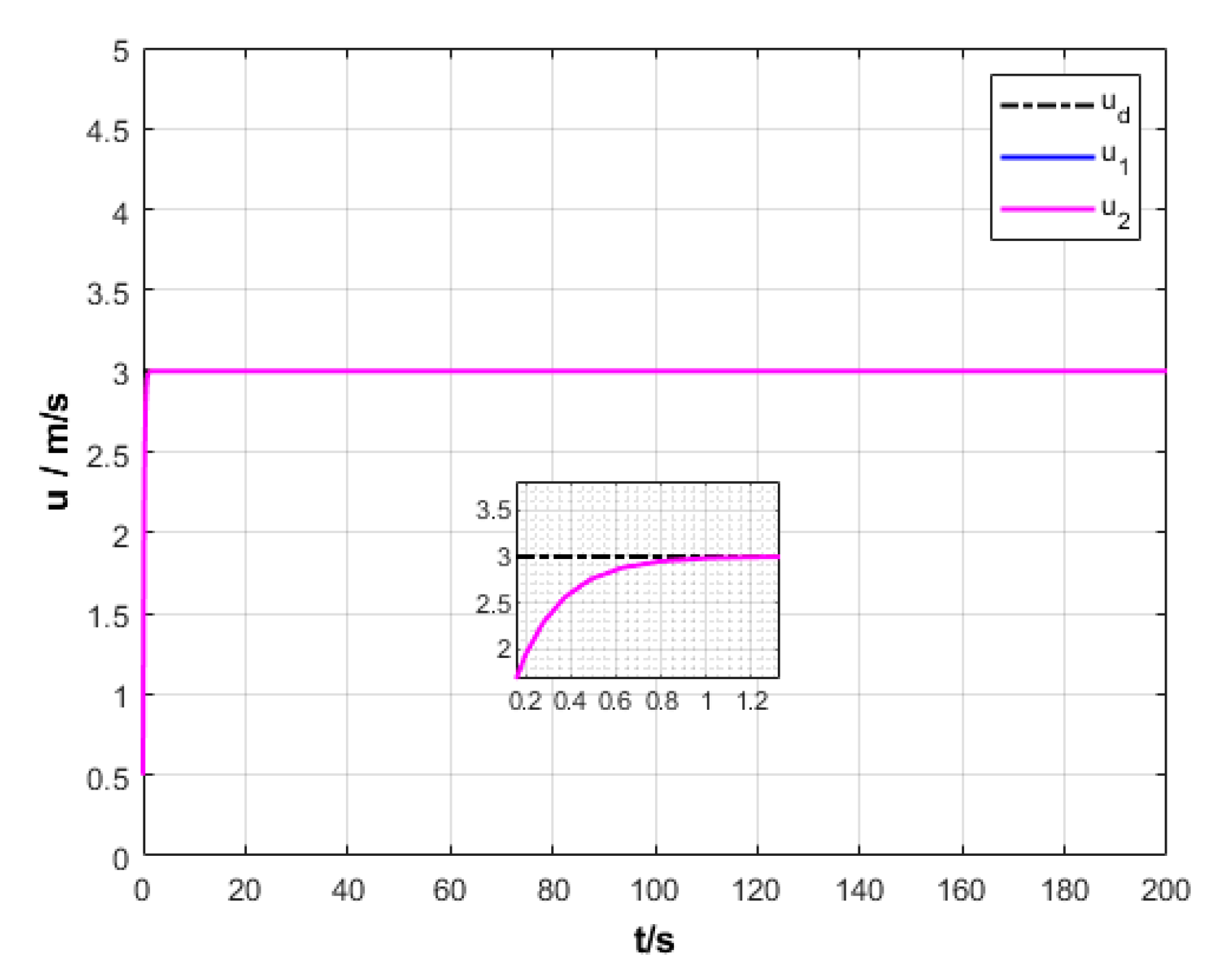
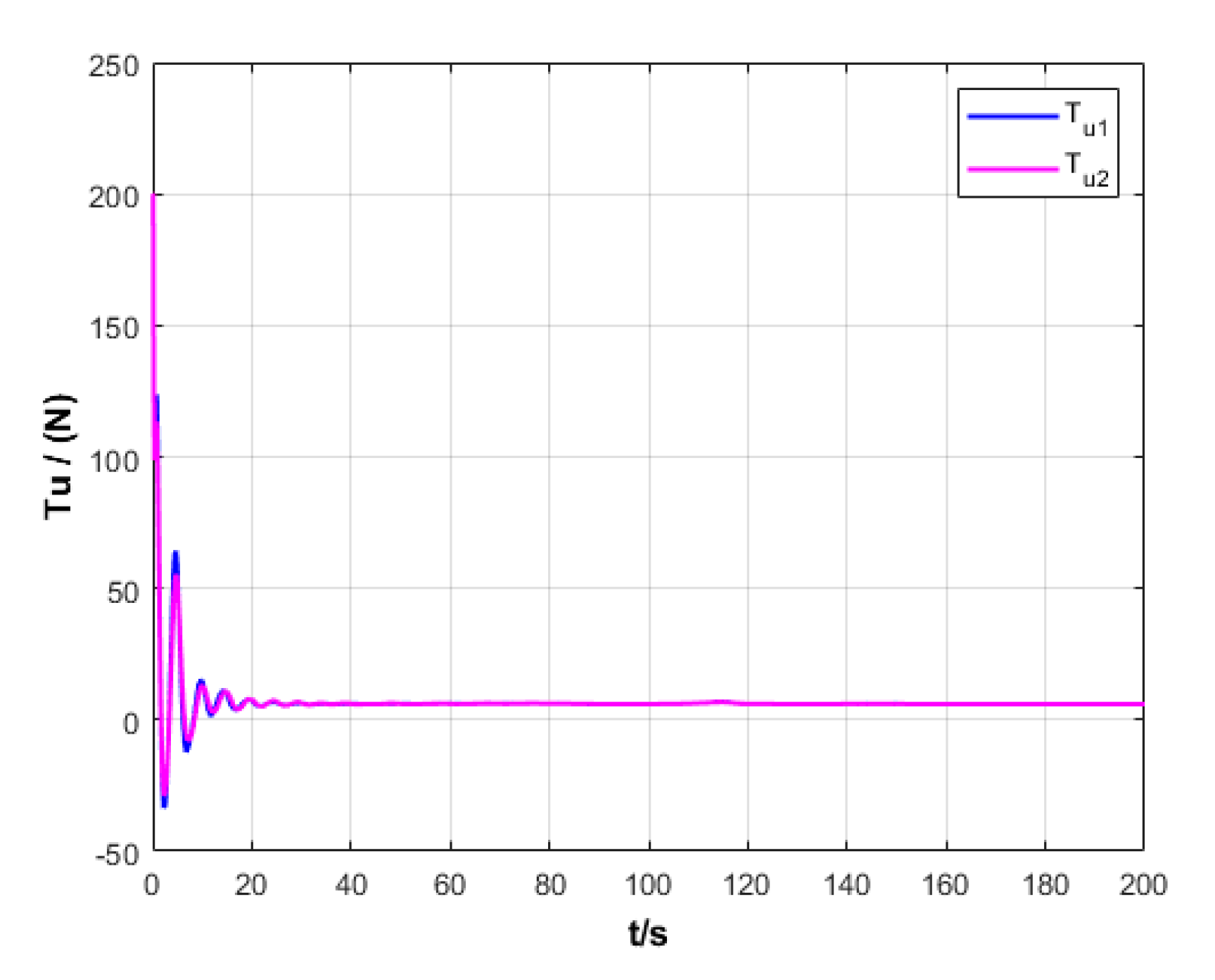
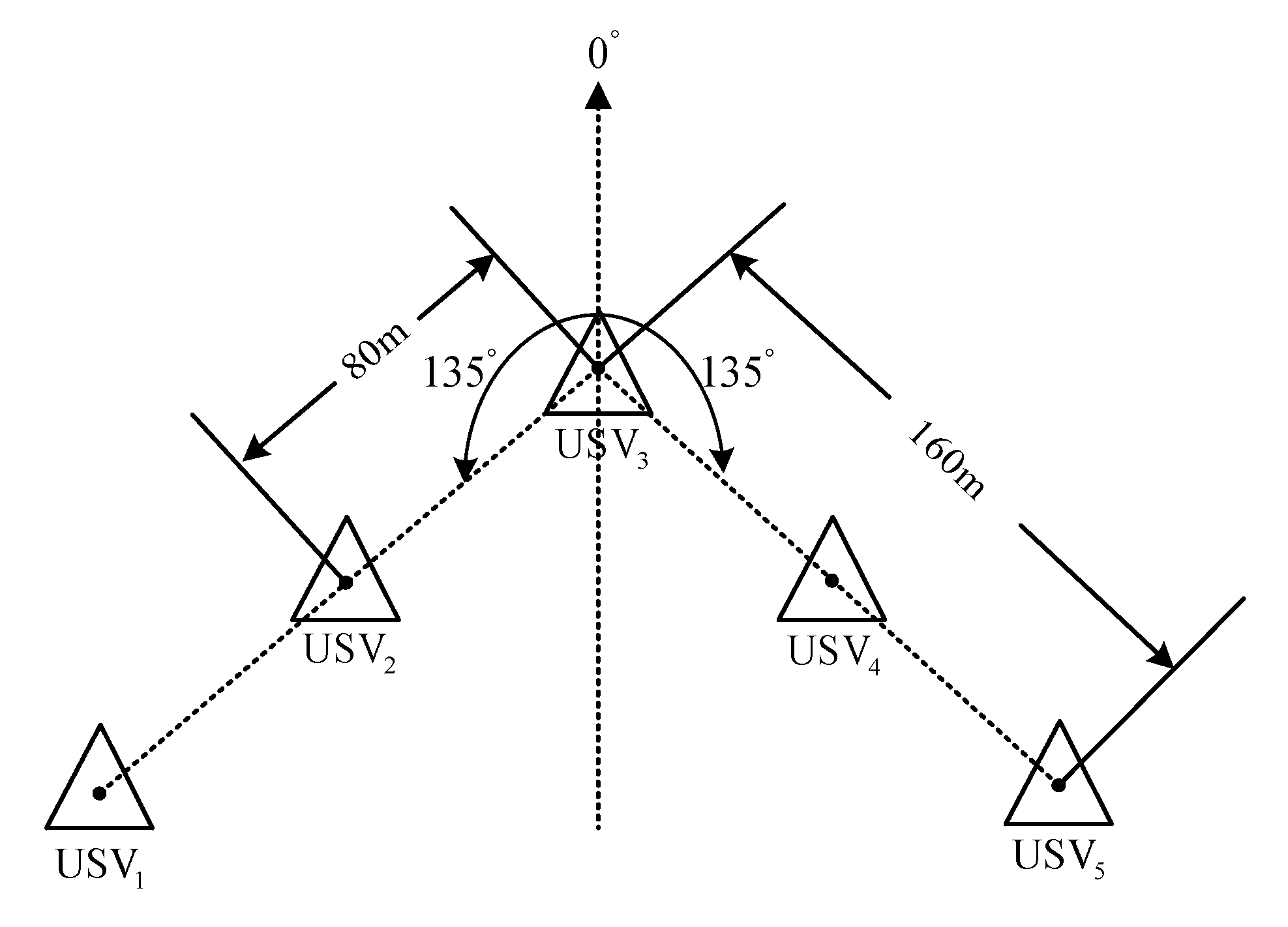
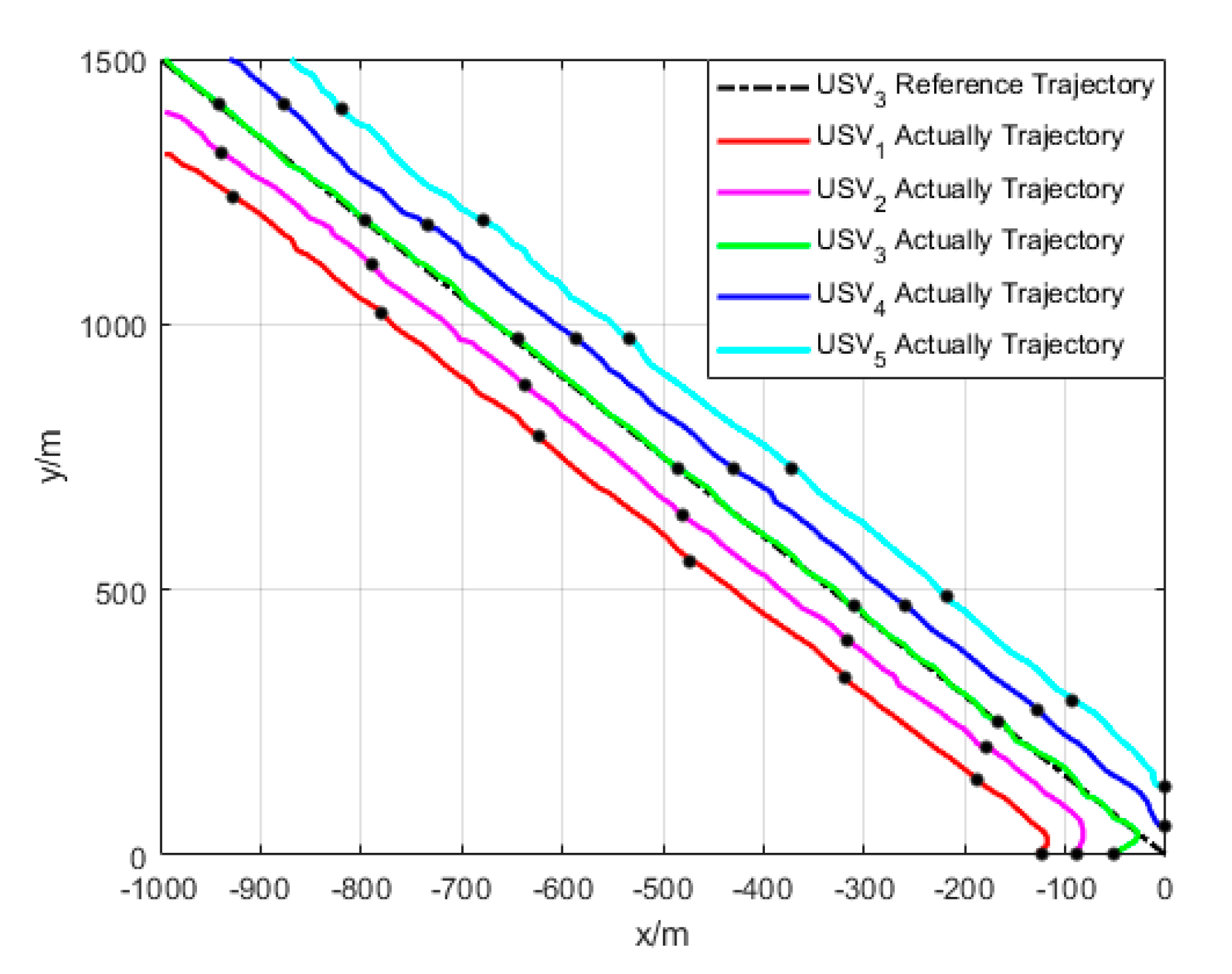
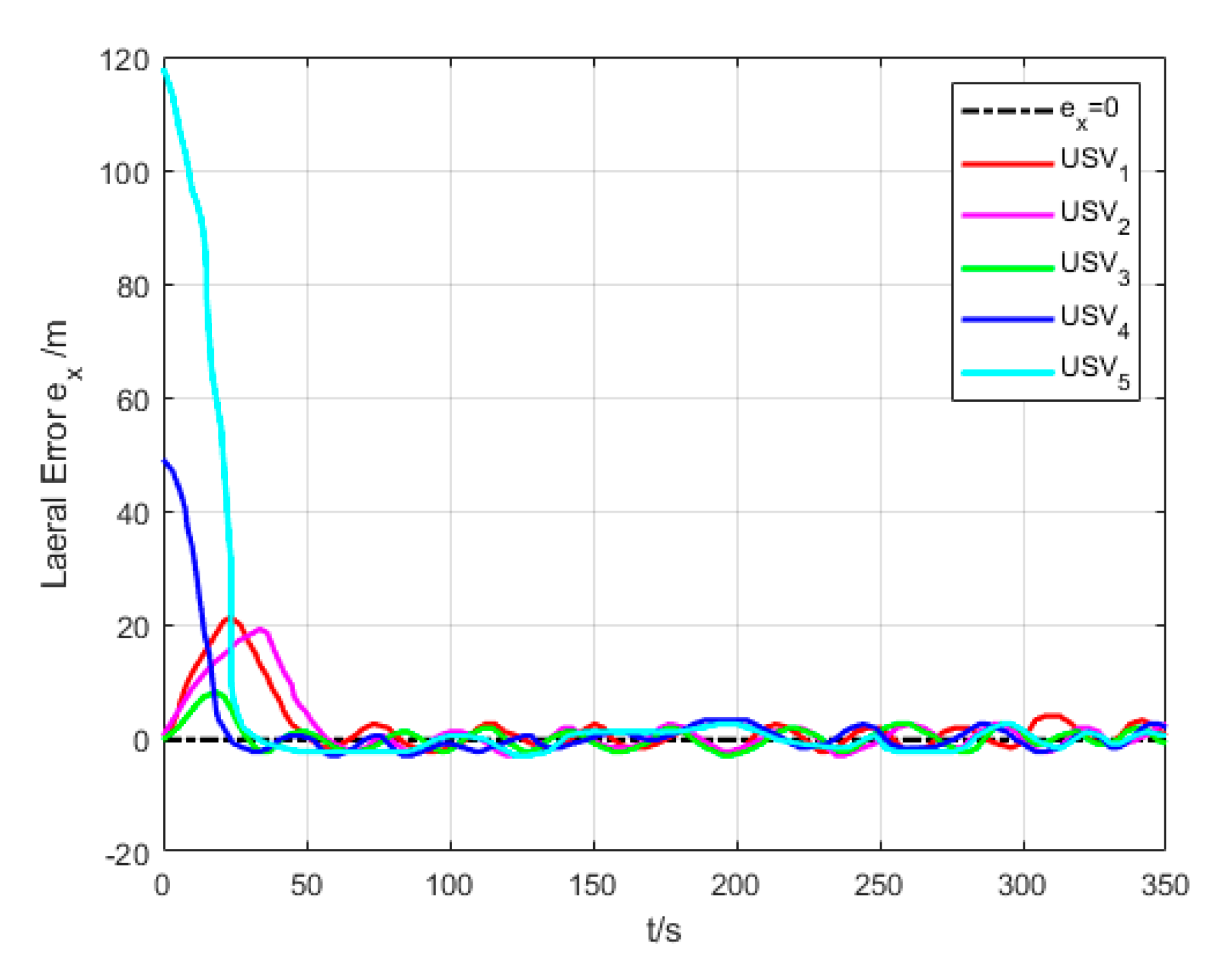
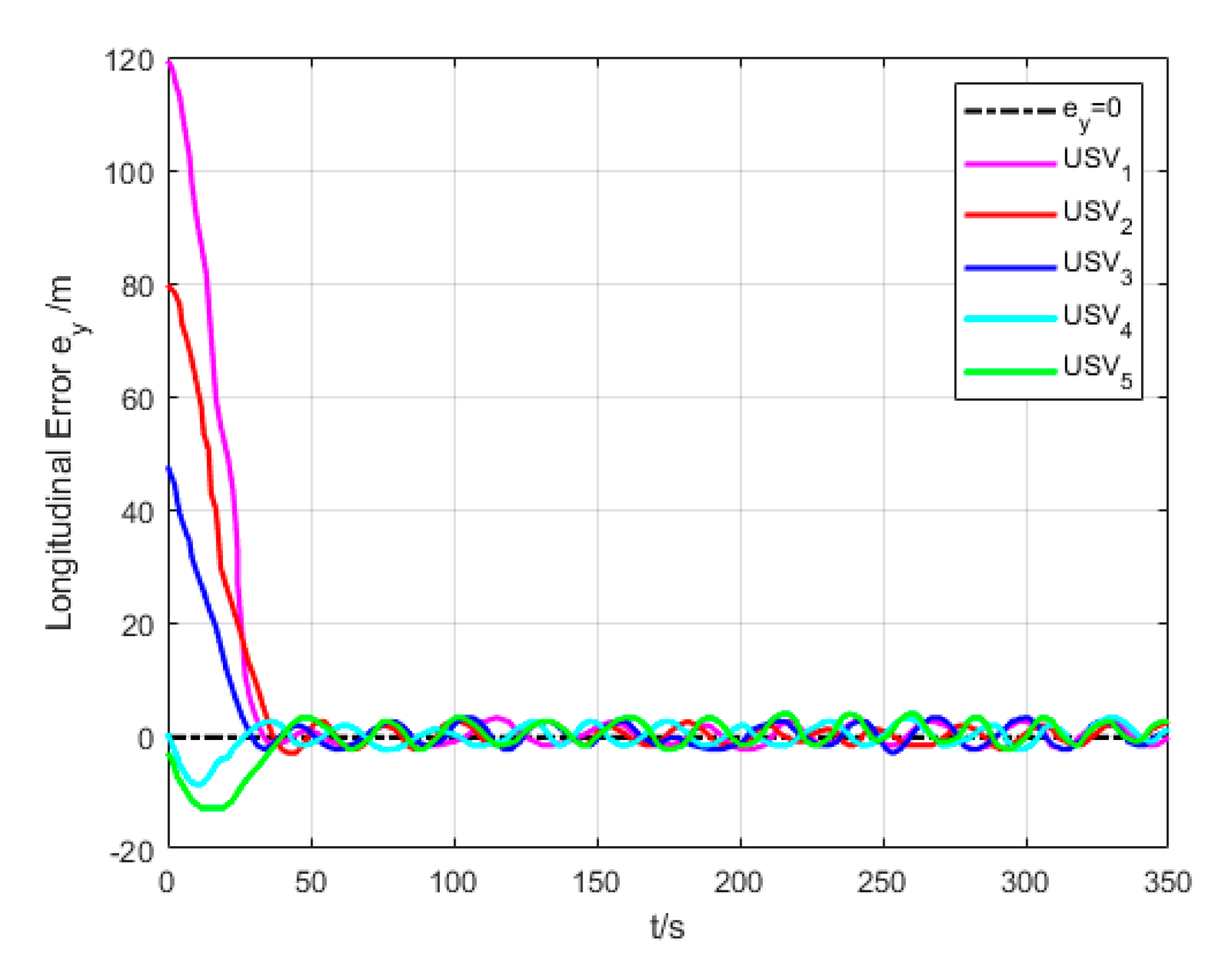
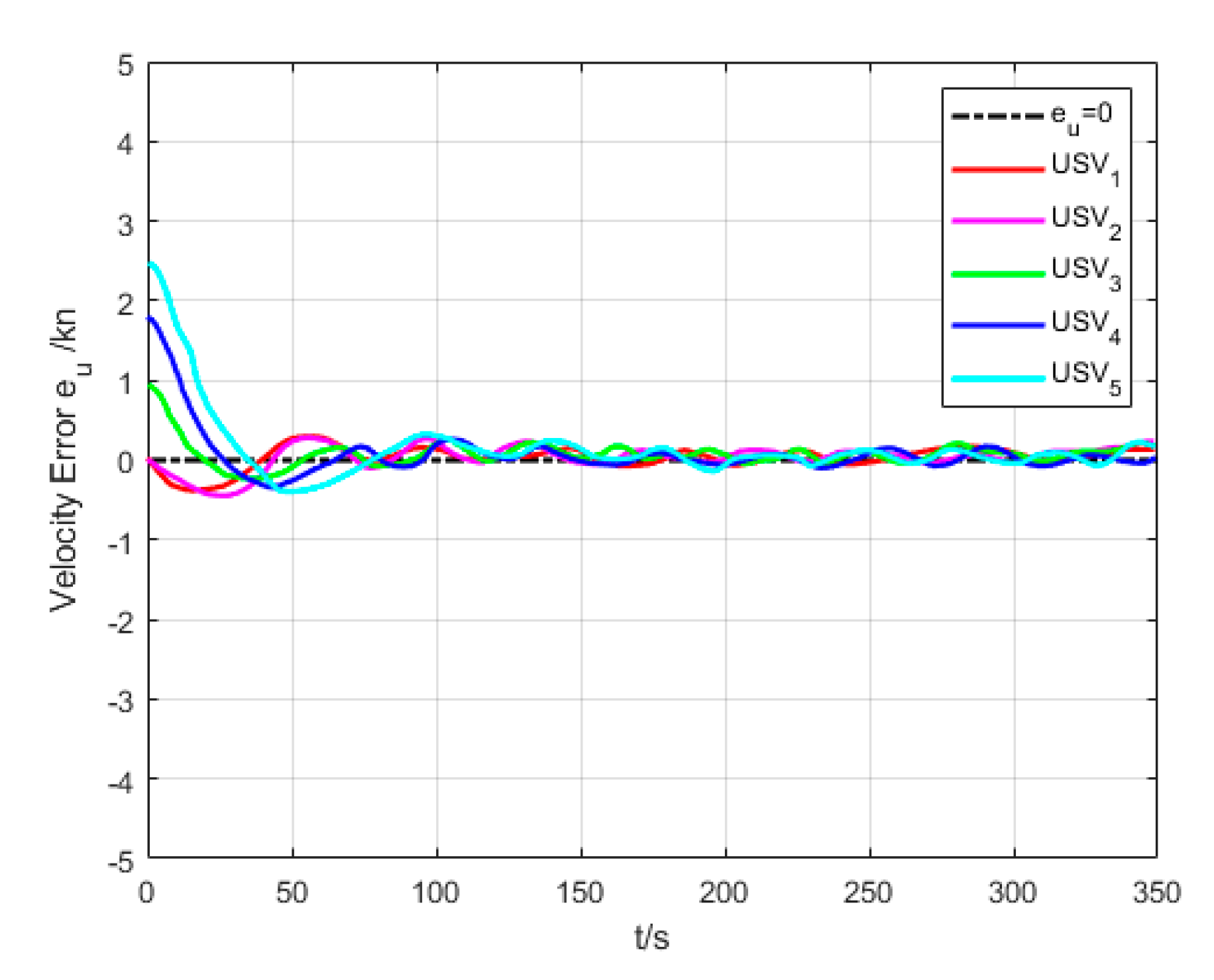
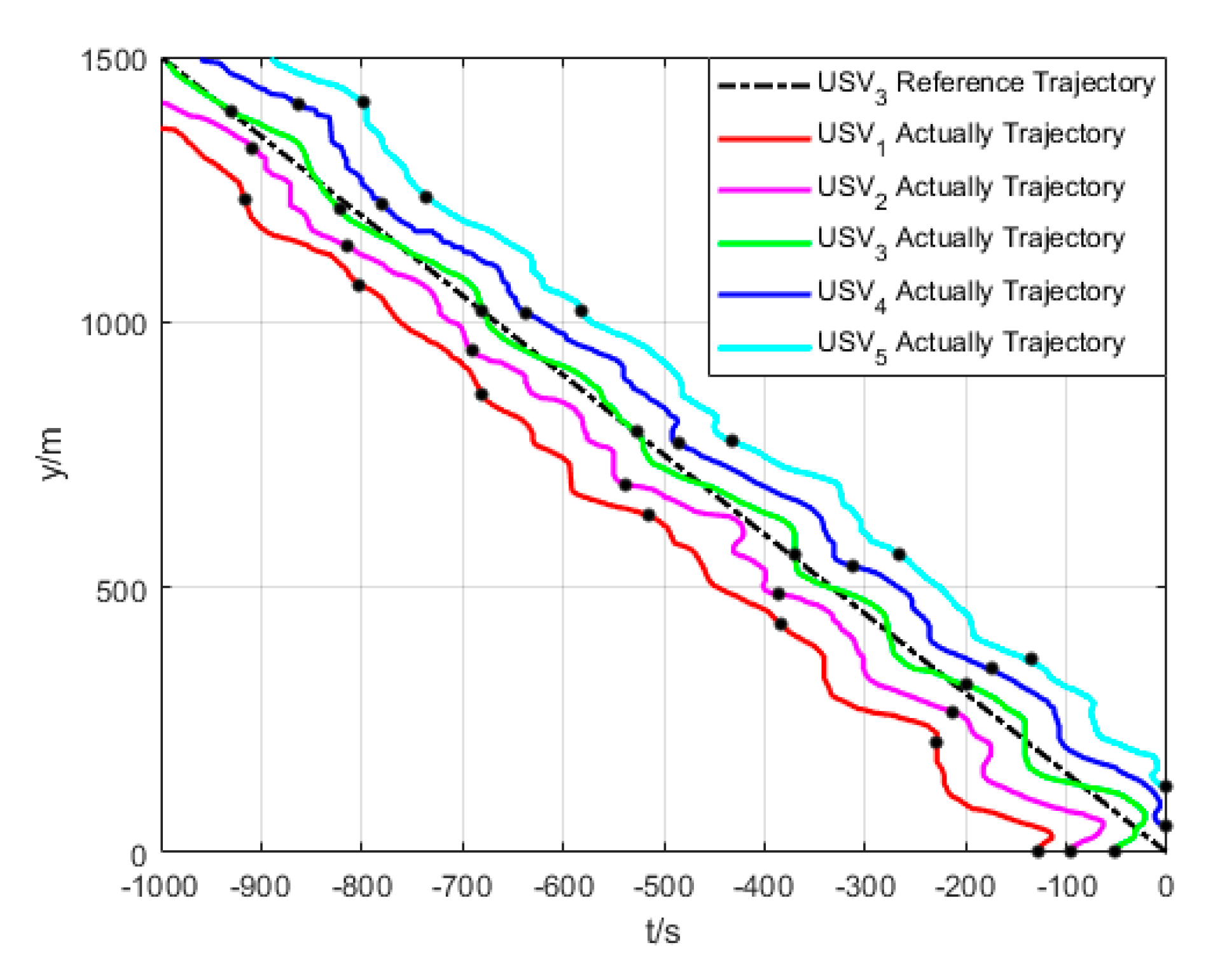
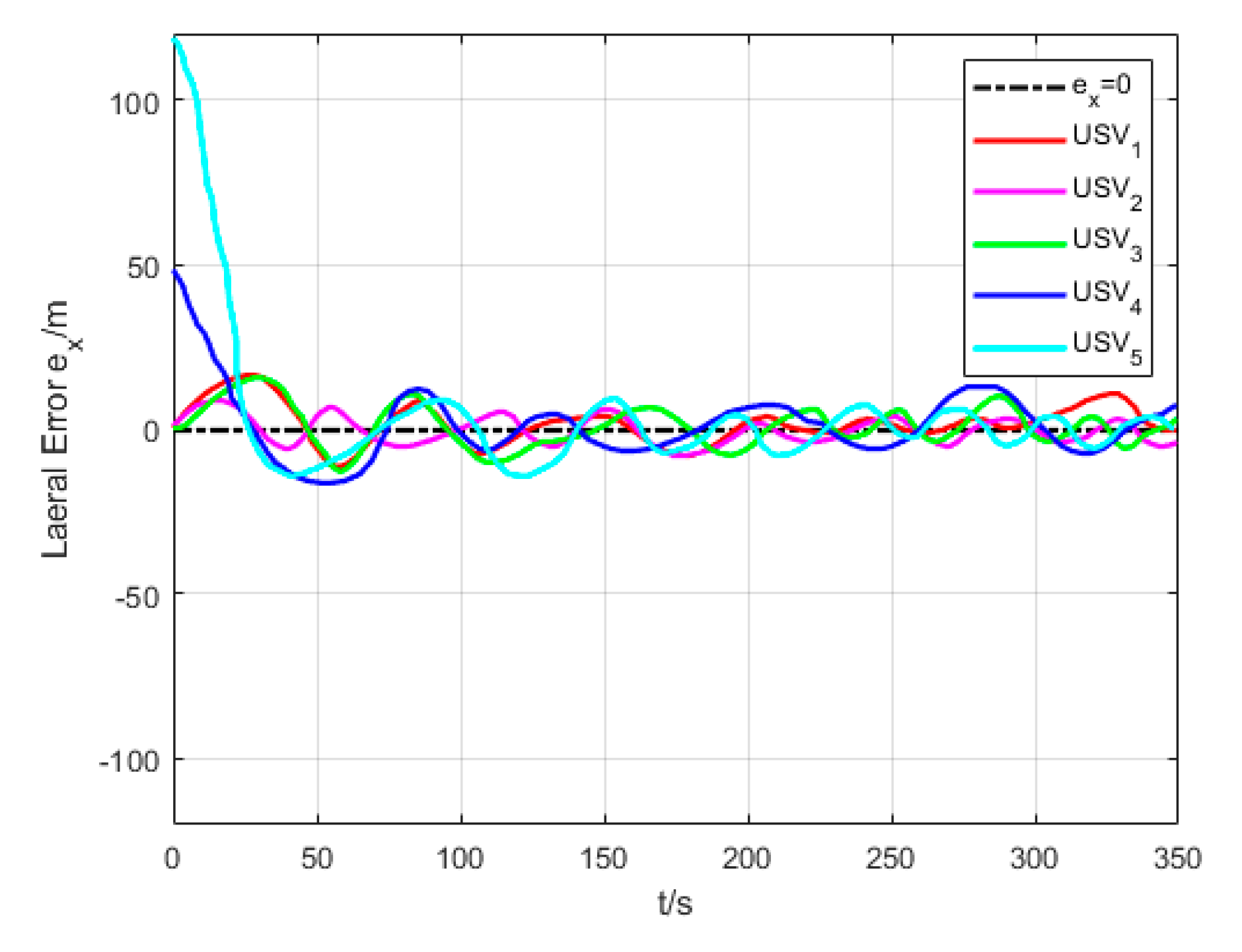
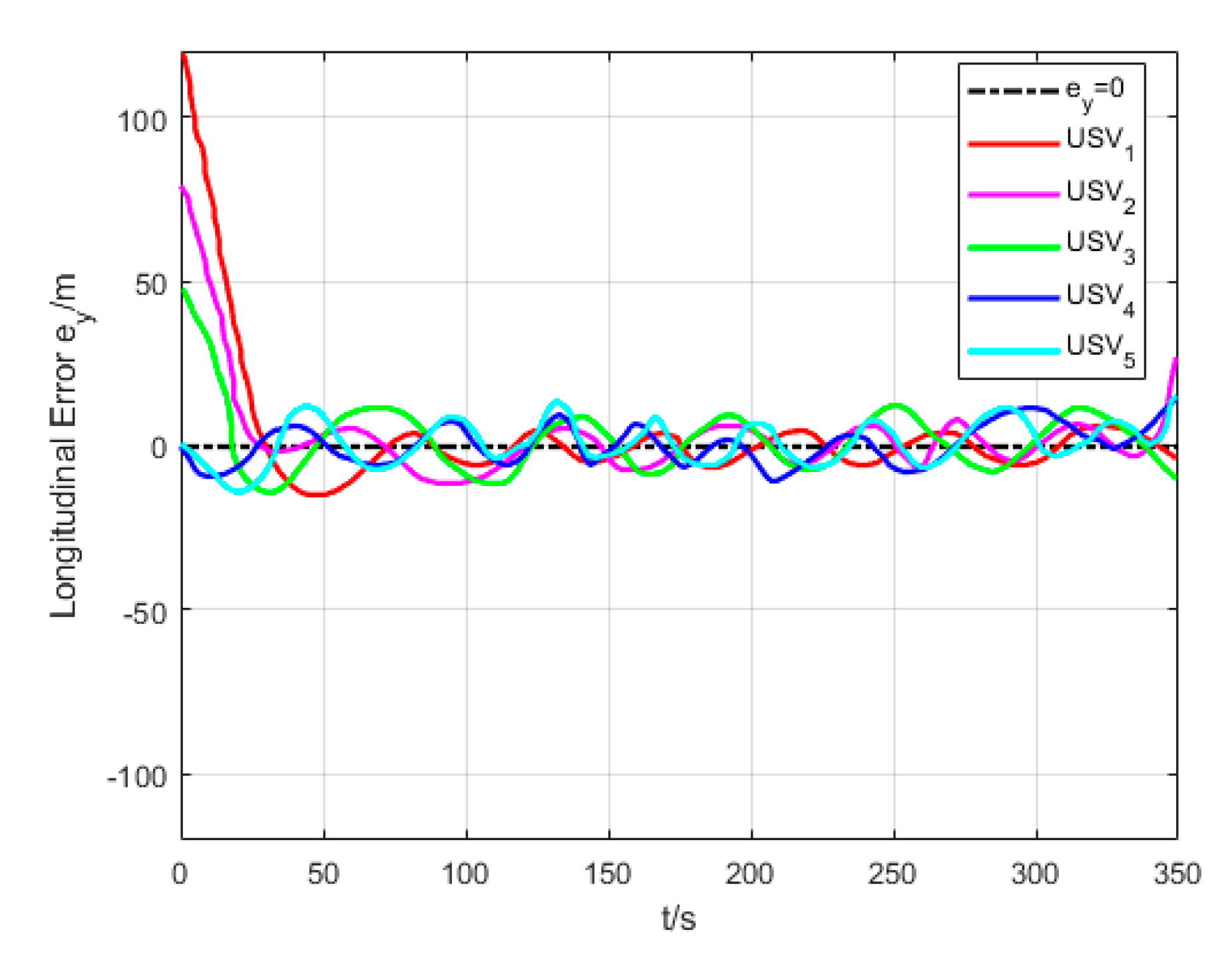
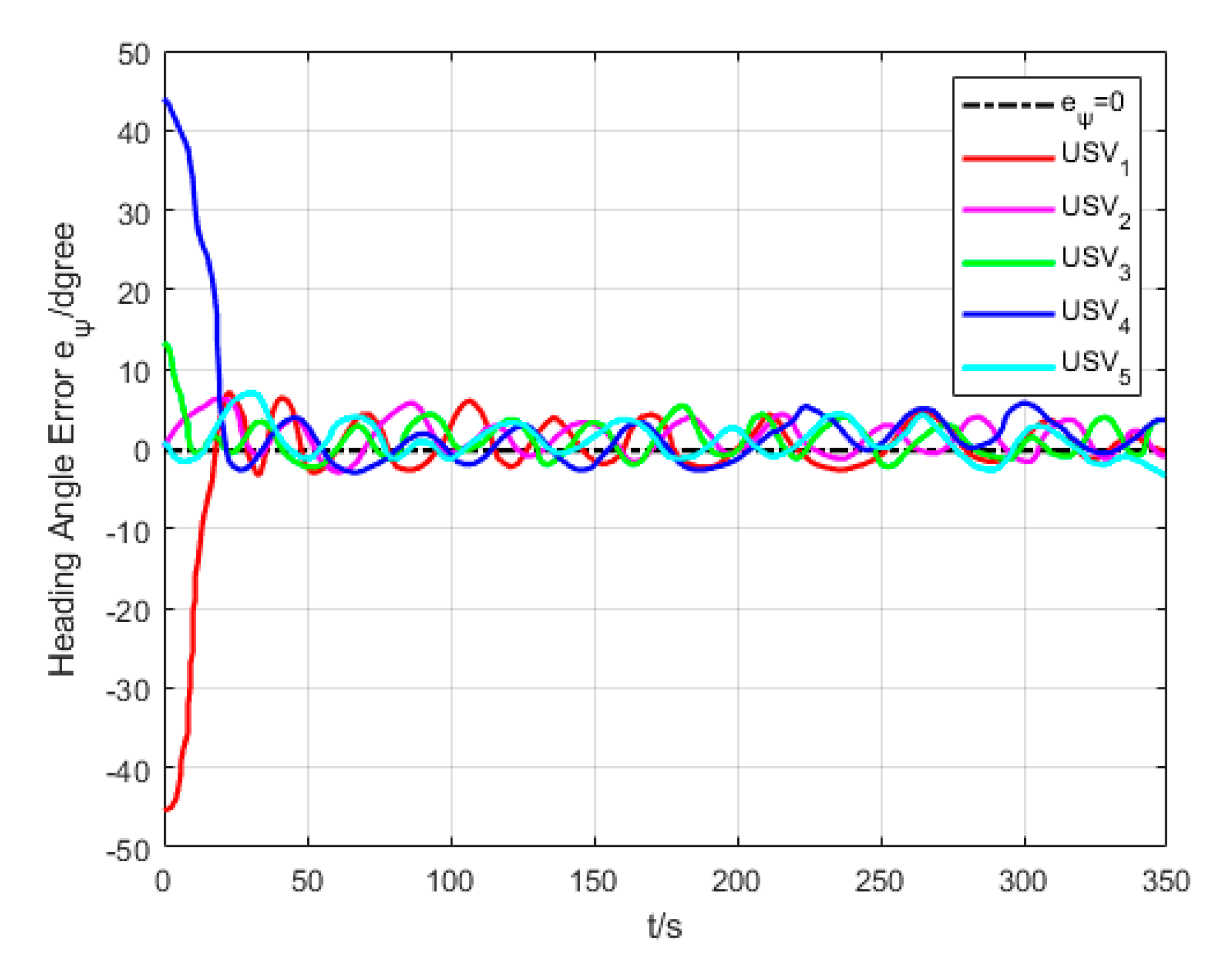
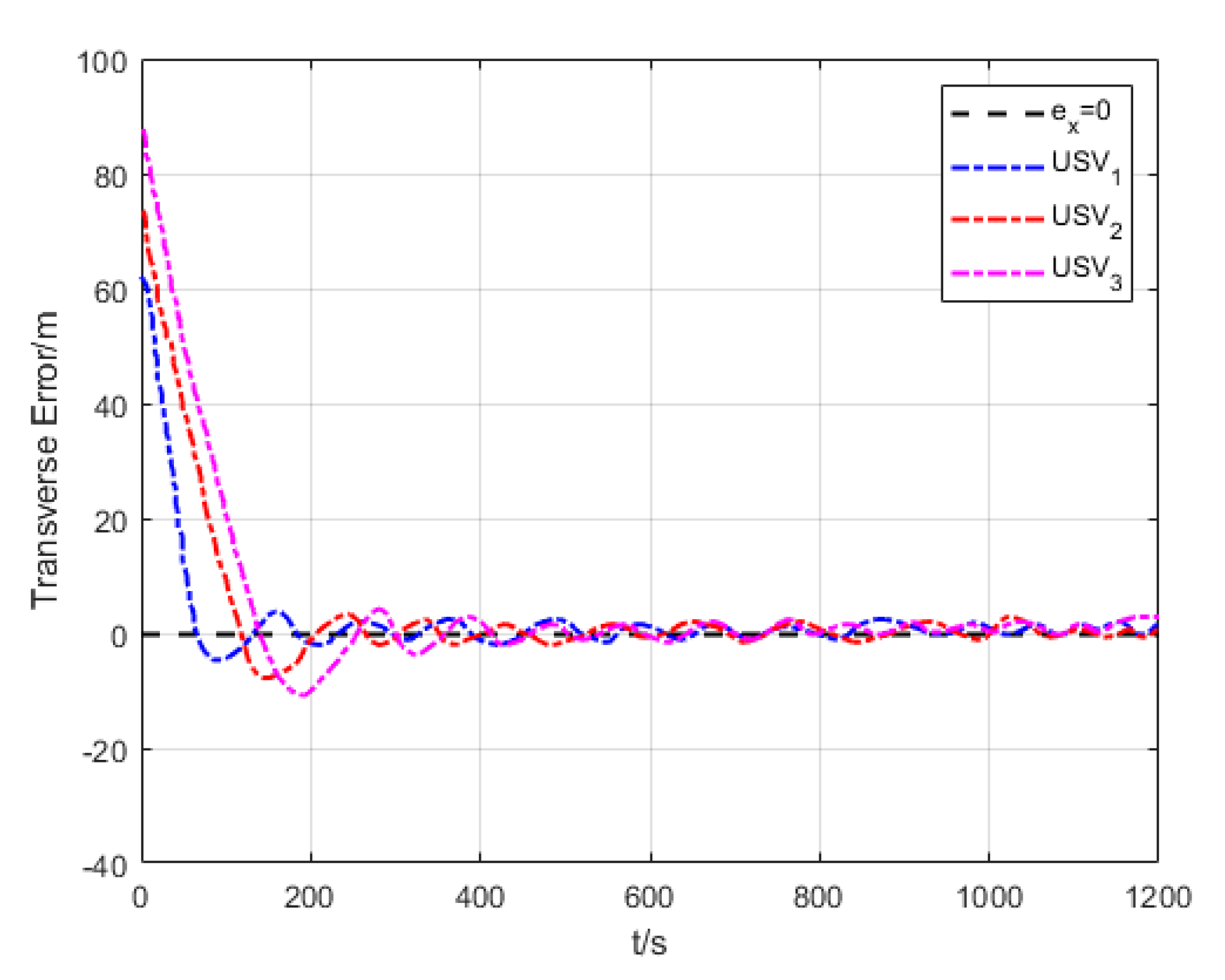
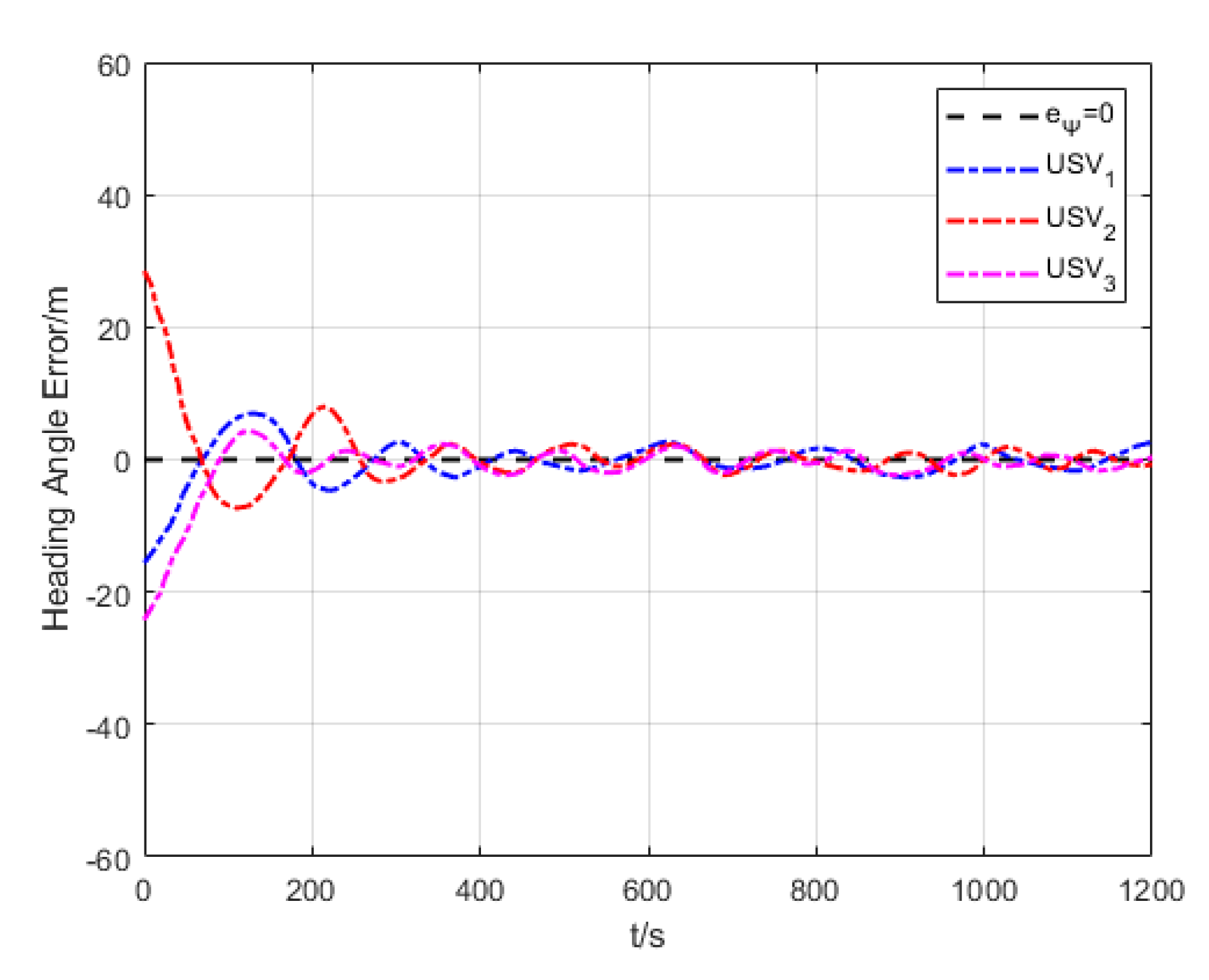
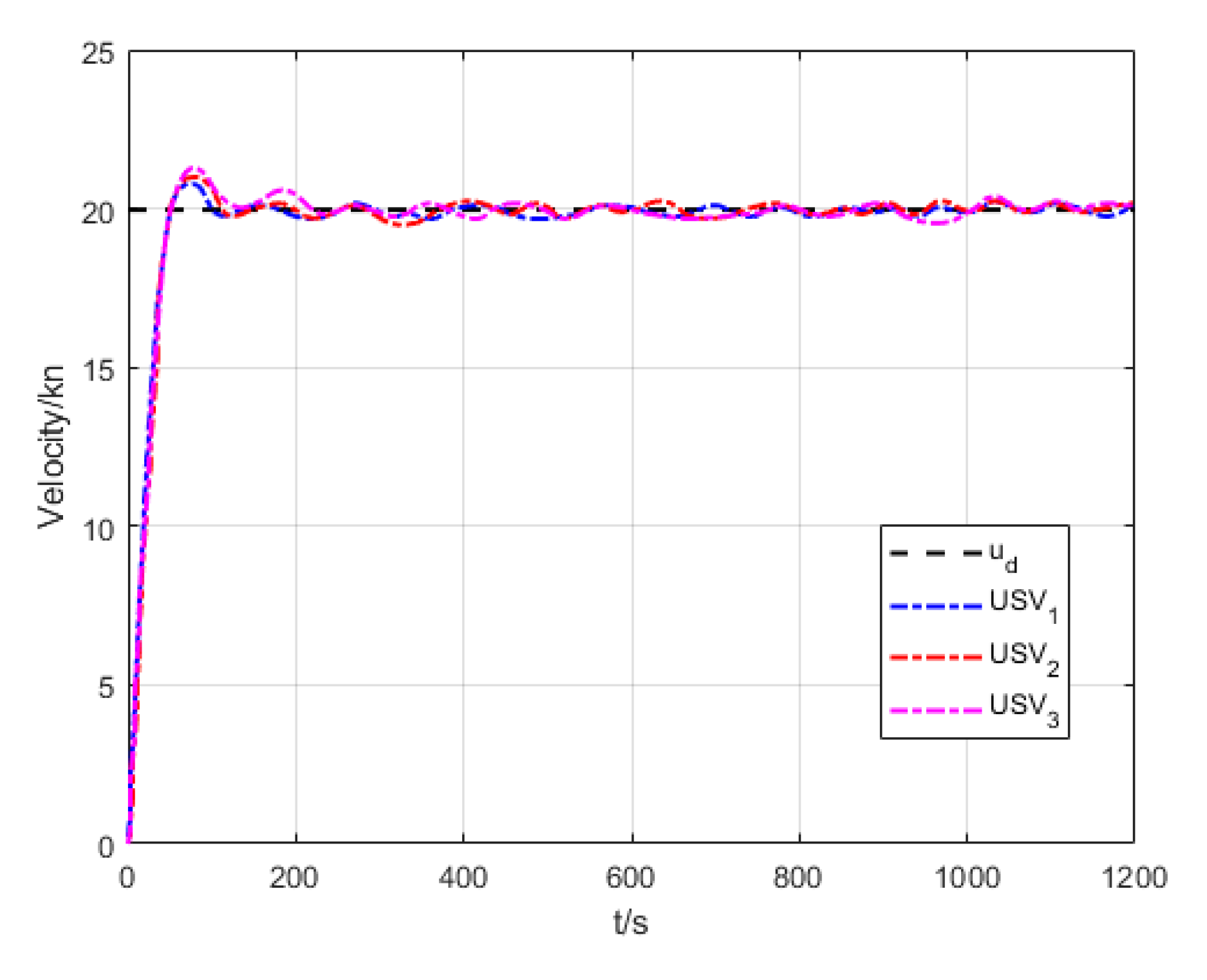
6.2. Formation Cruising Simulation
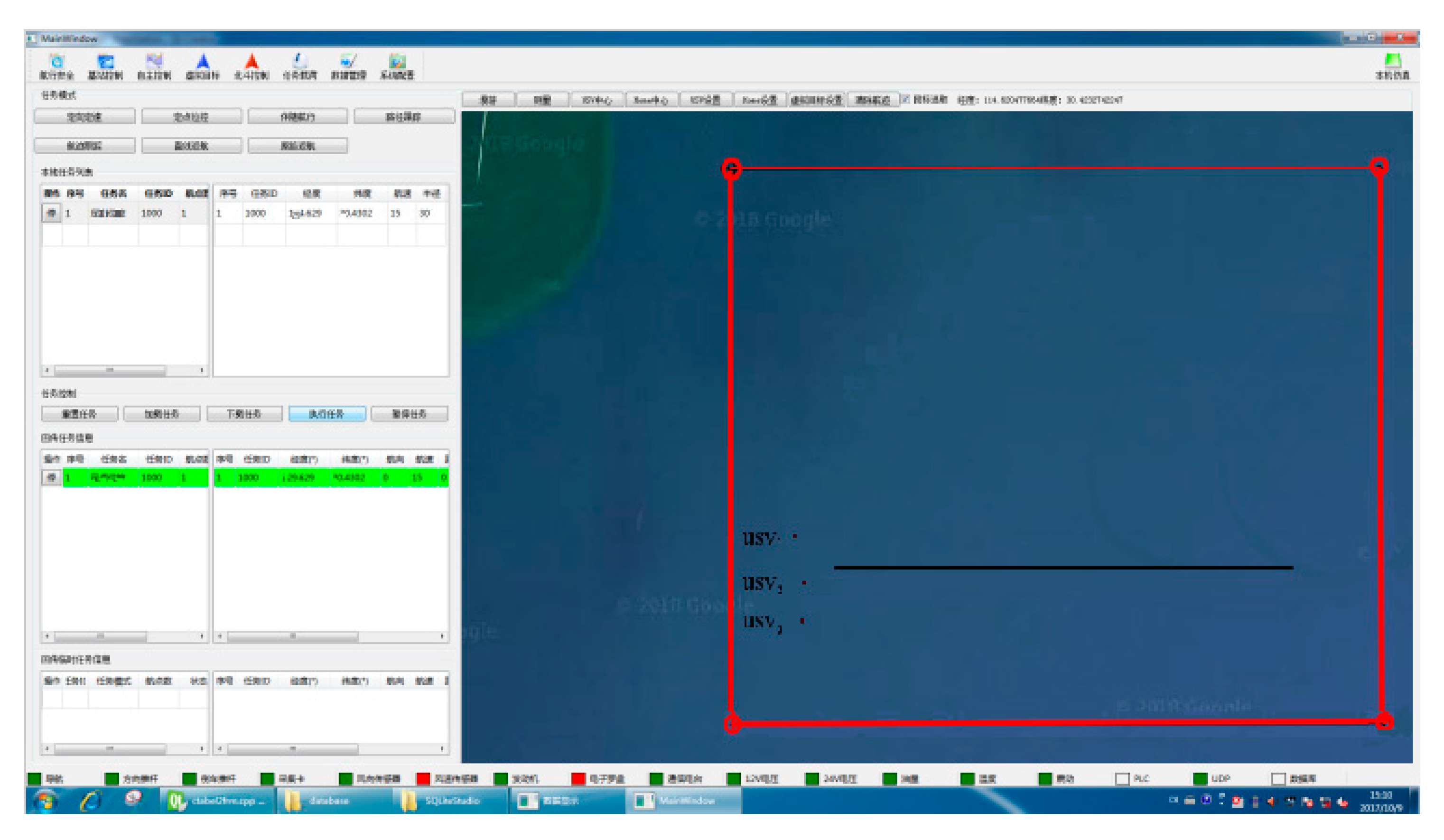
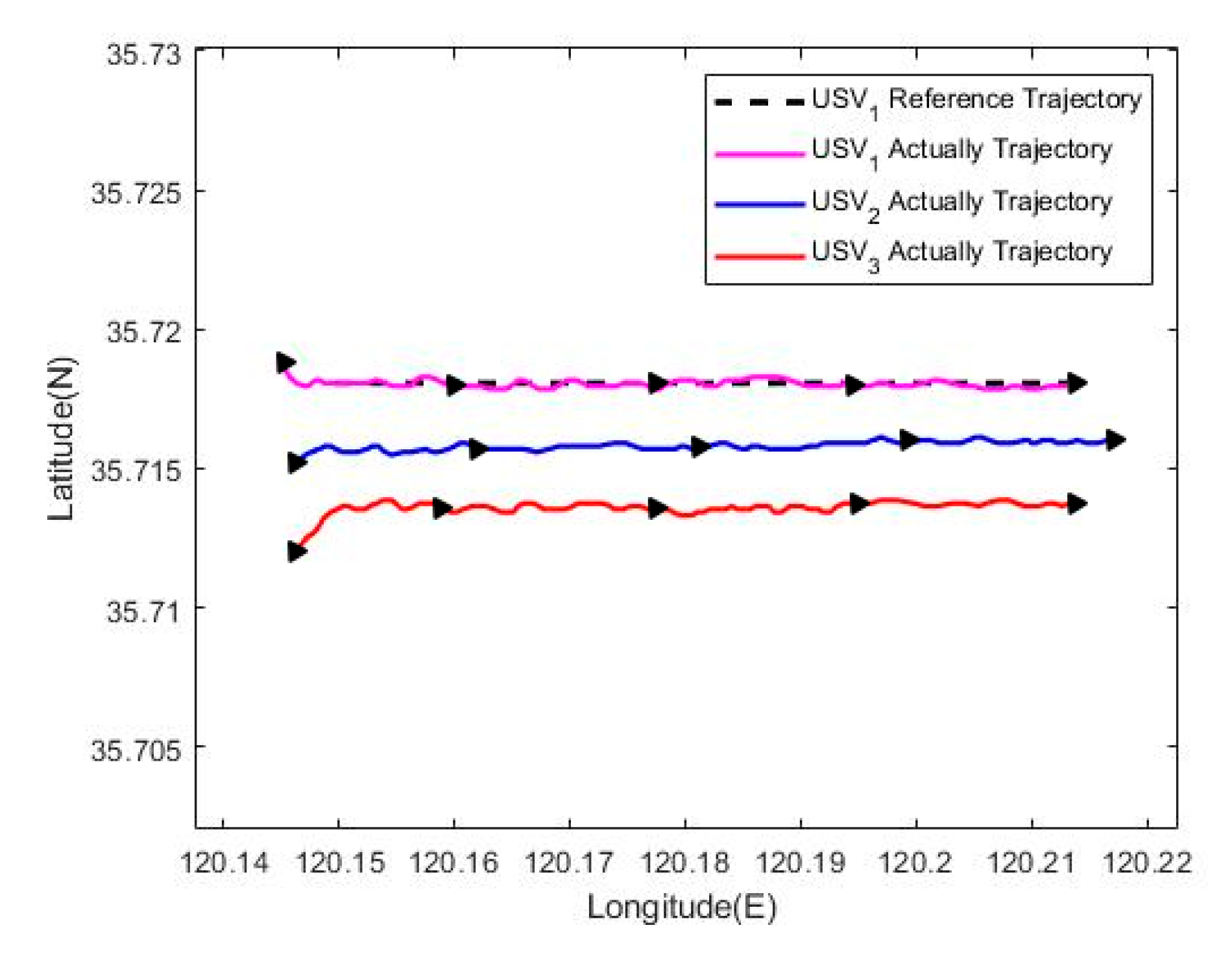
6.3. USV Formation Cruising Field Experiment
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, C.; Chu, X.; Wu, Q. A Review and Prospect of USV Research. Shipbuild. China 2014, 55, 194–205. [Google Scholar]
- Xue, C.; Huang, X.; Zhu, X. Status quo and development trends of foreign military’s unmanned systems. Radar ECM 2016, 36, 1–5. [Google Scholar]
- Li, J. Development and Application of USV. Fire Control Command Control 2012, 6, 203–207. [Google Scholar]
- Børhaug, E.; Pavlov, A.; Pettersen, K.Y. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 4984–4991. [Google Scholar]
- John, S.; Pedro, O.J. Neural network-based adaptive feedback linearization control of antilock braking system. Int. J. Artif. Intell. 2013, 10, 21–40. [Google Scholar]
- Caharija, W.; Pettersen, K.Y.; Sørensen, A.J. Relative velocity control and integral LOS for path following of autonomous surface vessels: Merging intuition with theory. Eng. Mar. Environ. 2014, 228, 180–191. [Google Scholar]
- Lekkas, A.M.; Fossen, T.I. Integral LOS path following for curved paths based on a monotone cubic Hermite spline parametrization. IEEE Trans. Control Syst. Technol. 2014, 22, 2287–2301. [Google Scholar] [CrossRef]
- Fredriksen, E.; Pettersen, K.Y. Global-exponential waypoint maneuver -ing of ships: Theory and Experiments. Automatica 2006, 42, 677–687. [Google Scholar] [CrossRef]
- Blažic, S. On periodic control laws for mobile robots. IEEE Trans. Ind. Electron. 2014, 61, 3660–3670. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, D.; Peng, Z. Design and validation of path tracking controller for USV along straight-lines. J. Dalian Marit. Univ. 2015, 4, 14–18. [Google Scholar]
- Takács, Á.; Kovács, L.; Rudas, I.J.; Precup, R.E.; Haidegger, T. Models for force control in telesurgical robot systems. Acta Polytech. Hung. 2015, 12, 95–114. [Google Scholar]
- Pozna, C.; Precup, R.E. An approach to the design of nonlinear state-space control systems. Stud. Inf. Control 2018, 27, 5–14. [Google Scholar] [CrossRef] [Green Version]
- Shojaei, K. Leader-follower formation control of underactuated autonomous marine surface vehicles with limited torque. Ocean Eng. 2015, 105, 196–205. [Google Scholar] [CrossRef]
- Shojaei, K. Observer-based neural adaptive formation control of autonomous surface vessels with limited torque. Robot. Auton. Syst. 2016, 78, 83–96. [Google Scholar] [CrossRef]
- Nair, R.R.; Karki, H.; Shukla, A. Fault-tolerant formation control of nonholonomic robots using fast adaptive gain nonsingular terminal sliding-mode control. IEEE Syst. J. 2017, 76, 1–12. [Google Scholar] [CrossRef]
- Xiao, X.; Dufek, J.; Woodbury, T.; Murphy, R. UAV assisted USV visual navigation for marine mass casualty incident response. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Columbia, DC, Canada, 24–28 September 2017; pp. 6105–6110. [Google Scholar]
- Ghommam, J.; Saad, M. Adaptive leader-follower formation control of underactuated surface vessels under asymmetric range and bearing constraints. IEEE Trans. Veh. Technol. 2018, 67, 852–865. [Google Scholar] [CrossRef]
- Wang, P.K.C. Navigation strategies for multiple autonomous robots moving in formation. J. Robot. Syst. 1991, 8, 177–195. [Google Scholar] [CrossRef]
- Farhimi, F. Sliding—Mode formation control for underactuated surface vessels. IEEE Trans. Robot. 2007, 23, 617–622. [Google Scholar] [CrossRef]
- Lewis, M.A.; Tan, K.H. High precision formation control of mobile robots using virtual structures. Auton. Robots 1997, 4, 387–403. [Google Scholar] [CrossRef]
- Mingyu, F.; Lingling, Y.; Jianfang, J. Formation control of autonomous surface vessels with saturation constraint. Control Theory Appl. 2017, 34, 663–670. [Google Scholar]
- Lin, A.; Jiang, D.; Zeng, J. Underactuated Ship Formation Control with Input Saturation. Acta Autom. Sin. 2018, 33, 1496–1504. [Google Scholar]
- Dunbar, W.B. Model Predictive Control: Extension to Coordinated Multi-Vehicle Formations and Real-Time Implementation; Califomia Institute of Technology: Pasadena, CA, USA, 2001; pp. 1–18. [Google Scholar]
- Soares, J.M.; Aguiar, A.P.; Pascoal, A. Joint ASV/AUV Range-based formation control: Theory and Experimental Results. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 5579–5585. [Google Scholar]
- Paliotta, C.; Belleter, J.W.D.; Pettersen, K.Y. Adaptive Source Seeking with Leader-Follower Formation Control. Ocean Eng. 2015, 105, 196–205. [Google Scholar]
- Lei, D.; Guo, G. Formation control for ship fleet based on backstepping. Control Decis. 2012, 27, 299–303. [Google Scholar]
- Zhen, Y.; Yan, W.; Zhilin, L. A sliding mode robust control method for under-actuated ship formations. Electr. Mach. Control 2014, 18, 90–96. [Google Scholar]
- Yang, L.; Chen, G. Control method of underactuated surface ship formation based on stable adaptive neural network control law. J. Traffic Transp. Eng. 2014, 14, 120–126. [Google Scholar]
- Anhui, L.; Desong, J.; Jianping, Z. Ship formation control via output feedback with unknown dynamics. Control Theory Appl. 2017, 34, 1222–1229. [Google Scholar]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Fierro, R.; Das, A. A modular architecture for formation control. In Proceedings of the 3rd International Workshop on Robot Motion and Control, Poznan, Poland, 11 November 2002; pp. 285–290. [Google Scholar]
- Hai, H.; Qiang, Z.; Shudi, Z. Adaptive formation control strategy for under-actuated AUVs. J. Harbin Eng. Univ. 2015, 36, 633–637. [Google Scholar]
- Yun, L.; Ying, J. Combination of leader-follower method and potential function about ship formation control. Control Theory Appl. 2016, 33, 1259–1264. [Google Scholar]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hudson County, NJ, USA, 2011. [Google Scholar]
- Wiig, M.S.; Pettersen, K.Y.; Krogstad, T.R. Uniform Semiglobal Exponential Stability of Integral Line-of-Sight Guidance Laws. IFAC Pap. Online 2015, 48, 61–68. [Google Scholar] [CrossRef] [Green Version]
- Breivik, M. Nonlinear Maneuvering Control of Underactuated Ships. Master’s Thesis, Norwegian University of Science and Technology, Gjøvik, Norway, 2003. [Google Scholar]
- Borhaug, E.; Pavlov, A.; Panteley, E. Straight line path following for formations of underactuated marine surface vessels. IEEE Trans. Control Syst. Technol. 2011, 19, 493–506. [Google Scholar] [CrossRef]














| Model Parameter | Value | Model Parameter | Value |
|---|---|---|---|
| 25.8 | 1 | ||
| 33.8 | 2.0 | ||
| −11.748 | 7.0 | ||
| −11.748 | −2.5425 | ||
| 6.813 | −2.5425 | ||
| 1 | 1.422 | ||
| 0 |
| 0 | 120 | 0° | 0 | 0 | 0 | |
| 0 | 85 | 45° | 0 | 0 | 0 | |
| 0 | 55 | 60° | 1 | 0 | 0 | |
| 70 | 0 | 90° | 2 | 1 | 0 | |
| 120 | 0 | 0° | 2.5 | 1 | 0.5 |
| Longitude | Latitude | |||||
|---|---|---|---|---|---|---|
| 137° | 0 | 0 | 0 | |||
| 52° | 0 | 0 | 0 | |||
| 43° | 0 | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Liu, Z.; Zhang, J. Multi-under-Actuated Unmanned Surface Vessel Coordinated Path Tracking. Sensors 2020, 20, 864. https://doi.org/10.3390/s20030864
Li Z, Liu Z, Zhang J. Multi-under-Actuated Unmanned Surface Vessel Coordinated Path Tracking. Sensors. 2020; 20(3):864. https://doi.org/10.3390/s20030864
Chicago/Turabian StyleLi, Zefang, Zhong Liu, and Jianqiang Zhang. 2020. "Multi-under-Actuated Unmanned Surface Vessel Coordinated Path Tracking" Sensors 20, no. 3: 864. https://doi.org/10.3390/s20030864
APA StyleLi, Z., Liu, Z., & Zhang, J. (2020). Multi-under-Actuated Unmanned Surface Vessel Coordinated Path Tracking. Sensors, 20(3), 864. https://doi.org/10.3390/s20030864




