A Highly Linear CMOS Image Sensor Design Based on an Adaptive Nonlinear Ramp Generator and Fully Differential Pipeline Sampling Quantization with a Double Auto-Zeroing Technique
Abstract
1. Introduction
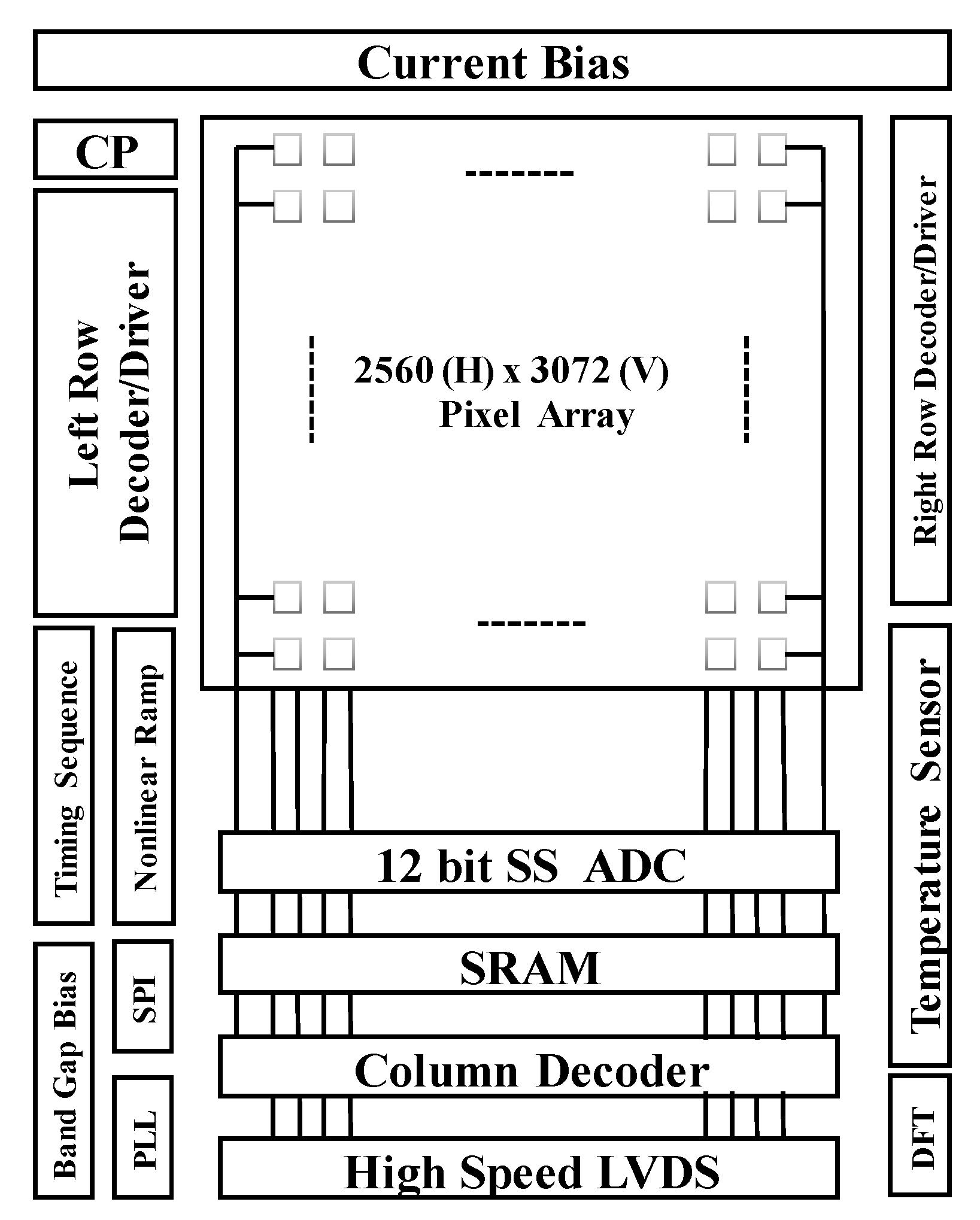
2. Image Sensor Architecture
3. Proposed Techniques
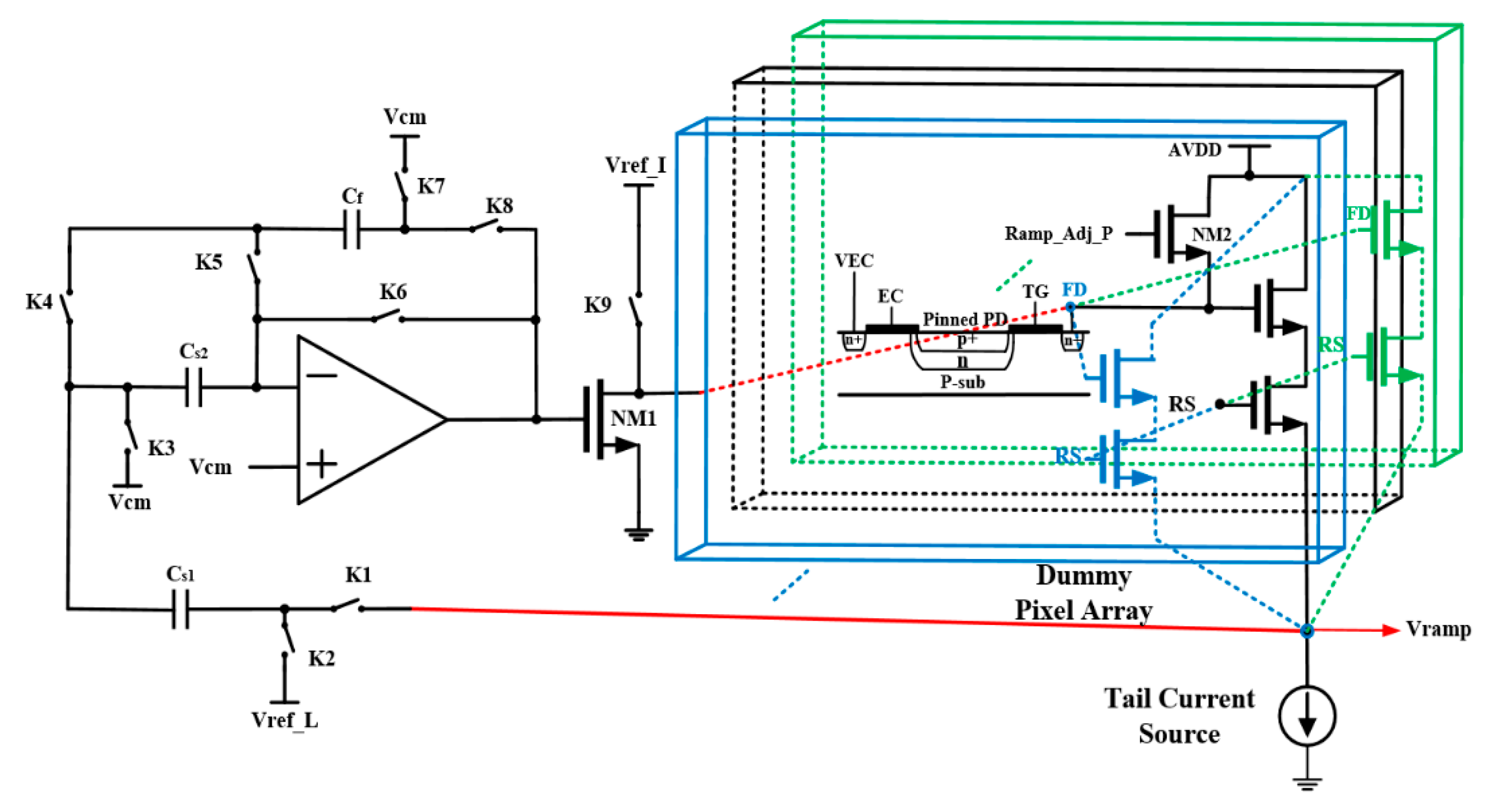
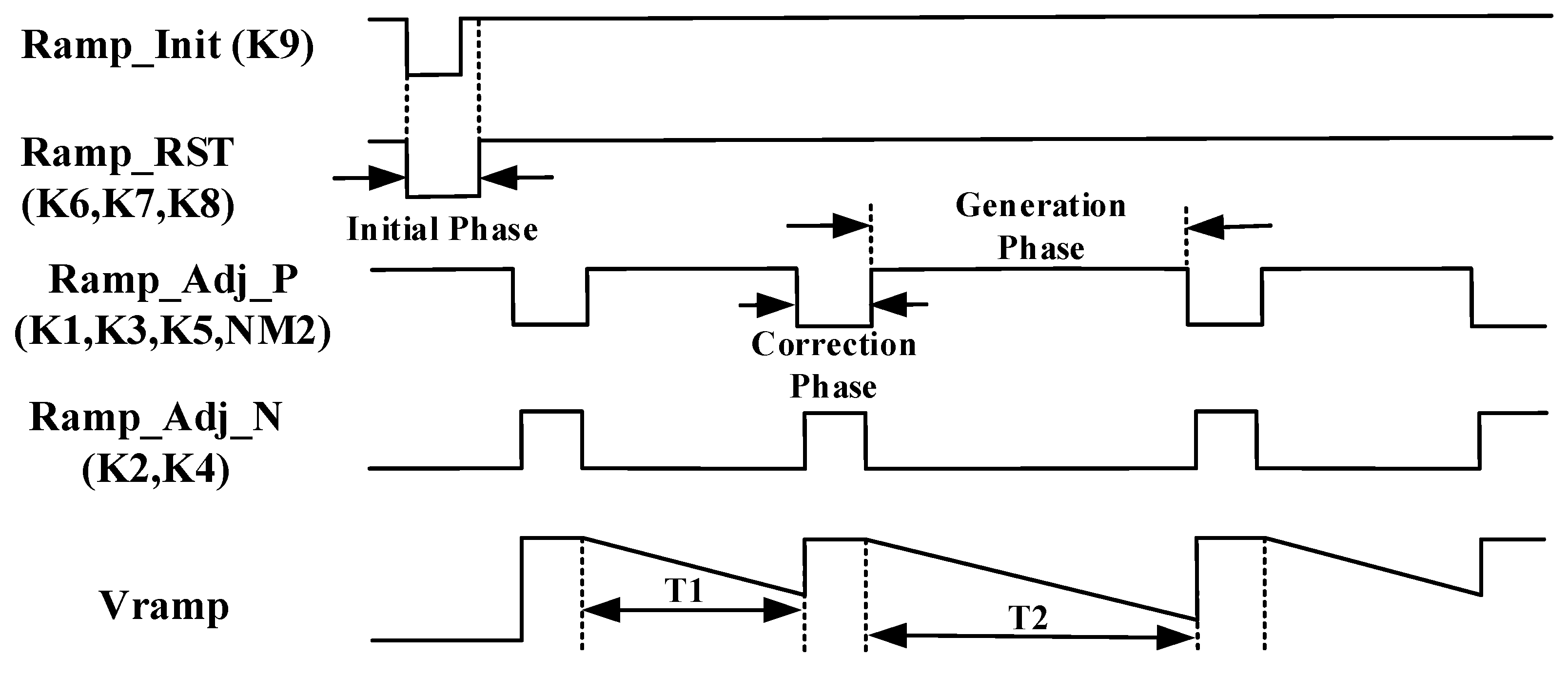
3.1. Nonlinear Ramp Generation Technique Based on Dummy Pixel Array
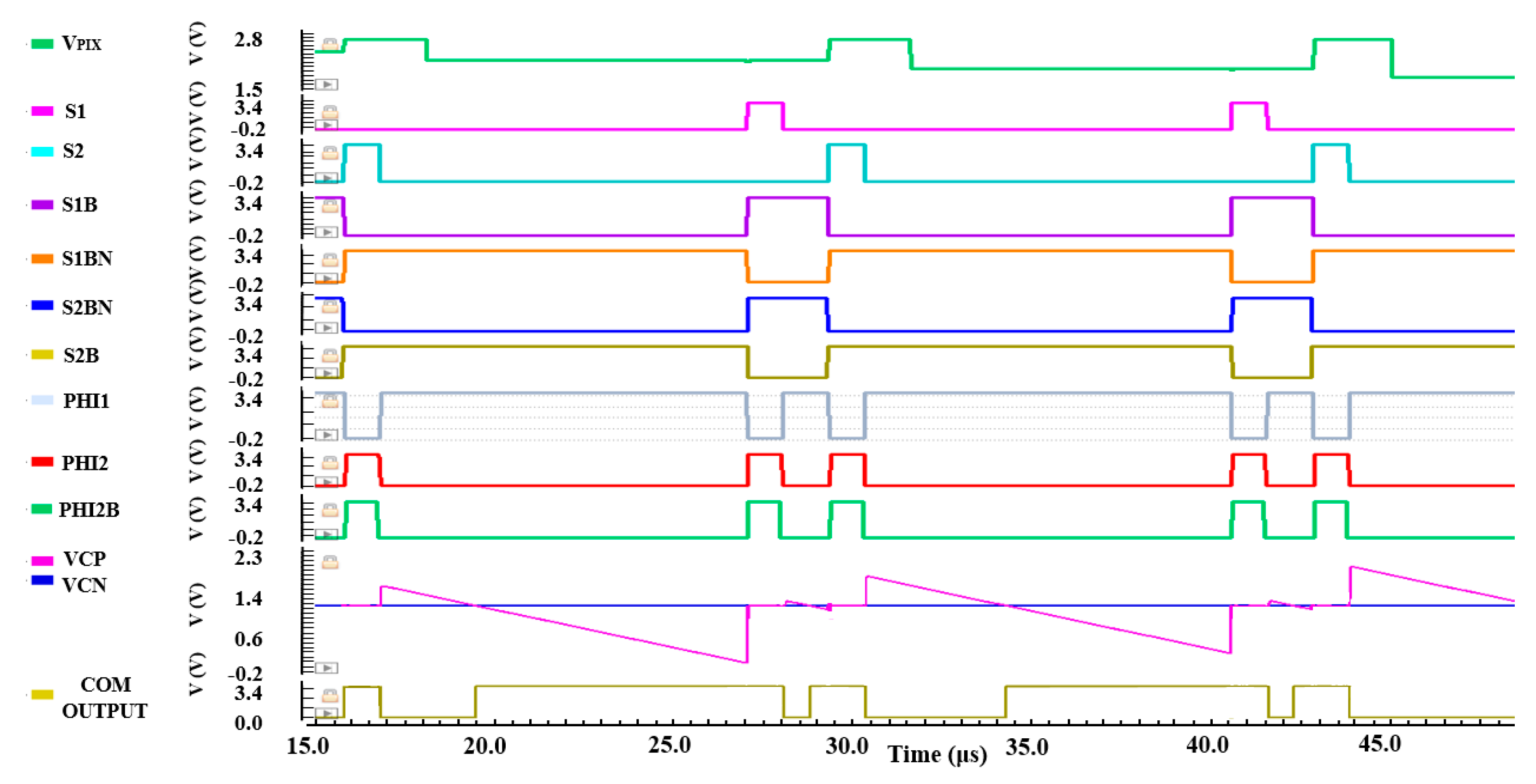
3.2. Fully Differential Pipeline Sampling Quantization Based on Double Auto-Zeroing Technique
4. Analysis of Proposed Techniques
4.1. Linearity Analysis of CMOS Image Sensor with Linear Ramp
4.2. Linearity Analysis of CMOS Image Sensor with Adaptive Nonlinear Ramp
5. Results
5.1. Simulation Results of Nonlinear Ramp Generation Circuit Based on Dummy Pixel
5.2. Simulation Results of Fully Differential Pipeline Sampling Quantization with Double Auto-Zeroing Technique
5.3. Experimental Result
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fei, W. Linearity Research of ACMOS Image Sensor; Delft University of Technology: Delft, The Netherlands, 2018. [Google Scholar]
- Wang, F.; Theuwissen, A.J.P. Pixel optimizations and digital calibration methods of a CMOS image sensor targeting high linearity. IEEE Trans. Circuit Syst. 2018, 66, 930–940. [Google Scholar] [CrossRef]
- Wang, F.; Han, L.; Theuwissen, A.J.P. Development and Evaluation of a Highly Linear CMOS Image sensor with a digitally assisted linearity calibration. IEEE J. Solid State Circuit 2018, 53, 2970–2981. [Google Scholar] [CrossRef]
- De Sá, L.B.; Dias, M.H.C.; Dupret, A.; Filho, A.C.D. A 99.95% linearity readout circuit with 72 dB dynamic range for active pixel sensors. Int. J. Circuit Theory Appl. 2018, 46, 1580–1592. [Google Scholar] [CrossRef]
- Wang, F.; Theuwissen, A.J.P. Techniques for pixel-level linearity optimization. In Proceedings of the Workshop CMOS Image Sensors High Performance Applications, Paris, France, 21–22 November 2017; pp. 1–20. [Google Scholar]
- Xiaoliang, G. The Design of a Global Shutter CMOS Image Sensor in 110nm Technology; Delft University: Delft, The Netherlands, 2012. [Google Scholar]
- Shoji, K. Column-parallel adcs for cmos image sensors and their fom-based evaluations. Ieice Trans. Electron. 2018, E101, 444–456. [Google Scholar]
- Qiyuan, L.; Edward, A.; Kinyua, M.; Soenen, E.G.; Silva-Martinez, J. A low power digitizer for back-illuminated 3-D-stacked CMOS image sensor readout with passing window and double auto-zeroing techniques. IEEE J. Solid State Circuits 2017, 52, 1591–1604. [Google Scholar]
- Samuel, S.I.; Blanca, P.G.; Espejo-Meana, S.; Ragel-Morales, A.; Ceballos-Cáceres, J.; Muñoz-Díaz, M.; Carranza-González, L.; Arias-Drake, A.; Mora-Gutiérrez, J.M.; Lagos-Florido, M.A. An adaptive approach to on-chip cmos ramp generation for high resolution single slope ADCs. In Proceedings of the 21st European Conference on Circuit Theory and Design, Dresden, Germany, 8–12 September 2012; Volume 12. [Google Scholar]
- Snoeij, M.F.; Gan, P.D.; Theuwissen, J.P.; Makinwa, K.A.A.; Huijsing, J.H. A Cmos Image Sensor with a column-level multiple-ramp single-slope adc. In Proceedings of the 2007 IEEE International Solid-State Circuits Conference. Digest of Technical Papers, San Francisco, CA, USA, 11–15 February 2007. [Google Scholar]
- Lim, S.; Cheon, J.; Ham, S.; Han, G. A new correlated double sampling and single slope ADC circuit for CMOS image sensors. Int. SoC Des. Conf. 2004, 10, 129–131. [Google Scholar]
- Chen, Y.; Theuwissen, J.P.; Chae, Y.C. Column parallel single slope ADC with digital correlated multiple sampling for low noise cmos image sensors. Procedia Eng. 2011, 25, 1265–1268. [Google Scholar] [CrossRef]
- Masood, T.; Jafar, S. An ultra-linear CMOS image sensor for a high—Accuracy imaging system. Int. J. Circuit Theory Appl. 2018, 3, 1593–1605. [Google Scholar]
- Masood, T. A highly linear and high-accurate CMOS image sensor. Analog Integr. Circuits Signal Proc. 2019, 10, 91–96. [Google Scholar]
- Sudhir, M.G.; Hyun, J.S.; Hon, S.P.W. Image Sensor with Dummy Pixel Array. US6344877B1, 12 February 2002. [Google Scholar]
- Benoit, P.; Sanchez-Sinencio, E. Auto-calibrating analog timer for on-chip testing. In Proceedings of the International Test Conference 1999 Proceedings, Atlantic City, NJ, USA, 30 September 1999; Volume 9. [Google Scholar]
- Benoit, P.; Sanchez-Sinencio, E. On-chip ramp generators for mixed-signal BIST and ADC self-test. IEEE J. Solid State Circuits 2003, 38, 263–273. [Google Scholar]









| Reference | This Work | [2] | [3] | [3] | [8] |
|---|---|---|---|---|---|
| Process (nm) | 180 | 180 | 180 | 180 | 40 |
| Linearity improvement techniques | Adaptive nonlinear ramp based on dummy pixel | Pixel optimization and calibration | Analog buffer | Off-chip digital calibration | Linear ramp and source follower buffer |
| Array size | 2560 × 3072 | 128 × 160 | 128 × 128 | 128 × 128 | NA |
| Global/Rolling shutter | GS/RS | RS | RS | RS | RS |
| ADC Architecture | 12/14 bit SS-ADC | 12 bit SS-ADC | 10 bit SS-ADC | 10 bit SS-ADC | 12 bit SS-ADC |
| Frame rate (fps) | 86 (400 MHz clock) | NA | 60 (12.5 MHz clock) | 60 | NA |
| Digital CDS | Y | Y | Y | Y | Y |
| Pixel size | 6.5 µm × 6.5 µm | 12 μm × 10 μm | 10 μm × 10 μm | 10 μm × 10 μm | NA |
| Fill factor | 100% (BSI) | 40% (FSI) | 47% (FSI) | 47% (FSI) | 100% (3D BSI) |
| Pixel type | 5T | CTIA | 4T | 4T | NA |
| Conversion gain | 17.4 μV/e− | 40 μV/e- | 56.8 μV/e- | 45.3 μV/e- | NA |
| Read noise | 7.9 e− | 16.4 (gain = 8) | 4.12 (gain = 8) | 4.17 (gain = 8) | 261.5 μVrms |
| Full well capacity | 91.7 ke− | 30.613 ke− | 17.27 ke− | 20.96 ke− | NA |
| Dynamic range(dB) | 81.3 | 65 | 72.4 | 74 | 71.8 |
| Column FPN (%) | 0.019 | NA | NA | NA | 0.028 |
| SNR (dB) | 49.4 | 44.2 | 42.1 | 42.9 | NA |
| Nonlinearity (%) | 0.047 | 0.095 | 0.058 | 0.06 | NA |
| Dark current | 8.3 pA/cm2@23 °C | NA | 5.6pA/cm2 | NA | NA |
| Per column Power | 96.3 μW | NA | NA | NA | 66.8 μW |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Han, B.; He, J.; Guo, Z.; Wu, L. A Highly Linear CMOS Image Sensor Design Based on an Adaptive Nonlinear Ramp Generator and Fully Differential Pipeline Sampling Quantization with a Double Auto-Zeroing Technique. Sensors 2020, 20, 1046. https://doi.org/10.3390/s20041046
Li C, Han B, He J, Guo Z, Wu L. A Highly Linear CMOS Image Sensor Design Based on an Adaptive Nonlinear Ramp Generator and Fully Differential Pipeline Sampling Quantization with a Double Auto-Zeroing Technique. Sensors. 2020; 20(4):1046. https://doi.org/10.3390/s20041046
Chicago/Turabian StyleLi, Chuangze, Benguang Han, Jie He, Zhongjie Guo, and Longsheng Wu. 2020. "A Highly Linear CMOS Image Sensor Design Based on an Adaptive Nonlinear Ramp Generator and Fully Differential Pipeline Sampling Quantization with a Double Auto-Zeroing Technique" Sensors 20, no. 4: 1046. https://doi.org/10.3390/s20041046
APA StyleLi, C., Han, B., He, J., Guo, Z., & Wu, L. (2020). A Highly Linear CMOS Image Sensor Design Based on an Adaptive Nonlinear Ramp Generator and Fully Differential Pipeline Sampling Quantization with a Double Auto-Zeroing Technique. Sensors, 20(4), 1046. https://doi.org/10.3390/s20041046




