Towards a Smart Smoking Cessation App: A 1D-CNN Model Predicting Smoking Events
Abstract
:1. Introduction
2. Classification Method: The 1D Convolutional Neural Network
3. Data Collection and Processing
3.1. Mobile App
3.2. Data Collection
4. Approach to Model Development
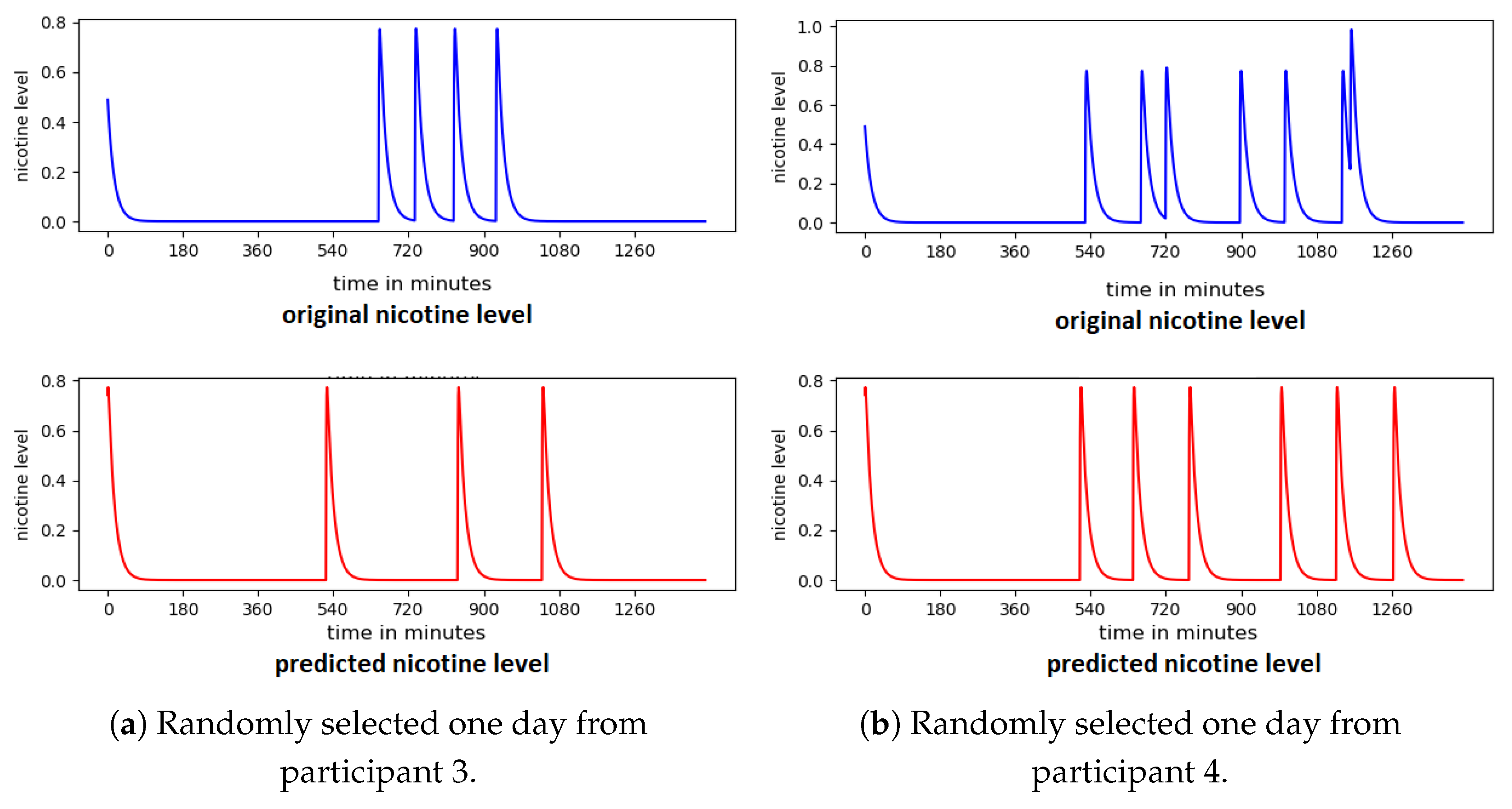
4.1. Control Theory Model of Smoking
4.2. Classification of Smoker Behavioural Data
5. Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- NHS. Adult Smoking Habits in the UK: 2016; Office of national statistics: London, UK, 2018.
- Abo-Tabik, M.; Costen, N.; Darby, J.; Benn, Y. Decision Tree Model of Smoking Behaviour. In Proceedings of the 2019 IEEE SmartWorld, Ubiquitous Intelligence and Computing, Advanced and Trusted Computing, Scalable Computing and Communications, Cloud and Big Data Computing, Internet of People and Smart City Innovation. IEEE, 2019, Leicester, UK, 19–23 August 2019; pp. 1746–1753. [Google Scholar]
- McClure, J.B.; Hartzler, A.L.; Catz, S.L. Design considerations for smoking cessation apps: Feedback from nicotine dependence treatment providers and smokers. JMIR mHealth uHealth 2016, 4, e17. [Google Scholar] [CrossRef] [PubMed]
- Naughton, F.; Hopewell, S.; Lathia, N.; Schalbroeck, R.; Brown, C.; Mascolo, C.; McEwen, A.; Sutton, S. A context-sensing mobile phone app (Q sense) for smoking cessation: A mixed-methods study. JMIR mHealth uHealth 2016, 4, e106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Businelle, M.S.; Ma, P.; Kendzor, D.E.; Frank, S.G.; Wetter, D.W.; Vidrine, D.J. Using intensive longitudinal data collected via mobile phone to detect imminent lapse in smokers undergoing a scheduled quit attempt. J. Med. Internet Res. 2016, 18, e275. [Google Scholar] [CrossRef] [PubMed]
- Schick, R.S.; Kelsey, T.W.; Marston, J.; Samson, K.; Humphris, G.W. MapMySmoke: Feasibility of a new quit cigarette smoking mobile phone application using integrated geo-positioning technology, and motivational messaging within a primary care setting. Pilot Feasibility Stud. 2018, 4, 19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dumortier, A.; Beckjord, E.; Shiffman, S.; Sejdić, E. Classifying smoking urges via machine learning. Comput. Methods Programs Biomed. 2016, 137, 203–213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Liu, J.; Zhang, Z.; Huang, J. Prediction of Daily Smoking Behavior Based on Decision Tree Machine Learning Algorithm. In Proceedings of the 2019 IEEE 9th International Conference on Electronics Information and Emergency Communication (ICEIEC), Beijing, China, 12–14 July 2019; pp. 330–333. [Google Scholar]
- Webb, T.L.; Chang, B.P.; Benn, Y. ‘The Ostrich Problem’: Motivated avoidance or rejection of information about goal progress. Soc. Personal. Psychol. Compass 2013, 7, 794–807. [Google Scholar] [CrossRef]
- Fibla, M.S.; Bernardet, U.; Verschure, P.F. Allostatic control for robot behaviour regulation: An extension to path planning. In Proceedings of the Intelligent Robots and Systems (IROS), 2010 IEEE/RSJ International Conference on, Taipei, Taiwan, 18–22 October 2010; pp. 1935–1942. [Google Scholar]
- Hughes, J.M. Real World Instrumentation with Python: Automated Data Acquisition and Control Systems; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2010. [Google Scholar]
- Gutkin, B.; Ahmed, S.H. Computational Neuroscience of Drug Addiction; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Ahmed, S.H.; Bobashev, G.; Gutkin, B.S. The simulation of addiction: Pharmacological and neurocomputational models of drug self-administration. Drug Alcohol Depend. 2007, 90, 304–311. [Google Scholar] [PubMed]
- Metin, S.; Sengor, N.S. From occasional choices to inevitable musts: A computational model of nicotine addiction. Comput. Intell. Neurosci. 2012, 2012, 18. [Google Scholar] [CrossRef] [Green Version]
- Solomon, R.L. The opponent-process theory of acquired motivation: The costs of pleasure and the benefits of pain. Am. Psychol. 1980, 35, 691. [Google Scholar] [CrossRef]
- Bobashev, G.; Holloway, J.; Solano, E.; Gutkin, B. A Control Theory Model of Smoking. Methods Rep. (RTI Press) 2017, 2017. [Google Scholar] [CrossRef]
- Timms, K.P.; Rivera, D.E.; Collins, L.M.; Piper, M.E. Control systems engineering for understanding and optimizing smoking cessation interventions. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 1964–1969. [Google Scholar]
- Bobashev, G.V.; Ellner, S.P.; Nychka, D.W.; Grenfell, B.T. Reconstructing susceptible and recruitment dynamics from measles epidemic data. Math. Population Stud. 2000, 8, 1–29. [Google Scholar] [CrossRef]
- Popa, D.; Pop, F.; Serbanescu, C.; Castiglione, A. Deep learning model for home automation and energy reduction in a smart home environment platform. Neural Comput. Appl. 2019, 31, 1317–1337. [Google Scholar] [CrossRef]
- Zahid, M.; Ahmed, F.; Javaid, N.; Abbasi, R.A.; Kazmi, Z.; Syeda, H.; Javaid, A.; Bilal, M.; Akbar, M.; Ilahi, M. Electricity price and load forecasting using enhanced convolutional neural network and enhanced support vector regression in smart grids. Electronics 2019, 8, 122. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Kalchbrenner, N.; Grefenstette, E.; Blunsom, P. A Convolutional Neural Network for Modelling Sentences. Available online: https://arxiv.org/abs/1404.2188 (accessed on 15 February 2020).
- Nguyen, T.H.; Grishman, R. Relation extraction: Perspective from convolutional neural networks. In Proceedings of the 1st Workshop on Vector Space Modeling for Natural Language Processing, Denver, Colorado, 31 May–5 June 2015; pp. 39–48. [Google Scholar]
- Sorokin, M.; Zhdanov, A.; Zhdanov, D. Recovery of Optical Parameters of a Scene Using Fully-Convolutional Neural Networks. Available online: http://ceur-ws.org/Vol-2344/short1.pdf (accessed on 15 February 2020).
- Deka, B. Pattern Recognition and Machine Intelligence: 8th International Conference, PReMI 2019, Tezpur, India, December 17–20, 2019, Proceedings, Part I; Springer Nature: Berlin, Germany, 2019. [Google Scholar]
- Camps, J.; Sama, A.; Martin, M.; Rodriguez-Martin, D.; Perez-Lopez, C.; Arostegui, J.M.M.; Cabestany, J.; Catala, A.; Alcaine, S.; Mestre, B.; et al. Deep learning for freezing of gait detection in Parkinson’s disease patients in their homes using a waist-worn inertial measurement unit. Knowl. Based Syst. 2018, 139, 119–131. [Google Scholar] [CrossRef]
- Michie, S.; Richardson, M.; Johnston, M.; Abraham, C.; Francis, J.; Hardeman, W.; Eccles, M.P.; Cane, J.; Wood, C.E. The behavior change technique taxonomy (v1) of 93 hierarchically clustered techniques: Building an international consensus for the reporting of behavior change interventions. Ann. Behav. Med. 2013, 46, 81–95. [Google Scholar] [CrossRef] [PubMed]
- Assaad, M.; Boné, R.; Cardot, H. A new boosting algorithm for improved time-series forecasting with recurrent neural networks. Inf. Fusion 2008, 9, 41–55. [Google Scholar] [CrossRef]














| Collected Data Group Name | Description |
|---|---|
| ID | This is unique ID that Identify the user data, it is set by the user at the start of the study. |
| Timing value | This is time stamp DD-MMYYYY, HH:MM:SS |
| Motion sensors data | Accelerometer, Gyroscope, Linear acceleration, Orientation, Rotation vector. |
| Environmental data | Magnetic field, Light level, Ambient temperature, Relative humidity, GPS location. |
| Activity labels | Google activity recognition API (Still, Running, Walking, Cycling, Tilting, and Driving). |
| Smoking labels | This is labelled by the user. |
| Calculated Accuracy Category | SVM | DT | 1D-CNN |
|---|---|---|---|
| Participant 1 smoking | 0.01 | 0.40 | 0.01 |
| Participant 1 not smoking | 0.98 | 0.70 | 1.00 |
| Participant 1 overall | 0.73 | 0.62 | 0.74 |
| Participant 2 smoking | 0.03 | 0.51 | 0.09 |
| Participant 2 not smoking | 0.99 | 0.95 | 0.98 |
| Participant 2 overall | 0.88 | 0.90 | 0.87 |
| Participant 3 smoking | 0.02 | 0.08 | 0.00 |
| Participant 3 not smoking | 0.99 | 0.91 | 1.00 |
| Participant 3 overall | 0.94 | 0.95 | 0.95 |
| Participant 4 smoking | 0.00 | 0.24 | 0.08 |
| Participant 4 not smoking | 1.00 | 0.81 | 1.00 |
| Participant 4 overall | 0.90 | 0.88 | 0.90 |
| Participant 5 smoking | 0.00 | 0.25 | 0.21 |
| Participant 5 not smoking | 1.00 | 0.97 | 0.97 |
| Participant 5 overall | 0.88 | 0.97 | 0.88 |
| Calculated Accuracy Category | SVM | DT | 1D-CNN |
|---|---|---|---|
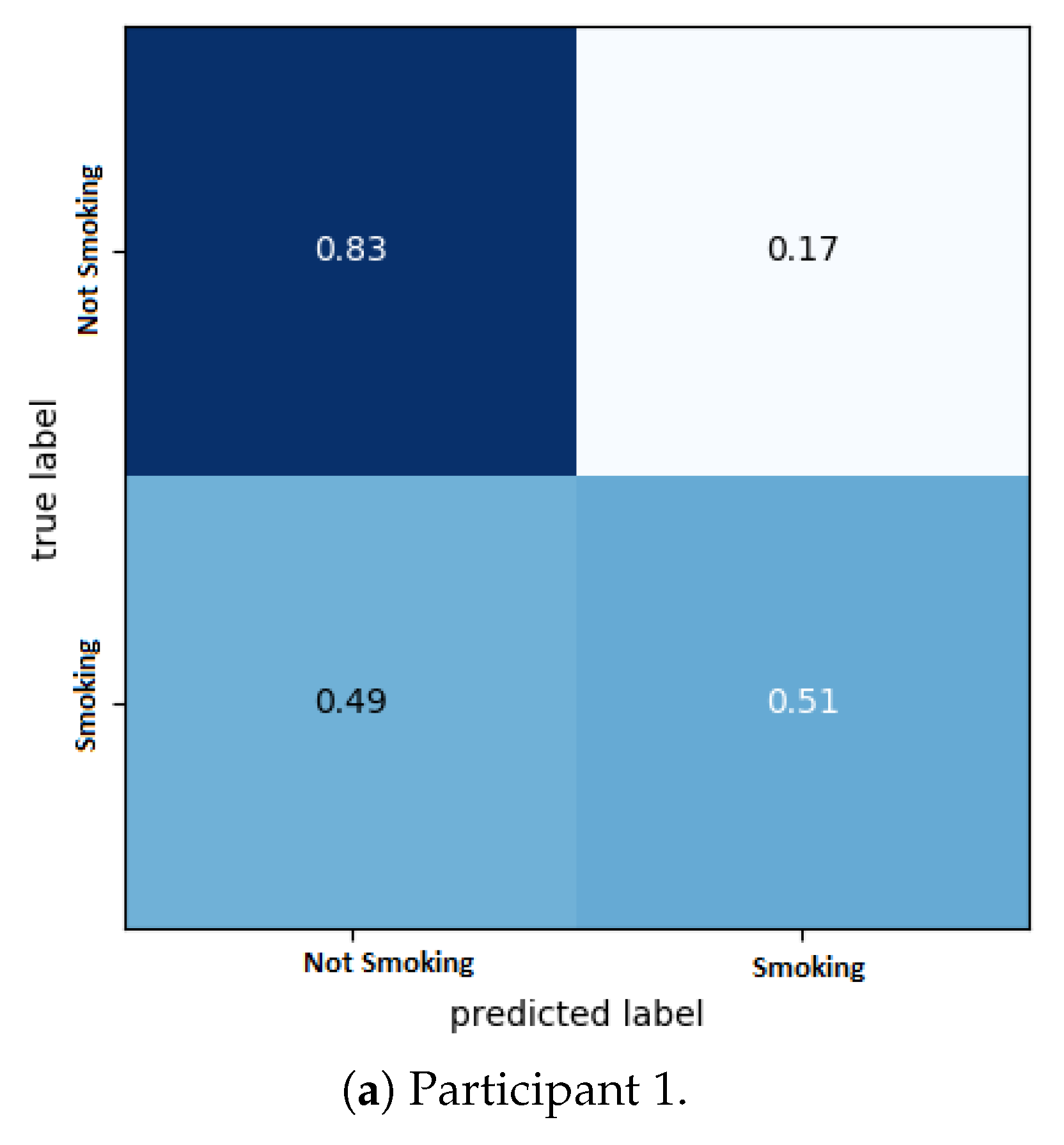
| Participant 1 smoking | 0.26 | 0.43 | 0.51 |
| Participant 1 not smoking | 0.74 | 0.75 | 0.83 |
| Participant 1 overall | 0.62 | 0.67 | 0.75 |
| Participant 2 smoking | 0.19 | 0.37 | 0.63 |
| Participant 2 not smoking | 0.88 | 0.89 | 0.95 |
| Participant 2 overall | 0.80 | 0.83 | 0.91 |
| Participant 3 smoking | 0.06 | 0.08 | 0.01 |
| Participant 3 not smoking | 0.95 | 0.94 | 1.00 |
| Participant 3 overall | 0.90 | 0.89 | 0.95 |
| Participant 4 smoking | 0.21 | 0.16 | 0.18 |
| Participant 4 not smoking | 0.91 | 0.93 | 0.97 |
| Participant 4 overall | 0.84 | 0.85 | 0.89 |
| Participant 5 smoking | 0.12 | 0.25 | 0.44 |
| Participant 5 not smoking | 0.95 | 0.95 | 0.94 |
| Participant 5 overall | 0.85 | 0.86 | 0.87 |
| Calculated Accuracy Category | SVM | DT | 1D-CNN |
|---|---|---|---|
| Participant 1 smoking | 0.24 | 0.41 | 0.59 |
| Participant 1 not smoking | 0.79 | 0.77 | 0.79 |
| Participant 1 overall | 0.65 | 0.68 | 0.73 |
| Participant 2 smoking | 0.04 | 0.50 | 0.64 |
| Participant 2 not smoking | 0.87 | 0.92 | 0.94 |
| Participant 2 overall | 0.78 | 0.87 | 0.89 |
| Participant 3 smoking | 0.05 | 0.11 | 0.03 |
| Participant 3 not smoking | 0.96 | 0.93 | 0.99 |
| Participant 3 overall | 0.91 | 0.89 | 0.94 |
| Participant 4 smoking | 0.14 | 0.28 | 0.20 |
| Participant 4 not smoking | 0.91 | 0.87 | 0.97 |
| Participant 4 overall | 0.83 | 0.81 | 0.89 |
| Participant 5 smoking | 0.12 | 0.26 | 0.47 |
| Participant 5 not smoking | 0.95 | 0.95 | 0.94 |
| Participant 5 overall | 0.85 | 0.86 | 0.88 |
| MSE | RMSE | NRMSE | |
|---|---|---|---|
| Participant 1 smoking | 0.07 | 0.26 | 0.23 |
| Participant 2 smoking | 0.05 | 0.22 | 0.20 |
| Participant 3 smoking | 0.02 | 0.14 | 0.15 |
| Participant 4 smoking | 0.03 | 0.18 | 0.21 |
| Participant 5 smoking | 0.03 | 0.15 | 0.17 |
| MSE | RMSE | NRMSE | |
|---|---|---|---|
| Participant 1 smoking | 0.07 | 0.27 | 0.24 |
| Participant 2 smoking | 0.03 | 0.16 | 0.17 |
| Participant 3 smoking | 0.01 | 0.10 | 0.11 |
| Participant 4 smoking | 0.03 | 0.16 | 0.20 |
| Participant 5 smoking | 0.01 | 0.12 | 0.15 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abo-Tabik, M.; Costen, N.; Darby, J.; Benn, Y. Towards a Smart Smoking Cessation App: A 1D-CNN Model Predicting Smoking Events. Sensors 2020, 20, 1099. https://doi.org/10.3390/s20041099
Abo-Tabik M, Costen N, Darby J, Benn Y. Towards a Smart Smoking Cessation App: A 1D-CNN Model Predicting Smoking Events. Sensors. 2020; 20(4):1099. https://doi.org/10.3390/s20041099
Chicago/Turabian StyleAbo-Tabik, Maryam, Nicholas Costen, John Darby, and Yael Benn. 2020. "Towards a Smart Smoking Cessation App: A 1D-CNN Model Predicting Smoking Events" Sensors 20, no. 4: 1099. https://doi.org/10.3390/s20041099
APA StyleAbo-Tabik, M., Costen, N., Darby, J., & Benn, Y. (2020). Towards a Smart Smoking Cessation App: A 1D-CNN Model Predicting Smoking Events. Sensors, 20(4), 1099. https://doi.org/10.3390/s20041099





