A Novel Method of Human Joint Prediction in an Occlusion Scene by Using Low-Cost Motion Capture Technique
Abstract
1. Introduction
2. Methodology
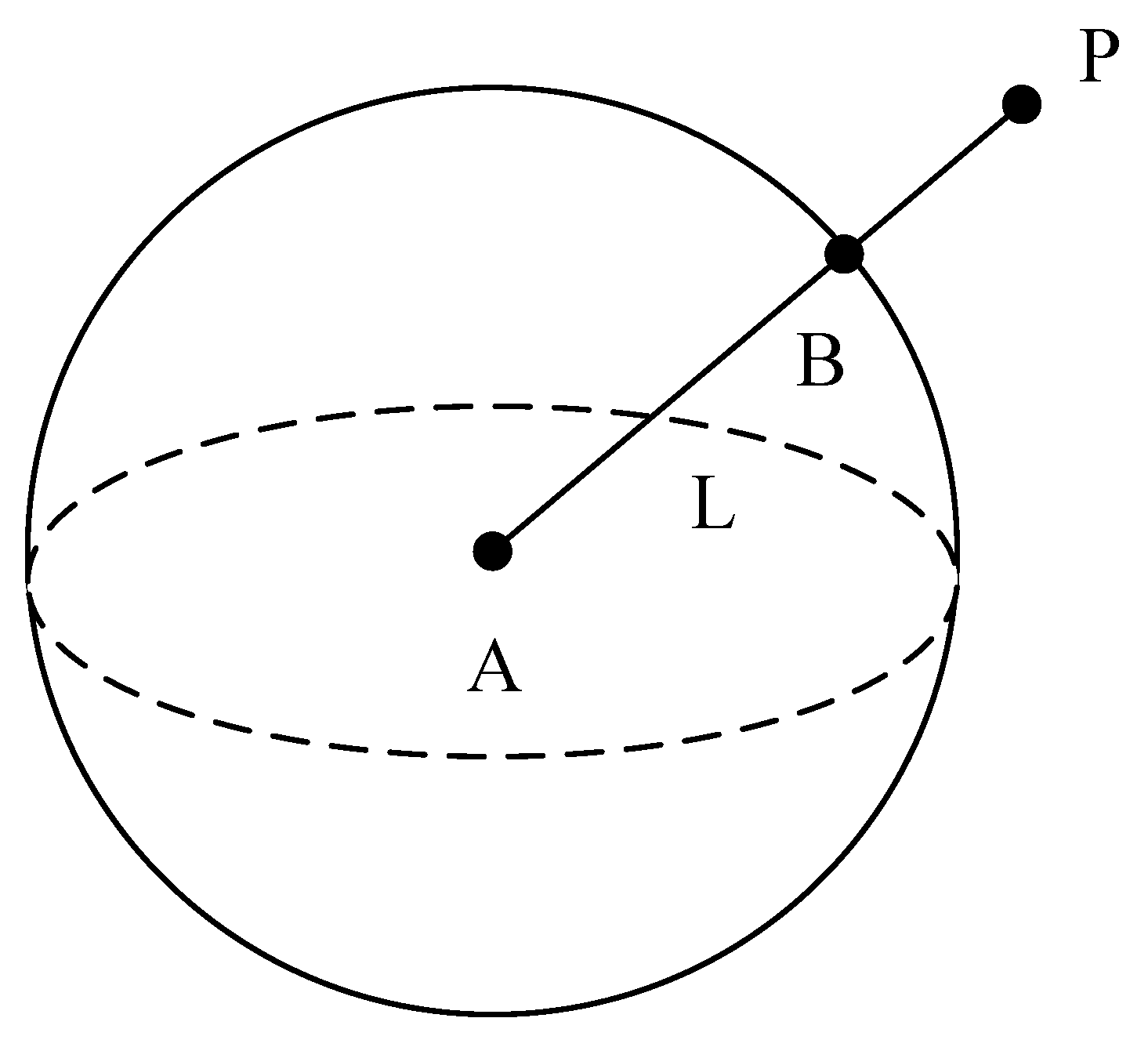
2.1. Reliability Measurement
2.2. Reliability Threshold
2.3. Algorithm to Handle Noise Data
2.4. Algorithm to Handle Erroneous Data
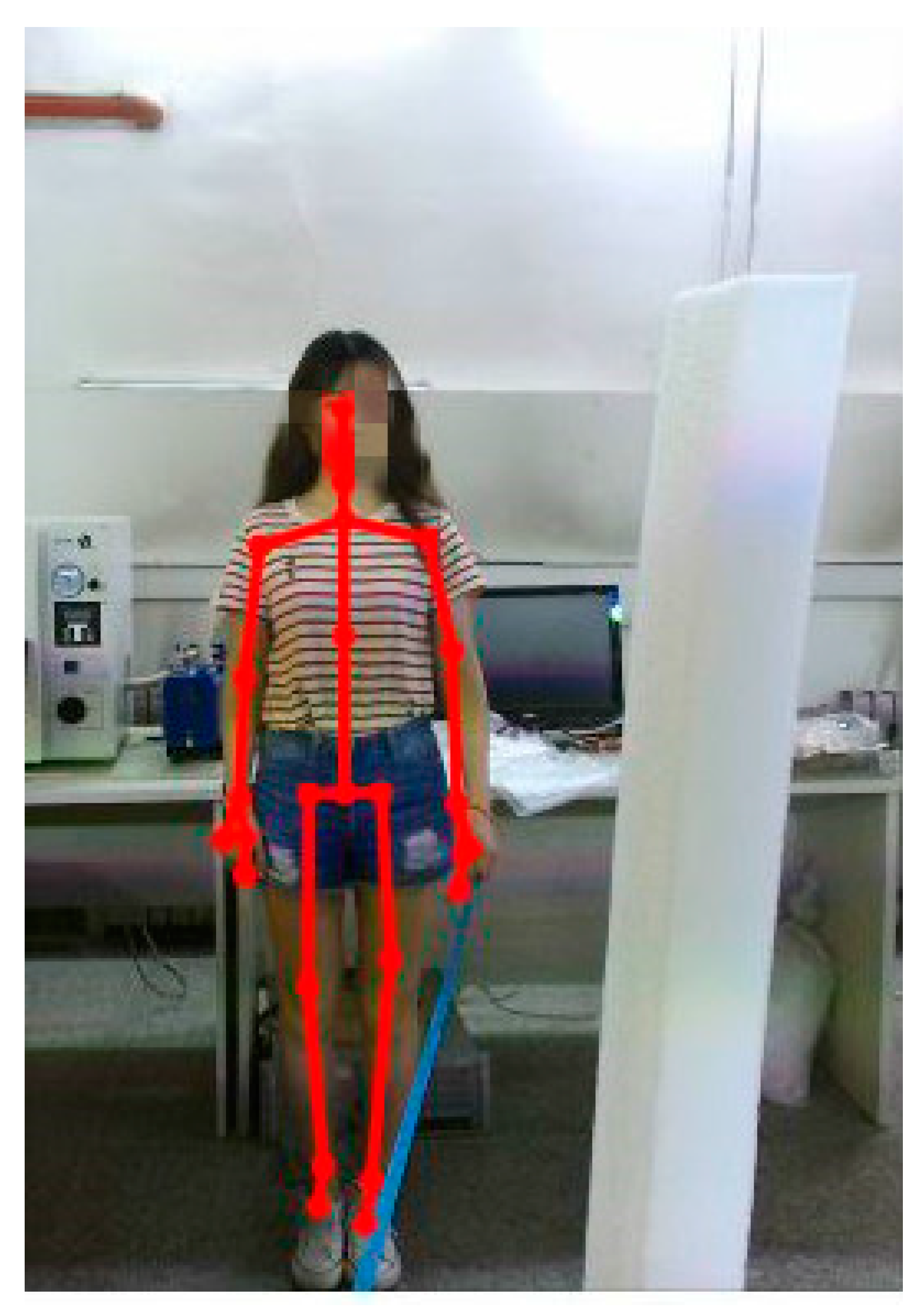
3. Experimental Setup
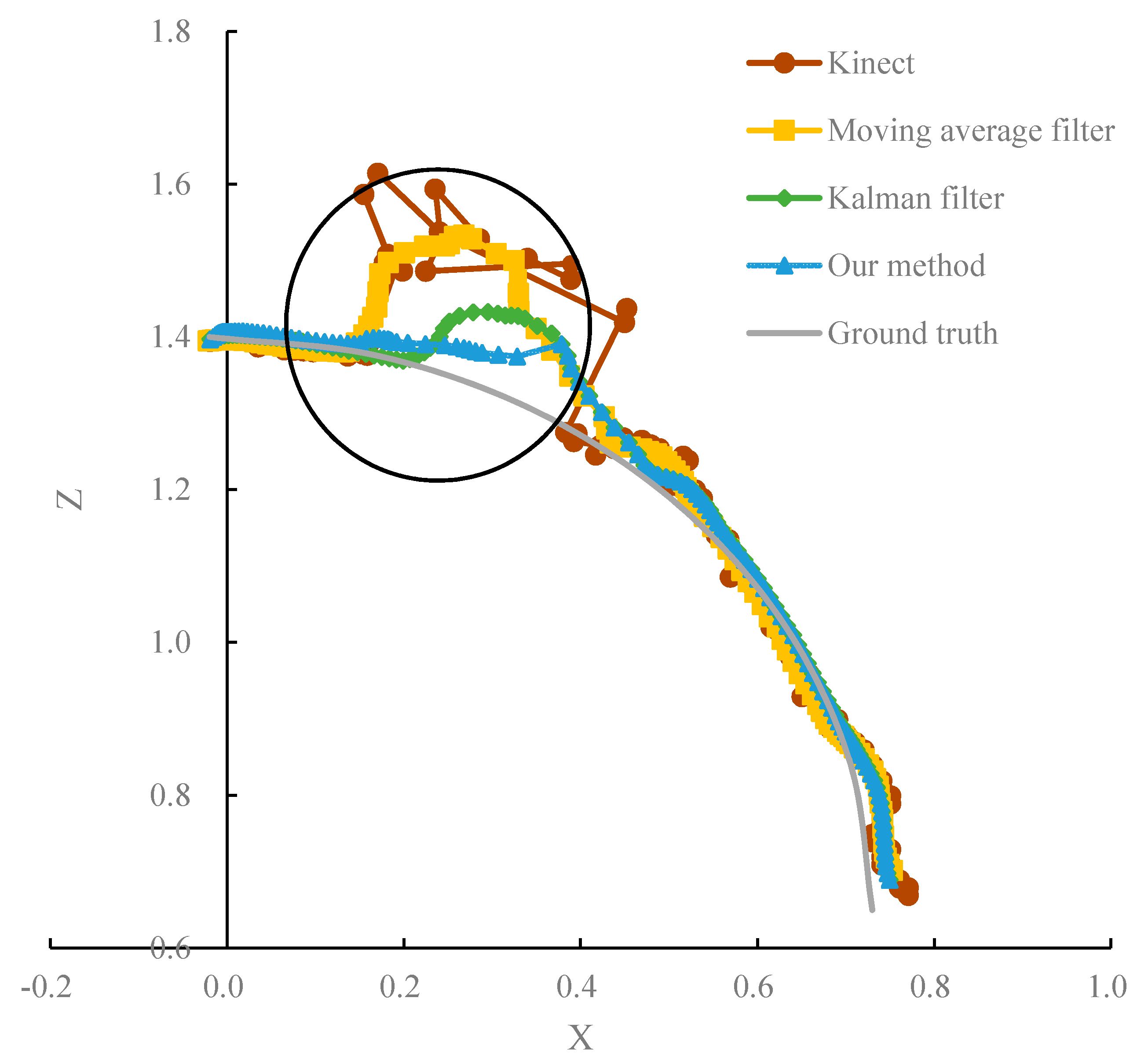
4. Results and Discussion
5. Conclusions and Future Work
Data Availability
Author Contributions
Funding
Conflicts of Interest
References
- Lasota, P.A.; Shah, J.A. A Multiple-Predictor Approach to Human Motion Prediction. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, Singapore, 29 May–3 June 2017. [Google Scholar]
- Haidegger, T.; Barreto, M.; Gonçalves, P.; Habib, M.K.; Ragavan, S.K.V.; Li, H.; Vaccarella, A.; Perrone, R.; Prestes, E. Applied ontologies and standards for service robots. Rob. Autom. Syst. 2013, 61, 1215–1223. [Google Scholar] [CrossRef]
- Habib, M.K.; Baudoin, Y.; Nagata, F. Robotics for rescue and risky intervention. In Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society (IECON 2011), Melbourne, VIC, Australia, 7–10 November 2011. [Google Scholar]
- Michalos, G.; Makris, S.; Papakostas, N.; Mourtzis, D.; Chryssolouris, G. Automotive assembly technologies review: challenges and outlook for a flexible and adaptive approach. CIRP J. Manuf. Sci. Technol. 2010, 2, 81–91. [Google Scholar] [CrossRef]
- Prakash, P.; Dhanasekaran, C.; Surya, K.; Pius, V.K.; Vishal, A.S.; Kumar, S.V. Gesture controlled dual six axis robotic arms with rover using MPU. Mater. Today Proc. 2019, 21, 547–556. [Google Scholar] [CrossRef]
- Kuhner, D.; Fiederer, L.D.J.; Aldinger, J.; Burget, F.; Völker, M.; Schirrmeister, R.T.; Do, C.; Boedecker, J.; Nebel, B.; Ball, T.; et al. A service assistant combining autonomous robotics, flexible goal formulation, and deep-learning-based brain–computer interfacing. Rob. Autom. Syst. 2019, 116, 98–113. [Google Scholar] [CrossRef]
- Tseng, S.H.; Chao, Y.; Lin, C.; Fu, L.C. Service robots: System design for tracking people through data fusion and initiating interaction with the human group by inferring social situations. Rob. Autom. Syst. 2016, 83, 188–202. [Google Scholar] [CrossRef]
- Paulius, D.; Sun, Y. A Survey of Knowledge Representation in Service Robotics. Rob. Autom. Syst. 2019, 118, 13–30. [Google Scholar] [CrossRef]
- Ramoly, N.; Bouzeghoub, A.; Finance, B. A Framework for Service Robots in Smart Home: An Efficient Solution for Domestic Healthcare. IRBM 2018, 39, 413–420. [Google Scholar] [CrossRef]
- Tseng, R.Y.; Do, E.Y.L. Facial Expression Wonderland: A Novel Design Prototype of Information and Computer Technology for Children with Autism Spectrum Disorder. In Proceedings of the 1st ACM International Health Informatics Symposium (IHI 2010), Arlington, VA, USA, 11–12 November 2010. [Google Scholar]
- Blanchard, S.; Freiman, V.; Lirrete-Pitre, N. Strategies used by elementary schoolchildren solving robotics-based complex tasks: innovative potential of technology. Procedia Soc. Behav. Sci. 2010, 2, 2851–2857. [Google Scholar] [CrossRef]
- Nergui, M.; Imamoglu, N.; Yoshida, Y.; Gonzalez, J.; Sekine, M.; Kawamura, K.; Yu, W.W. Human Behavior Recognition by a Mobile Robot Following Human Subjects. In Evaluating AAL Systems Through Competitive Benchmarking; Springer: Berlin/Heidelberg, Germany, 2013; pp. 159–172. [Google Scholar]
- Carse, B.; Meadows, B.; Bowers, R.; Rowe, P. Affordable clinical gait analysis: An assessment of the marker tracking accuracy of a new low-cost optical 3d motion analysis system. Physiotherapy 2013, 99, 347–351. [Google Scholar] [CrossRef]
- Pfister, A.; West, A.; Bronner, S.; Noah, J.A. Comparative Abilities of Microsoft Kinect and Vicon 3D Motion Capture for Gait Analysis. J. Med. Eng. Technol. 2014, 38, 274–280. [Google Scholar] [CrossRef]
- Shen, W.; Bai, X.; Hu, R.; Wang, H.Y.; Latecki, L.J. Skeleton Growing and Pruning with Bending Potential Ratio. Pattern Recognit. 2011, 44, 196–209. [Google Scholar] [CrossRef]
- Kean, S.; Hall, J.; Perry, P. Meet the Kinect: An Introduction to Programming Natural User Interfaces; Apress: New York, NY, USA, 2011. [Google Scholar]
- Tripathy, S.R.; Chakravarty, K.; Sinha, A.; Chatterjee, D.; Saha, S.K. Constrained Kalman Filter For Improving Kinect Based Measurements. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017. [Google Scholar]
- Das, P.; Chakravarty, K.; Chowdhury, A.; Chatterjee, D.; Sinha, A.; Pal, A. Improving joint position estimation of Kinect using anthropometric constraint based adaptive Kalman filter for rehabilitation. Biomed. Phys. Eng. Express 2018, 4, 035002. [Google Scholar] [CrossRef]
- Clark, R.A.; Mentiplay, B.F.; Hough, E.; Pua, Y.H. Three-dimensional cameras and skeleton pose tracking for physical function assessment: A review of uses, validity, current developments and Kinect alternatives. Gait Posture 2019, 68, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Shu, J.; Hamano, F.; Angus, J. Application of extended Kalman filter for improving the accuracy and smoothness of Kinect skeleton-joint estimates. J. Eng. Math. 2014, 88, 161–175. [Google Scholar] [CrossRef]
- Wochatz, M.; Tilgner, N.; Mueller, S.; Rabe, S.; Eichler, S.; John, M.; Völler, H.; Mayer, F. Reliability and validity of the Kinect V2 for the assessment of lower extremity rehabilitation exercises. Gait Posture 2019, 70, 330–335. [Google Scholar] [CrossRef]
- Sarsfield, J.; Brown, D.; Sherkat, N.; Langensiepen, C.; Lewis, J.; Taheri, M.; McCollin, C.; Barnett, C.; Selwood, L.; Standen, P.; et al. Clinical assessment of depth sensor based pose estimation algorithms for technology supervised rehabilitation applications. Int. J. Med. Informatics 2019, 121, 3038. [Google Scholar] [CrossRef]
- Manghisi, V.M.; Uva, A.E.; Fiorentino, M.; Bevilacqua, V.; Trotta, G.F.; Monno, G. Real time RULA assessment using Kinect v2 sensor. Appl. Ergon. 2017, 65, 481–491. [Google Scholar] [CrossRef]
- Xu, X.; Robertson, M.; Chen, K.B.; Lin, J.H.; McGorry, R.W. Using the Microsoft Kinect™ to assess 3-D shoulder kinematics during computer use. Appl. Ergon. 2017, 65, 418–423. [Google Scholar]
- Plantard, P.; Shum, H.P.H.; Pierres, A.S.L.; Multon, F. Validation of an ergonomic assessment method using Kinect data in real workplace conditions. Appl. Ergon. 2017, 65, 562–569. [Google Scholar] [CrossRef]
- Edwards, M.; Green, R. Low-latency filtering of kinect skeleton data for video game control. In Proceedings of the 29th International Conference on Image and Vision Computing New Zealand, Hamilton, New Zealand, 19–21 November 2014. [Google Scholar]
- Du, G.L.; Zhang, P. Markerless Human-Robot Interface for Dual Robot Manipulators Using Kinect Sensor. Rob. Comput. Integr. Manuf. 2014, 30, 150–159. [Google Scholar] [CrossRef]
- Rosado, J.; Silva, F.; Santos, V. A Kinect-Based Motion Capture System for Robotic Gesture Imitation. In ROBOT 2013: First Iberian Robotics Conference; Springer: Cham, Switzerland, 2014; Volume 1, pp. 585–595. [Google Scholar]
- Wang, Q.F.; Kurillo, G.; Ofli, F.; Bajcsy, R. Remote Health Coaching System and Human Motion Data Analysis for Physical Therapy with Microsoft Kinect. Available online: https://arxiv.org/abs/1512.06492 (accessed on 1 January 2020).
- Shen, W.; Deng, K.; Bai, X.; Leyvand, T.; Guo, B.N.; Tu, Z.W. Exemplar-Based Human Action Pose Correction and Tagging. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Shum, H.P.H.; Ho, E.S.L. Real-Time Posture Reconstruction for Microsoft Kinect. IEEE Trans. Cybern. 2013, 43, 1357–1369. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.G.; Zhou, L.Y.; Leung, H.; Shum, H.P.H. Kinect Posture Reconstruction Based on a Local Mixture of Gaussian Process Models. IEEE Trans. Visual Comput. Graphics 2016, 22, 2437–2450. [Google Scholar] [CrossRef] [PubMed]
- Plantard, P.; Shum, H.P.H.; Multon, F. Filtered Pose Graph for Efficient Kinect Pose Reconstruction. Multimedia Tools Appl. 2017, 76, 4291–4312. [Google Scholar] [CrossRef]
- Morasso, P. Spatial Control of Arm Movements. Exp. Brain Res. 1981, 42, 223–227. [Google Scholar] [CrossRef]
- Huber, M.E.; Seitz, A.L.; Leeser, M.; Sternad, D. Validity and Reliability of Kinect Skeleton for Measuring Shoulder Joint Angles: A Feasibility Study Chartered Society of Physiotherapy. Physiotherapy 2015, 101, 389–393. [Google Scholar] [CrossRef]
- Shotton, J.; Sharp, T.; Kipman, A.; Girshick, R.; Fitzgibbon, A.; Cook, M.; Finocchio, M.; Moore, R.; Kohli, P.; Criminisi, A.; et al. Difficient Human Pose Estimation from Single depth Images. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2821–2840. [Google Scholar] [CrossRef]



| Experiment | Reliability Threshold | ||||
|---|---|---|---|---|---|
| Subject 1 | Subject 2 | Subject 3 | Subject 4 | Subject 5 | |
| 1 | 0.69 | 0.68 | 0.74 | 0.72 | 0.79 |
| 2 | 0.70 | 0.73 | 0.65 | 0.77 | 0.75 |
| 3 | 0.72 | 0.69 | 0.64 | 0.76 | 0.66 |
| 4 | 0.75 | 0.74 | 0.63 | 0.73 | 0.73 |
| 5 | 0.66 | 0.65 | 0.66 | 0.69 | 0.69 |
| Kinect | Moving Mean Filter | Kalman Filter | Our Method | |||||
|---|---|---|---|---|---|---|---|---|
| Error | SD | Error | SD | Error | SD | Error | SD | |
| 1 | 0.081 | 0.008 | 0.065 | 0.007 | 0.043 | 0.003 | 0.032 | 0.003 |
| 2 | 0.076 | 0.004 | 0.061 | 0.005 | 0.041 | 0.002 | 0.031 | 0.003 |
| 3 | 0.071 | 0.004 | 0.054 | 0.010 | 0.036 | 0.003 | 0.028 | 0.005 |
| 4 | 0.069 | 0.007 | 0.051 | 0.009 | 0.039 | 0.002 | 0.030 | 0.002 |
| 5 | 0.078 | 0.005 | 0.062 | 0.004 | 0.042 | 0.004 | 0.036 | 0.004 |
| Mean | 0.075 | 0.006 | 0.059 | 0.007 | 0.040 | 0.003 | 0.031 | 0.003 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, J.; Wang, X.; Wang, D.; Ran, L. A Novel Method of Human Joint Prediction in an Occlusion Scene by Using Low-Cost Motion Capture Technique. Sensors 2020, 20, 1119. https://doi.org/10.3390/s20041119
Niu J, Wang X, Wang D, Ran L. A Novel Method of Human Joint Prediction in an Occlusion Scene by Using Low-Cost Motion Capture Technique. Sensors. 2020; 20(4):1119. https://doi.org/10.3390/s20041119
Chicago/Turabian StyleNiu, Jianwei, Xiai Wang, Dan Wang, and Linghua Ran. 2020. "A Novel Method of Human Joint Prediction in an Occlusion Scene by Using Low-Cost Motion Capture Technique" Sensors 20, no. 4: 1119. https://doi.org/10.3390/s20041119
APA StyleNiu, J., Wang, X., Wang, D., & Ran, L. (2020). A Novel Method of Human Joint Prediction in an Occlusion Scene by Using Low-Cost Motion Capture Technique. Sensors, 20(4), 1119. https://doi.org/10.3390/s20041119





