1. Introduction
Heterogeneous multi-sensor data fusion has extensive research and applications in mobile robots [
1], driverless cars [
2], and other fields. Compared with a single-sensor system, multi-sensor fusion systems [
3] can provide richer environmental information and complete higher-level tasks such as target detection [
4], autonomous location [
5], and path planning [
6]. The combined application of 3D light detection and ranging (LiDAR) and camera is very common. LiDAR has high resolution, strong anti-interference ability, wide detection range, and can accurately obtain the distance and angle information of the detection target [
7]. The camera has a small size, low cost, and can obtain the shape and color information of the target. They can complement each other functionally. However, LiDAR and the camera are in different spatial positions in the multi-sensor system. Therefore, the calibration of the spatial coordinate system must be completed before data fusion.
The calibration of 3D LiDAR and camera is essentially the process of obtaining the mutual conversion relationship between the LiDAR coordinate system and camera pixel coordinate system. Through that, the spatial information detected by two sensors can be correlated and fused. Commonly used calibration methods can be divided into two categories: global matching optimization method and calibration tool assisted method. The global matching optimization method uses the structural similarity between the LiDAR point cloud and image data to perform global matching and optimize the calibration results. Pandey et al. [
8] completed the calibration by maximizing the mutual information between the intensity of the LiDAR frame and the gray information of the image. Castorena et al. [
9] used the natural alignment of depth and intensity edges in combination with a Gaussian mixture model to solve the calibration result. It is easy to analyze a global matching optimization method that is automatic, targetless, and completely data-driven. However, because of the requirement to use features such as point cloud structures and image edges, this method requires high-precision LiDAR data and is very sensitive to image distortion. This will place high demands on the hardware system. The calibration tool assisted method completes the calibration by using auxiliary tools such as a calibration board. Due to the different forms of information obtained on the auxiliary tools, this method can also be divided into two categories: vector constraint method and feature point method. The vector constraint method was originally proposed by Zhang [
10]. This type of method needs to solve the intrinsic parameters of the camera [
11] first. Then use the camera and LiDAR to detect calibration aids (such as a black and white checkerboard [
10], an arbitrary trihedron [
12], two non-coplanar triangle checkers [
13], some boxes of known size [
14], etc.) at the same time. The position constraint of the plane normal vectors or other selected vectors in the two coordinate systems on the auxiliary tool is used to establish the vector constraint equations and solve the external parameters. Finally, the nonlinear optimization is generally performed to refine the solution parameters. Obviously, the vector constraint method can clearly and directly solve the intrinsic parameters of the camera and the conversion parameters between the camera and LiDAR, but this method has a large calculation cost and cumbersome steps. Moreover, multi-step calibration will introduce a large cumulative error. The feature point method directly obtains the transformation relationship between LiDAR coordinate system and the camera pixel coordinate system by selecting the feature points and obtaining their coordinates in the above two systems based on the calibration board, then calculating the transformation matrix and the intrinsic and external parameters [
15] by solving the calibration matrix conversion equation [
16] or using method like supervised learning [
17], etc. The feature point method has low calculation cost, wide applicability, and is easy to implement. In addition, the solved transformation matrix can be directly used for point cloud projection, which can effectively avoid the cumulative error generated by the multi-step calibration.
The calibration accuracy of the feature point method mainly depends on the accuracy of the extracted feature points’ coordinates. Coordinates of feature points can be acquired by infrared imager [
18] or directly using a calibration board through calculation or other methods. Infrared imagers can visualize LiDAR scanning points, but the cost of the instrument is high and it must be ensured that the sensitive frequency matches the LiDAR light frequency. In view of cost and applicability, calibration boards are commonly used in related researches.
The form of the calibration boards and their corresponding calibration methods are different. Liu [
19] constructed trapezoidal and rectangular deep depressions on a white flat board, and completed the single-line LiDAR and camera calibration by using the scanning points at the intersection of the plane and the depression as the feature points. However, the angle of the depth depression of the calibration board was variable which made the calibration board unstable. However, manual labeling was used to determine the pixel coordinates of the calibration board, which led to many manual errors that seriously affected the accuracy of the calibration. The work of Dong et al. [
20] and Zhuang et al. [
21] is a little similar. They constructed hollow circular holes in the center of the black and white checkerboard lattices, and used the centers of the circular holes as the feature points for calibration. Without obvious features in the LiDAR point cloud, the coordinates of centers could only be approximately calculated from the point cloud of the entire circular hole. Analogously, Velas et al. [
22] proposed a method for extrinsic calibration. They designed a calibration board containing four circular holes, then used the circle centers and the radius of the 3D LiDAR data and 2D image to comply a coarse calibration. Finally, a fine calibration was performed by the 3D LiDAR data captured along the circle edges and the inverse distance transform of the camera image. Ha [
23] used a black and white checkerboard with a triangular hole, where he took the two intersections of the scanning line and the hole as feature points, and determined the absolute position of the laser scan data on the plane by the relative positions of the feature points. Due to the lateral resolution of LiDAR and the non-coplanarity between the hole scan data and the flat scan data, the feature points cannot be obtained by fitting and intersecting, which brought many errors into the extracted feature point coordinates. Park et al. [
24] used a white diamond-shaped board as the calibration board and the vertexes of the diamond-shaped board as the feature points. Then solved the coordinates of the feature points in the LiDAR coordinate system by fitting the edge points of the diamond-shaped board. White flat board can avoid extra LiDAR noise caused by texture and some special structures. However, because of the limited lateral resolution of the LiDAR, there was no guarantee that the laser could sweep to the edge of the rhombus, which affected the solution of the coordinates of the vertex of the rhombus. There are also some researchers who use light-absorbing flat boards [
25] or V-shaped boards with special shapes [
26] as calibration boards. Inevitably, they all introduced large calibration error limited by the design of the calibration boards and calibration methods. It can be seen from the analysis that the feature point method is widely used for 3D LiDAR and camera calibration, the form of the calibration board is arbitrary, and the calibration methods are diverse. However, due to the design of the calibration board and corresponding method, there are too many manual interventions or approximate estimates when determining the coordinates of the feature points, which makes the feature point coordinates not accurate enough and affects the accuracy of the calibration. Moreover, there is currently no reasonable method for verifying calibration results.
This article conducts the following research on the above issues. Firstly, because one of the reasons of the error introduction is the design of the calibration board, a novel calibration board with local gradient depth information and main plane square corner information (BWDC) was specially designed. The calibration board has gradient depth information, plane corner information, and position information, which is easy to experiment and adjust. Secondly, since another factor that affects the calibration accuracy is the calibration method, this paper proposed the "three-step fitting interpolation method" for selecting feature points and accurately obtaining the coordinates of the feature points in the LiDAR coordinate system and camera pixel coordinate system. Then, we discussed various conditions that should be satisfied during the calibration to reduce artificial and random errors and improve the accuracy of the calibration results. Thirdly, we designed and carried out calibration experiments and verification experiments to evaluate the calibration results.
To present the proposed method, we organize the remainder of this paper as follows. In
Section 2, we describe the basic method of 3D LiDAR and camera calibration using feature points. In
Section 3, we propose the design of BWDC and corresponding calibration method.
Section 4 presents the experiments and analysis, followed with conclusions and future work in
Section 5, and related patents in
Section 6.
2. Basic Method of 3D LiDAR and Camera Feature Point Calibration
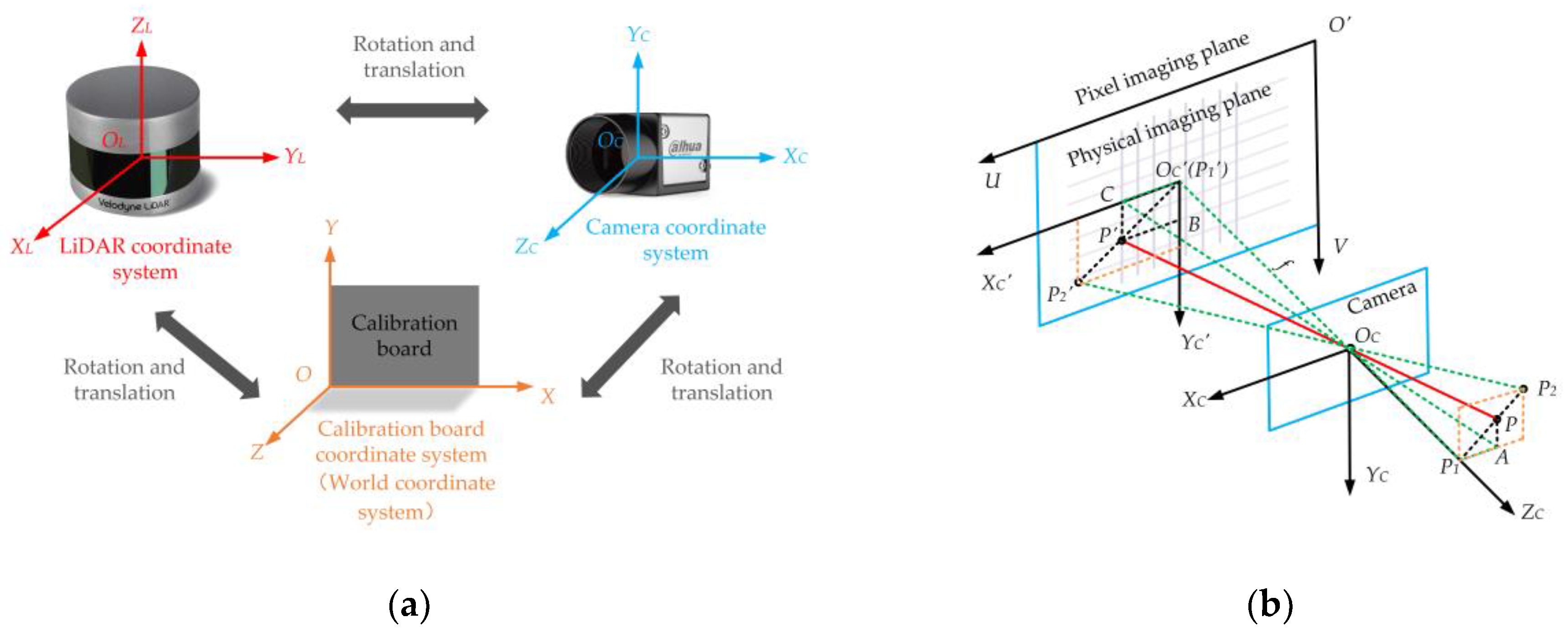
The coordinate conversion relationship of a typical feature point calibration system is shown in
Figure 1.
Figure 1a includes the LiDAR coordinate system
(the origin
is at the scan center of the LiDAR), the camera coordinate system
(the origin
is at the camera’s optical center), and the calibration board coordinate system
(the origin
is at the first corner point at the bottom left). These coordinate systems can be converted to each other by rotation and translation.
Figure 1b is an ideal pinhole camera imaging transformation model. An object is imaged on the image plane through the camera’s optical center pinhole
. Coordinate system
is the image physical coordinate system with the intersection
of the optical axis and the image plane as the coordinate origin. Coordinate system
is the image pixel coordinate system with the vertex
of the imaging plane as the coordinate origin. The object points
,
, and
are imaged at points
,
, and
respectively. The camera focal length is
.
The first thing that should be clear is that the purpose of calibration is to solve the conversion relationship between the LiDAR coordinate system and the camera pixel coordinate system. We can obtain the above conversion relationship by solving the rotation vector and translation vector between the LiDAR coordinate system and the camera coordinate system, as well as the intrinsic parameters of the camera.
The feature point calibration method is to solve the above parameters by using a sufficient number of different coordinates in two coordinate systems of the feature points. The transformation process of feature points can be divided into the following two processes: One is the linear transformation of the points between the LiDAR coordinate system and the camera coordinate system, which is the boresight alignments between camera and LiDAR and depends on the rotation vector and translation vector between the LiDAR coordinate system and the camera coordinate system. The other is the process of imaging a point in the camera coordinate system to a pixel coordinate system, which depends on the intrinsic parameters of the camera.
Firstly, according to the conversion relationship shown in
Figure 1a, if the coordinate of a point
P in LiDAR coordinate system is
and its coordinate in camera coordinate system is
. Then we have
where
R is a
rotation matrix, which represents the angular rotation relationship between the two coordinate systems.
,
, and
respectively represent the angles of rotation along the
x,
y, and
z axes during rotating the LiDAR coordinate system to the camera coordinate system in the right-hand coordinate system.
T is a
translation vector, which represents the relative position relationship between the two coordinate systems. The value is the coordinate of the origin of the LiDAR coordinate system in the camera coordinate system.
Secondly, as shown in
Figure 1b, object point
P is imaged by the camera to a point
on the pixel plane. Assume that the coordinate of point
P in camera coordinate system is
and the corresponding coordinate in image physical coordinate system is
. Since the feature point calibration method is not particularly sensitive to camera distortion, camera distortion parameters are generally ignored in related studies. According to the similar triangle principle, we have
According to the translation relationship between image physical coordinate system and image pixel coordinate system, the image physical coordinate
can be converted to the image pixel coordinate
:
Here, is the coordinate of the pixel center of the image, that is, the pixel coordinates of the intersection of the optical axis of the camera and the physical imaging plane. , respectively represent the pixel unit distances of the camera in the x direction and the y direction.
By Equation (2) and Equation (3), we can obtain the conversion formula of points between camera coordinate system and image pixel coordinate system:
where
and
are the equivalent focal lengths in the
x direction and the
y direction respectively.
,
,
, and
are the intrinsic parameters of the camera, which are generally provided by the camera manufacturer.
can be ignored when solving equations, since homogeneous coordinates multiplied by non-zero express the same meaning.
Therefore, a total of ten parameters are required in calibration. There are three angle variables: ,, in rotation vector, three position variables: ,, in translation vector, and four intrinsic parameters of the camera:,,,.
Here, we can use the conversion equation between the LiDAR coordinate system and camera coordinate system (1), the conversion equation between camera coordinate system and pixel coordinate system (4) to derive the conversion equation between LiDAR coordinate system and image pixel coordinate system as:
where
Q is a conversion matrix with a size of
. It can be seen from the calculation process of the equation that each parameter in the matrix is a composite calculated value of several calibration intrinsic and external parameters. At this time, we transform the problem of solving the above ten calibration parameters into a problem of solving the transformation matrix
Q. This matrix can be calculated when the corresponding coordinates of a sufficient number of feature points are obtained. We can use this matrix to perform data space fusion directly, or solve the calibration parameters. That is, when matrix
Q is solved, we can acquire twelve equations with ten unknown calibration parameters for each element in the matrix
Q that is a compound operation of the calibration parameters. Through the above processes, we obtain a one-to-one correspondence between the LiDAR coordinates and the camera pixel coordinates, and complete the calibration.
When solving the matrix Q according to the Equation (5), there is a total of twelve unknown variables, so at least four feature points which are not coplanar are needed to solve the equation, and any three of them should be non-collinear. In the feature point calibration method, we use a calibration board and a corresponding calibration method to obtain the coordinates of the feature points in two coordinate systems.
4. Experiments and Analysis
The LiDAR model is Velodyne VLP-32C for the experiments, with a detectable range of 0–200 m, a vertical field of view angle of −25° to 15°, a horizontal field of view angle of 360°, and a horizontal lateral resolution of 0.4°. The minimum vertical lateral resolution of LiDAR is 0.33°, the detection accuracy is ±5 cm when the detection distance is less than 50 m, and the detection accuracy is ±10 cm when the detection distance is between 50 m and 200 m. The camera model is A5131CU210 from HUARAY TECHNOLOGY (Guangdong, China) with a resolution of 1280 1024 and a cell size of 4.8 μm 4.8 μm. The lens model is MH0820S from HUARAY TECHNOLOGY (Guangdong, China) with the field of view of 60.8° 42.7°, the focal length of 8 mm, and distortion of less than 0.1%. The design calibration board parameter L is 0.2 m, so the calibration board size is 1.8 m 3.6 m.
The experimental test scenario is shown in
Figure 6. LiDAR and camera are respectively fixed on two sliders. The sliders can both be moved on a slide rail equipped with a ruler, wherein the camera fixed slider is provided with a readable angle rotation device.
4.1. Calibration Experiments
According to the discussion in
Section 2 and
Section 3.4, at least four feature points not coplanar and any three of them not collinear are needed in a calibration experiment. For this reason, we placed the calibration board at the distance of 5 m and 10 m away from the sensors, and adjusted the calibration board to meet the calibration conditions. For each experimental distance, we selected three laser scanning lines in the effective scanning area. Therefore, we got twenty-four sets of feature point coordinates at the end, which is enough to complete the calibration. The data acquired by camera and LiDAR are shown in
Figure 7.
Calculate the corresponding coordinates of the twenty-four feature points in the two coordinate systems. Then substitute them into Equation (5) and solve the function by the linear least square method. Calibration results are shown in
Table 1.
According to the camera’s nominal value, we can obtain: , ,. Comparing the experimental value with the nominal value, the error is within 4%, which can initially indicate that the results of the calibration are basically accurate.
In order to verify the stability of the calibration results, without changing the relative position of the sensor and the placement distance of the calibration board, multiple calibration experiments and result calculations were performed under the same conditions. Then each calibration result was compared with the average of multiple calibration results. The rotation angle vector, translation vector, and the parameters of the camera’s parameters have a dynamic range of 0.2%. Therefore, the results of this calibration are relatively stable and not accidental data.
4.2. Incremental Verification Experiments
The actual relative position of LiDAR and the camera is difficult to obtain, so it is hard to quantitatively verify the calibration results by comparing experimental values with actual values. This is also the more difficult problem in the current calibration of the LiDAR and camera. For this purpose, we specially designed incremental verification experiments to indirectly verify the accuracy of the calibration results. For the experiments in
Section 4.1, the relative distance and rotation angle of LiDAR and the camera were changed separately. Then we compared the changes in the calibration results with the actual values.
4.2.1. Translation Incremental Verification
Keep LiDAR stationary and move the slider carrying the camera 11 cm on the guide rail. The calibration results before and after changing only the relative translation position are shown in
Table 2.
Calculate the translation variation according to the two calibration results. Hence, we have
The difference between the experimental value and the nominal value is 0.0007 m, which is within the tolerance range.
4.2.2. Rotation Increment Verification
Keep LiDAR stationary and rotate the angle adjustment device on the camera slider. Rotate the camera 8° counterclockwise. The calibration results before and after changing the relative rotation position are shown in
Table 3.
Since the rotation direction of the camera coordinate is unknown, we use a random vector combined with an arbitrary axis rotation matrix and a multi-objective constrained programming method [
27] to calculate the value. The rotation angle is 7.9542°.
The difference between the experimental value and the nominal value is 0.0458°, which is within the allowable range of the error.
Through the above two single-parameter incremental test experiments, the accuracy of this calibration method was indirectly verified.
4.3. Reprojection Error Evaluation
We use the more commonly known verification method in the calibration field to evaluate accuracy of this calibration method, that is the reprojection error. For the calibration experiments in
Section 4.1, the pixel coordinates of the feature points after reprojection are used as experimental values here, and the pixel coordinates of feature points calculated by the "three-step fitting interpolation method" are used as theoretical values. Then, we have the reprojection error as:
Here, N is the number of selected feature points. is the theoretical coordinate. is the experimental coordinate.
In order to initially verify the accuracy of our calibration experiment, we placed the calibration board at 2, 5, 7.5, 10, 15, and 20 m respectively, then used the transformation matrix
Q obtained by the experiment in
Section 4.1 to solve the reprojection errors at different distances. The results are shown in
Table 4.
It can be seen from the above values that the reprojection errors at different distances are all about 1.8 pixels, which can also verify the accuracy of this calibration method. Moreover, the amount of change at each distance is within 0.1 pixels. Based on this, we believe that this calibration method is basically not affected by the placement distance of the calibration board.
Finally, taking the re-projection error at various distances into consideration, we compare the results of our method with others, as shown in
Table 5.
As can be seen from
Table 5, the reprojection error of the method proposed in this paper is 1.8312 pixels, which is second only to the supervised learning calibration method. However, compared with our method, the supervised learning method requires a larger number of feature point samples, and the workload of the feature point acquisition process is enormous. The mutual information calibration method directly performs global optimization, and the accuracy is relatively high. However, the amount of calculation is large, and the sensor accuracy and image distortion requirements are stricter. The method adopted by Xie et al. and Jia et al. is the feature point method. It is not difficult to analyze that the accuracy is lower due to the inaccuracy of obtaining the feature point coordinates. The bi-parallel plate method is a vector constraint method. It has successively performed three calibration processes: LiDAR and car body calibration, camera and car body calibration, and camera and LiDAR calibration. The process is tedious, and the accumulated calibration errors in each process cause the overall calibration accuracy to be low. Considering the calibration accuracy, calibration workload, and convenience, the calibration method proposed in this paper has higher practical and popularization value.
5. Conclusions and Future Work
At present, the calibration of LiDAR and the camera using the feature point method is not perfect due to the inadequacy of the design of the calibration board and the calibration method, which results in a large error in calibration. Aiming at the above problems, this paper designs BWDC, and puts forward the "three-step fitting interpolation method" to obtain a sufficient number of accurate coordinate points of the feature points to solve the calibration matrix and the intrinsic and external parameters. The designed calibration board has both gradient depth information and corner point information. It has only one design parameter, which facilitates the control of processing errors. In addition, it has a certain self-calibration function, and is widely applicable. By applying the calibration method proposed in this paper, the corresponding coordinates of the feature points in the two coordinate systems can be directly calculated without manual labeling or approximate estimation, which greatly improves the accuracy of the feature point coordinates and further improves the calibration accuracy. It is verified by experiments that the calibration method has high accuracy, stability and accuracy. Moreover, it is not difficult to see from the general method that the proposed method is also applicable to single-line LiDAR, although developed around multi-line LiDAR.
However, the verification method proposed in this paper is still inadequate. Because the true orientation of LiDAR and the camera coordinate systems cannot be obtained, we can only use the preliminary comparison of actual and experimental values, incremental verification methods, and scanning line reprojection to verify the correctness of the calibration performance indirectly. In the future, we will consider using infrared cameras to assist verification. Other than that, this calibration method is slightly inadequate in calibration accuracy. The calibration equation is an over-constrained equation. The linear least square method used in this paper is only one of its solutions. Later, we will consider increasing the number of extracted feature points, using other optimization methods such as Gauss Newton, or training the neural networks to solve the calibration equation to further improve the calibration accuracy.