Design of Signal Generators Using Active Elements Developed in I3T25 CMOS Technology Single IC Package for Illuminance to Frequency Conversion
Abstract
:1. Introduction
- (a)
- A simple electronic control of the repeating frequency (f0) by bias current,
- (b)
- Bias voltage driving threshold voltages of the Schmitt trigger,
- (c)
- Hypothetical elements are not used,
- (d)
- (e)
- High amplitude of the output voltage levels in comparison with other solutions, where output levels are in tens of mV (similarly to as in simulated waveforms, e.g., see [21]).
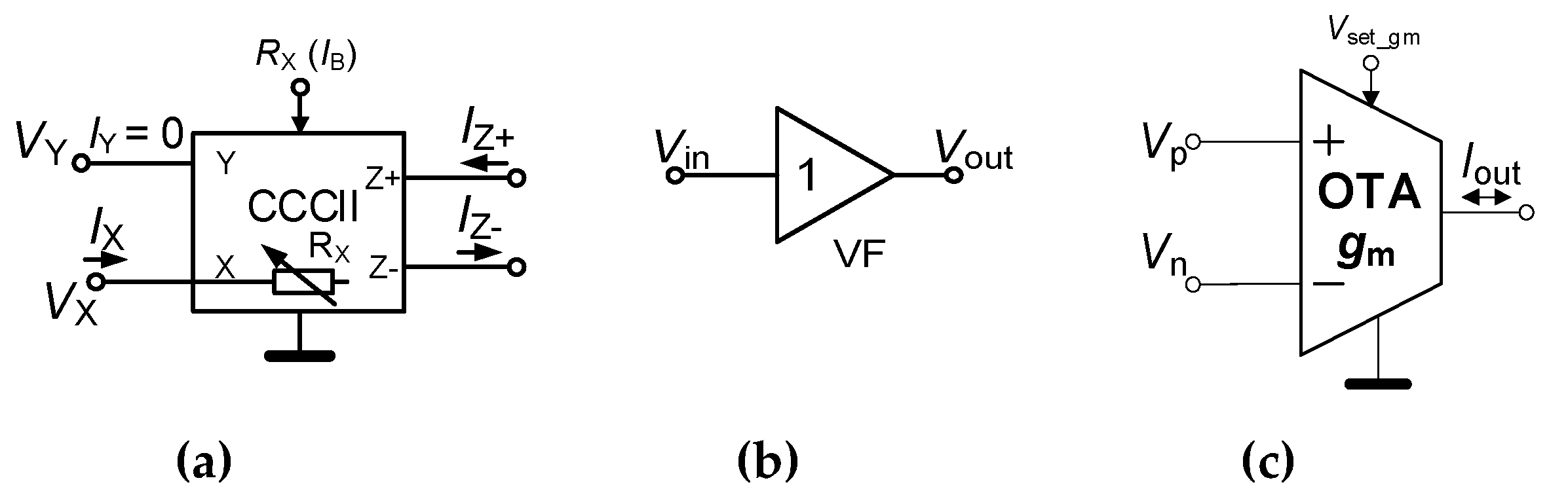
2. Description of Active Elements
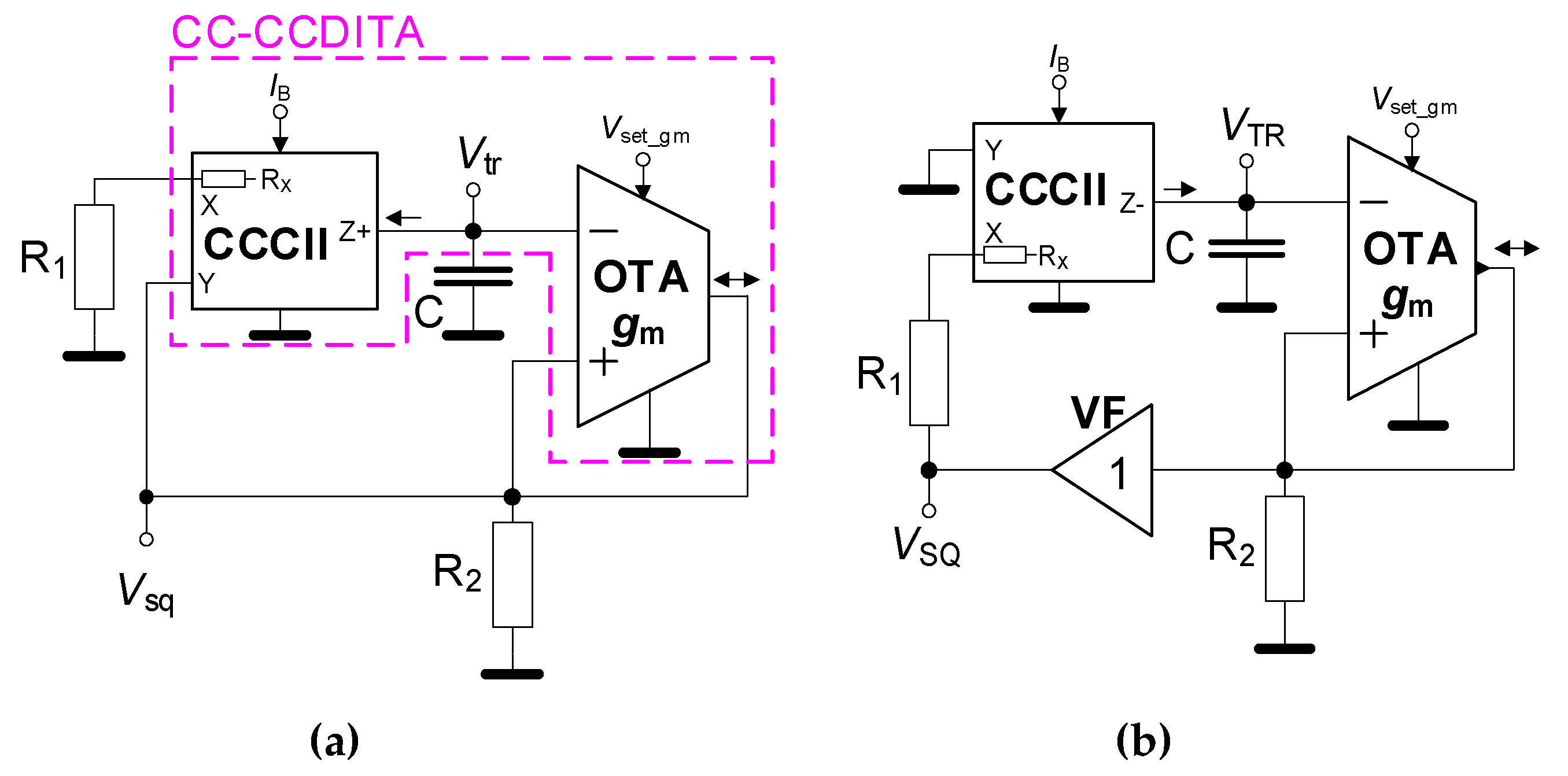
3. Generator Based on Schmitt Trigger with OTA and Current Controlled Integrator Using CCCII
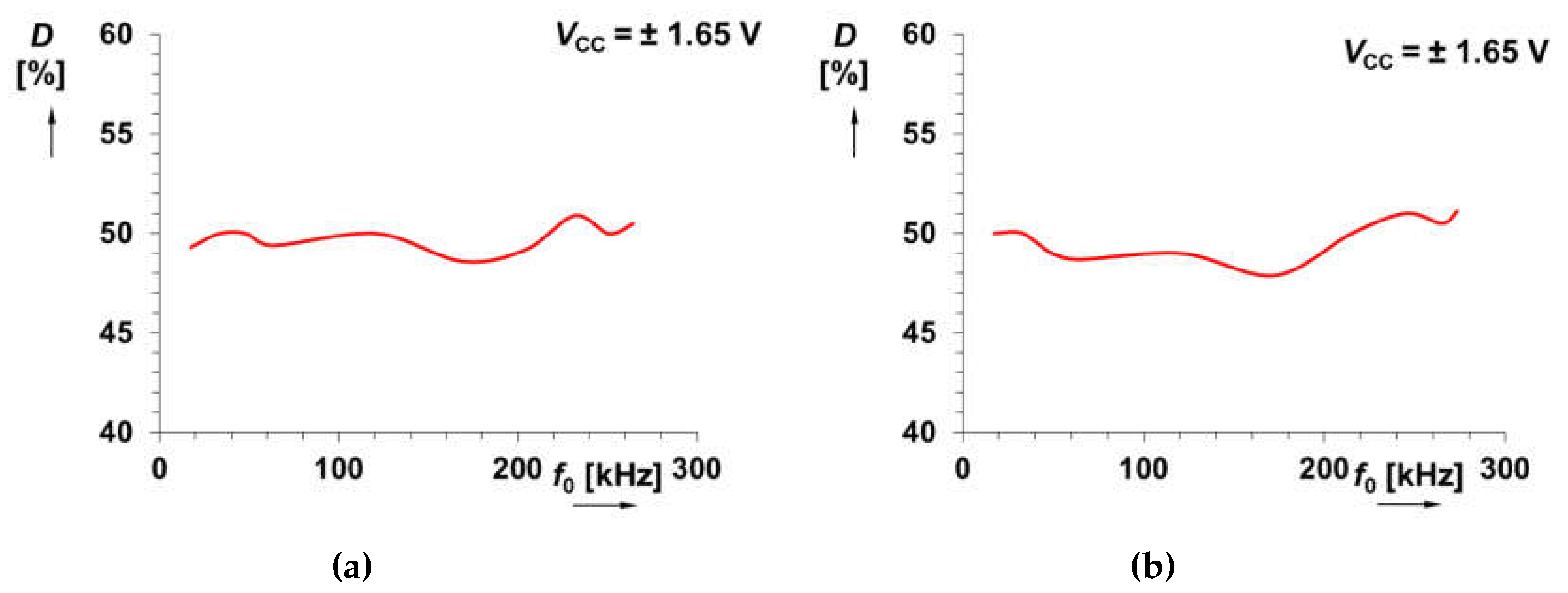
4. Comparison of the Proposed Concepts with Previous Works
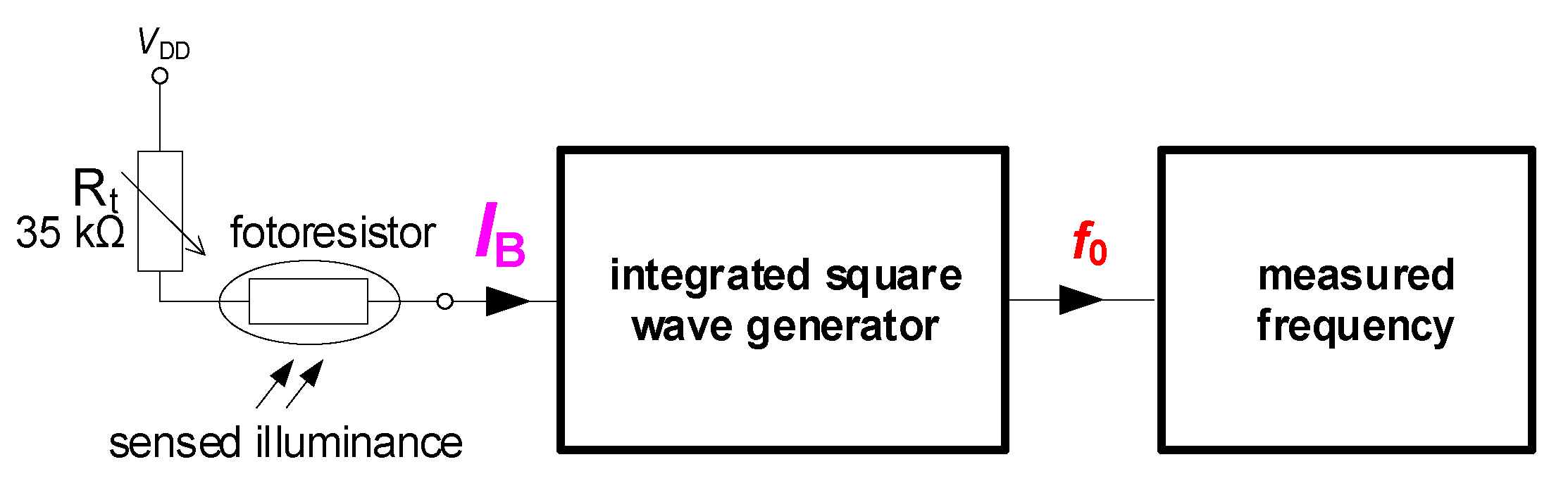
5. Illuminance to Frequency Converter—A Sensing Application
Sensing Applications—A Brief Discussion of the State-of-the-Art
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Senani, R.; Bhaskar, D.R.; Singh, V.K.; Sharma, R.K. Sinusoidal Oscillators and Waveform Generators Using Modern Electronic Circuit Building Blocks; Springer International Publishing AG: Cham, Switzerland, 2016; pp. 1–622. [Google Scholar]
- Biolek, D.; Senani, R.; Biolkova, V.; Kolka, Z. Active elements for analog signal processing: Classification, Review and New Proposals. Radioengineering 2008, 17, 15–32. [Google Scholar]
- Senani, R.; Bhaskar, D.R.; Singh, V.K. Current Conveyors: Variants, Applications and Hardware Implementations; Springer International Publishing: Berlin/Heidelberg, Switzerland, 2015; pp. 1–560. [Google Scholar]
- Polak, L.; Sotner, R.; Petrzela, J.; Jerabek, J. CMOS Current Feedback Operational Amplifier-Based Relaxation Generator for Capacity to Voltage Sensor Interface. Sensors 2018, 18, 4488. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chung, W.S.; Kim, H.; Cha, H.-W. Triangular/square-wave generator with independently controllable frequency and amplitude. IEEE Trans. Instrum. Meas. 2005, 54, 105–109. [Google Scholar] [CrossRef]
- Siripruchyanun, M.; Wardkein, P. A full independently adjustable, integrable simple current controlled oscillator and derivative PWM signal generator. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2003, 86, 3119–3126. [Google Scholar]
- Kumbun, J.; Siripruchyanun, M. MO-CTTA-based electronically controlled current-mode square/triangular wave generator. In Proceedings of the 1st International Conference on Technical Education (ICTE2009), Bangkok, Thailand, 21–22 January 2010; pp. 158–162. [Google Scholar]
- Silapan, P.; Siripruchyanun, M. Fully and electronically controllable current-mode Schmitt triggers employing only single MO-CCCDTA and their applications. Analog Integr. Circuits Signal Process. 2011, 68, 111–128. [Google Scholar] [CrossRef]
- Srisakul, T.; Silapan, P.; Siripruchyanun, M. An electronically controlled current-mode triangular/square wave generator employing MO-CCCCTAs. In Proceedings of the 8th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications, and Information Technology (ECTICON), Khon Kaen, Thailand, 17–19 May 2011; pp. 82–85. [Google Scholar]
- Janecek, M.; Kubanek, D.; Vrba, K. Voltage-Controlled Square/Triangular Wave Generator with Current Conveyors and Switching Diodes. Int. J. Adv. Telecommun. Electrotech. Signals Syst. 2012, 1, 76–79. [Google Scholar]
- Sotner, R.; Jerabek, J.; Herencsar, N. Voltage Differencing Buffered/Inverted Amplifiers and Their Applications for Signal Generation. Radioengineering 2013, 22, 490–504. [Google Scholar]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Dostal, T.; Vrba, K. Design of Z-copy controlled-gain voltage differencing current conveyor based adjustable functional generator. Microelectron. J. 2015, 46, 143–152. [Google Scholar] [CrossRef]
- Jerabek, J.; Sotner, R.; Dostal, T.; Vrba, K. Simple Resistor-less Generator Utilizing Z-copy Controlled Gain Voltage Differencing Current Conveyor for PWM Generation. Elektronika Ir Elektrotechnika 2015, 21, 28–34. [Google Scholar] [CrossRef] [Green Version]
- Sotner, R.; Petrzela, J.; Jerabek, J.; Domansky, O.; Langhammer, L. Special Electronically Reconfigurable Lossy/Lossless Integrator in Application of Functional Generator. In Proceedings of the 27th International Conference Radioelektronika, Brno, Czech Republic, 19–20 April 2017; pp. 1–5. [Google Scholar]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Prokop, R.; Vrba, K.; Petrzela, J.; Dostal, T. Simply Adjustable Triangular and Square Wave Generator Employing Controlled Gain Current and Differential Voltage Amplifier. In Proceedings of the 23th International Conference Radioelektronika, Pardubice, Czech Republic, 16–17 April 2013; pp. 109–114. [Google Scholar]
- Sotner, R.; Jerabek, J.; Herencsar, N.; Lahiri, A.; Petrzela, J.; Vrba, K. Practical Aspects of Operation of Simple Triangular and Square Wave Generator Employing Diamond Transistor and Controllable Amplifiers. In Proceedings of the 36th International Conference on Telecommunications and Signal Processing (TSP), Rome, Italy, 2–4 July 2013; pp. 431–435. [Google Scholar]
- Sotner, R.; Jerabek, J.; Herencsar, N. Study of impact of voltage gain of comparator on performance of newly designed functional generator. Optik 2018, 172, 203–219. [Google Scholar] [CrossRef]
- Chaturvedi, B.; Kumar, A. A novel linear square/triangular wave generator with tunable duty cycle. AEU Int. J. Electron. Commun. 2018, 84, 206–209. [Google Scholar] [CrossRef]
- Kumar, A.; Chaturvedi, B. Single Active Element-Based Tunable Square/Triangular Wave Generator with Grounded Passive Components. Circuits Syst. Signal Process. 2017, 36, 3875–3900. [Google Scholar] [CrossRef]
- Siripruchyanun, M.; Payakkakul, K.; Pipatthitikorn, P.; Satthaphol, P. A Current-mode Square/Triangular ware Generator based on Multiple-output VDTAs. Procedia Comput. Sci. 2016, 86, 152–155. [Google Scholar] [CrossRef] [Green Version]
- Chaturvedi, B.; Kumar, A. Fully Electronically Tunable and Easily Cascadable Square/Triangular Wave Generator with Duty Cycle Adjustment. J. Circuits Syst. Comput. 2018, 28, 1950105. [Google Scholar] [CrossRef]
- Kumar, A.; Chaturvedi, B.; Maheshwari, S. A fully electronically controllable Schmitt trigger and duty cycle-modulated waveform generator. Int. J. Circuit Theory Appl. 2017, 45, 2157–2180. [Google Scholar] [CrossRef]
- Chaturvedi, B.; Kumar, A. Novel CMOS MO-CFDITA based fully electronically controlled square/triangular wave generator with adjustable duty cycle. IET Circuits Devices Syst. 2018, 12, 817–826. [Google Scholar] [CrossRef]
- Chien, H.C. A current-/voltage-controlled four-slope operation square-/triangular-wave generator and a dual-mode pulse width modulation signal generator employing current-feedback operational amplifiers. Microelectron. J. 2014, 45, 634–647. [Google Scholar] [CrossRef]
- Zafar, Z.N.; Maktoomi, M.A.; Hashmi, M.S. A new adjustable square/triangular-wave generator using CCII/CCCII and OTA. In Proceedings of the 26th International Conference on Microelectronics (ICM), Doha, Qatar, 14–17 December 2014; pp. 104–107. [Google Scholar]
- Chien, H.C. Voltage-controlled dual slope operation square/triangular wave generator and its applications as a dual mode operation pulse width modulator employing differential voltage current conveyors. Microelectron. J. 2013, 43, 962–974. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Prokop, R.; Kledrowetz, V.; Polak, J. A CMOS Multiplied Input Differential Difference Amplifier: A New Active Device and Its Applications. Appl. Sci. 2017, 7, 106. [Google Scholar] [CrossRef] [Green Version]
- Prokop, R.; Musil, V. Modular approach to design of modern circuit blocks for current signal processing and new device CCTA. In Proceedings of the 7th International Conference on Signal and Image Processing, Honolulu, HI, USA, 15–17 August 2005; pp. 494–499. [Google Scholar]
- Prokop, R.; Musil, V. New modular current devices for true current mode signal processing. Electronics 2007, 16, 36–42. [Google Scholar]
- Sotner, R.; Jerabek, J.; Polak, L.; Prokop, R.; Kledrowetz, V. Integrated Building Cells for a Simple Modular Design of Electronic Circuits with Reduced External Complexity: Performance, Active Element Assembly, and an Application Example. Electronics 2019, 8, 568. [Google Scholar] [CrossRef] [Green Version]
- Token. CDS Light-Dependent Photoresistors PGM/LDR5516. 2010, p. 7. Available online: https://www.tme.eu/Document/0b7aec6d26675b47f9e54d893cd4521b/PGM5506.pdf (accessed on 8 December 2019).
- Malik, S.; Kishore, K.; Sharma, D.; Maharana, M.; Akbar, S.A.; Islam, T. A CCII-based wide frequency range square/triangular wave generator. In Proceedings of the 2nd International Conference on Recent Trends in Information Systems (ReTIS), Kolkata, India, 9–11 July 2015; pp. 446–449. [Google Scholar]
- Do, T.-H.; Yo, M. Performance Analysis of Visible Light Communication Using CMOS Sensors. Sensors 2016, 16, 309. [Google Scholar] [CrossRef] [PubMed]
- De Marcellis, A.; Ferri, G. Physical and Chemical Sensors. In Analog Circuits and Systems for Voltage-Mode and Current-Mode Sensor Interfacing Applications; Springer: Heidelberg, Germany, 2011; pp. 1–35. [Google Scholar]
- Lee, C.; Koo, S.-M.; Oh, J.-M.; Moon, K.-S.; Lee, D. Selectable Titanium-oxide Based Critical and Differential Temperature Sensor in a Single Device. IEEE Electron Device Lett. 2018, 39, 1058–1060. [Google Scholar] [CrossRef]
- Wei, Q.; He, C.; Chen, J.; Chen, D.; Wang, J. Wireless Passive Intracranial Pressure Sensor Based on a Microfabricated Flexible Capacitor. IEEE Trans. Electron Devices 2018, 65, 2592–2600. [Google Scholar] [CrossRef]
- Shin, K.; Jeon, J.; West, J.E.; Moon, W. A Micro-Machined Microphone Based on a Combination of Electret and Field-Effect Transistor. Sensors 2015, 15, 20232–20249. [Google Scholar] [CrossRef] [Green Version]
- Vargas-Bernal, R.; Carlos, A.; Gómez-Polo, C. Electrical Circuit Modeling of Sensor Magneto-Impedances with a Square-Root Frequency Dependence. IEEE Sens. J. 2018, 18, 623–628. [Google Scholar] [CrossRef]
- Yu, X.; Chen, X.; Ding, X.; Zhao, X. A High-Stability Quartz Crystal Resonator Humidity Sensor Based on Tuning Capacitor. IEEE Trans. Instrum. Meas. 2018, 67, 715–721. [Google Scholar] [CrossRef]
- Piotto, M.; Del Cesta, S.; Bruschi, P. Precise Measurement of Gas Volumes by Means of Low-Offset MEMS Flow Sensors with μL/min Resolution. Sensors 2017, 17, 2497. [Google Scholar] [CrossRef] [Green Version]
- Parente, F.R.; Giovanni, S.D.; Ferri, G.; Stornelli, V.; Pennanzza, G.; Santonico, M. An Analog Bootstrapped Biosignal Read-Out Circuit With Common-Mode Impedance Two-Electrode Compensation. IEEE Sens. J. 2018, 18, 2861–2869. [Google Scholar] [CrossRef]
- Depari, A.; Sisinni, E.; Flammini, A.; Ferri, G.; Stornelli, V.; Barile, G.; Parente, F.R. Autobalancing Analog Front End for Full-Range Differential Capacitive Sensing. IEEE Trans. Instrum. Meas. 2018, 67, 885–893. [Google Scholar] [CrossRef]
- De Marcellis, A.; Ferri, G.; Mantenuto, P. A CCII-based non-inverting Schmitt trigger and its application as astable multivibrator for capacitive sensor interfacing. Int. J. Circ. Theor. Appl. 2017, 45, 1060–1076. [Google Scholar] [CrossRef]
- Preto, S.; Gomes, C.C. Lighting in the Workplace: Recommended Illuminance (lux) at Workplace Environs. In International Conference on Applied Human Factors and Ergonomics (AHFE 2018): Advances in Design for Inclusion; Springer International Publishing: Cham, Germany, 2018; pp. 180–191. [Google Scholar]
- Li, D.H.W.; Tsang, E.K.W. An analysis of measured and simulated daylight illuminance and lighting savings in a daylight corridor. Build. Environ. 2005, 40, 973–982. [Google Scholar] [CrossRef]
- Waddington, C.; Kofman, J. Analysis of measurement sensitivity to illuminance and fringe-pattern gray levels for fringe-pattern projection adaptive to ambient lighting. Opt. Lasers Eng. 2010, 48, 251–256. [Google Scholar] [CrossRef]
- Lavery, L.L.; Whiting, G.L.; Arias, A.C. All ink-jet printed polyfluorene photosensor for high illuminance detection. Org. Electron. 2011, 12, 682–685. [Google Scholar] [CrossRef]
- Moon, S.-J.; Lim, Y.-S. Image Sensor Module for Detection Space Illuminance in Indoor Environment. J. Korea Inst. Inf. Commun. Eng. 2019, 23, 771–778. [Google Scholar]
- Kuo, W.; Chiang, C.; Huang, Y. An Automatic Light Monitoring System with Light-to-Frequency Converter for Flower Planting. In Proceedings of the International IEEE Instrumentation and Measurement Technology Conference (IMTC), Victoria, BC, Canada, 12–15 May 2008; pp. 1146–1149. [Google Scholar]
- Germer, S.; Cherkouk, C.; Rebohle, L.; Helm, M.; Skorupa, W. Si-based light emitter in an integrated photonic circuit for smart biosensor applications. In Proceedings of the Integrated Photonics: Materials, Devices, and Applications II, SPIE Microtechnologies, Grenoble, France, 22 May 2013; Volume 8767, pp. 876710-1–876710-13. [Google Scholar]
- Xu, K.; Chen, Y.; Okhai, T.A.; Snyman, L.W. Micro optical sensors based on avalanching silicon light-emitting devices monolithically integrated on chips. Opt. Mater. Express 2019, 9, 3985–3997. [Google Scholar] [CrossRef]





| Reference | Number of Passive Elements (in Lab. Experiments) | Number of Active Elements | Number of IC Packages (in Laboratory Experiments) | Compact IC Device Including All Active Elements | Maximal Current (ICmax) Charging C Independent on Linear Operation of the AE | Integrator Uses Different Part than OTA (Where ICmax ≅ Ibias) | Type of Active Element(s) | Number of Internal Functional Subparts of Active Device | Classification of Active Element(s) Used in Verification | Verification | Power Consumption |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [5] | 3 | 3 | 3 | No | Yes | No | OTA | N/A | standard | M | N/A |
| [6] | 3 | 3 | N/A | No | Yes | No | OTA | N/A | standard | S | N/A |
| [7] | 1 | 2 | N/A | No | Yes | No | MO-CTTA | 2 | hypothetical | S | N/A |
| [8] | 1 | 2(8) | N/A | No | Yes | No | MO-CCCDTA | 2 | hypothetical | S | N/A |
| [9] | 1 | 2 | N/A | No | Yes | No | MO-CCCCTA | 2 | hypothetical | S | 1.6 mW |
| [10] | 8 | 2 | 1 | Yes | Yes | Yes | UCC + CCII | N/A | fabricated (CMOS) | S | N/A |
| [11] | 3 | 2 | N/A | No | Yes | No | VDBA | 2 | hypothetical | S | N/A |
| [12] | 3 | 1 | 5 | No | Yes | No | ZC-CG-VDCC | 2 | hypothetical | S | 6.3 mW |
| [13] | 1 | 1 | 8 | No | Yes | No | ZC-CG-VDCC | 2 | hypothetical | M | N/A |
| [14] | 4 | 3 | 3 | No | No | Yes | ECCII + VGA + OPAMP | N/A | standard | S | N/A |
| [15] | 2 | 1 | N/A | No | No | Yes | CG-CDVA | 2 | hypothetical | S | N/A |
| [16] | 2 | 3 | 3 | No | Yes | Yes | DT + VGA | N/A | standard | M | N/A |
| [17] | 2 | 2 | 2 | No | No | Yes | ECCII + VGA | N/A | standard | M | N/A |
| [18] | 2(4) | 1 | 7 | No | Yes | No | MO-DXCCTA | 2 | hypothetical | M | N/A |
| [19] | 2(4) | 1 | 6 | No | Yes | No | MO-DVCCTA | 2 | hypothetical | M | 226 mW |
| [20] | 3 | 2 | N/A | No | Yes | No | MO-VDTA | 2 | hypothetical | S | 14.3 mW |
| [21] | 2(4) | 1 | 8 | No | Yes | No | MO-DXCCTA | 2 | hypothetical | S | 1 mW |
| [22] | 1(2) | 1 | 5 | No | Yes | No | MO-CIDITA | 2 | hypothetical | M | 1 |
| [23] | 1(2) | 1 | 4 | No | Yes | No | MO-CFDITA | 2 | hypothetical | M | 2 |
| * [24] | 2(3) | 4(5) | 2(3) | No | No | Yes | CFOA | N/A | standard | M | 458 mW |
| [25] | 4 | 2 | 2 | No | No | Yes | CCII/CCCII + OTA | N/A | standard | M | 192 mW |
| * [26] | 4 | 2(3) | 6(9) | No | No | Yes | DVCC | 1 | hypothetical | M | 763 mW |
| Proposed | |||||||||||
| Figure 1a | 3 | 2 | 1 | Yes | Yes | Yes | CCCII + OTA | N/A | fabricated (CMOS I3T) | M | 67 mW |
| Figure 1b | 3 | 3 | 1 | Yes | Yes | Yes | CCCII + OTA + VF | N/A | fabricated (CMOS I3T) | M | 86 mW |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sotner, R.; Jerabek, J.; Polak, L.; Kledrowetz, V.; Prokop, R. Design of Signal Generators Using Active Elements Developed in I3T25 CMOS Technology Single IC Package for Illuminance to Frequency Conversion. Sensors 2020, 20, 1198. https://doi.org/10.3390/s20041198
Sotner R, Jerabek J, Polak L, Kledrowetz V, Prokop R. Design of Signal Generators Using Active Elements Developed in I3T25 CMOS Technology Single IC Package for Illuminance to Frequency Conversion. Sensors. 2020; 20(4):1198. https://doi.org/10.3390/s20041198
Chicago/Turabian StyleSotner, Roman, Jan Jerabek, Ladislav Polak, Vilem Kledrowetz, and Roman Prokop. 2020. "Design of Signal Generators Using Active Elements Developed in I3T25 CMOS Technology Single IC Package for Illuminance to Frequency Conversion" Sensors 20, no. 4: 1198. https://doi.org/10.3390/s20041198





