Batch Processing through Particle Swarm Optimization for Target Motion Analysis with Bottom Bounce Underwater Acoustic Signals †
Abstract
:1. Introduction
2. Problem Formulation
2.1. Dynamic Model
2.2. Measurement Model
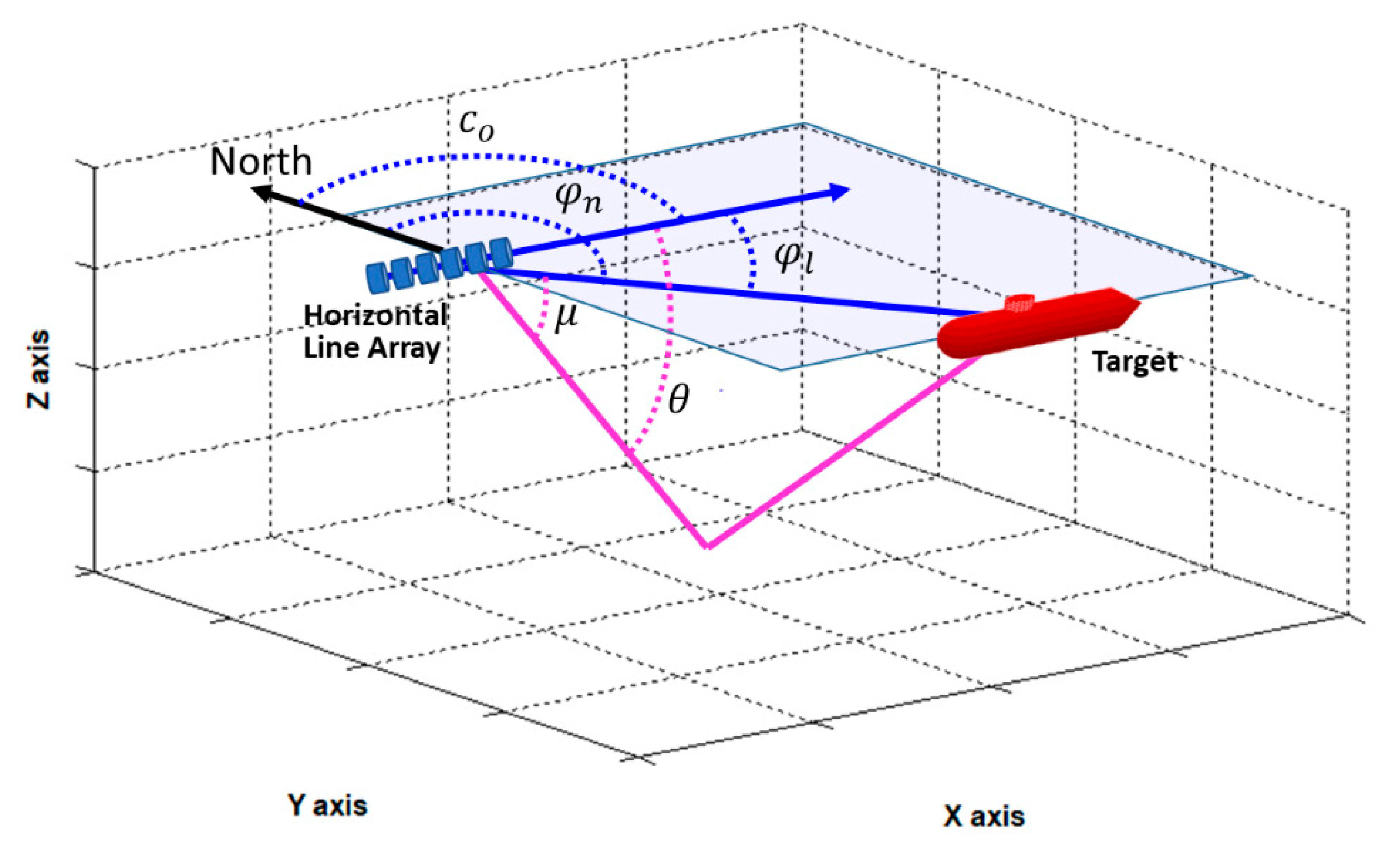
3. Target Motion Analysis with Bottom Bounce Path
3.1. Bearing Lines of Bottom Bounce Path
3.2. Particle Swarm Optimization
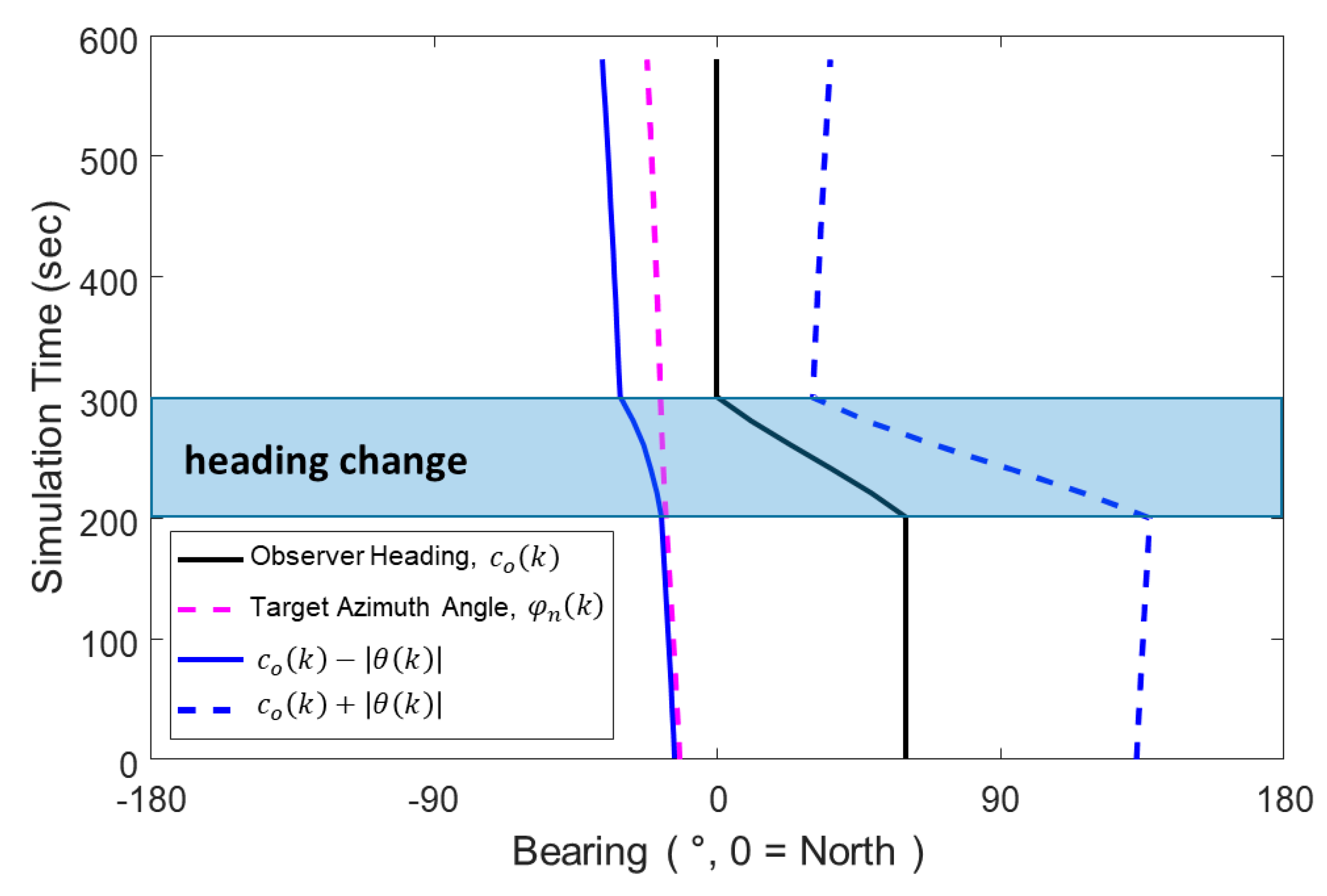
4. Simulation Result
5. Summary and Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Abraham, D.A. Underwater Acoustic Signal Processing: Modeling, Detection, and Estimation, Modern Acoustics and Signal Processing; Springer Nature Switzerland AG: Cham, Switzerland, 2019. [Google Scholar]
- Aidala, V.J.; Hammel, S.E. Utilization of Modified Polar Coordinates for Bearings-Only Tracking. IEEE Trans. Autom. Control 1983, AC-28, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Aidala, V.J.; Nardone, S.C. Biased Estimation Properties of the Pseudolinear Tracking Filter. IEEE Trans. Aerosp. Electron. Syst. 1982, AES-18, 432–441. [Google Scholar] [CrossRef]
- Song, T.L.; Speyer, J.L. A stochastic analysis of a modified gain extended Kalman filter with applications to estimation with bearings only measurements. IEEE Trans. Autom. Control 1985, AC-30, 940–949. [Google Scholar] [CrossRef]
- Arulampalam, S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal process. 2002, 50, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Beard, M.; Vo, B.T.; Vo, B.N.; Arulampalam, S. A partially uniform target birth model for gaussian mixture PHD/CPHD Filtering. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2835–2844. [Google Scholar] [CrossRef]
- Zhang, Q.; Song, T.L. Improved bearings-only multi-target tracking with GM-PHD filtering. Sensors 2016, 16, 1469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xie, Y.; Song, T.L. Bearings-only multi-target tracking using an improved labeled multi-Bernoulli filter. Signal Process. 2018, 151, 32–44. [Google Scholar] [CrossRef]
- Kirubarajan, T.; Shalom, Y.B.; Lerro, D. Bearings-Only Tracking of Maneuvering Targets Using a Batch-Recursive Estimator. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 770–780. [Google Scholar] [CrossRef]
- Oh, R.; Gu, B.S.; Kim, S.; Song, T.L.; Choi, J.W.; Son, S.U.; Kim, W.K.; Bae, H.S. Estimation of bearing error of line array sonar system caused by bottom bounced path. J. Acoust. Soc. Korea 2018, 37, 412–421. [Google Scholar]
- Jauffret, C.; Pillon, D. Observability in Passive Target Motion Analysis. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1290–1300. [Google Scholar] [CrossRef]
- Hammel, S.E.; Aidala, V.J. Observability Requirements for Three-Dimensional Tracking via Angle Measurements. IEEE Trans. Aerosp. Electron. Syst. 1985, AES-21, 200–207. [Google Scholar] [CrossRef]
- Heaney, K.D.; Campbell, R.L.; Murray, J.J. Deep water towed array measurements at close range. J. Acoust. Soc. Am. 2013, 134, 3230–3241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics, AIP Series in Modern Acoustics and Signal Processing; American Institute of Physics: New York, NY, USA, 1994. [Google Scholar]
- Porter, M.B.; Bucker, H.P. Gaussian beam tracing for computing ocean acoustic fields. J. Acoust. Soc. Am. 1987, 82, 1349–1359. [Google Scholar] [CrossRef]
- Oh, R.; Song, T.L.; Choi, J.W. Bearings-Only Target Motion Analysis using Ray Tracing. In Proceedings of the 8th International Conference on Control Automation & Information Sciences, Chengdu, China, 23–26 October 2019. [Google Scholar]
- Song, T.L. Observability of target tracking with bearings-only measurements. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1468–1472. [Google Scholar] [CrossRef]
- Munk, W.H. Sound channel in an exponentially stratified ocean with application to SOFAR. J. Acoust. Soc. Am. 1974, 55, 220–226. [Google Scholar] [CrossRef]
- Kennedy, J. Particle Swarm Optimization. In Encyclopedia of Machine Learning; Springer: New York, NY, USA, 2011; pp. 760–766. [Google Scholar]
- Kim, S.; Choi, J.W. Optimal Deployment of Sensor Nodes Based on Performance Surface of Underwater Acoustic Communication. Sensors 2017, 17, 2389–2403. [Google Scholar]








| Parameter | Symbol | Value |
|---|---|---|
| Number of particles | 200 | |
| Number of dimensions | 4 | |
| Number of generations | m and m/s | |
| Acceleration weight constants | 0.73 | |
| Acceleration weight constants | 0.1 | |
| Acceleration weight constants | 0.2 | |
| Random number | 0―1 | |
| Random number | 0―1 |
[m, m, m/s, m/s] | ||
|---|---|---|
| 0.2° | ||
| 0.4° | ||
| 0.6° |
[m, m, m/s, m/s] | ||
|---|---|---|
| 15 | ||
| 30 | ||
| 60 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, R.; Song, T.L.; Choi, J.W. Batch Processing through Particle Swarm Optimization for Target Motion Analysis with Bottom Bounce Underwater Acoustic Signals. Sensors 2020, 20, 1234. https://doi.org/10.3390/s20041234
Oh R, Song TL, Choi JW. Batch Processing through Particle Swarm Optimization for Target Motion Analysis with Bottom Bounce Underwater Acoustic Signals. Sensors. 2020; 20(4):1234. https://doi.org/10.3390/s20041234
Chicago/Turabian StyleOh, Raegeun, Taek Lyul Song, and Jee Woong Choi. 2020. "Batch Processing through Particle Swarm Optimization for Target Motion Analysis with Bottom Bounce Underwater Acoustic Signals" Sensors 20, no. 4: 1234. https://doi.org/10.3390/s20041234
APA StyleOh, R., Song, T. L., & Choi, J. W. (2020). Batch Processing through Particle Swarm Optimization for Target Motion Analysis with Bottom Bounce Underwater Acoustic Signals. Sensors, 20(4), 1234. https://doi.org/10.3390/s20041234







