Method to Determine the Far-Field Beam Pattern of A Long Array From Subarray Beam Pattern Measurements
Abstract
1. Introduction
2. Materials and Methods
2.1. Beam Pattern
2.2. Proposed Measurement Method
3. Results and Discussion
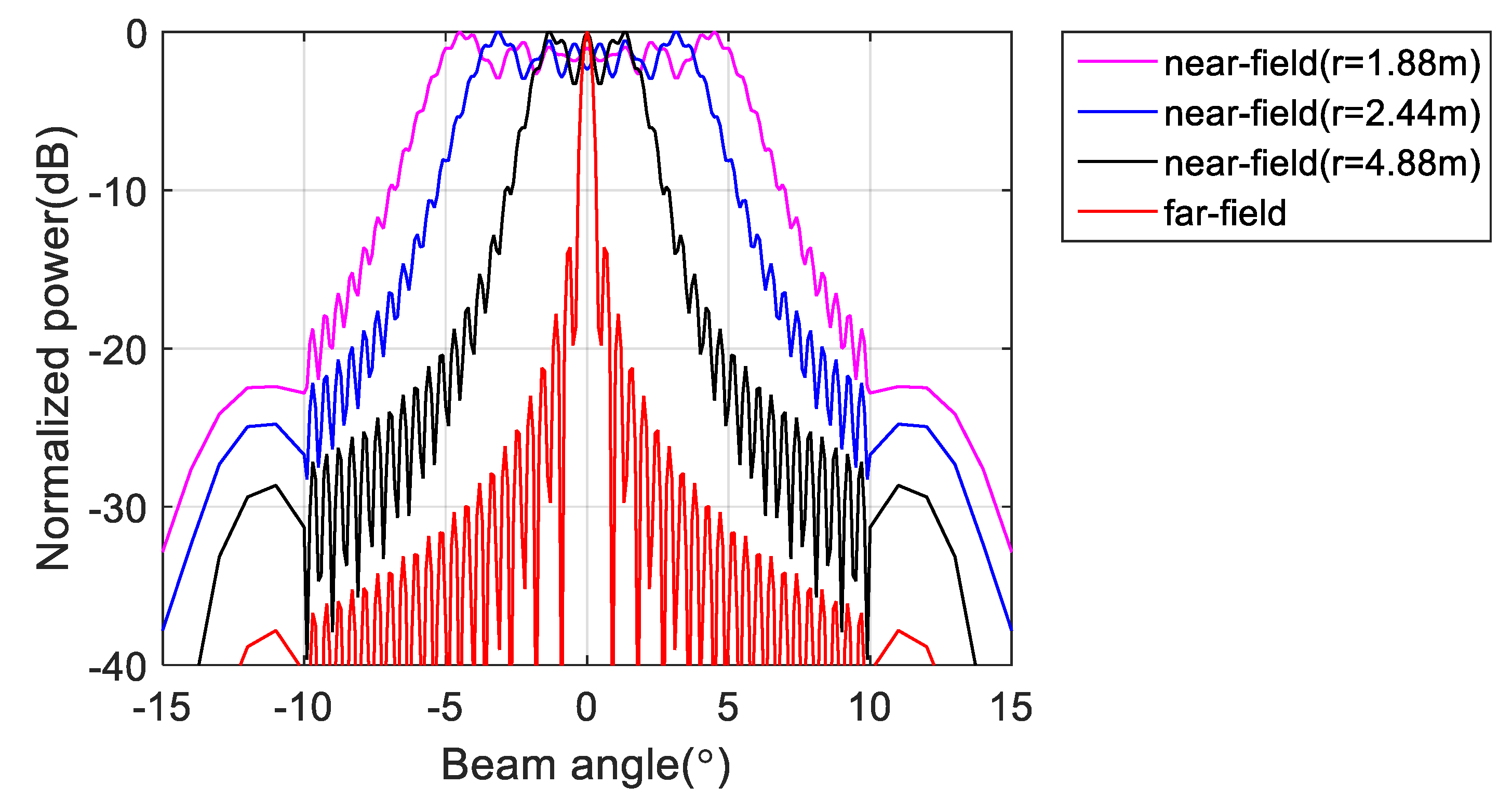
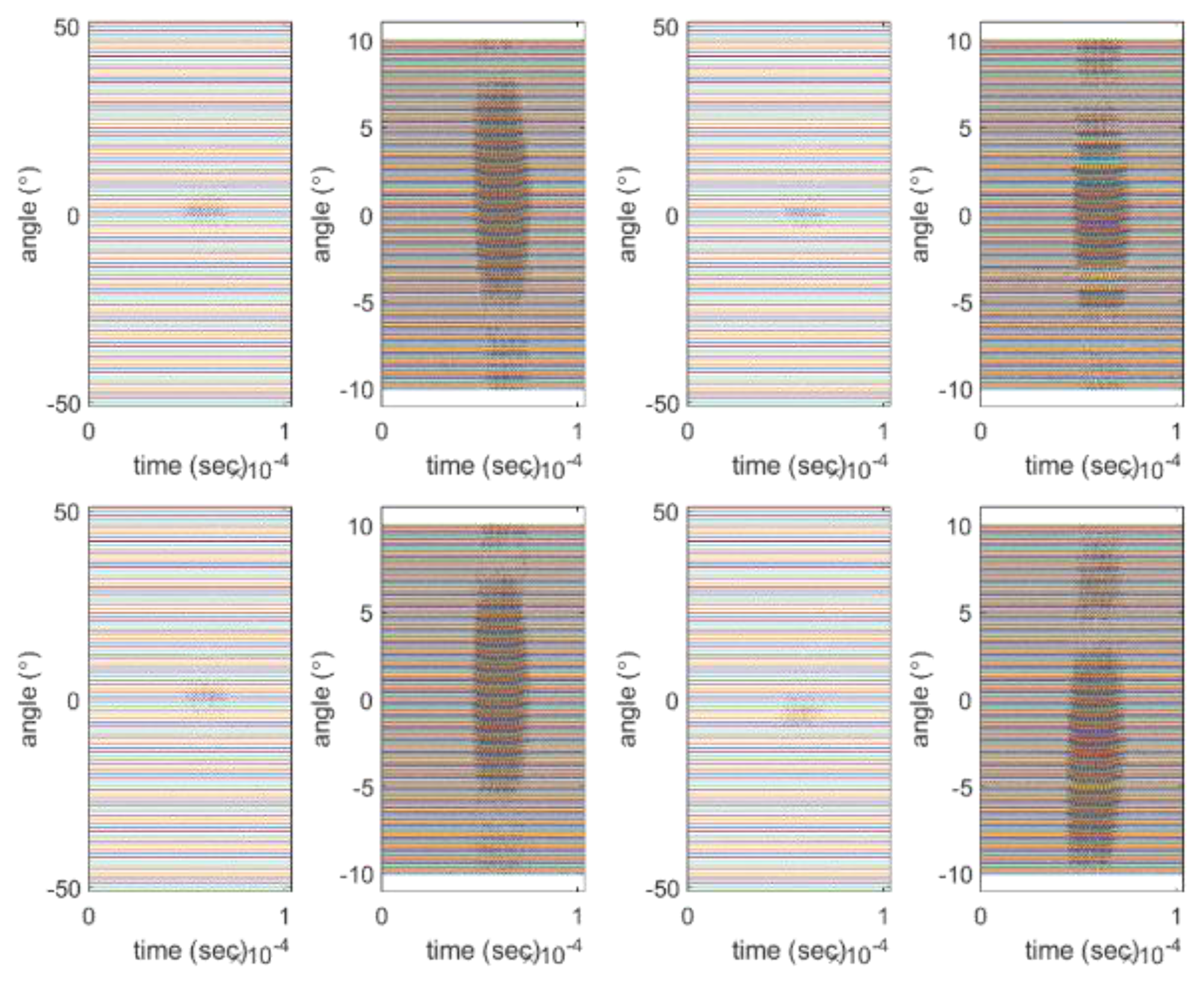
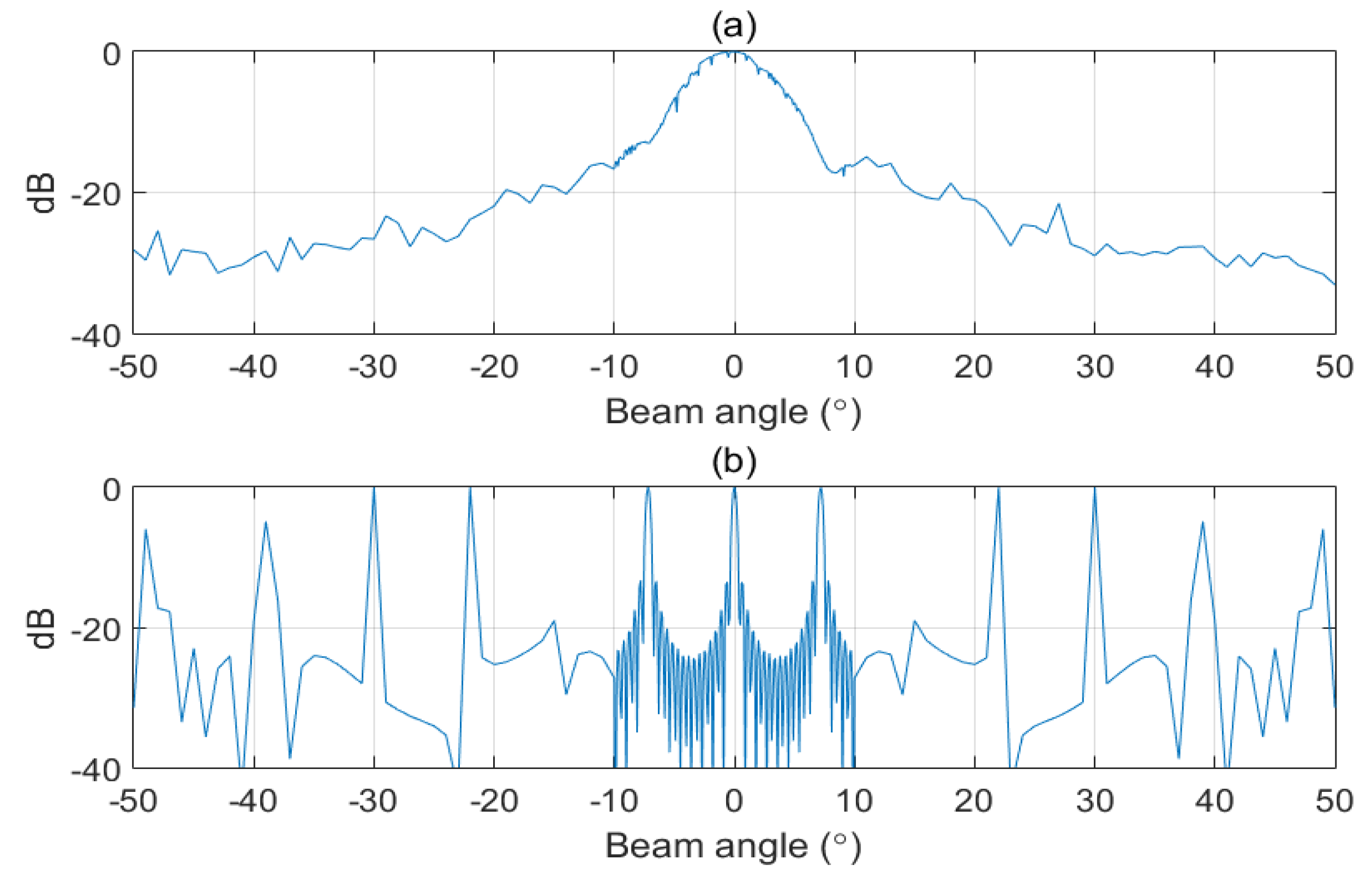
3.1. Simulation
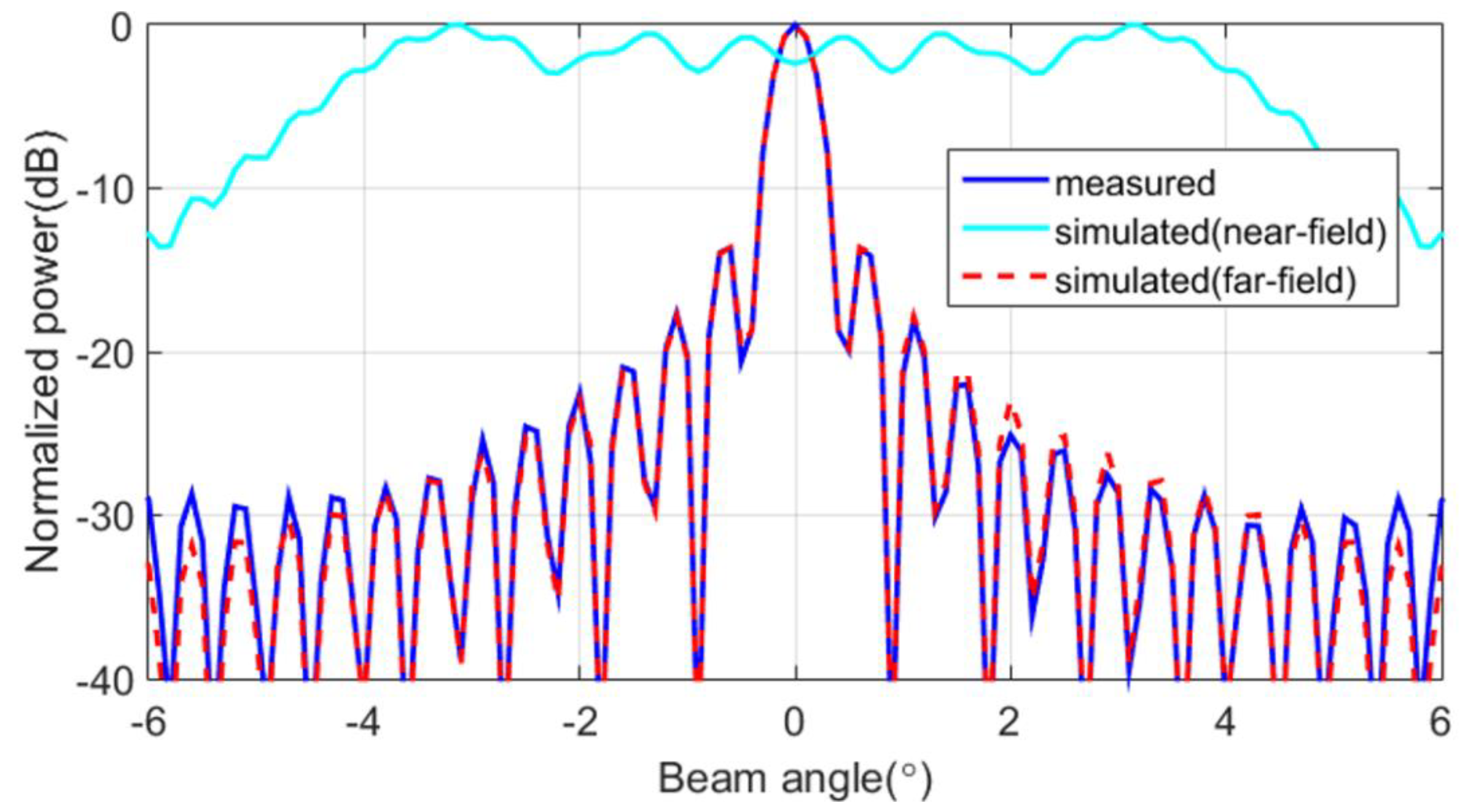
3.2. Near-Field Measurement Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Johnson, R.; Ecker, H.; Moore, R. Compact range techniques and measurements. IEEE Trans. Antennas Propag. 1969, 17, 568–576. [Google Scholar] [CrossRef]
- Odendaal, J.W.; Joubert, J. Radar cross section measurements using near-field radar imaging. IEEE Trans. Instrum. Meas. 1996, 45, 948–954. [Google Scholar] [CrossRef]
- Brown, J.; Jull, E.V. The prediction of aerial radiation patterns from near-field measurements. Proc. IEE Part B Electron. Commun. Eng. 1961, 108, 635. [Google Scholar] [CrossRef]
- KERNS, D.M. Plane-Wave Scattering-Matrix Theory of Antennas and Antenna-Antenna Interactions; US Department of Commerce, National Bureau of Standards: Gaithersburg, MD, USA, 1981.
- Wacker, P.F. Near-Field Antenna Measurements Using a Spherical Scan: Efficient Data Reduction with Probe Correction. In Proceedings of the Conference on Precision Electromagnetic Measurements, London, UK, 1–5 July 1974; pp. 286–288. [Google Scholar]
- Wacker, P.F. Non-Planar Near-Field Measurements: Spherical Scanning. Final Report, Oct. 1973–Jul. 1974; National Bureau of Standards, Boulder, CO. Electromagnetics Div.: Gaithersburg, MD, USA, 1975; Volume 1. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/IR/nbsir75-809.pdf (accessed on 24 February 2020).
- Yaghjian, A. An overview of near-field antenna measurements. IEEE Trans. Antennas Propag. 1986, 34, 30–45. [Google Scholar] [CrossRef]
- Appel-Hansen, J. Near-field far-field antenna measurements. In Antenna Handbook; Springer: Boston, MA, USA, 1988; pp. 2175–2205. [Google Scholar]
- Ludwig, A. Near-field far-field transformations using spherical-wave expansions. IEEE Trans. Antennas Propag. 1971, 19, 214–220. [Google Scholar] [CrossRef]
- Kennedy, R.A.; Abhayapala, T.D.; Ward, D.B. Broadband nearfield beamforming using a radial beampattern transformation. IEEE Trans. Signal Process. 1998, 46, 2147–2156. [Google Scholar] [CrossRef]
- Kennedy, R.A.; Ward, D.B.; Abhayapala, T.D. Nearfield beamforming using radial reciprocity. IEEE Trans. Signal Process. 1999, 47, 33–40. [Google Scholar] [CrossRef]
- Isernia, T.; Leone, G.; Pierri, R. Radiation pattern evaluation from near-field intensities on planes. IEEE Trans. Antennas Propag. 1996, 44, 701. [Google Scholar] [CrossRef]
- Zheng, Y.R.; Goubran, R.A.; El-Tanany, M. Robust Near-Field Adaptive Beamforming with Distance Discrimination. IEEE Trans. Speech Audio Process. 2004, 12, 478–488. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, N.; Xu, J. A novel algorithm based stepped-frequency system about extrapolating near-field to far-field. In Proceedings of the 2012 8th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP), Poznan, Poland, 18–20 July 2012; pp. 1–4. [Google Scholar]
- Kobayashi, H.; Singh, D.; Yamaguchi, Y. Near-field to far-field transformation by using antenna array factor. In Proceedings of the 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR 2011), Seoul, Korea, 26–30 September 2011; Volume 2, pp. 892–895. [Google Scholar]
- Kobayashi, H.; Yamaguchi, Y.; Cui, Y. Simple Near-field to Far-field Transformation Method Using Antenna Array-factor. J. Wirel. Netw. Commun. 2012, 2, 43–48. [Google Scholar] [CrossRef]
- Jung, D.; Kim, J.; Byun, G. Numerical modeling and simulation technique in time-domain for multibeam echo sounder. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 225–234. [Google Scholar] [CrossRef]
- Ioannides, P.; Balanis, C.A. Uniform circular and rectangular arrays for adaptive beamforming applications. IEEE Antennas Wirel. Propag. Lett. 2005, 4, 351–354. [Google Scholar] [CrossRef]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, D.; Kim, J. Method to Determine the Far-Field Beam Pattern of A Long Array From Subarray Beam Pattern Measurements. Sensors 2020, 20, 1236. https://doi.org/10.3390/s20041236
Jung D, Kim J. Method to Determine the Far-Field Beam Pattern of A Long Array From Subarray Beam Pattern Measurements. Sensors. 2020; 20(4):1236. https://doi.org/10.3390/s20041236
Chicago/Turabian StyleJung, Donghwan, and Jeasoo Kim. 2020. "Method to Determine the Far-Field Beam Pattern of A Long Array From Subarray Beam Pattern Measurements" Sensors 20, no. 4: 1236. https://doi.org/10.3390/s20041236
APA StyleJung, D., & Kim, J. (2020). Method to Determine the Far-Field Beam Pattern of A Long Array From Subarray Beam Pattern Measurements. Sensors, 20(4), 1236. https://doi.org/10.3390/s20041236




