Increase of Input Resistance of a Normal-Mode Helical Antenna (NMHA) in Human Body Application
Abstract
:1. Introduction
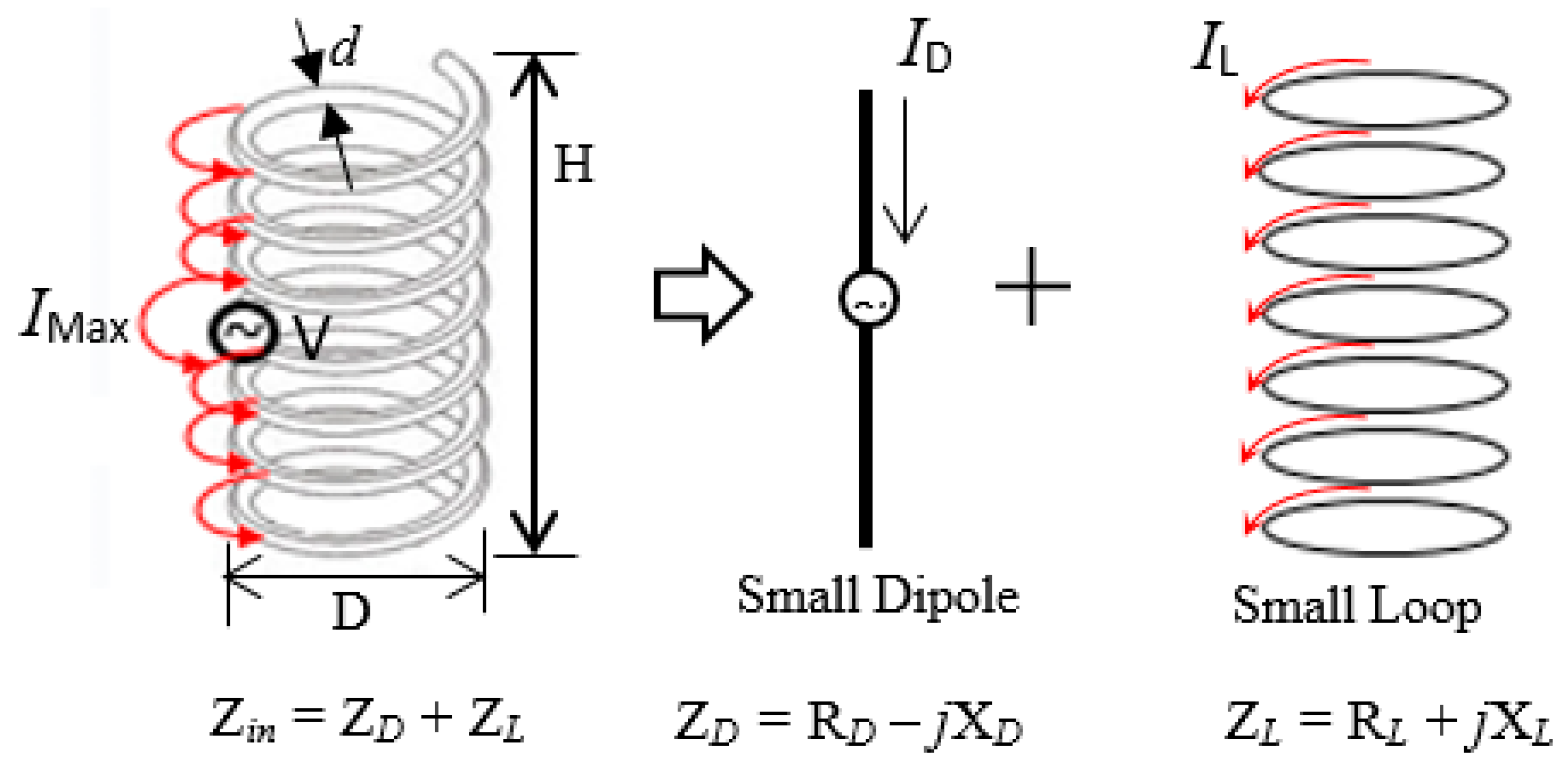
2. Fundamental Equations of NMHA
3. Electromagnetic Simulation of NMHA in Human Body Conditions
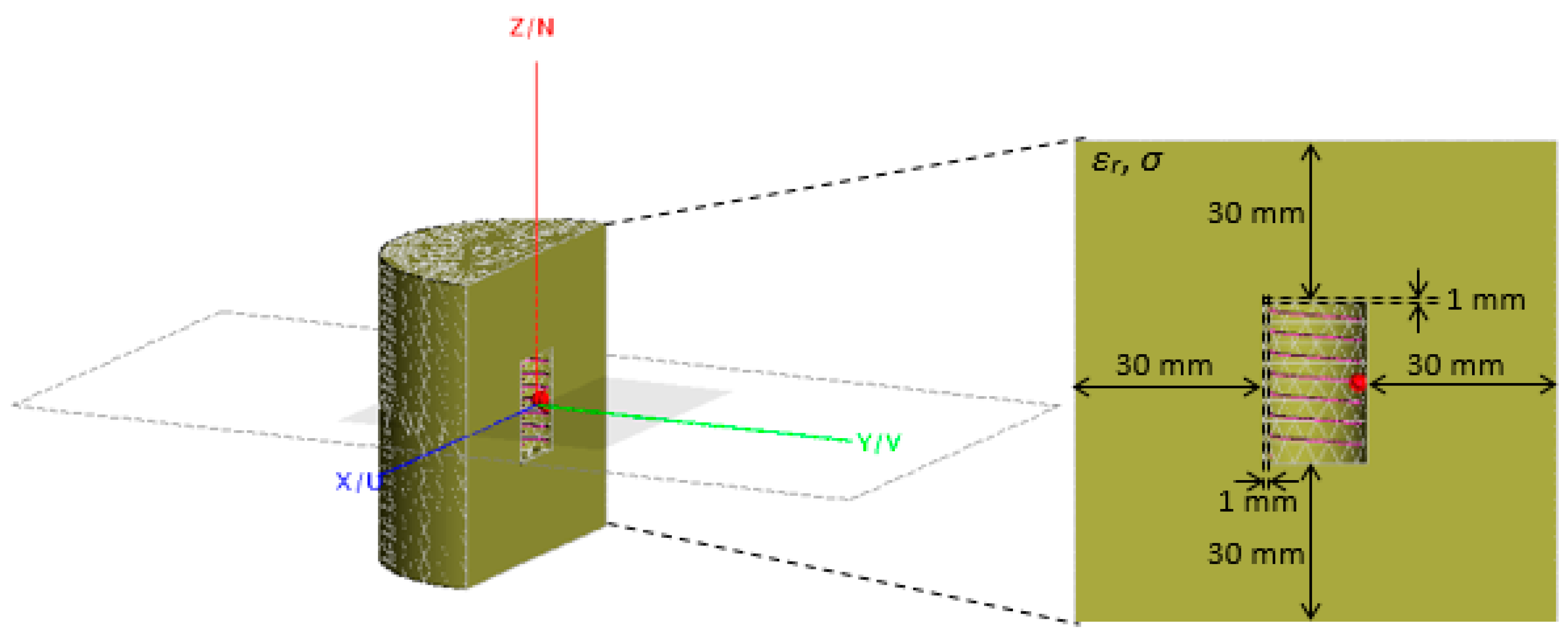
3.1. Simulation Model
3.2. Simulation Parameters
4. Simulation Results
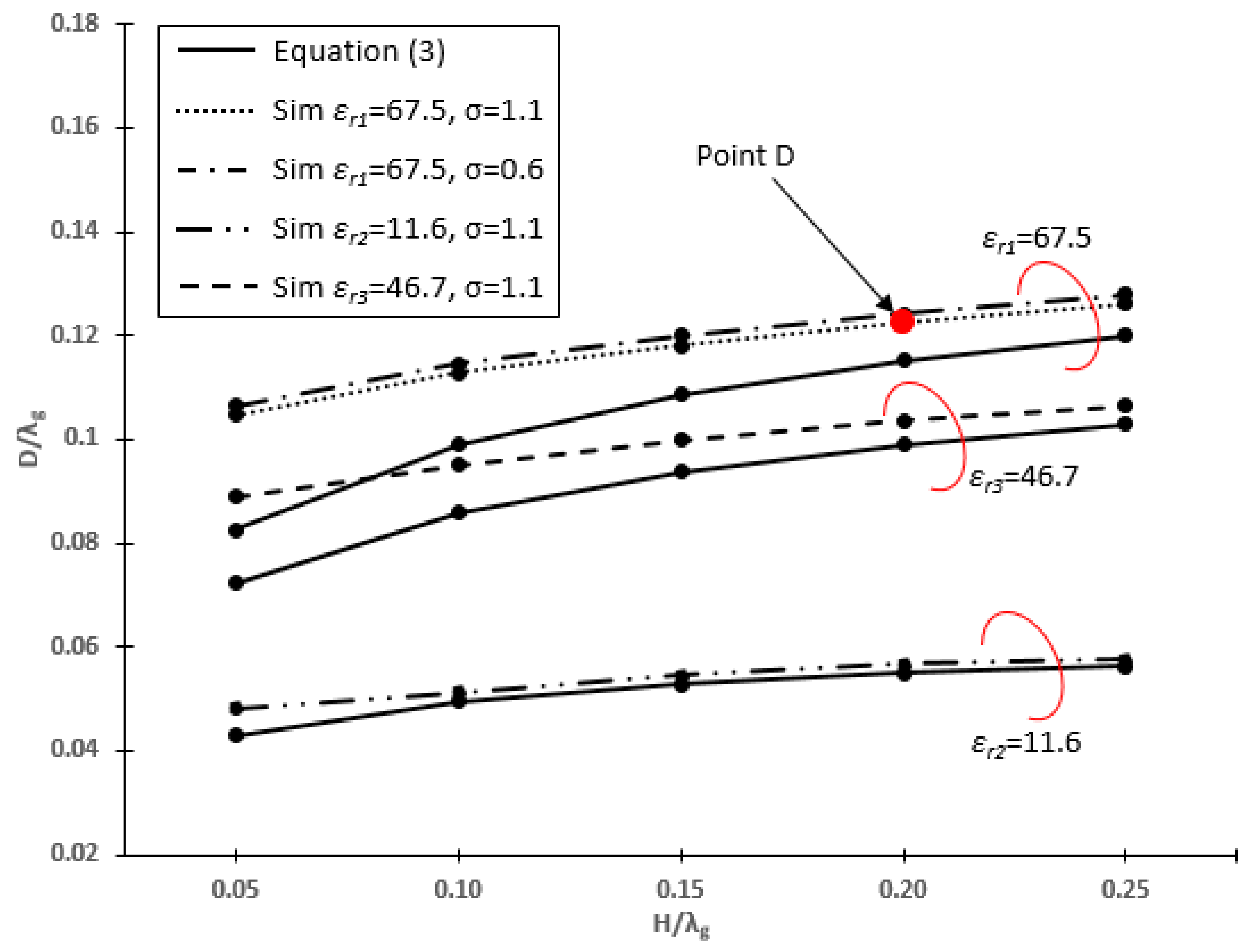
4.1. Self-Resonant Structure
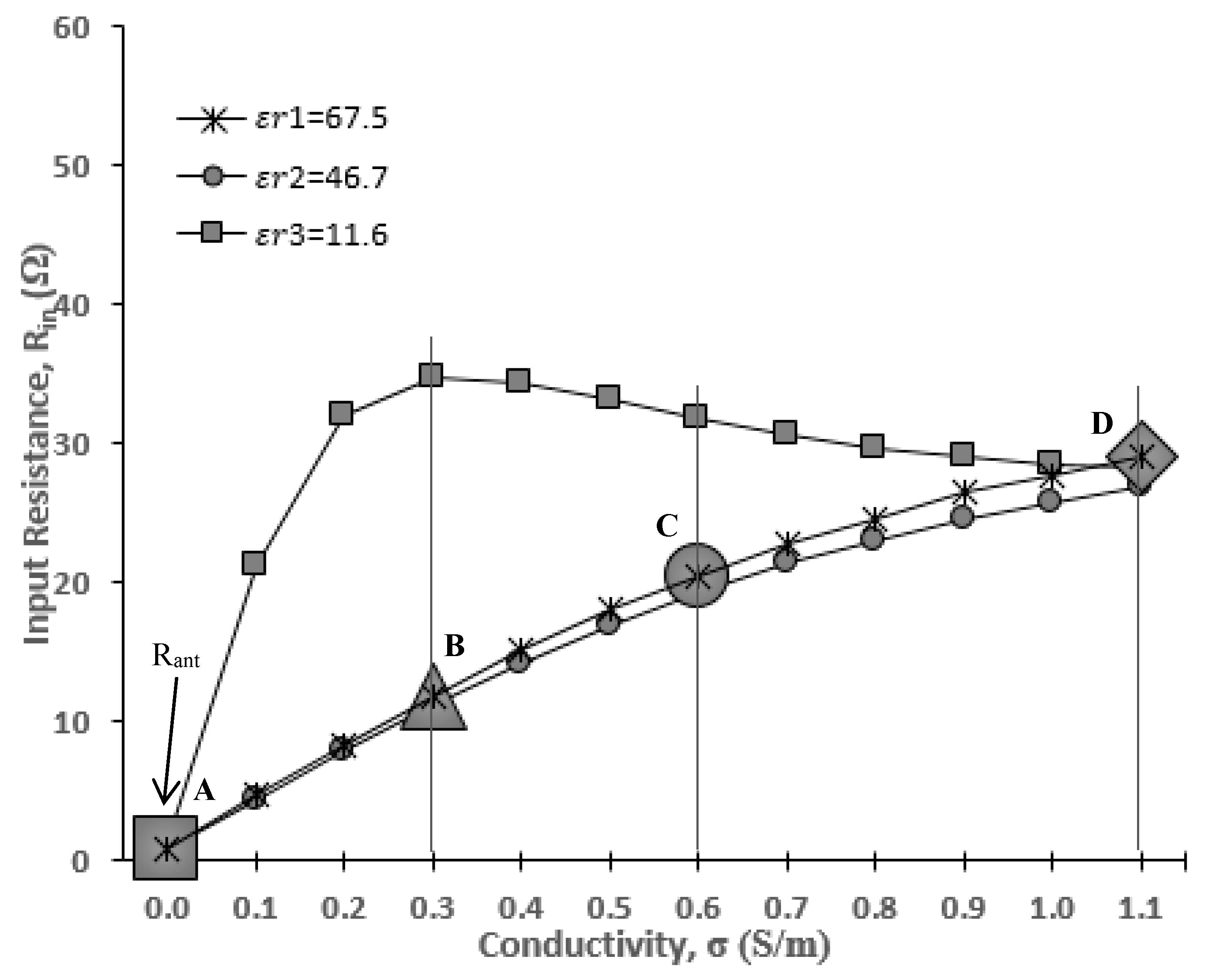
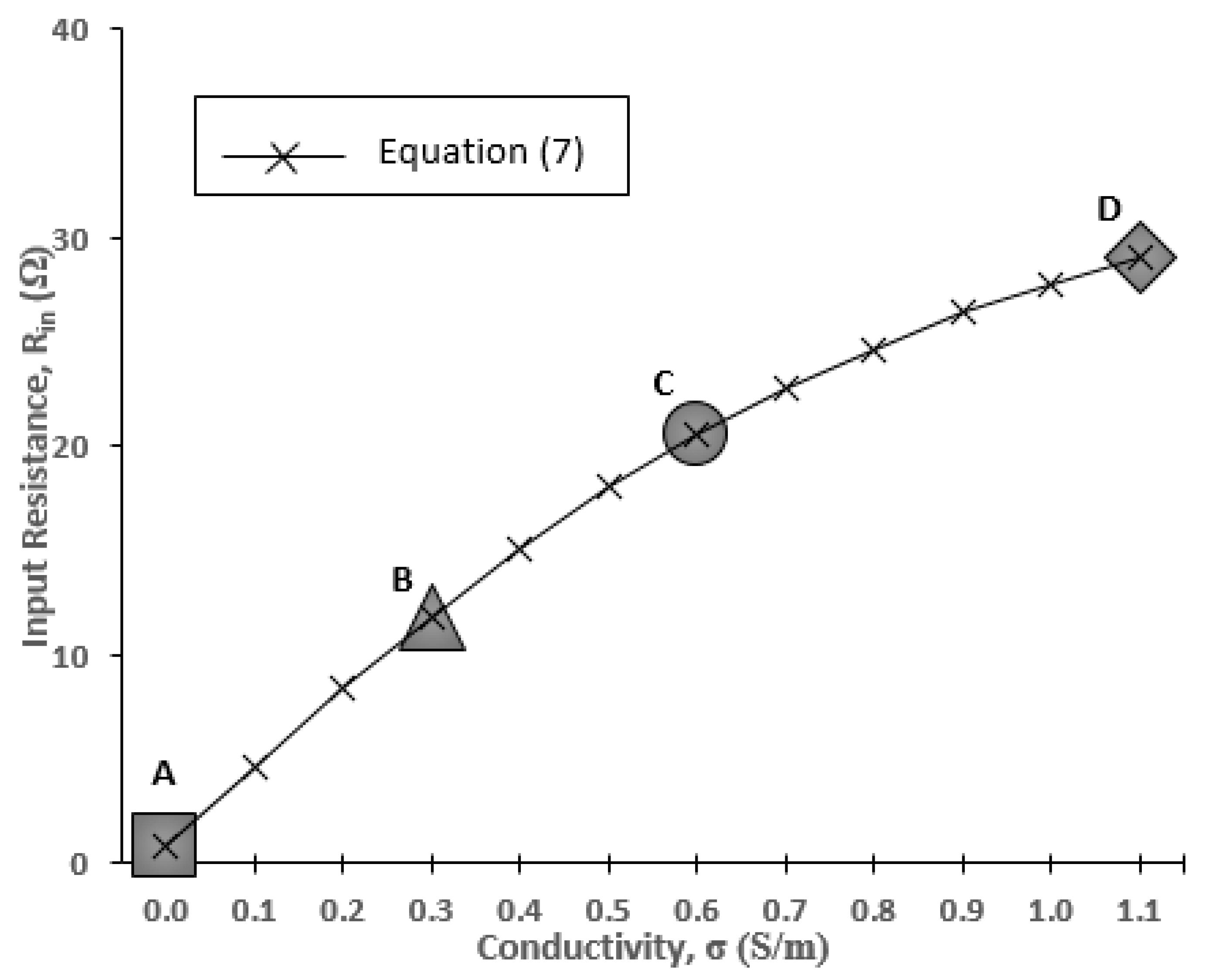
4.2. Input Resistance
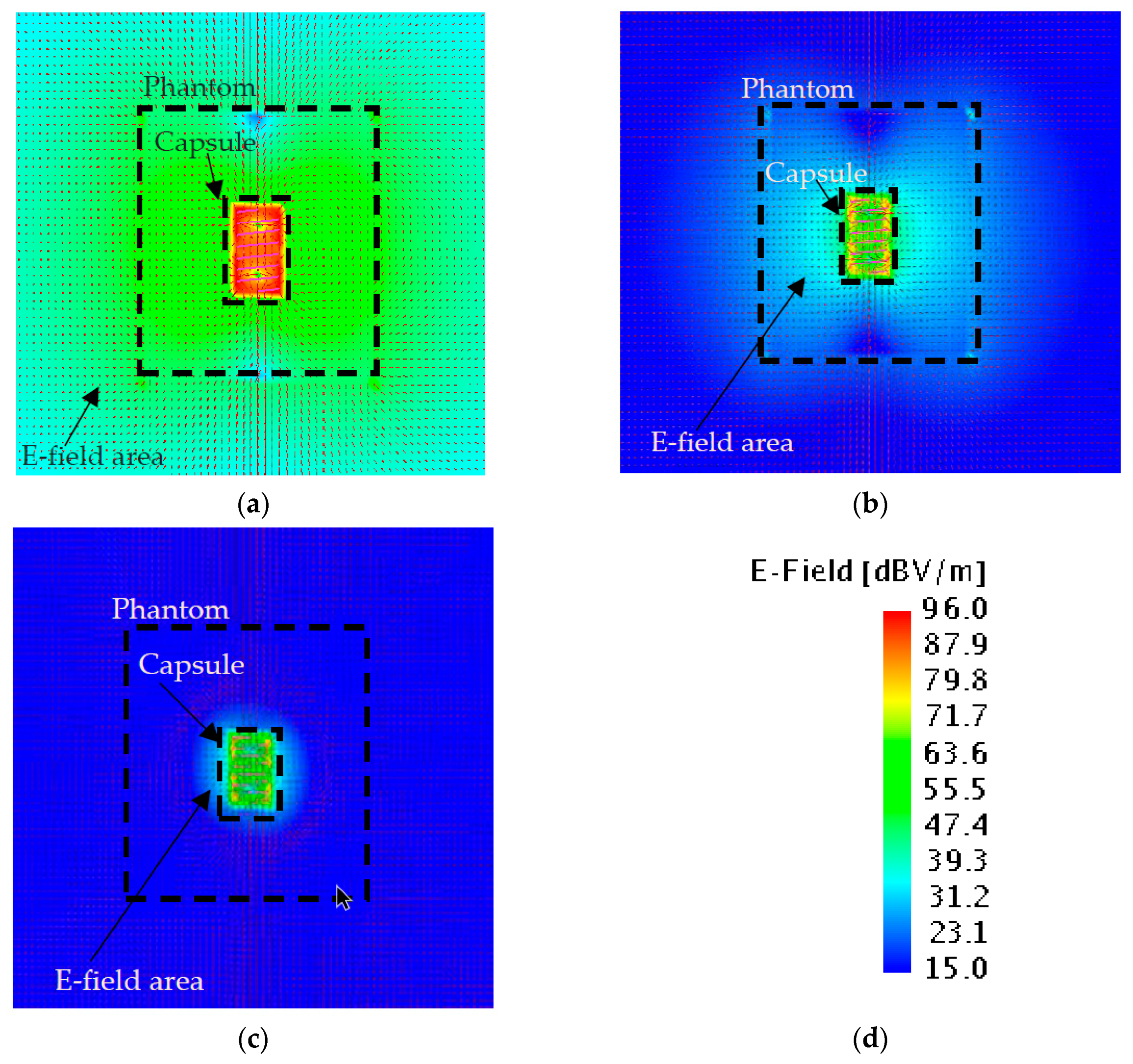
4.3. Electric Field
4.4. Current Distribution
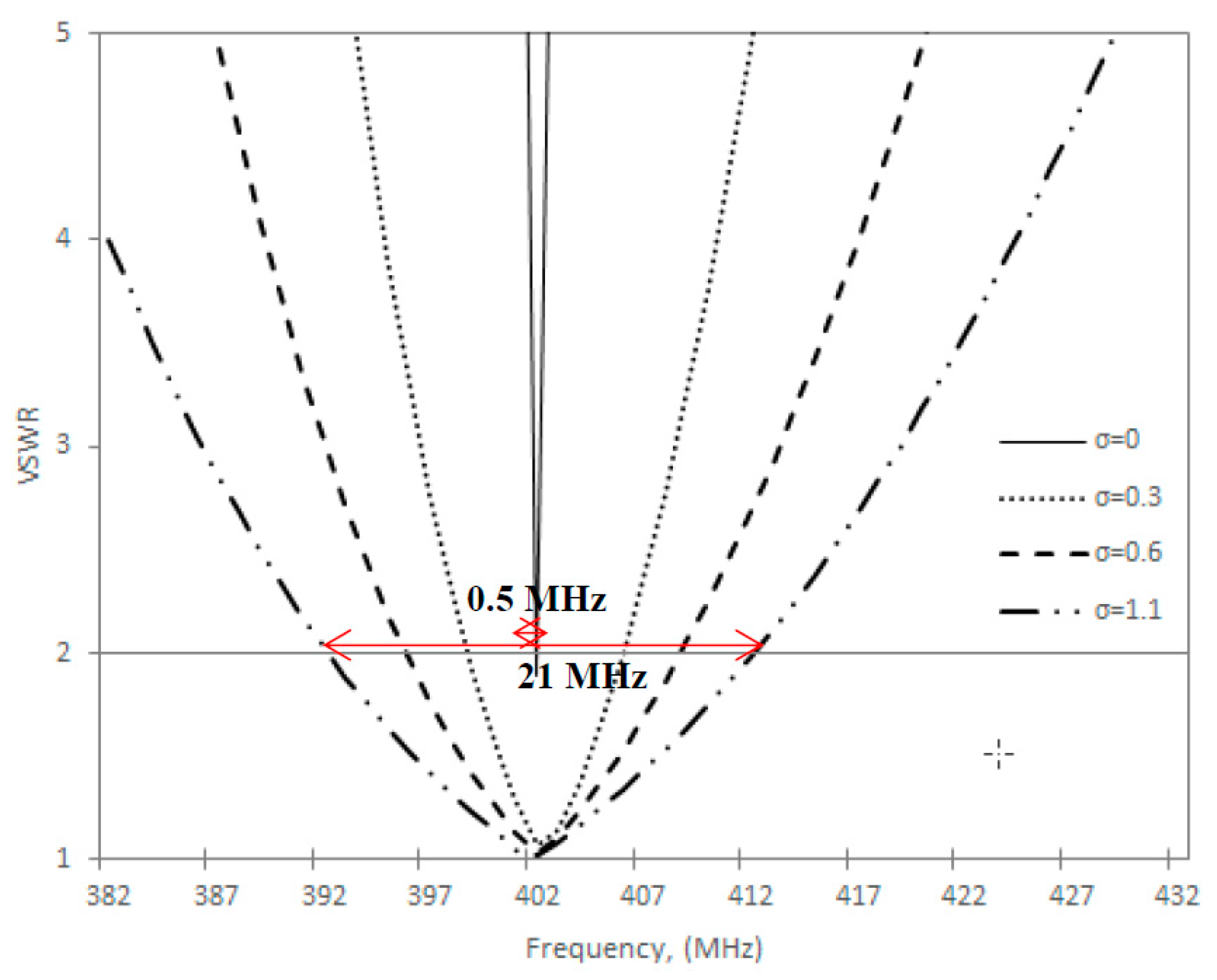
4.5. Bandwidth
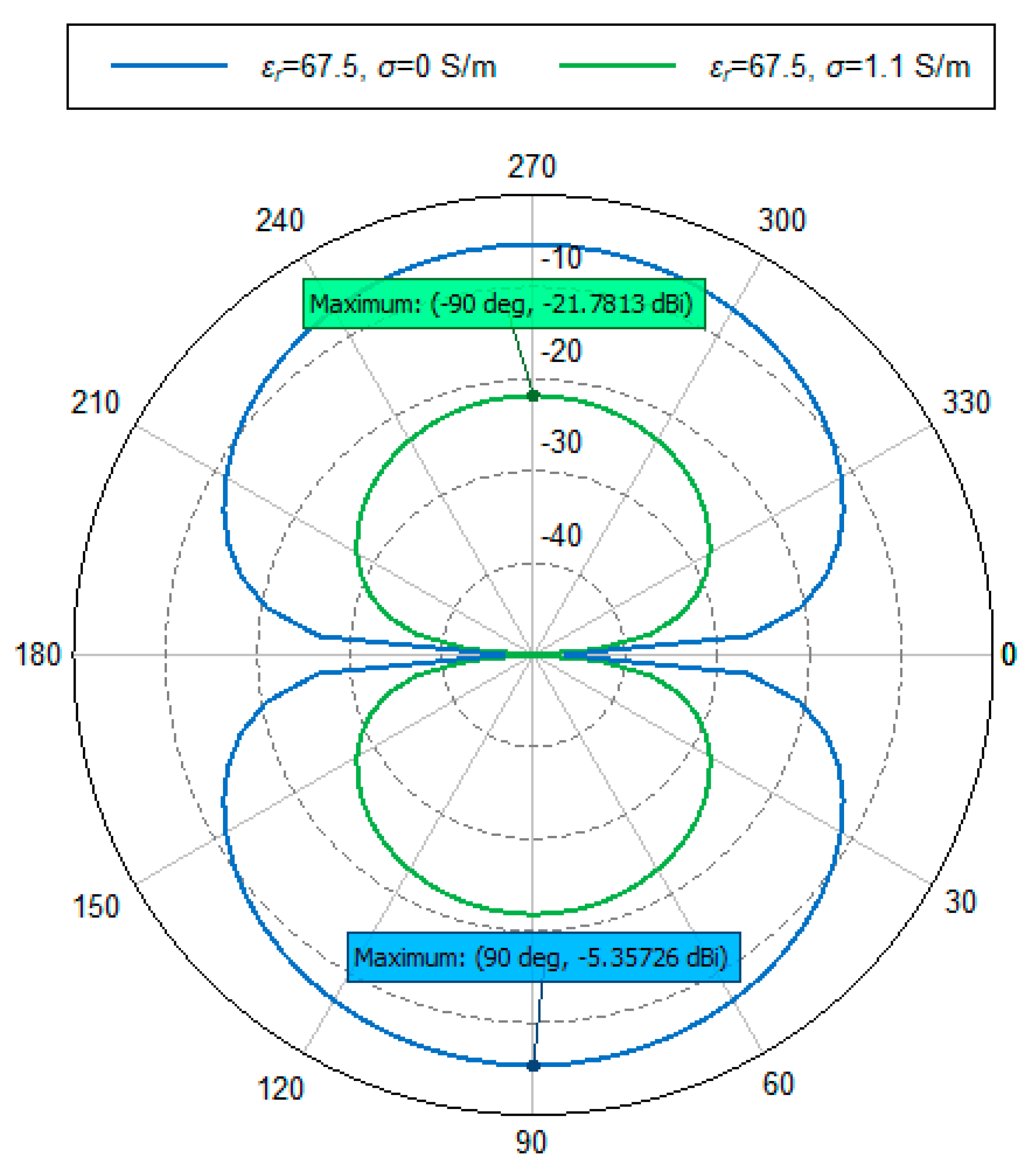
4.6. Radiation Pattern
5. Measurement Setup
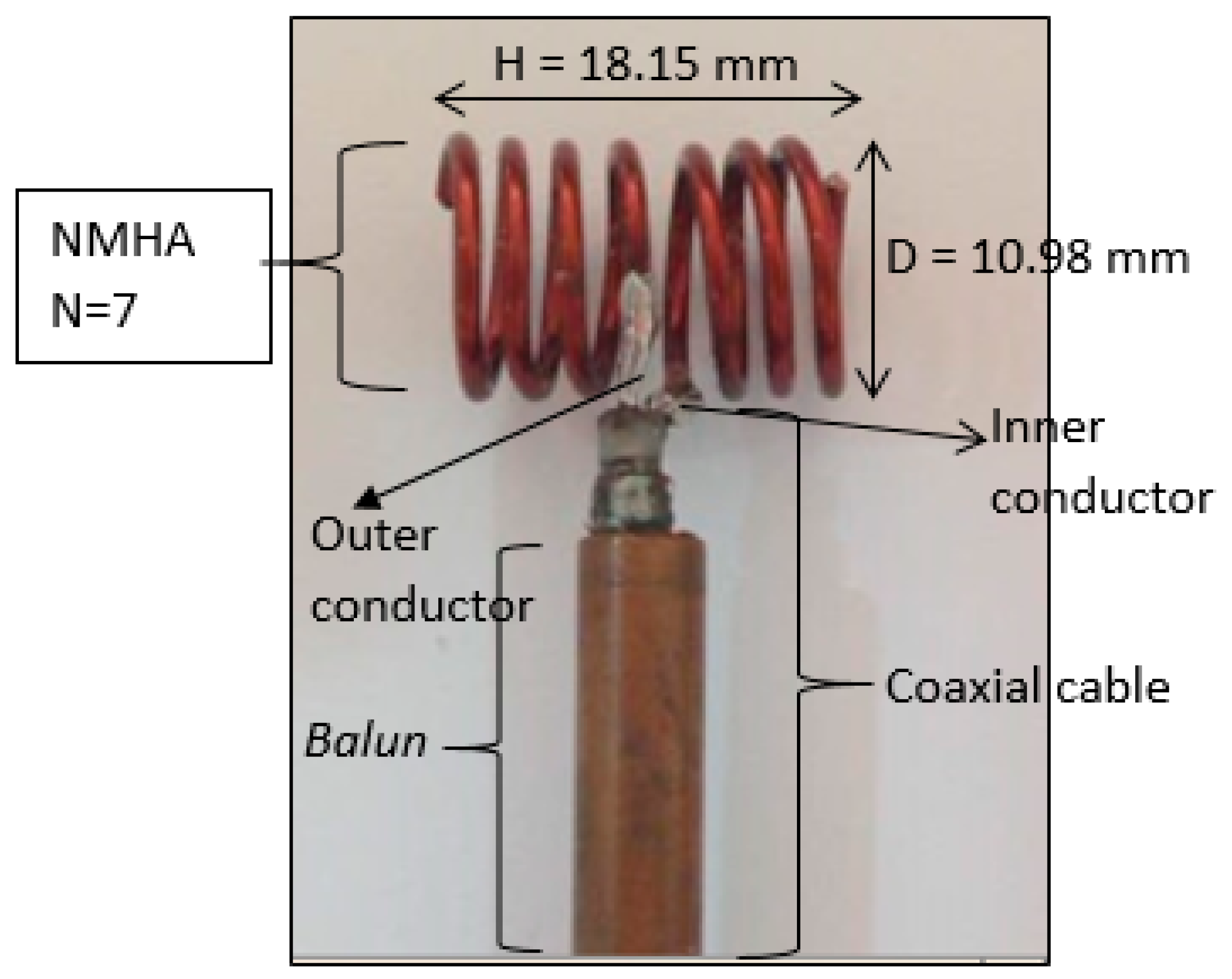
5.1. Antenna Fabrication
5.2. Phantom Fabrication and Measurement
5.3. Antenna Measurement Setup
6. Measurement Results
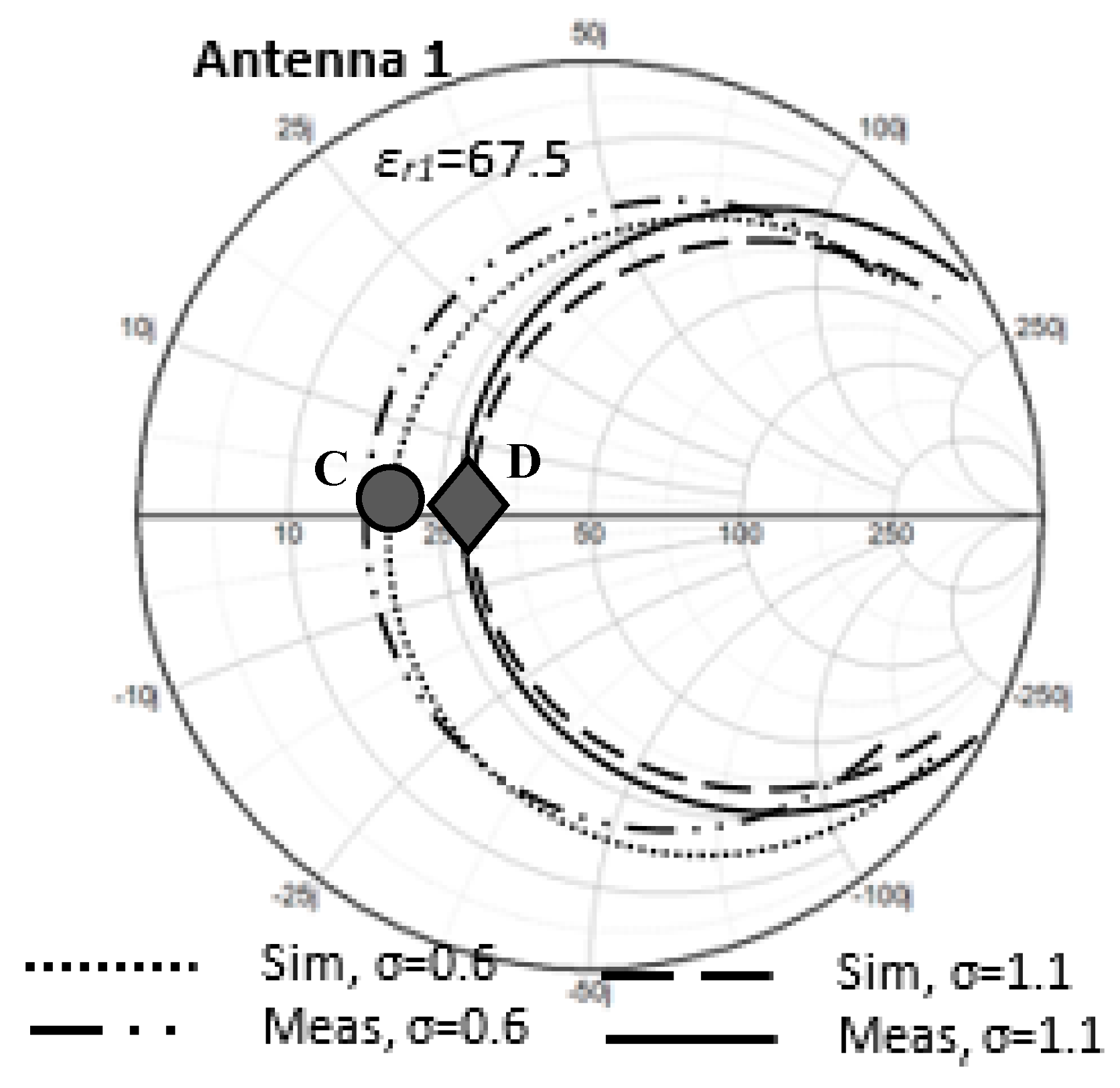
6.1. Input Resistance
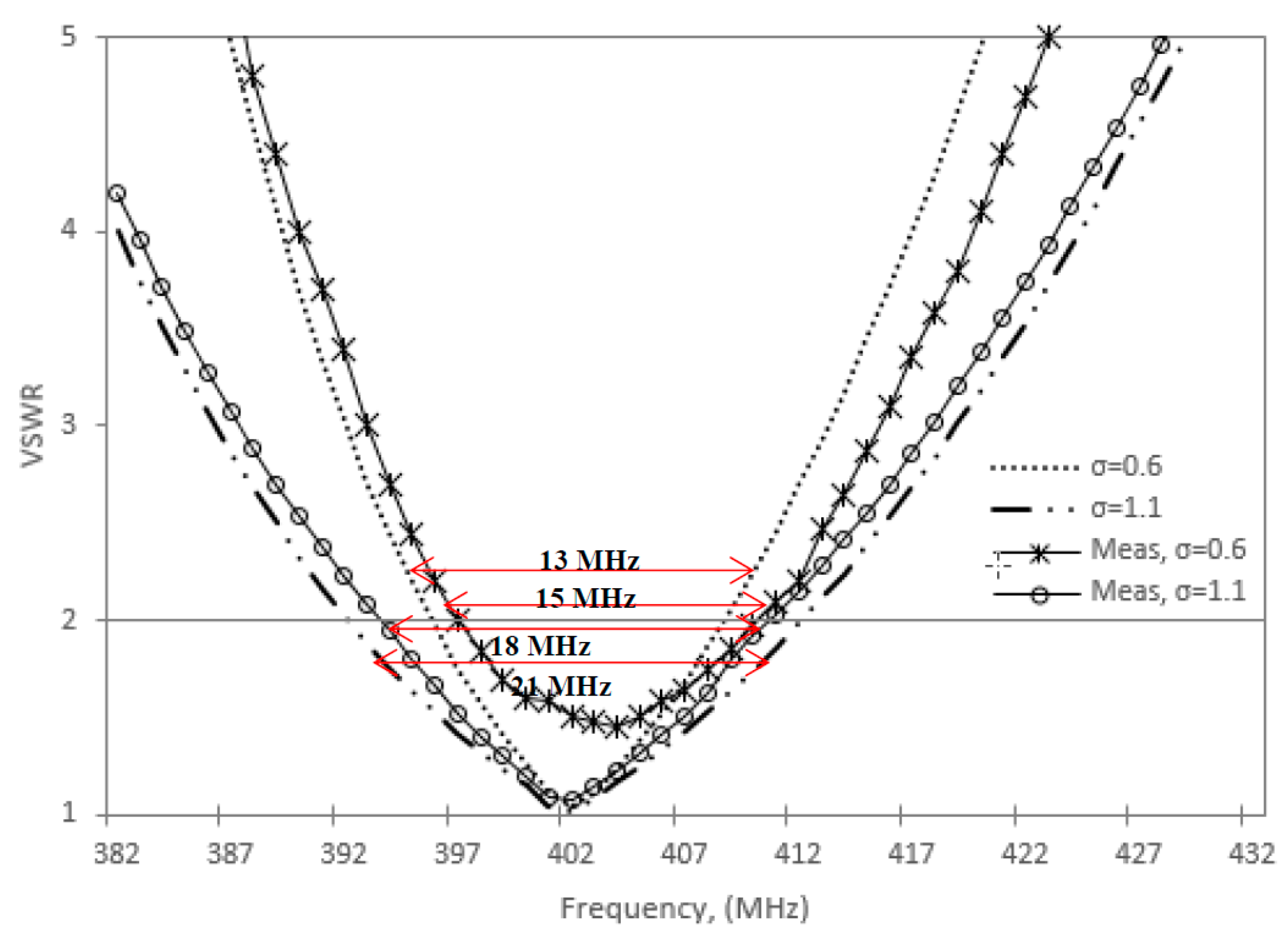
6.2. Bandwidth
7. Discussion
- The relation between the increase of input resistance (Rin) and dielectric permittivity (εr) and conductivity (σ).
- The relation between input resistance (Rin) and current distributions.
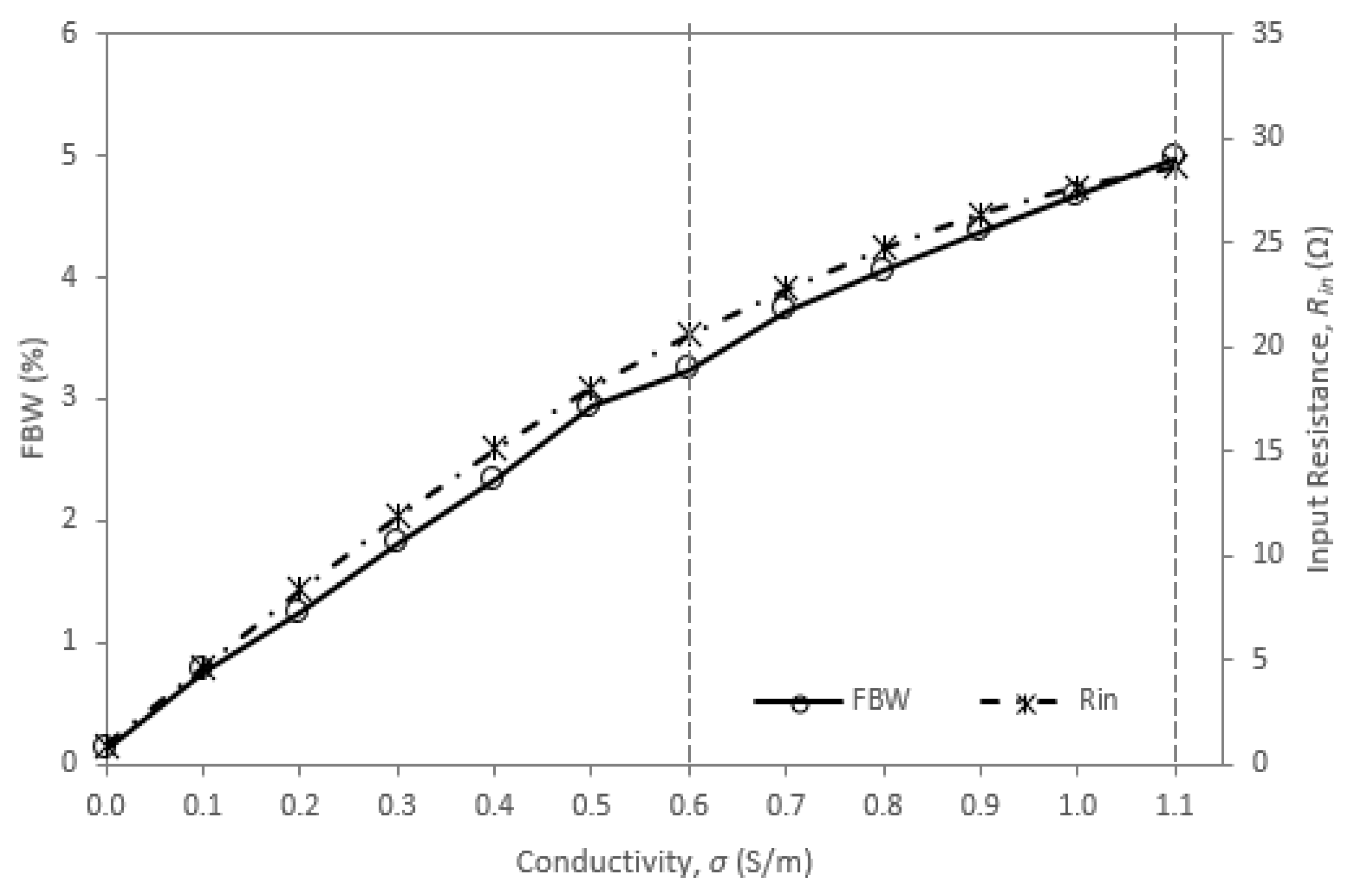
- The relation between input resistance (Rin) and bandwidth (BW).
- Input resistance (Rin).
- Bandwidth (BW).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Singh, K. Biotelemetry: Could technological developments assist healthcare in rural india. Int. Electron. J. Rural Remote Heal. Res. Educ. Pract. Policy 2001, 3, 6. [Google Scholar]
- Tanaka, T.; Sonoda, K.; Okochi, S.; Chan, A.; Nii, M.; Kanda, K.; Fujita, T.; Higuchi, K.; Maenaka, K. Wearable Health Monitoring System and its Applications. In Proceedings of the Fourth International Conference on Emerging Trends in Engineering & Technology (ICETET), Port Louis, Mauritius, 18–20 November 2011; pp. 143–146. [Google Scholar]
- Loktongbam, P.; Pal, D.; Koley, C. Design of an implantable antenna for biotelemetry applications. J. Microsyst. Technol. 2019, 1–10. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.L.H.; Vuong, T.P.; Chan, A.; Nii, M. A Printed Wearable Dual Band Antenna for Remote Healthcare Monitoring Device. In Proceedings of the 2019 IEEE-RIVF International Conference on Computing and Communication Technologies (RIVF), Danang, Vietnam, 20–22 March 2019; pp. 1–5. [Google Scholar]
- Palandoken, M. Compact bioimplantable MICS and ISM band antenna design for wireless biotelemetry applications. Radioengineering 2017, 26, 917–918. [Google Scholar] [CrossRef]
- Pantelopoulos, A.; Bourbakis, N.G. A survey on wearable sensor-based systems for health monitoring and prognosis. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2010, 40, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Long, V.S.; To, T.L.; Dung, T.H. Heart-Rate Monitoring Device based on Fluxgate Sensors. In Proceedings of the 2019 International Conference on System Science and Engineering (ICSSE), Dong Hoi, Vietnam, 20–21 July 2019; pp. 437–440. [Google Scholar]
- Sato, H.; Yoshimura, K.; Nakamoto, H.; Ishibashi, D.; Nakata, Y.; Yaginuma, Y.; Masui, S. 19.2 cm3 flexible fetal heart rate sensor for improved quality of pregnancy life. In Proceedings of the IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, China, 17–19 October 2016; pp. 140–143. [Google Scholar]
- Schires, E.; Georgiou, P.; Lande, T.S. Vital Sign Monitoring Through the Back Using an UWB Impulse Radar With Body Coupled Antennas. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 292–302. [Google Scholar] [CrossRef]
- Kachuee, M.; Kiani, M.M.; Mohammaadzade, H.; Shabany, M. Cuffless Blood Pressure Estimation Algorithms for Continuous Health-Care Monitoring. IEEE Trans. Biomed. Eng. 2017, 64, 859–869. [Google Scholar] [CrossRef]
- Cong, P.; Ko, W.H.; Young, D.J. Wireless Batteryless Implantable Blood Pressure Monitoring Microsystem for Small Laboratory Animals. IEEE Sens. J. 2010, 10, 243–254. [Google Scholar] [CrossRef]
- Ullah, S.; Higgins, H.; Braem, B.; Latre, B.; Blondia, C.; Moerman, I.; Saleem, S.; Rahman, Z.; Kwak, K.S. A comprehensive survey of wireless body area networks on PHY, MAC, and network layers solutions. J. Med. Syst. 2012, 36, 1065–1094. [Google Scholar] [CrossRef] [Green Version]
- Presti, D.L.; Massaroni, C.; D’Abbracio, J.; Massari, L.; Caponero, M.; Longo, U.G.; Formica, D.; Oddo, C.M.; Schena, E. Wearable System Based on Flexible FBG for Repiratory and Cardiac Moniroring. IEEE Sens. J. 2019, 19, 7391–7398. [Google Scholar] [CrossRef]
- Ren, H.; Jin, H.; Chen, C.; Ghayvat, H.; Chen, W. A Novel cardiac Auscultation Monitoring System for Healthcare. IEEE J. Transl. Eng. Health Med. 2018, 6, 1–12. [Google Scholar] [CrossRef]
- Holmer, M.; Sandberg, F.; Solem, K.; Grigonytė, E.; Olde, B.; Sörnmo, L. Extracting a cardiac Signal From the Extracorporeal Pressure Sensors of a Hemodialysis Machine. IEEE Trans. Biomed. Eng. 2015, 62, 2343–2352. [Google Scholar] [CrossRef] [PubMed]
- Turicchia, L.; Valle, B.D.; Bohorquez, J.L.; Sanchez, W.R.; Misra, V.; Fay, L.; Tavakoli, M.; Sarpeshkar, R. Ultralow-Power Electronics for Cardiac-Monitoring. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 2279–2290. [Google Scholar] [CrossRef]
- Nemati, E.; Deen, M.J.; Mondal, T. A wireless wearable ECG sensor for long-term applications. IEEE Commun. Mag. 2012, 50, 36–43. [Google Scholar] [CrossRef]
- Zainudin, N.; Abdul Latef, T.; Yamada, Y.; Kamardin, K.; Aridas, N.K.; Baharin, R.H.M. Measured Results of Input Resistance of NMHA in a Body Phantom. In Proceedings of the 2nd International Conference on Telematics and Future Generation Networks (TAFGEN 2018), Kuching, Malaysia, 24–26 July 2018; pp. 87–92. [Google Scholar]
- Baharin, R.H.M.; Uno, T.; Arima, T.; Zainudin, N.; Yamada, Y.; Kamardin, K.; Michishita, N. Effects of the permittivity and conductivity of human body for normal-mode helical antenna performance. IEICE Electron. Express 2019, 16, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Guo, Y.X.; Xiao, S. Circularly polarized helical antenna for ISM-band ingestible capsule endoscope systems. IEEE Trans. Antennas Propag. 2014, 62, 6027–6039. [Google Scholar] [CrossRef]
- Baharin, R.H.M.; Yamada, Y.; Kamardin, K.; Dinh, N.Q.; Michishita, N. Input resistances of small normal-mode helical antennas in dielectric materials. In Proceedings of the 2017 IEEE Asia Pacific Microwave Conference (APMC), Kuala Lumpar, Malaysia, 13–16 November 2017; pp. 1175–1178. [Google Scholar]
- Hatmi, F.E.L.; Grzeskowiak, M.; Alves, T.; Protat, S.; Picon, O. Magnetic loop antenna for wireless capsule endoscopy inside the human body operating at 315 MHz: Near field behavior. In Proceedings of the 2011 11th Mediterranean Microwave Symposium (MMS), Hammamet, Tunisia, 8–10 September 2011; pp. 81–87. [Google Scholar]
- Merli, F.; Bolomey, L.; Zurcher, J.-F.; Corradini, G.; Meurville, E.; Skrivervik, A.K. Design, realization and measurements of a miniature antenna for implantable wireless communication systems. IEEE Trans. Antennas Propag. 2011, 59, 3544–3555. [Google Scholar]
- Huang, B.; Yan, G.Z.; Zan, P. Design of ingested small microstrip antenna for radiotelemetry capsules. Electron. Lett. 2007, 43, 1178–1179. [Google Scholar] [CrossRef]
- Kwak, S.I.; Chang, K.; Yoon, Y.J. The helical antenna for the capsule endoscope. In Proceedings of the 2005 IEEE Antennas and Propagation Society International Symposium, Washington, DC, USA, 3–8 July 2005; pp. 804–807. [Google Scholar]
- Cheng, X.; Wu, J.; Blank, R.; Senior, D.E.; Yoon, Y.-K. An omnidirectional wrappable compact patch antenna for wireless endoscope applications. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1667–1670. [Google Scholar] [CrossRef]
- Das, R.; Yoo, H. A wideband circularly polarized conformal endoscopic antenna system for high-speed data transfer. IEEE Trans. Antennas Propag. 2017, 65, 2816–2826. [Google Scholar] [CrossRef]
- Wang, J.; Leach, M.; Lim, E.G.; Wang, Z.; Pei, R.; Huang, Y. An implantable and conformal antenna for wireless capsule endoscopy. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1153–1157. [Google Scholar] [CrossRef]
- Alrawashdeh, R.; Huang, Y.; Cao, P.; Lim, E. A new small conformal antenna for capsule endoscopy. In Proceedings of the 2013 7th European Conference on Antennas and Propagation (EuCAP), Gothenburg, Sweden, 8–12 April 2013; pp. 220–223. [Google Scholar]
- Houzen, T.; Takahashi, M.; Ito, K. Implanted Antenna for an Artificial Cardiac Pacemaker System. In Proceedings of the Progress in Electromagnetics Research Symposium, Prague, Czech Republic, 27–30 August 2007; pp. 51–54. [Google Scholar]
- Yun, S.; Kim, K.; Nam, S. Outer-Wall Loop Antenna for Ultrawideband Capsule Endoscope System. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 1135–1138. [Google Scholar] [CrossRef]
- Lim, E.G.; Wang, Z.; Yu, F.Z.; Tillo, T.; Man, K.L.; Wang, J.C.; Zhang, M. Transmitter antennas for wireless capsule endoscopy. In Proceedings of the 2012 International SoC Design Conference (ISOCC), Jeju Island, South Korea, 4–7 November 2012; pp. 269–272. [Google Scholar]
- Lee, S.H.; Lee, J.; Yoon, Y.J.; Park, S.; Cheon, C.; Kim, K.; Nam, S. A Wideband Spiral Antenna for Ingestible Capsule Endoscope Systems: Experimental Results in a Human Phantom and a Pig. IEEE Trans. Biomed. Eng. 2011, 58, 1734–1741. [Google Scholar] [PubMed]
- Mohd Baharin, R.H.; Tuan, N.T.; Yamada, Y.; Kamardin, K. Electrical characteristic changes by setting conditions of Normal-Mode Helical Antenna in a phantom. In Proceedings of the 2016 IEEE Asia-Pacific Conference on Applied Electromagnetics (APACE), Langkawi, Malaysia, 11–13 December 2016; pp. 73–78. [Google Scholar]
- Liao, Y.; Zhang, Y.; Liang, Z.C.; Fang, J.P.; Gao, W. Effects of Dielectric Materials on Impedance Characteristics of Embedded Small Normal Mode Helical Antenna. Appl. Mech. Mater. 2014, 446, 1059–1063. [Google Scholar] [CrossRef]
- Tuan, N.T.; Dinh, N.Q.; Yamada, Y.; Mohd Baharin, R.H.; Kamardin, K.; Dung, D.T.; Michishita, N. Deterministic Equation of Self-Resonant Structures for Normal-Mode Helical Antennas Implanted in a Human Body. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1377–1381. [Google Scholar] [CrossRef]
- ERC RECOMMENDATION 70-03 (Tromsø 1997 and Subsequent Amendments). Available online: http://docplayer.net/5081624-Erc-recommendation-70-03-tromso-1997-and-subsequent-amendments-relating-to-the-use-of-short-range-devices-srd.html (accessed on 6 February 2020).
- Kim, J.; Rahmat-samii, Y. Implanted Antennas Inside a Human Body: Simulations, Designs, and Characterizations. IEEE Trans. Microw. Theory Tech. 2004, 52, 1934–1943. [Google Scholar] [CrossRef]







| Aspect | Parameter | |
|---|---|---|
| Simulator | FEKO 2018 | Method of Moment |
| Frequency | MICS Band | 402 MHz |
| Antenna | Height, H/λg | 0.2 |
| Diameter, D/λg | 0.0965~0.1210 | |
| Number of turns, N | 7 | |
| Diameter of wire, d | 1.2 mm | |
| Mesh size, Δl | λg/100 | |
| Metallic Wire, Copper | 5.8 × 106 (S/m) | |
| Dielectric (Human Body) | Permittivity, εr | 67.5, 46.7, 11.6 |
| Permeability, μr | 1 | |
| Conductivity, σ | 0~1.1 | |
| Wavelength material, λg | 90.77 mm, | |
| Mesh size, Δm | λg/100 | |
| εr1 = 67.5 | Ra [Ω] | Rin(σ) [Ω] | ηa [dBi] | GA (sim) [dBi] |
|---|---|---|---|---|
| σ = 0 [S/m] | 0.227 | 0.8 | −5.47 | −5.357 |
| σ = 1.1 [S/m] | 0.217 | 29.02 | −21.26 | −21.78 |
| Human Stomach Phantom | |||
|---|---|---|---|
| Materials | Function | Phantom 1 εr1 = 67.5, σ = 1.1 | Phantom 2 εr1 = 67.5, σ = 0.6 |
| Distilled water | Main material | 400 mL | 400 mL |
| Polyethylene powder | Permittivity | 6 g | 6 g |
| Agar | Forming material | 17.5 g | 17.5 g |
| Sodium Chloride (NaCl) | Conductivity | 1.925 g | 0.9 g |
| Xanthan | Thickener | 15 g | 15 g |
| Sodium Dehydro-acetat | Preservative | 0.25 g | 0.25 g |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zainudin, N.; Abdul Latef, T.; Aridas, N.K.; Yamada, Y.; Kamardin, K.; Abd Rahman, N.H. Increase of Input Resistance of a Normal-Mode Helical Antenna (NMHA) in Human Body Application. Sensors 2020, 20, 958. https://doi.org/10.3390/s20040958
Zainudin N, Abdul Latef T, Aridas NK, Yamada Y, Kamardin K, Abd Rahman NH. Increase of Input Resistance of a Normal-Mode Helical Antenna (NMHA) in Human Body Application. Sensors. 2020; 20(4):958. https://doi.org/10.3390/s20040958
Chicago/Turabian StyleZainudin, Norsiha, Tarik Abdul Latef, Narendra Kumar Aridas, Yoshihide Yamada, Kamilia Kamardin, and Nurul Huda Abd Rahman. 2020. "Increase of Input Resistance of a Normal-Mode Helical Antenna (NMHA) in Human Body Application" Sensors 20, no. 4: 958. https://doi.org/10.3390/s20040958





