Optimizing the Calibration Error of Refraction Angles in Ultrasonic Angle Beam Testing
Abstract
:1. Introduction
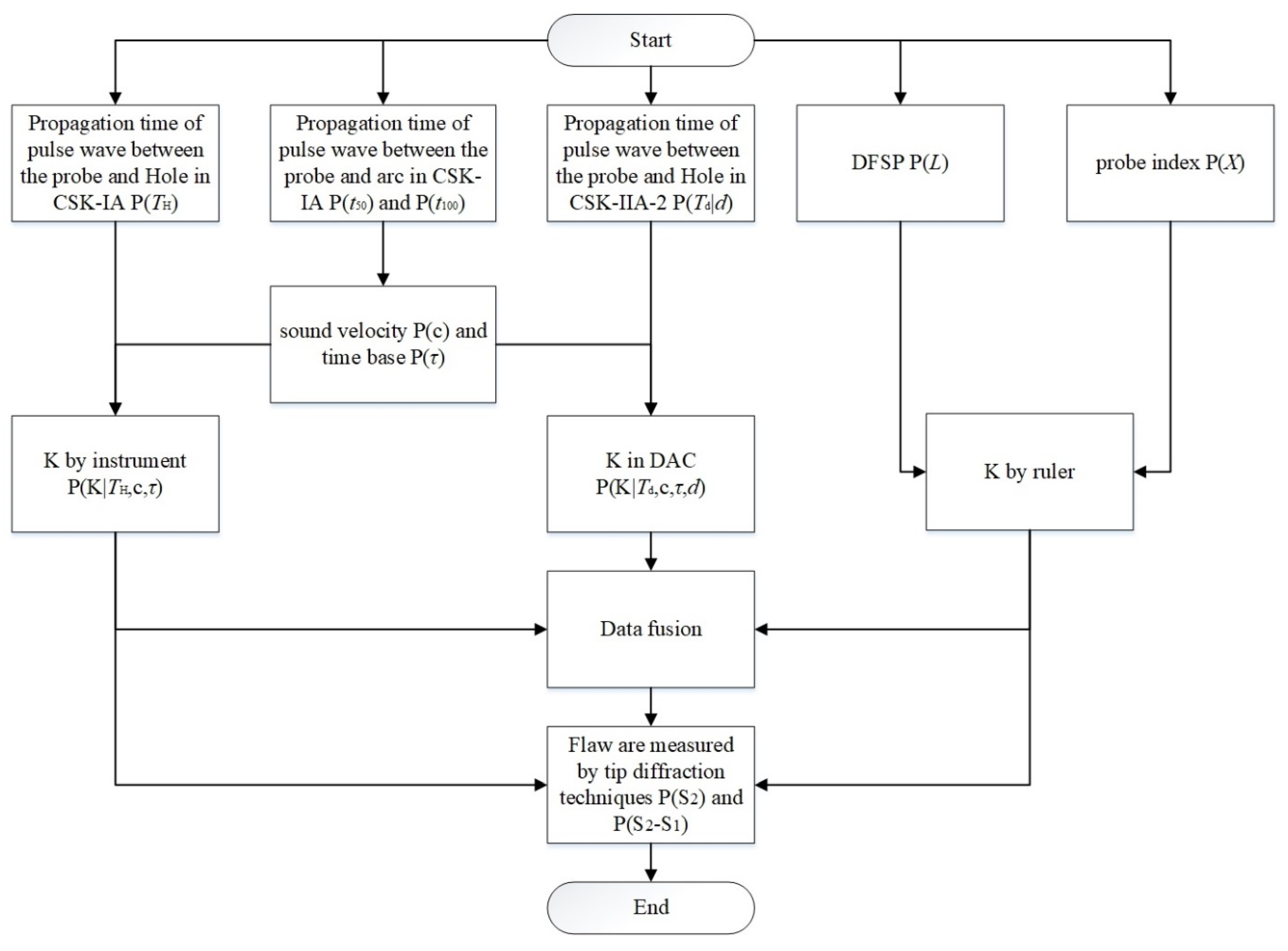
2. Methods
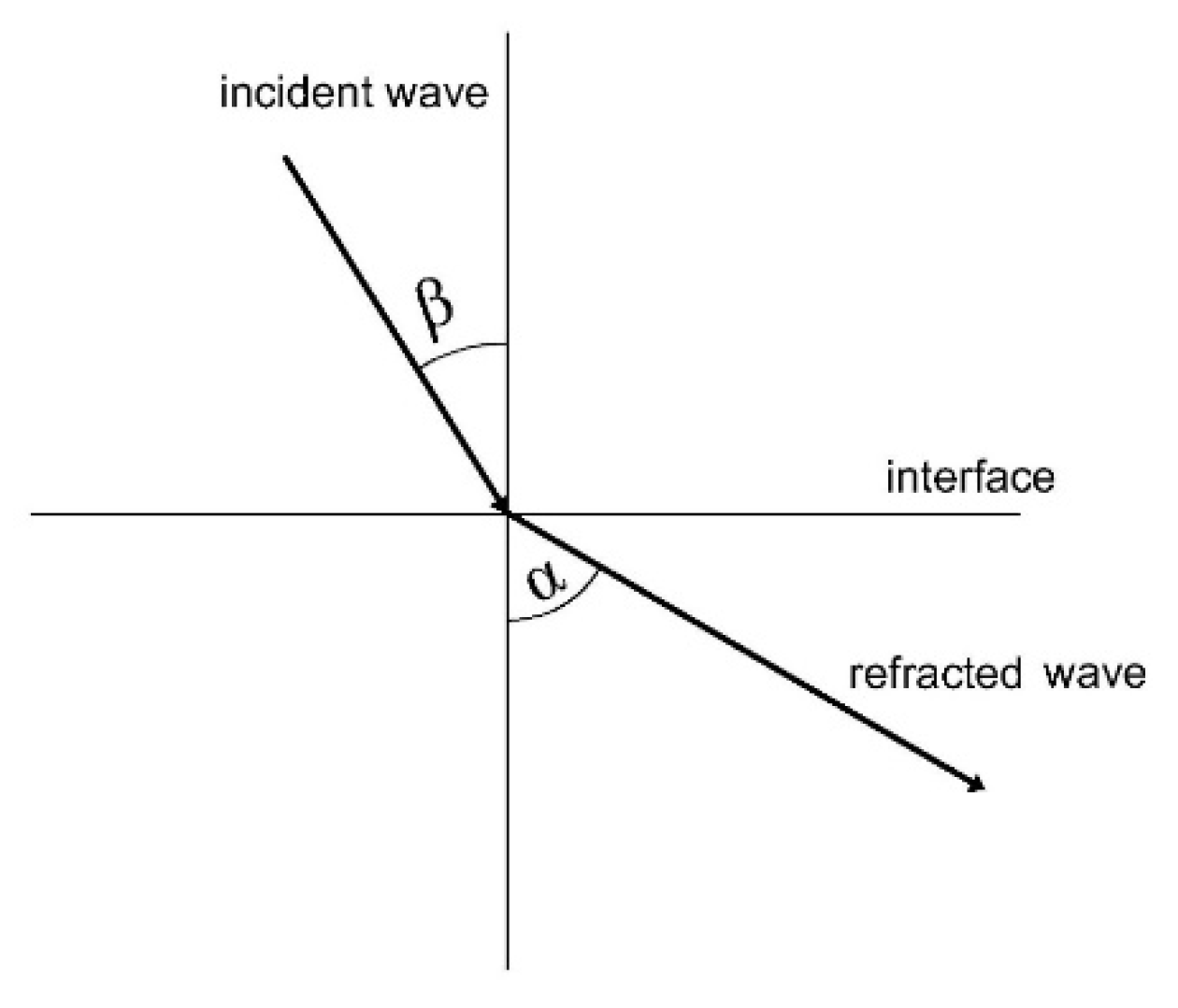
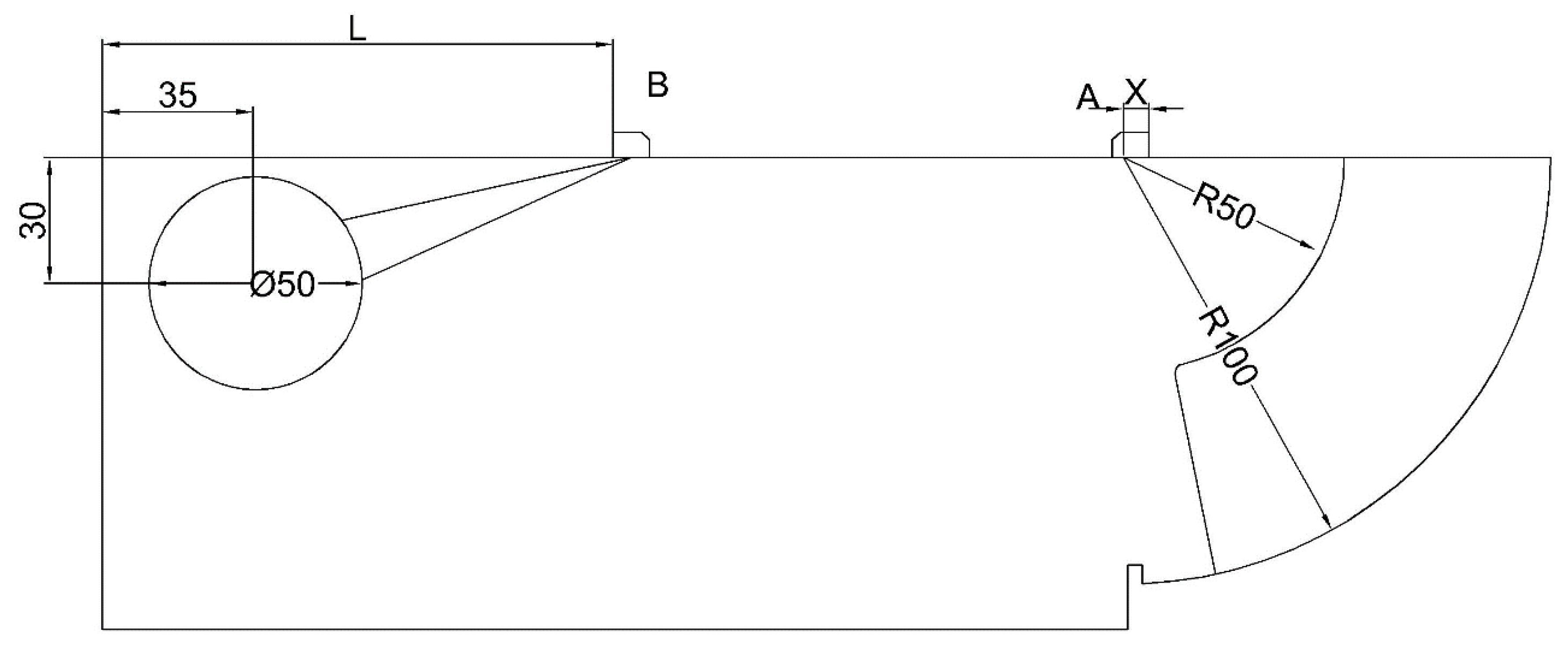
2.1. Methods of Calibration
2.2. Methods for Obtaining Flaw Height
2.3. Optimizing the Values of the Refraction Angle in the DAC Calibration Procedure
2.4. Experiments
2.5. Monte Carlo Simulation
3. Results and Discussion
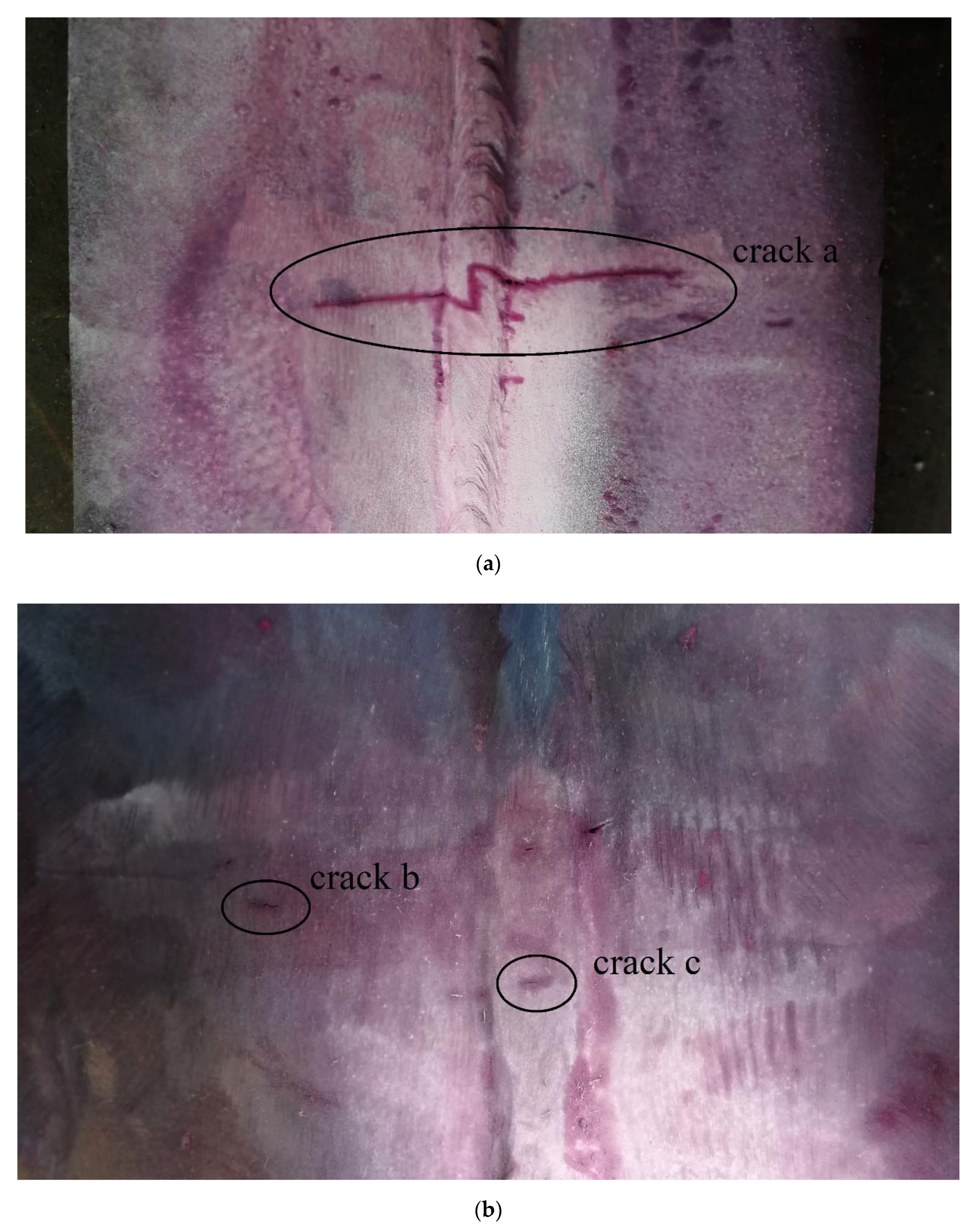
3.1. Results of the Experiment
3.2. Results of Monte Carlo Simulation of Data Fusion K
3.3. Results of Monte Carlo Simulation and Experiments for Measurement Flaw Size
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Carvalho, A.; Rebello, J.; Souza, M.; Sagrilo, L.; Soares, S. Reliability of non-destructive test techniques in the inspection of pipelines used in the oil industry. Int. J. Press. Vessel. Pip. 2008, 85, 745–751. [Google Scholar] [CrossRef]
- Di Ianni, T.; De Marchi, L.; Perelli, A.; Marzani, A. Compressive sensing of full wave field data for structural health monitoring applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2015, 62, 1373–1383. [Google Scholar] [CrossRef] [PubMed]
- Duan, X.; Wang, M.; Kozluk, M. Acceptance criterion for probabilistic structural integrity assessment: Prediction of the failure pressure of steam generator tubing with fretting flaws. Nucl. Eng. Des. 2015, 281, 154–162. [Google Scholar] [CrossRef]
- ISO 16810:2012(E), Non-Destructive Testing-Ultrasonic Testing-General Principles; International Organization for Standardization: Geneva, Switzerland, 2012.
- Wronkowicz-Katunin, A.; Dragan, K.; Lis, K. Assessment of uncertainty in damage evaluation by ultrasonic testing of composite structures. Compos. Struct. 2018, 203, 71–84. [Google Scholar] [CrossRef]
- Li, J.W.; Chen, J.M. NDT Handbook, 1st ed.; China Machine Press: Beijing, China, 2002; pp. 163–166. (In Chinese) [Google Scholar]
- Gandossi, L.; Simola, K. Bayesian analysis of flaw sizing data of the NESC III exercise. Int. J. Press. Vessel. Pip. 2006, 83, 654–662. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, J.; Zhou, S.; Rasselkorde, E.M.; Abbasi, W. Probabilistic modeling and sizing of embedded flaws in ultrasonic non-destructive inspections for fatigue damage prognostics and structural integrity assessment. NDT E Int. 2014, 61, 1–9. [Google Scholar] [CrossRef]
- Bettayeb, F.; Rachedi, T.; Benbartaoui, H. An improved automated ultrasonic NDE system by wavelet and neuron networks. Ultrasonics 2004, 42, 853–858. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Su, Z.; Cheng, L. Quantitative evaluation of orientation-specific damage using elastic waves and probability-based diagnostic imaging. Mech. Syst. Signal Process. 2011, 25, 2135–2156. [Google Scholar] [CrossRef]
- He, J.; Ran, Y.; Liu, B.; Yang, J.; Guan, X. A Fatigue Crack Size Evaluation Method Based on Lamb Wave Simulation and Limited Experimental Data. Sensors 2017, 17, 2097. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; He, J.; Guan, X.; Wang, D.; Chen, H.; Zhang, W.; Liu, Y. A probabilistic crack size quantification method using in-situ Lamb wave test and Bayesian updating. Mech. Syst. Signal Process. 2016, 78, 118–133. [Google Scholar] [CrossRef]
- Zhang, J.; Drinkwater, B.W.; Wilcox, P. The Use of Ultrasonic Arrays to Characterize Crack-Like Defects. J. Nondestruct. Eval. 2010, 29, 222–232. [Google Scholar] [CrossRef]
- De Marchi, L.; Marzani, A.; Miniaci, M. A dispersion compensation procedure to extend pulse-echo defects location to irregular waveguides. NDT E Int. 2013, 54, 115–122. [Google Scholar] [CrossRef]
- De Marchi, L.; Marzani, A.; Miniaci, M.; Perelli, A.; Testoni, N. Localization of defects in irregular waveguides by dispersion compensation and pulse compression. In Proceedings of the Health Monitoring of Structural and Biological Systems, San Diego, CA, USA, 10–14 March 2013; Volume 8695, p. 869517. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Guide Waves in Solid Media; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Trtnik, G.; Kavčič, F.; Turk, G. Prediction of concrete strength using ultrasonic pulse velocity and artificial neural networks. Ultrasonics 2009, 49, 53–60. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- NB/T47013-2015, Nondestructive Testing of Pressure Equipments; Xinhua Publishing House: Beijing, China, 2015.
- ISO 16811:2012(E), Non-Destructive Testing-Ultrasonic Testing-Sensitivity and Range Setting; International Organization for Standardization: Geneva, Switzerland, 2012.
- ASME V-2017, Nondestructive Examination; ASME Press: New York, NY, USA, 2015.
- ISO 16827:2012(E), Non-Destructive Testing-Ultrasonic Testing-Characterization and Sizing of Discontinuities; International Organization for Standardization: Geneva, Switzerland, 2012.
- Eriksen, B.; Eriksson, A.; Houghton, R. Final results of the NESC-III non-destructive testing blind round robin trials on dissimilar metal welds. Insight Non-Destr. Test. Cond. Monit. 2008, 50, 616–622. [Google Scholar] [CrossRef]
- Matsuura, H.; Kaji, A. Evaluation of Tensile Strength of Partial Penetration Butt Welded Joints by Ultrasonic Testing. JSME Int. J. Ser. A 2001, 44, 514–519. [Google Scholar] [CrossRef]



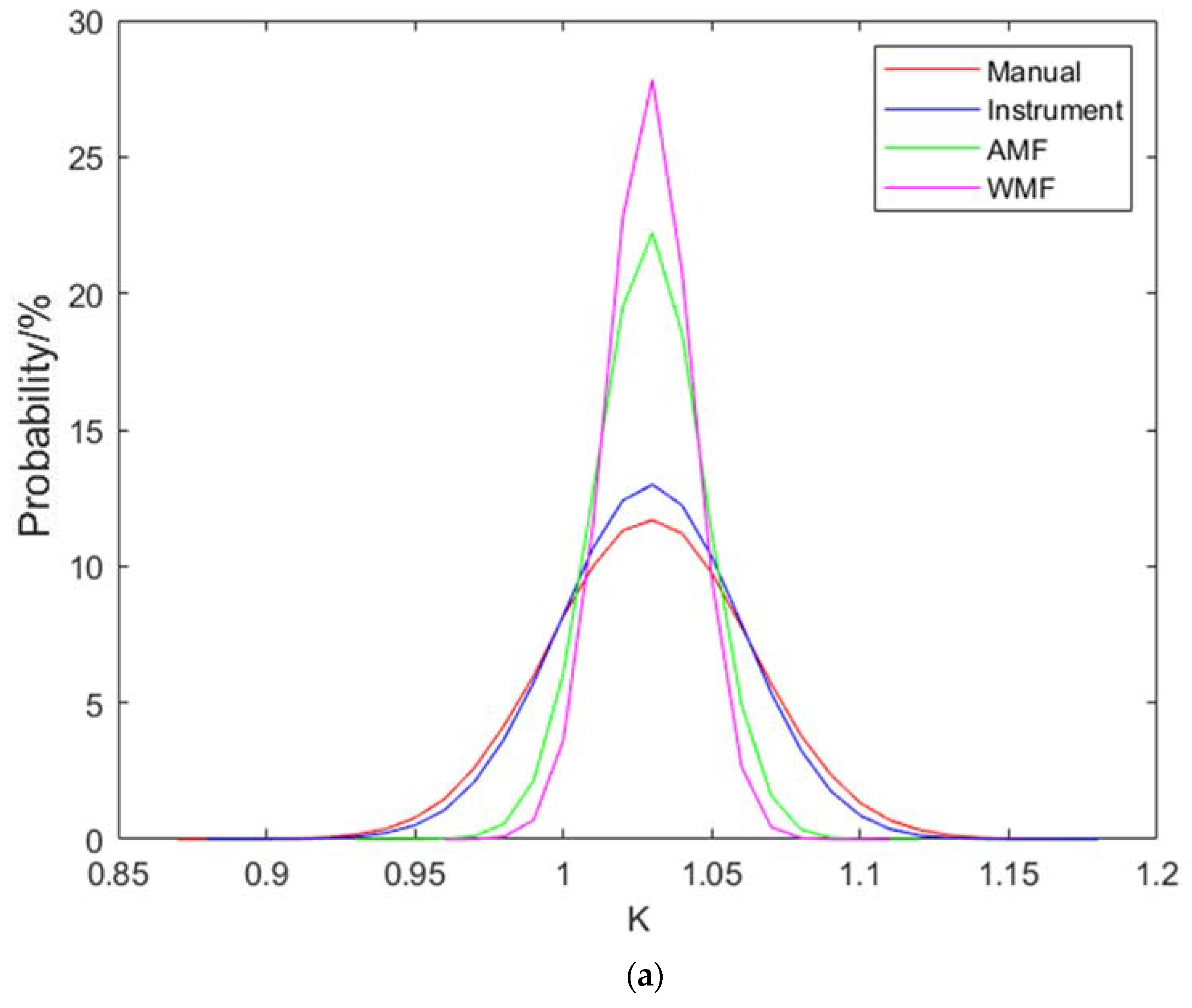

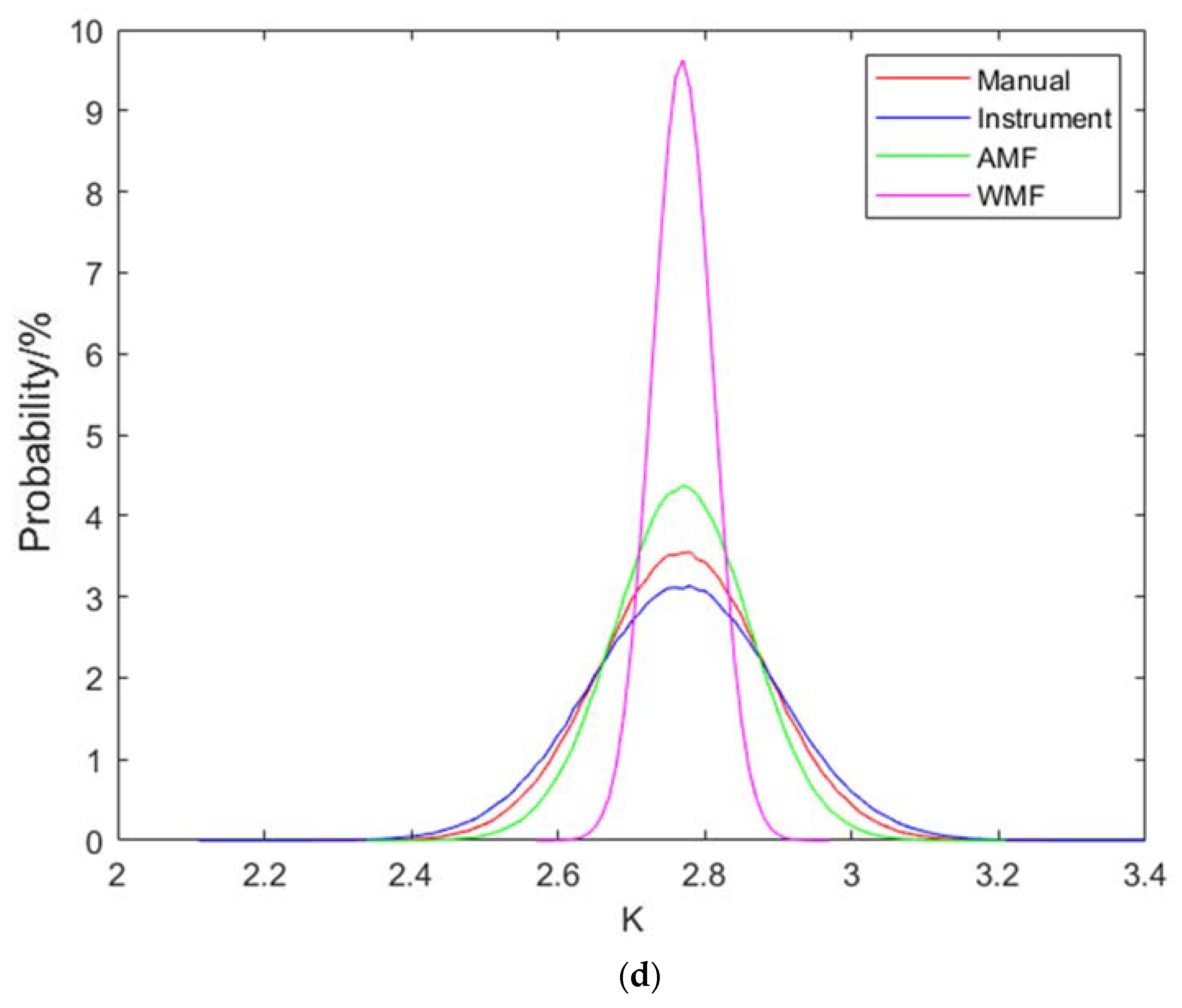
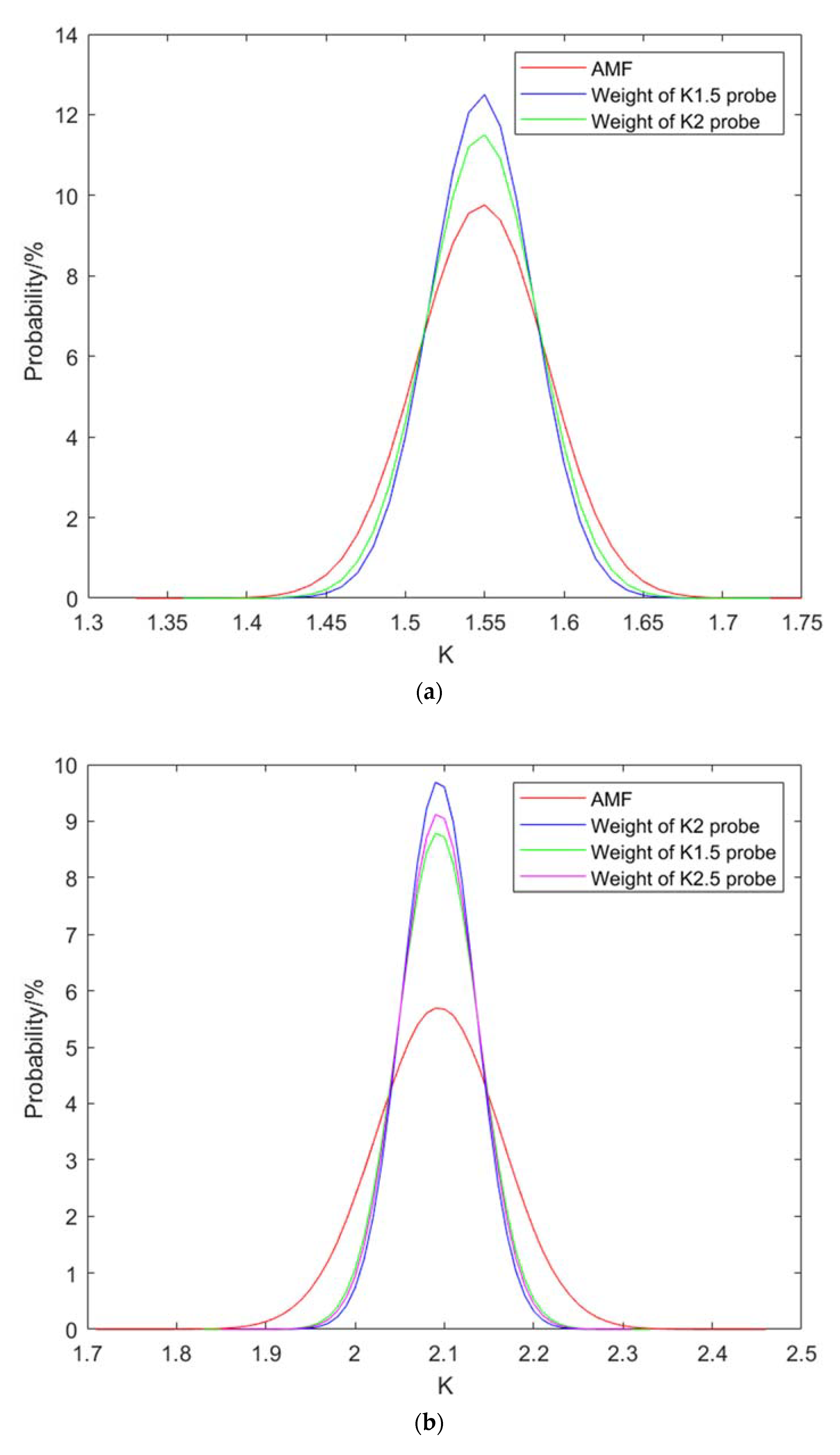

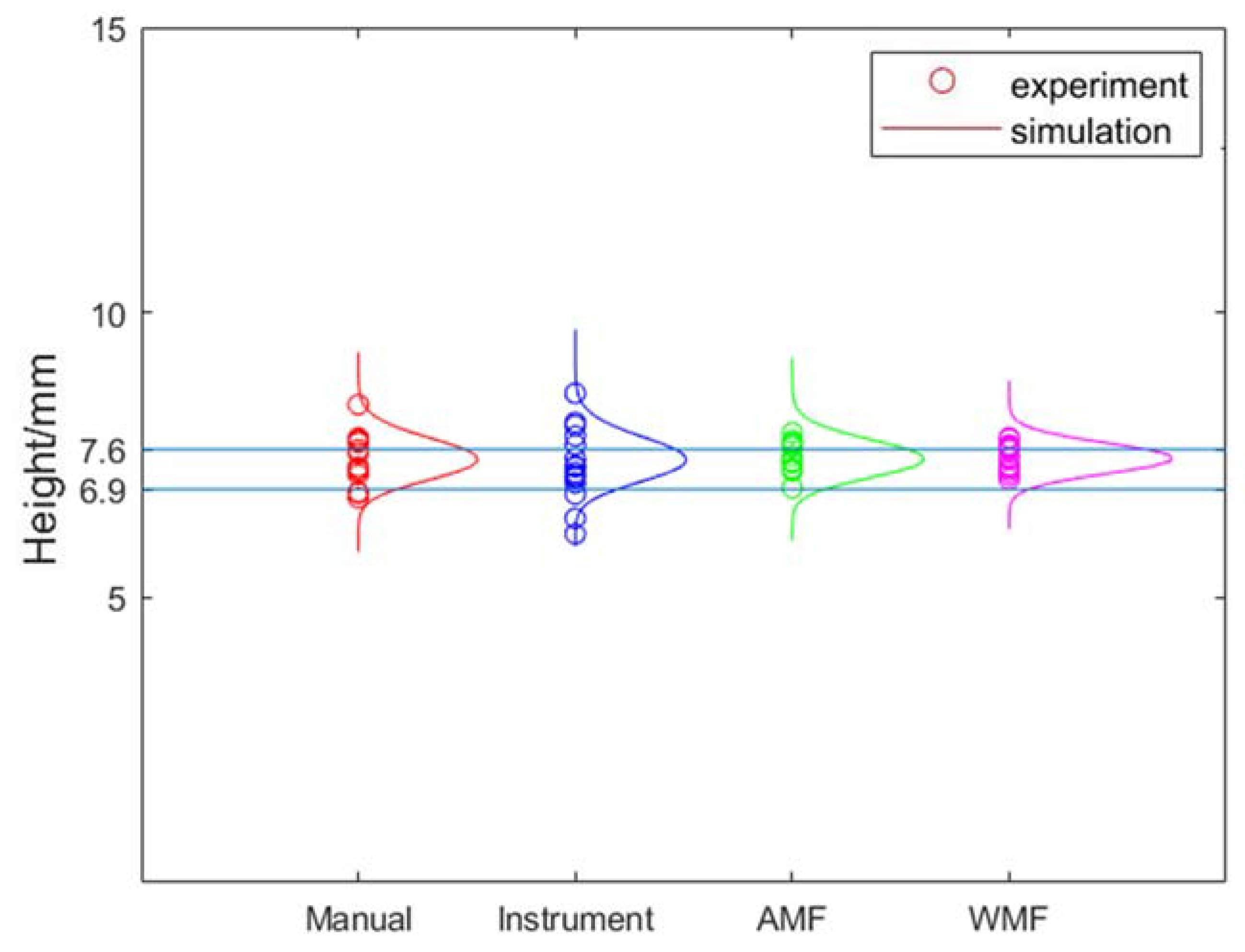
| Item | Probe | Mean | Standard Deviation | Times | P Value for KS-Test |
|---|---|---|---|---|---|
| t100 | K1 | 68.22 µs | 0.31 | 39 | 0.73 |
| K1.5 | 68.67 µs | 0.35 | 17 | 0.8 | |
| K2 | 70.03 µs | 0.84 | 23 | 0.98 | |
| K2.5 | 68.85 µs | 1.15 | 41 | 0.89 | |
| t50 | K1 | 37.3 µs | 0.3 | 39 | 0.7 |
| K1.5 | 37.84 µs | 0.4 | 17 | 0.83 | |
| K2 | 39.21 µs | 0.9 | 23 | 0.9 | |
| K2.5 | 38 µs | 1.1 | 41 | 0.79 | |
| X | K1 | 9.51 mm | 0.71 | 39 | 0.89 |
| K1.5 | 8.49 mm | 0.62 | 17 | 0.97 | |
| K2 | 9.39 mm | 0.74 | 23 | 0.99 | |
| K2.5 | 12.94 mm | 0.91 | 41 | 0.65 | |
| L | K1 | 56.62 mm | 0.72 | 39 | 0.49 |
| K1.5 | 73.22 mm | 1.76 | 17 | 0.55 | |
| K2 | 88.52 mm | 2.48 | 23 | 0.93 | |
| K2.5 | 106.06 mm | 3.24 | 41 | 0.91 | |
| TD | K1 | 17.44 µs | 0.27 | 39 | 0.64 |
| K1.5 | 25.56 µs | 0.88 | 17 | 0.88 | |
| K2 | 35.83 µs | 1.44 | 23 | 0.98 | |
| K2.5 | 45.7 µs | 1.94 | 41 | 0.73 |
| Probe | K1 | K1.5 | K2 | K2.5 |
|---|---|---|---|---|
| t100 and t50 | 0.96 | 0.98 | 0.99 | 0.99 |
| L and TD | 0.71 | 0.78 | 0.9 | 0.93 |
| Probe | c | τ | K by Ruler | K by Instrument |
|---|---|---|---|---|
| K1 | 3234.88/9.16 | 6.39/0.33 | 1.04/0.035 | 1.02/0.029 |
| K1.5 | 3243.46/9.22 | 7/0.46 | 1.56/0.056 | 1.54/0.056 |
| K2 | 3245.13/12.55 | 8.4/0.99 | 2.1/0.079 | 2.09/0.088 |
| K2.5 | 3242.79/18.26 | 7.17/1.08 | 2.8/0.11 | 2.74/0.128 |
| Depth | K1 | K1.5 | K2 | K2.5 |
|---|---|---|---|---|
| 10 | - | 18.18/0.38 | 22.52/0.47 | 27.72/1.78 |
| 30 | 32.33/0.52 | 40.39/1.03 | 50.14/1.2 | 60.25/2.03 |
| 50 | 49.82/0.61 | 62.73/1.31 | 77.94/2.11 | 98.55/1.87 |
| 70 | 67.74/0.68 | 86.36/1.95 | 106.81/2.25 | 137.72/2.01 |
| 90 | 85.3/0.71 | - | - | - |
| t2 | t2–t1 | Times | |
|---|---|---|---|
| K1 with crack a | - | 6.33/0.82 | 15 |
| K1.5 with crack a | 16.07/0.73 | 8.21/0.77 | 15 |
| K2 with crack a | 19.47/0.81 | 9.8/0.77 | 15 |
| K2.5 with crack a | 20.93/0.52 | 13.53/0.44 | 15 |
| K2.5 with crack b | - | 2.84/0.31 | 6 |
| Crack a | Crack b | Crack c | |
|---|---|---|---|
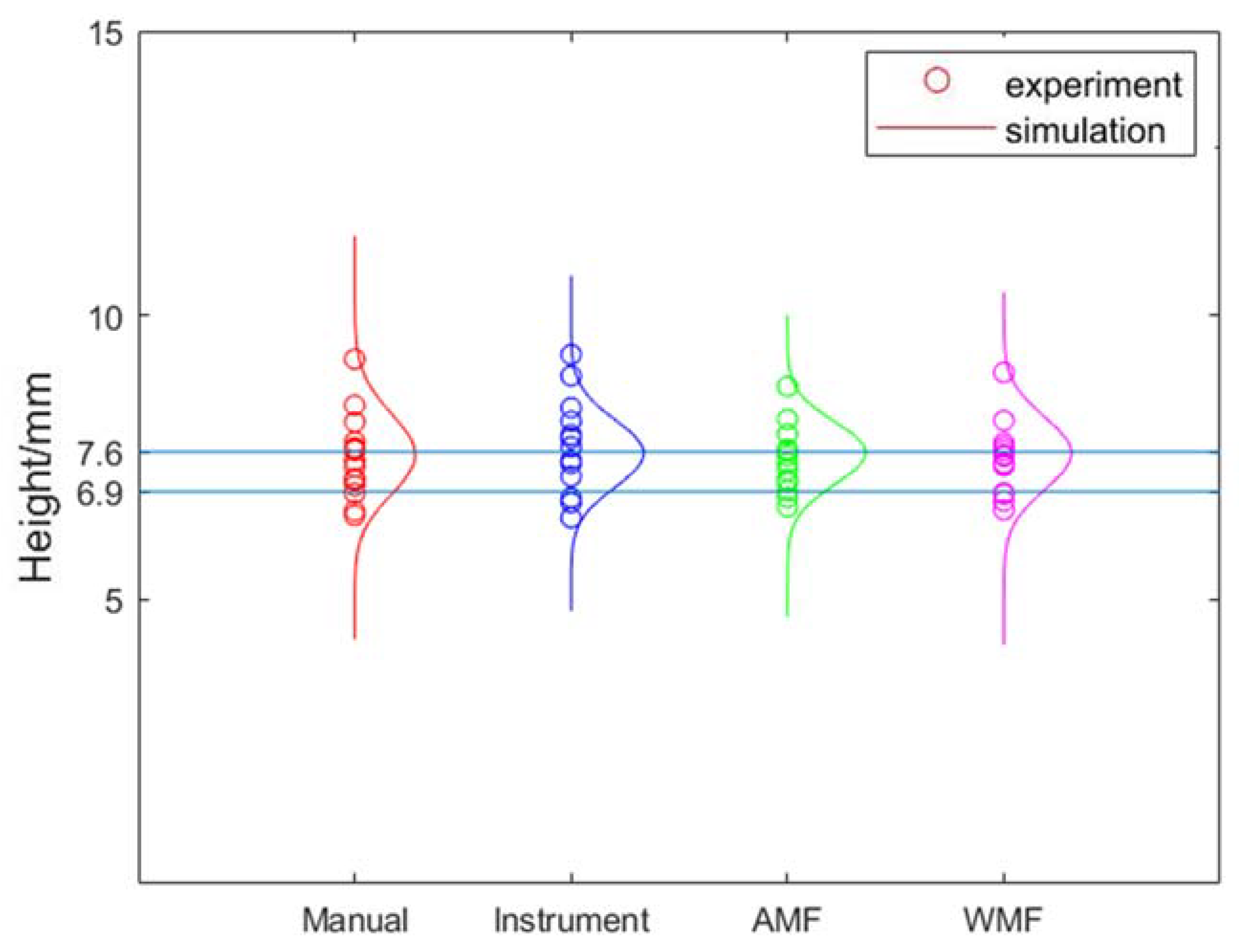
| HMIN | 6.9 | 2.1 | - |
| HMAX | 7.6 | 2.7 | 1.2 |
| Ruler | Instrument | 10 | 30 | 50 | 70 | 90 | |
|---|---|---|---|---|---|---|---|
| K1 | 0.2179 | −0.0943 | 0.0309 | 0.1516 | 0.2602 | 0.4337 | - |
| K1.5 | 0.2828 | −0.0256 | - | −0.0108 | 0.1485 | 0.3121 | 0.2390 |
| K2 | 0.4176 | −0.2245 | - | −0.0357 | 0.2021 | 0.2243 | 0.4163 |
| K2.5 | 0.3549 | −0.2454 | - | −0.0074 | 0.0709 | 0.2997 | 0.5272 |
| Crack | Probe | Location | Manual | Instrument | AMF | WMF |
|---|---|---|---|---|---|---|
| a | K1 | Bottom-surface | 7.1417/7.1846 | 7.1423/7.1467 | 7.1416/7.1467 | 7.1412/7.1448 |
| a | K1.5 | Bottom-surface | 7.2201/7.18 | 7.2217/7.2192 | 7.2191/7.2106 | 7.2175/7.195 |
| a | K1.5 | Top-surface | 7.09/7.0708 | 7.086/7.1012 | 7.0834/7.0442 | 7.0852/7.0299 |
| a | K2 | Bottom-surface | 6.8489/6.835 | 6.8535/6.9414 | 6.848/6.8694 | 6.8437/6.8341 |
| a | K2 | Top-surface | 7.7363/7.8083 | 7.7255/7.8431 | 7.7192/7.8047 | 7.7274/7.8675 |
| a | K2.5 | Bottom-surface | 7.4517/7.4138 | 7.4551/7.3315 | 7.4503/7.4463 | 7.444/7.4507 |
| a | K2.5 | Top-surface | 7.5789/7.4934 | 7.5706/7.5751 | 7.5655/7.4878 | 7.5686/7.4519 |
| b | K2.5 | Bottom-surface | 2.5342/2.5105 | 2.5353/2.4641 | 2.5337/2.4832 | 2.5315/2.5369 |
| Crack | Probe | Location | Manual | Instrument | AMF | WMF |
|---|---|---|---|---|---|---|
| a | K1 | Bottom-surface | 0.9377/0.9861 | 0.9362/0.9613 | 0.9318/0.9285 | 0.931/0.9264 |
| a | K1.5 | Bottom-surface | 0.71/0.6907 | 0.712/0.7324 | 0.693/0.6947 | 0.6877/0.69 |
| a | K1.5 | Top-surface | 0.7838/0.8326 | 0.7355/0.8558 | 0.7154/0.7189 | 0.7492/0.6897 |
| a | K2 | Bottom-surface | 0.5825/0.5992 | 0.6043/0.6756 | 0.5665/0.5961 | 0.5454/0.5859 |
| a | K2 | Top-surface | 0.9277/0.96 | 0.8052/0.9262 | 0.7686/0.836 | 0.8721/1.0377 |
| a | K2.5 | Bottom-surface | 0.3617/0.4438 | 0.3897/0.6439 | 0.3265/0.2693 | 0.2612/0.2305 |
| a | K2.5 | Top-surface | 0.7153/0.7198 | 0.5949/0.8554 | 0.5535/0.5595 | 0.6396/0.602 |
| b | K2.5 | Bottom-surface | 0.2954/0.2828 | 0.2996/0.2972 | 0.2905/0.3082 | 0.2805/0.3136 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Z.; Jin, Z.; Zhu, L.; Li, Y.; Lei, Y.; Gao, Z. Optimizing the Calibration Error of Refraction Angles in Ultrasonic Angle Beam Testing. Sensors 2020, 20, 1427. https://doi.org/10.3390/s20051427
Cai Z, Jin Z, Zhu L, Li Y, Lei Y, Gao Z. Optimizing the Calibration Error of Refraction Angles in Ultrasonic Angle Beam Testing. Sensors. 2020; 20(5):1427. https://doi.org/10.3390/s20051427
Chicago/Turabian StyleCai, Zhihui, Zhangmin Jin, Linyi Zhu, Yuebing Li, Yuebao Lei, and Zengliang Gao. 2020. "Optimizing the Calibration Error of Refraction Angles in Ultrasonic Angle Beam Testing" Sensors 20, no. 5: 1427. https://doi.org/10.3390/s20051427
APA StyleCai, Z., Jin, Z., Zhu, L., Li, Y., Lei, Y., & Gao, Z. (2020). Optimizing the Calibration Error of Refraction Angles in Ultrasonic Angle Beam Testing. Sensors, 20(5), 1427. https://doi.org/10.3390/s20051427





