Novel Magnetic Field Modulation Concept Using Multiferroic Heterostructure for Magnetoresistive Sensors
Abstract
:1. Introduction
2. Principle
3. Theoretical Model
3.1. Establishment of the Equivalent Magnetic Circuit Model (EMCM)
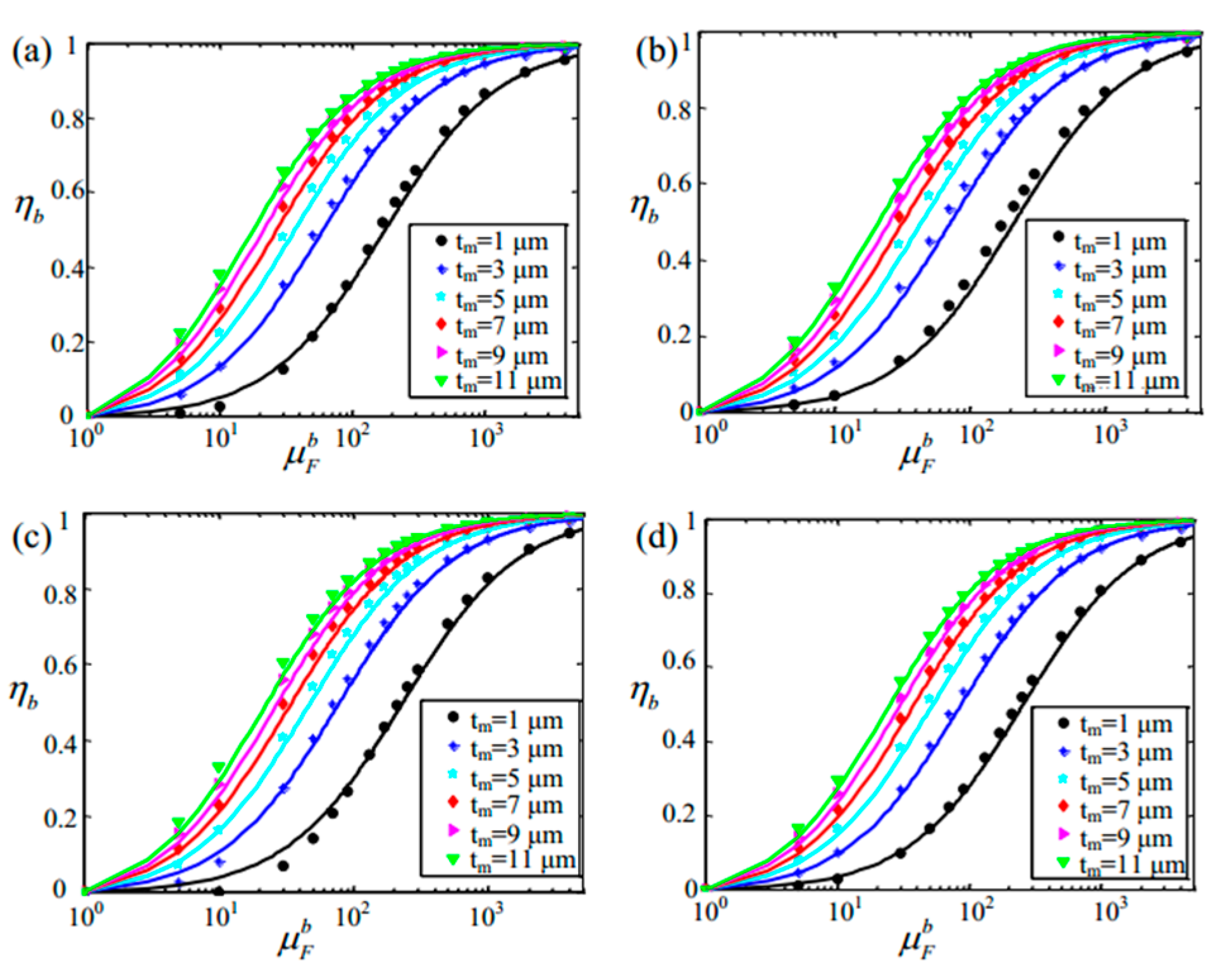
3.2. Verification of the EMCM
4. The Method to Improve Modulation Efficiency
4.1. Size Optimization of Modulation Structure
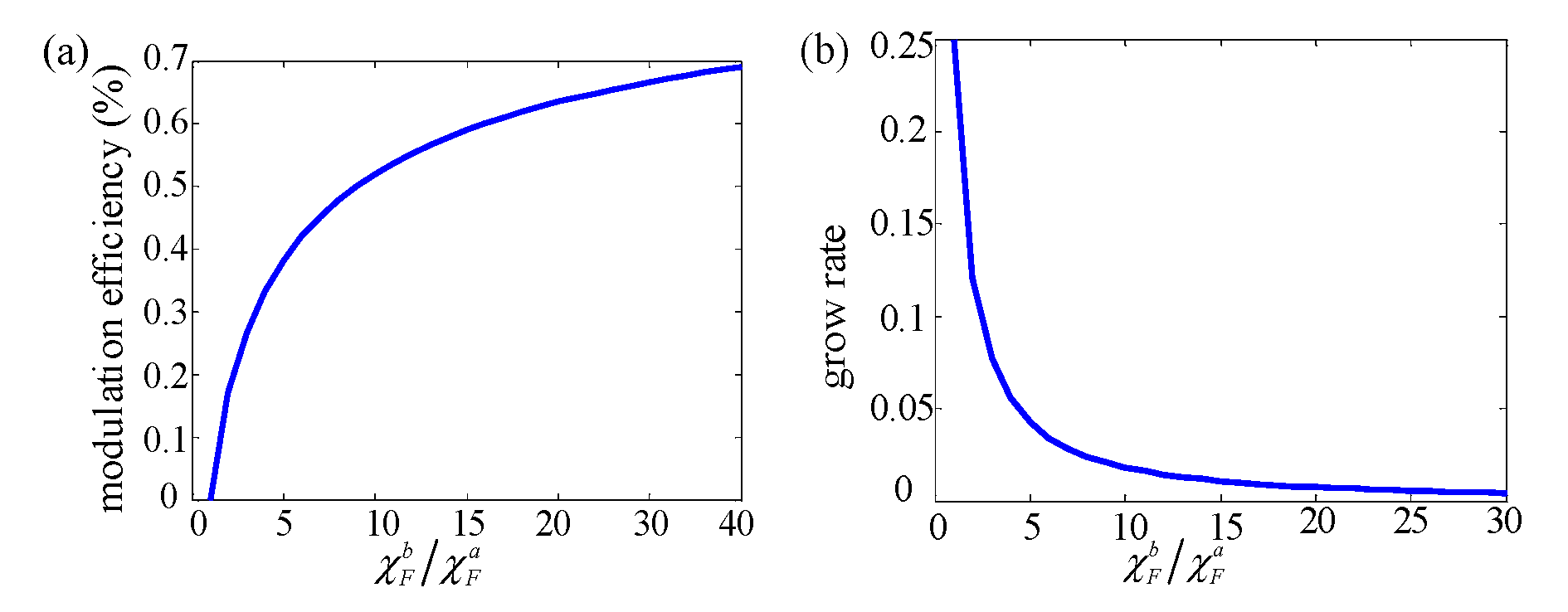
4.2. Materials Optimization FE Layer and FMF Layer
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, J.; Hu, J.; Tian, W.; Hu, J.; Pan, M. Designs of novel magnetic flux guides for three-Axis magnetic sensor. IEEE Trans. Magn. 2015, 51, 1–6. [Google Scholar] [CrossRef]
- Ribeiro, P.; Khan, M.A.; Alfadhel, A.; Kosel, J.; Franco, F.; Cardoso, S.; Bernardino, A.; Santos-Victor, J.; Jamone, L. A miniaturized force sensor based on hair-like flexible magnetized cylinders deposited over a giant magnetoresistive sensor. IEEE Trans. Magn. 2017, 53, 1–5. [Google Scholar] [CrossRef]
- Ribeiro, P.; Neto, M.; Cardoso, S. Strategy for determining a magnet position in a 2-D space using 1-D sensors. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Chaves, R.C.; Freitas, P.P.; Ocker, B.; Maass, W. Low frequency picotesla field detection using hybrid MgO based tunnel sensors. Appl. Phys. Lett. 2007, 91, 102504. [Google Scholar] [CrossRef]
- Jander, A.; Nordman, C.A.; Pohm, A.V.; Anderson, J.M. Chopping techniques for low-frequency nanotesla spin-dependent tunneling field sensors. J. Appl. Phys. 2003, 93, 8382–8384. [Google Scholar] [CrossRef]
- Egelhoff, W.F.; Pong, P.W.T.; Unguris, J.; McMichael, R.D.; Nowak, E.R.; Edelstein, A.S.; Burnette, J.E.; Fischer, G.A. Critical challenges for picoTesla magnetic-tunnel-junction sensors. Sens. Actuators A Phys. 2009, 155, 217–225. [Google Scholar] [CrossRef]
- Hu, J.; Pan, M.; Tian, W.; Chen, D.; Zhao, J. Magnetostati detection using magnetoresistive sensors with vertical motion flux modulation. Rev. Sci. Instrum. 2012, 83, 055009. [Google Scholar] [CrossRef]
- Valadeiro, J.; Cardoso, S.; Macedo, R.; Guedes, A.; Gaspar, J.; Freitas, P.P. Hybrid integration of magnetorisistive sensors with MEMS as a strategy to detect ultra-low magnetic fields. Micromachines 2016, 7, 88. [Google Scholar] [CrossRef] [Green Version]
- Edelstein, A.S.; Fischer, G. Minimizing 1/f nosie in magnetic sensors using a microelectromechanical system flux concentrator. J. Appl. Phys. 2002, 91, 7795–7797. [Google Scholar] [CrossRef]
- Hu, J.; Pan, M.; Tian, W.; Chen, D.; Luo, F. Integrating magnetoresistive sensors with microelectromechanical systems for noise reduction. Appl. Phys. Lett. 2012, 101, 234101. [Google Scholar] [CrossRef]
- Liu, M.; Sun, N.X. Voltage control of magnetism in multiferroic heterostructures. Philos. Trans. A Math. Phys. Eng. Sci. 2014, 372, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Zhou, Z.; Nan, T.; Howe, B.M.; Brown, G.J.; Sun, N.X. Voltage tuning of ferromagnetic resonance with bistable magnetization switching in energy-efficient magnetoelectric composites. Adv. Mater. 2013, 25, 1435–1439. [Google Scholar] [CrossRef] [PubMed]
- Lahtinen, T.H.; Franke, K.J.; van Dijken, S. Electric-field control of magnetic domain wall motion and local magnetization reversal. Sci. Rep. 2012, 2, 258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.; Zhao, Y.G.; Li, P.S.; Yang, J.J.; Rizwan, S.; Zhang, J.X.; Seidel, J.; Qu, T.L.; Yang, Y.J.; Luo, Z.L. Electric-field control of nonvolatile magnetization in Co40Fe40B20/Pb(Mg1/3Nb2/3)0.7Ti0.3O3 structure at room temperature. Phys. Rev. Lett. 2012, 108, 137203. [Google Scholar] [CrossRef]
- Li, P.; Chen, A.; Li, D.; Zhao, Y.; Zhang, S.; Yang, L.; Liu, Y.; Zhu, M.; Zhang, H.; Han, X. Electric field manipulation of magnetization rotation and tunneling magnetoresistance of magnetic tunnel junctions at room temperature. Adv. Mater. 2014, 6, 4320–4325. [Google Scholar] [CrossRef]
- Li, P.; Zhao, Y.; Zhang, S.; Chen, A.; Li, D.; Ma, J.; Liu, Y.; Pierce, D.T.; Unguris, J.; Piao, H.G. Spatially resolved ferroelectric domain-switching-contralled magnetism in Co40Fe40B20/Pb(Mg1/3Nb2/3)0.7Ti0.3O3 multiferroic heterostructure. ACS Appl. Mater. Interfaces 2017, 9, 2642–2649. [Google Scholar] [CrossRef] [Green Version]
- Lou, J.; Reed, D.; Liu, M.; Sun, N.X. Electrostatically tunable magnetoelectric inductors with large inductance tunability. Appl. Phys. Lett. 2009, 94, 112508. [Google Scholar] [CrossRef]
- Tkach, A.; Kehlberger, A.; Büttner, F.; Jakob, G.; Eisebitt, S.; Kläui, M. Electric field modification of magnetotransport in Ni thin films on (011) PMN-PT piezosubstrates. Appl. Phys. Lett. 2015, 106, 062404. [Google Scholar] [CrossRef]
- Phuoc, N.N.; Ong, C.K. Role of crystal orientation on electrical tuning of dynamic permeability in strain-mediated multiferroic structures. Mater. Res. Express 2017, 4, 066101. [Google Scholar] [CrossRef]
- Hu, J.; Pan, M.; Tian, W.; Chen, D.; Zhao, J.; Luo, F. 1/f noise suppression of giant magnetoresistive sensors with vertical motion flux modulation. Appl. Phys. Lett. 2012, 100, 244102. [Google Scholar] [CrossRef] [Green Version]
- Phuoc, N.N.; Ong, C.K. Control of ferromagnetic resonance frequency and frequency linewidth by electrical fields in FeCo/[Pb(Mg1/3Nb2/3)O3]0.68-[PbTiO3]0.32(011) heterostructures. J. Electron. Mater. 2016, 45, 4999–5005. [Google Scholar] [CrossRef]
- Tkach, A.; Kehlberger, A.; Büttner, F.; Jakob, G.; Eisebitt, S.; Kläui, M. Quantitative analysis of magnetization reversal in Ni thin films on unpoled and poled (011) [PbMg1/3Nb2/3O3]0.68–[PbTiO3]0.32 piezoelectric substrates. J. Phys. D Appl. Phys. 2016, 49, 335004. [Google Scholar] [CrossRef]
- Kokernak, J.M.; Torrey, D.A. Magnetic circuit model for the mutually coupled switched-reluctance machine. IEEE Trans. Magn. 2000, 36, 500–507. [Google Scholar] [CrossRef]
- Pan, M.; Hu, J.; Tian, W.; Chen, D.; Zhao, J. Magnetic flux vertical motion modulation for 1/f noise reduction of magnetic tunnel junctions. Sens. Actuators A Phys. 2012, 179, 92–97. [Google Scholar] [CrossRef]
- Edelstein, A.S.; Fischer, G.; Pulskamp, J.; Pedersen, M.; Bernard, W.; Cheng, S.F. Minimizing the effect of 1/f noise with a MEMS flux concentrator. Sens. Proc. IEEE 2004, 3, 1562–1565. [Google Scholar]
- Cubells-Beltran, M.D.; Reig, C.; Madrenas, J.; De Marcellis, A.; Santos, J.; Cardoso, S.; Freitas, P.P. Integration of GMR sensors with different technologies. Sensors 2016, 16, 939. [Google Scholar] [CrossRef]
- Tannous, C.; Gieraltowski, J. The Stoner–Wohlfarth model of ferromagnetism. Eur. J. Phys. 2012, 29, 475–487. [Google Scholar] [CrossRef]
- Yan, Y.; Geng, L.D.; Zhang, L.; Gao, X.; Gollapudi, S.; Song, H.C.; Dong, S.; Sanghadasa, M.; Ngo, K.; Wang, Y.U. Correlation between tenability and anisotropy in magnetoelectric voltage tunable inductor (VTI). Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Gazda, P.; Nowicki, M.; Szewczyk, R. Comparison of stress-impedance effect in amorphous ribbons with positive and negative magnetostrction. Materials 2019, 12, 275. [Google Scholar] [CrossRef] [Green Version]
- Sun, E.; Zhang, S.; Luo, J.; Shrout, T.R.; Cao, W. Elastic, dielectric, and piezoelectric constants of Pb(In1/2Nb1/2)O3–Pb(Mg1/3Nb2/3)O3–PbTiO3 single crystal poled along [011]c. Appl. Phys. Lett. 2010, 97, 032902. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Jamali, M.; D’Souza, N.; Zhang, D.; Bandyopadhyay, S.; Atulasimha, J.; Wang, J.P. Giant voltage manipulation of MgO-based magnetic tunnel junctions via localized anisotropic strain: A potential pathway to unltra-energy-efficient memory technology. Appl. Phys. Lett. 2016, 109, 092403. [Google Scholar] [CrossRef] [Green Version]
- Roy, K.; Bandyopadhyay, S.; Atulasimha, J. Hybrid spintronics and straintronics: A magnetic technology for urtra low energy computing and signal processing. Appl. Phys. Lett. 2011, 99, 063108. [Google Scholar] [CrossRef] [Green Version]
- Chu, Z.; Dong, C.; Tu, C.; Liang, X.; Chen, H.; Sun, C.; Yu, Z.; Dong, S.; Sun, N.X. A low-power and high-sensitivity magnetic field sensor based on converse magnetoelectric effect. Appl. Phys. Lett. 2019, 115, 162901. [Google Scholar] [CrossRef]
- Srinnivasan, G.; Vreugd, C. Resonant magnetoelectric coupling on trilayers of ferromagnetic alloys and piezoelectric lead zirconate titanate: The influence of bias magnetic field. Phys. Rev. B 2005, 71, 184423. [Google Scholar] [CrossRef]
- Guedes, G.; Patil, S.B.; Wisniowski, P.; Chu, V.; Conde, J.P.; Freitas, P.P. Hybrid magnetic tunnel junction-MEMS high frequency field modulator for 1/f noise suppression. IEEE Trans. Magn. 2008, 44, 2554–2557. [Google Scholar] [CrossRef]


| Situations | tfc (μm) | lg (μm) (length of gap) | wfc (μm) | Permeability of FC | k (solved parameter) |
|---|---|---|---|---|---|
| a | 5 | 30 | 300 | 500 | 2.92 × 10−2 |
| b | 10 | 30 | 300 | 500 | 4.94 × 10−2 |
| c | 5 | 40 | 300 | 500 | 2.21 × 10−2 |
| d | 10 | 40 | 300 | 500 | 4.07 × 10−2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, L.; Pan, M.; Hu, J.; Hu, Y.; Che, Y.; Yu, Y.; Wang, N.; Qiu, W.; Li, P.; Peng, J.; et al. Novel Magnetic Field Modulation Concept Using Multiferroic Heterostructure for Magnetoresistive Sensors. Sensors 2020, 20, 1440. https://doi.org/10.3390/s20051440
Pan L, Pan M, Hu J, Hu Y, Che Y, Yu Y, Wang N, Qiu W, Li P, Peng J, et al. Novel Magnetic Field Modulation Concept Using Multiferroic Heterostructure for Magnetoresistive Sensors. Sensors. 2020; 20(5):1440. https://doi.org/10.3390/s20051440
Chicago/Turabian StylePan, Long, Mengchun Pan, Jiafei Hu, Yueguo Hu, Yulu Che, Yang Yu, Nan Wang, Weicheng Qiu, Peisen Li, Junping Peng, and et al. 2020. "Novel Magnetic Field Modulation Concept Using Multiferroic Heterostructure for Magnetoresistive Sensors" Sensors 20, no. 5: 1440. https://doi.org/10.3390/s20051440
APA StylePan, L., Pan, M., Hu, J., Hu, Y., Che, Y., Yu, Y., Wang, N., Qiu, W., Li, P., Peng, J., & Jiang, J. (2020). Novel Magnetic Field Modulation Concept Using Multiferroic Heterostructure for Magnetoresistive Sensors. Sensors, 20(5), 1440. https://doi.org/10.3390/s20051440






