A Survey of Heart Anomaly Detection Using Ambulatory Electrocardiogram (ECG)
Abstract
1. Introduction
2. ECG Monitoring and Its Signals
2.1. Standard 12-lead ECG
2.2. Three-lead vs. 12-lead ECGs
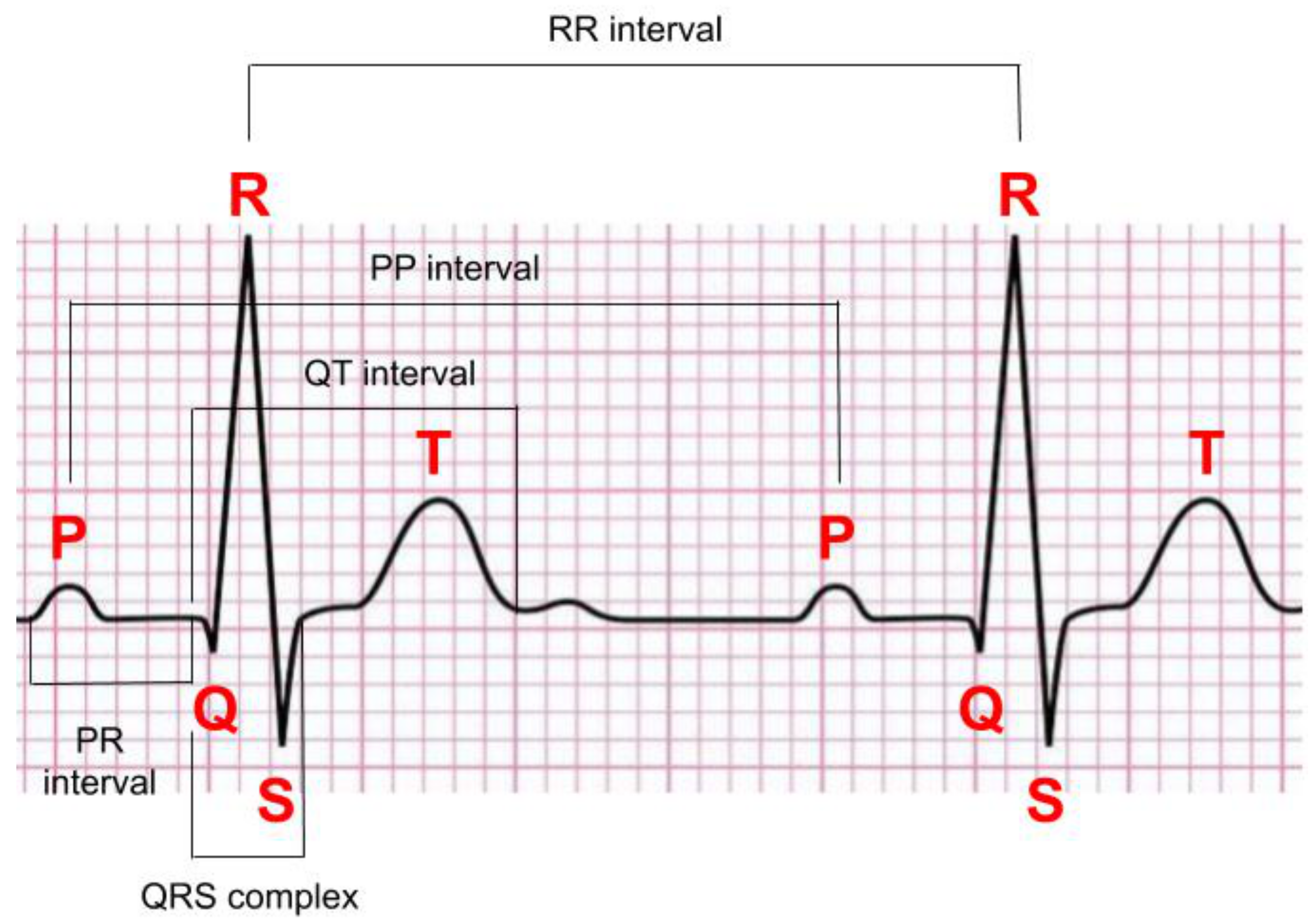
2.3. Normal ECG Signals
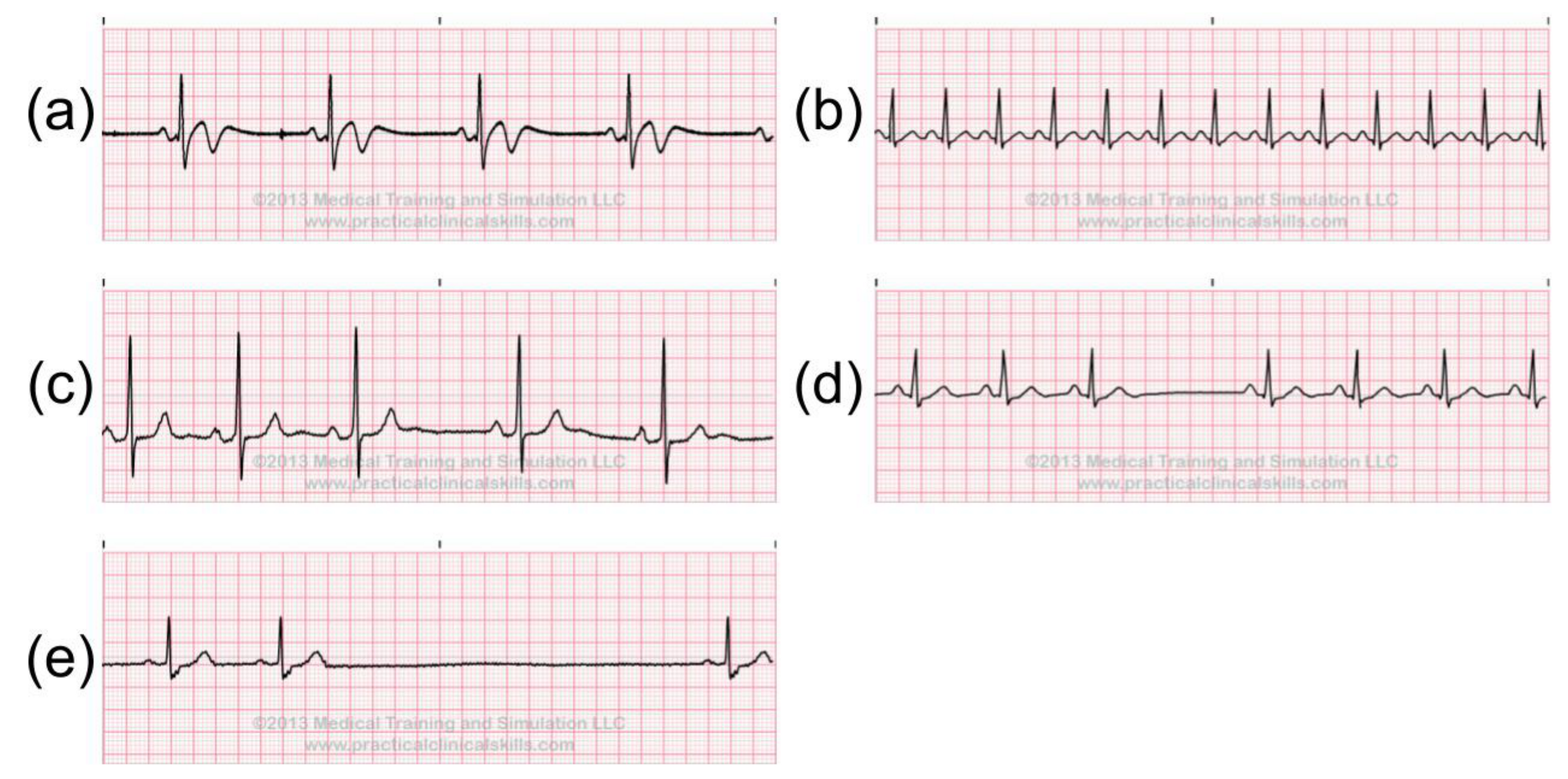
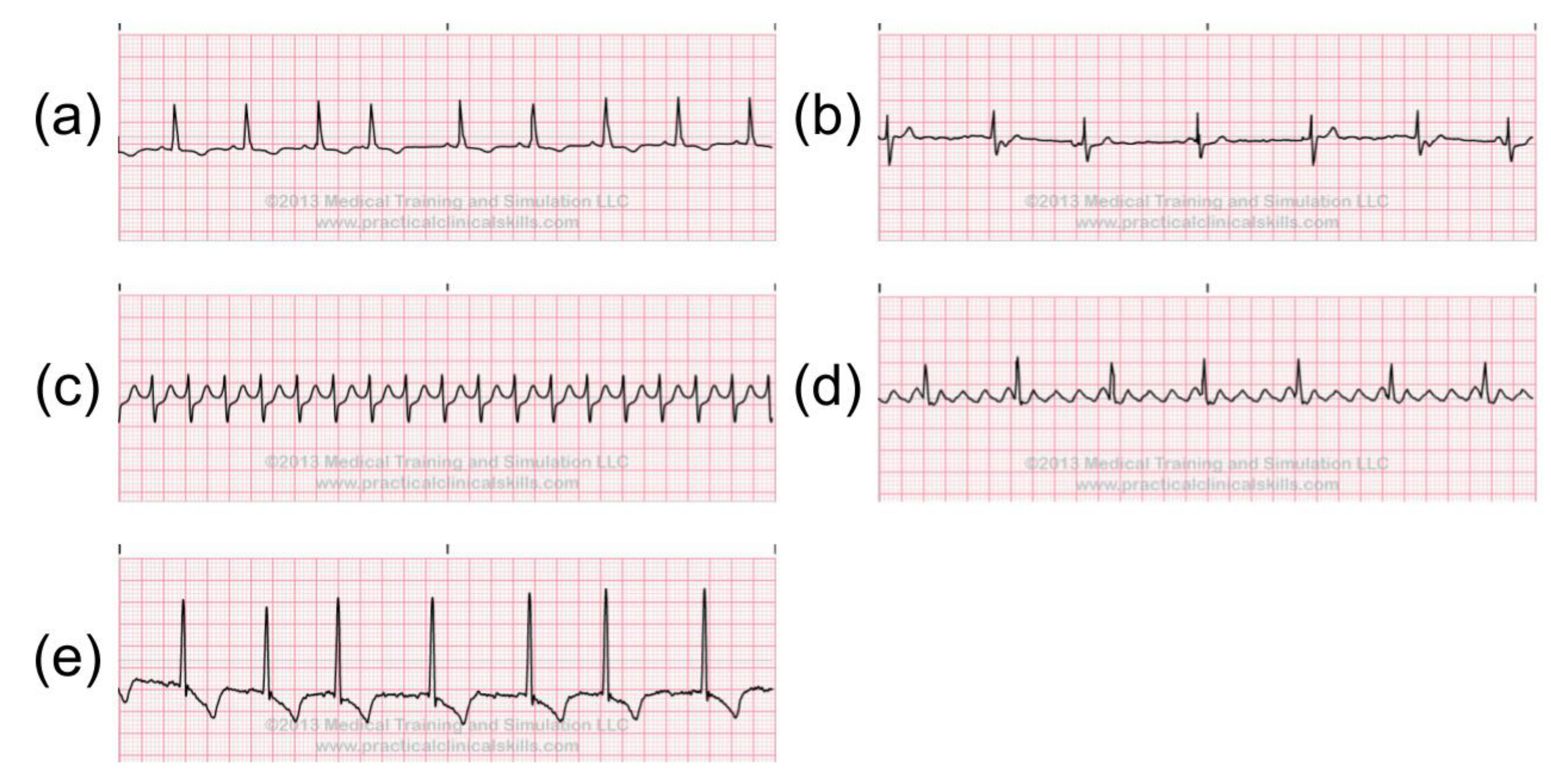
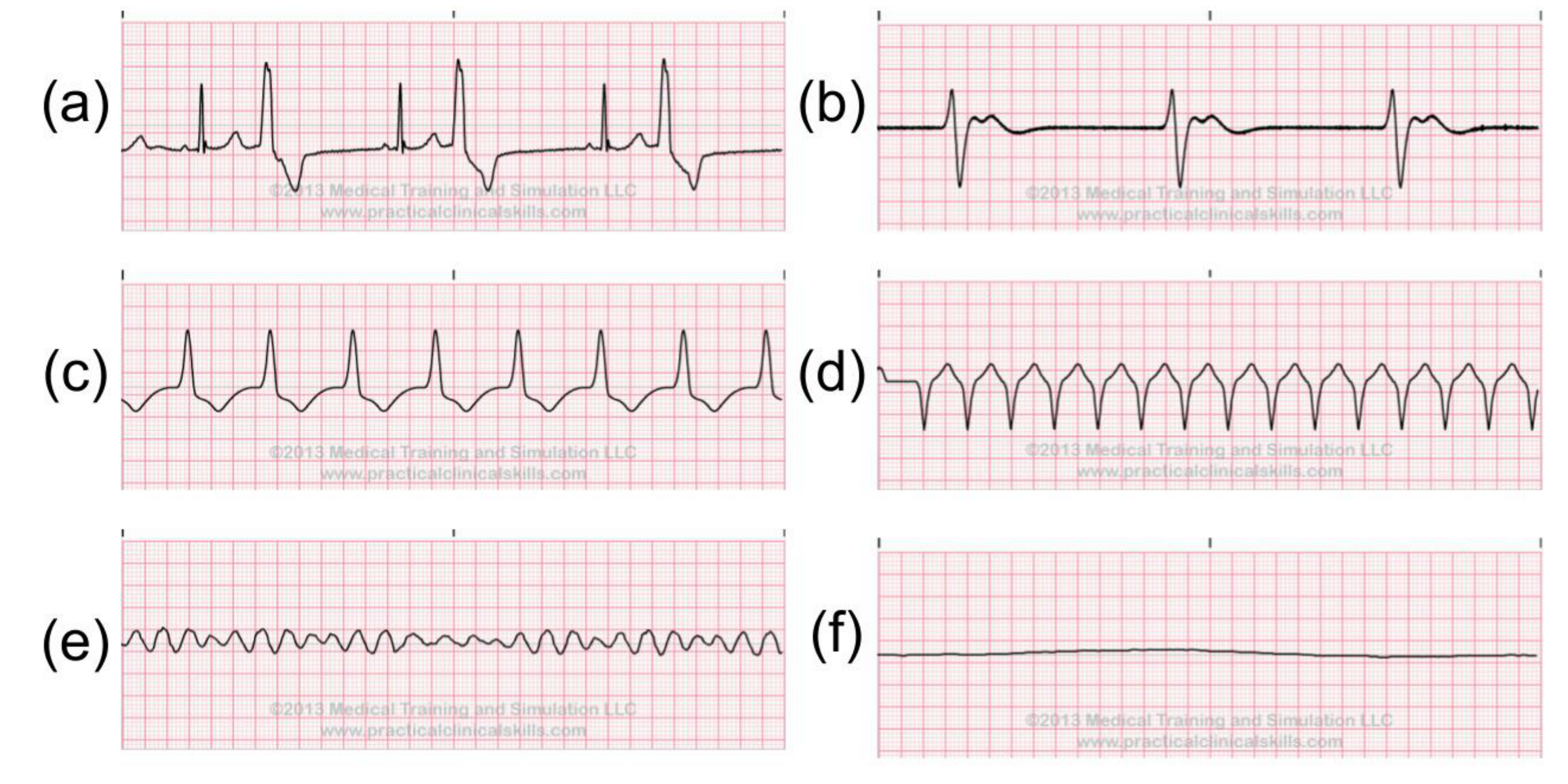
2.4. Abnormal ECG Signals
3. Automatic Heart Anomaly Detection: A State-of-the-Art
3.1. Automatic Heart Anomaly Detection
3.1.1. MIT-BIH Database
- Normal (N)
- Left bundle branch block beat (LBBB)
- Right bundle branch block beat (RBBB)
- Atrial premature beat (PAC/APC)
- Aberrated atrial rremature beat (a)
- Nodal(junctional) premature beat (J)
- Supraventricular premature beat (S)
- Premature ventricular contraction (PVC)
- Fusion of ventricular and normal beat (F)
- Atrial escape beat (e)
- Nodal (junctional) escape beat (j)
- Ventricular escape beat (E)
- Paced beat (P)
- Fusion of paced and normal beat (f)
- Classifiable beat (Q)
- Atrial/Ventricular flutter beat (!).
- Atrial bigeminy (AB)
- Atrial fibrillation (AF)
- Atrial flutter (AFL)
- Ventricular bigeminy (B)
- 2 Heart block (BII)
- Idioventricular rhythm (IVR)
- Normal sinus rhythm (NSR)
- Nodal (A-V junction) rhythm
- Paced rhythm (PR)
- Pre-excitation (PREX)
- Sinus bradycardia (SBR)
- Supraventricular tachyarrhythmia (SVTA)
- Ventricular trigeminy (T)
- Ventricular flutter (VFL)
- Ventricular tachycardia (VT).
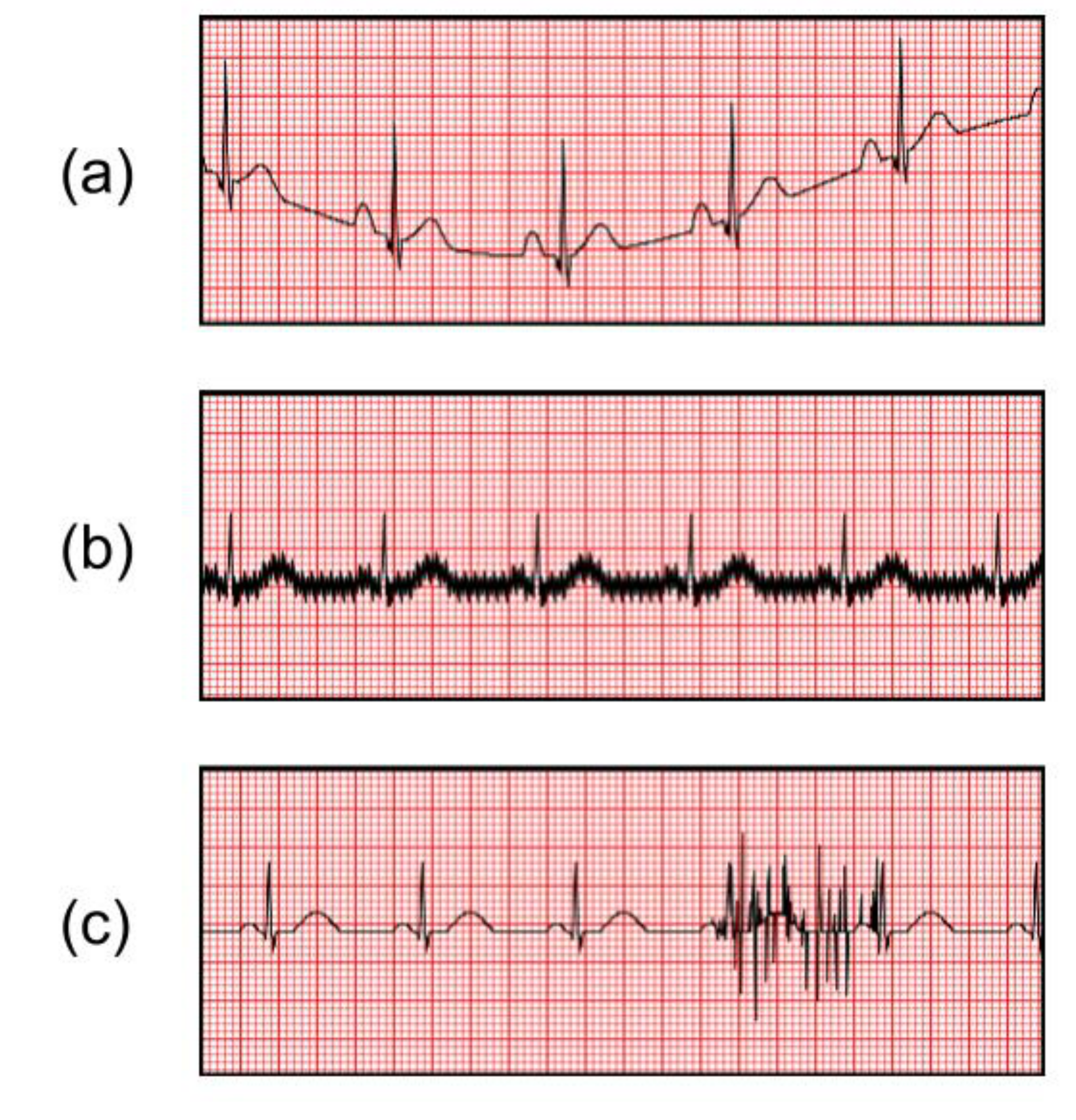
3.2. Noise Removal
- The number of extremas and zero-crossings must be equal or differ at most by one;
- All local maximas and minimas must be symmetric to zero.
3.3. Heartbeat Detection and Segmentation
- TP: Number of correctly detected heartbeats
- FP: Number of incorrectly detected heartbeats
- FN: Number of missed heartbeats
- Sensitivity (SEN) = TP / (TP+FN)
- Positive Detection (+P) = TP / (TP+FP)
- Detection Error Rate(DER) = (FP+FN) / TP
- Accuracy (ACC) = TP / (TP+FP+FN).
3.4. Irregular Heartbeat Classification
3.4.1. Feature Extraction
- Vectorcardiography (VCG) vector;
- DWT coefficients produced by Discrete Wavelet Transform (DWT);
- Independent components from Independent Component Analysis (ICA);
- PCA components generated from Principal Component Analysis (PCA);
- IMFs from Empirical Mode Decomposition (EMD)/Ensemble EMD (EEMD);
- DTCWT coefficients from Dual Tree Complex Wavelet Transform;
- Eigenvector methods;
- Dynamic Time Warping (DTW) distance.
3.4.2. Model Training
3.5. Irregular Rhythm Classification
3.6. Heartbeat/Rhythm Classification Algorithm Comparison
- TP: Number of correctly detected abnormal heartbeats
- FP: Number of incorrectly detected abnormal heartbeats
- TN: Number of correctly detected normal heartbeats
- FN: Number of incorrectly detected normal heartbeats
- Sensitivity = TP/(TP+FN)
- False Alarm Rate= 1 - Specificity = FP/(FP+TN)
- Accuracy = (TP+TN)/(TP+FP+TN+FN)
4. Discussion
4.1. Challenges for Heart Anomaly Detection with Ambulatory Electrocardiograms
- ECG signals may be contaminated with motion noise as the patient is constantly moving. The noisy signal may have a similar morphology to abnormal cardiac signals resulting in false positive. It is easy for the human eye to identify these conditions; however, for computers, it is much harder to separate the noise from the signal.
- The model training requires a labeled ECG signal. In order to label the ECG data set, trained personnel are needed. In addition, the labeling process is very time consuming. For example, a 10 s one ECG signal has 2500 data points, and the continuous monitoring usually takes 24–48 h.
- The ECG heartbeat data is highly imbalanced. Over 99% of the heartbeat data is the normal case and only 1% of the heartbeat data presents 16 abnormal cases. Therefore, the highly imbalanced dataset makes it more difficult to adjust the learning step. Several options could be explored to reduce the effect of imbalanced data, such as database re-sampling or using the cost-sensitive method, kernel based method, or active learning [97].
4.2. Future Works
4.3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- World Health Organization. Cardiovascular Diseases. 2017. Available online: https://www.who.int/health-topics/cardiovasculardiseases/tab=tab3 (accessed on 4 March 2020).
- Zipes, D.P.; Libby, P.; Bonow, R.O.; Mann, D.L.; Tomaselli, G.F. Braunwald’s Heart Disease E-Book: A Textbook of Cardiovascular Medicine; Elsevier Health Sciences: Philadelphia, PA, USA, 2018. [Google Scholar]
- Apple Inc. Apple Watch Series 4. 2018. Available online: https://www.apple.com/ca/apple-watch-series-4/health (accessed on 4 March 2020).
- AliveCor Inc. Alive cor. 2020. Available online: https://www.alivecor.com/ (accessed on 4 March 2020).
- Omron Healthcare Asia. Omron ecg Monitor hcg-801. 2020. Available online: https://zenicor.com/zenicor-ekg/ (accessed on 4 March 2020).
- Qardio Inc. Qardiomd. 2018. Available online: https://www.getqardio.com/qardiomd-ecg/ (accessed on 4 March 2020).
- Carre Technologies Inc. Hexoskin Smart Shirt. 2012. Available online: https://www.hexoskin.com/ (accessed on 4 March 2020).
- Hampton, J. The ECG Made Easy E-Book; Elsevier Health Sciences: St. Louis, MO, USA, 2013. [Google Scholar]
- Frank, E. An accurate, clinically practical system for spatial vectorcardiography. Circulation 1956, 13, 737–749. [Google Scholar] [CrossRef] [PubMed]
- Antonicelli, R.; Ripa, C.; Abbatecola, A.M.; Capparuccia, C.A.; Ferrara, L.; Spazzafumo, L. Validation of the 3-lead tele-ECG versus the 12-lead tele-ECG and the conventional 12-lead ECG method in older people. J. Telemed. Telecare 2012, 18, 104–108. [Google Scholar] [CrossRef] [PubMed]
- Kristensen, A.N.; Jeyam, B.; Riahi, S.; Jensen, M.B. The use of a portable three-lead ECG monitor to detect atrial fibrillation in general practice. Scand. J. Primary Health Care 2016, 34, 304–308. [Google Scholar] [CrossRef] [PubMed]
- Mehri-Dehnavi, A.; Salehpour, N.; Rabbani, H.; Farahabadi, A.; Farahabadi, E. Automatic Analysis of Vectorcardiogram Signal for Detection of Cardiovascular Diseases. Ph.D. Thesis, Isfahan University of Medical Sciences, Isfahan, Iran, 2013. [Google Scholar]
- Augustyniak, P. On the Equivalence of the 12-Lead ECG and the VCG Representations of the Cardiac Electrical Activity. In Proceedings of the 10th International Conference on System-Modelling-Control, Zakopane, Poland, 21–25 May 2001; pp. 51–56. [Google Scholar]
- Atoui, H.; Fayn, J.; Rubel, P. A novel neural-network model for deriving standard 12-lead ECGs from serial three-lead ECGs: Application to self-care. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 883–890. [Google Scholar] [CrossRef]
- Figueiredo, C.; Mendes, P. Towards Wearable And Continuous 12-Lead Electrocardiogram Monitoring-Synthesis of the 12-lead Electrocardiogram using 3 Wireless Single-lead Sensors. In International Conference on Biomedical Electronics and Devices; SCITEPRESS: Setúbal, Portugal, 2012; Volume 2. [Google Scholar]
- Zhu, H.; Pan, Y.; Cheng, K.T.; Huan, R. A lightweight piecewise linear synthesis method for standard 12-lead ECG signals based on adaptive region segmentation. PLoS ONE 2018, 13, e0206170. [Google Scholar] [CrossRef]
- Nelwan, S.P.; Kors, J.A.; Meij, S.H.; van Bemmel, J.H.; Simoons, M.L. Reconstruction of the 12-lead electrocardiogram from reduced lead sets. J. Electrocardiol. 2004, 37, 11–18. [Google Scholar] [CrossRef]
- Drew, B.J.; Adams, M.G.; Pelter, M.M.; Wung, S.F.; Caldwell, M.A. Comparison of standard and derived 12-lead electrocardiograms for diagnosis of coronary angioplasty-induced myocardial ischemia. Am. J. Cardiol. 1997, 79, 639–644. [Google Scholar] [CrossRef]
- Drew, B.J.; Pelter, M.M.; Brodnick, D.E.; Yadav, A.V. Comparison of a new reduced lead set ECG with the standard ECG for diagnosing cardiac arrhythmias and myocardial ischemia. J. Electrocardiol. 2002, 35, 13. [Google Scholar] [CrossRef]
- Tomasic, I.; Trobec, R.; Lindén, M. Can the regression trees be used to model relation between ECG leads? In International Internet of Things Summit; Springer: Rome, Italy, 2015; pp. 467–472. [Google Scholar]
- M. Training and S. LLC. Ekg reference. 2019. Available online: https://www.practicalclinicalskills.com/ekg-reference (accessed on 4 March 2020).
- Goldberger, A.L.; Goldberger, Z.D.; Shvilkin, A. Clinical Electrocardiography: A Simplified Approach E-Book: A Simplified Approach; Elsevier Health Sciences: Philadelphia, PA, USA, 2017. [Google Scholar]
- Morris, F.; Brady, W.J. ABC of clinical electrocardiography: Acute myocardial infarction—Part I. Bmj 2002, 324, 831–834. [Google Scholar] [CrossRef]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Harrigan, R.A.; Chan, T.C.; Brady, W.J. Electrocardiographic electrode misplacement, misconnection, and artifact. J. Emerg. Med. 2012, 43, 1038–1044. [Google Scholar] [CrossRef]
- Jané, R.; Laguna, P.; Thakor, N.V.; Caminal, P. Adaptive baseline wander removal in the ECG: Comparative analysis with cubic spline technique. In Proceedings Computers in Cardiology; IEEE: Durham, NC, USA, 1992; pp. 143–146. [Google Scholar]
- Thakor, N.V.; Zhu, Y.S. Applications of adaptive filtering to ECG analysis: Noise cancellation and arrhythmia detection. IEEE Trans. Biomed. Eng. 1991, 38, 785–794. [Google Scholar] [CrossRef] [PubMed]
- MAUVILA.COM. Ecg Artifacts. 2018. Available online: http://www.mauvila.com/ECG/ecgartifact:htm (accessed on 4 March 2020).
- Christov, I.; Gómez-Herrero, G.; Krasteva, V.; Jekova, I.; Gotchev, A.; Egiazarian, K. Comparative study of morphological and time-frequency ECG descriptors for heartbeat classification. Med. Eng. Phys. 2006, 28, 876–887. [Google Scholar] [CrossRef]
- De Chazal, P.; Reilly, R.B. A patient-adapting heartbeat classifier using ECG morphology and heartbeat interval features. IEEE Trans. Biomed. Eng. 2006, 53, 2535–2543. [Google Scholar] [CrossRef]
- Thomas, M.; Das, M.K.; Ari, S. Automatic ECG arrhythmia classification using dual tree complex wavelet based features. AEU-Int. J. Electron. Commun. 2015, 69, 715–721. [Google Scholar] [CrossRef]
- Rajesh, K.N.; Dhuli, R. Classification of ECG heartbeats using nonlinear decomposition methods and support vector machine. Comput. Biol. Med. 2017, 87, 271–284. [Google Scholar] [CrossRef] [PubMed]
- Sivaraks, H.; Ratanamahatana, C.A. Robust and accurate anomaly detection in ECG artifacts using time series motif discovery. Comput. Math. Methods Med. 2015, 453214. [Google Scholar] [CrossRef]
- Patel, A.M.; Gakare, P.K.; Cheeran, A. Real time ECG feature extraction and arrhythmia detection on a mobile platform. Int. J. Comput. Appl. 2012, 44, 40–45. [Google Scholar]
- Kiranyaz, S.; Ince, T.; Gabbouj, M. Real-time patient-specific ECG classification by 1-D convolutional neural networks. IEEE Trans. Biomed. Eng. 2015, 63, 664–675. [Google Scholar] [CrossRef]
- Velayudhan, A.; Peter, S. Noise Analysis and Different Denoising Techniques of ECG Signal-A Survey. IOSR J. Electron. Commun. Eng. (IOSR-JECE) 2016, 2278–2834, 40–44. [Google Scholar]
- Llamedo, M.; Martínez, J.P. Heartbeat classification using feature selection driven by database generalization criteria. IEEE Trans. Biomed. Eng. 2010, 58, 616–625. [Google Scholar] [CrossRef] [PubMed]
- Rai, H.M.; Trivedi, A.; Shukla, S. ECG signal processing for abnormalities detection using multi-resolution wavelet transform and Artificial Neural Network classifier. Measurement 2013, 46, 3238–3246. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Lih, O.S.; Hagiwara, Y.; Tan, J.H.; Adam, M. Automated detection of arrhythmias using different intervals of tachycardia ECG segments with convolutional neural network. Inf. Sci. 2017, 405, 81–90. [Google Scholar] [CrossRef]
- Rai, H.M.; Trivedi, A. De-noising of ECG Waveforms based on Multi-resolution Wavelet Transform. Int. J. Comput. Appl. 2012, 45, 25–30. [Google Scholar]
- Singh, B.N.; Tiwari, A.K. Optimal selection of wavelet basis function applied to ECG signal denoising. Digit. Signal Process. 2006, 16, 275–287. [Google Scholar] [CrossRef]
- Lin, H.Y.; Liang, S.Y.; Ho, Y.L.; Lin, Y.H.; Ma, H.P. Discrete-wavelet-transform-based noise removal and feature extraction for ECG signals. Irbm 2014, 35, 351–361. [Google Scholar] [CrossRef]
- Labate, D.; La Foresta, F.; Occhiuto, G.; Morabito, F.C.; Lay-Ekuakille, A.; Vergallo, P. Empirical mode decomposition vs. wavelet decomposition for the extraction of respiratory signal from single-channel ECG: A comparison. IEEE Sens. J. 2013, 13, 2666–2674. [Google Scholar] [CrossRef]
- Weng, B.; Blanco-Velasco, M.; Barner, K.E. ECG denoising based on the empirical mode decomposition. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 1–4. [Google Scholar]
- Blanco-Velasco, M.; Weng, B.; Barner, K.E. ECG signal denoising and baseline wander correction based on the empirical mode decomposition. Comput. Biol. Med. 2008, 38, 1–13. [Google Scholar] [CrossRef]
- Chang, K.M. Arrhythmia ECG noise reduction by ensemble empirical mode decomposition. Sensors 2010, 10, 6063–6080. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Jenitta, J.; Rajeswari, A. Denoising of ECG signal based on improved adaptive filter with EMD and EEMD. In Proceedings of the 2013 IEEE Conference on Information & Communication Technologies, Thuckalay, Tamil Nadu, India, 11–12 April 2013; pp. 957–962. [Google Scholar]
- Zhidong, Z.; Yi, L.; Qing, L. Adaptive noise removal of ECG signal based on ensemble empirical mode decomposition. In Adaptive Filtering Applications; IntechOpen: London, UK, 2011; ISBN 978-953-307-306-4. [Google Scholar] [CrossRef]
- Singh, G.; Kaur, G.; Kumar, V. ECG denoising using adaptive selection of IMFs through EMD and EEMD. In Proceedings of the 2014 International Conference on Data Science & Engineering (ICDSE), Kochi, India, 26–28 August 2014; pp. 228–231. [Google Scholar]
- Lisheng, X.; Kuanquan, W.; Zhang, D.; Cheng, S. Adaptive baseline wander removal in the pulse waveform. In Proceedings of the 15th IEEE Symposium on Computer-Based Medical Systems (CBMS 2002), Maribor, Slovenia, 4–7 June 2002; pp. 143–148. [Google Scholar]
- Haykin, S.S.; Widrow, B.; Widrow, B. Least-Mean-Square Adaptive Filters; Wiley Online Library: Hoboken, NJ, USA, 2003; Volume 31. [Google Scholar]
- Thenua, R.K.; Agarwal, S. Simulation and performance analysis of adaptive filter in noise cancellation. Int. J. Eng. Sci. Technol. 2010, 2, 4373–4378. [Google Scholar]
- Raya, M.A.D.; Sison, L.G. Adaptive noise cancelling of motion artifact in stress ECG signals using accelerometer. In Proceedings of the Second Joint 24th Annual Conference and the Annual Fall Meeting of the Biomedical Engineering Society Engineering in Medicine and Biology, Houston, TX, USA, 23–26 October 2002; Volume 2, pp. 1756–1757. [Google Scholar]
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef]
- Afonso, V.X.; Tompkins, W.J.; Nguyen, T.Q.; Luo, S. ECG beat detection using filter banks. IEEE Trans. Biomed. Eng. 1999, 46, 192–202. [Google Scholar] [CrossRef]
- Chen, S.W.; Chen, H.C.; Chan, H.L. A real-time QRS detection method based on moving-averaging incorporating with wavelet denoising. Comput. Methods Progr. Biomed. 2006, 82, 187–195. [Google Scholar] [CrossRef]
- Choi, S.; Adnane, M.; Lee, G.J.; Jang, H.; Jiang, Z.; Park, H.K. Development of ECG beat segmentation method by combining lowpass filter and irregular R–R interval checkup strategy. Expert Syst. Appl. 2010, 37, 5208–5218. [Google Scholar] [CrossRef]
- Yeh, Y.C.; Wang, W.J. QRS complexes detection for ECG signal: The Difference Operation Method. Comput. Methods Progr. Biomed. 2008, 91, 245–254. [Google Scholar] [CrossRef]
- Zidelmal, Z.; Amirou, A.; Adnane, M.; Belouchrani, A. QRS detection based on wavelet coefficients. Comput. Methods Progr. Biomed. 2012, 107, 490–496. [Google Scholar] [CrossRef]
- Bouaziz, F.; Boutana, D.; Benidir, M. Multiresolution wavelet-based QRS complex detection algorithm suited to several abnormal morphologies. IET Signal Process. 2014, 8, 774–782. [Google Scholar] [CrossRef]
- Manikandan, M.S.; Soman, K. A novel method for detecting R-peaks in electrocardiogram (ECG) signal. Biomed. Signal Process. Control 2012, 7, 118–128. [Google Scholar] [CrossRef]
- Zhu, H.; Dong, J. An R-peak detection method based on peaks of Shannon energy envelope. Biomed. Signal Process. Control 2013, 8, 466–474. [Google Scholar] [CrossRef]
- Rakshit, M.; Panigrahy, D.; Sahu, P. An improved method for R-peak detection by using Shannon energy envelope. Sādhanā 2016, 41, 469–477. [Google Scholar] [CrossRef]
- Park, J.S.; Lee, S.W.; Park, U. R peak detection method using wavelet transform and modified Shannon energy envelope. J. Healthc. Eng. 2017. [Google Scholar] [CrossRef] [PubMed]
- Pal, S.; Mitra, M. Detection of ECG characteristic points using multiresolution wavelet analysis based selective coefficient method. Measurement 2010, 43, 255–261. [Google Scholar] [CrossRef]
- Banerjee, S.; Gupta, R.; Mitra, M. Delineation of ECG characteristic features using multiresolution wavelet analysis method. Measurement 2012, 45, 474–487. [Google Scholar] [CrossRef]
- Karimipour, A.; Homaeinezhad, M.R. Real-time electrocardiogram P-QRS-T detection–delineation algorithm based on quality-supported analysis of characteristic templates. Comput. Biol. Med. 2014, 52, 153–165. [Google Scholar] [CrossRef]
- De Chazal, P.; O’Dwyer, M.; Reilly, R.B. Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans. Biomed. Eng. 2004, 51, 1196–1206. [Google Scholar] [CrossRef]
- Ye, C.; Kumar, B.V.; Coimbra, M.T. Heartbeat classification using morphological and dynamic features of ECG signals. IEEE Trans. Biomed. Eng. 2012, 59, 2930–2941. [Google Scholar]
- Yang, S.; Shen, H. Heartbeat classification using discrete wavelet transform and kernel principal component analysis. In Proceedings of the IEEE 2013 Tencon-Spring, Sydney, Australia, 17–19 April 2013; pp. 34–38. [Google Scholar]
- Jekova, I.; Bortolan, G.; Christov, I. Assessment and comparison of different methods for heartbeat classification. Med. Eng. Phys. 2008, 30, 248–257. [Google Scholar] [CrossRef]
- Zhang, Z.; Dong, J.; Luo, X.; Choi, K.S.; Wu, X. Heartbeat classification using disease-specific feature selection. Comput. Biol. Med. 2014, 46, 79–89. [Google Scholar] [CrossRef]
- Sahoo, S.; Kanungo, B.; Behera, S.; Sabut, S. Multiresolution wavelet transform based feature extraction and ECG classification to detect cardiac abnormalities. Measurement 2017, 108, 55–66. [Google Scholar] [CrossRef]
- Chuah, M.C.; Fu, F. ECG anomaly detection via time series analysis. In Proceedings of the International Symposium on Parallel and Distributed Processing and Applications, Niagara Falls, ON, Canada, 29–31 August 2007; pp. 123–135. [Google Scholar]
- Li, P.; Chan, K.L.; Fu, S.; Krishnan, S.M. An abnormal ecg beat detection approach for long-term monitoring of heart patients based on hybrid kernel machine ensemble. In Proceedings of the International Workshop on Multiple Classifier Systems, Seaside, CA, USA, 13–15 June 2005; pp. 346–355. [Google Scholar]
- Li, K.; Du, N.; Zhang, A. Detecting ECG abnormalities via transductive transfer learning. In Proceedings of the 2012 ACM Conference on Bioinformatics, Computational Biology and Biomedicine, Orlando, FL, USA, 8–10 October 2012; pp. 210–217. [Google Scholar]
- Chauhan, S.; Vig, L. Anomaly detection in ECG time signals via deep long short-term memory networks. In Proceedings of the IEEE International Conference on Data Science and Advanced Analytics (DSAA), Paris, France, 19–21 October 2015; pp. 1–7. [Google Scholar]
- Burch, G.E. The history of vectorcardiography. Med. History 1985, 29, 103–131. [Google Scholar] [CrossRef] [PubMed]
- Kingsbury, N. Complex wavelets for shift invariant analysis and filtering of signals. Appl. Comput. Harmon. Anal. 2001, 10, 234–253. [Google Scholar] [CrossRef]
- Wess, M.; Manoj, P.S.; Jantsch, A. Neural network based ECG anomaly detection on FPGA and trade-off analysis. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Übeyli, E.D. Combining recurrent neural networks with eigenvector methods for classification of ECG beats. Digit. Signal Process. 2009, 19, 320–329. [Google Scholar] [CrossRef]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. In Proceedings of the KDD Workshop, Seattle, WA, USA, 31 July –1 August 1994; Volume 10, pp. 359–370. [Google Scholar]
- Pham, N.D.; Le, Q.L.; Dang, T.K. HOT aSAX: A novel adaptive symbolic representation for time series discords discovery. In Proceedings of the Asian Conference on Intelligent Information and Database Systems, Hue City, Vietnam, 24–26 March 2010; pp. 113–121. [Google Scholar]
- Veeravalli, B.; Deepu, C.J.; Ngo, D. Real-time, personalized anomaly detection in streaming data for wearable healthcare devices. In Handbook of Large-Scale Distributed Computing in Smart Healthcare; Springer: New York, NY, USA, 2017; pp. 403–426. [Google Scholar]
- Gretton, A.; Smola, A.; Huang, J.; Schmittfull, M.; Borgwardt, K.; Schölkopf, B. Covariate shift by kernel mean matching. Dataset Shift Mach. Learn. 2009, 3, 5. [Google Scholar]
- Biel, L.; Pettersson, O.; Philipson, L.; Wide, P. ECG analysis: A new approach in human identification. IEEE Trans. Instrum. Meas. 2001, 50, 808–812. [Google Scholar] [CrossRef]
- Hu, Y.H.; Palreddy, S.; Tompkins, W.J. A patient-adaptable ECG beat classifier using a mixture of experts approach. IEEE Trans. Biomed. Eng. 1997, 44, 891–900. [Google Scholar]
- Jiang, W.; Kong, S.G. Block-based neural networks for personalized ECG signal classification. IEEE Trans. Neural Netw. 2007, 18, 1750–1761. [Google Scholar] [CrossRef]
- Ince, T.; Kiranyaz, S.; Gabbouj, M. A generic and robust system for automated patient-specific classification of ECG signals. IEEE Trans. Biomed. Eng. 2009, 56, 1415–1426. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Hamila, R.; Gabbouj, M. Convolutional neural networks for patient-specific ecg classification. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milano, Italy, 25–29 August 2015; pp. 2608–2611. [Google Scholar]
- Luo, K.; Li, J.; Wang, Z.; Cuschieri, A. Patient-specific deep architectural model for ECG classification. J. Healthc. Eng. 2017, 2017. [Google Scholar] [CrossRef]
- Ge, D.; Srinivasan, N.; Krishnan, S.M. Cardiac arrhythmia classification using autoregressive modeling. Biomed. Eng. Online 2002, 1, 5. [Google Scholar] [CrossRef]
- Özbay, Y.; Ceylan, R.; Karlik, B. Integration of type-2 fuzzy clustering and wavelet transform in a neural network based ECG classifier. Expert Syst. Appl. 2011, 38, 1004–1010. [Google Scholar] [CrossRef]
- Rajpurkar, P.; Hannun, A.Y.; Haghpanahi, M.; Bourn, C.; Ng, A.Y. Cardiologist-level arrhythmia detection with convolutional neural networks. arXiv 2017, arXiv:1707.01836. [Google Scholar]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Gravina, R.; Alinia, P.; Ghasemzadeh, H.; Fortino, G. Multi-sensor fusion in body sensor networks: State-of-the-art and research challenges. Inf. Fusion 2017, 35, 68–80. [Google Scholar] [CrossRef]
- Ghosh, S.; Banerjee, A.; Ray, N.; Wood, P.W.; Boulanger, P.; Padwal, R. Using accelerometric and gyroscopic data to improve blood pressure prediction from pulse transit time using recurrent neural network. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 935–939. [Google Scholar]











| Method | Year | Total Heartbeats | TP | FP | FN | SEN | +P | DER | ACC |
|---|---|---|---|---|---|---|---|---|---|
| Pan–Tompkins [56] | 1985 | 116,137 | 115,860 | 507 | 277 | 99.76% | 99.56% | 0.68% | 99.33% |
| FBBBD [57] | 1999 | 91,283 | 90,909 | 406 | 374 | 99.59% | 99.56% | 0.86% | 99.15% |
| S.W.Chen [58] | 2006 | 102,654 | 102,195 | 529 | 459 | 99.55% | 99.49% | 0.97% | 99.04% |
| DOM [60] | 2008 | 116,137 | 115,971 | 58 | 166 | 99.86% | 99.95% | 0.19% | 99.81% |
| S.Choi [59] | 2010 | 109,494 | 109,118 | 218 | 376 | 99.66% | 99.80% | 0.54% | 99.46% |
| Z.Zidelmal [61] | 2012 | 109,494 | 109,101 | 193 | 393 | 99.64% | 99.82% | 0.54% | 99.47% |
| SEEHT [63] | 2012 | 109,496 | 109,417 | 140 | 79 | 99.93% | 99.87% | 0.2% | 99.80% |
| S.Banerjee [68] | 2012 | 19140 | 19126 | 20 | 20 | 99.90% | 99.90% | 0.21% | 99.79% |
| PSEE [64] | 2013 | 109,494 | 109,401 | 91 | 93 | 99.92% | 99.92% | 0.17% | 99.83% |
| F.Bouaziz [62] | 2014 | 109,494 | 109,354 | 232 | 140 | 99.87% | 99.79% | 0.34% | 99.66% |
| A.Karimipour [69] | 2014 | 116,137 | 115,945 | 308 | 192 | 99.83% | 99.74% | 0.43% | 99.57% |
| ISEE [65] | 2016 | 109,532 | 109,474 | 116 | 58 | 99.95% | 99.89% | 0.16% | 99.84% |
| WTSEE [66] | 2017 | 109,494 | 109,415 | 99 | 79 | 99.93% | 99.91% | 0.16% | 99.84% |
| Features | Description | Reference |
|---|---|---|
| QRS complex duration | The time interval between the onsite of the Q wave and offsite of the S wave | [30,31,38] [73,74,75] |
| QRS velociy left | The QRS slope velocity calculated for the time-interval between the QRS complex onset and the first peak | [30,73] |
| QRS velociy right | The QRS slope velocity calculated for the time-interval between the first peak and the second peaks | [30,73] |
| QRS complex area | The sum of the positive area and absolute negative area in the QRS complex | [30,73] |
| QRS complex morphology | Sample points from the QRS onsite to the QRS offsite | [31] |
| QRS complex AC power | The total power content of the QRS complex signal | [32] |
| QRS complex Kurtosis | The kurtosis indicates the peakedness of the QRS complex | [32] |
| QRS complex Skewness | The skewness measures the symmetry of the distribution of the QRS complex | [32] |
| Q wave valley | The valley value of Q wave | [75] |
| S wave valley | The valley value of S wave | [75] |
| T wave peak | The peak value of T wave | [75] |
| T wave duration | The duration from the QRS offsite to the T wave offsite | [31] |
| T wave morphology | Sample points from the QRS offsite to the T wave offsite | [31] |
| P wave flag | A Boolean value indicates the presence or absence of the P wave | [31] |
| P wave duration | The duration from the P wave onsite to the P wave offsite | [74] |
| P wave morphology | Sample points from the P wave onsite to the P wave offsite | [34,74] |
| PR interval duration | The duration from the P wave onsite to the QRS complex onsite | [74] |
| PR interval morphology | Sample points from the P wave onsite to the QRS complex onsite | [34] |
| QT interval duration | The duration from the QRS complex onsite to the T wave offsite | [74] |
| QT interval morphology | Sample points from the QRS complex onsite to the T wave offsite | [34,75] |
| ST interval morphology | Sample points from the S wave valley to the T wave offsite | [75] |
| Max peak(R peak) value | The maximum amplitude of the heartbeat | [30,73,75] |
| Min peak value | The minimum amplitude of the heartbeat | [30,73] |
| Positive QRS complex area | The area of the positive sample points in the QRS complex | [30,73,74] |
| Negative QRS complex area | The area of the negative sample points in the QRS complex | [30,73,74] |
| Positive P wave area | The area of the positive sample points in the P wave | [74] |
| Negative P wave area | The area of the negative sample points in the P wave | [74] |
| Positive T wave area | The area of the positive sample points in the T wave | [74] |
| Negative T wave area | The area of the negative sample points in the T wave | [74] |
| Absolute velocity sum | Sum of the absolute velocities in the pattern interval | [30,73] |
| Ima | Time-interval from the QRS complex onset to the maximal peak | [30,73] |
| Imi | Time-interval from the QRS complex onset to the minimal peak | [30,73] |
| Pre-RR interval | The RR interval between the heartbeat and its previous heartbeat | [31,71,74] |
| Post-RR interval | The RR interval between the heartbeat and its following heartbeat | [31,71,74] |
| Post-PP interval | The PP interval between the heartbeat and its following heartbeat | [74] |
| Average-RR interval | The average value of all valid RR intervals in the ECG record | [31,71,74] [32,75] |
| Local Average-RR interval | The average value of ten valid RR intervals surrounding the heartbeat | [31,71,74] |
| Normalized signal | The heartbeat sample points are normalized and down-sampled to have a mean of zero and standard deviation of one | [76,77,78] |
| Raw/downsampled ECG signal | The unprocessed ECG signal or the only processing on the signal is downsampled | [36,79] |
| Features | Method | Description | Reference |
|---|---|---|---|
| VCG amplitude | VCG | Maximal amplitude of the VCG vector | [30,38] |
| VCG sine angle | VCG | Sine component of the angle of the maximal amplitude vector | [30,38] |
| VCG cosine angle | VCG | Cosine component of the angle of the maximal amplitude vector | [30,38] |
| DTW distance | DTW | The Dynamic Time Warping distance between a heartbeat segment and the median heartbeat segment of the recording | [74,76] |
| Positive peak of the QRS complex | DWT | The positive peak amplitude of QRS complex on the fourth scale of the DWT | [38] |
| Negative peak of the QRS complex | DWT | The absolute negative peak amplitude of QRS complex on the fourth scale of the DWT | [38] |
| Positive peak of T wave | DWT | The positive peak amplitude of the T wave on the fourth scale of the DWT | [38] |
| Absolute T wave offsite | DWT | The absolute amplitude of the T wave offsite on the fourth scale of the DWT | [38] |
| R-S interval distance | DWT | The relative distance between the R peak and S valley on the fourth scale of the DWT | [38] |
| S-T interval distance 1 | DWT | The relative distance between the S valley to the T wave peak on the fourth scale of the DWT | [38] |
| S-T interval distance 2 | DWT | The relative distance between the S valley to the T wave offsite on the fourth scale of the DWT | [38] |
| Absolute maximum | DWT | The absolute maximum value and location on the fourth scale of the DWT signal | [38] |
| Zero crossing | DWT | The zero crossing location on the fourth scale of DWT signal | [38] |
| Wavelet scale | DWT | Calculate which scale the QRS complex is centered on | [38] |
| DWT coefficients | DWT | The down-sampled third and fourth detail coefficients and the fourth approximation coefficients | [71] |
| Independent Components | ICA | Independent components calculated with a fast fixed point algorithm | [71] |
| Fourier spectrum | DTCWT | Compute the absolute value of fourth and 5th scale DTCWT detail coefficients(dc). Then 1D FFT is applied to the selected DC to obtain the Fourier spectrum. Then take logarithm value of the Fourier spectrum | [32] |
| IMF sample entropy | EMD/EEMD | The sample entropy is measured of regularity of a time series used to quantify the complexity of heartbeat dynamics | [33] |
| IMF variation coefficient | EMD/EEMD | The coefficient of variation is a statistical parameter defined as / . | [33] |
| IMF singular values | EMD/EEMD | The singular value decomposition | [33] |
| IMF band power values | EMD/EEMD | The band power is the average power of each IMF | [33] |
| PCA components | PCA | PCA components for size reduction | [82] |
| Pisarenko PSD | Eigenvector | Power spectral density estimates generated with Pisarenko method | [83] |
| MUSCI PSD | Eigenvector | Power spectral density estimates generated with Multiple signal classification method | [83] |
| Minimum-Norm PSD | Eigenvector | Power spectral density estimates generated with Minimum-Norm methods | [83] |
| Method | Year | Abnormal/Normal | Heartbeat Types | TP | FP | TN | FN | Sensitivity | False Alarm | Accuracy |
|---|---|---|---|---|---|---|---|---|---|---|
| Christov et al. [30]-morphology | 2006 | 18,378/47,239 | 5 | 180,42 | 1604 | 45,635 | 336 | 98.17% | 3.40% | 97.04% |
| Christov et al. [30]-frequency | 2006 | 18,378/47,239 | 5 | 17,590 | 1459 | 45,780 | 788 | 95.71% | 3.09% | 96.58% |
| Chazal et al. [31]-frequency | 2006 | 4317/34,394 | 5 | 4108 | 1962 | 32,432 | 209 | 95.16% | 5.70% | 94.39% |
| Ubeyli et al. [83] | 2009 | 269/90 | 4 | 268 | 2 | 88 | 2 | 99.26% | 2.22% | 99.89% |
| Llamedo et al. [38] | 2010 | 5441/44,188 | 3 | 4752 | 2238 | 41,950 | 689 | 87.34% | 5.06% | 94.10% |
| Ye et al. [71]-rejection | 2012 | 19,913/64,042 | 16 | 19,815 | 93 | 63,949 | 98 | 99.51% | 0.15% | 99.77% |
| Ye et al. [71]-bayesian | 2012 | 20,745/65,264 | 16 | 20,557 | 286 | 64,978 | 188 | 99.09% | 0.44% | 99.45% |
| Zhang et al. [74] | 2014 | 5653/44,011 | 4 | 5248 | 4869 | 39,142 | 405 | 92.84% | 11.06% | 89.38% |
| Thomas et al. [32] | 2015 | 26,626/672,68 | 5 | 22,900 | 1300 | 65,968 | 3726 | 86.01% | 1.93% | 94.65% |
| Kiranyaz et al. [36] | 2015 | 7366/42,191 | 5 | 6539 | 1228 | 40,963 | 827 | 88.77% | 2.97% | 95.85% |
| Rajesh et al. [33] | 2017 | 8000/2000 | 5 | 7677 | 33 | 1967 | 323 | 95.96% | 1.65% | 96.44% |
| Sahoo et al. [75] | 2017 | 807/244 | 4 | 798 | 5 | 239 | 9 | 98.88% | 2.04% | 98.67% |
| Method | Year | Abnormal/Normal | Rhythm Types | Rhythm Length | TP | FP | TN | FN | Sensitivity | False Alarm | Accuracy |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ge et al. [94] | 2002 | 713/143 | 6 | 1.2 s | 706 | 10 | 133 | 7 | 88.77% | 6.99% | 98.01% |
| U. Acharya Net A [40] | 2017 | 20807/902 | 4 | 2 s | 19,160 | 62 | 840 | 1647 | 92.08% | 6.87% | 92.13% |
| U. Acharya Net B [40] | 2017 | 8322/361 | 4 | 5 s | 7946 | 376 | 294 | 67 | 95.48% | 18.56% | 94.9% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Boulanger, P. A Survey of Heart Anomaly Detection Using Ambulatory Electrocardiogram (ECG). Sensors 2020, 20, 1461. https://doi.org/10.3390/s20051461
Li H, Boulanger P. A Survey of Heart Anomaly Detection Using Ambulatory Electrocardiogram (ECG). Sensors. 2020; 20(5):1461. https://doi.org/10.3390/s20051461
Chicago/Turabian StyleLi, Hongzu, and Pierre Boulanger. 2020. "A Survey of Heart Anomaly Detection Using Ambulatory Electrocardiogram (ECG)" Sensors 20, no. 5: 1461. https://doi.org/10.3390/s20051461
APA StyleLi, H., & Boulanger, P. (2020). A Survey of Heart Anomaly Detection Using Ambulatory Electrocardiogram (ECG). Sensors, 20(5), 1461. https://doi.org/10.3390/s20051461





