Figure 1.
An instance of mobile 2D LiDAR used for data acquisition in this study. During the inspection, the 2D LiDAR scans the OCS infrastructure on the plane perpendicular to the rail direction, and the odometer sensor records the traveled distance of each scan line.
Figure 1.
An instance of mobile 2D LiDAR used for data acquisition in this study. During the inspection, the 2D LiDAR scans the OCS infrastructure on the plane perpendicular to the rail direction, and the odometer sensor records the traveled distance of each scan line.
Figure 2.
Data processing framework. Points are classified scan line by scan line. Firstly, data of a scan line are transformed into a 3D coordinate system. Secondly, point features with 3D contexts are extracted at multiple scales by the iterative point partitioning algorithm and the SFN. Finally, the multi-scale local features are concatenated together and then input to a classifier to yield point scores.
Figure 2.
Data processing framework. Points are classified scan line by scan line. Firstly, data of a scan line are transformed into a 3D coordinate system. Secondly, point features with 3D contexts are extracted at multiple scales by the iterative point partitioning algorithm and the SFN. Finally, the multi-scale local features are concatenated together and then input to a classifier to yield point scores.
Figure 3.
An MLS system carried by an inspection device at the starting point. The front view is shown on the left, and the left view is shown on the right. Since the device moves on the rail, the defined 3D Cartesian coordinate system is relative to rail tracks.
Figure 3.
An MLS system carried by an inspection device at the starting point. The front view is shown on the left, and the left view is shown on the right. Since the device moves on the rail, the defined 3D Cartesian coordinate system is relative to rail tracks.
Figure 4.
Definitions of region size and region span. Assume that there are region A and region B, respectively, in plane A and plane B which are perpendicular to the z-axis. In region A, and are the remotest pair of points. The distance between and denotes the region size of region A. The distance between plane A and plane B denotes the region span between region A and region B.
Figure 4.
Definitions of region size and region span. Assume that there are region A and region B, respectively, in plane A and plane B which are perpendicular to the z-axis. In region A, and are the remotest pair of points. The distance between and denotes the region size of region A. The distance between plane A and plane B denotes the region span between region A and region B.
Figure 5.
The architecture of SFN. In the PointNet, MLP denotes a multilayer perceptron, and batch normalization is applied to each layer of the MLP with ReLU. For feature fusion, both LSMTs are single hidden-layer. The hidden layer sizes of the LSTM and the LSTM are, respectively, 8 and 128 so that k and m are, respectively, 8 and 128 with the usage of UDLSTMs. Note that UDLSTMs are without backward hidden states. With the usage of BDLSTMs, outputs of the forward process and backward process are combined so that k and m are, respectively, 16 and 512.
Figure 5.
The architecture of SFN. In the PointNet, MLP denotes a multilayer perceptron, and batch normalization is applied to each layer of the MLP with ReLU. For feature fusion, both LSMTs are single hidden-layer. The hidden layer sizes of the LSTM and the LSTM are, respectively, 8 and 128 so that k and m are, respectively, 8 and 128 with the usage of UDLSTMs. Note that UDLSTMs are without backward hidden states. With the usage of BDLSTMs, outputs of the forward process and backward process are combined so that k and m are, respectively, 16 and 512.
Figure 6.
An instance of single-scale feature extraction with the region size threshold
. Symbols formatted as
,
,
, and
are depicted in
Section 3.2. At the beginning of the iterative process of point partitioning,
is initialized as ∅. Then, regions and region-to-region relationships are produced by the iterative point partitioning algorithm (IPPA). The region-to-region relationships are informed by the superscript
n of the region data, which are formatted as
. Note that the regions without points (e.g., region data
) are discarded for feature extraction. Based on the region-to-region relationships, region data are reorganized in sequences (e.g., sequence
). SFNs extract and fuse features among the sequential region data to acquire the point features with 3D contexts. We share the weights of SFNs for processing data at a single scale. The output
is the set of point features corresponding to the input points
.
Figure 6.
An instance of single-scale feature extraction with the region size threshold
. Symbols formatted as
,
,
, and
are depicted in
Section 3.2. At the beginning of the iterative process of point partitioning,
is initialized as ∅. Then, regions and region-to-region relationships are produced by the iterative point partitioning algorithm (IPPA). The region-to-region relationships are informed by the superscript
n of the region data, which are formatted as
. Note that the regions without points (e.g., region data
) are discarded for feature extraction. Based on the region-to-region relationships, region data are reorganized in sequences (e.g., sequence
). SFNs extract and fuse features among the sequential region data to acquire the point features with 3D contexts. We share the weights of SFNs for processing data at a single scale. The output
is the set of point features corresponding to the input points
.
![Sensors 20 02224 g006]()
Figure 7.
Overhead Contact System configuration of Chinese high-speed railway tagged with sixteen classes: (a) an image; and (b–d) MLS data ((b,c) sections of insulated overlap and (d) a section with mid-point anchor).
Figure 7.
Overhead Contact System configuration of Chinese high-speed railway tagged with sixteen classes: (a) an image; and (b–d) MLS data ((b,c) sections of insulated overlap and (d) a section with mid-point anchor).
Figure 8.
Results of iterative point partitioning: (a) = 0.5 m; (b) = 2 m; and (c) = 7 m. The points grouped into regions are tagged with their region colors. Regions with the same color are related together for feature fusion.
Figure 8.
Results of iterative point partitioning: (a) = 0.5 m; (b) = 2 m; and (c) = 7 m. The points grouped into regions are tagged with their region colors. Regions with the same color are related together for feature fusion.
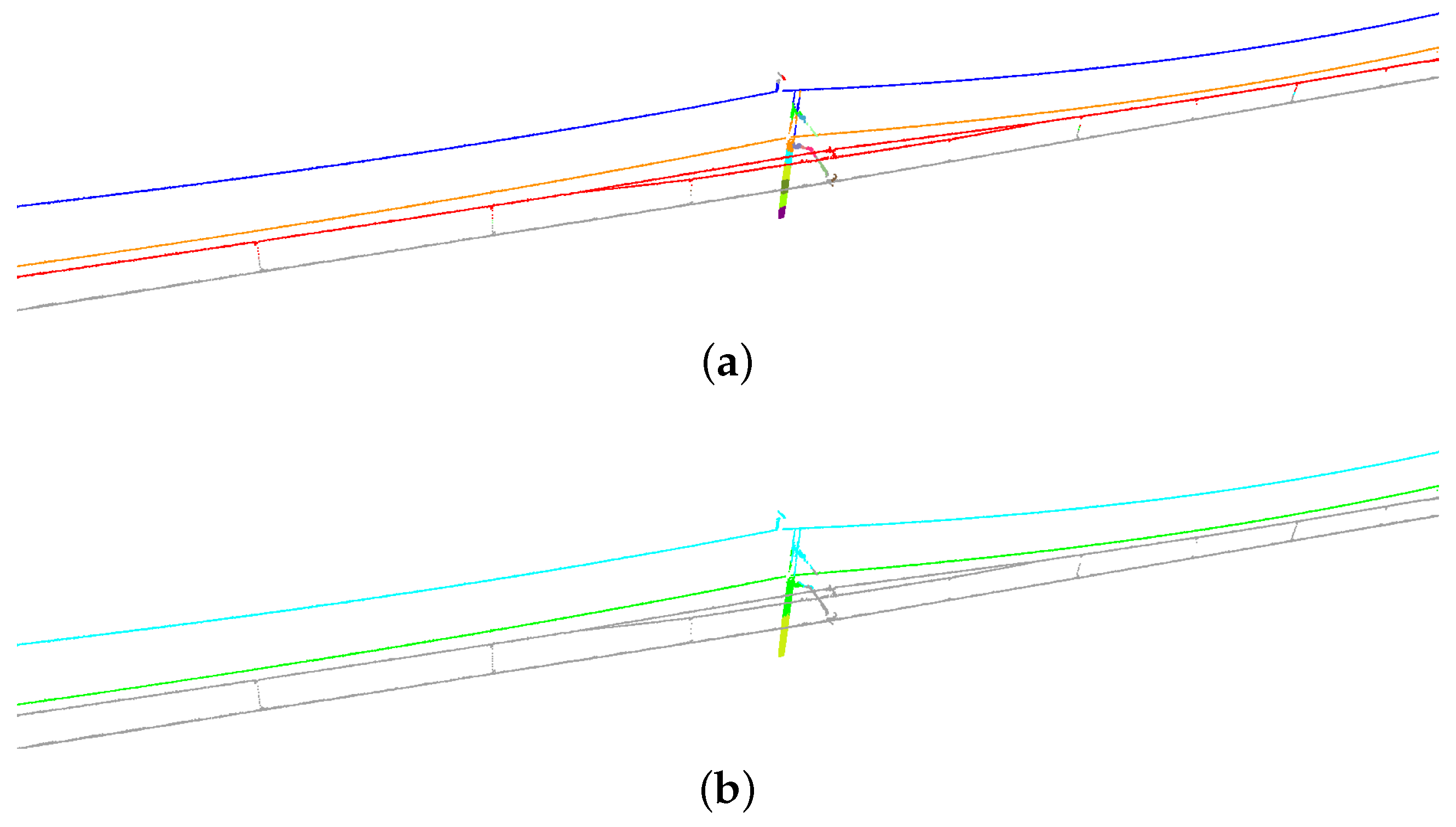
Figure 9.
Segmentation results of non-insulated overlap section: (
a) unidirectional mode; and (
b) bidirectional mode. In each subfigure, predictions are shown above and errors are highlighted in red below (the same as
Figure 10 and
Figure 11).
Figure 9.
Segmentation results of non-insulated overlap section: (
a) unidirectional mode; and (
b) bidirectional mode. In each subfigure, predictions are shown above and errors are highlighted in red below (the same as
Figure 10 and
Figure 11).
Figure 10.
Segmentation results of insulated overlap section: (a) unidirectional mode; and (b) bidirectional mode.
Figure 10.
Segmentation results of insulated overlap section: (a) unidirectional mode; and (b) bidirectional mode.
Figure 11.
Segmentation results of a scene with spreaders: (a) non-feature fusion mode; (b) unidirectional mode; and (c) bidirectional mode.
Figure 11.
Segmentation results of a scene with spreaders: (a) non-feature fusion mode; (b) unidirectional mode; and (c) bidirectional mode.
Table 1.
Parameters of our MLS system.
Table 1.
Parameters of our MLS system.
| Parameters | Value |
|---|
| scaning frequency | 25 Hz |
| angular resolution | |
| field of view | |
| range | 80 m |
| travelling speed | approximately 1 m/s |
Table 2.
The point proportions and object quantities of each class. Note that “-” in this table means that the class is uncountable.
Table 2.
The point proportions and object quantities of each class. Note that “-” in this table means that the class is uncountable.
| Class | Training Dataset | Test Dataset |
|---|
| Points (%) | Quantity | Points (%) | Quantity |
|---|
| COW | 17.90 | - | 4.18 | - |
| CAW | 12.75 | - | 2.84 | - |
| CTLV | 4.18 | 338 | 1.11 | 92 |
| DRO | 0.52 | 1982 | 0.12 | 536 |
| SW | 3.31 | 275 | 0.95 | 76 |
| pole | 8.05 | 278 | 2.15 | 76 |
| SPD | 0.61 | 124 | 0.15 | 32 |
| RW | 14.71 | - | 3.59 | - |
| FW | 13.31 | - | 3.29 | - |
| SI | 0.08 | 220 | 0.03 | 55 |
| PB | 0.69 | 34 | 0.13 | 8 |
| TW | 1.64 | 34 | 0.30 | 8 |
| GW | 0.78 | 108 | 0.24 | 26 |
| MPAW | 1.00 | 10 | 0.08 | 1 |
| MPAAW | 0.13 | 20 | 0.01 | 2 |
| EC | 0.1 | 29 | 0.02 | 8 |
| others | 0.94 | - | 0.12 | - |
Table 3.
Per-class precision, recall, and IoU in the unidirectional mode and the bidirectional mode.
Table 3.
Per-class precision, recall, and IoU in the unidirectional mode and the bidirectional mode.
| Class | Unidirectional Mode | Bidirectional Mode |
|---|
| Precision (%) | Recall (%) | IoU (%) | Precision (%) | Recall (%) | IoU (%) |
|---|
| COW | 99.92 | 99.91 | 99.83 | 99.93 | 99.91 | 99.84 |
| CAW | 99.26 | 96.38 | 95.69 | 99.12 | 99.01 | 98.15 |
| CTLV | 99.39 | 99.19 | 98.59 | 99.36 | 99.21 | 98.59 |
| DRO | 96.50 | 93.90 | 90.80 | 97.04 | 92.91 | 90.35 |
| SW | 90.37 | 98.31 | 88.98 | 97.12 | 97.83 | 95.07 |
| pole | 99.61 | 99.68 | 99.29 | 99.55 | 99.76 | 99.32 |
| SPD | 97.20 | 98.86 | 96.13 | 98.24 | 97.77 | 96.08 |
| RW | 99.92 | 99.92 | 99.84 | 99.99 | 99.94 | 99.93 |
| FW | 99.99 | 99.99 | 99.98 | 99.99 | 99.98 | 99.97 |
| SI | 99.34 | 98.41 | 97.77 | 98.29 | 99.02 | 97.34 |
| PB | 97.89 | 99.41 | 97.32 | 99.06 | 99.25 | 98.32 |
| TW | 99.47 | 98.93 | 98.41 | 99.28 | 99.28 | 98.57 |
| GW | 98.93 | 97.72 | 96.70 | 99.18 | 99.12 | 98.31 |
| MPAW | 96.05 | 99.33 | 95.43 | 97.17 | 99.89 | 97.06 |
| MPAAW | 95.11 | 99.53 | 94.69 | 98.62 | 99.69 | 98.32 |
| EC | 95.35 | 90.59 | 86.75 | 96.77 | 90.90 | 88.23 |
| others | 98.41 | 99.36 | 97.79 | 98.94 | 99.56 | 98.51 |
| mean | 97.81 | 98.20 | 96.12 | 98.69 | 98.41 | 97.17 |
Table 4.
Confusion matrix of partial classes in the unidirectional mode. Values denote the point proportion of the reference.
Table 4.
Confusion matrix of partial classes in the unidirectional mode. Values denote the point proportion of the reference.
| Reference | Prediction (%) | Total (%) |
|---|
| COW | CAW | CTLW | DRO | SW | EC |
|---|
| COW | 99.91 | 0.00 | 0.05 | 0.03 | 0.00 | 0.00 | 99.99 |
| CAW | 0.00 | 96.38 | 0.04 | 0.05 | 3.41 | 0.01 | 99.89 |
| CTLV | 0.05 | 0.16 | 99.19 | 0.00 | 0.09 | 0.00 | 99.49 |
| DRO | 1.99 | 2.10 | 0.03 | 93.90 | 1.49 | 0.36 | 99.87 |
| SW | 0.01 | 1.58 | 0.04 | 0.04 | 98.31 | 0.00 | 99.98 |
| EC | 1.20 | 2.02 | 1.96 | 4.23 | 0.00 | 90.59 | 100 |
Table 5.
Confusion matrix of partial classes in the bidirectional mode. Values denote the point proportion of the reference.
Table 5.
Confusion matrix of partial classes in the bidirectional mode. Values denote the point proportion of the reference.
| Reference | Prediction (%) | Total (%) |
|---|
| COW | CAW | CTLW | DRO | SW | EC |
|---|
| COW | 99.91 | 0.00 | 0.05 | 0.03 | 0.00 | 0.00 | 99.99 |
| CAW | 0.00 | 99.01 | 0.05 | 0.03 | 0.83 | 0.01 | 99.93 |
| CTLV | 0.04 | 0.12 | 99.21 | 0.00 | 0.08 | 0.00 | 99.45 |
| DRO | 1.91 | 2.39 | 0.01 | 92.91 | 2.67 | 0.10 | 99.99 |
| SW | 0.01 | 2.12 | 0.03 | 0.01 | 97.83 | 0.00 | 100 |
| EC | 1.20 | 2.08 | 0.00 | 5.62 | 0.13 | 90.90 | 99.93 |
Table 6.
Model size and Time. Value of model size denotes the total size of the model parameters. Value of time denotes the average time of processing per scan line on the test dataset. In the unidirectional mode and the bidirectional mode, scan lines are processed in batch. In the scan line-by-scan line (SLSL) unidirectional mode, scan lines are processed in sequence with the same model parameters as the unidirectional mode, which means that segmentation results of the unidirectional mode and SLSL unidirectional mode are the same.
Table 6.
Model size and Time. Value of model size denotes the total size of the model parameters. Value of time denotes the average time of processing per scan line on the test dataset. In the unidirectional mode and the bidirectional mode, scan lines are processed in batch. In the scan line-by-scan line (SLSL) unidirectional mode, scan lines are processed in sequence with the same model parameters as the unidirectional mode, which means that segmentation results of the unidirectional mode and SLSL unidirectional mode are the same.
| Mode | Model Size (MB) | Time (ms) |
|---|
| unidirectional | 1.11 | 1.80 |
| bidirectional | 1.74 | 1.95 |
| unidirectional (SLSL) | 1.11 | 8.99 |
Table 7.
Comparison of different settings of region size threshold .
Table 7.
Comparison of different settings of region size threshold .
| Settings of | Unidirectional Mode | Bidirectional Mode |
|---|
| mIoU (%) | OA (%) | mIoU (%) | OA (%) |
|---|
| 0.5 | 84.29 | 97.80 | 88.73 | 98.35 |
| 2 | 77.73 | 96.32 | 82.47 | 95.96 |
| 7 | 87.99 | 96.95 | 90.24 | 97.85 |
| 0.5, 7 | 95.10 | 99.17 | 97.09 | 99.52 |
| 0.5, 2, 7 | 96.12 | 99.36 | 97.17 | 99.54 |
Table 8.
Comparison of the results with multi-scale feature extraction () in the non-feature fusion mode, the unidirectional mode, and the bidirectional mode.
Table 8.
Comparison of the results with multi-scale feature extraction () in the non-feature fusion mode, the unidirectional mode, and the bidirectional mode.
| Mode | mIoU (%) | OA (%) |
|---|
| non-feature fusion | 93.53 | 98.29 |
| unidirectional | 96.12 | 99.36 |
| bidirectional | 97.17 | 99.54 |