Laser Spot Center Location Method for Chinese Spaceborne GF-7 Footprint Camera
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specifications of GF-7 Footprint Camera
2.2. Laser Spot Center Location Method of GF-7 Satellite
2.2.1. Geometric Registration Model
2.2.2. Brightness Conversion Model
2.3. Introduction to the Experimental Data
3. Results and Discussion
3.1. Evaluation Metric
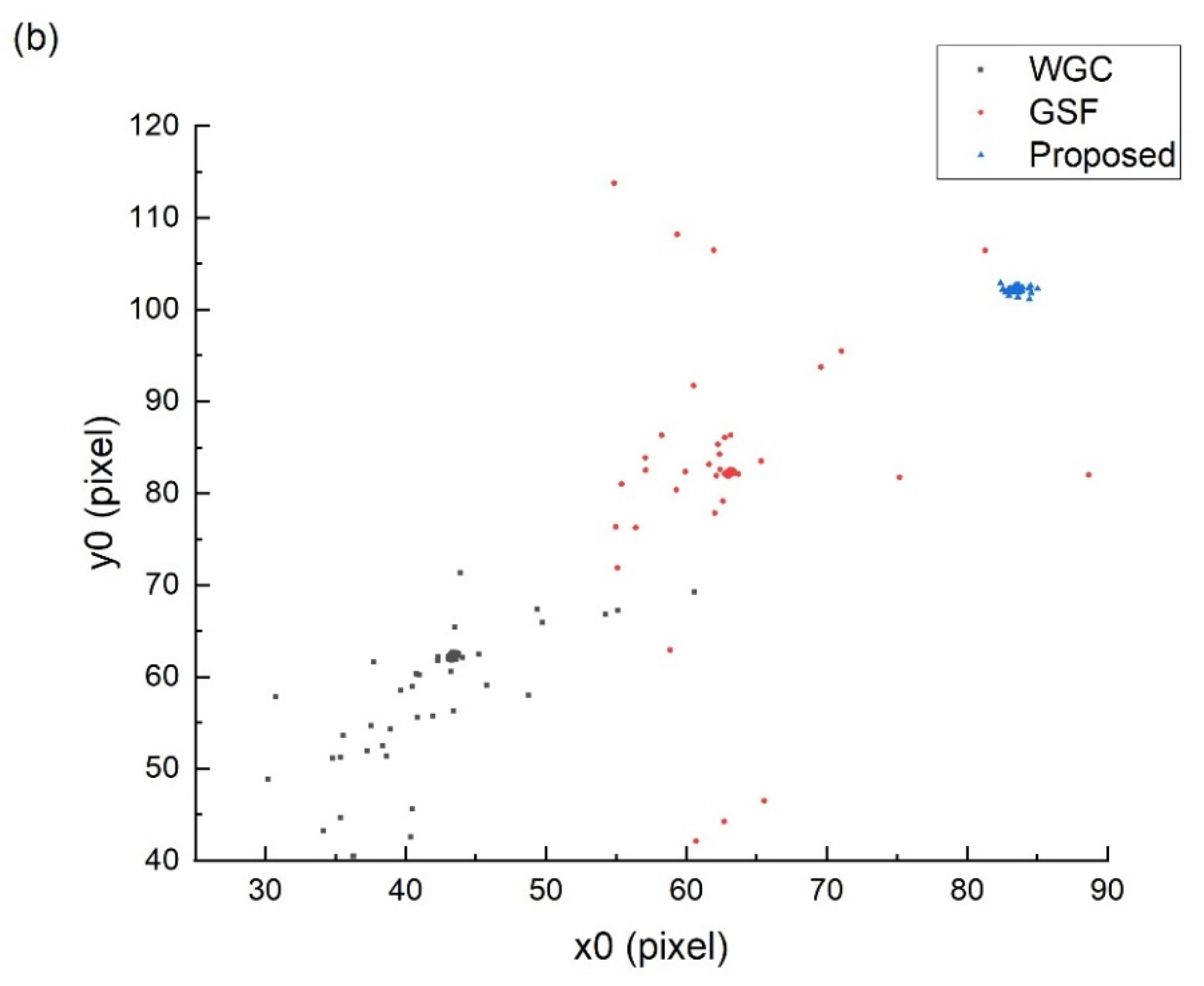
3.2. Validation of the Accuracy of Geometric Registration
3.3. Validation of the Positioning Accuracy of the Laser Spot Center
- (1)
- The first type is that the epipolar error is consistent with the RMSE of image EI and EIII, which basically does not exceed 0.3 pixel. By analyzing the specific processing process, it is found that the results of this type are all based on the feature matching to complete the geometric registration. Therefore, after positioning the fitted spot center to the footprint image, its epipolar error is consistent with the RMSE of footprint image EI and EIII.
- (2)
- The second type is that the epipolar error exceeds the RMSE of image EI and EIII but does not exceed 0.7 pixel. The results of this type are based on template matching to complete the geometric registration, and the accuracy of the spot center positioning is consistent with the template accuracy.
- (3)
- The third type is the epipolar error exceeds 1 pixel. In Figure 12, a part of the spot images with an epipolar distance error more than 2 pixels is deleted for the convenience display. The epipolar error of this type is too large because its geometric registration process fails. The reason for geometric registration failure is that the original image is covered by clouds, shadows, or the image lacks texture information.
4. Conclusions
- (1)
- The fitting accuracy of the spot center is mainly affected by the geometric registration accuracy. The epipolar error of the spot center based on the feature matching method is less than 0.3 pixel. The epipolar error of the spot center based on the template matching method is less than 0.7 pixel.
- (2)
- The results of this method are more reliable. The epipolar error can effectively represent the accuracy of the spot center, and the results with epipolar errors exceeding 1 pixel will be eliminated and cannot be used for the combined adjustment of laser altimeter and stereo images.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tang, X.; Xie, J.; Wang, X.; Jiang, W. High-Precision Attitude Post-Processing and Initial Verification for the ZY-3 Satellite. Remote Sens. 2015, 7, 111–134. [Google Scholar] [CrossRef]
- Li, R.; Niu, X.; Liu, C.; Wu, B.; Deshpande, S. Impact of Imaging Geometry on 3D Geopositioning Accuracy of Stereo Ikonos Imagery. Photogramm. Eng. Remote Sens. 2009, 75, 1119–1125. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Xu, K.; Jia, P.; Hao, X.; Li, D. Integrating Stereo Images and Laser Altimeter Data of the ZY3-02 Satellite for Improved Earth Topographic Modeling. Remote Sens. 2019, 11, 2453. [Google Scholar]
- Abshire, J.B.; Sun, X.; Riris, H.; Sirota, M.; Palm, S.; Ketchum, E.A. Geoscience laser altimeter system (GLAS) on the ICESat mission: Pre-launch and on-orbit measurement performance. In Proceedings of the Conference on Lasers and Electro-Optics 2003, Baltimore, MD, USA, 1–6 June 2003. [Google Scholar]
- Shan, J.; Yoon, J.-S.; Lee, D.S.; Kirk, R.L.; Neumann, G.A.; Acton, C.H. Photogrammetric Analysis of the Mars Global Surveyor Mapping Data. Photogramm. Eng. Remote Sens. 2005, 71, 97–108. [Google Scholar] [CrossRef]
- Tang, X.; Xie, J.F.; Fu, X.K.; Mo, F.; Li, S.N.; Dou, X. ZY3-02 Laser Altimeter On-orbit Geometrical Calibration and Test. Acta Geod. Et Cartogr. Sin. 2017, 46, 714–723. [Google Scholar]
- Xie, J.; Tang, X.; Mo, F.; Tang, H.; Wang, Z.; Wang, X.; Liu, Y.; Tian, S.; Liu, R.; Xia, X. In-orbit geometric calibration and experimental verification of the ZY3-02 laser altimeter. Photogramm. Rec. 2018, 33, 341–362. [Google Scholar]
- Kong, B.; Wang, Z.; Tan, Y. Algorithm of Laser Spot Detection Based on Circle Fitting. Infrared Laser Eng. 2002, 31, 275–279. [Google Scholar]
- Wang, Z.; Xu, R.; Hu, B. Algorithm of Semicircular Laser Spot Detection Based on Circle Fitting. Laser Infrared 2013, 43, 708–711. [Google Scholar]
- Zhou, P.; Wang, X.; Huang, Q.; Ma, C. Laser Spot Center Detection Based on Improved Circled Fitting Algorithm. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018. [Google Scholar]
- Zhu, J.; Xu, Z.; Fu, D.; Hu, C. Laser Spot Center Detection and Comparison Test. Photonic Sens. 2018, 9, 49–52. [Google Scholar] [CrossRef] [Green Version]
- Feng, X. Fast Algorithms on Center Location of Two Dimensional Gaussian Distribution Spot. Acta Opt. Sin. 2012, 32, 0512002. [Google Scholar] [CrossRef]
- Wang, L.L.; Hu, Z.-W.; Ji, H.-X. Laser spot center location algorithm based on Gaussian fitting. J. Appl. Opt. 2012, 33, 985–990. [Google Scholar]
- Zhang, H.; Li, G.; Zhang, Y.; Hu, S. Spot centroid extraction algorithm based on three-dimensional arctangent function fitting. Infrared Laser Eng. 2019, 48, 226001. [Google Scholar]
- Wang, D.; Liao, Y.; Min, Z. Analysis of Precisions of Parameters Calculated by Ellipse Fitting in Double Beam Interferometer. Acta Opt. Sin. 2016, 36, 0312002. [Google Scholar]
- Tang, Y.; Gu, G.; Qian, W.; Chen, Q.; Zhang, J. Laser spot center location algorithm of four-quadrant detector based on Gaussian distribution. Infrared Laser Eng. 2017, 46, 206003. [Google Scholar] [CrossRef]
- Wang, H.Y.; Pan, D.L.; Xia, D.S. Fast algorithm for two-dimensional Otsu adaptive threshold algorithm. J. Image Graph. 2007, 33, 969–970. [Google Scholar]
- Rother, C.; Kolmogorov, V.; Blake, A. “GrabCut”: Interactive foreground extraction using iterated graph cuts. Acm Trans. Graph. 2004, 23, 309–314. [Google Scholar] [CrossRef]
- Sun, X.; Xu, T.; Zhang, J.; Zhao, Z.; Li, Y. An Automatic Multi-Target Independent Analysis Framework for Non-Planar Infrared-Visible Registration. Sensors 2017, 17, 1696. [Google Scholar] [CrossRef] [Green Version]
- Ayaz, S.M.; Khan, D.; Kim, M.Y. Three-Dimensional Registration for Handheld Profiling Systems Based on Multiple Shot Structured Light. Sensors 2018, 18, 1146. [Google Scholar] [CrossRef] [Green Version]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Wu, C. SiftGPU: A GPU Implementation of Scale Invariant Feature Transform (SIFT). Available online: http://ccwu.me/vsfm/ (accessed on 21 February 2020).
- Siddique, M.A.; Sarfraz, S.M.; Bornemann, D.; Hellwich, O. Automatic registration of SAR and optical images based on mutual information assisted Monte Carlo. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1813–1816. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. Acm 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Taguchi, Y.; Jian, Y.D.; Ramalingam, S.; Chen, F. Point-plane SLAM for hand-held 3D sensors. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Kai, T.; Grand, S.P.; Niu, F. Full-waveform inversion of triplicated data using a normalized-correlation-coefficient-based misfit function. Geophys. J. Int. 2017, 210, 1517–1524. [Google Scholar]
- Hsieh, C.; Huang, Y.; Chen, Y.; Fuh, C.; Ho, W. Video Super-resolution by Integrating SAD and NCC matching criterion for multiple moving objects. In Proceedings of the 10th IASTED International Conference on Computer Graphics and Imaging, Innsbruck, Austria, 13–15 February 2008. [Google Scholar]
- Moulon, P.; Duisit, B.; Monasse, P. Global Multiple-View Color Consistency. In Proceedings of the CVMP, London, UK, 6–7 November 2013; p. 00873517. [Google Scholar]
- Agarwal, S.; Mierle, K. Ceres Solver. Available online: http://ceres-solver.org (accessed on 24 February 2020).







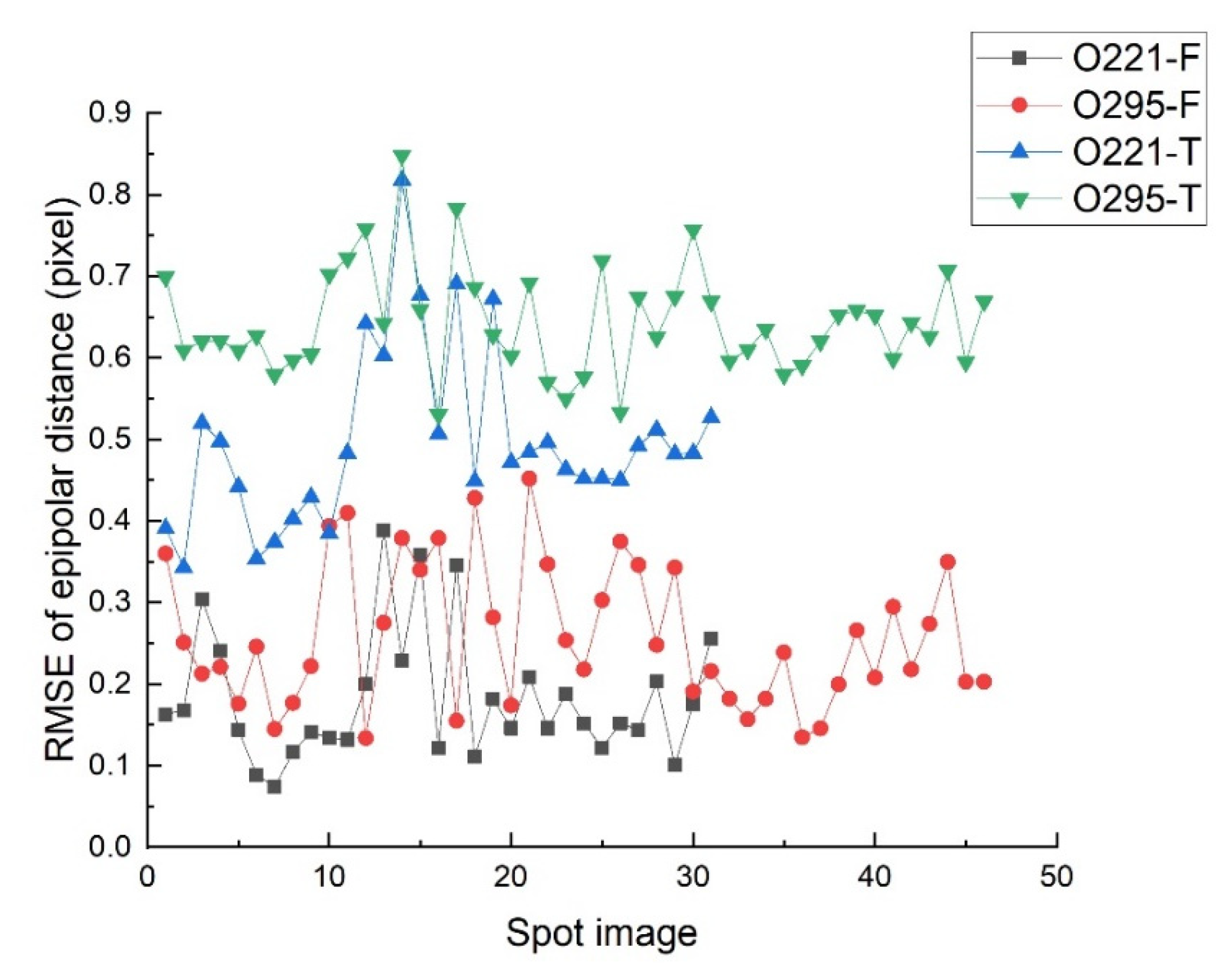




| Method | Max Error (pixel) | Min Error (pixel) | Average Error (pixel) |
|---|---|---|---|
| O221-F | 0.389 | 0.073 | 0.182 |
| O221-T | 0.818 | 0.343 | 0.495 |
| O295-F | 0.452 | 0.134 | 0.259 |
| O295-T | 0.848 | 0.530 | 0.643 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, C.; Xie, J.; Zhi, X.; Yang, Y.; Yang, S. Laser Spot Center Location Method for Chinese Spaceborne GF-7 Footprint Camera. Sensors 2020, 20, 2319. https://doi.org/10.3390/s20082319
Ren C, Xie J, Zhi X, Yang Y, Yang S. Laser Spot Center Location Method for Chinese Spaceborne GF-7 Footprint Camera. Sensors. 2020; 20(8):2319. https://doi.org/10.3390/s20082319
Chicago/Turabian StyleRen, Chaofeng, Junfeng Xie, Xiaodong Zhi, Yun Yang, and Shuai Yang. 2020. "Laser Spot Center Location Method for Chinese Spaceborne GF-7 Footprint Camera" Sensors 20, no. 8: 2319. https://doi.org/10.3390/s20082319





