An Ultra-Short Baseline Underwater Positioning System with Kalman Filtering
Abstract
:1. Introduction
- (1)
- Considering the error source and its impact on the positioning results, we present the Kalman filter-based, non-equidistant quaternary array. We organically combine the Kalman filtering and array element to accurately capture the acoustic signals.
- (2)
- During the USBL positioning process, we utilize an array element and a corresponding processing method to eliminate the ambiguity problem of a phase difference, which can improve the accuracy of our proposed USBL positioning system.
- (3)
- Based on the capture of the acoustic signal and calculation of the phase difference, we present an ultra-short baseline underwater positioning system with Kalman filtering to enhance the positioning accuracy.
2. Related Works
2.1. The Array Types
2.2. Positioning Methods
3. The USBL Positioning System Based on Kalman Filtering
3.1. The Framework of the USBL Positioning Method Based on Kalman Filtering
3.1.1. Array Deployment
3.1.2. Kalman Filtering
3.1.3. Positioning Computing
3.2. Array Deployment
3.2.1. Traditional Array
3.2.2. Non-Equidistant, Quaternary Array
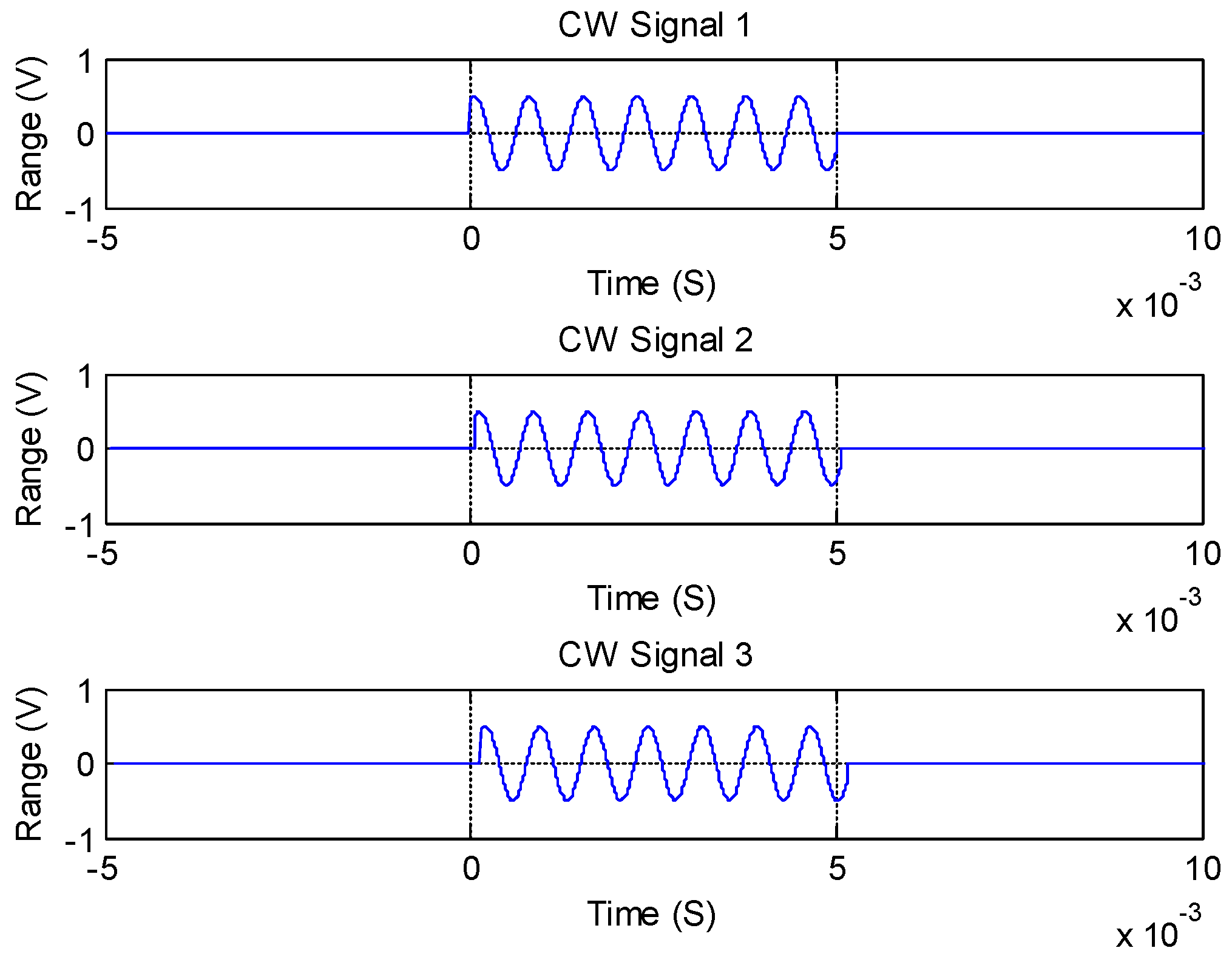
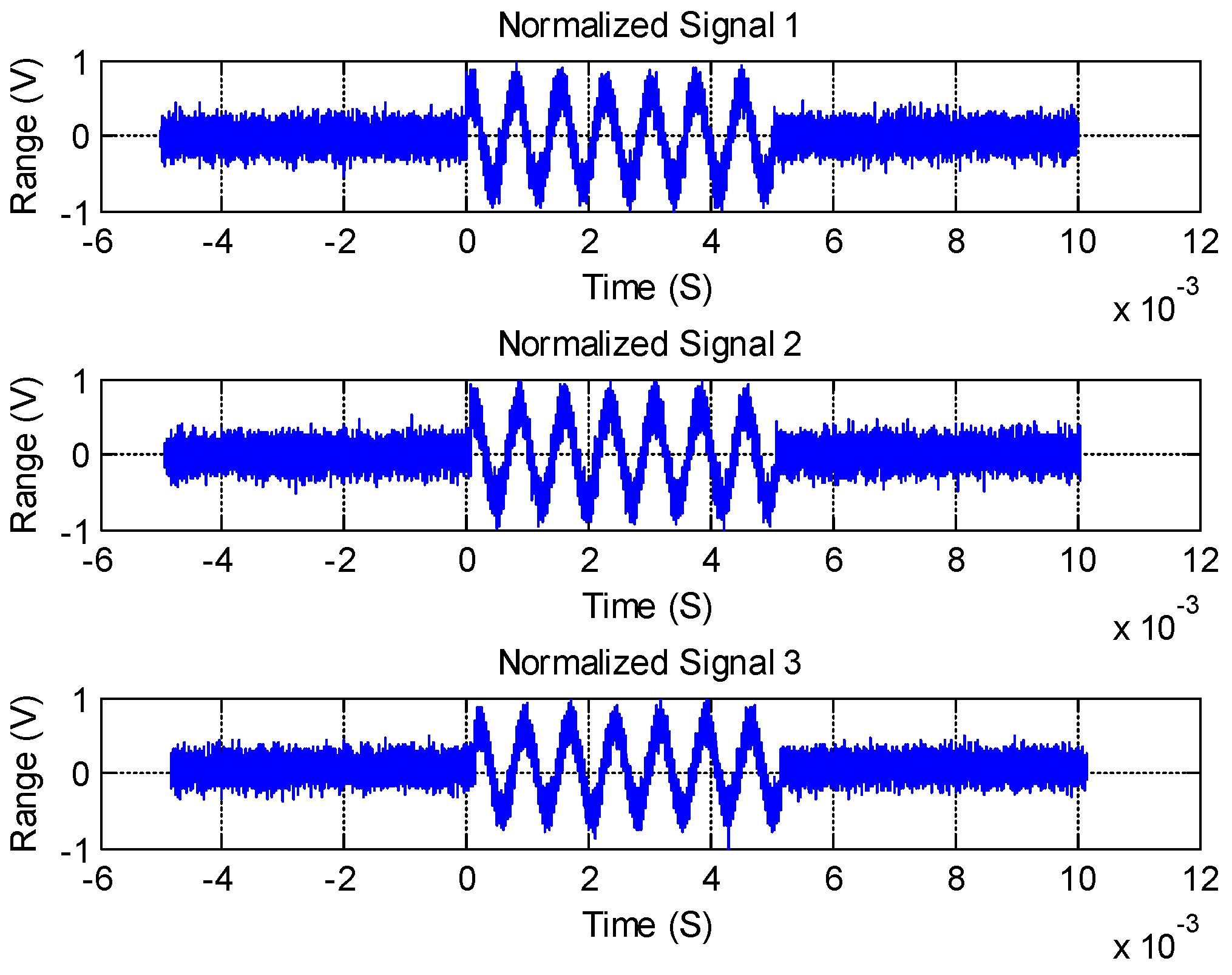
3.3. Signal Noise Reduction
3.4. Positioning Computing
3.4.1. Positioning Principle
3.4.2. Ambiguity Problem Solution for the Phase Difference
4. Performance Evaluation and Analysis
4.1. Evaluation Environment Setup
4.1.1. Evaluation Design
4.1.2. Parameters Setting
4.1.3. Evaluation Metrics
4.1.4. Reference Methods
4.2. Impact Analysis of Sampling Frequency on Positioning Accuracy
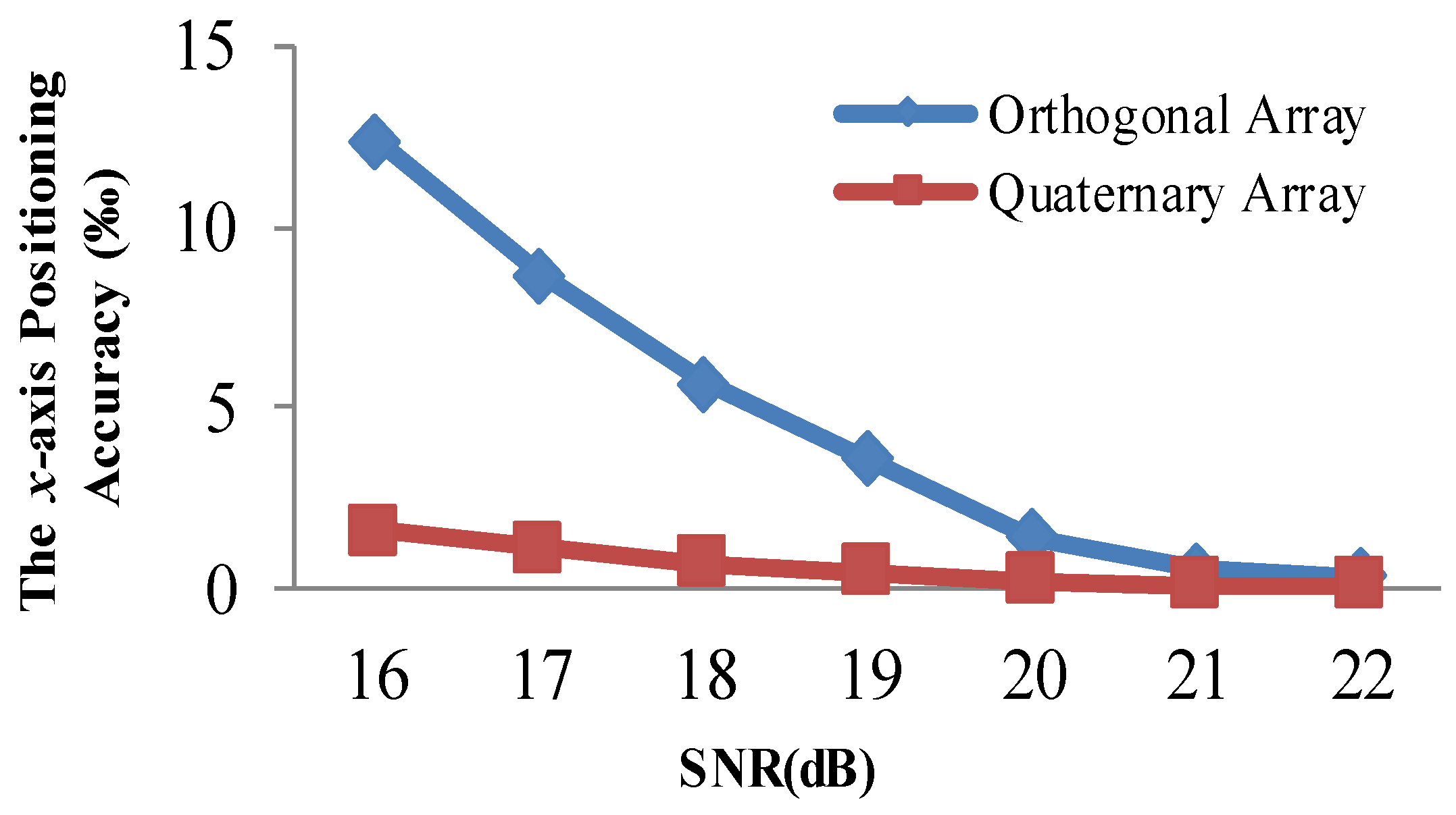
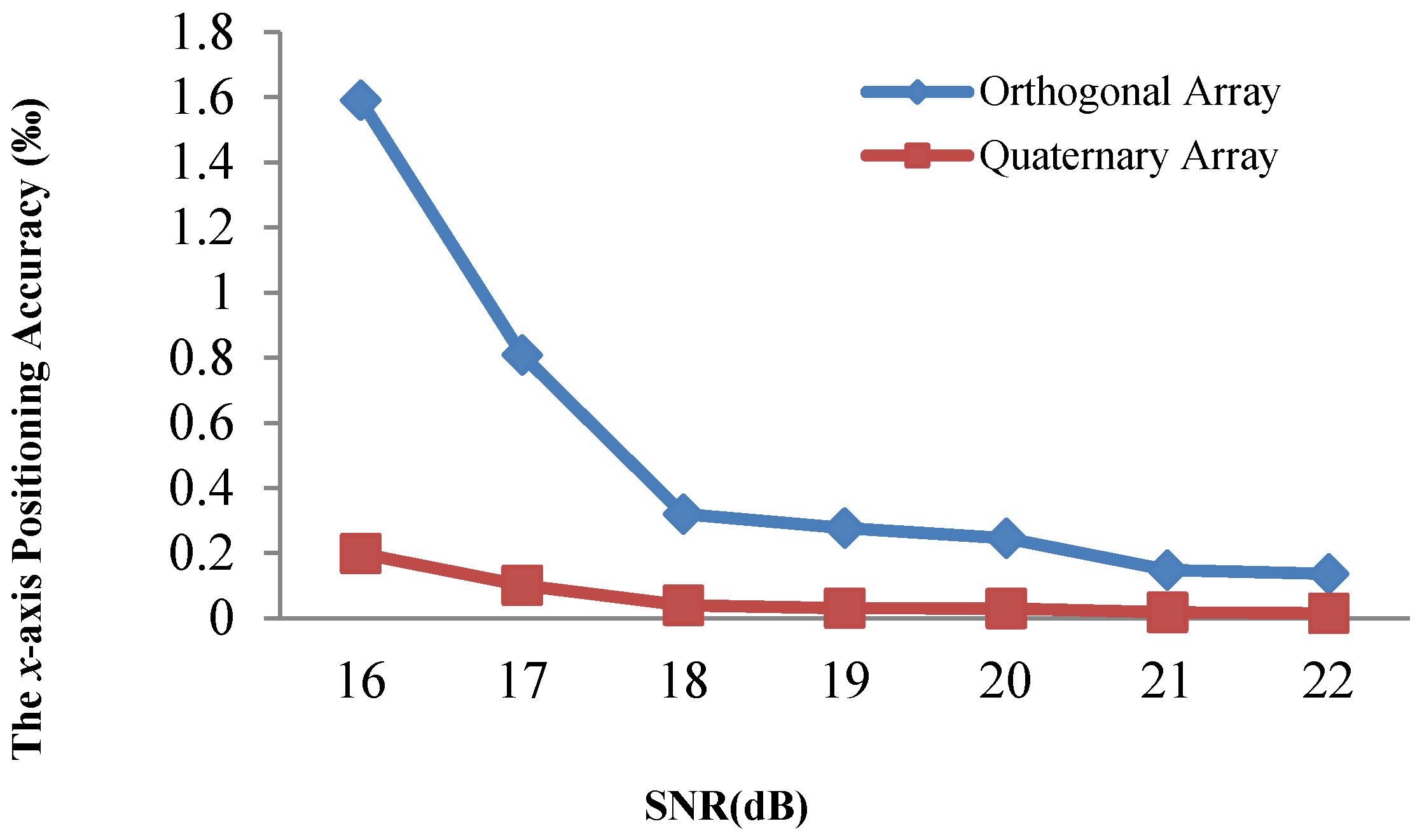
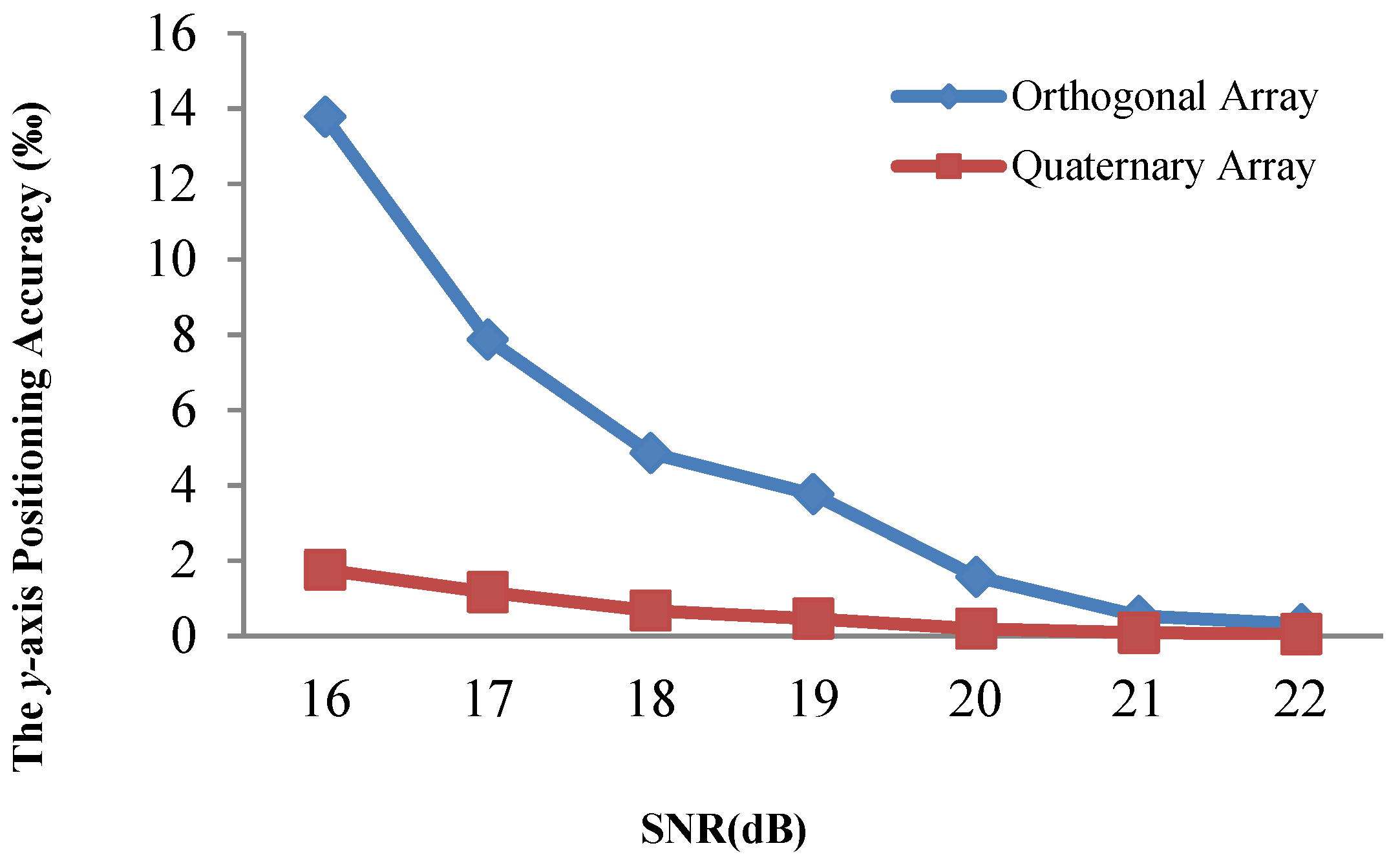
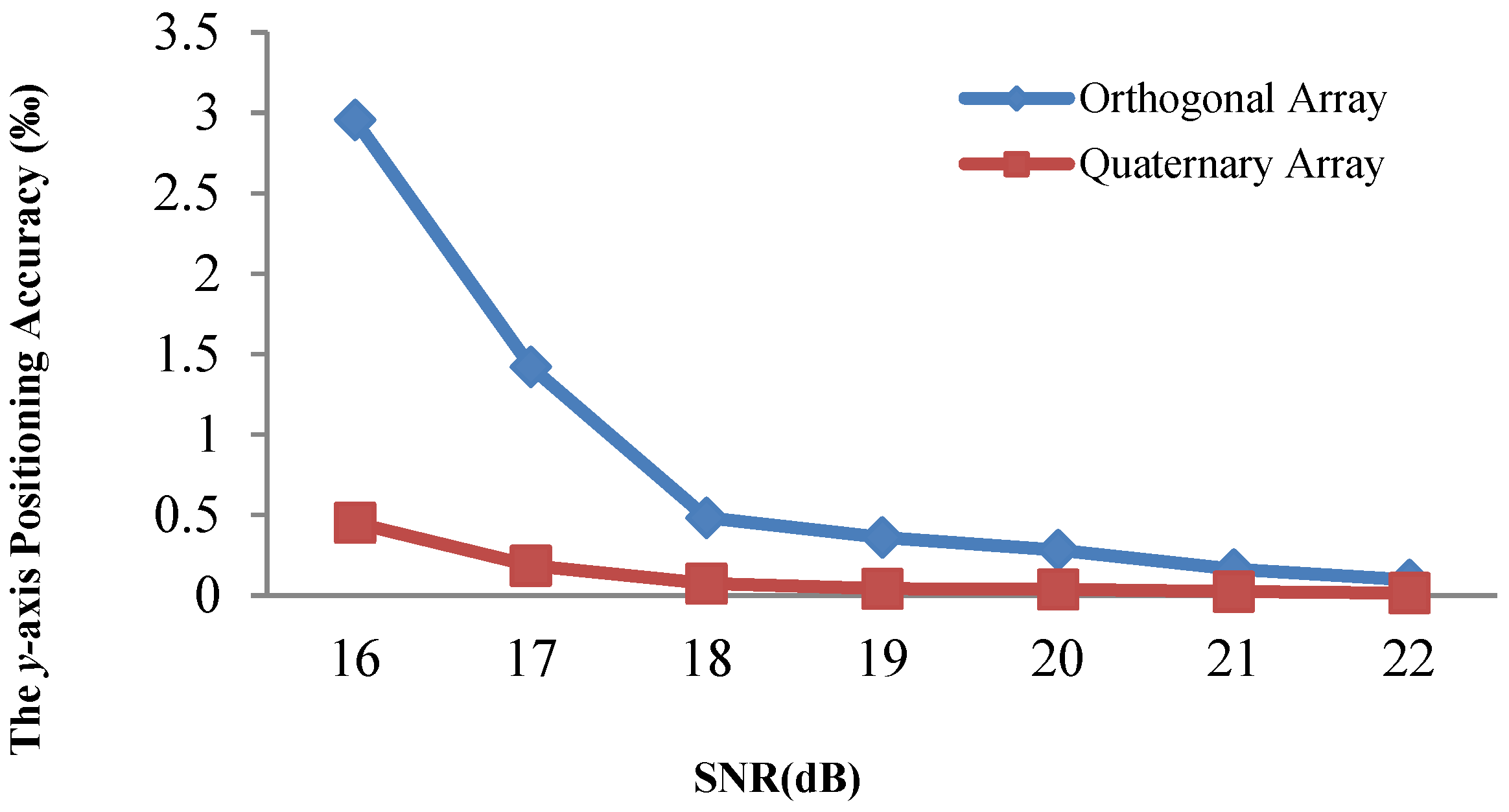
4.3. Positioning Accuracy Evaluation with Traditional Array
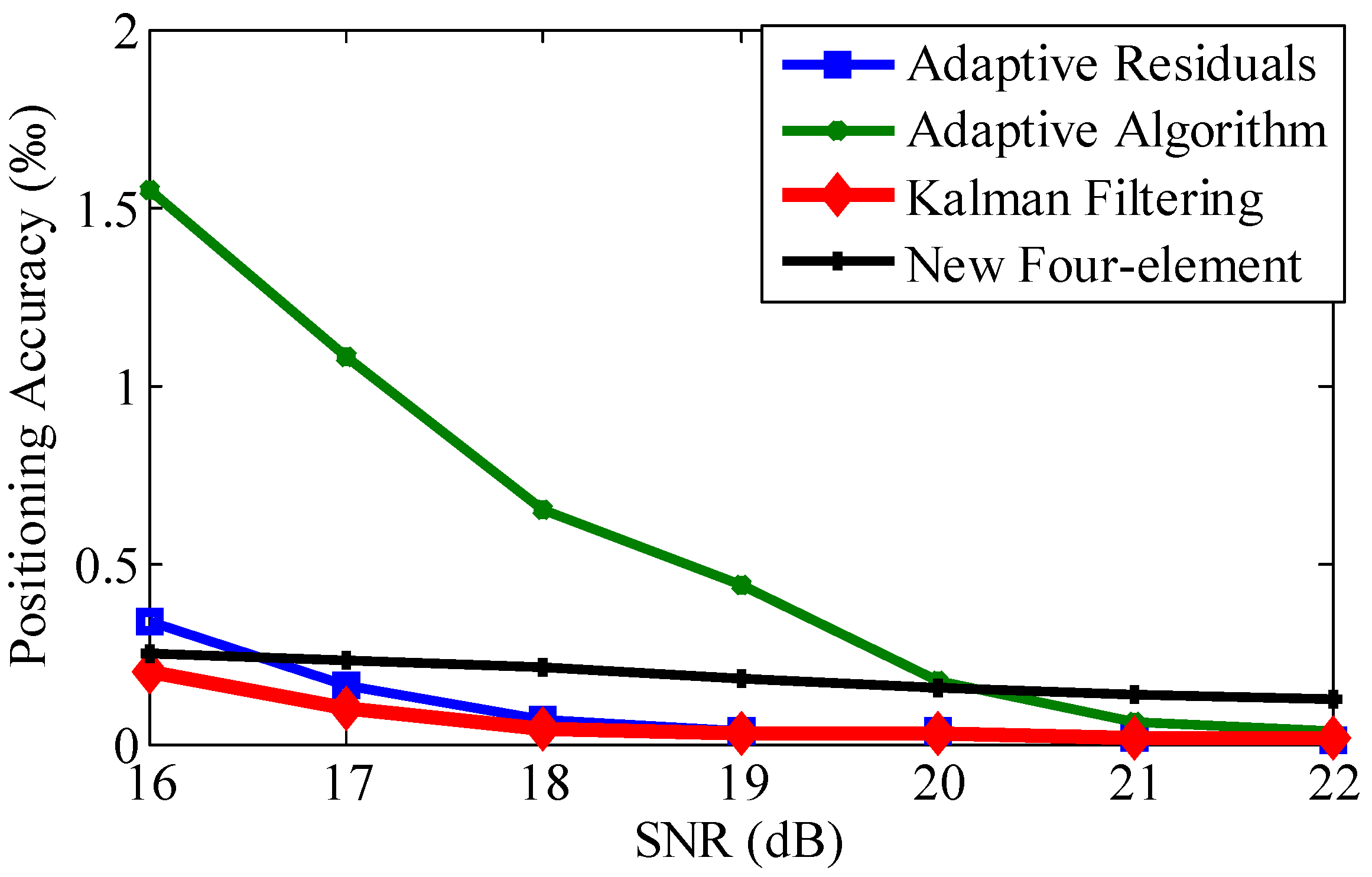
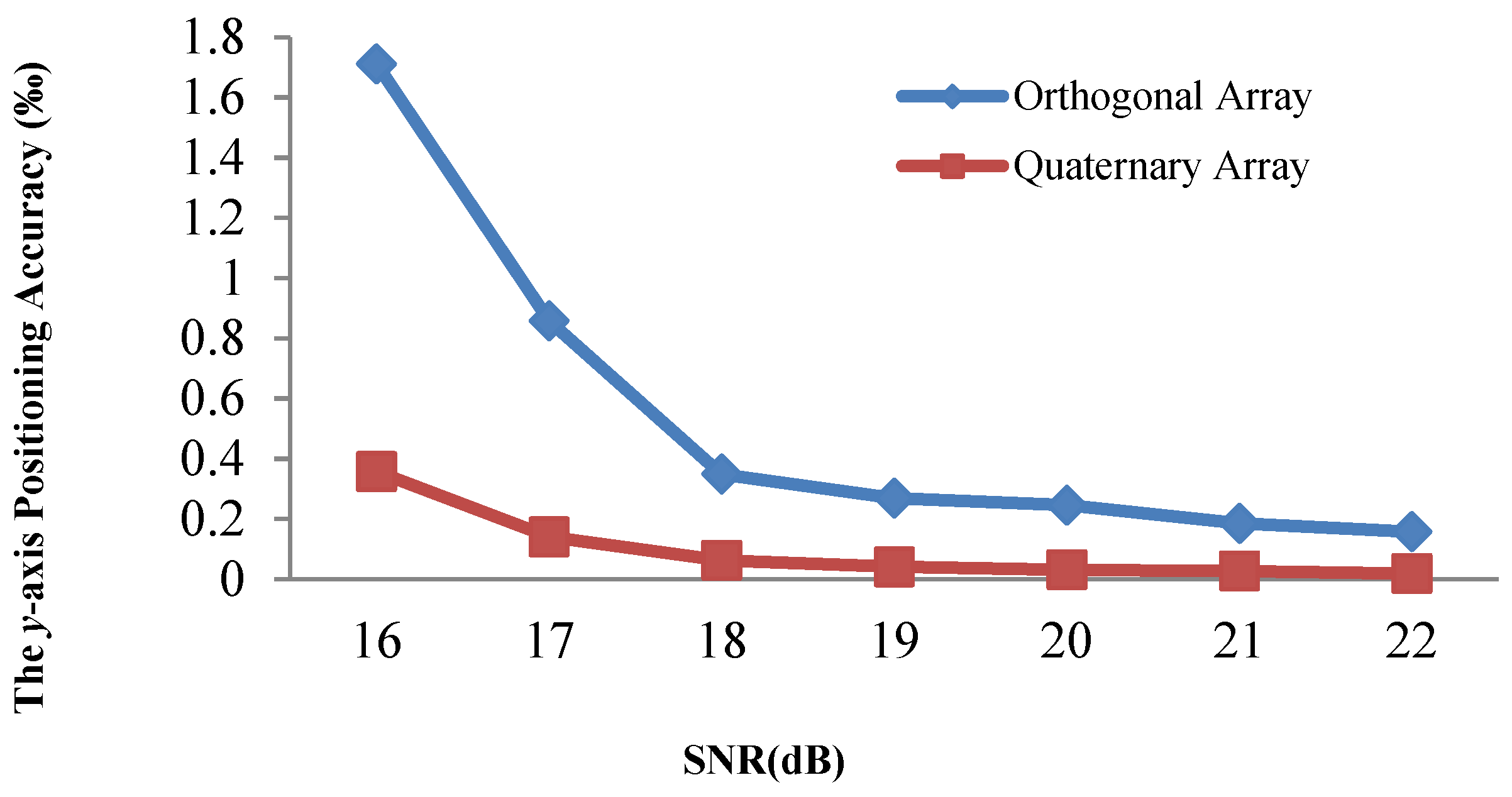
4.4. Positioning Accuracy Evaluation with a Quaternary Array
4.5. Positioning Efficiency Evaluation
4.6. Discussion
4.6.1. Discussion on Array Type
4.6.2. Discussion on the Positioning Accuracy of Different Methods
4.6.3. Discussion on the Generalization of the Proposed Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| LBL | Long Baseline |
| SBL | Short Baseline |
| USBL | Ultra-Short Baseline |
| SDN | Software-Defined Networking |
| AUVs | Autonomous Underwater Vehicles |
| UWNs | Underwater Wireless Networks |
| DVL | Doppler Velocity Log |
References
- Yao, Y.; Xu, X.; Yang, D.; Xu, X. An IMM-UKF aided SINS/USBL calibration solution for underwater vehicles. IEEE Trans. Veh. Technol. 2020, 69, 3740–3747. [Google Scholar] [CrossRef]
- Tong, J.; Xiaosu, X.; Zhang, T.; Liang, Z.; Yao, L. Study on installation error analysis and calibration of acoustic transceiver array based on SINS/USBL integrated system. IEEE Access 2018, 6, 66923–66939. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, T.; Jin, B.; Zhu, Y.; Tong, J. Student’s t-based robust kalman filter for a SINS/USBL integration navigation strategy. IEEE Sens. J. 2020, 20, 5540–5553. [Google Scholar] [CrossRef]
- Zhao, L.; Kang, Y.; Cheng, J.; Wu, M. A fault-tolerant polar grid SINS/DVL/USBL integrated navigation algorithm based on the centralized filter and relative position measurement. Sensors 2019, 19, 3899. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Gu, Q.; Chen, Y.; Sun, G.; Huang, H. A combined ray tracing method for improving the precision of the USBL positioning system in smart ocean. Sensors 2018, 18, 3586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joon, C.H.; Sang-Ki, J.; Dae-Hyeong, J.; Tran, N.-H.; Vu, M.T.; Choi, H. Study on control system of integrated unmanned surface vehicle and underwater vehicle. Sensors 2020, 20, 2633. [Google Scholar]
- Keisaku, T.; Shingo, Y.; Tomoya, T.; Saito, T. Multipath error reduction for underwater acoustic direction of arrival estimation. In Proceedings of the OCEANS 2019 MTS/IEEE Seattle, Seattle, WA, USA, 27–31 October 2019; pp. 1–4. [Google Scholar]
- Xu, Y.; Liu, W.; Ding, X.; Lv, P.; Feng, C.; He, B.; Yan, T. USBL positioning system based adaptive kalman filter in AUV. In Proceedings of the 2018 OCEANS—MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–4. [Google Scholar]
- Tong, J.; Xu, X.; Hou, L.; Li, Y.; Wang, J.; Zhang, L. An ultra-short baseline positioning model based on rotating array & reusing elements and its error analysis. Sensors 2019, 19, 4373. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, Z.; Shan, R.; He, K.; Zhao, S. Research into the integrated navigation of a deep-sea towed vehicle with USBL/DVL and pressure gauge. Appl. Acoust. 2020, 159, 107052. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, T.; Jin, B.; Xu, X.X. Technology of SINS/USBL highly tightly coupled integrated navigation based on phase dif-ference measurements. In Proceedings of the 2019 DGON Inertial Sensors and Systems, Braunschweig, Germany, 10–11 September 2019. [Google Scholar]
- Sun, D.; Ding, J.; Zheng, C.; Huang, W. An underwater acoustic positioning algorithm for compact arrays with arbitrary con-figuration. IEEE J. Sel. Top. Signal Process. 2019, 13, 120–130. [Google Scholar] [CrossRef]
- Sun, D.; Ding, J.; Zheng, C.; Huang, W. Angular misalignment calibration method for ultra-short baseline positioning system based on matrix decomposition. IET Radar Sonar Navig. 2019, 13, 456–463. [Google Scholar] [CrossRef]
- Tong, J.; Xu, X.; Zhang, T.; Li, Y.; Yao, Y.; Weng, C.; Hou, L.; Zhang, L. A misalignment angle error calibration method of underwater acoustic array in strapdown inertial navigation system/ultrashort baseline integrated navigation system based on single transponder mode. Rev. Sci. Instrum. 2019, 90, 085001. [Google Scholar] [CrossRef] [PubMed]
- Min, Y. Research on long range ultra short baseline system. Ph.D. Thesis, Harbin Engineer University, Harbin, China, 2006. [Google Scholar]
- Md, K.; Sagarika, M.; Bikramaditya, D. UWB Saleh–Valenzuela model for underwater acoustic sensor network. Int. J. Inf. Technol. 2020, 12, 1073–1083. [Google Scholar] [CrossRef]
- Rossi, P.S.; Ciuonzo, D.; Ekman, T.; Dong, H. Energy detection for MIMO decision fusion in underwater sensor networks. IEEE Sens. J. 2015, 15, 1630–1640. [Google Scholar] [CrossRef]
- Lin, C.; Han, G.J.; Guizani, M.; Bi, Y.; Du, J.; Shu, L. An SDN architecture for AUV-based underwater wireless networks to enable cooperative under-water Search. IEEE Wirel. Commun. 2020, 27, 132–139. [Google Scholar] [CrossRef]
- Zheng, E.; Chen, X.; Sun, C.; Yu, H. An innovation four-element array to achieve high-precision positioning of the ul-tra-short baseline. Appl. Acoust. 2013, 32, 15–22. [Google Scholar]
- Luo, Q.H.; Ju, C.Y.; Yan, X.Z.; Hu, C.; Wang, C.T.; Din, J.F. Accurate underwater localization through phase difference. In Proceedings of the 2020 IEEE International Conference on Smart Internet of Things (SmartIoT), Beijing, China, 14–16 August 2020; pp. 38–42. [Google Scholar]
- Mikhail, A.; Leon, H.D. A design method and algorithm for USBL systems with skew three-element arrays. Int. J. Circuits Syst. Signal Process. 2011, 5, 382–390. [Google Scholar]
- Wu, X.; Bao, G.; Tao, C.; Gu, C.; Zhang, K. Ultra-short baseline underwater acoustic location data processing. J. Hangzhou Dianzi Univ. 2011, 31, 53–56. [Google Scholar]
- Huang, M.; Feng, H.; Pan, X.; Liu, B. A method to improve the positioning accuracy of USBL positioning system. Tech. Acoust. 2013, 32, 281–283. [Google Scholar]
- Huang, Y.; Zhang, Y. A new process uncertainty robust student’s t based kalman filter for SINS/GPS integration. IEEE Access 2017, 5, 14391–14404. [Google Scholar] [CrossRef]
- Xiong, J.; Shu, L.; Wang, Q.; Xu, W.; Zhu, C. A scheme on indoor tracking of ship dynamic positioning based on distrib-uted multi-sensor data fusion. IEEE Access 2017, 5, 379–392. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Chen, L.; Yan, Y. Underwater positioning algorithm based on SINS/LBL integrated system. IEEE Access 2018, 6, 7157–7163. [Google Scholar] [CrossRef]






| Symbol | Quantity | Value or Means |
|---|---|---|
| R | Target slant distance | 3000 m |
| c | Acoustic velocity | 1500 m/s |
| d | Adjacent array spacing | 40 mm < 0.5 λ |
| L | Maximum array spacing | 8 d = 320 mm |
| f0 | Transponder frequency | 1.35 kHz |
| fs | Sampling frequency | 2000 kHz |
| Tw | Pulse width | 5 ms |
| SNR | Signal-to-noise ratio (SNR) | 20 dB |
| Symbol | Means | Setting |
|---|---|---|
| f0 | Transponder frequency | 1.35 kHz |
| fs | Sampling frequency | 2000 kHz |
| SNR | Signal-to-noise ratio | 16 dB–22 dB |
| d | Element distance | 10 mm |
| SNR (dB) | 16 | 17 | 18 | 19 | 20 | 21 | 22 | Improvement |
|---|---|---|---|---|---|---|---|---|
| Adaptive Algorithm | 12.3937 | 8.6505 | 5.6543 | 3.5464 | 1.3875 | 0.4869 | 0.3025 | 81.57% |
| Adaptive Residuals | 2.7354 | 1.3014 | 0.4495 | 0.2836 | 0.2578 | 0.1453 | 0.0922 | 9.34% |
| Kalman Filtering | 1.5905 | 0.8085 | 0.3197 | 0.2768 | 0.2456 | 0.1483 | 0.1367 | - |
| SNR (dB) | 16 | 17 | 18 | 19 | 20 | 21 | 22 | Improvement |
|---|---|---|---|---|---|---|---|---|
| Adaptive Algorithm | 1.5492 | 1.0813 | 0.6569 | 0.4433 | 0.1734 | 0.0609 | 0.0378 | 82.49% |
| Adaptive Residuals | 0.3419 | 0.1627 | 0.0687 | 0.0367 | 0.0322 | 0.0182 | 0.0115 | 16.14% |
| New Four-Element | 0.2502 | 0.2334 | 0.2127 | 0.1850 | 0.1537 | 0.1355 | 0.1242 | 70.97% |
| Kalman Filtering | 0.1988 | 0.1011 | 0.0400 | 0.0308 | 0.0295 | 0.0185 | 0.0151 | - |
| Positioning Method | Adaptive Residuals | Adaptive Algorithm | New Four-Element | Kalman Filtering |
|---|---|---|---|---|
| Positioning time (s) | 552 | 11 | 1.2 | 48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Q.; Yan, X.; Ju, C.; Chen, Y.; Luo, Z. An Ultra-Short Baseline Underwater Positioning System with Kalman Filtering. Sensors 2021, 21, 143. https://doi.org/10.3390/s21010143
Luo Q, Yan X, Ju C, Chen Y, Luo Z. An Ultra-Short Baseline Underwater Positioning System with Kalman Filtering. Sensors. 2021; 21(1):143. https://doi.org/10.3390/s21010143
Chicago/Turabian StyleLuo, Qinghua, Xiaozhen Yan, Chunyu Ju, Yunsai Chen, and Zhenhua Luo. 2021. "An Ultra-Short Baseline Underwater Positioning System with Kalman Filtering" Sensors 21, no. 1: 143. https://doi.org/10.3390/s21010143
APA StyleLuo, Q., Yan, X., Ju, C., Chen, Y., & Luo, Z. (2021). An Ultra-Short Baseline Underwater Positioning System with Kalman Filtering. Sensors, 21(1), 143. https://doi.org/10.3390/s21010143





