Calibrating Range Measurements of Lidars Using Fixed Landmarks in Unknown Positions
Abstract
:1. Introduction
1.1. Literature Review
- Certain assumptions about the sensor movement and about the surrounding environment, in which the calibration process is shaped as joint parameters and state estimation, for example, lidar calibration from linear motion [10].
- Another strategy for substituting ground truth information with some other information is to implement appropriate sensor fusion strategies, i.e., to combine redundant information from independent distance sensors. Such a strategy has been used in [10,11], where approximated Expectation Maximization (EM) procedures (in the former) and Markov chain Monte Carlo (MCMC) techniques under Bayesian frameworks (in the later) are used for joint parameter and state estimation combining information from lidars, odometry, and ultrasound sensors. Calibrating the intrinsic parameters of one beam based on other beams of rotating multi-beam lidar attracted large amount of research, for example, in [12,13,14,15]. We note that sensor fusion is a vast topic and there are many publications on calibrating other sensors, for example, magnetometer calibration using inertial sensors in [16], camera and IMU calibration in [17], and lidar and camera calibration in [18]. However, here, we are interested only in calibration that is related to lidars.
- The last strategy is to use assumptions on the environment, for example, odometer calibration with localization [19]. Another example is to use the planar feature in the environment to calibrate lidars. Originally plane-based calibration was presented for calibrating airborne lidars in [20,21]. Then, the authors of [22] introduced a mathematical model and static calibration for the Velodyne HDL-64E lidar using planar feature and least squares solution. The authors of [23] calibrated a 3D lidar for both the geometric and temporal parameters based on Rényi Quadratic Entropy to formulate an optimization problem that maximizes the quality of the point cloud.
- triangulation, where the position is determined through measuring the angles between the sensing device and the known landmarks (see, e.g., in [24]);
1.2. Statement of Contributions
1.3. Organization of the Manuscript
2. Problem Formulation
- (A1)
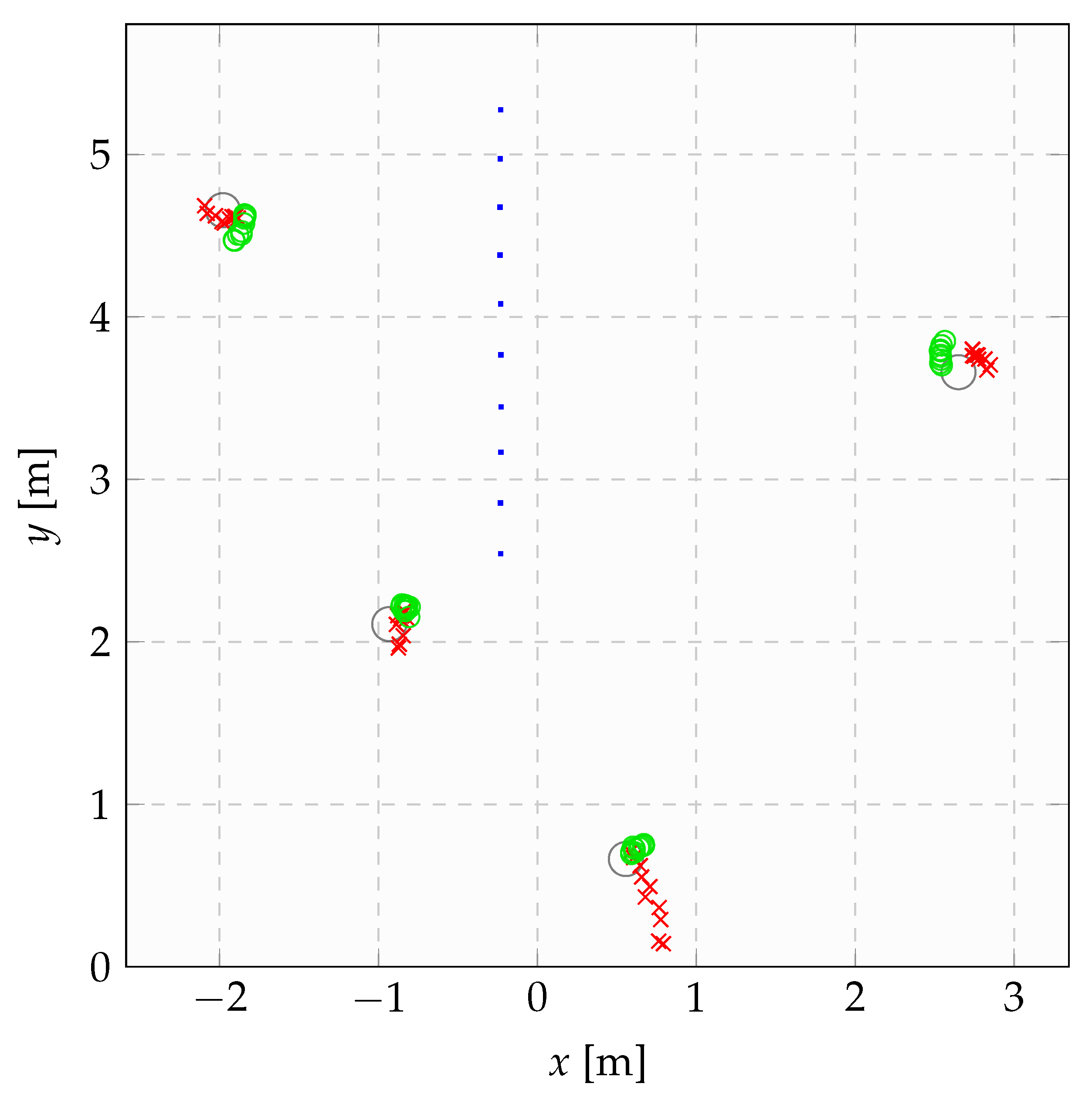
- The environment from which we collect the measurements to be used for the calibration process has particular structures that produce easily recognizable features in the sensor readings. For example, the situation is as in Figure 3, where corners and poles produce clear features in the 2D plane of the measurements. Note that this means that our strategy cannot work in environments that miss these easily recognizable structures (such as natural places like deserts, or flat areas without trees). However, generally we consider applications where robots shall move precisely in the surroundings, and this calls for objects to be avoided. If there are no such obstacles/structures then the need for precise calibration becomes feeble. Given this, without loss of generality we require static and detectable landmarks; in this paper, we will use cylinders with known radius, but it could be anything as long as we have a detector for it.
- (A2)
- The sensor measurements lie in a 2D plane that is parallel to the ground. Moreover, the objects that produce the above mentioned features develop orthogonally w.r.t. the ground. This implies that the distances measurements are not affected by tilt effects. This requirement may not hold in generic situations; however, our envisioned calibration strategy is to be carried out within a building, where the conditions above hold. The problem of removing these assumptions is considered as a potential future extension.
- (A3)
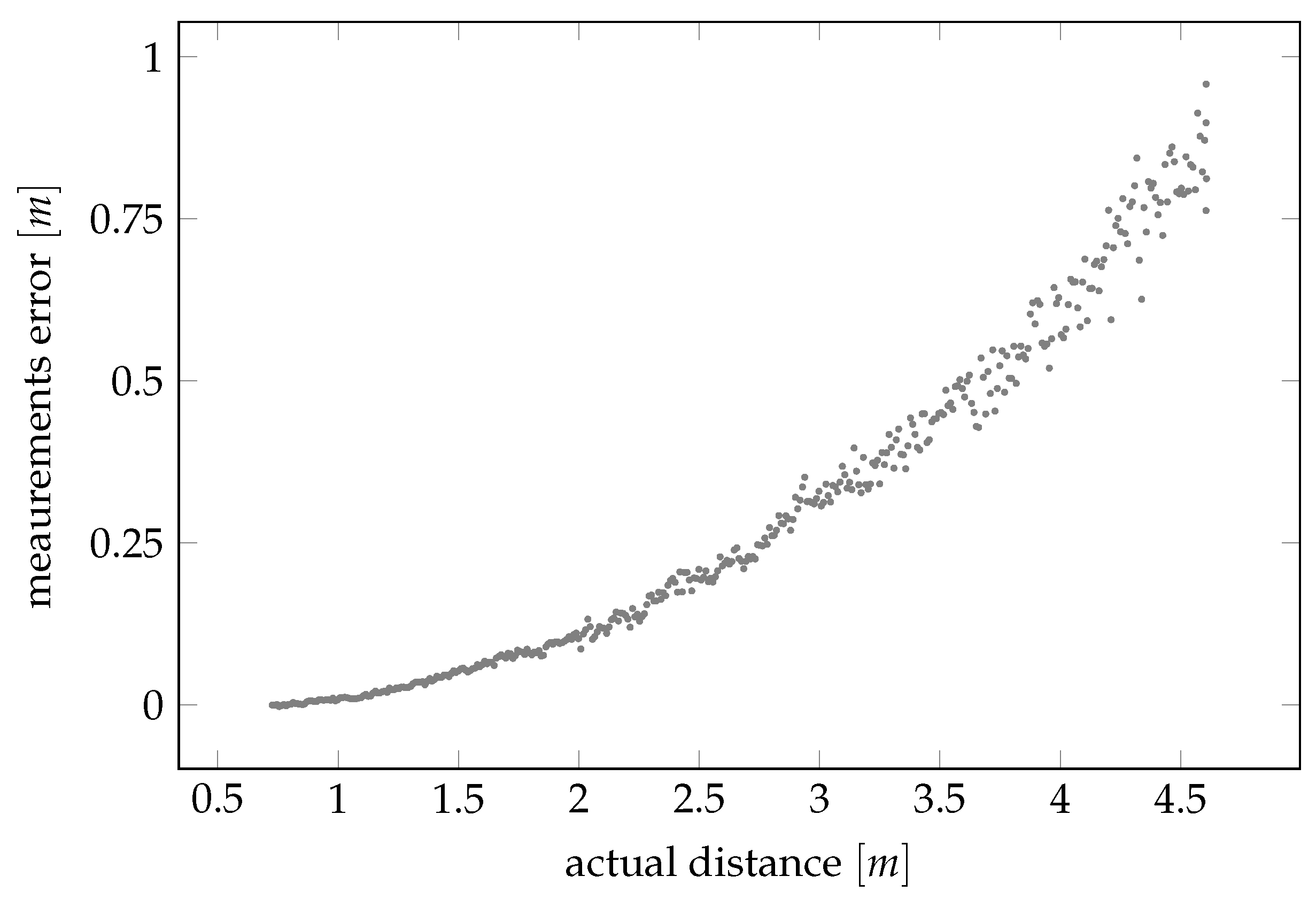
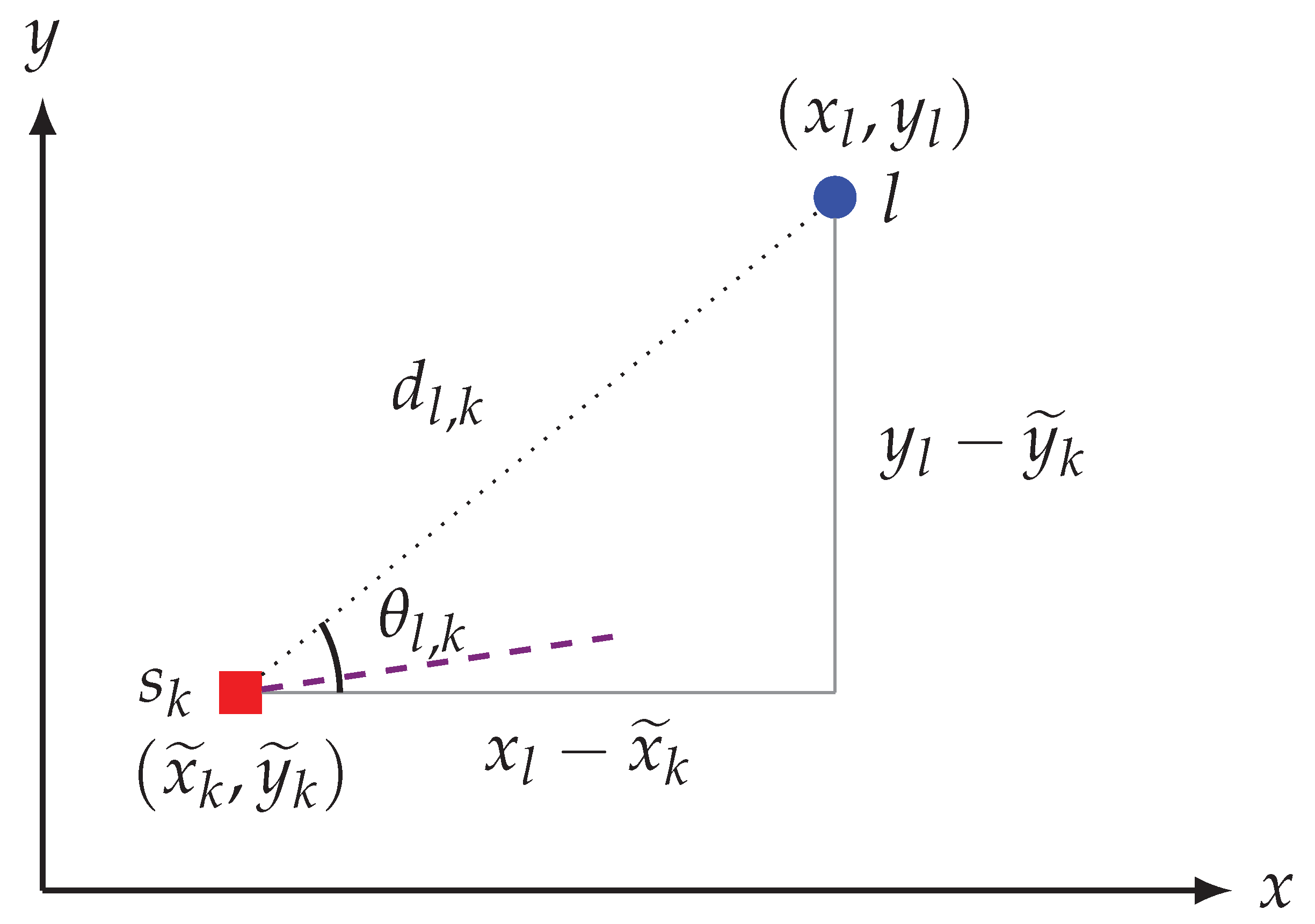
- The statistical model underlying the distance readings contains heteroskedastic noise (for which the variance of the noise increases with the actual distance that shall be measured) and a bias whose amplitude also increases with the distance above. More specifically, we will focus on the situation where there exist objects in the environment, and places where the sensor can be placed. We then let and be, respectively, the Cartesian coordinates of the L objects and of the K sensor positions. Accordingly, the actual distance between the sensor position k and the object placement l isWe then assume that the distance readings are distributed as the polynomial modelwith iid. The model parameters are thus , , with n being the corresponding model order (hereafter assumed for simplicity equal for both the bias and noise terms, i.e., ). Note that in the following we may also use a simplified distance model that, for the sake of numerical tractability, neglects the heteroskedastic term in (3) so that the model reduces toWe will refer to this model as to the “simplified distance model”.
- (A4)
- Finally, we also assume that the angular readings are noisy measurements of the actual angles from which the object l is seen by the sensor at position k with respect to the reference frame of the horizontal axis. More precisely, we assumewhere the measurement noise is iid. Note that in practice this is a simplificative assumption that we use for analytical tractability reasons and that, a posteriori, is motivated by the numerical results we got during our experiments (For the sake of precision, it would be more formally correct to model the angle measurement noise through a Von Mises distribution with circular mean and noncircular concentration parameter. However, such a distribution converges to a normal one as the concentration parameter grows larger. In our case thus the approximation is justified in practice). Note, moreover, that this assumption implies that is an unknown parameter of the model. We also assume that the error characteristics of (3)–(5) are time-invariant and do not depend on the absolute positions of the landmark (while they obviously depend on the relative distances “sensor vs. obstacle”). The angle is thus the sum of the angle from which the object l is seen by the sensor with respect to the robot reference frame, plus the robot heading angle plus the rotation angle of the lidar’s internal coordinate system with the robot coordinate system which is assumed to be a known constant. Note also that the measurement noise in (5) incorporates imprecisions in the knowledge of the robot heading and rotation angle.
- (P1)
- design a statistically optimal or near-optimal (in the Mean Squared Error (MSE) sense) algorithm that can be computed using closed-form expressions, and that can simultaneously estimate: the sensor coordinates for each sampling position k, the position of the objects for each object l, the model order and the model parameters vector above;
- (P2)
- quantitatively characterize the statistical performance of these estimators using appropriate mathematical analysis and field tests.
3. A Triangulateration Strategy for Calibrating Distance Sensors
- Assume to know that there exist L landmarks, and to be able to identify and label them at each time instant from the raw measurements stream;
- place the sensor in a finite number of ideally equally spaced positions along an ideally straight line (say where );
- estimate the 2D positions of the L landmarks in the inertial frame based on the sensor angle measurements only, using the strategy defined in Section 3.1 below; and
- given the estimated landmark positions above, and the measured distances , estimate the model order and model parameters (i.e., do the actual sensor calibration step) with the strategy proposed in Section 3.2 below.
3.1. Estimating the 2D Positions of Circular Landmarks
3.2. Calibrating the Sensor
- phase#1: model parameters estimation. After obtaining the estimates of the distances between the sensor and landmarks, estimate the parameters casting the problem as a linear regression on (26) and the measurement vector for model orders , where is a user-defined parameter. This means solving for each potential n the problemwhich has the closed-form solutionNote that, once again, the estimator is unbiased; however, due to the simplification of the noise term in (3) (i.e., ignoring the heteroskedastic part of the noise), will not be efficient.
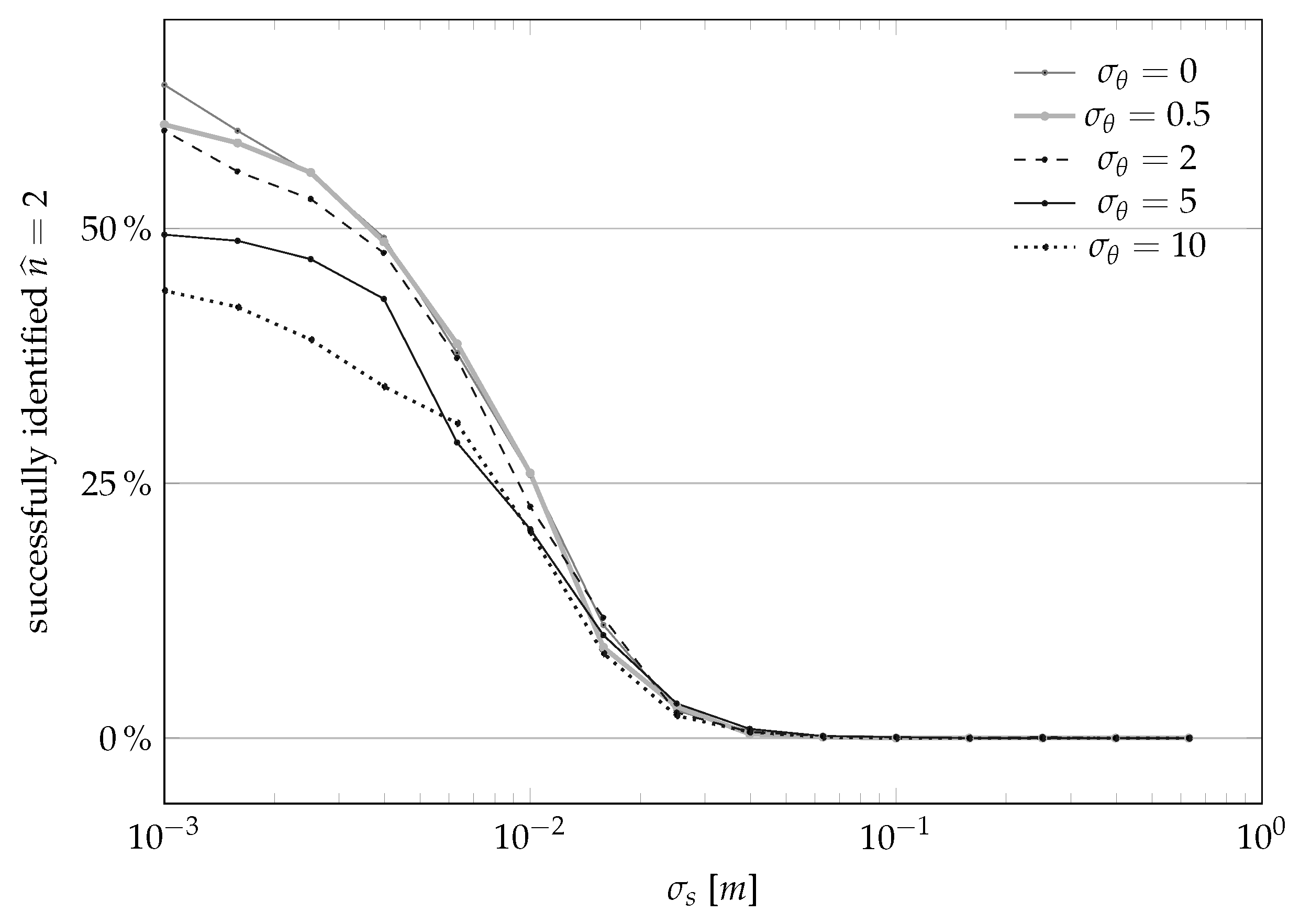
- phase#2: model order selection. We note that there exist various alternatives for selecting the optimal model order : fitting opportune test sets, using crossvalidation, or also using model order selection criteria, for example, AIC. In the setups we considered for this paper we actually found that the model order selection problem has quite clear solutions, implying that all the various alternatives clearly indicated the very same number (see Section 4), implying in its turn that for our specific case all the various approaches tend to give equivalent results. It may, however, be that in other cases different strategies lead to different results;
- phase#3: filtering new measurements. Once the model order selection and the model parameters estimation problems are solved, this means rewriting the “object distance vs. sensor reading” measurement model (3) aswhere is the raw measurement, and d is the actual distance. To estimate d from and the trained model one should thus invert (29). This inversion is not immediate; for example, one may solve the Least Squares (LS)-type optimization problemwhich requires finding the roots of a polynomial of order . Thus, despite its apparent simplicity, the problem of finding polynomial roots requires numerical methods for polynomial orders greater than 3.
4. Numerical Results
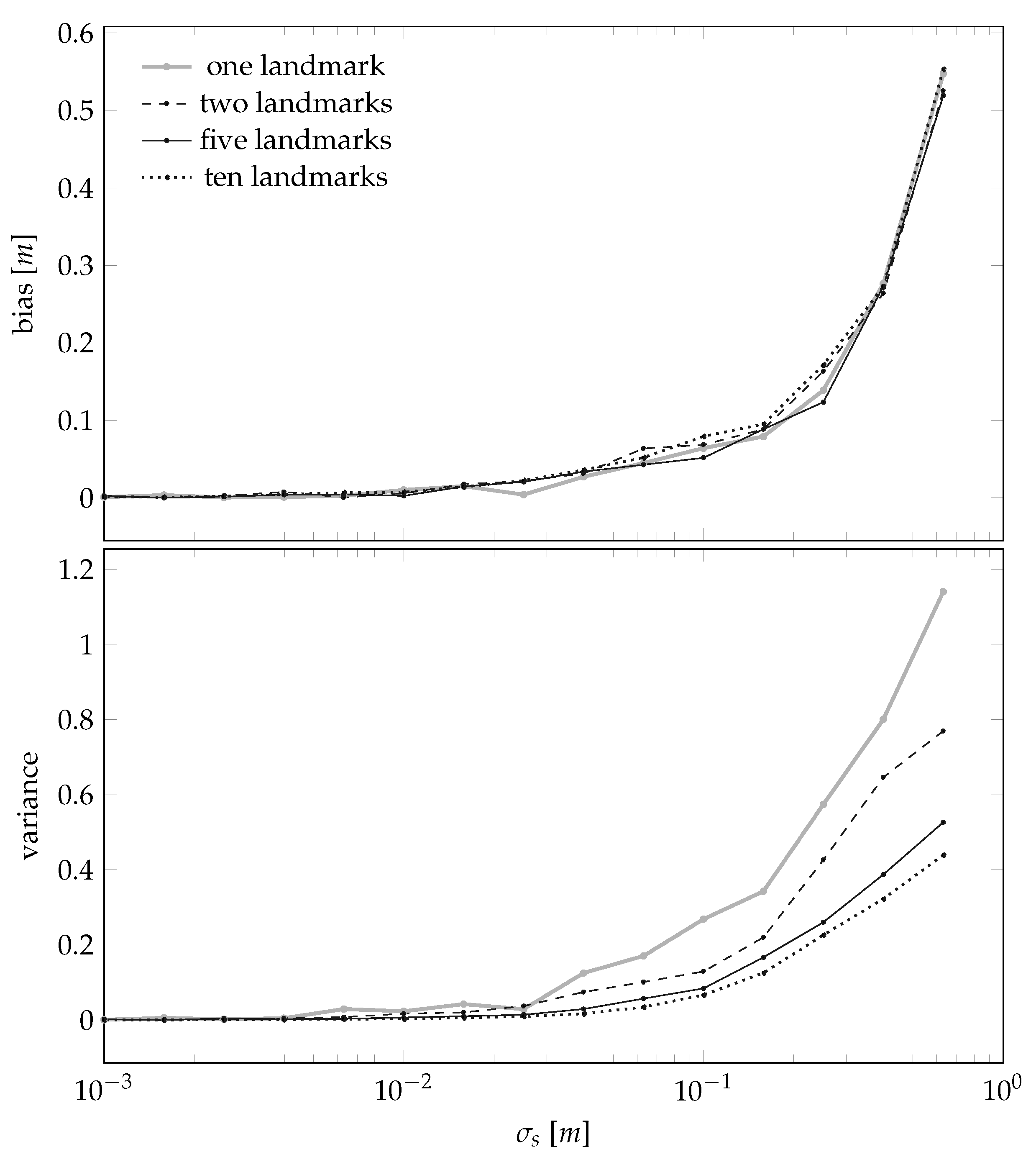
4.1. Analyzing the Statistical Properties of the Landmark Position Estimator through Simulation Results
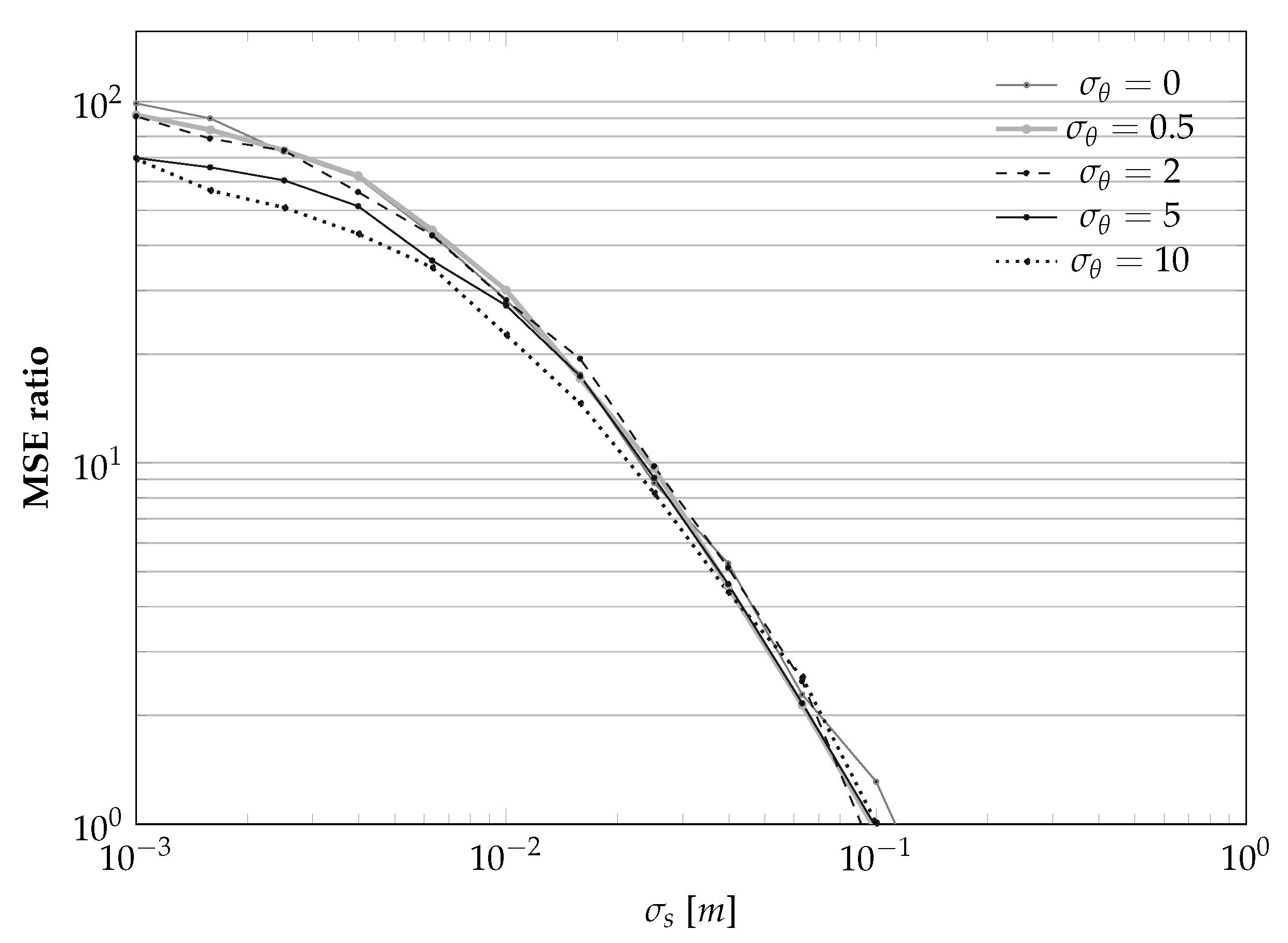
4.2. Analyzing the Statistical Properties of the Sensor Calibration Procedure through Simulation Results
4.3. Field Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Organization for Standardization. Uncertainty of Measurement-Part 3: Guide to the Expression of Uncertainty in Measurement (GUM: 1995); ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Alhashimi, A. Statistical Sensor Calibration Algorithms. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2018. [Google Scholar]
- Schwarz, B. LIDAR: Mapping the world in 3D. Nat. Photonics 2010, 4, 429–430. [Google Scholar] [CrossRef]
- Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial LiDAR technology in forest science: Application fields, benefits and challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef] [Green Version]
- Akay, A.E.; Oğuz, H.; Karas, I.R.; Aruga, K. Using LiDAR technology in forestry activities. Environ. Monit. Assess. 2009, 151, 117–125. [Google Scholar] [CrossRef] [PubMed]
- Burguera, A.; González, Y.; Oliver, G. Sonar sensor models and their application to mobile robot localization. Sensors 2009, 9, 10217–10243. [Google Scholar] [CrossRef]
- Noykov, S.; Roumenin, C. Calibration and interface of a polaroid ultrasonic sensor for mobile robots. Sens. Actuators Phys. 2007, 135, 169–178. [Google Scholar] [CrossRef]
- Dogruer, C.U. Online identification of odometer parameters of a mobile robot. In Proceedings of the International Joint Conference SOCO’14-CISIS’14-ICEUTE’14, Bilbao, Spain, 25–27 June 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 195–206. [Google Scholar]
- Karam, S.; Vosselman, G.; Peter, M.; Hosseinyalamdary, S.; Lehtola, V. Design, Calibration, and Evaluation of a Backpack Indoor Mobile Mapping System. Remote Sens. 2019, 11, 905. [Google Scholar] [CrossRef] [Green Version]
- Alhashimi, A.; Varagnolo, D.; Gustafsson, T. Calibrating Distance Sensors for Terrestrial Applications Without Groundtruth Information. IEEE Sens. J. 2017, 17, 3698–3709. [Google Scholar] [CrossRef] [Green Version]
- Alhashimi, A.; Del Favero, S.; Varagnolo, D.; Gustafsson, T.; Pillonetto, G. Bayesian strategies for calibrating heteroskedastic static sensors with unknown model structures. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2447–2453. [Google Scholar]
- Muhammad, N.; Lacroix, S. Calibration of a rotating multi-beam lidar. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 5648–5653. [Google Scholar]
- Levinson, J.; Thrun, S. Unsupervised calibration for multi-beam lasers. In Experimental Robotics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 179–193. [Google Scholar]
- Sheehan, M.; Harrison, A.; Newman, P. Automatic self-calibration of a full field-of-view 3D n-laser scanner. In Experimental Robotics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 165–178. [Google Scholar]
- Nouira, H.; Deschaud, J.E.; Goulette, F. Point cloud refinement with a target-free intrinsic calibration of a mobile multi-beam LiDAR system. In Proceedings of the ISPRS Congress 2016 International Society for Photogrammetry and Remote Sensing, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Kok, M.; Schön, T.B. Magnetometer calibration using inertial sensors. IEEE Sens. J. 2016, 16, 5679–5689. [Google Scholar] [CrossRef] [Green Version]
- Rehder, J.; Siegwart, R. Camera/IMU calibration revisited. IEEE Sens. J. 2017, 17, 3257–3268. [Google Scholar] [CrossRef]
- Zhou, L. A new minimal solution for the extrinsic calibration of a 2D LIDAR and a camera using three plane-line correspondences. IEEE Sens. J. 2013, 14, 442–454. [Google Scholar] [CrossRef]
- Martinelli, A.; Tomatis, N.; Siegwart, R. Simultaneous localization and odometry self calibration for mobile robot. Auton. Robot. 2007, 22, 75–85. [Google Scholar] [CrossRef]
- Filin, S. Recovery of systematic biases in laser altimetry data using natural surfaces. Photogramm. Eng. Remote Sens. 2003, 69, 1235–1242. [Google Scholar] [CrossRef]
- Skaloud, J.; Lichti, D. Rigorous approach to bore-sight self-calibration in airborne laser scanning. ISPRS J. Photogramm. Remote Sens. 2006, 61, 47–59. [Google Scholar] [CrossRef]
- Glennie, C.; Lichti, D.D. Static calibration and analysis of the Velodyne HDL-64E S2 for high accuracy mobile scanning. Remote Sens. 2010, 2, 1610–1624. [Google Scholar] [CrossRef] [Green Version]
- Sheehan, M.; Harrison, A.; Newman, P. Self-calibration for a 3D laser. Int. J. Robot. Res. 2012, 31, 675–687. [Google Scholar] [CrossRef] [Green Version]
- Hartley, R.I.; Sturm, P. Triangulation. Comput. Vis. Image Underst. 1997, 68, 146–157. [Google Scholar] [CrossRef]
- Manolakis, D.E. Efficient solution and performance analysis of 3-D position estimation by trilateration. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1239–1248. [Google Scholar] [CrossRef]
- Alwan, N.A.S.; Mahmood, A.S. On Gradient Descent Localization in 3-D Wireless Sensor Networks. J. Eng. 2015, 21, 85–97. [Google Scholar]
- Berle, F. Mixed triangulation/trilateration technique for emitter location. In IEE Proceedings F (Communications, Radar and Signal Processing); IET: London, UK, 1986; Volume 133, pp. 638–641. [Google Scholar]
- Thomas, N.J.; Cruickshank, D.G.M.; Laurenson, D.I. Performance of a TDOA-AOA hybrid mobile location system. In Proceedings of the Second International Conference on 3G Mobile Communication Technologies, London, UK, 26–28 March 2001; pp. 216–220. [Google Scholar] [CrossRef]
- Leonard, J.J.; Durrant-Whyte, H.F. Mobile robot localization by tracking geometric beacons. IEEE Trans. Robot. Autom. 1991, 7, 376–382. [Google Scholar] [CrossRef]
- Betke, M.; Gurvits, L. Mobile robot localization using landmarks. IEEE Trans. Robot. Autom. 1997, 13, 251–263. [Google Scholar] [CrossRef] [Green Version]
- Esteves, J.S.; Carvalho, A.; Couto, C. Generalized geometric triangulation algorithm for mobile robot absolute self-localization. In Proceedings of the 2003 IEEE International Symposium on Industrial Electronics (ISIE’03), Rio de Janeiro, Brazil, 9–11 June 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 1, pp. 346–351. [Google Scholar]
- Thomas, F.; Ros, L. Revisiting trilateration for robot localization. IEEE Trans. Robot. 2005, 21, 93–101. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Liu, Y. Quality of trilateration: Confidence-based iterative localization. IEEE Trans. Parallel Distrib. Syst. 2010, 21, 631–640. [Google Scholar] [CrossRef]
- del Peral-Rosado, J.A.; Raulefs, R.; López-Salcedo, J.A.; Seco-Granados, G. Survey of cellular mobile radio localization methods: From 1G to 5G. IEEE Commun. Surv. Tutor. 2017, 20, 1124–1148. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. Sensor fusion IV: Control paradigms and data structures. Int. Soc. Opt. Photonics 1992, 1611, 586–606. [Google Scholar]
- Biber, P.; Straßer, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003)(Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 3, pp. 2743–2748. [Google Scholar]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan registration for autonomous mining vehicles using 3D-NDT. J. Field Robot. 2007, 24, 803–827. [Google Scholar] [CrossRef] [Green Version]
- Campos, D.; Santos, J.; Gonçalves, J.; Costa, P. Modeling and simulation of a hacked neato XV-11 laser scanner. In Robot 2015: Second Iberian Robotics Conference; Springer: Berlin/Heidelberg, Germany, 2016; pp. 425–436. [Google Scholar]
- Lima, J.; Gonçalves, J.; Costa, P.J. Modeling of a low cost laser scanner sensor. In CONTROLO’2014—Proceedings of the 11th Portuguese Conference on Automatic Control; Springer: Berlin/Heidelberg, Germany, 2015; pp. 697–705. [Google Scholar]
- Alhashimi, A.; Varagnolo, D.; Gustafsson, T. Statistical modeling and calibration of triangulation Lidars. In Proceedings of the Informatics in Control, Automation and Robotics: 13th International Conference, ICINCO 2016, Lisbon, Portugal, 29–31 July 2016; SCITEPRESS: Setubal, Portugal, 2016; Volume 1, pp. 308–317. [Google Scholar]
- Alhashimi, A.; Pierobon, G.; Varagnolo, D.; Gustafsson, T. Modeling and Calibrating Triangulation Lidars for Indoor Applications. In Proceedings of the Informatics in Control, Automation and Robotics: 13th International Conference, ICINCO 2016, Lisbon, Portugal, 29–31 July 2016; Springer International Publishing: Cham, Switzerland, 2018; pp. 342–366. [Google Scholar]
- Konolige, K.; Augenbraun, J.; Donaldson, N.; Fiebig, C.; Shah, P. A low-cost laser distance sensor. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 3002–3008. [Google Scholar]
- Aitken, A.C. On least squares and linear combination of observations. Proc. R. Soc. Edinb. 1936, 55, 42–48. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhashimi, A.; Magnusson, M.; Knorn, S.; Varagnolo, D. Calibrating Range Measurements of Lidars Using Fixed Landmarks in Unknown Positions. Sensors 2021, 21, 155. https://doi.org/10.3390/s21010155
Alhashimi A, Magnusson M, Knorn S, Varagnolo D. Calibrating Range Measurements of Lidars Using Fixed Landmarks in Unknown Positions. Sensors. 2021; 21(1):155. https://doi.org/10.3390/s21010155
Chicago/Turabian StyleAlhashimi, Anas, Martin Magnusson, Steffi Knorn, and Damiano Varagnolo. 2021. "Calibrating Range Measurements of Lidars Using Fixed Landmarks in Unknown Positions" Sensors 21, no. 1: 155. https://doi.org/10.3390/s21010155
APA StyleAlhashimi, A., Magnusson, M., Knorn, S., & Varagnolo, D. (2021). Calibrating Range Measurements of Lidars Using Fixed Landmarks in Unknown Positions. Sensors, 21(1), 155. https://doi.org/10.3390/s21010155





