Timely Reliability Analysis of Virtual Machines Considering Migration and Recovery in an Edge Server
Abstract
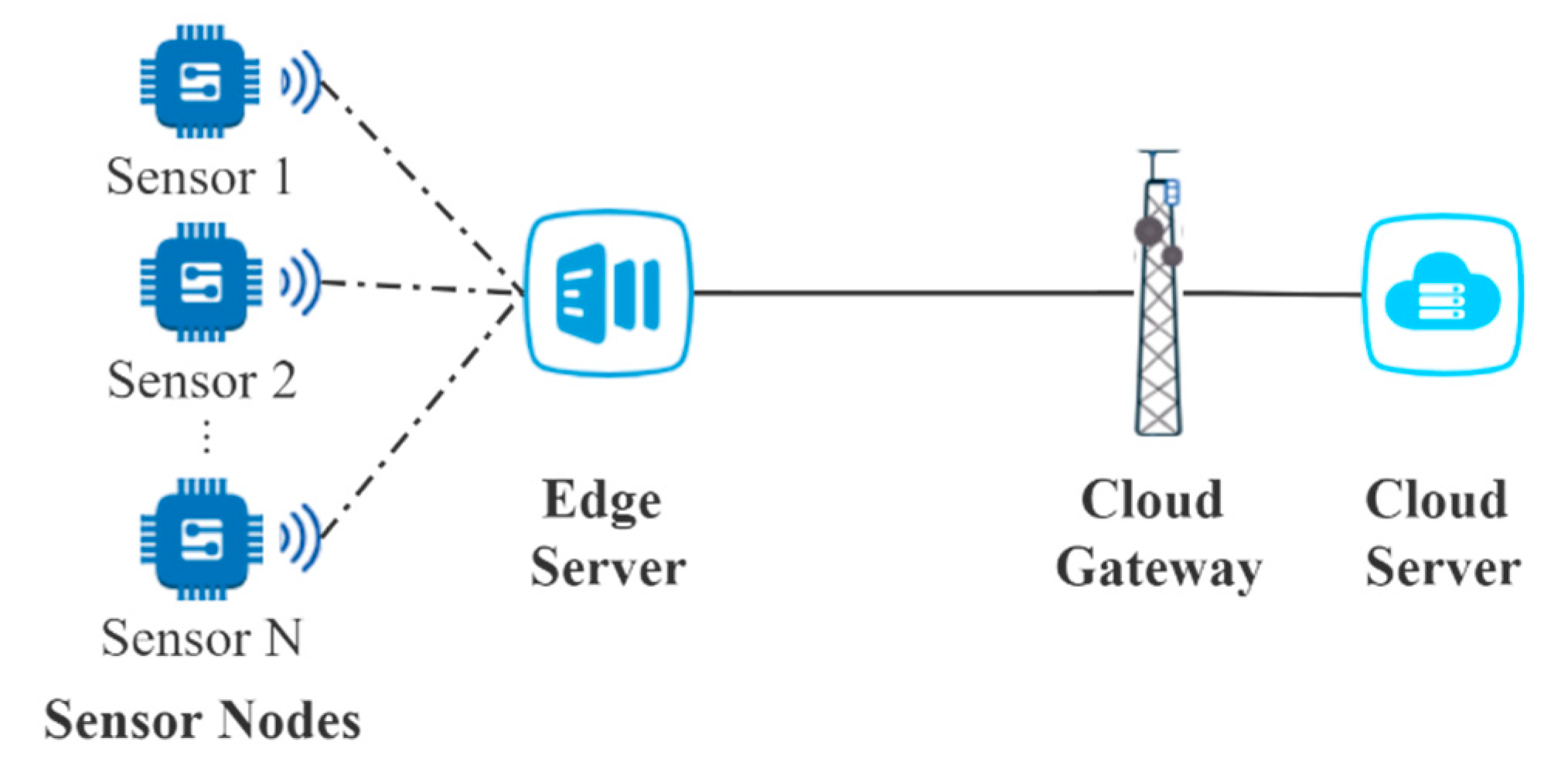
1. Introduction
2. Related Work
2.1. Network Delay Analysis
| Delay | Feature | Description | ||
|---|---|---|---|---|
| Transmission delay | -- | Transmission delay is the ratio of the data size and the transmission rate. Factors such as task length, data size, and bandwidth are considered to obtain the transmission delay [31,35,36,37]. | ||
| Propagation delay | -- | Propagation delay is the ratio of the distance and the propagation speed and is often treated as a function of distance. Factors such as distance [31,33] considered to obtain the propagation delay. | ||
| Processing delay | -- | Processing delay depends on the computing capability of the server and the computing complex of the tasks. It is usually modeled by exponential distribution [24,25,29,31,33,35] or constant [18], etc., and acquired by combining with queue delay. | ||
| Queueing delay | Fixed queues | Homogeneous servers | M/M/c | Model the two-stage queues inside a server [25] or multi-stage queues [24,27] of the edge/cloud computing network, consisting of end equipment, edge nodes, and cloud, etc. Queue theory is employed to obtain average metrics such as mean queue length and mean delay, etc. Virtual machines are considered as queue servers [24] and the modeled virtual machine (VM) states only include busy and idle. Server failure of the queue is not considered, and the probability density function (PDF) of end-to-end delay is not obtained. |
| Non-M/M/c | Consider tasks arriving with an arbitrary probability distribution [27] or service time following arbitrary probability distribution [30]. Average metrics such as mean queue length and mean delay, are obtained. Virtual machines are considered as queue servers [30] and the modeled VM states only include busy and idle. Server failure of the queue is not considered, and the PDF of end-to-end delay is not obtained. | |||
| Heterogeneous servers | Different resource requests lead to heterogeneous queueing servers. The situation where the task requires VMs with different numbers of cores is analyzed [29,38]. The modeled VM states only include busy and idle. The number of jobs in waiting, the number of jobs under provisioning, the number of busy cores, and the number of jobs in service, etc., are employed to define the state space. CTMC is employed to calculate the mean delay. Server failure of the queue is not considered, and the PDF of end-to-end delay is not obtained. | |||
| Stochastic queues | Build the queueing models with probabilities according to different offloading mechanisms [31,33]. M/M/c queue model is employed to calculate the mean delay. Server failure of the queue is not considered, and the PDF of end-to-end delay is not obtained. | |||
2.2. VMs Timely Reliability Analysis
2.3. End-to-End Timely Reliability Analysis
3. Problem Description
3.1. Analysis of Delay at the VMs in the Edge Server
- All the tasks are equal in data size;
- The failures of VM are all transient failures, which can be recovered by rebooting in a short time;
- Idle VMs do not fail;
- The working times of VMs in the server are independent and identically distributed with the exponential distribution where is the mean time to failure.
3.2. Analysis of End-to-End Delay
4. Mathematical Model
4.1. Queueing Model of the Edge Server
4.2. Timely Reliability Model
4.2.1. VMs Timely Reliability
4.2.2. End-to-End Timely Reliability
4.3. Algorithm
| Algorithm1 Algorithm for obtaining PDF of the sojourn time at the edge server |
| Input: Arrival rate of tasks: Number of sensors: Service rate of VM: Number of TVMs: Number of BVMs: Capacity of the buffer: Failure rate of VMs: Migration rate of VMs: Reboot rate of VMs: Output: PDF of the sojourn time at the edge server: |
| 1. initialize 2. vector % The number of columns of block 3. vector % The number of total columns from block 1 to block 4. for i = 1: Z + 1 do % Transitions caused by arrival or departure of tasks 5. for j = 1: Y do 6. for k = 1: min((j), i) do 7. x = (j) − (j) + k 8. y = (j + 1) − (j + 1) + k 9. 10. (y, x) = min (min (Z + 1 − i, S), j − k) * 11. end for 12. end for 13. end for 14. for i = 1: Z + 1 do % Transitions caused by migration of VMs 15. for j = 2: Y + 1 do 16. for k = (j): −1: 2 do 17. x = (j) − (j) + k 18. {i, i} (x, x − 1) = min (k − 1, Z + 1 − i − min (min (Z + 1 − i, S), j − k)) * 19. end for 20. end for 21. end for 22. for j = 2: Y + 1 do % Transitions caused by migration of VMs 23. for k = 1: (j) − 1 do 24. for i = 1: Z do 25. 26. (Z + 1 − i, ), j − k) * 27. end for 28. end for 29. end for 30. for j = 1: Y + 1 do % Transitions caused by reboot of VMs 31. for k = 1: (j) do 32. for i = 2: Z + 1 do 33. x = (j) − (j) + k 34. {i, i − 1} (x, x) = i 35. end for 36. end for 37. end for 38. for j = Z + 1: Y + 1 do % Transitions caused by reboot without migration when all the VMs are failed-unmigrated 39. k = (j) 40. x = (j) − (j) + k 41. {Z + 1, Z} (x, x−1) = (k − 1) * 42. end for 43. Q = 44. for j = 1: size (,2) do % Identify pseudo-states 45. for k = 1: (j) do 46. for i = 1: Z + 1 do 47. if 48. x = (i − 1) * (Y + 1) + (j) − (j) + k 49. replace row x of Q with 0 50. replace column x of Q with 0 51. end if 52. end for 53. end for 54. end for 55. replace the rows and columns of absorbing states with 0 56. record the row number (or column number) of the states whose value is 0 57. revise the diagonal elements of Q to ensure the sum of each row equal to 0 58. delete the rows and columns whose value is 0 59. the steady-state probability vector: % is a column vector whose last element is 1, and the other elements are 0 60. M = A 61. set the arrival rate to 0 in M 62. revise the diagonal elements of M to ensure the sum of each row equals to 0 63. delete the rows and columns of the states of block 1 % The states of block 1 represent that the edge server is empty 64. delete the rows and columns that equals to 0 65. delete the probability of empty states in the stable probability vector and name the new vector as 66. let 67. 68. calculate the PDF of sojourn time at the edge server: 69. return |
5. Results and Discussion
5.1. Experimental Setup
5.2. Simulation Experiments
5.3. Timely Reliability Analysis
5.3.1. Analysis of Failure Rate, Migration Rate, and Reboot Rate
5.3.2. Analysis of the Number of VMs
5.3.3. Management of VMs
5.4. Section Summary
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hassan, S.R.; Ahmad, I.; Ahmad, S.; Alfaify, A.; Shafiq, M. Remote Pain Monitoring Using Fog Computing for e-Healthcare: AnEfficient Architecture. Sensors 2020, 20, 6574. [Google Scholar] [CrossRef] [PubMed]
- Qadri, Y.A.; Nauman, A.; Zikria, Y.B.; Vasilakos, A.V.; Kim, S.W. The Future of Healthcare Internet of Things: A Survey of Emerging Technologies. IEEE Commun. Surv. Tutor. 2020, 22, 1121–1167. [Google Scholar] [CrossRef]
- Osanaiye, O.; Chen, S.; Yan, Z.; Lu, R.; Choo, K.-K.R.; Dlodlo, M. From Cloud to Fog Computing: A Review and a Conceptual Live VM Migration Framework. IEEE Access 2017, 5, 8284–8300. [Google Scholar] [CrossRef]
- Tao, Z.; Xia, Q.; Hao, Z.; Li, C.; Ma, L.; Yi, S.; Li, Q. A Survey of Virtual Machine Management in Edge Computing. Proc. IEEE 2019, 107, 1482–1499. [Google Scholar] [CrossRef]
- Jennings, B.; Stadler, R. Resource Management in Clouds: Survey and Research Challenges. J. Netw. Syst. Manag. 2015, 23, 567–619. [Google Scholar] [CrossRef]
- Grigorescu, S.; Cocias, T.; Trasnea, B.; Margheri, A.; Lombardi, F.; Aniello, L. Cloud2Edge Elastic AI Framework for Prototyping and Deployment of AI Inference Engines in Autonomous Vehicles. Sensors 2020, 20, 5450. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Liu, G.; Fu, X.; Yahyapour, R. A Survey on Virtual Machine Migration: Challenges, Techniques, and Open Issues. IEEE Commun. Surv. Tutor. 2018, 20, 1206–1243. [Google Scholar] [CrossRef]
- Nkenyereye, L.; Nkenyereye, L.; Adhi Tama, B.; Reddy, A.G.; Song, J. Software-Defined Vehicular Cloud Networks: Architecture, Applications and Virtual Machine Migration. Sensors 2020, 20, 1092. [Google Scholar] [CrossRef]
- Garraghan, P.; Townend, P.; Xu, J. An Empirical Failure-Analysis of a Large-Scale Cloud Computing Environment. In Proceedings of the 2014 IEEE 15th International Symposium on High-Assurance Systems Engineering, Miami Beach, FL, USA, 9–11 September 2014; pp. 113–120, ISBN 978-1-4799-3466-9. [Google Scholar]
- Xu, J.; Kalbarczyk, Z.; Iyer, R.K. Networked Windows NT system field failure data analysis. In Proceedings of the 1999 Pacific Rim International Symposium on Dependable Computing, Hong Kong, China, 16–17 December 1999; pp. 178–185, ISBN 0-7695-0371-3. [Google Scholar]
- Bernstein, P.A.; Newcomer, E. System Recovery, In Principles of Transaction Processing; Morgan Kaufmann: San Francisco, CA, USA, 2009; pp. 185–222. ISBN 9781558606234. [Google Scholar]
- Voorsluys, W.; Broberg, J.; Venugopal, S.; Buyya, R. Cost of Virtual Machine Live Migration in Clouds: A Performance Evaluation. In Cloud Computing; Hutchison, D., Kanade, T., Kittler, J., Kleinberg, J.M., Mattern, F., Mitchell, J.C., Naor, M., Nierstrasz, O., Pandu Rangan, C., Steffen, B., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 254–265. ISBN 978-3-642-10664-4. [Google Scholar]
- Noshy, M.; Ibrahim, A.; Ali, H.A. Optimization of live virtual machine migration in cloud computing: A survey and future directions. J. Netw. Comput. Appl. 2018, 110, 1–10. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, F.; Lin, C. Delay guaranteed live migration of Virtual Machines. In Proceedings of the IEEE INFOCOM 2014-IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 574–582, ISBN 978-1-4799-3360-0. [Google Scholar]
- Li, S.; Huang, N.; Chen, J.; Kang, R. Analysis for application reliability parameters of communication networks. In Proceedings of the 2012 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Chengdu, China, 15–18 June 2012; pp. 206–210, ISBN 978-1-4673-0788-8. [Google Scholar]
- Zhao, F.; Huang, N.; Chen, J.X. Impact Analysis of Communication Network Reliability Based on Node Failure. Appl. Mech. Mater. 2013, 347–350, 2100–2105. [Google Scholar] [CrossRef]
- Babay, A.; Wagner, E.; Dinitz, M.; Amir, Y. Timely, Reliable, and Cost-Effective Internet Transport Service Using Dissemination Graphs. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; pp. 1–12, ISBN 978-1-5386-1792-2. [Google Scholar]
- Li, R.; Li, M.; Liao, H.; Huang, N. An efficient method for evaluating the end-To-End transmission time reliability of a switched Ethernet. J. Netw. Comput. Appl. 2017, 88, 124–133. [Google Scholar] [CrossRef]
- Zurawski, R. The Industrial Information Technology Handbook; CRC Press: Boca Raton, FL, USA, 2005; ISBN 0-8493-1985-4. [Google Scholar]
- Liou, C.-D. Markovian queue optimisation analysis with an unreliable server subject to working breakdowns and impatient customers. Int. J. Syst. Sci. 2015, 46, 2165–2182. [Google Scholar] [CrossRef]
- Yang, D.-Y.; Wu, Y.-Y. Analysis of a finite-capacity system with working breakdowns and retention of impatient customers. J. Manuf. Syst. 2017, 44, 207–216. [Google Scholar] [CrossRef]
- Jiang, T.; Xin, B.; Chang, B.; Liu, L. Analysis of a queueing system in random environment with an unreliable server and geometric abandonments. RAIRO-Oper. Res. 2018, 52, 903–922. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Shruti; Kulshrestha, R. A queueing model with server breakdowns, repairs, vacations, and backup server. Oper. Res. Perspect. 2020, 7, 100131. [Google Scholar] [CrossRef]
- El Kafhali, S.; Salah, K. Efficient and dynamic scaling of fog nodes for IoT devices. J. Supercomput. 2017, 73, 5261–5284. [Google Scholar] [CrossRef]
- Pereira, P.; Araujo, J.; Torquato, M.; Dantas, J.; Melo, C.; Maciel, P. Stochastic performance model for web server capacity planning in fog computing. J. Supercomput. 2020, 4, 33. [Google Scholar] [CrossRef]
- Ke, J.-C.; Lin, C.-H.; Yang, J.-Y.; Zhang, Z.G. Optimal (d, c) vacation policy for a finite buffer M/M/c queue with unreliable servers and repairs. Appl. Math. Model. 2009, 33, 3949–3962. [Google Scholar] [CrossRef]
- Liu, C.-F.; Bennis, M.; Poor, H.V. Latency and Reliability-Aware Task Offloading and Resource Allocation for Mobile Edge Computing. In Proceedings of the 2017 IEEE Globecom Workshops (GC Wkshps), Singapore, 4–8 December 2017; pp. 1–7, ISBN 978-1-5386-3920-7. [Google Scholar]
- Xie, M.; Haenggi, M. Towards an end-To-End delay analysis of wireless multihop networks. Ad. Hoc. Netw. 2009, 7, 849–861. [Google Scholar] [CrossRef]
- Wang, B.; Chang, X.; Liu, J. Modeling Heterogeneous Virtual Machines on IaaS Data Centers. IEEE Commun. Lett. 2015, 19, 537–540. [Google Scholar] [CrossRef]
- Chang, X.; Wang, B.; Muppala, J.K.; Liu, J. Modeling Active Virtual Machines on IaaS Clouds Using an M/G/m/m+K Queue. IEEE Trans. Serv. Comput. 2016, 9, 408–420. [Google Scholar] [CrossRef]
- Li, L.; Guo, M.; Ma, L.; Mao, H.; Guan, Q. Online Workload Allocation via Fog-Fog-Cloud Cooperation to Reduce IoT Task Service Delay. Sensors 2019, 19, 3830. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.; Chen, Y.; Hou, D.; Xing, L.; Kang, R. Application reliability for communication networks and its analysis method. J. Syst. Eng. Electron. 2011, 22, 1030–1036. [Google Scholar] [CrossRef]
- Yousefpour, A.; Ishigaki, G.; Gour, R.; Jue, J.P. On Reducing IoT Service Delay via Fog Offloading. IEEE Internet Things J. 2018, 5, 998–1010. [Google Scholar] [CrossRef]
- Yang, D.-Y.; Chen, Y.-H.; Wu, C.-H. Modelling and optimisation of a two-Server queue with multiple vacations and working breakdowns. Int. J. Prod. Res. 2020, 58, 3036–3048. [Google Scholar] [CrossRef]
- Gu, X.; Ji, C.; Zhang, G. Energy-Optimal Latency-Constrained Application Offloading in Mobile-Edge Computing. Sensors 2020, 20, 3064. [Google Scholar] [CrossRef]
- Rodrigues, T.G.; Suto, K.; Nishiyama, H.; Kato, N. Hybrid Method for Minimizing Service Delay in Edge Cloud Computing Through VM Migration and Transmission Power Control. IEEE Trans. Comput. 2017, 66, 810–819. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, F.; Shu, R.; Huang, T.; Liu, Y. Guaranteeing Delay of Live Virtual Machine Migration by Determining and Provisioning Appropriate Bandwidth. IEEE Trans. Comput. 2016, 65, 2910–2917. [Google Scholar] [CrossRef]
- Khazaei, H.; Miic, J.; Miic, V.B.; Mohammadi, N.B. Modeling the Performance of Heterogeneous IaaS Cloud Centers. In Proceedings of the 2013 IEEE 33rd International Conference on Distributed Computing Systems Workshops, Philadelphia, PA, USA, 8–77 July 2013; pp. 232–237, ISBN 978-1-4799-3248-1. [Google Scholar]
- Liu, B.; Chang, X.; Liu, B.; Chen, Z. Performance Analysis Model for Fog Services under Multiple Resource Types. In Proceedings of the 2017 International Conference on Dependable Systems and Their Applications (DSA), Beijing, China, 31 October–2 November 2017; pp. 110–117, ISBN 978-1-5386-3690-9. [Google Scholar]
- Fernando, D.; Terner, J.; Gopalan, K.; Yang, P. Live Migration Ate My VM: Recovering a Virtual Machine after Failure of Post-Copy Live Migration. In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 343–351, ISBN 978-1-7281-0515-4. [Google Scholar]
- Groesbrink, S. Virtual Machine Migration as a Fault Tolerance Technique for Embedded Real-Time Systems. In Proceedings of the 2014 IEEE Eighth International Conference on Software Security and Reliability-Companion, San Francisco, CA, USA, 30 June–2 July 2014; pp. 7–12, ISBN 978-1-4799-5843-6. [Google Scholar]
- Callegati, F.; Cerroni, W. Live Migration of Virtualized Edge Networks: Analytical Modeling and Performance Evaluation. In Proceedings of the 2013 IEEE SDN for Future Networks and Services (SDN4FNS), Trento, Italy, 11–13 November 2013; pp. 1–6, ISBN 978-1-4799-2781-4. [Google Scholar]
- Chen, P.-C.; Lin, C.-I.; Huang, S.-W.; Chang, J.-B.; Shieh, C.-K.; Liang, T.-Y. A Performance Study of Virtual Machine Migration vs. Thread Migration for Grid Systems. In Proceedings of the 22nd International Conference on Advanced Information Networking and Applications-Workshops (Aina Workshops 2008), Gino-Wan, Japan, 25–28 March 2008; pp. 86–91, ISBN 978-0-7695-3096-3. [Google Scholar]
- He, T.; Toosi, N.A.; Buyya, R. Performance evaluation of live virtual machine migration in SDN-Enabled cloud data centers. J. Parallel Distrib. Comput. 2019, 131, 55–68. [Google Scholar] [CrossRef]
- Kumar, N.; Zeadally, S.; Chilamkurti, N.; Vinel, A. Performance analysis of Bayesian coalition game-Based energy-aware virtual machine migration in vehicular mobile cloud. IEEE Netw. 2015, 29, 62–69. [Google Scholar] [CrossRef]
- Li, S.; Huang, J. GSPN-Based Reliability-Aware Performance Evaluation of IoT Services. In Proceedings of the 2017 IEEE International Conference on Services Computing (SCC), Honolulu, HI, USA, 25–30 June 2017; pp. 483–486, ISBN 978-1-5386-2005-2. [Google Scholar]
- Liu, H.; Jin, H.; Xu, C.-Z.; Liao, X. Performance and energy modeling for live migration of virtual machines. Cluster. Comput. 2013, 16, 249–264. [Google Scholar] [CrossRef]
- Begam, R.; Wang, W.; Zhu, D. TIMER-Cloud: Time-Sensitive VM Provisioning in Resource-Constrained Clouds. IEEE Trans. Cloud Comput. 2020, 8, 297–311. [Google Scholar] [CrossRef]
- Chaufournier, L.; Sharma, P.; Le, F.; Nahum, E.; Shenoy, P.; Towsley, D. Fast transparent virtual machine migration in distributed edge clouds. In Proceedings of the Second ACM/IEEE Symposium on Edge Computing, San Jose, CA, USA, 12–14 October 2017; Zhang, J., Chiang, M., Maggs, B., Eds.; ACM: New York, NY, USA, 2017; pp. 1–13, ISBN 9781450350877. [Google Scholar]
- Genez, T.A.L.; Tso, F.P.; Cui, L. Latency-Aware joint virtual machine and policy consolidation for mobile edge computing. In Proceedings of the 2018 15th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 12–15 January 2018; pp. 1–6, ISBN 978-1-5386-4790-5. [Google Scholar]
- Wang, X.; Chen, X.; Yuen, C.; Wu, W.; Zhang, M.; Zhan, C. Delay-Cost tradeoff for virtual machine migration in cloud data centers. J Netw. Comput. Appl. 2017, 78, 62–72. [Google Scholar] [CrossRef]
- Elbamby, M.S.; Perfecto, C.; Liu, C.-F.; Park, J.; Samarakoon, S.; Chen, X.; Bennis, M. Wireless Edge Computing With Latency and Reliability Guarantees. Proc. IEEE 2019, 107, 1717–1737. [Google Scholar] [CrossRef]
- Liu, Y.; Li, R.; Li, Q. Reliability Analysis of Cloud Computing Systems with Different Scheduling Strategies under Dynamic Demands. In Proceedings of the 2017 4th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 21–23 July 2017; pp. 1108–1113, ISBN 978-1-5386-3013-6. [Google Scholar]
- Klimenok, V.; Breuer, L.; Tsarenkov, G.; Dudin, A. The tandem queue with losses. Perform. Eval. 2005, 61, 17–40. [Google Scholar] [CrossRef]
- Gómez-Corral, A.; Martos, M.E. Marked Markovian Arrivals in a Tandem G-Network with Blocking. Methodol. Comput. Appl. Probab. 2009, 11, 621–649. [Google Scholar] [CrossRef]
- Phung-Duc, T. An explicit solution for a tandem queue with retrials and losses. Oper. Res. Int. J. 2012, 12, 189–207. [Google Scholar] [CrossRef]
- Kim, C.; Dudin, A.; Dudina, O.; Dudin, S. Tandem queueing system with infinite and finite intermediate buffers and generalized phase-type service time distribution. Eur. J. Oper. Res. 2014, 235, 170–179. [Google Scholar] [CrossRef]
- Wu, K.; Shen, Y.; Zhao, N. Analysis of tandem queues with finite buffer capacity. IISE Trans. 2017, 49, 1001–1013. [Google Scholar] [CrossRef]
- Li, R.; Huang, N.; Kang, R. Modeling and simulation for network transmission time reliability. In Proceedings of the 2010 Proceedings-Annual Reliability and Maintainability Symposium (RAMS), San Jose, CA, USA, 25–28 January 2010; pp. 1–6, ISBN 978-1-4244-5102-9. [Google Scholar]
- He, W.; Liu, X.; Zheng, L.; Yang, H. Reliability Calculus: A Theoretical Framework to Analyze Communication Reliability. In Proceedings of the 2010 IEEE 30th International Conference on Distributed Computing Systems, Genoa, Italy, 21–25 June 2010; pp. 159–168, ISBN 978-1-4244-7261-1. [Google Scholar]
- Shen, J.; He, W.-b.; Liu, X.; Wang, Z.-b.; Wang, Z.; Yao, J.-G. End-To-End delay analysis for networked systems. Front. Inf. Technol. Electron. Eng. 2015, 16, 732–743. [Google Scholar] [CrossRef]
- Burke, P. Output process and tandem queues. In Proceedings of the Symposium on Computer-Communications Networks and Teletraffic, New York, NY, USA, 4–6 April 1972; pp. 419–428. [Google Scholar]
- Gass, S.I.; Fu, M.C. Encyclopedia of Operations Research and Management Science; Springer: Boston, MA, USA, 2013; ISBN 978-1-4419-1153-7. [Google Scholar]
- Ross, S.M. Queueing Theory. In Introduction to Probability Models; Academic Press: Salt Lake City, UT, USA, 2019; pp. 507–589. ISBN 9780128143469. [Google Scholar]
- Sarker, V.K.; Queralta, J.P.; Gia, T.N.; Tenhunen, H.; Westerlund, T. A Survey on LoRa for IoT: Integrating Edge Computing. In Proceedings of the 2019 Fourth International Conference on Fog and Mobile Edge Computing (FMEC), Rome, Italy, 10–13 June 2019; pp. 295–300, ISBN 978-1-7281-1796-6. [Google Scholar]
- Ortin, J.; Cesana, M.; Redondi, A. Augmenting LoRaWAN Performance with Listen Before Talk. IEEE Trans. Wirel. Commun. 2019, 18, 3113–3128. [Google Scholar] [CrossRef]














| Notation | Description |
|---|---|
| Arrival rate of tasks | |
| Number of sensors | |
| Service rate of virtual machine (VM) | |
| Number of task VMs (TVMs) | |
| Number of backup VMs (BVMs) | |
| Capacity of the buffer of the edge server | |
| Total number of VMs | |
| Maximum capacity of the edge server | |
| Failure rate of VM | |
| Migration rate of VM | |
| Reboot rate of VM | |
| The proportion of tasks requiring cloud service | |
| Service rate of cloud gateway | |
| Capacity of cloud gateway | |
| Service rate of cloud server | |
| Capacity of cloud server | |
| Maximum allowable delay at the edge server | |
| Maximum allowable end-to-end delay | |
| Number of available VMs | |
| Number of tasks in the edge server | |
| Number of failed-unmigrated VMs | |
| State row number | |
| State block number | |
| State column number inside the block | |
| Number of about-to-fail VMs | |
| Number of migrating VMs | |
| The -th block of the CTMC | |
| Set of all the states in row of the CTMC |
| Parameter | Description | Value |
|---|---|---|
| Arrival rate of tasks | 180 per s | |
| Number of sensors | 10 | |
| Service rate of VM | 1000 per s | |
| Number of TVMs | 5 | |
| Number of BVMs | 2 | |
| Capacity of the buffer of the edge server | 180 | |
| Total number of VMs | 7 | |
| Maximum capacity of the edge server | 187 | |
| Failure rate of VM | 0.0002 per s | |
| Migration rate of VM | 0.2 per s | |
| Reboot rate of VM | 0.002 per s | |
| The proportion of tasks requiring cloud service | 1% | |
| Service rate of cloud gateway | 200 per s | |
| Capacity of cloud gateway | 100 | |
| Service rate of cloud server | 300 per s | |
| Capacity of cloud server | 100 | |
| Maximum allowable delay at the edge server | 0.04 s | |
| Maximum allowable end-to-end delay | 0.04 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Guo, L.; Wang, Y.; Chen, X. Timely Reliability Analysis of Virtual Machines Considering Migration and Recovery in an Edge Server. Sensors 2021, 21, 93. https://doi.org/10.3390/s21010093
Liu K, Guo L, Wang Y, Chen X. Timely Reliability Analysis of Virtual Machines Considering Migration and Recovery in an Edge Server. Sensors. 2021; 21(1):93. https://doi.org/10.3390/s21010093
Chicago/Turabian StyleLiu, Kangkai, Linhan Guo, Yu Wang, and Xianyu Chen. 2021. "Timely Reliability Analysis of Virtual Machines Considering Migration and Recovery in an Edge Server" Sensors 21, no. 1: 93. https://doi.org/10.3390/s21010093
APA StyleLiu, K., Guo, L., Wang, Y., & Chen, X. (2021). Timely Reliability Analysis of Virtual Machines Considering Migration and Recovery in an Edge Server. Sensors, 21(1), 93. https://doi.org/10.3390/s21010093






