Noise Floor Reduction in Frequency Delta-Sigma Modulation Microphone Sensors
Abstract
:1. Introduction
2. Frequency Delata-Sigma Modulation
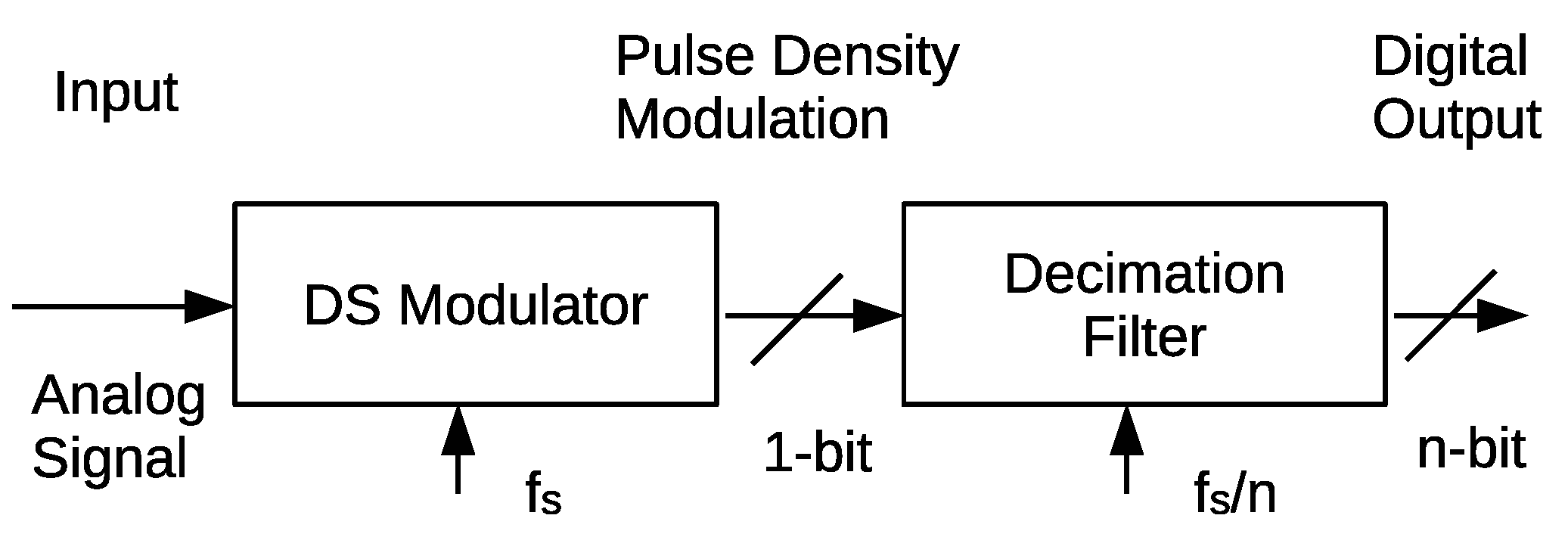
2.1. Delta-Sigma ADCs and Delta-Sigma Modulators
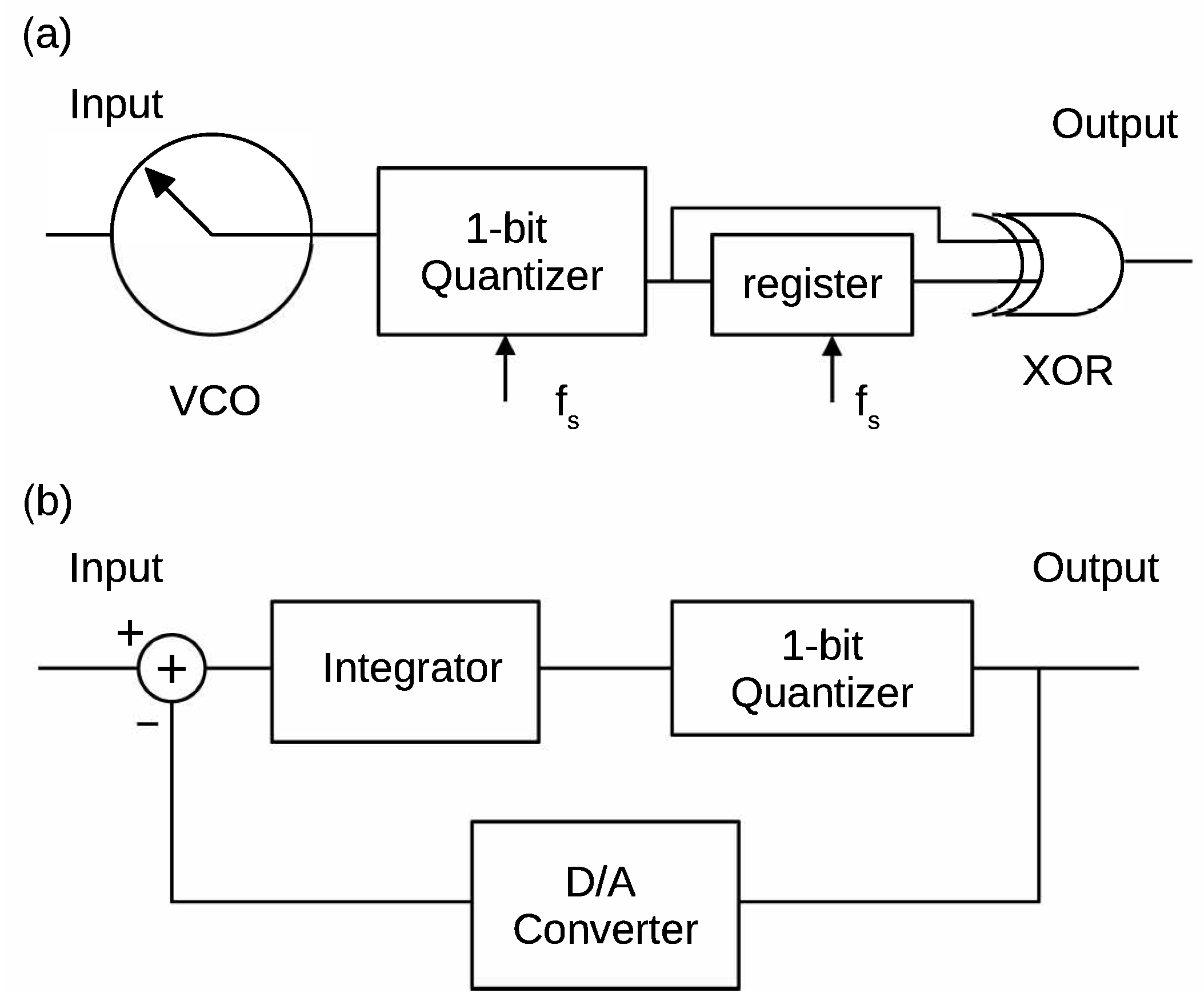
2.2. Frequency Delta-Sigma Modulators
3. FDSM Microphone Sensor
4. Origin of the Noise Floor
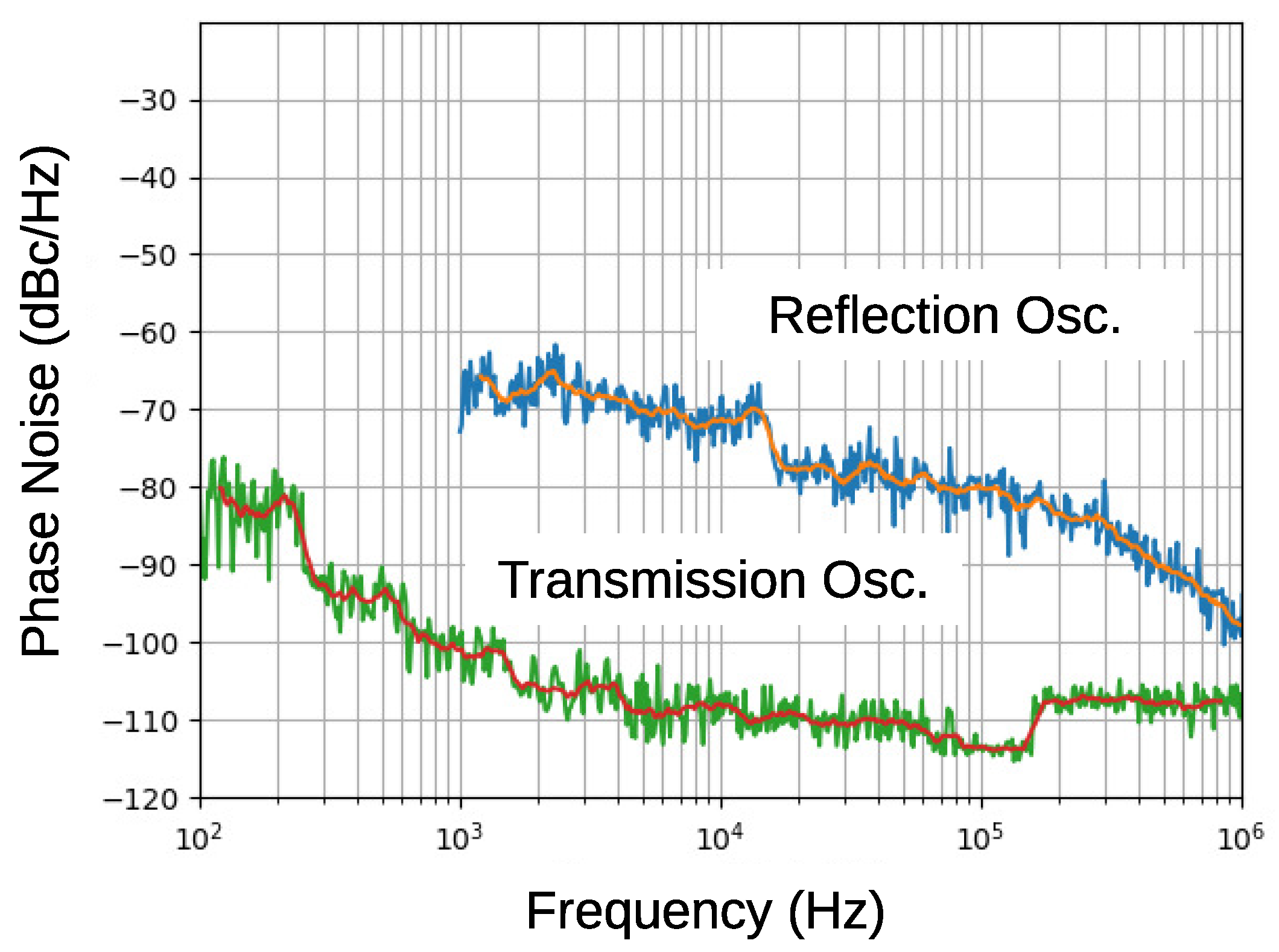
5. Cavity Resonator Oscillators with Lower Phase Noise
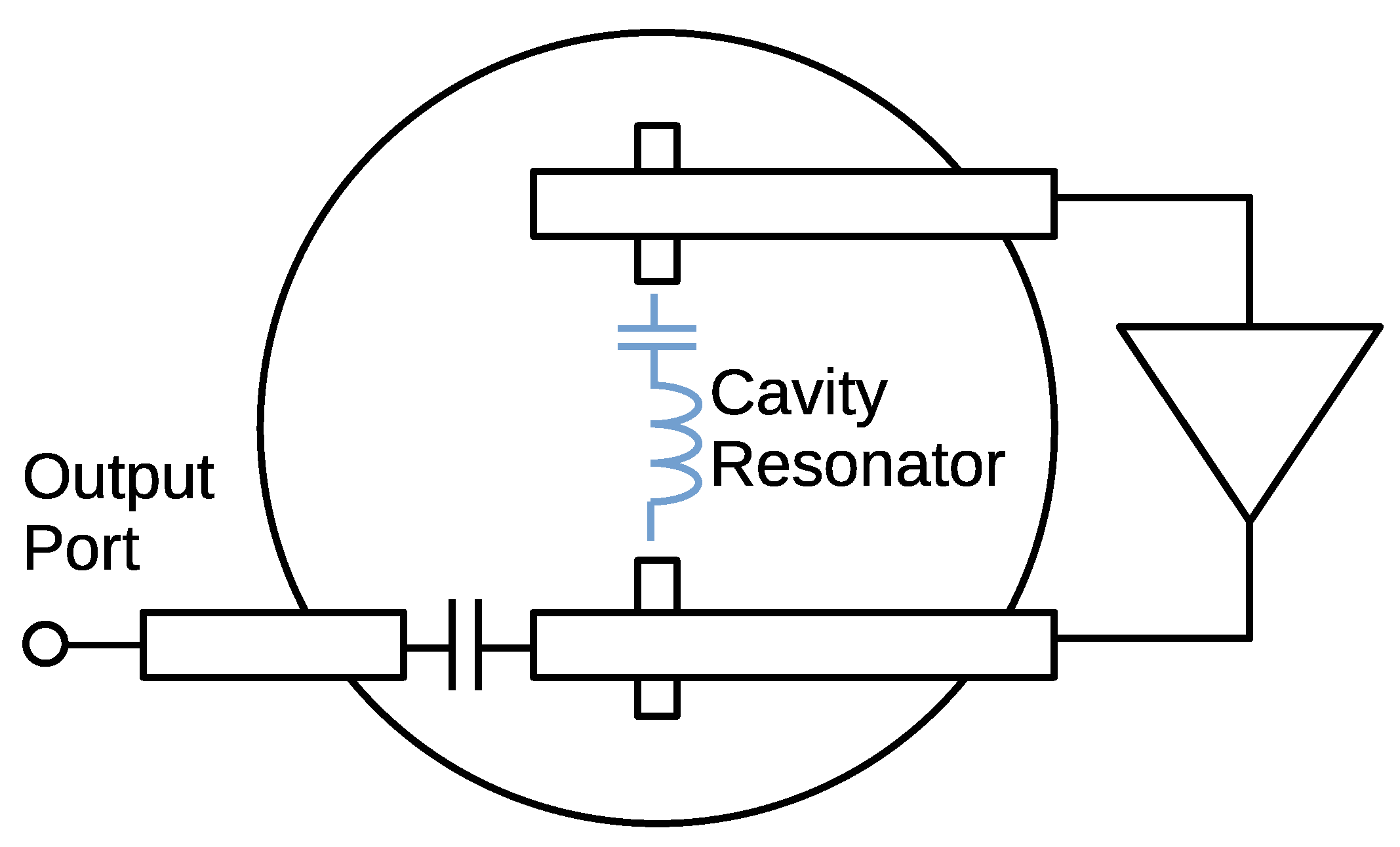
5.1. Cavity Resonators
5.2. Oscillator Circuit Design
6. Experimental Results of the FDSM Microphone Sensors
6.1. FDSM Analyzer Circuit on an FPGA
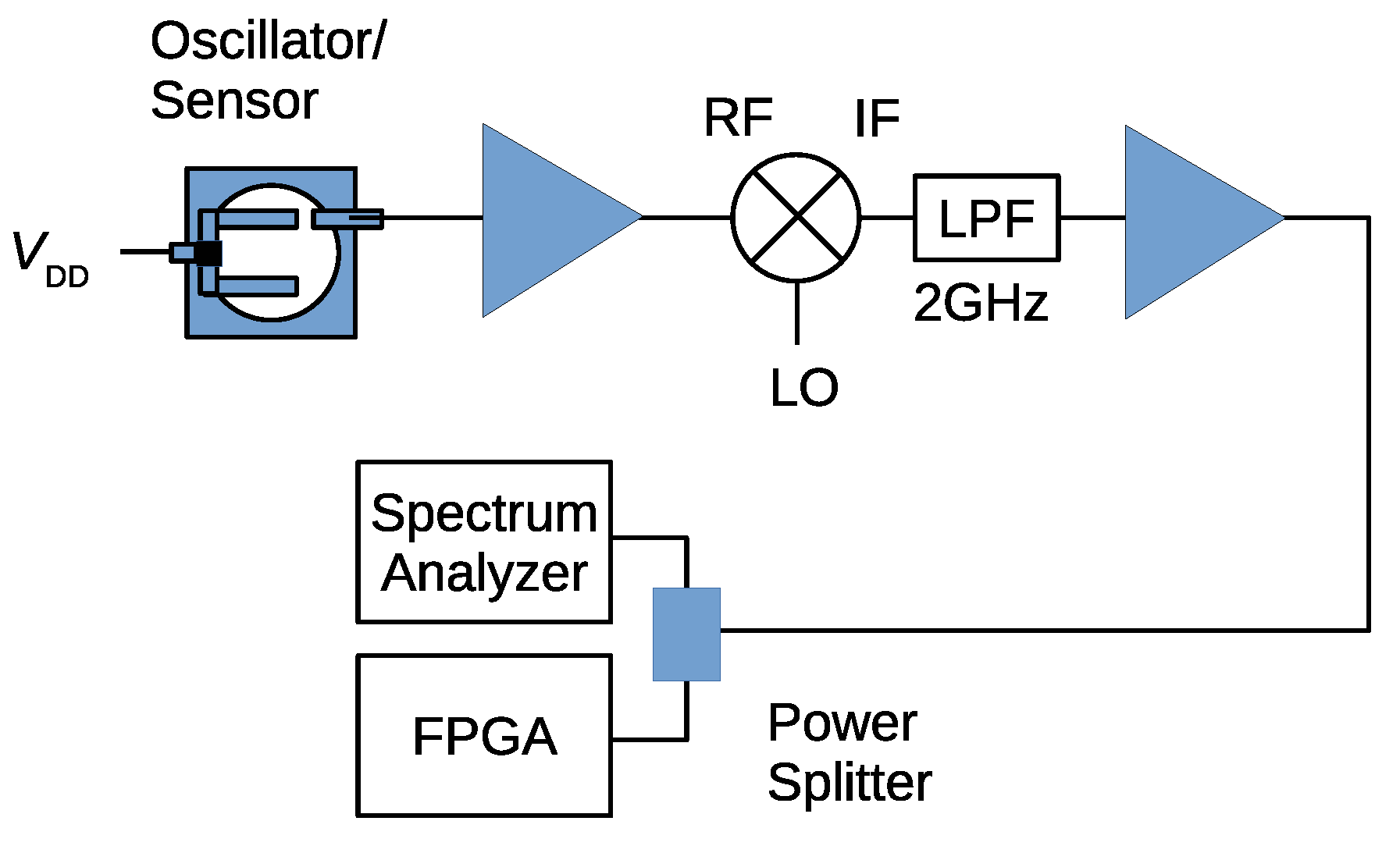
6.2. Experimental Setup
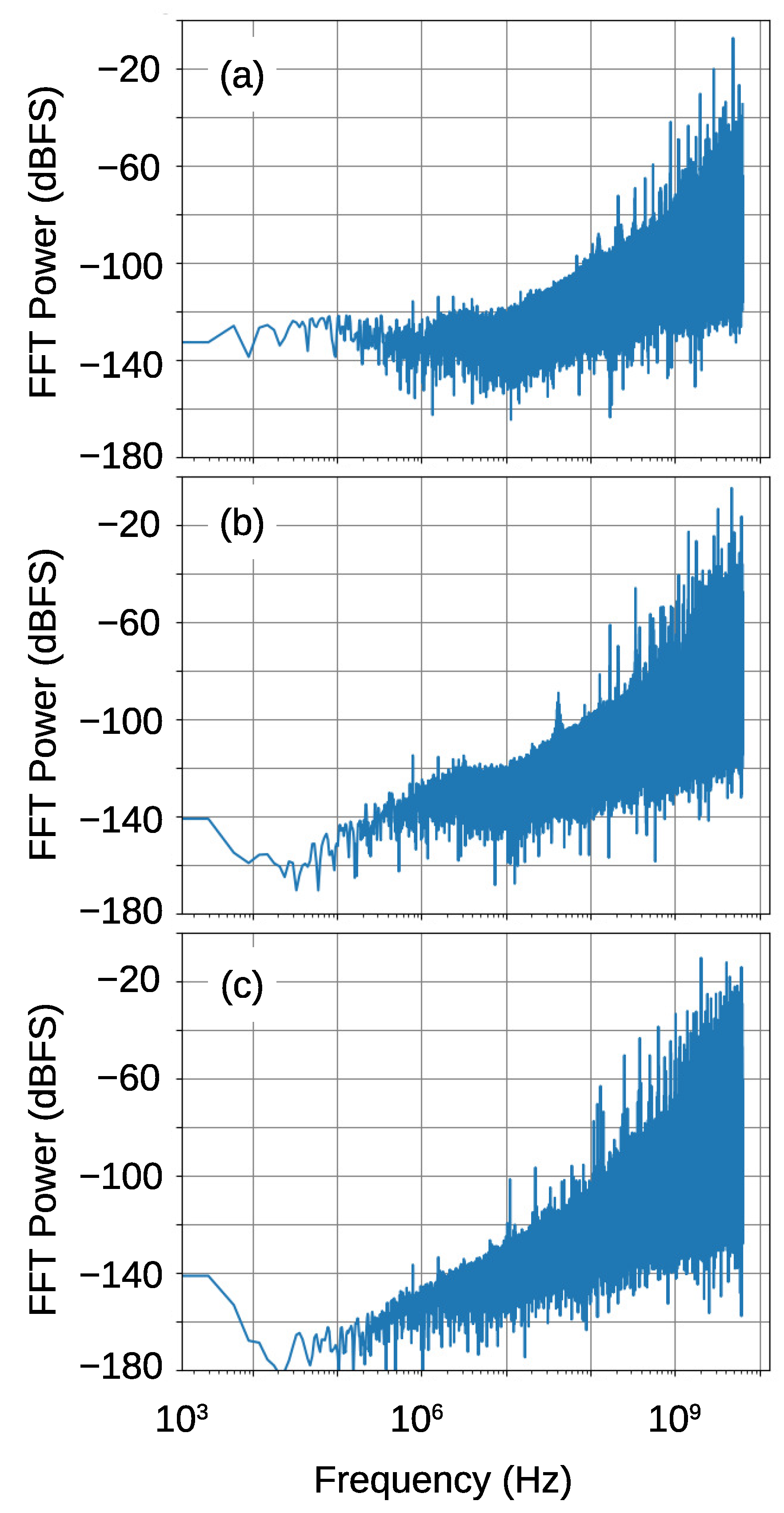
6.3. Noise Floor and Total in-Band Noise Power
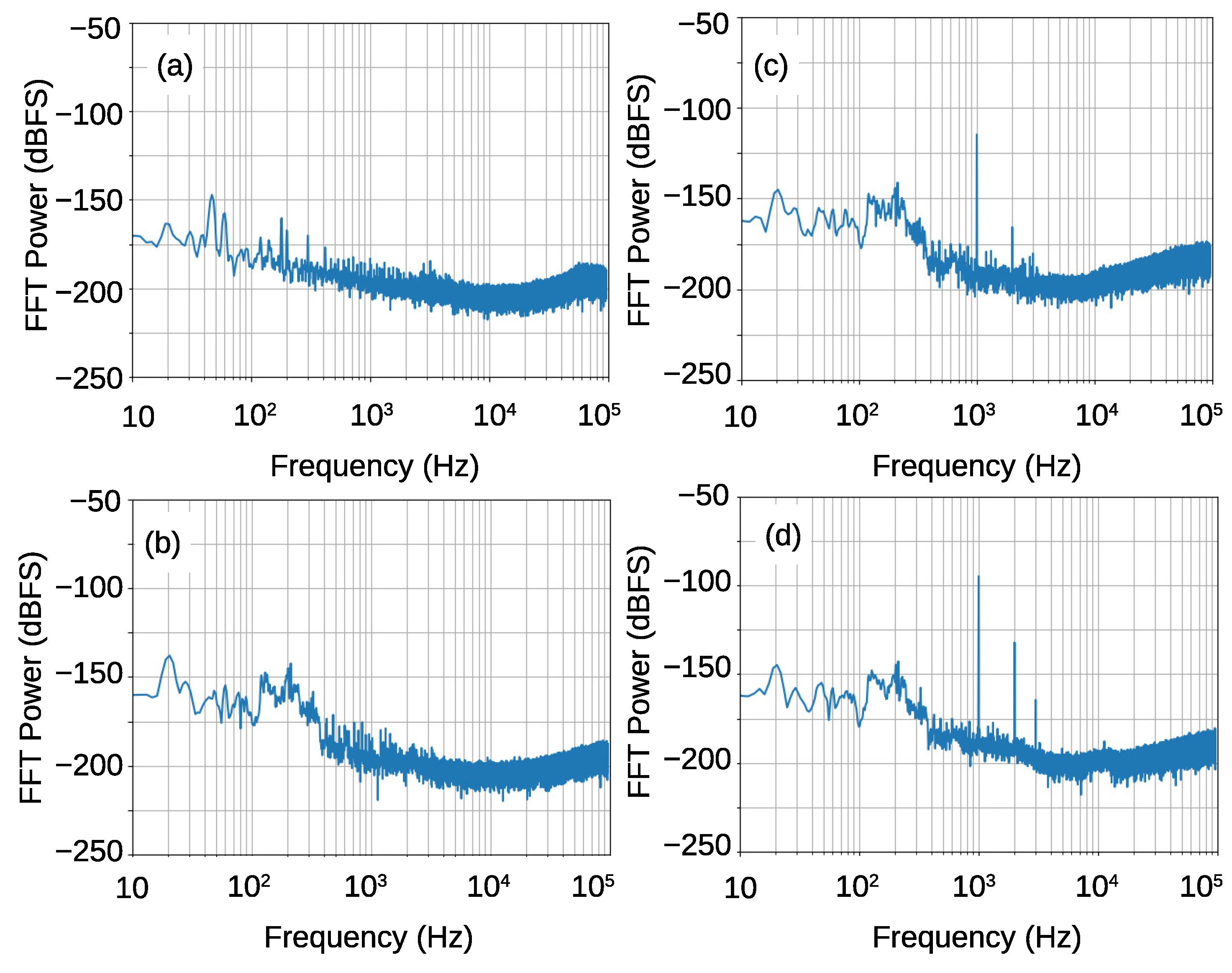
6.4. Sound Spectra
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ADC | Analog-Digital Converter |
| DSM | Delta-Sigma Modulator |
| PDM | Pulse Density Modulation |
| DAC | Digital-Analog Converter |
| FDSM | Frequency Delta-Sigma Modulator |
| FM | Frequency Modulation |
| VCO | Voltage Controlled Oscillator |
| FET | Field Effect Transistor |
| FFT | Fast Fourier Transform |
| FEM | Finite Element Method |
| FWHM | Full Width of Half Maximum |
| pHEMT | pseudomorphic High Electron Mobility Transistor |
| FPGA | Field Programmable Gate Way |
| CIC | Cascaded Integrator-Comb |
| LO | Local Oscillator |
| SNR | Signal-to-Noise Ratio |
| DR | Dynamic Range |
| dBSPL | decibel sound pressure lebel |
| dBFS | decibel full-scale |
References
- Candy, C. A Use of Limit Cycle Oscillations to Obtain Robust Analog-to-Digital Converters. IEEE Trans. Commun. 1974, 22, 298–305. [Google Scholar]
- Norsworthy, S.R.; Schreier, R.; Temes, C.G. Delta-Sigma Data Converters; IEEE Press: New York, NY, USA, 1996. [Google Scholar]
- Pavan, S.R.; Schreier, R.; Temes, G.C. Understanding Delta-Sigma Data Converters, 2nd ed.; Willey & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Høvin, M.; Lande, T.S.; Toumazou, C. Delta-Sigma Modulators Using Frequency-Modulated Intermediate Values. IEEE J. Solid-State Circuits 1997, 32, 13–22. [Google Scholar] [CrossRef]
- Iwata, A.; Sakimura, N.; Nagata, M.; Morie, T. The Architecture of Delta Sigma Analog-to-Digital Converters Using a Voltage-Controlled Oscillator as a Multibit Quantizer. IEEE Trans. Circuits Syst. 1999, 46, 941–945. [Google Scholar] [CrossRef]
- Maezawa, K.; Sakou, M.; Matsubara, W.; Mizutani, T. Resonant tunneling delta-sigma modulator suitable for high-speed operation. Electron. Lett. 2006, 42, 20063215. [Google Scholar]
- Li, S.; Sanyal, A.; Lee, K.; Yoon, Y.; Tang, X.; Zhong, Y.; Ragab, K.; Sun, N. Advances in Voltage-Controlled-Oscillator-Based Delta Sigma ADCs. IEICE Trans. Electron. 2019, E102-C, 509–519. [Google Scholar] [CrossRef]
- Maezawa, K.; Sakou, M.; Matsubara, W.; Mizutani, T. Dual-clock MASH delta-sigma modulator employing a frequency modulated intermediate signal. IEICE Electron. Express 2006, 3, 459–463. [Google Scholar] [CrossRef] [Green Version]
- Straayer, M.Z.; Perrott, M.H. A 12-bit, 10-MHz bandwidth, continuous-time ADC with a 5-bit, 950-MS/s VCO-based quantizer. IEEE J. Solid-State Circuits 2008, 43, 805. [Google Scholar] [CrossRef]
- Park, M.; Perrott, M.H. A VCO-based analog-to-digital converter with second-order Sigma-Delta noise shaping. In Proceedings of the IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 3130–3133. [Google Scholar]
- Voelker, M.; Pashmineh, S.; Hauer, J.; Ortmanns, M. Current Feedback Linearization Applied to Oscillator Based ADCs. IEEE Trans. Circuits Syst. I 2014, 61, 3066–3074. [Google Scholar] [CrossRef]
- Lee, K.; Yoon, Y.; Sun, N. A Scaling-Friendly Low-Power Small-Area ADC with VCO-Based Integrator and Intrinsic Mismatch Shaping Capability. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 561–573. [Google Scholar] [CrossRef]
- Xing, X.; Zhu, P.; Liu, H.; Gielen, G. Fully-VCO-based 0-2 MASH CT ΔΣ ADC. Electron. Lett. 2018, 54, 1018–1020. [Google Scholar] [CrossRef]
- Jayaraj, A.; Danesh, M.; Chandrasekaran, S.T.; Sanyal, A. Highly Digital Second-Order VCO ADC. IEEE Trans. Circuits Syst. I 2019, 66, 2415–2425. [Google Scholar] [CrossRef]
- Fujino, S.; Mizuno, Y.; Takaoka, K.; Nakano, J.; Mori, M.; Maezawa, K. Experimental Demonstration of Noise Shaping in the Digital Microphone Employing Frequency ΔΣ Modulation. IEICE Trans. Electron. (Jpn. Ed.) 2013, J96-C, 554–555. [Google Scholar]
- Maezawa, K.; Fujino, S.; Yamaoka, T.; Mori, M. Delta Sigma Modulation Microphone Sensors Using a Microwave Cavity Resonator. Electron. Lett. 2016, 52, 1651–1652. [Google Scholar] [CrossRef]
- Tajika, T.; Kakutani, Y.; Mori, M.; Maezawa, K. Experimental demonstration of strain detection using resonant tunneling delta-sigma modulation sensors. Phys. Status Solidi A 2016, 214, 1600548. [Google Scholar] [CrossRef]
- Maezawa, K.; Takumi, T.; Mori, M. 1 MHz strain detection using resonant tunneling delta sigma modulation sensors. In Proceeding of the 2018 Asia-Pacific Workshop on Fundamentals and Applications of Advanced Semiconductor Devices (AWAD 2018), Kitakyushu, Japan, 2–4 July 2018. [Google Scholar]
- Maezawa, K.; Ito, T.; Mori, M. Delta-sigma modulation microphone sensors employing a resonant tunneling diode with a suspended microstrip resonator. Sens. Rev. 2020, 40, 535–542. [Google Scholar] [CrossRef]
- Maezawa, K.; Mori, M. Effects of oscillator phase noise on frequency delta sigma modulators with a high oversampling ratio for sensor applications. IEICE Trans. Electron. 2021, E104-C. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; ISBN 978-0-470-63155-3. [Google Scholar]
- Leeson, D.B. A simple model of feedback oscillator noise spectrum. Proc. IEEE 1966, 54, 329–330. [Google Scholar] [CrossRef] [Green Version]
- Hajimiri, A.; Lee, T.H. A General Theory of Phase Noise in Electrical Oscillators. IEEE J. Solid-State Circuits 1998, 33, 179–194. [Google Scholar] [CrossRef] [Green Version]
- Rubiola, E. Phase Noise and Frequency Stability in Oscillators; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Itoh, K. Basis of Microwave Synthesizers [I]: Foundation of Low Noise PLL Frequency Synthesizers. J. IEICE 2005, 88, 995–1001. [Google Scholar]
- Medeiro, F.; Verdu, B.P.; Vazquez, A.R. Top-Down Design of High-Performance Sigma-Delta Modulators; Kluwer Academic Publishers: Boston, MA, USA, 1999; pp. 79–80. [Google Scholar]
- Gronefeld, A.; Gronefeld, I. Ultra-Low Phase Noise Oscillators with Attosecond Jitter. Available online: https://www.microwavejournal.com/articles/print/30053-ultra-low-phase-noise-oscillators-with-attosecond-jitter (accessed on 7 April 2021).
- Everard, J.K.A. A Review of Low Noise Oscillator. In Proceedings of the International Frequency Control Symposium, Orlando, FL, USA, 30 May 1997; pp. 909–918. [Google Scholar]
- Galani, Z.; Bianchini, M.J.; Waterman, R.C., Jr.; Dibiase, R.; Laton, R.W.; Cole, J.B. Analysis and Design of a Single-Resonator GaAs FET Oscillator with Noise Degeneration. IEEE Trans. Microwave Theory Tech. 1984, 32, 1556–1565. [Google Scholar] [CrossRef]
- Høvin, M. First-Order Frequency Δ-Σ Modulation. Ph.D. Thesis, University of Oslo, Oslo, Norway, 2000; pp. 76–82. [Google Scholar]











| Sample | Measured | Calculated (dBFS) | ||
|---|---|---|---|---|
| (dBFS) | Total | Quantization Noise | Phase Noise | |
| Ref. Osc. down-conv. | −114 | −112 | −141 | −112 |
| Trans. Osc. direct | −133 | −141 | −141 | −150 |
| Trans. Osc. down-conv. | −143 | −141 | −141 | −152 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maezawa, K.; Mori, M.; Andoh, H. Noise Floor Reduction in Frequency Delta-Sigma Modulation Microphone Sensors. Sensors 2021, 21, 3470. https://doi.org/10.3390/s21103470
Maezawa K, Mori M, Andoh H. Noise Floor Reduction in Frequency Delta-Sigma Modulation Microphone Sensors. Sensors. 2021; 21(10):3470. https://doi.org/10.3390/s21103470
Chicago/Turabian StyleMaezawa, Koichi, Masayuki Mori, and Hiroya Andoh. 2021. "Noise Floor Reduction in Frequency Delta-Sigma Modulation Microphone Sensors" Sensors 21, no. 10: 3470. https://doi.org/10.3390/s21103470
APA StyleMaezawa, K., Mori, M., & Andoh, H. (2021). Noise Floor Reduction in Frequency Delta-Sigma Modulation Microphone Sensors. Sensors, 21(10), 3470. https://doi.org/10.3390/s21103470







