Force-Free Control for Direct Teaching of a Surgical Assistant Robot End Effector with Wire-Driven Bidirectional Telescopic Mechanism
Abstract
:1. Introduction
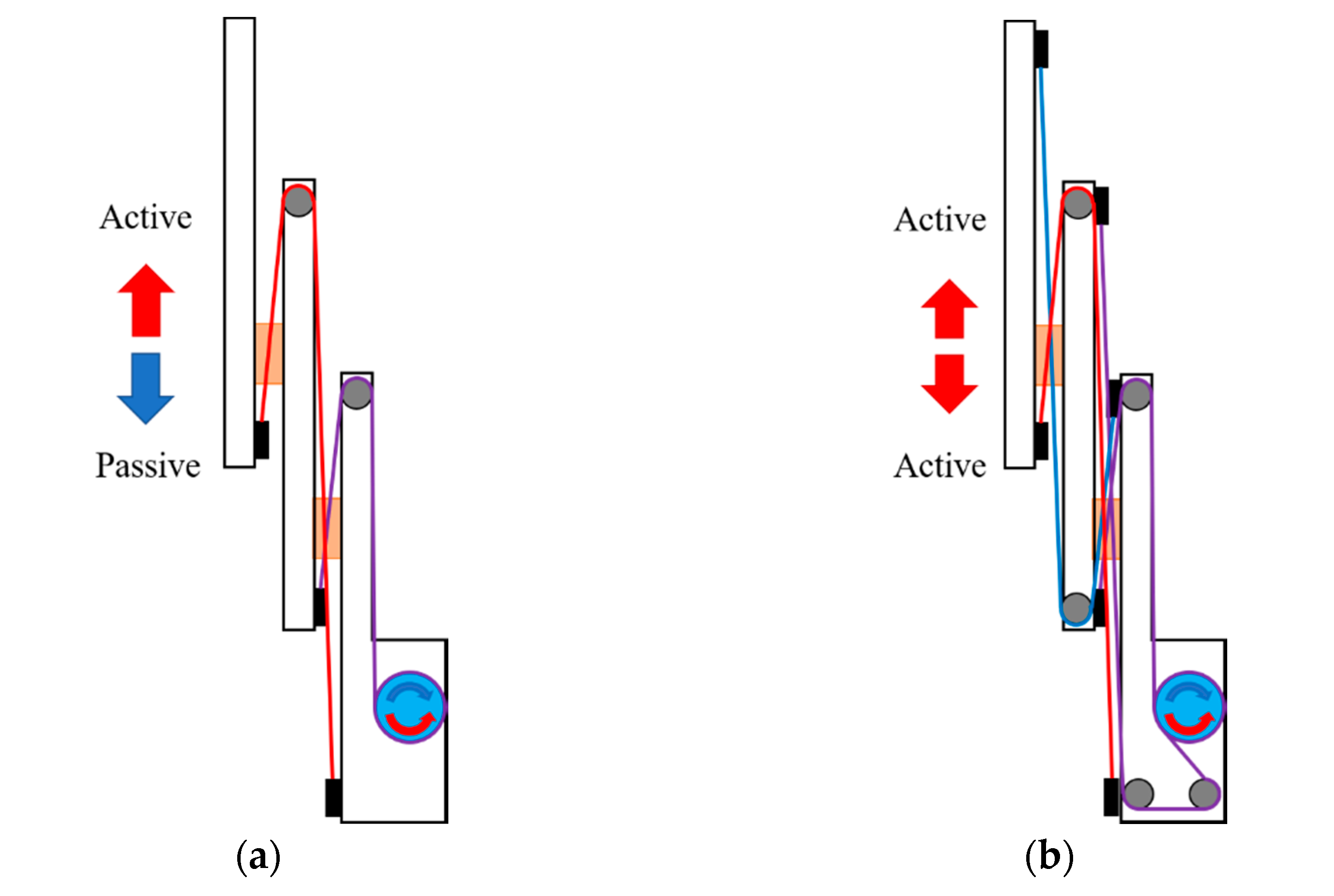
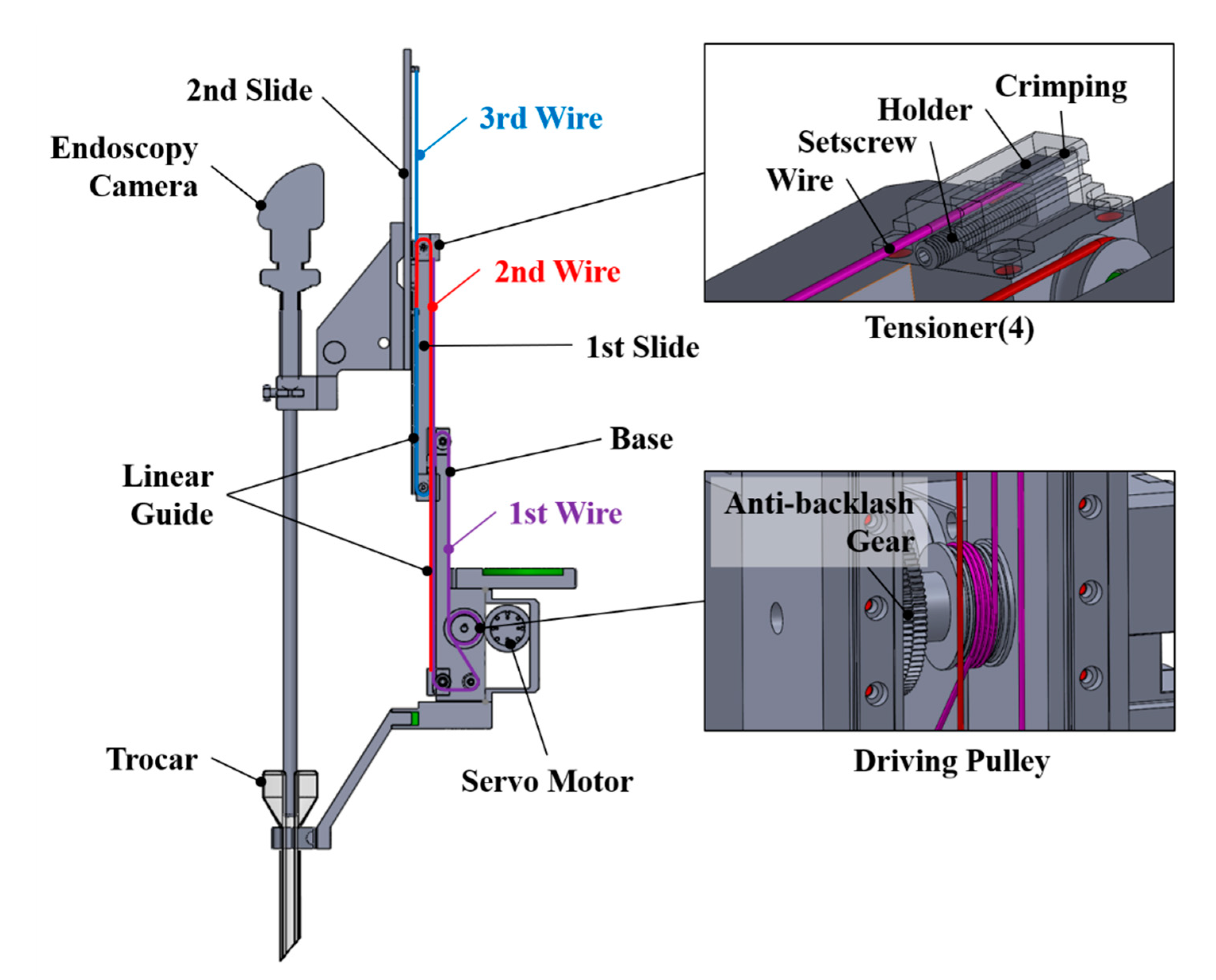
2. Bidirectional Telescopic Mechanism
2.1. Description of Mechanism
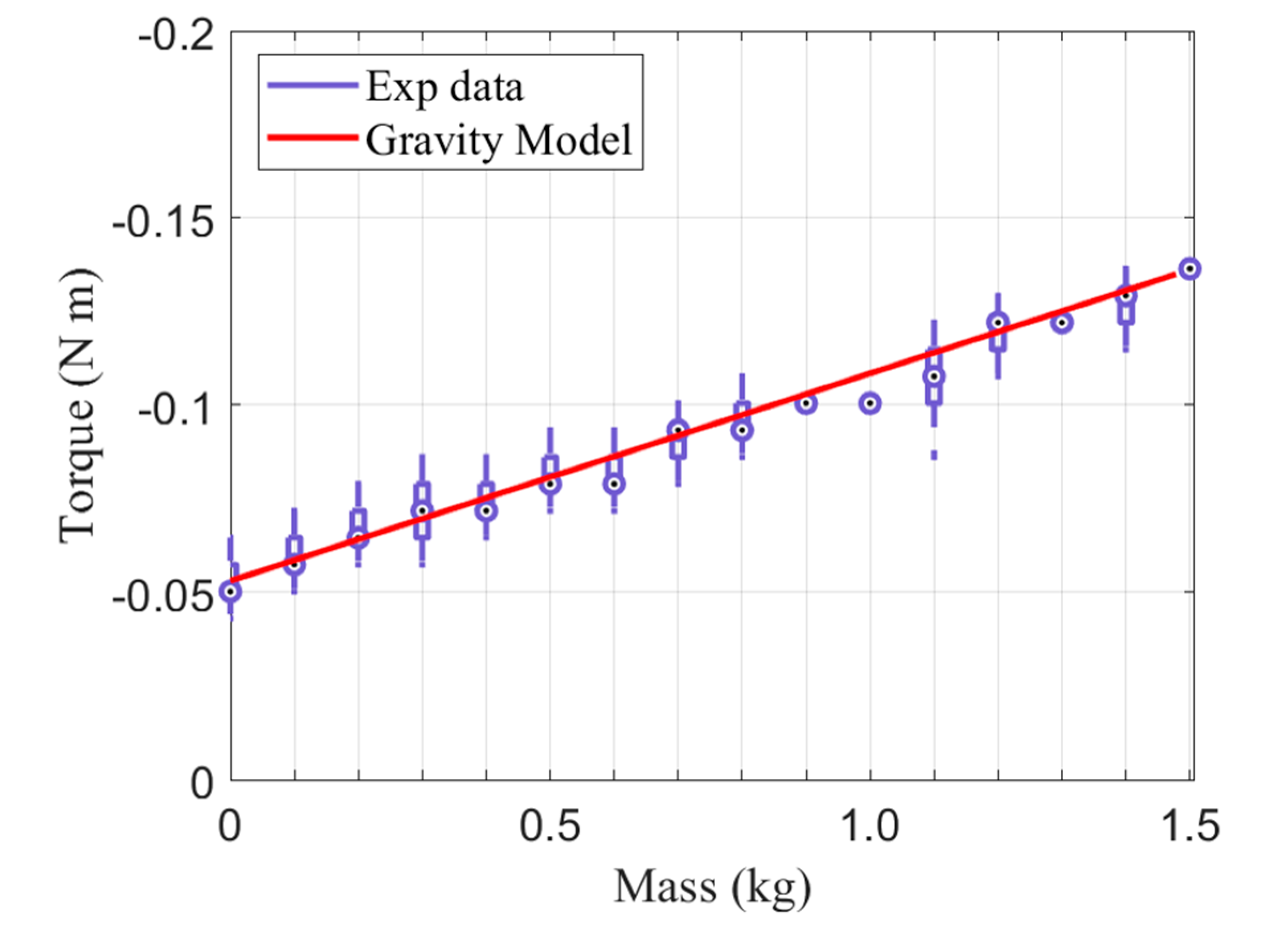
2.2. Static Modeling
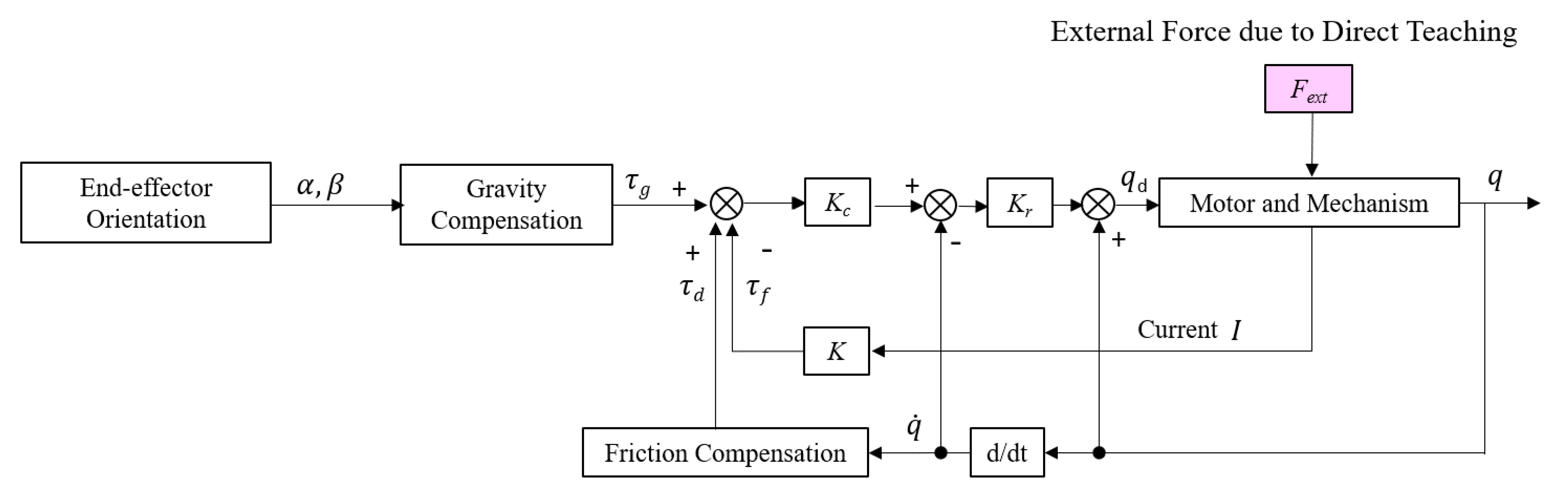
3. Force-Free Control with Compensation
3.1. Gravity Compensation
3.2. Friction Compensation
3.2.1. Estimating Static Parameters
3.2.2. Estimating Dynamic Parameters
3.3. Design of Force-Free Control
4. Experiment of Direct Teaching Performance
4.1. Description of Experimental Apparatus
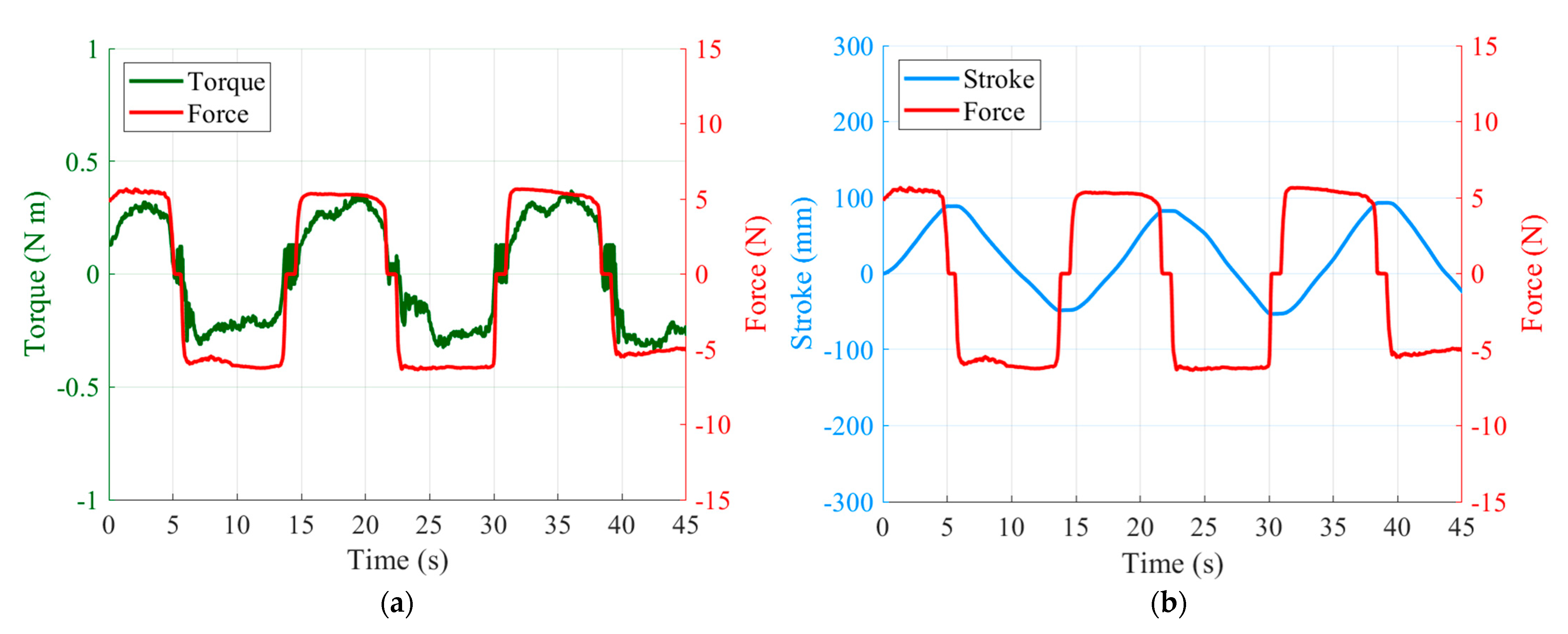
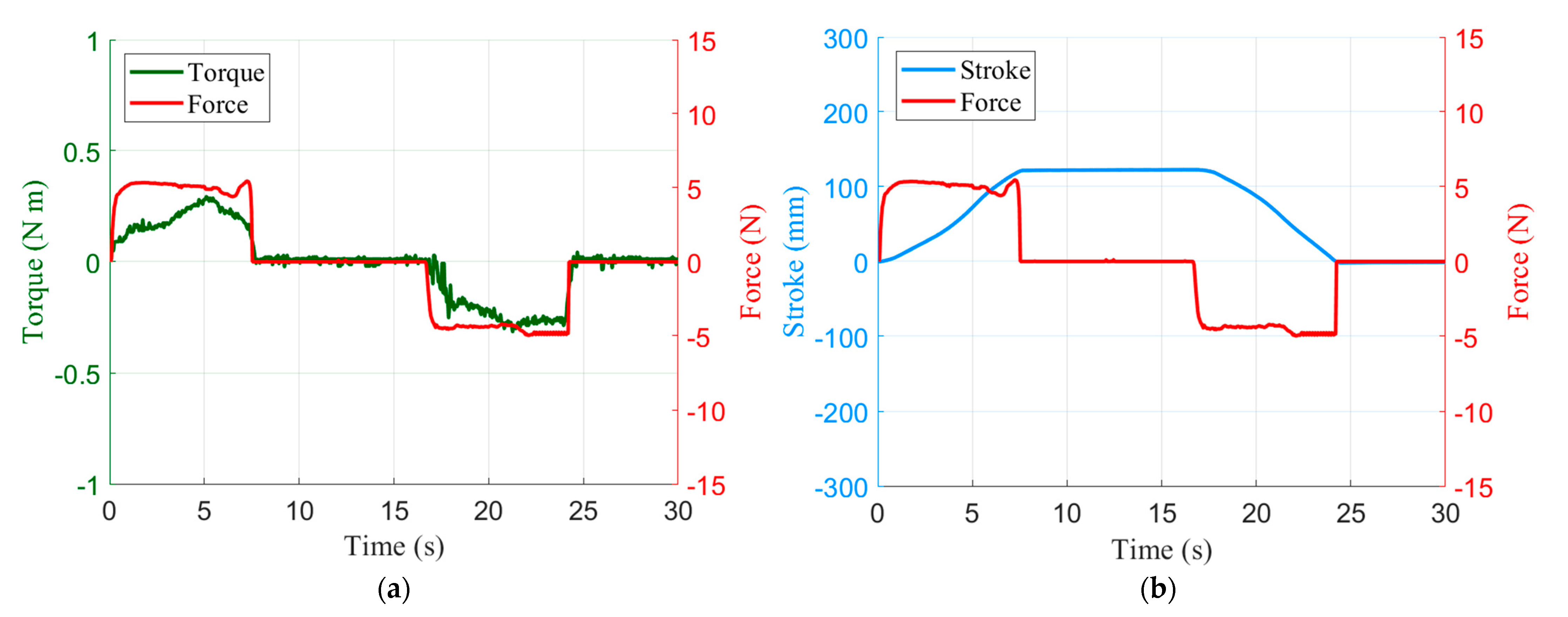
4.2. Hand Guiding Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, M.; Zhang, Y.; Jin, S. Control Strategy for Direct Teaching of Non-Mechanical Remote Center Motion of Surgical Assistant Robot with Force/Torque Sensor. Appl. Sci. 2021, 11, 4279. [Google Scholar] [CrossRef]
- Lee, D.; Chang, D.; Shin, Y.I.; Son, D.; Kim, T.-W.; Lee, K.-Y.; Kim, J. Design and application of a wire-driven bidirectional telescopic mechanism for workspace expansion with a focus on shipbuilding tasks. Adv. Robot. 2011, 25, 699–715. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Yuan, J.; Han, Z.; Qian, Y. Current-Based Direct Teaching for Industrial Manipulator. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 1647–1652. [Google Scholar] [CrossRef]
- Yen, S.H.; Tang, P.C.; Lin, Y.C.; Lin, C.Y. Development of a Virtual Force Sensor for a Low-Cost Collaborative Robot and Applications to Safety Control. Sensors 2019, 19, 2603. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Luo, M.; Jiang, G.; Abdelaziz, O. Collaborative robot zero moment control for direct teaching based on self-measured gravity and friction. Int. J. Adv. Robot. Syst. 2018, 15, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Ubeda, R.; Zotovic-Stanisic, R.; Gutiérrez, S.C. Force Control Improvement in Collaborative Robots through Theory Analysis and Experimental Endorsement. Appl. Sci. 2020, 10, 4329. [Google Scholar] [CrossRef]
- Lee, S.D.; Ahn, K.H.; Song, J.B. Torque control based sensorless hand guiding for direct robot teaching. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 740–750. [Google Scholar] [CrossRef]
- Kallu, K.D.; Abbasi, S.J.; Khan, H.; Wang, J.; Lee, M.C. Implementation of a TSMCSPO controller on a 3-dof hydraulic manipulator for position tracking and sensor-less force estimation. IEEE Access 2019, 7, 177035–177047. [Google Scholar] [CrossRef]
- Nakamura, H.; Ohishi, K.; Yokokura, Y.; Kamiya, N.; Miyazaki, T.; Tsukamoto, A. Force sensorless fine force control based on notch-type friction-free disturbance observers. IEEJ J. Ind. Appl. 2018, 7, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Goto, S. Forcefree Control for Flexible Motion of Industrial Articulated Robot Arms. In Industrial Robotics: Theory, Modelling and Control; IntechOpen: Mammendorf, Germany, December 2006; pp. 813–840. [Google Scholar] [CrossRef] [Green Version]
- Kushida, D.; Nakamura, M.; Goto, S.; Kyura, N. Human direct teaching of industrial articulated robot arms based on force-free control. Artif. Life Robot. 2001, 5, 26–32. [Google Scholar] [CrossRef]
- Pennestrì, E.; Rossi, V.; Salvini, P.; Valentini, P.P. Review and comparison of dry friction force models. Nonlinear Dynammics 2016, 83, 1785–1801. [Google Scholar] [CrossRef]
- Do, T.N.; Tjahjowidodo, T.; Lau, M.W.S.; Phee, S. Nonlinear friction modelling and compensation control of hysteresis phenomena for a pair of tendon-sheath actuated surgical robots. Mech. Syst. Signal. Process. 2015, 60, 770–784. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S. High performance adaptive control of mechanical servo system with LuGre friction model: Identification and compensation. J. Dyn. Syst. Meas. Control. 2012, 134, 770–784. [Google Scholar] [CrossRef] [Green Version]
- Freidovich, L.; Robertsson, A.; Shiriaev, A.; Johansson, R. LuGre-Model-Based Friction Compensation. IEEE Trans. Control. Syst. Technol. 2010, 18, 194–200. [Google Scholar] [CrossRef]
- Ishikawa, J.; Tei, S.; Hoshino, D.; Izutsu, M.; Kamamichi, N. Friction compensation based on the LuGre friction model. In Proceedings of the SICE Annual Conference 2010, Taipei, Taiwan, 18–21 August 2010; pp. 9–12. [Google Scholar]
- Piatkowski, T. Dahl and LuGre dynamic friction models. Anal. Sel. Prop. Mech. Mach. Theory 2014, 73, 91–100. [Google Scholar] [CrossRef]
- Wen, Y.; Chu, M.; Sun, H. Friction parameters identification and compensation of LuGre model base on genetic algorithms. In 2015 International Symposium on Computers & Informatics; Atlantis Press: Beijing, China, 2015; pp. 229–238. [Google Scholar] [CrossRef]





| Parameters | Value | |
|---|---|---|
| Height | min | max |
| 256 mm | 492 mm | |
| Width | 57 mm | |
| Whole body weight | 2.09 kg | |
| Parameters | Description | Value |
|---|---|---|
| m1 | Mass of the first slide | 0.176 kg |
| m2 | Mass of the second slide | 0.427 kg |
| K | Torque coefficient | 2.67 N·m/A |
| N1 | Gear ratio of the anti-backlash gears | 6:7 |
| N2 | Gear ratio of the motor reducer | 1:152.3 |
| Parameters | Description | Value |
|---|---|---|
| τc | Coulomb friction level | 0.070 N·m |
| τs | Static friction level | 0.030 N·m |
| σ2 | Viscous damping coefficient | 0.155 N m·s/rad |
| ω2 | Stribeck velocity | 0.090 rad−1 |
| Parameters | Description | Value |
|---|---|---|
| σ0 | Bristle stiffness | 0.051 N·m/rad |
| σ1 | Bristle damping coefficient | 0.297 N·m·s/rad |
| Parameters | Description | Value |
|---|---|---|
| Kr | Command conversion gain | 2.05 |
| Kc | Control loop gain | 1.68 |
| K | Torque coefficient | 2.67 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Jeong, C.-S.; Kim, M.; Jin, S. Force-Free Control for Direct Teaching of a Surgical Assistant Robot End Effector with Wire-Driven Bidirectional Telescopic Mechanism. Sensors 2021, 21, 3498. https://doi.org/10.3390/s21103498
Zhang Y, Jeong C-S, Kim M, Jin S. Force-Free Control for Direct Teaching of a Surgical Assistant Robot End Effector with Wire-Driven Bidirectional Telescopic Mechanism. Sensors. 2021; 21(10):3498. https://doi.org/10.3390/s21103498
Chicago/Turabian StyleZhang, Youqiang, Cheol-Su Jeong, Minhyo Kim, and Sangrok Jin. 2021. "Force-Free Control for Direct Teaching of a Surgical Assistant Robot End Effector with Wire-Driven Bidirectional Telescopic Mechanism" Sensors 21, no. 10: 3498. https://doi.org/10.3390/s21103498






