THz Sensing of Human Skin: A Review of Skin Modeling Approaches
Abstract
:1. Introduction
1.1. Terahertz Radiation and Systems
1.2. Biomedical Applications of THz Imaging
1.3. Variables Affecting In Vivo THz Measurements of Skin
1.4. Aim of this Review
2. New Advances of THz Measurement and Modeling of Skin
2.1. Dielectric Model
2.1.1. Double Debye Model
2.1.2. Effective Medium Theory
2.2. Structural Models for THz Waves
2.2.1. Single Layer Model
2.2.2. Two-Layer Model
2.2.3. Model with Depth-Dependent Water Concentration
- Stratified media model:
- Fresnel equation-based model:
2.2.4. Model with Anisotropic Stratum Corneum
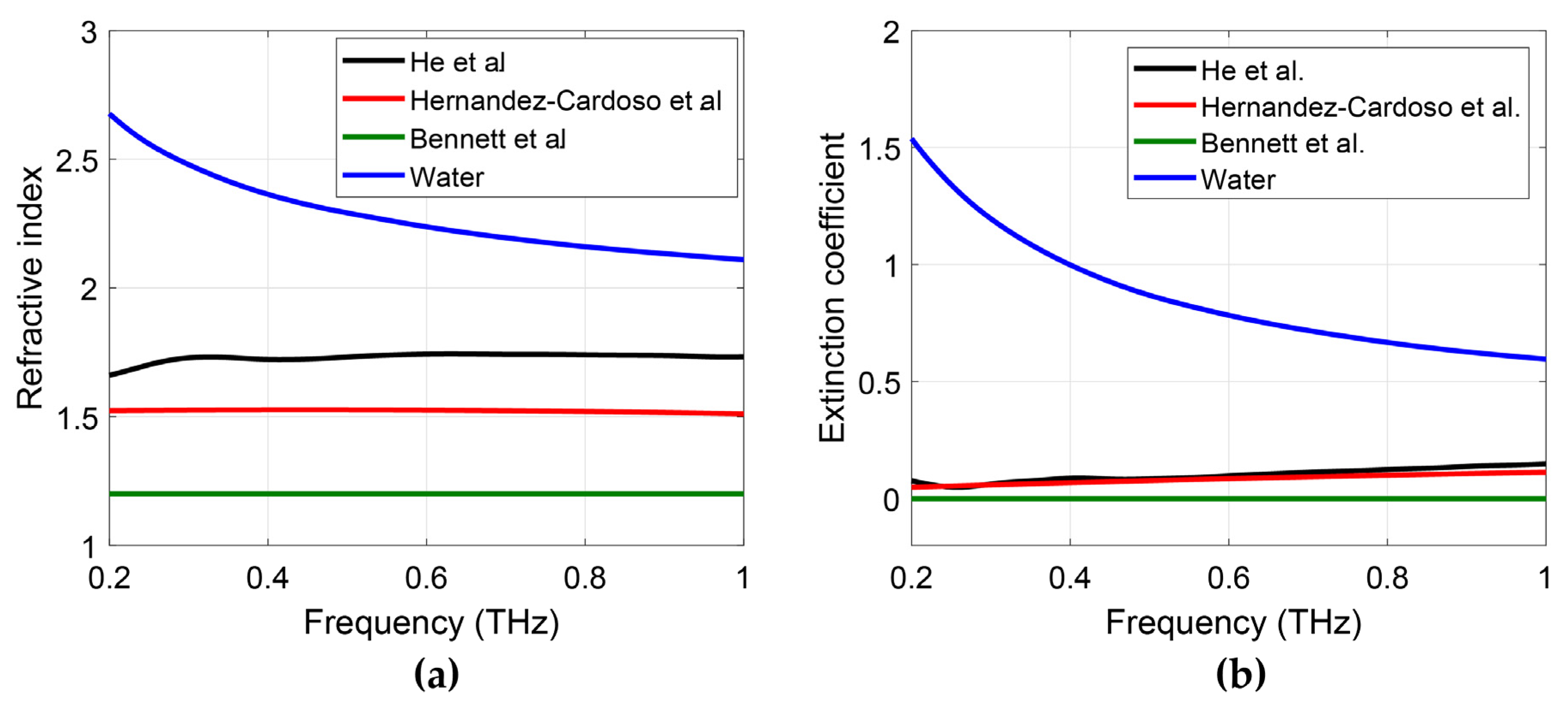
2.3. Comparison of Different Models
3. Future Perspective
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liebe, H.J.; Hufford, G.A.; Manabe, T. A model for the complex permittivity of water at frequencies below 1 THz. Int. J. Infrared Millim. Waves 1991, 12, 659–675. [Google Scholar] [CrossRef]
- Cal, K.; Stefanowska, J.; Zakowiecki, D. Current tools for skin imaging and analysis. Int. J. Dermatol. 2009, 48, 1283–1289. [Google Scholar] [CrossRef] [PubMed]
- Rallan, D.; Harland, C.C. Skin imaging: Is it clinically useful? Clin. Exp. Dermatol. 2004, 29, 453–459. [Google Scholar] [CrossRef] [PubMed]
- Boyd, A.; Cain, O.; Chauhan, A.; Webb, G.J. Medical liver biopsy: Background, indications, procedure and histopathology. Front. Gastroenterol. 2020, 11, 40–47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bergh, B.A.I.V.D.; Swartzendruber, D.C.; Hoogstraate, J.J.; Schrijvers, A.H.G.J.; Boddé, H.E.; Junginger, H.E.; Bouwstra, J.A.; Der Geest, A.B.-V. Development of an optimal protocol for the ultrastructural examination of skin by transmission electron microscopy. J. Microsc. 1997, 187, 125–133. [Google Scholar] [CrossRef] [PubMed]
- White, N.S.; Errington, R.J. Fluorescence techniques for drug delivery research: Theory and practice. Adv. Drug Deliv. Rev. 2005, 57, 17–42. [Google Scholar] [CrossRef]
- Kilpatrick-Liverman, L.; Kazmi, P.; Wolff, E.; Polefka, T.G. The use of near-infrared spectroscopy in skin care applications. Ski. Res. Technol. 2006, 12, 162–169. [Google Scholar] [CrossRef]
- Caspers, P.; Lucassen, G.; Puppels, G. Combined In Vivo Confocal Raman Spectroscopy and Confocal Microscopy of Human Skin. Biophys. J. 2003, 85, 572–580. [Google Scholar] [CrossRef] [Green Version]
- Eberhardt, K.; Stiebing, C.; Matthäus, C.; Schmitt, M.; Popp, J. Advantages and limitations of Raman spectroscopy for molecular diagnostics: An update. Expert Rev. Mol. Diagn. 2015, 15, 773–787. [Google Scholar] [CrossRef] [PubMed]
- Welzel, J.; Lankenau, E.; Birngruber, R.; Engelhardt, R. Optical coherence tomography of the human skin. J. Am. Acad. Dermatol. 1997, 37, 958–963. [Google Scholar] [CrossRef]
- Schwartz, M.; Levine, A.; Markowitz, O. Optical coherence tomography in dermatology. Cutis 2017, 100, 163–166. [Google Scholar]
- Goldman, L.W. Principles of CT: Radiation Dose and Image Quality. J. Nucl. Med. Technol. 2007, 35, 213–225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, S.-Y.; Boone, J.M.; Yang, K.; Kwan, A.L.C.; Packard, N.J. The effect of skin thickness determined using breast CT on mammographic dosimetry. Med. Phys. 2008, 35, 1199–1206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mirrashed, F.; Sharp, J.C. In vivo morphological characterisation of skin by MRI micro-imaging methods. Ski. Res. Technol. 2004, 10, 149–160. [Google Scholar] [CrossRef]
- Mirbeik-Sabzevari, A.; Tavassolian, N. Ultrawideband, Stable Normal and Cancer Skin Tissue Phantoms for Millimeter-Wave Skin Cancer Imaging. IEEE Trans. Biomed. Eng. 2018, 66, 176–186. [Google Scholar] [CrossRef] [PubMed]
- Fear, E.C. Microwave Imaging of the Breast. Technol. Cancer Res. Treat. 2005, 4, 69–82. [Google Scholar] [CrossRef] [Green Version]
- Owda, A.Y.; Salmon, N.; Casson, A.J.; Owda, M. The Reflectance of Human Skin in the Millimeter-Wave Band. Sensors 2020, 20, 1480. [Google Scholar] [CrossRef] [Green Version]
- Owda, A.Y.; Salmon, N.; Harmer, S.W.; Shylo, S.; Bowring, N.J.; Rezgui, N.D.; Shah, M. Millimeter-wave emissivity as a metric for the non-contact diagnosis of human skin conditions. Bioelectromagnetics 2017, 38, 559–569. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, N.; Matsumoto, M.; Sakai, S. In vivo measurement of the water content in the dermis by confocal Raman spectroscopy. Ski. Res. Technol. 2010, 16, 137–141. [Google Scholar] [CrossRef]
- Chen, X.; Parrott, E.P.J.; Ung, B.S.-Y.; Pickwell-MacPherson, E. A Robust Baseline and Reference Modification and Acquisition Algorithm for Accurate THz Imaging. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 493–501. [Google Scholar] [CrossRef]
- Rakić, A.D.; Taimre, T.; Bertling, K.; Lim, Y.L.; Dean, P.; Valavanis, A.; Indjin, D. Sensing and imaging using laser feedback interferometry with quantum cascade lasers. Appl. Phys. Rev. 2019, 6, 021320. [Google Scholar] [CrossRef] [Green Version]
- Rakić, A.D.; Lim, Y.L.; Taimre, T.; Agnew, G.; Qi, X.; Bertling, K.; Han, S.; Wilson, S.J.; Kundu, I.; Grier, A.; et al. Optical feedback effects on terahertz quantum cascade lasers: Modelling and applications. In Infrared, Millimeter-Wave, and Terahertz Technologies IV; International Society for Optics and Photonics: Beijing, China, 2016; p. 1003016. [Google Scholar]
- Rakic, A.D.; Taimre, T.; Bertling, K.; Lim, Y.L.; Wilson, S.J.; Nikolić, M.; Valavanis, A.; Indjin, D.; Linfield, E.H.; Davies, A.G.; et al. THz QCL self-mixing interferometry for biomedical applications. In Terahertz Emitters, Receivers, and Applications V; International Society for Optics and Photonics: San Diego, CA, USA, 2014; p. 91990M. [Google Scholar]
- Shi, L.; Shumyatsky, P.; Rodríguez-Contreras, A.; Alfano, R. Terahertz spectroscopy of brain tissue from a mouse model of Alzheimer’s disease. J. Biomed. Opt. 2016, 21, 015014. [Google Scholar] [CrossRef] [Green Version]
- Hou, D.; Li, X.; Cai, J.; Ma, Y.; Kang, X.; Huang, P.; Zhang, G. Terahertz spectroscopic investigation of human gastric normal and tumor tissues. Phys. Med. Biol. 2014, 59, 5423–5440. [Google Scholar] [CrossRef]
- Wang, J.; Lindley-Hatcher, H.; Liu, K.; Pickwell-MacPherson, E. Evaluation of transdermal drug delivery using terahertz pulsed imaging. Biomed. Opt. Express 2020, 11, 4484–4490. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Stantchev, R.I.; Wang, J.; Parrott, E.P.J.; Cottenden, A.; Chiu, T.-W.; Ahuja, A.T.; Pickwell-MacPherson, E. In vivo estimation of water diffusivity in occluded human skin using terahertz reflection spectroscopy. J. Biophotonics 2018, 12, e201800145. [Google Scholar] [CrossRef] [PubMed]
- Lindley-Hatcher, H.; Hernandez-Serrano, A.I.; Wang, J.; Cebrian, J.; Hardwicke, J.; Pickwell-MacPherson, E. Evaluation of in vivo THz sensing for assessing human skin hydration. J. Phys. Photonics 2021, 3, 014001. [Google Scholar] [CrossRef]
- Pickwell, E.; Cole, B.E.; Fitzgerald, A.J.; Pepper, M.; Wallace, V.P. In vivo study of human skin using pulsed terahertz radiation. Phys. Med. Biol. 2004, 49, 1595. [Google Scholar] [CrossRef]
- Fitzgerald, A.J.; Wallace, V.P.; Jimenez-Linan, M.; Bobrow, L.; Pye, R.J.; Purushotham, A.D.; Arnone, D.D. Terahertz Pulsed Imaging of Human Breast Tumors. Radiology 2006, 239, 533–540. [Google Scholar] [CrossRef]
- Ji, Y.B.; Oh, S.J.; Kang, S.-G.; Heo, J.; Kim, S.-H.; Choi, Y.; Song, S.; Son, H.Y.; Kim, S.H.; Lee, J.H.; et al. Terahertz reflectometry imaging for low and high grade gliomas. Sci. Rep. 2016, 6, 36040. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wallace, V.P.; Fitzgerald, A.J.; Shankar, S.; Flanagan, N.; Pye, R.; Cluff, J.; Arnone, D.D. Terahertz pulsed imaging of basal cell carcinoma ex vivo and in vivo. Br. J. Dermatol. 2004, 151, 424–432. [Google Scholar] [CrossRef]
- Cole, B.E.; Woodward, R.M.; Crawley, D.A.; Wallace, V.P.; Arnone, D.D.; Pepper, M. Terahertz imaging and spectroscopy of human skin in vivo. In Commercial and Biomedical Applications of Ultrashort Pulse Lasers; Laser Plasma Generation and Diagnostics; International Society for Optics and Photonics: San Jose, CA, USA, 2001; pp. 1–10. [Google Scholar]
- Fan, S.; Ung, B.S.Y.; Parrott, E.P.J.; Wallace, V.P.; Pickwell-MacPherson, E. In vivo terahertz reflection imaging of human scars during and after the healing process. J. Biophotonics 2016, 10, 1143–1151. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Sun, Q.; Stantchev, R.I.; Chiu, T.-W.; Ahuja, A.T.; Pickwell-MacPherson, E. In vivo terahertz imaging to evaluate scar treatment strategies: Silicone gel sheeting. Biomed. Opt. Express 2019, 10, 3584–3590. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.W.; Kim, K.-S.; Kim, H.; Lee, S.H.; Park, J.-H.; Han, J.-H.; Seok, S.-H.; Park, J.; Choi, Y.; Kim, Y.I.; et al. Terahertz dynamic imaging of skin drug absorption. Opt. Express 2012, 9, 9476–9484. [Google Scholar] [CrossRef]
- Kim, K.W.; Kim, H.; Park, J.; Han, J.K.; Son, J.-H. Terahertz Tomographic Imaging of Transdermal Drug Delivery. IEEE Trans. Terahertz Sci. Technol. 2011, 2, 99–106. [Google Scholar] [CrossRef]
- Wang, J.; Stantchev, R.I.; Sun, Q.; Chiu, T.-W.; Ahuja, A.T.; MacPherson, E.P. THz in vivo measurements: The effects of pressure on skin reflectivity. Biomed. Opt. Express 2018, 9, 6467–6476. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Parrott, E.P.; He, Y.; Pickwell-MacPherson, E. In vivo THz imaging of human skin: Accounting for occlusion effects. J. Biophotonics 2017, 11, e201700111. [Google Scholar] [CrossRef]
- Lindley-Hatcher, H.; I Hernandez-Serrano, A.; Sun, Q.; Wang, J.; Cebrian, J.; Blasco, L.; Pickwell-MacPherson, E. A Robust Protocol for In Vivo THz Skin Measurements. J. Infrared Millim. Terahertz Waves 2019, 40, 980–989. [Google Scholar] [CrossRef] [Green Version]
- Pickwell, E.; Cole, B.E.; Fitzgerald, A.J.; Wallace, V.P.; Pepper, M. Simulation of terahertz pulse propagation in biological systems. Appl. Phys. Lett. 2004, 84, 2190–2192. [Google Scholar] [CrossRef]
- Zaytsev, K.I.; Dolganova, I.N.; Chernomyrdin, N.V.; Katyba, G.M.; Gavdush, A.A.; Cherkasova, O.P.; Komandin, G.; Shchedrina, M.A.; Khodan, A.N.; Ponomarev, D.S.; et al. The progress and perspectives of terahertz technology for diagnosis of neoplasms: A review. J. Opt. 2019, 22, 013001. [Google Scholar] [CrossRef]
- Truong, B.C.Q.; Tuan, H.D.; Fitzgerald, A.J.; Wallace, V.P.; Nguyen, H.T. High correlation of double Debye model parameters in skin cancer detection. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; Volume 2014, pp. 718–721. [Google Scholar]
- Yada, H.; Nagai, M.; Tanaka, K. Origin of the fast relaxation component of water and heavy water revealed by terahertz time-domain attenuated total reflection spectroscopy. Chem. Phys. Lett. 2008, 464, 166–170. [Google Scholar] [CrossRef]
- Stantchev, R.I.; Yu, X.; Blu, T.; Pickwell-MacPherson, E. Real-time terahertz imaging with a single-pixel detector. Nat. Commun. 2020, 11, 2535. [Google Scholar] [CrossRef]
- Gente, R.; Born, N.; Voß, N.; Sannemann, W.; Léon, J.; Koch, M.; Castro-Camus, E. Determination of Leaf Water Content from Terahertz Time-Domain Spectroscopic Data. J. Infrared Millim. Terahertz Waves 2013, 34, 316–323. [Google Scholar] [CrossRef]
- He, Y.; Liu, K.; Au, C.; Sun, Q.; Parrott, E.P.J.; Pickwell-MacPherson, E. Determination of terahertz permittivity of dehydrated biological samples. Phys. Med. Biol. 2017, 62, 8882–8893. [Google Scholar] [CrossRef]
- Scheller, M.; Jansen, C.; Koch, M. Applications of Effective Medium Theories in the Terahertz Regime. In Recent Opt. Photonic Technol; IntechOpen: London, UK, 2010; pp. 231–250. [Google Scholar] [CrossRef] [Green Version]
- Hernandez-Cardoso, G.G.; Rojas-Landeros, S.C.; Alfaro-Gomez, M.; Hernandez-Serrano, A.I.; Salas-Gutierrez, I.; Lemus-Bedolla, E.; Castillo-Guzman, A.R.; Lopez-Lemus, H.L.; Castro-Camus, E. Terahertz imaging for early screening of diabetic foot syndrome: A proof of concept. Sci. Rep. 2017, 7, srep42124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hernandez-Cardoso, G.G.; Singh, A.K.; Castro-Camus, E. Empirical comparison between effective medium theory models for the dielectric response of biological tissue at terahertz frequencies. Appl. Opt. 2020, 59, D6–D11. [Google Scholar] [CrossRef]
- Bennett, D.B.; Li, W.; Taylor, Z.D.; Grundfest, W.S.; Brown, E.R. Stratified Media Model for Terahertz Reflectometry of the Skin. IEEE Sens. J. 2010, 11, 1253–1262. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Q.; Wang, J.; Pickwell-MacPherson, E. Skin Surface Feature Influence on Terahertz in vivo Measurements. In Proceedings of the 2020 45th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Institute of Electrical and Electronics Engineers (IEEE), Paris, France, 1–6 September 2020; pp. 1–2. [Google Scholar]
- Chen, X.; Sun, Q.; Wang, J.; Lindley-Hatcher, H.; Pickwell-MacPherson, E. Exploiting Complementary Terahertz Ellipsometry Configurations to Probe the Hydration and Cellular Structure of Skin In Vivo. Adv. Photonics Res. 2021, 2, 2000024. [Google Scholar] [CrossRef]
- Nibali, V.C.; Havenith, M. New Insights into the Role of Water in Biological Function: Studying Solvated Biomolecules Using Terahertz Absorption Spectroscopy in Conjunction with Molecular Dynamics Simulations. J. Am. Chem. Soc. 2014, 136, 12800–12807. [Google Scholar] [CrossRef] [PubMed]
- Menon, G.K.; Cleary, G.W.; Lane, M.E. The structure and function of the stratum corneum. Int. J. Pharm. 2012, 435, 3–9. [Google Scholar] [CrossRef]
- Tippavajhala, V.K.; Magrini, T.D.; Matsuo, D.C.; Silva, M.G.P.; Favero, P.P.; De Paula, L.R.; Martin, A.A. In Vivo Determination of Moisturizers Efficacy on Human Skin Hydration by Confocal Raman Spectroscopy. AAPS PharmSciTech 2018, 19, 3177–3186. [Google Scholar] [CrossRef]
- Dąbrowska, A.K.; Adlhart, C.; Spano, F.; Rotaru, G.-M.; Derler, S.; Zhai, L.; Spencer, N.D.; Rossi, R.M. In vivo confirmation of hydration-induced changes in human-skin thickness, roughness and interaction with the environment. Biointerphases 2016, 11, 031015. [Google Scholar] [CrossRef] [Green Version]
- Egawa, M.; Hirao, T.; Takahashi, M. In vivo Estimation of Stratum Corneum Thickness from Water Concentration Profiles Obtained with Raman Spectroscopy. Acta Derm. Venereol. 2007, 87, 4–8. [Google Scholar] [CrossRef] [Green Version]
- Smith, G.D. Numerical Solution of Partial Differential Equations: Finite Difference Methods; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Hale, D.K. The physical properties of composite materials. J. Mater. Sci. 1976, 11, 2105–2141. [Google Scholar] [CrossRef]
- Rawlings, A.V. Ethnic skin types: Are there differences in skin structure and function? Int. J. Cosmet. Sci. 2006, 28, 79–93. [Google Scholar] [CrossRef] [PubMed]
- Farage, M.A.; Miller, K.W.; Elsner, P.; Maibach, H.I. Structural Characteristics of the Aging Skin: A Review. Cutan. Ocul. Toxicol. 2007, 26, 343–357. [Google Scholar] [CrossRef]
- Baumann, L. Skin ageing and its treatment. J. Pathol. 2007, 211, 241–251. [Google Scholar] [CrossRef] [PubMed]
- Firooz, A.; Sadr, B.; Babakoohi, S.; Sarraf-Yazdy, M.; Fanian, F.; Kazerouni-Timsar, A.; Nassiri-Kashani, M.; Naghizadeh, M.M.; Dowlati, Y. Variation of Biophysical Parameters of the Skin with Age, Gender, and Body Region. Sci. World J. 2012, 2012, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Ehlers, C.; Ivens, U.I.; Møller, M.L.; Senderovitz, T.; Serup, J. Females have lower skin surface pH than men: A study on the influence of gender, forearm site variation, right/left difference and time of the day on the skin surface pH. Ski. Res. Technol. 2001, 7, 90–94. [Google Scholar] [CrossRef]
- Wilhelm, K.P.; Cua, A.B.; Maibach, H.I. Skin Aging: Effect on Transepidermal Water Loss, Stratum Corneum Hydration, Skin Surface pH, and Casual Sebum Content. Arch. Dermatol. 1991, 127, 1806–1809. [Google Scholar] [CrossRef]
- Barker, X.R.; Pickwell-MacPherson, E. In vivo THz Measurements of Human Skin: Investigating the Dependence on Ethnicity and Arm Dominance. In Proceedings of the 2019 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Institute of Electrical and Electronics Engineers (IEEE), Paris, France, 1–6 September 2019; pp. 1–2. [Google Scholar]
- Peralta, X.G.; Lipscomb, D.; Wilmink, G.J.; Echchgadda, I. Terahertz spectroscopy of human skin tissue models with different melanin content. Biomed. Opt. Express 2019, 10, 2942–2955. [Google Scholar] [CrossRef] [PubMed]
- Clegg, J.; Robinson, M.P. A genetic algorithm used to fit Debye functions to the dielectric properties of tissues. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Clegg, J.; Robinson, M.P. A genetic algorithm for optimizing multi-pole Debye models of tissue dielectric properties. Phys. Med. Biol. 2012, 57, 6227–6243. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Yang, F.; Yu, X.; Li, M.; Gao, B.; Fang, Y.; Huang, X. Optimization of Data Fitting Algorithm for Tissue Dielectric Properties in THz-band using Genetic Algorithm. In Proceedings of the 2019 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Institute of Electrical and Electronics Engineers (IEEE), Paris, France, 1–6 September 2019; pp. 1–2. [Google Scholar]
- Truong, B.C.Q.; Tuan, H.D.; Kha, H.H.; Nguyen, H.T. Global optimization for human skin investigation in terahertz. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, IEEE, San Diego, CA, USA, 28 August–1 September 2012; Volume 2012, pp. 5474–5477. [Google Scholar]
- Truong, B.C.Q.; Tuan, H.D.; Kha, H.H.; Nguyen, H.T. Debye Parameter Extraction for Characterizing Interaction of Terahertz Radiation with Human Skin Tissue. IEEE Trans. Biomed. Eng. 2013, 60, 1528–1537. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Chopra, N.; Abbasi, Q.H.; Qaraqe, K.A.; Alomainy, A. Collagen Analysis at Terahertz Band Using Double-Debye Parameter Extraction and Particle Swarm Optimisation. IEEE Access 2017, 5, 27850–27856. [Google Scholar] [CrossRef]















| Model | Merits | Limitations |
|---|---|---|
| Double Debye model | Physical properties obtained Very little prior knowledge needed | Accuracy for dry tissues is questionable |
| Effective medium theory | Direct extraction of the water content Very few fitting parameters | Requires a prior knowledge on the biological background EMT assumptions may not be satisfied |
| Single-layer model | Simple characterization | Oversimplified Cannot distinguish different tissues No comparability between different setups |
| Double-layer model | Differentiate SC and epidermis Good accuracy | Dielectric models needed |
| Stratified media model/Fresnel Theory | Clear water concentration distribution Good consistency with Raman spectroscopy | Pre-defined water profile needed More difficult convergence |
| Anisotropic SC model | Birefringence induced by SC cellular structure considered No dielectric model used Both hydration and structural information obtained | Needs multiple uncorrelated measurements for a convergent fit |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Lindley-Hatcher, H.; Chen, X.; Pickwell-MacPherson, E. THz Sensing of Human Skin: A Review of Skin Modeling Approaches. Sensors 2021, 21, 3624. https://doi.org/10.3390/s21113624
Wang J, Lindley-Hatcher H, Chen X, Pickwell-MacPherson E. THz Sensing of Human Skin: A Review of Skin Modeling Approaches. Sensors. 2021; 21(11):3624. https://doi.org/10.3390/s21113624
Chicago/Turabian StyleWang, Jiarui, Hannah Lindley-Hatcher, Xuequan Chen, and Emma Pickwell-MacPherson. 2021. "THz Sensing of Human Skin: A Review of Skin Modeling Approaches" Sensors 21, no. 11: 3624. https://doi.org/10.3390/s21113624






