A Multifunctional Smart Meter Using ANN-PSO Flux Estimation and Harmonic Active Compensation with Fuzzy Voltage Regulation
Abstract
1. Introduction
2. Material and Methods
2.1. Artificial Neural Network and PSO
2.2. Smart Systems
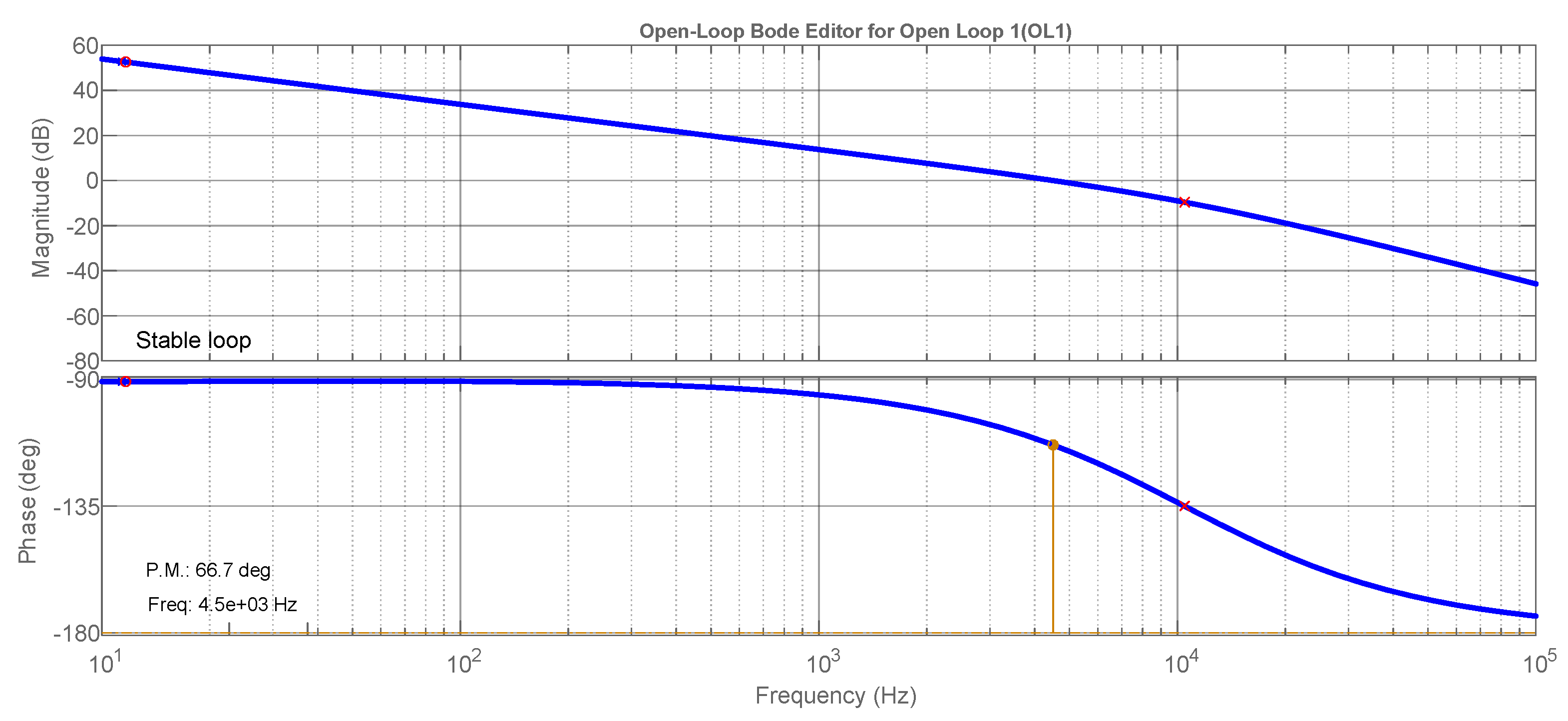
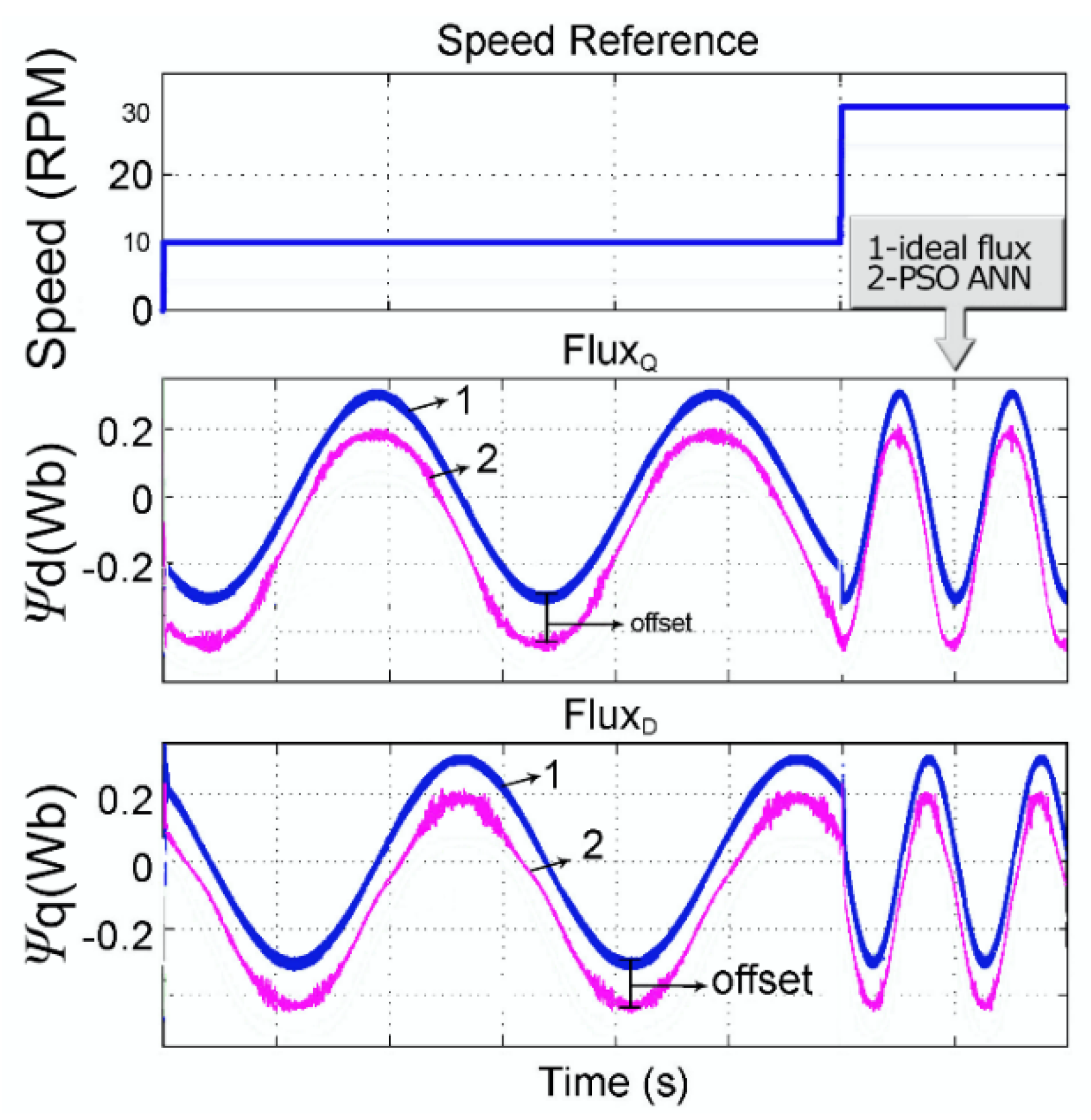
3. Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhosale, S.S.; Bhosale, Y.N.; Chavan, U.M.; Malvekar, S.A. Power quality improvement by using UPQC: A review. In Proceedings of the 2018 International Conference on Control, Power, Communication and Computing Technologies (ICCPCCT), Kannur, India, 23–24 March 2018; pp. 375–380. [Google Scholar]
- Barcenas, E.B.; Cardenas, V.; Roffiel, J.A. Review of power factor correction in three-phase three wire systems. In Proceedings of the 2006 IEEE International Power Electronics Congress, Puebla, Mexico, 16–18 October 2006; pp. 1–6. [Google Scholar]
- Das, J. Passive filters-potentialities and limitations. In Proceedings of the Conference Record of the 2003 Annual Pulp and Paper Industry Technical Conference, Charleston, SC, USA, 16–20 June 2003; pp. 187–197. [Google Scholar]
- Wang, F.; Yang, F.; Liu, T.; Hu, X. Measuring energy meter of three-phase electricity-stealing defense system. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 11–15. [Google Scholar]
- Da Silva, S.A.O.; Modesto, R.A. Active power line compensation applied to a three-phase line interactive UPS system using SRF method. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 12–16 June 2005; pp. 2358–2362. [Google Scholar]
- Chang, L.; Diduch, C.; Song, P. Development of standards for interconnecting distributed generators with electric power systems. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 12–16 June 2005; pp. 1–7. [Google Scholar]
- Bhattacharyya, S.; Van Lumig, M.; Cobben, S.; Myrzik, J.; Kling, W. Consequences of poor power quality for grid operators. In Proceedings of the International Conference and Exhibition on Electricity Distribution, Prague, Czech Republic, 8–11 June 2009; pp. 8–11. [Google Scholar]
- Li, E.; Sheng, W.; Wang, X.; Wang, B. Combined compensation strategies based on instantaneous reactive power theory for reactive power compensation and load balancing. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Yichang, China, 16–18 September 2011; pp. 5788–5791. [Google Scholar]
- Kanagavel, R.; Vairavasundaram, I.; Padmanaban, S. Design and prototyping of single-phase shunt active power filter for harmonics elimination using model predictive current control. Int. Trans. Electr. Energy Syst. 2020, 30. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic—A personal perspective. Fuzzy Sets Syst. 2015, 281, 4–20. [Google Scholar] [CrossRef]
- Bessaad, T.; Taleb, R.; Chabni, F.; Iqbal, A. Fuzzy adaptive control of a multimachine system with single inverter supply. Int. Trans. Electr. Energy Syst. 2019, 29. [Google Scholar] [CrossRef]
- Zhou, Y.-S.; Lai, L.-Y. Optimal design for fuzzy controllers by genetic algorithms. IEEE Trans. Ind. Appl. 2002, 36, 93–97. [Google Scholar] [CrossRef]
- Akpan, V.A.; Hassapis, G. Adaptive predictive control using recurrent neural network identification. In Proceedings of the 2009 17th Mediterranean Conference on Control and Automation, Thessaloniki, Greece, 24–26 June 2009; pp. 61–66. [Google Scholar]
- Krishnamoorthy, S.; Sanjeevikumar, P.; Holm-Nielsen, J.B.; Raja Singh, R.; Rajesh, M. Torque ripple minimization of PMSM using an adaptive Elman neural network-controlled feedback linearization-based direct torque control strategy. Int. Trans. Electr. Energy Syst. 2021, 31. [Google Scholar] [CrossRef]
- Costa, B.L.G.; Graciola, C.L.; Angélico, B.A.; Goedtel, A.; Castoldi, M.F.; Pereira, W.C.D.A. A practical framework for tuning DTC-SVM drive of three-phase induction motors. Control. Eng. Pract. 2019, 88, 119–127. [Google Scholar] [CrossRef]
- Gong, Y.-J.; Shen, M.; Zhang, J.; Kaynak, O.; Chen, W.-N.; Zhan, Z.-H. Optimizing RFID network planning by using a particle swarm optimization algorithm with redundant reader elimination. IEEE Trans. Ind. Inform. 2012, 8, 900–912. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C.; Shi, Y. Swarm Intelligence; Elsevier: Amsterdam, The Netherlands, 2001; p. 512. [Google Scholar]
- Del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.-C.; Harley, R.G. Particle swarm optimization: Basic concepts, variants and applications in power systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimisation: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Serov, A.N.; Serov, N.A.; Lupachev, A.A. The application of digital filtration for the active power measurement. In Proceedings of the 2018 IEEE International Conference on Electrical Engineering and Photonics (EExPolytech), St. Petersburg, Russia, 22–23 October 2018; pp. 88–92. [Google Scholar]
- Chatterjee, D.; Dalapati, S. Single-phase average power measurement using instantaneous power theory in a fixed point processor. In Proceedings of the 2020 IEEE Calcutta Conference (CALCON), Kolkata, India, 28–29 February 2020; pp. 297–301. [Google Scholar]
- Acosta, J.; Gonzalez, A.; Martínez, Z. FPGA based control scheme for active power filter. In Proceedings of the 2006 IEEE/PES Transmission & Distribution Conference and Exposition: Latin America, Caracas, Venezuela, 15–18 August 2006; pp. 1–4. [Google Scholar]
- Dai, W.; Wang, B.; Xie, Y. A novel fuzzy logic controller for active power filter. In Proceedings of the 2009 IEEE International Conference on Computational Intelligence for Measurement Systems and Applications, Hong Kong, China, 11–13 May 2009; pp. 118–123. [Google Scholar]
- Saavedra, E.; Del Campo, G.; Santamaria, A. Smart Metering for Challenging Scenarios: A Low-Cost, Self-Powered and Non-Intrusive IoT Device. Sensors 2020, 20, 7133. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, R. Electric Motor Drives—Modeling. Analysis and Control; Prentice Hall: Upper Saddle River, NJ, USA, 2001; 626p. [Google Scholar]
- Teja, A.V.R.; Chakraborty, C.; Maiti, S.; Hori, Y. A new model reference adaptive controller for four quadrant vector controlled induction motor drives. IEEE Trans. Ind. Electron. 2011, 59, 3757–3767. [Google Scholar] [CrossRef]
- Joice, C.S.; Paranjothi, S.R.; Kumar, V.J.S. Digital control strategy for four quadrant operation of three phase BLDC motor with load variations. IEEE Trans. Ind. Informatics 2012, 9, 974–982. [Google Scholar] [CrossRef]
- Jin, T.; Li, L.; Smedley, K.M. A universal vector controller for four-quadrant three-phase power converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 377–390. [Google Scholar] [CrossRef]
- Ogata, K. Discrete Time Control Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2000; 745p. [Google Scholar]
- Mikulovic, J.; Skrbic, B.; Durisic, Z. Power definitions for polyphase systems based on Fortescue’s symmetrical com-ponents. Int. J. Electr. Power Energy Syst. 2018, 98, 455–462. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Kluwer Academic Publishers: New York, NY, USA, 2001; 900p. [Google Scholar]
- Rahmani, S.; Hamadi, A.; Al-Haddad, K.; Dessaint, L.A. A combination of shunt hybrid power filter and thyris-tor-controlled reactor for power quality. IEEE Trans. Ind. Electron. 2014, 61, 2152–2164. [Google Scholar] [CrossRef]
- Limongi, L.R.; Bojoi, I.R.; Griva, G.B.; Tenconi, A. Digital current-control schemes. IEEE Ind. Electron. Mag. 2009, 3, 20–31. [Google Scholar] [CrossRef]
- Cai, C.; Wang, L.; Yin, G. A three-phase active power filter based on park transformation. In Proceedings of the 2009 4th International Conference on Computer Science & Education, Nanning, China, 25–28 July 2009; pp. 1221–1224. [Google Scholar]
- Pelusi, D. Optimization of a fuzzy logic controller using genetic algorithms. In Proceedings of the 2011 Third International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2011; Volume 2, pp. 143–146. [Google Scholar]
- Chukhrova, N.; Johannssen, A. Fuzzy regression analysis: Systematic review and bibliography. Appl. Soft Comput. 2019, 84, 1–29. [Google Scholar] [CrossRef]
- Augeby, J.; Angeby, J. Estimating signal parameters using the nonlinear instantaneous least squares approach. IEEE Trans. Signal Process. 2000, 48, 2721–2732. [Google Scholar] [CrossRef]
- Tomioka, S.; Nisiyama, S.; Enoto, T. Nonlinear least square regression by adaptive domain method with multiple genetic algorithms. IEEE Trans. Evol. Comput. 2007, 11, 1–16. [Google Scholar] [CrossRef]




















| Coefficient | Value |
|---|---|
| k0 | 9.13 × |
| k1 | 2.739 × |
| k2 | 2.39 × |
| k3 | 9.13 × |
| k4 | −2.987 |
| k5 | 2.975 |
| k6 | −0.9875 |
| Symbol | Description | Value |
|---|---|---|
| Lc | Inductance | 700 μH |
| Vdc | DC bus voltage | 400 V |
| fs | Switching frequency | 30 kHz |
| ΔiLC | Current ripple | 10% |
| Vgridpeak | Grid peak voltage | 311 V |
| Current sensor | 1/10 | |
| Compensator gain | 3545 | |
| Zero | 73.2 | |
| Pole | 65,820 |
| u(k) | e(k) | |||||
|---|---|---|---|---|---|---|
| de(k) | NB | NS | Z | PS | B | |
| NB | NB | NB | NS | NS | Z | |
| Z | NS | NS | Z | PS | PS | |
| PB | Z | PS | PS | PB | PB | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batista, E.A.; de Brito, M.A.G.; Siqueira, J.C.; Dias, J.C.; Gomez, R.C.; Catharino, M.F.R.; Gomes, M.B. A Multifunctional Smart Meter Using ANN-PSO Flux Estimation and Harmonic Active Compensation with Fuzzy Voltage Regulation. Sensors 2021, 21, 4154. https://doi.org/10.3390/s21124154
Batista EA, de Brito MAG, Siqueira JC, Dias JC, Gomez RC, Catharino MFR, Gomes MB. A Multifunctional Smart Meter Using ANN-PSO Flux Estimation and Harmonic Active Compensation with Fuzzy Voltage Regulation. Sensors. 2021; 21(12):4154. https://doi.org/10.3390/s21124154
Chicago/Turabian StyleBatista, Edson A., Moacyr A. G. de Brito, João C. Siqueira, Jeandro C. Dias, Raphael C. Gomez, Maurilio F. R. Catharino, and Matheus B. Gomes. 2021. "A Multifunctional Smart Meter Using ANN-PSO Flux Estimation and Harmonic Active Compensation with Fuzzy Voltage Regulation" Sensors 21, no. 12: 4154. https://doi.org/10.3390/s21124154
APA StyleBatista, E. A., de Brito, M. A. G., Siqueira, J. C., Dias, J. C., Gomez, R. C., Catharino, M. F. R., & Gomes, M. B. (2021). A Multifunctional Smart Meter Using ANN-PSO Flux Estimation and Harmonic Active Compensation with Fuzzy Voltage Regulation. Sensors, 21(12), 4154. https://doi.org/10.3390/s21124154






