Design and Optimization of Sensitivity Enhancement Package for MEMS-Based Thermal Acoustic Particle Velocity Sensor †
Abstract
:1. Introduction
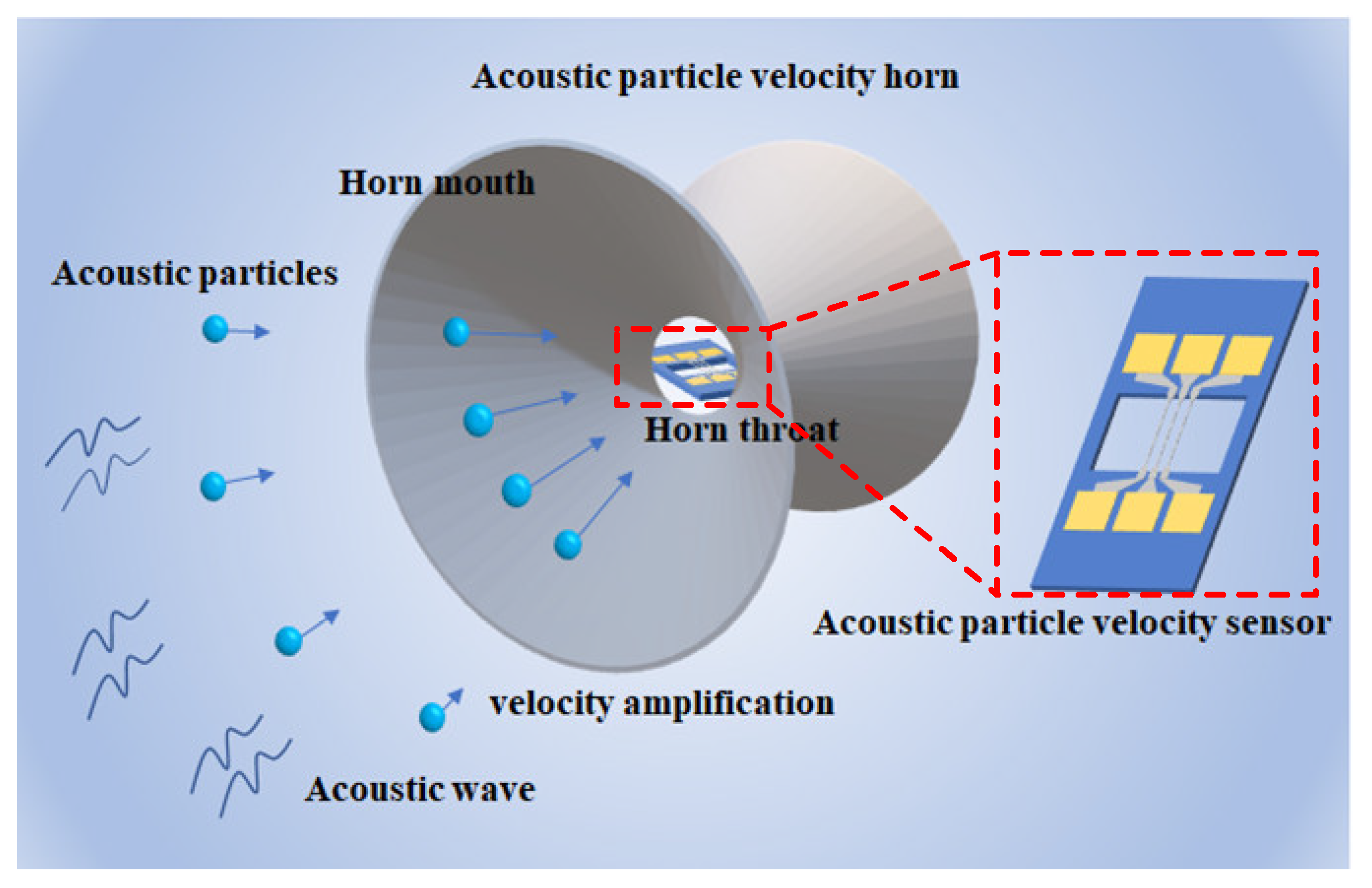
2. Theory and Simulation
2.1. Theory
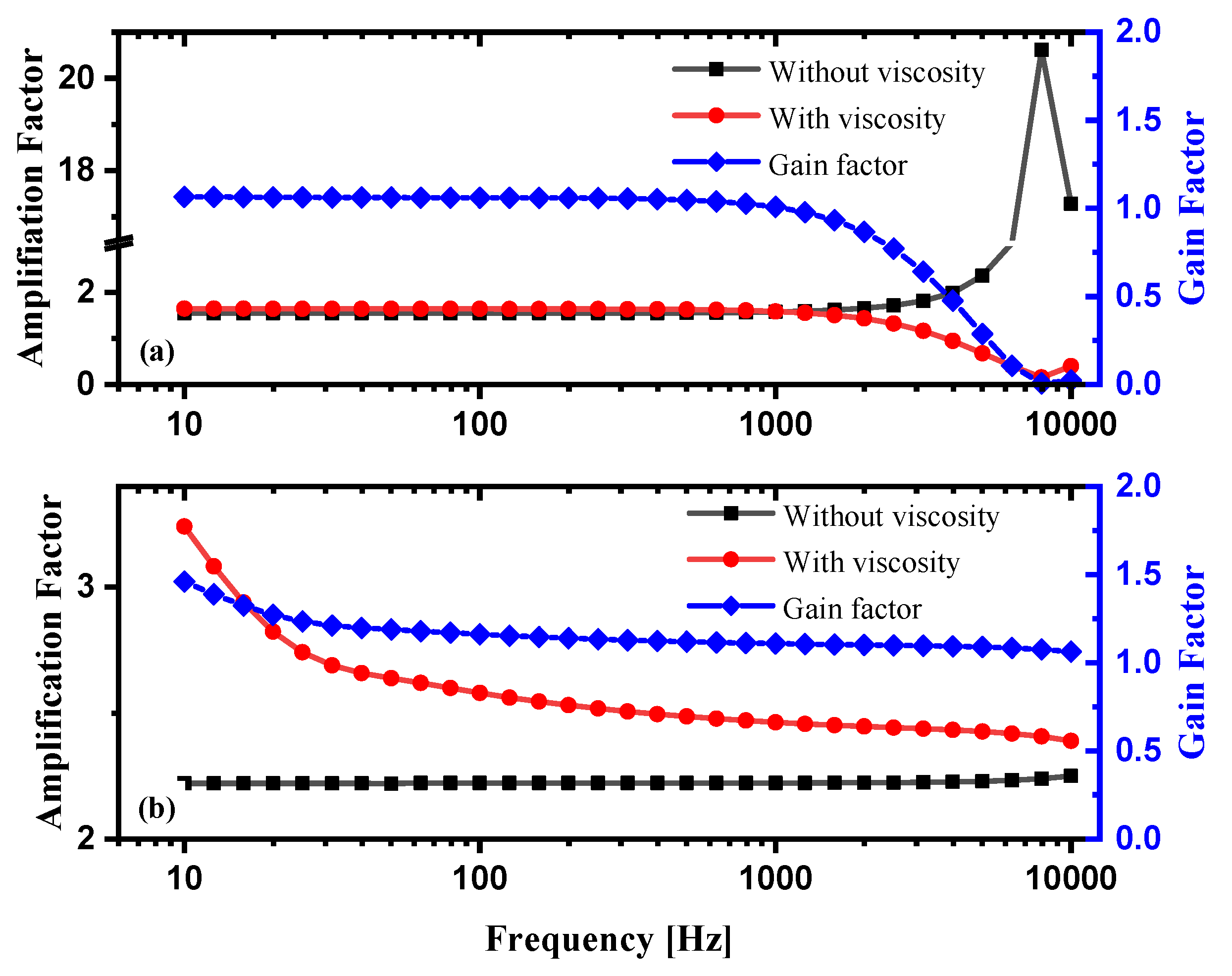
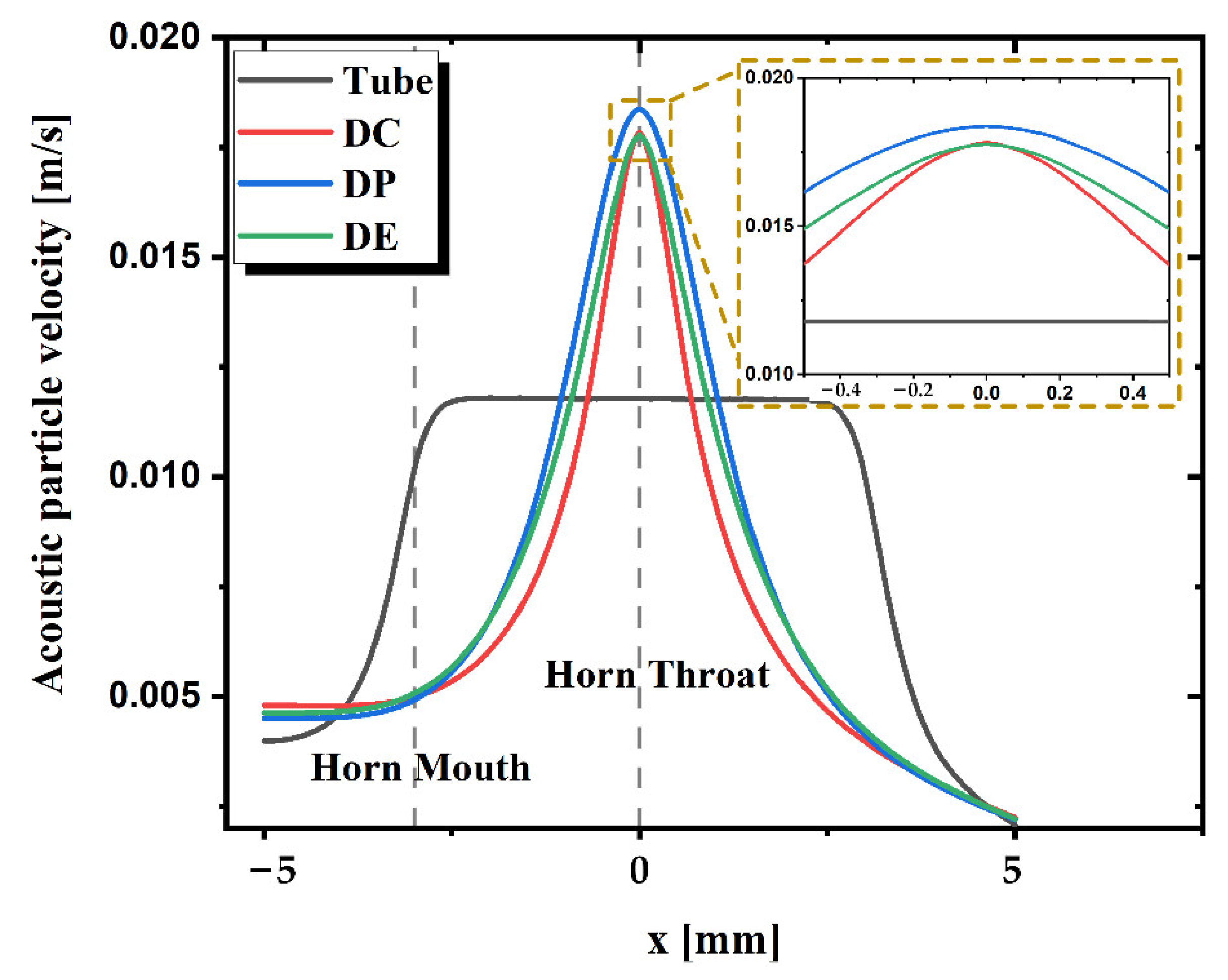
2.2. Simulation
3. Fabrication
4. Experiments
4.1. Experimental Setup
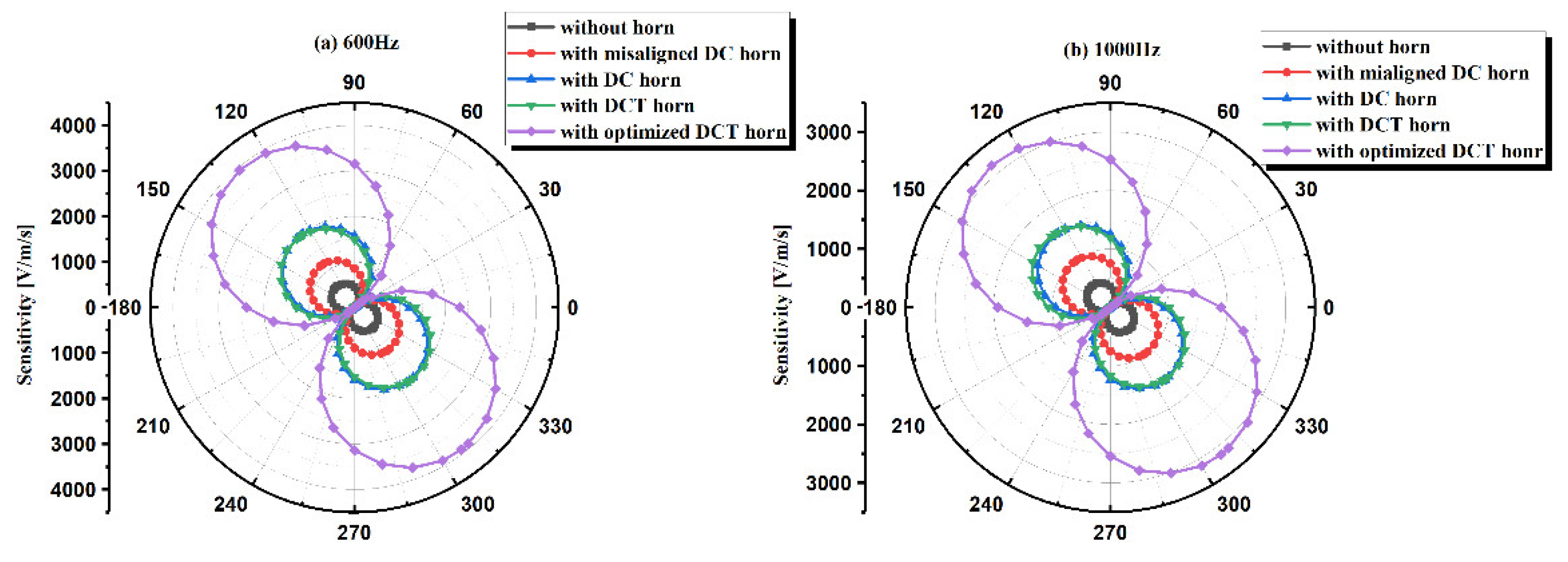
4.2. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kino, G. Acoustic Waves: Devices, Imaging, and Analog Signal Processing; Prentice Hall: Hoboken, NJ, USA, 1987. [Google Scholar]
- De Bree, H.-E. The Microflown: An Acoustic Particle Velocity Sensor. Acoust. Aust. 2003, 31, 91–94. [Google Scholar]
- Chang, W.; Li, Z.; Cheng, S.; Sun, S.; Gao, C.; Hao, Y. A Gas Medium Approach To Sensitivity Improvement Of MEMS-Based Thermal Acoustic Particle Velocity Sensors. In Proceedings of the 2019 International Conference on IC Design and Technology (ICICDT), Suzhou, China, 17–19 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Li, Z.; Chang, W.; Gao, C.; Hao, Y. Three-Hot-Wire Acoustic Particle Velocity Sensor with Improved Detection Capability. Electron. Lett. 2019, 55, 201–202. [Google Scholar] [CrossRef]
- Jacobsen, F.; Bree, H.-E. A Comparison of Two Different Sound Intensity Measurement Principles. J. Acoust. Soc. Am. 2005, 118. [Google Scholar] [CrossRef] [Green Version]
- Fernandez Comesaña, D.; Steltenpool, S.; Korbasiewicz, M.; Tijs, E. Direct Acoustic Vector Field Mapping: New Scanning Tools for Measuring 3D Sound Intensity in 3D Space. In Proceedings of the Euronoise, Maastricht, The Netherlands, 31 May–3 June 2015; pp. 891–895. [Google Scholar]
- Fernandez Comesaña, D.; Nambur Ramamohan, K.; Cabo, D.; Pousa, G. Modelling and Localizing Low Frequency Noise of a Wind Turbine Using an Array of Acoustic Vector Sensors. In Proceedings of the 7th Wind Turbine Noise Conference, Rotterdam, The Netherlands, 2–5 May 2017. [Google Scholar]
- Comesaña, D.; Tijs, E.; de Bree, H.E. Exploring the properties of acoustic particle velocity sensors for near-field noise source localisation applications. In Proceedings of the Forum Acusticum, Krakow, Poland, 7–12 September 2014. [Google Scholar]
- Van Zon, T.; Evers, L.; Vossen, R.; Ainslie, M. Direction of Arrival Estimates with Vector Sensors: First Results of an Atmospheric Infrasound Array in the Netherlands. In Proceedings of the 3rd Internationnal Conference on Underwater Acoustic Measurements: Technologies and Results, Nafplion, Greece, 21–26 June 2009. [Google Scholar]
- Comesana, D.F.; Korbasiewicz, M. Evaluation of electric vehicle interior noise focused on sound source identification and transfer path analysis. In Proceedings of the Aachen Acoustics Colloquium, Aachen, Germany, 23–25 November 2015. [Google Scholar]
- Fernandez Comesaña, D.; Holland, K.R.; Fernandez-Grande, E. Spatial Resolution Limits for the Localization of Noise Sources Using Direct Sound Mapping. J. Sound Vib. 2016, 375, 53–62. [Google Scholar] [CrossRef] [Green Version]
- Cabo, D.; Bree, H.-E.; Fernandez Comesaña, D.; Seoane, M. Real Life Harmonic Source Localization Using a Network of Acoustic Vector Sensors. In Proceedings of the EuroNoise, Maastricht, The Netherlands, 31 May–3 June 2015; pp. 2333–2338. [Google Scholar]
- Vries, J.; Bree, H.-E. Scan & Listen: A Simple and Fast Method to Find Sources; SAE International: Warrendale, PA, USA, 2008. [Google Scholar] [CrossRef]
- Adaileh, W.M. Engine Fault Diagnosis Using Acoustic Signals. In Applied Mechanics and Materials; Trans Tech Publications: Baech, Switzerland, 2013. [Google Scholar]
- Allam, S.; Abdo, M.; Rabie, M. Diesel engine fault detection using vibration and acoustic emission signals. Int. J. Adv. Sci. Res. Eng. 2018, 4, 86–93. [Google Scholar] [CrossRef]
- Ning, D.; Hou, J.; Gong, Y.; Zhang, Z.; Sun, C. Auto-Identification of Engine Fault Acoustic Signal through Inverse Trigonometric Instantaneous Frequency Analysis. Adv. Mech. Eng. 2016, 8, 1687814016641840. [Google Scholar] [CrossRef] [Green Version]
- Fernandez Comesaña, D.; Tijs, E.; Kim, D. Direct Sound Radiation Testing on a Mounted Car Engine. SAE Int. J. Passeng. Cars-Mech. Syst. 2014, 7, 1229–1235. [Google Scholar] [CrossRef]
- De Bree, H.E.; Wind, J.W. The acoustic vector sensor: A versatile battlefield acoustics sensor. In Proceedings of the Ground/Air Multisensor Interoperability, Integration, and Networking for Persistent ISR II, Orlando, FL, USA, 25–29 April 2011; International Society for Optics and Photonics: Bellingham, WA, USA, 2011; Volume 8047. [Google Scholar] [CrossRef]
- Tijs, E. High-resolution Absorption Mapping with a Pu Surface Impedance Method. J. Acoust. Soc. Am. 2010, 9, 015003. [Google Scholar] [CrossRef]
- Guiot, M.; Fernandez Comesaña, D.; Korbasiewicz, M.; Pousa, G. Turbo-Compressor and Piping Noise Assessment Using a Particle Velocity Based Sound Emission Method. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Dubrovnik, Croatia, 9–12 August 2015. [Google Scholar]
- Li, Z.; Chang, W.; Gao, C.; Hao, Y. A Novel Five-Wire Micro Anemometer with 3D Directionality for Low Speed Air Flow Detection and Acoustic Particle Velocity Detecting Capability. J. Micromech. Microeng. 2018, 28, 044004. [Google Scholar] [CrossRef]
- De Bree, H.-E. An Overview of Microflown Technologies. Acta Acust. United Acust. 2003, 89, 163–172. [Google Scholar]
- De Bree, H.-E.; Druyvesteyn, W.F.; Berenschot, E.; Elwenspoek, M. Three-Dimensional Sound Intensity Measurements Using Microflown Particle Velocity Sensors. In Proceedings of the Technical Digest. In Proceedings of the Twelfth IEEE International Conference on Micro Electro Mechanical Systems (Cat. No. 99CH36291), MEMS 99, Orlando, FL, USA, 17–21 January 1999; IEEE: Piscataway, NJ, USA, 1999; pp. 124–129. [Google Scholar]
- Saine, K.; Gao, Z. Five DB Noise Reduction for Large Medium Speed Diesel Engines. In Proceedings of the Aachen Acoustics Colloquium (AAC), Aachen, Germany, 21–23 November 2016. [Google Scholar]
- Carrillo Pousa, G.; Fernandez Comesana, D.; Wild, J. Acoustic Particle Velocity for Fault Detection of Rotating Machinery Using Tachless Order Analysis. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference, San Francisco, CA, USA, 9–12 August 2015; Institute of Noise Control Engineering: Reston, VA, USA, 2015; Volume 250, pp. 6074–6081. [Google Scholar]
- Lee, J.-H.; Kim, J. Study on Sound Transmission Characteristics of a Cylindrical Shell Using Analytical and Experimental Models. Appl. Acoust. 2003, 64, 611–632. [Google Scholar] [CrossRef]
- Oliazadeh, P.; Farshidianfar, A. Analysis of Different Techniques to Improve Sound Transmission Loss in Cylindrical Shells. J. Sound Vib. 2017, 389, 276–291. [Google Scholar] [CrossRef]
- White, P.H. Sound Transmission through a Finite, Closed, Cylindrical Shell. J. Acoust. Soc. Am. 1966, 40, 1124–1130. [Google Scholar] [CrossRef]
- Smith, P.W. Sound Transmission through Thin Cylindrical Shells. J. Acoust. Soc. Am. 1957, 29, 721–729. [Google Scholar] [CrossRef]
- Webster, A.G. Acoustical Impedance and the Theory of Horns and of the Phonograph. Proc. Natl. Acad. Sci. USA 1919, 5, 275–282. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stewart, G.W.; Lindsay, R.B. Acoustics: A Text on Theory and Applications; D. Van Nostrand Company: New York, NY, USA, 1930. [Google Scholar]
- Donskoy, D.M.; Cray, B.A. Horns as Particle Velocity Amplifiers. J. Acoust. Soc. Am. 2011, 130, EL311–EL315. [Google Scholar] [CrossRef] [PubMed]
- Donskoy, D.M.; Cray, B.A. Acoustic Particle Velocity Horns. J. Acoust. Soc. Am. 2012, 131, 3883–3890. [Google Scholar] [CrossRef] [PubMed]
- Donskoy, D.M.; Hassan, S.E. Sound Amplification and Flow Noise Reduction with Acoustic Velocity Horns. In Proceedings of the Meetings on Acoustics 167ASA, San Francisco, CA, USA, 27–31 October 2014. [Google Scholar]
- Van Honschoten, J.W.; Yntema, D.R.; Wiegerink, R.J.; Elwenspoek, M. Analysis of a Three-Dimensional Particle Velocity Sensor for Design Optimization. J. Micromech. Microeng. 2007, 17, S137–S146. [Google Scholar] [CrossRef]
- Chang, W.; Yang, L.; Zhu, Z.; Yang, Z.; Gao, C.; Hao, Y. Modeling of Small-Sized Acoustic Particle Velocity Horn for MEMS Thermal Acoustic Particle Velocity Sensor. In Proceedings of the 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), San Diego, CA, USA, 25–29 January 2021; pp. 697–700. [Google Scholar]
- Chandrika, U.K.; Hari, V.N. A Vector Sensing Scheme for Underwater Acoustics Based on Particle Velocity Measurements. In Proceedings of the OCEANS 2015-MTS/IEEE, Washington, DC, USA, 19–22 October 2015; IEEE: Washington, DC, USA, 2015; pp. 1–7. [Google Scholar]
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2019; ISBN 978-3-030-11214-1. [Google Scholar]
- De Bree, H.E. The Microflown e-Book; Microflown Technologies: Arnhem, The Netherlands, 2007; Available online: https://www.microflown.com/resources/e-books/e-book-the-microflown-e-book (accessed on 24 June 2021).











| Radius of Horn Throat RT | Radius of Horn Mouth RM | Length of Horn L | |
|---|---|---|---|
| Horn 1 | 0.5 mm | 2 mm | 5 mm |
| Horn 2 | 10 mm | 30 mm | 50 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, W.; Yang, L.; Zhu, Z.; Yang, Z.; Hao, Y.; Gao, C. Design and Optimization of Sensitivity Enhancement Package for MEMS-Based Thermal Acoustic Particle Velocity Sensor. Sensors 2021, 21, 4337. https://doi.org/10.3390/s21134337
Chang W, Yang L, Zhu Z, Yang Z, Hao Y, Gao C. Design and Optimization of Sensitivity Enhancement Package for MEMS-Based Thermal Acoustic Particle Velocity Sensor. Sensors. 2021; 21(13):4337. https://doi.org/10.3390/s21134337
Chicago/Turabian StyleChang, Wenhan, Lingmeng Yang, Zhezheng Zhu, Zhenchuan Yang, Yilong Hao, and Chengchen Gao. 2021. "Design and Optimization of Sensitivity Enhancement Package for MEMS-Based Thermal Acoustic Particle Velocity Sensor" Sensors 21, no. 13: 4337. https://doi.org/10.3390/s21134337
APA StyleChang, W., Yang, L., Zhu, Z., Yang, Z., Hao, Y., & Gao, C. (2021). Design and Optimization of Sensitivity Enhancement Package for MEMS-Based Thermal Acoustic Particle Velocity Sensor. Sensors, 21(13), 4337. https://doi.org/10.3390/s21134337





