Statistical Study of the Method of Radius-Change Sphericity Measurements
Abstract
1. Introduction
2. State of the Art of Sphericity Measurements
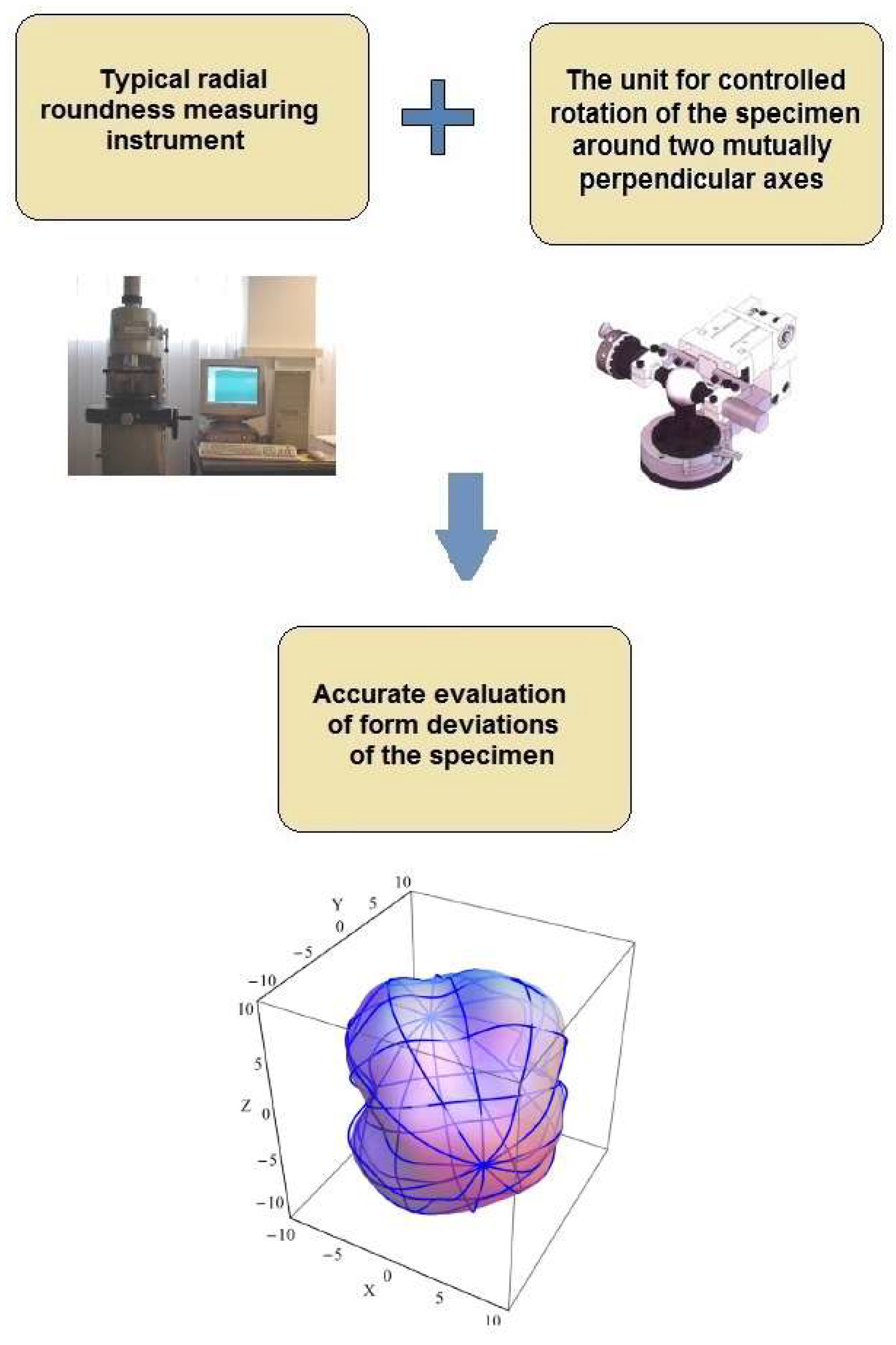
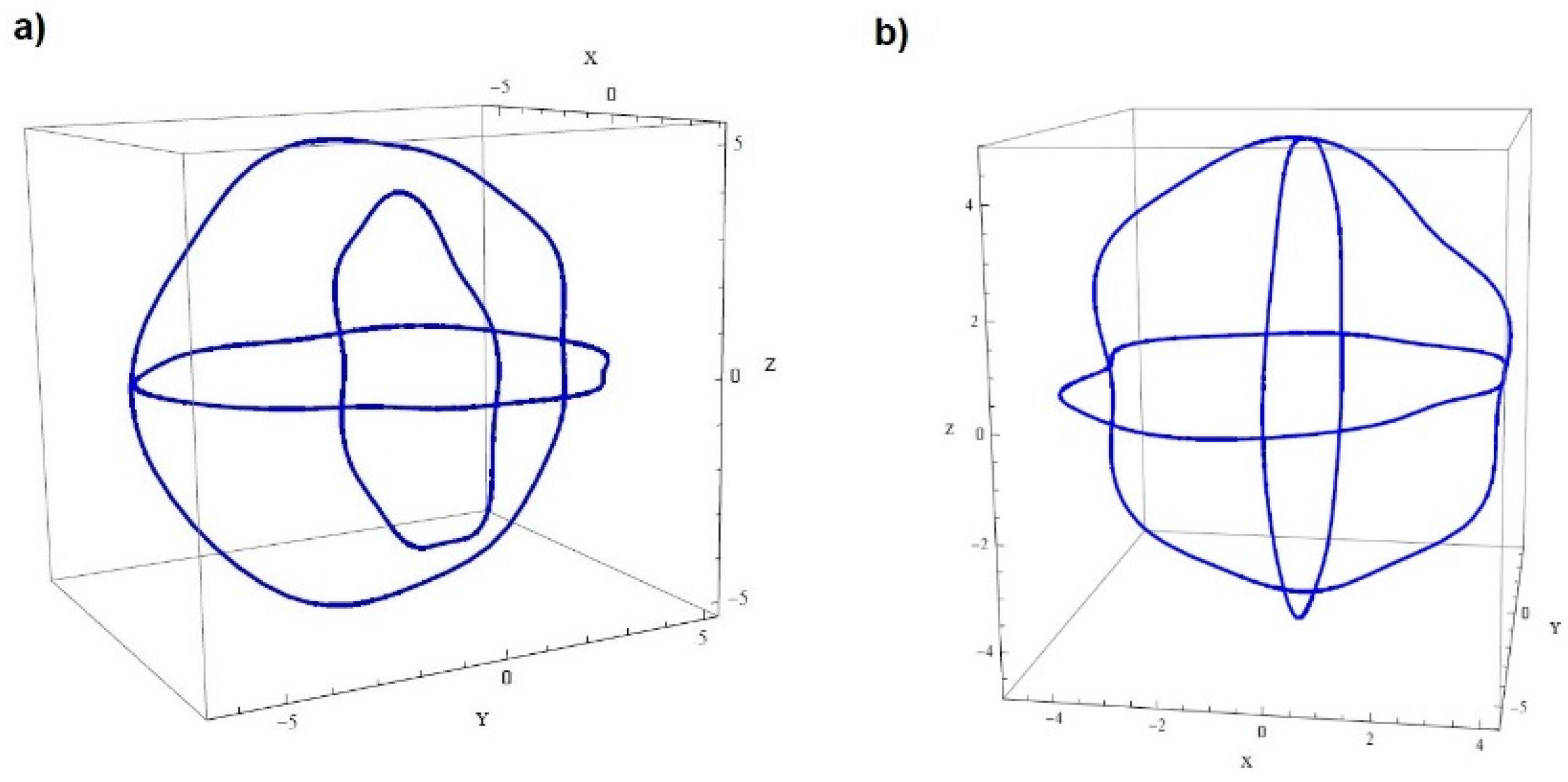
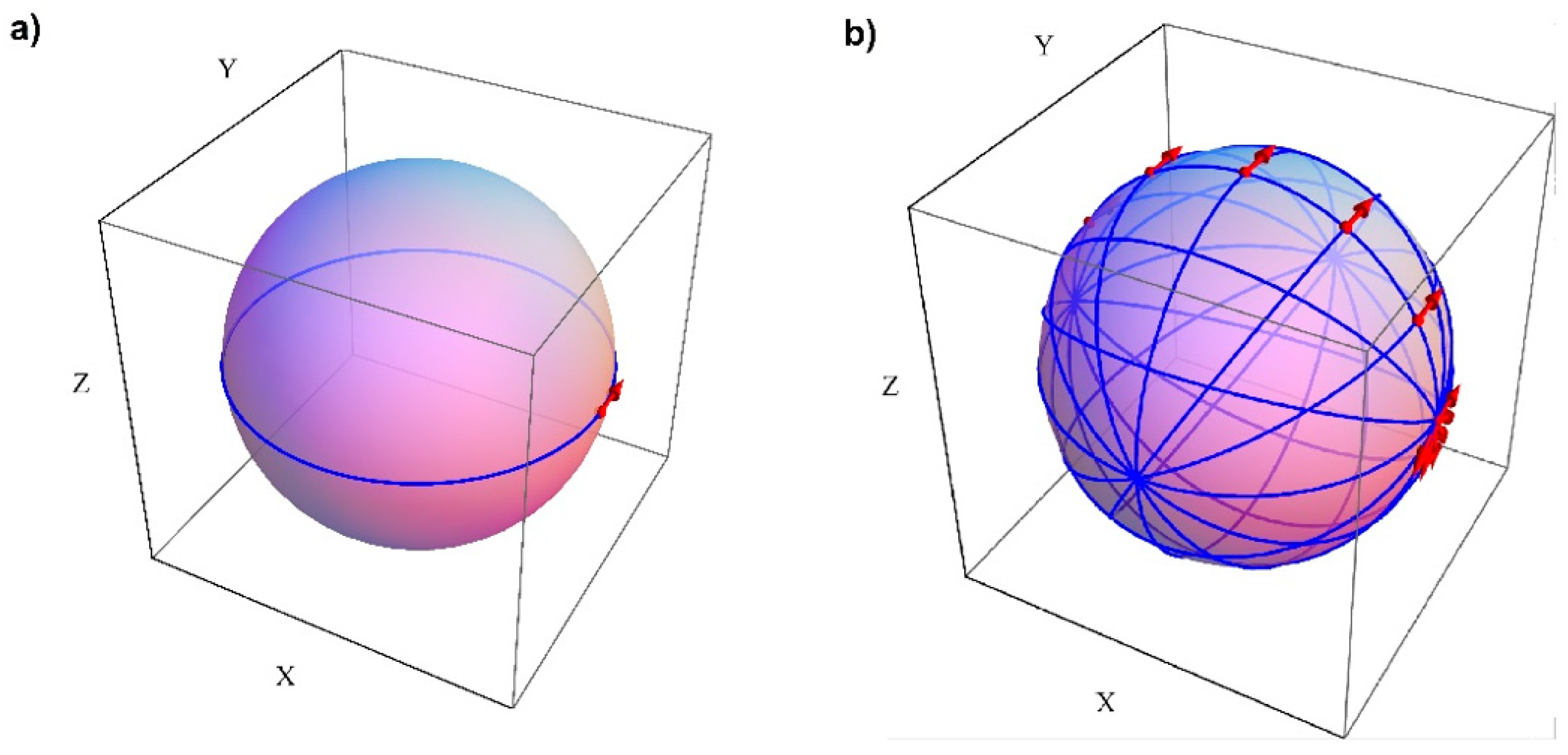
3. Concept of Radius Change Measurement of Sphericity
4. Experiment
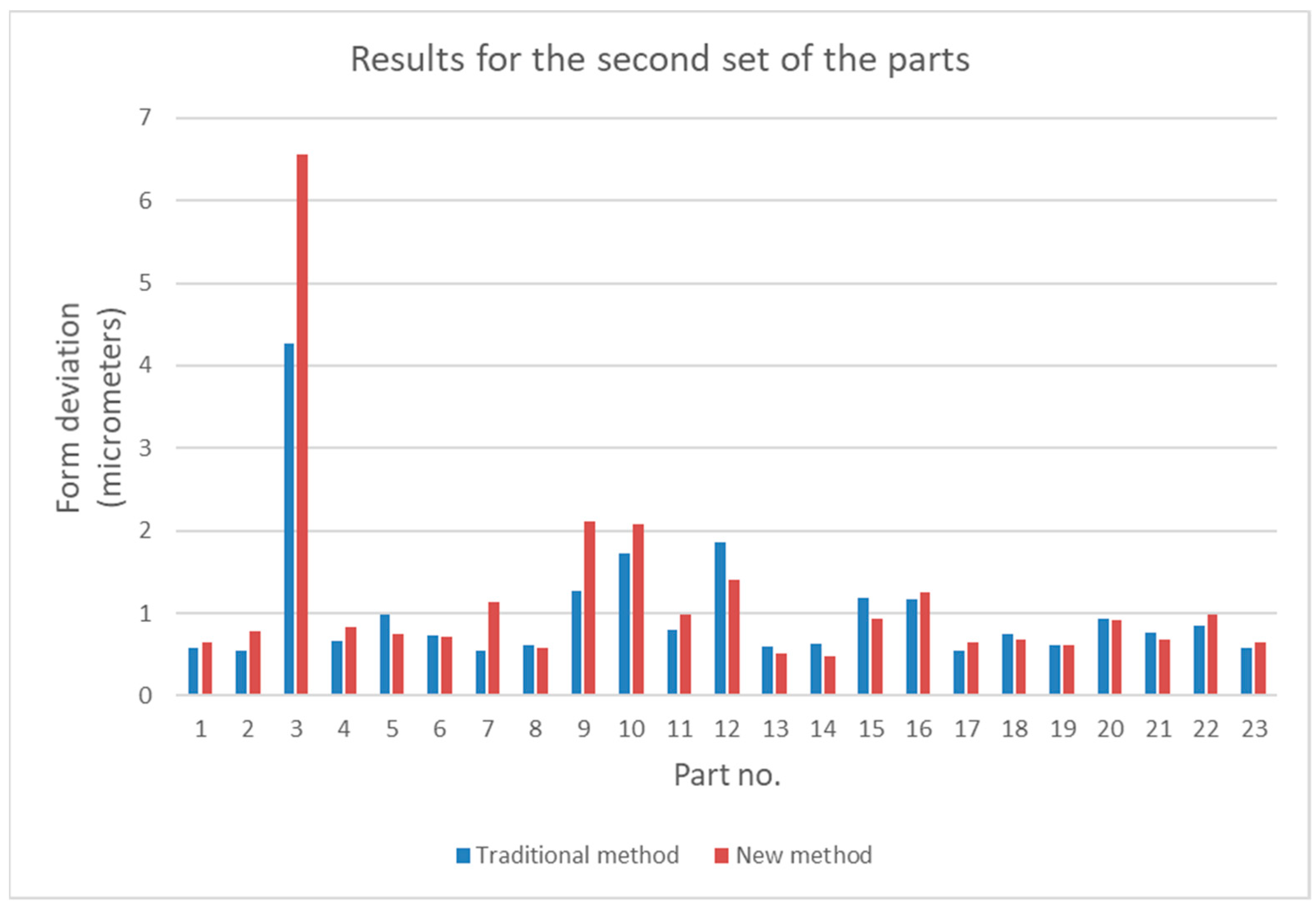
5. Results
6. The Statistical Analysis of the Results and Discussion
6.1. The Analysis of Differences between the Results Obtained by the New and Traditional Methods
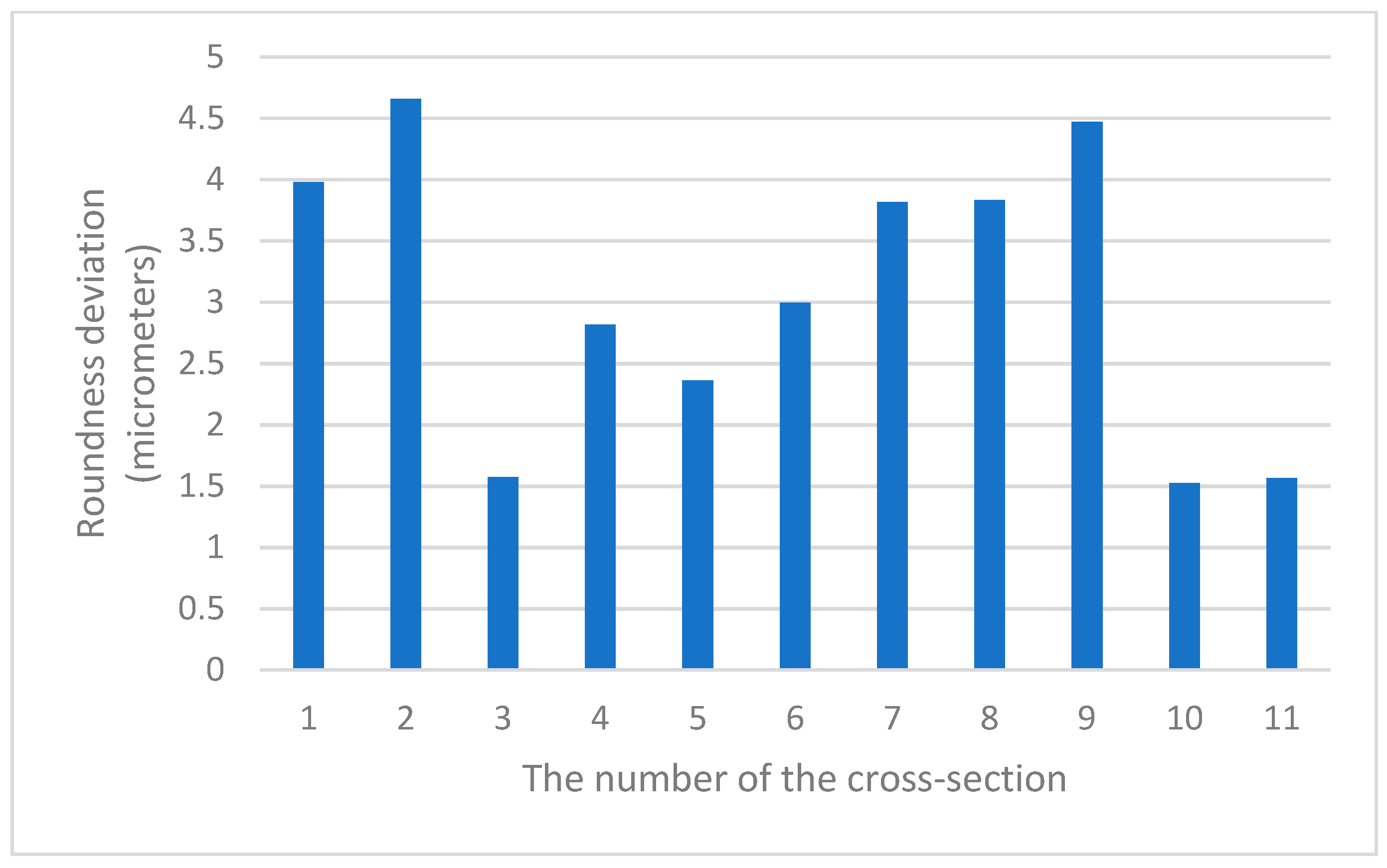
6.2. Analysis of Differences in Values of the Roundness Deviation in Various Cross-Sections of the Same Spherical Part
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Stepien, K. Verification of the concept of sphericity measurements by the radial method under industrial conditions. In Proceedings of the XI International Symposium on Measurement and Quality Control-ISMQC 2013, Cracow-Kielce, Poland, 11–13 September 2013. [Google Scholar]
- Ratajczyk, E. Quality control of surfaces of rolling bearing with the use of AVIKO automated systems. Mechanik 1968, 4, 203–207. (In Polish) [Google Scholar]
- Hagino, T.; Yokoyama, Y.; Kuriyama, Y.; Haitjema, H. Sphericity Measurement Using Stitching Interferometry. Key Eng. Mater. 2012, 523–524, 883–888. [Google Scholar] [CrossRef]
- Bartl, G.; Krystek, M.; Nicolaus, A.; Giardini, W. Interferometric determination of the topographies of absolute sphere radii using the sphere interferometer of PTB. Meas. Sci. Technol. 2010, 21, 115101. [Google Scholar] [CrossRef]
- Halkaci, H.S.; Mavi, Ö.; Yigit, O. Evaluation of form error at semi-spherical tools by use of image processing. Measurement 2007, 40, 860–867. [Google Scholar] [CrossRef]
- Song, L.M.; Zhou, X.; Qu, X.; Xu, K.; Lv, L. Novel 3D sphericity evaluation based on SFS-NDT. NDT E Int. 2005, 38, 442–447. [Google Scholar] [CrossRef]
- Samuel, G.L.; Shunmugam, M.S. Evaluation of circularity and sphericity from coordinate measurement data. J. Mater. Process. Technol. 2003, 139, 90–95. [Google Scholar] [CrossRef]
- Poniatowska, M.; Werner, A. Fitting spatial models of geometric deviations of free-form surfaces determined in coordinate measurements. Metrol. Meas. Syst. 2010, 17, 599–610. [Google Scholar] [CrossRef][Green Version]
- Chen, L.-C. Automatic 3D surface reconstruction and sphericity measurement of micro spherical balls of miniaturized coordinate measuring probes. Meas. Sci. Technol. 2007, 18, 1748–1755. [Google Scholar] [CrossRef]
- Samuel, G.; Shunmugam, M. Evaluation of sphericity error from form data using computational geometric techniques. Int. J. Mach. Tools Manuf. 2002, 42, 405–416. [Google Scholar] [CrossRef]
- Huang, J. An exact minimum zone solution for sphericity evaluation. Comput. Des. 1999, 31, 845–853. [Google Scholar] [CrossRef]
- Fana, K.-C.; Lee, J.-C. Analysis of minimum zone sphericity error using minimum potential energy theory. Precis. Eng. 1999, 23, 65–72. [Google Scholar] [CrossRef]
- Kanada, T. Estimation of sphericity by means of statistical processing for roundness of spherical parts. Precis. Eng. 1997, 20, 117–122. [Google Scholar] [CrossRef]
- Cai, W.; Kim, D.W.; Zhou, P.; Parks, R.E.; Burge, J.H. Interferometer Calibration using the Random Ball Test. In Proceedings of the Optical Fabrication and Testing 2010, Jackson Hole, WY, USA, 13–17 June 2010. [Google Scholar]
- Zhou, P.; Burge, J.H. Limits for interferometer calibration using the random ball test. In Proceedings of the SPIE 7426, Optical Manufacturing and Testing VIII, San Diego, CA, USA, 21 August 2009; Volume 7426, p. 7426U. [Google Scholar]
- Janecki, D.; Adamczak, S.; Stępień, K. Problem of profile matching in sphericity measurements by the radial method. Metrol. Meas. Syst. 2012, 19/4, 703–714. [Google Scholar] [CrossRef]
- Janecki, D.; Stępień, K.; Adamczak, S. Sphericity measurements by the radial method: I. Mathematical fundamentals. Meas. Sci. Technol. 2016, 27, 015005. [Google Scholar] [CrossRef]
- Janecki, D.; Stępień, K.; Adamczak, S. Sphericity measurements by the radial method: II. Experimental verification. Meas. Sci. Technol. 2016, 27, 015006. [Google Scholar] [CrossRef]
- Adamczak, S.; Janusiewicz, A.; Makieła, W.; Stępień, K. Statistical validation of the method for measuring radius variations of components on the machine tool. Metrol. Meas. Syst. 2011, 18/1, 35–46. [Google Scholar] [CrossRef]




| Form Deviation Measured by the Traditional Method (Micrometers) | Form Deviation Measured by the New Method (Micrometers) |
|---|---|
| 0.505 | 0.64 |
| 0.743 | 0.819 |
| 0.568 | 1.175 |
| 0.522 | 1.014 |
| 0.597 | 0.778 |
| 0.513 | 0.786 |
| 0.968 | 0.824 |
| 0.83 | 0.923 |
| 0.525 | 0.943 |
| 0.723 | 0.471 |
| 1.046 | 1.048 |
| 0.719 | 0.771 |
| 0.597 | 0.592 |
| 0.647 | 0.685 |
| 0.613 | 0.641 |
| 0.432 | 0.479 |
| 0.499 | 0.403 |
| 0.561 | 0.666 |
| 0.922 | 1.42 |
| 0.456 | 1.072 |
| 0.892 | 0.505 |
| 0.457 | 0.825 |
| 0.903 | 0.87 |
| Form Deviation Measured by the Traditional Method (Micrometers) | Form Deviation Measured by the New Method (Micrometers) |
|---|---|
| 0.585 | 0.649 |
| 0.548 | 0.775 |
| 4.267 | 6.566 |
| 0.669 | 0.824 |
| 0.975 | 0.745 |
| 0.725 | 0.708 |
| 0.545 | 1.129 |
| 0.615 | 0.581 |
| 1.275 | 2.107 |
| 1.731 | 2.084 |
| 0.799 | 0.978 |
| 1.855 | 1.399 |
| 0.598 | 0.512 |
| 0.628 | 0.479 |
| 1.193 | 0.936 |
| 1.175 | 1.259 |
| 0.772 | 0.329 |
| 0.545 | 0.65 |
| 0.746 | 0.678 |
| 0.607 | 0.606 |
| 0.936 | 0.916 |
| 0.772 | 0.682 |
| 0.843 | 0.987 |
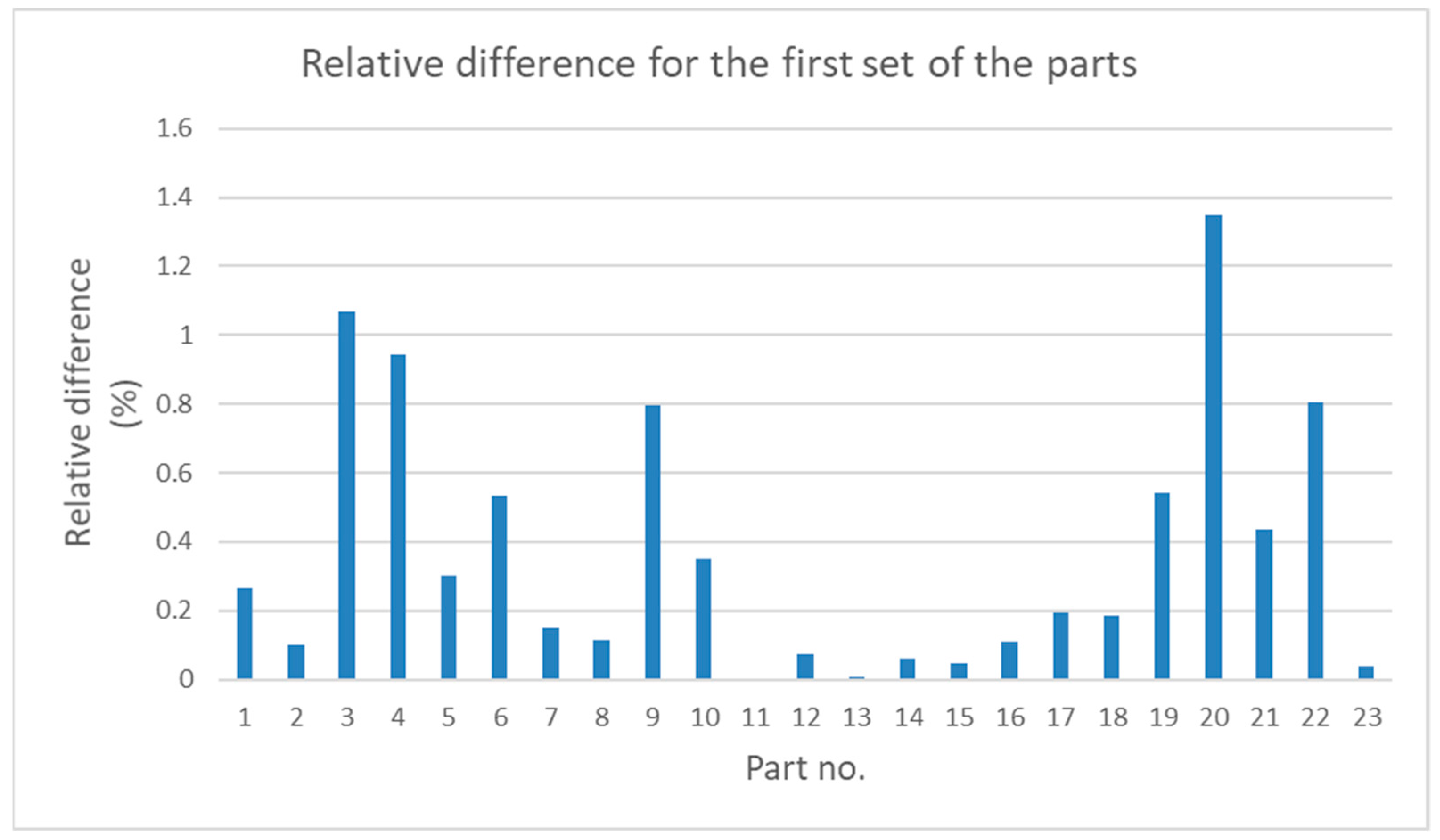
| Parameter Name | Parameter Value for the first Set of the Parts (%) | Parameter Value for the second Set of the Parts (%) |
|---|---|---|
| Mean value of the relative difference | 36.8 | 25.4 |
| Maximum value of the relative difference | 135.1 | 107.2 |
| Minimum value of the relative difference | 0.19 | 0.16 |
| Standard deviation | 38.2 | 25 |
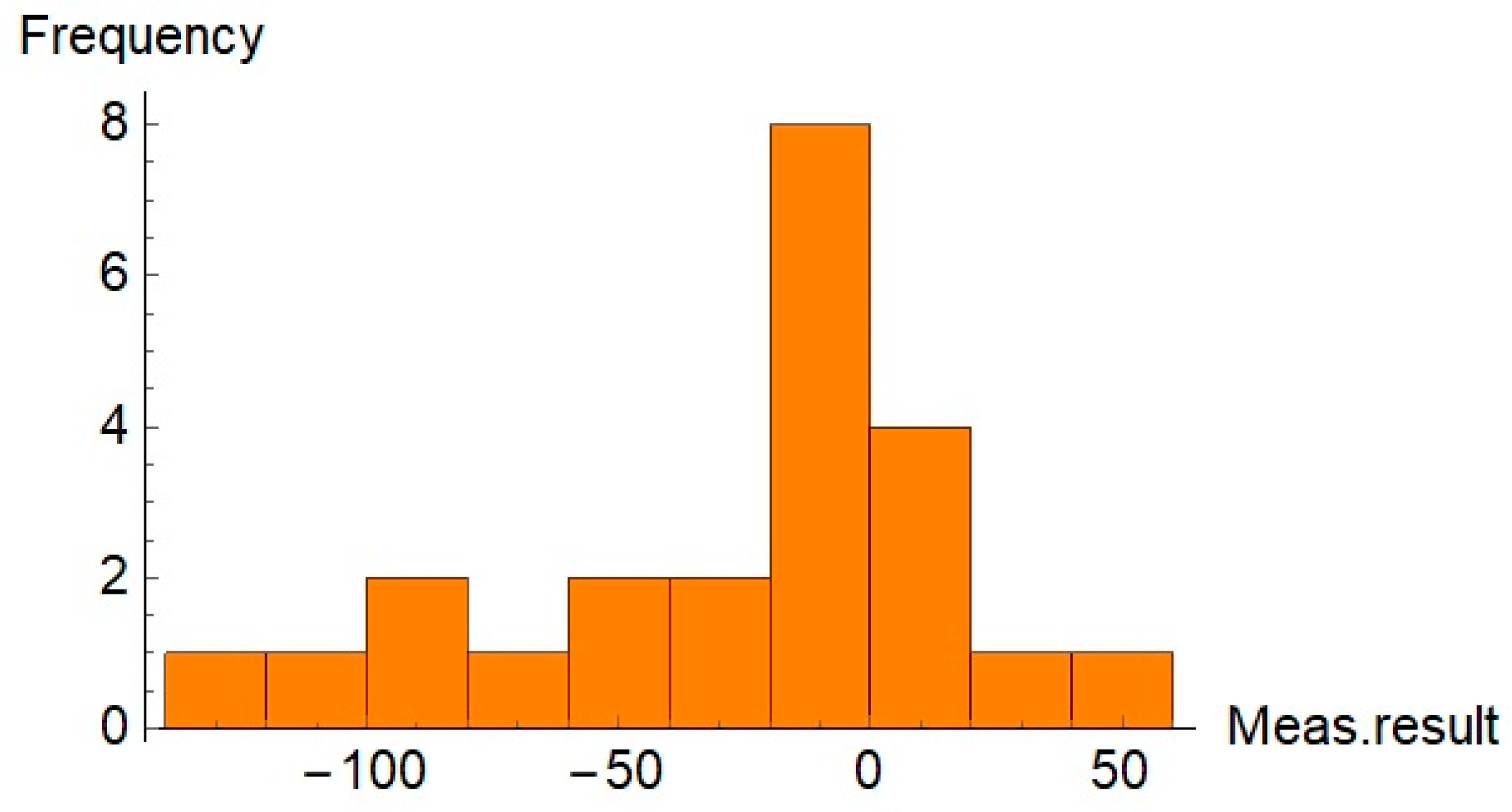
| The Number of the Measurement Dataset | Distribution Type and Its Parameters |
|---|---|
| First set | Uniform distribution (min. value: −135.088, max. value: 43.3857) |
| Second set | NormalDistribution [mean value: −9.66936, standard deviation: 40.513] |
| The Number of the Measurement Dataset | Confidence Interval |
|---|---|
| First set | |
| Second set |
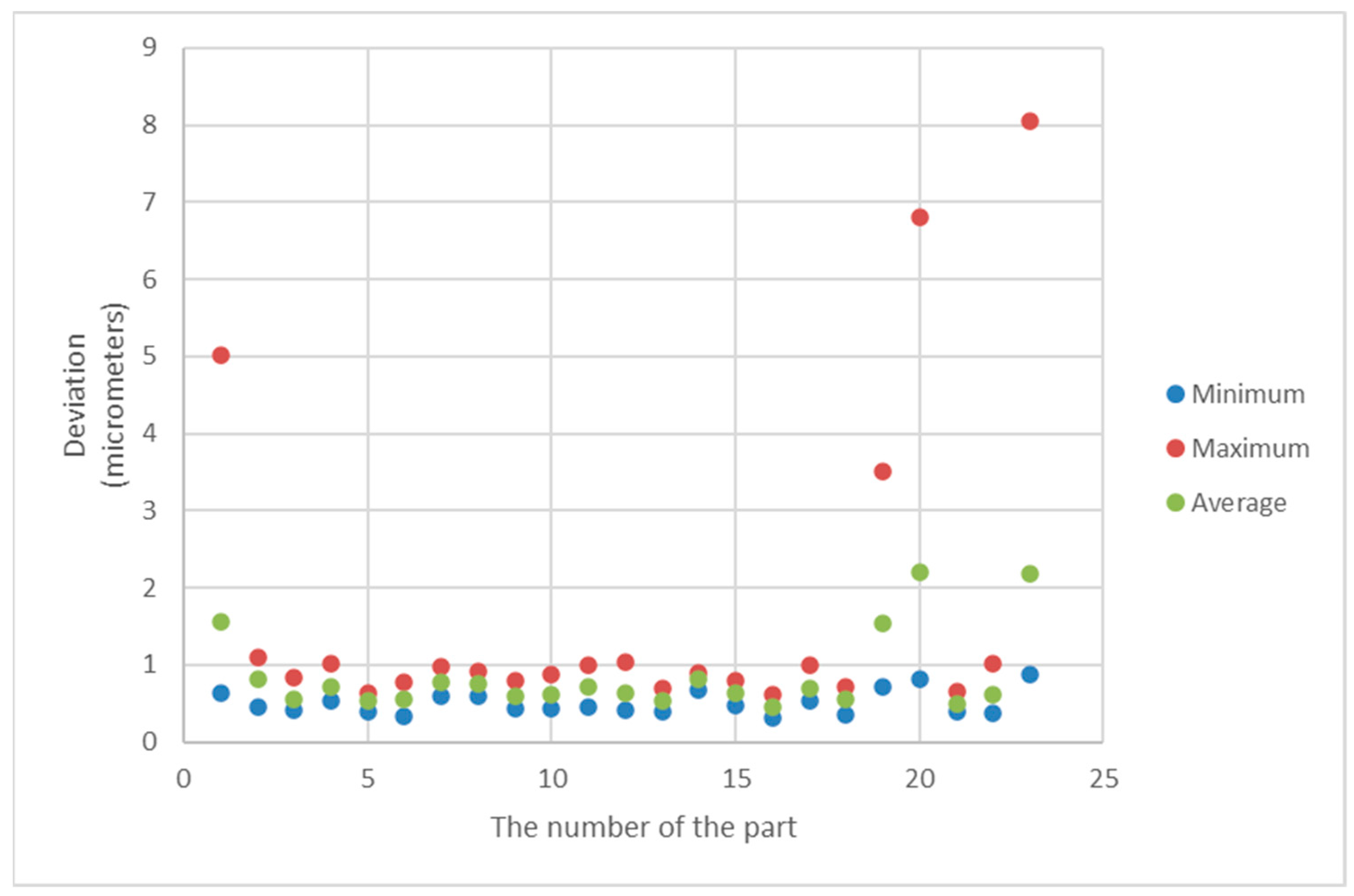
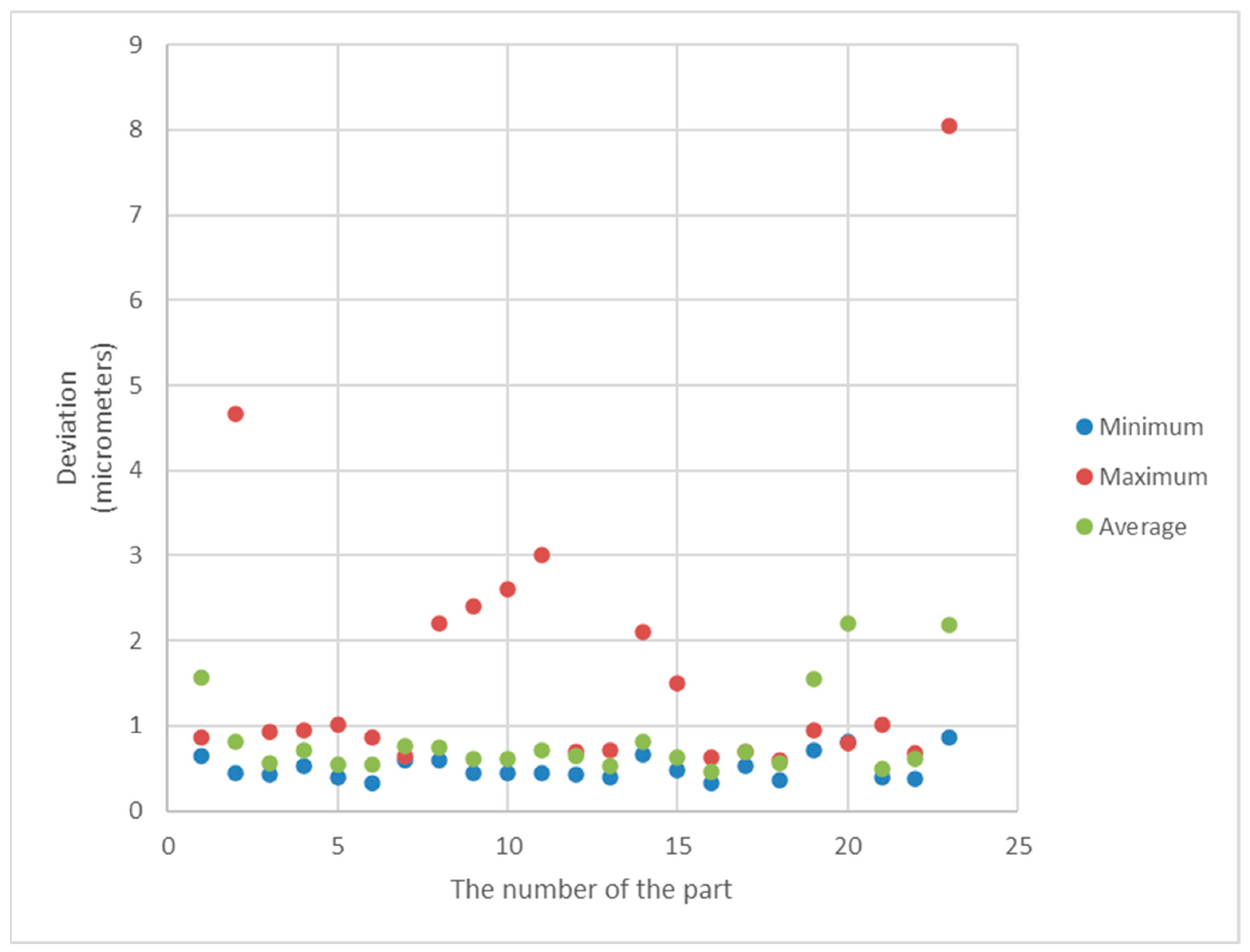
| Minimum Value | Maximum Value | Range | Average Value | Standard Deviation |
|---|---|---|---|---|
| 0.641 | 5.01 | 4.369 | 1.561 | 1.275 |
| 0.451 | 1.105 | 0.654 | 0.814 | 0.186 |
| 0.42 | 0.841 | 0.421 | 0.556 | 0.118 |
| 0.531 | 1.021 | 0.49 | 0.717 | 0.134 |
| 0.401 | 0.634 | 0.233 | 0.539 | 0.082 |
| 0.323 | 0.781 | 0.458 | 0.554 | 0.130 |
| 0.593 | 0.986 | 0.393 | 0.768 | 0.125 |
| 0.601 | 0.911 | 0.31 | 0.752 | 0.113 |
| 0.437 | 0.805 | 0.368 | 0.604 | 0.114 |
| 0.442 | 0.882 | 0.44 | 0.610 | 0.129 |
| 0.452 | 0.991 | 0.539 | 0.716 | 0.163 |
| 0.421 | 1.032 | 0.611 | 0.643 | 0.172 |
| 0.391 | 0.693 | 0.302 | 0.534 | 0.112 |
| 0.671 | 0.896 | 0.225 | 0.806 | 0.074 |
| 0.471 | 0.79 | 0.319 | 0.630 | 0.096 |
| 0.321 | 0.617 | 0.296 | 0.460 | 0.091 |
| 0.526 | 0.993 | 0.467 | 0.694 | 0.148 |
| 0.362 | 0.71 | 0.348 | 0.561 | 0.113 |
| 0.705 | 3.504 | 2.799 | 1.549 | 0.958 |
| 0.811 | 6.801 | 5.99 | 2.207 | 1.785 |
| 0.401 | 0.658 | 0.257 | 0.490 | 0.079 |
| 0.381 | 1.012 | 0.631 | 0.605 | 0.184 |
| 0.87 | 8.055 | 7.185 | 2.186 | 2.095 |
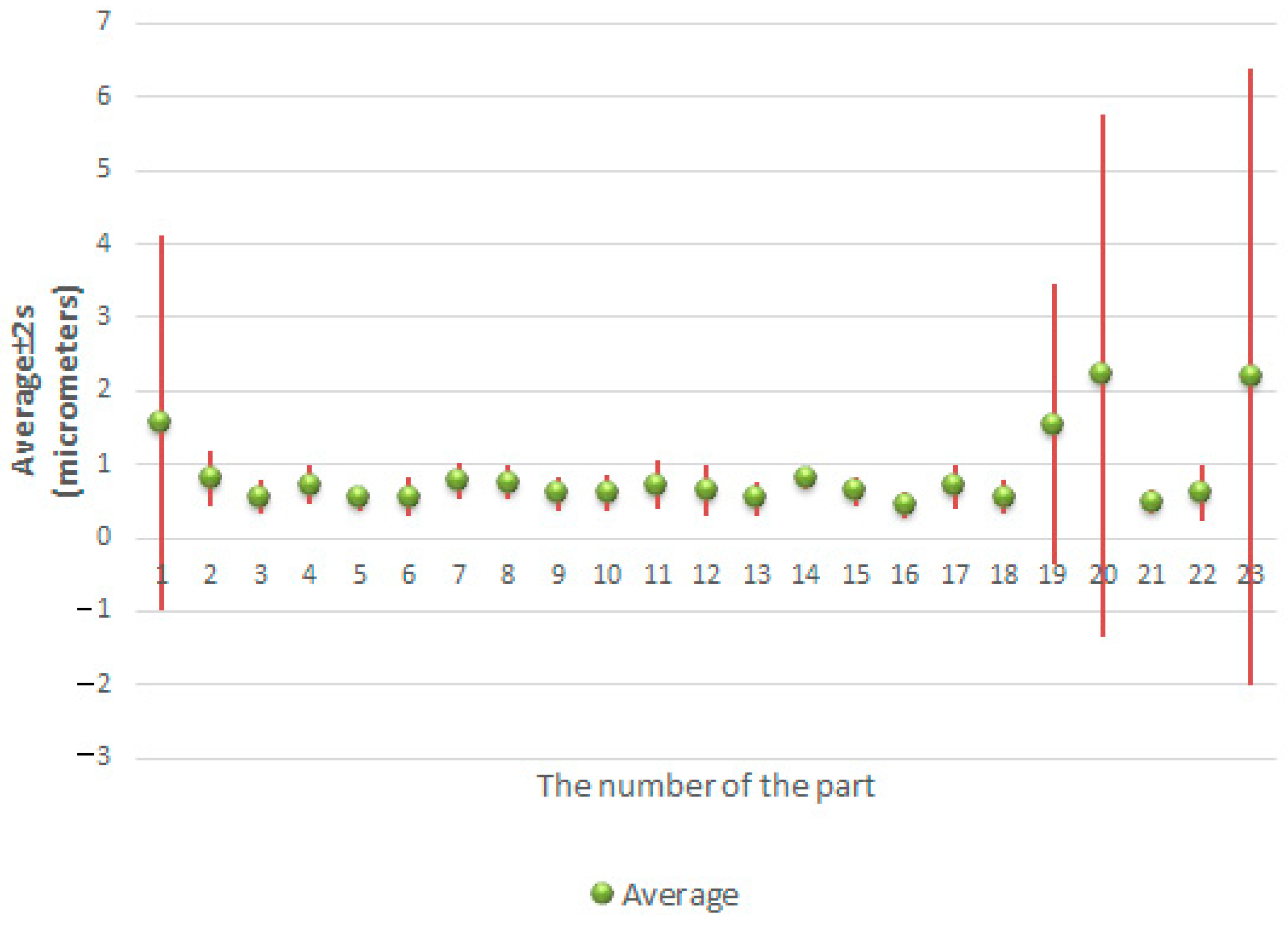
| Minimum Value | Maximum Value | Range | Average Value | Standard Deviation |
|---|---|---|---|---|
| 0.31 | 0.86 | 0.55 | 0.581 | 0.154 |
| 1.527 | 4.658 | 3.131 | 3.054 | 1.179 |
| 0.277 | 0.924 | 0.647 | 0.563 | 0.221 |
| 0.511 | 0.941 | 0.43 | 0.670 | 0.143 |
| 0.453 | 1.01 | 0.557 | 0.724 | 0.169 |
| 0.502 | 0.871 | 0.369 | 0.725 | 0.124 |
| 0.352 | 0.654 | 0.302 | 0.464 | 0.083 |
| 1.3 | 2.202 | 0.902 | 1.759 | 0.322 |
| 1.23 | 2.402 | 1.172 | 1.937 | 0.397 |
| 0.824 | 2.602 | 1.778 | 1.451 | 0.501 |
| 1.115 | 3.001 | 1.886 | 2.113 | 0.507 |
| 0.311 | 0.7 | 0.389 | 0.489 | 0.126 |
| 0.315 | 0.708 | 0.393 | 0.508 | 0.158 |
| 0.746 | 2.108 | 1.362 | 1.374 | 0.448 |
| 0.554 | 1.504 | 0.95 | 1.085 | 0.327 |
| 0.343 | 0.621 | 0.278 | 0.456 | 0.084 |
| 0.411 | 0.7 | 0.289 | 0.596 | 0.103 |
| 0.352 | 0.6 | 0.248 | 0.464 | 0.096 |
| 0.441 | 0.953 | 0.512 | 0.703 | 0.154 |
| 0.332 | 0.801 | 0.469 | 0.596 | 0.129 |
| 0.51 | 1.015 | 0.505 | 0.672 | 0.157 |
| 0.401 | 0.675 | 0.274 | 0.566 | 0.091 |
| 0.31 | 0.86 | 0.55 | 0.581 | 0.154 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stępień, K.; Janecki, D.; Adamczak, S. Statistical Study of the Method of Radius-Change Sphericity Measurements. Sensors 2021, 21, 4563. https://doi.org/10.3390/s21134563
Stępień K, Janecki D, Adamczak S. Statistical Study of the Method of Radius-Change Sphericity Measurements. Sensors. 2021; 21(13):4563. https://doi.org/10.3390/s21134563
Chicago/Turabian StyleStępień, Krzysztof, Dariusz Janecki, and Stanisław Adamczak. 2021. "Statistical Study of the Method of Radius-Change Sphericity Measurements" Sensors 21, no. 13: 4563. https://doi.org/10.3390/s21134563
APA StyleStępień, K., Janecki, D., & Adamczak, S. (2021). Statistical Study of the Method of Radius-Change Sphericity Measurements. Sensors, 21(13), 4563. https://doi.org/10.3390/s21134563






