A Study on the Failure Behavior of Sand Grain Contacts with Hertz Modeling, Image Processing, and Statistical Analysis
Abstract
:1. Introduction
2. Methodology
2.1. Materials, Experimental Setup, and Testing Program
2.2. Analytical Method
3. Results and Discussion
3.1. Analysis of Local Radius and Contact Radius
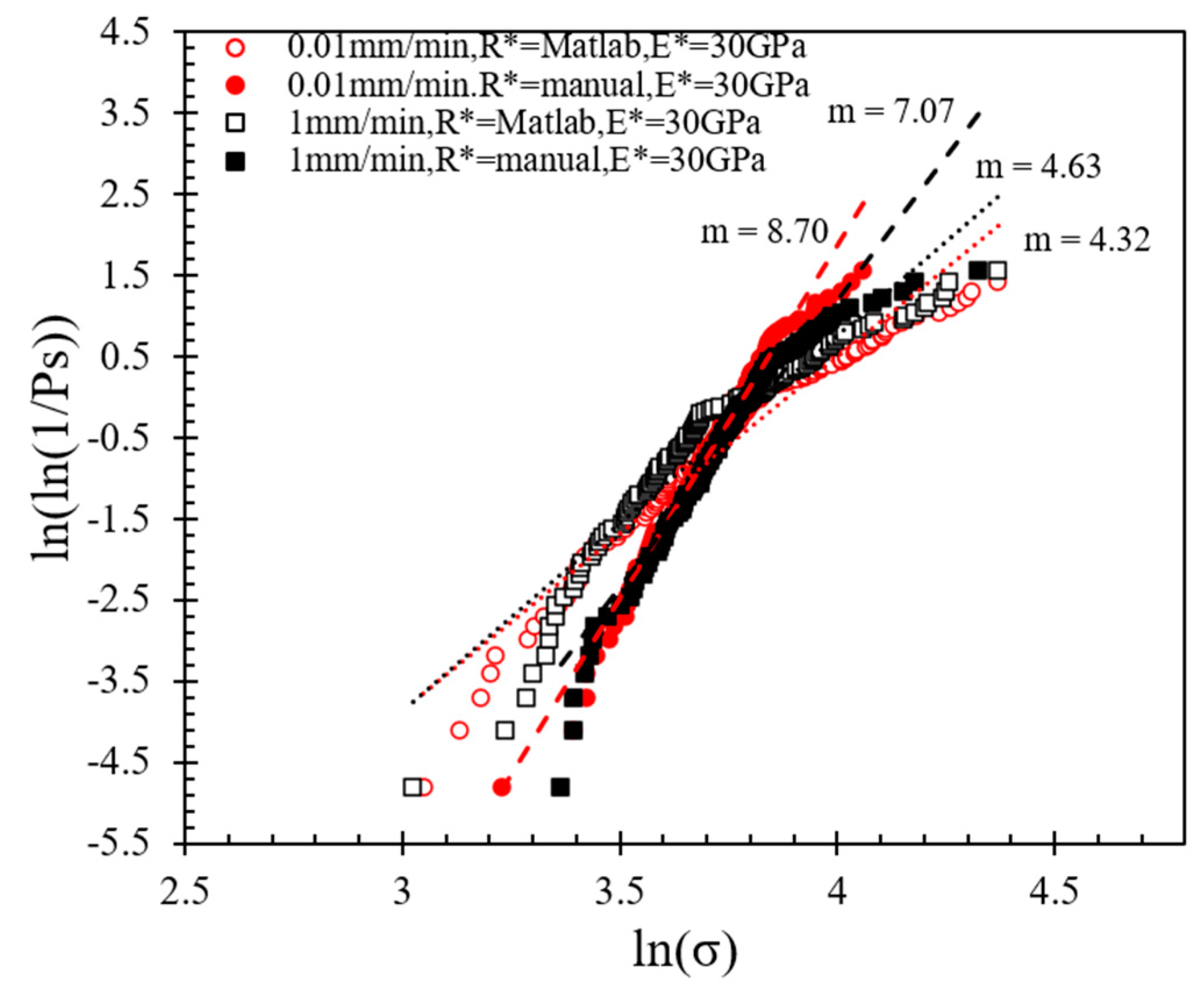
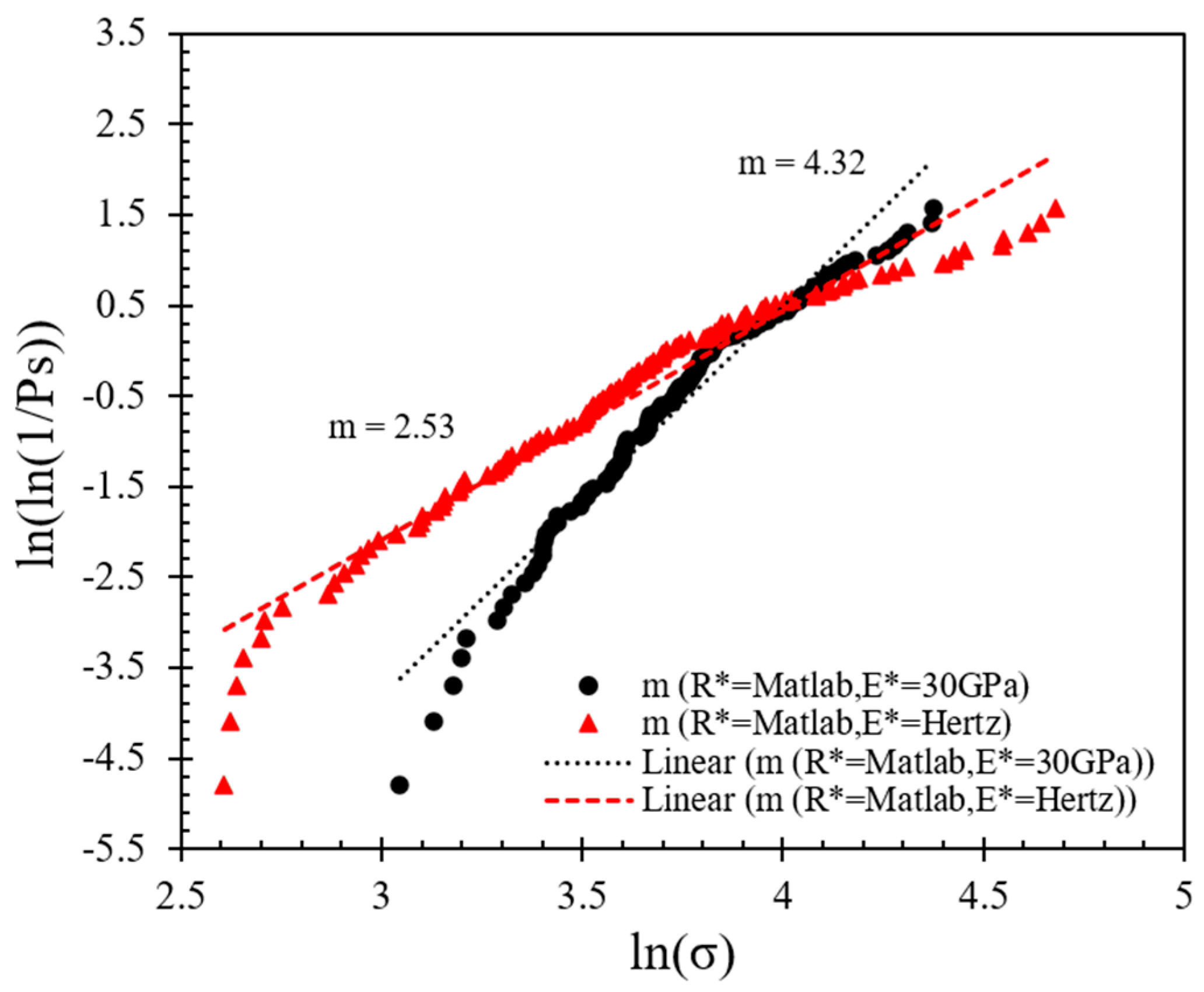
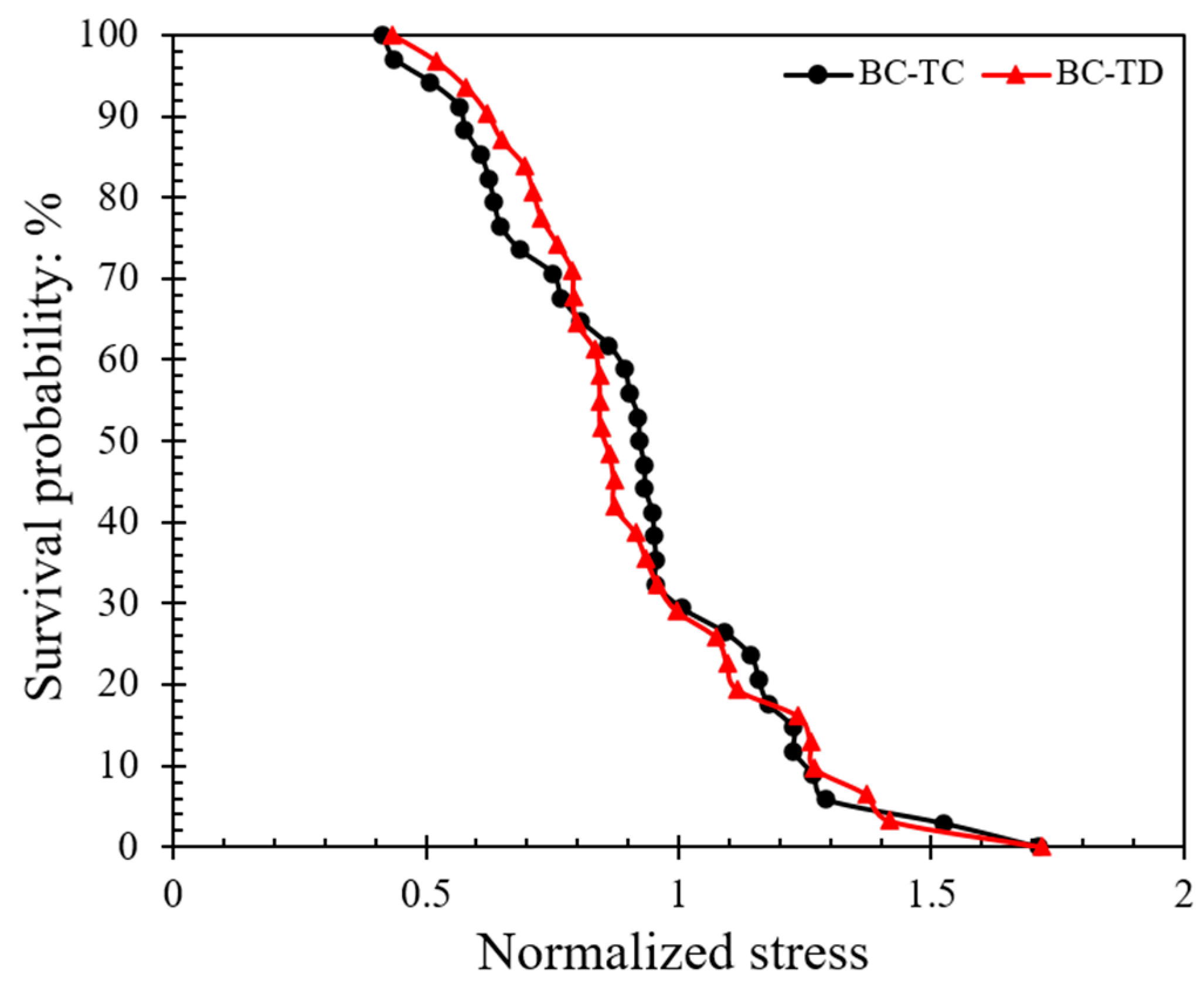
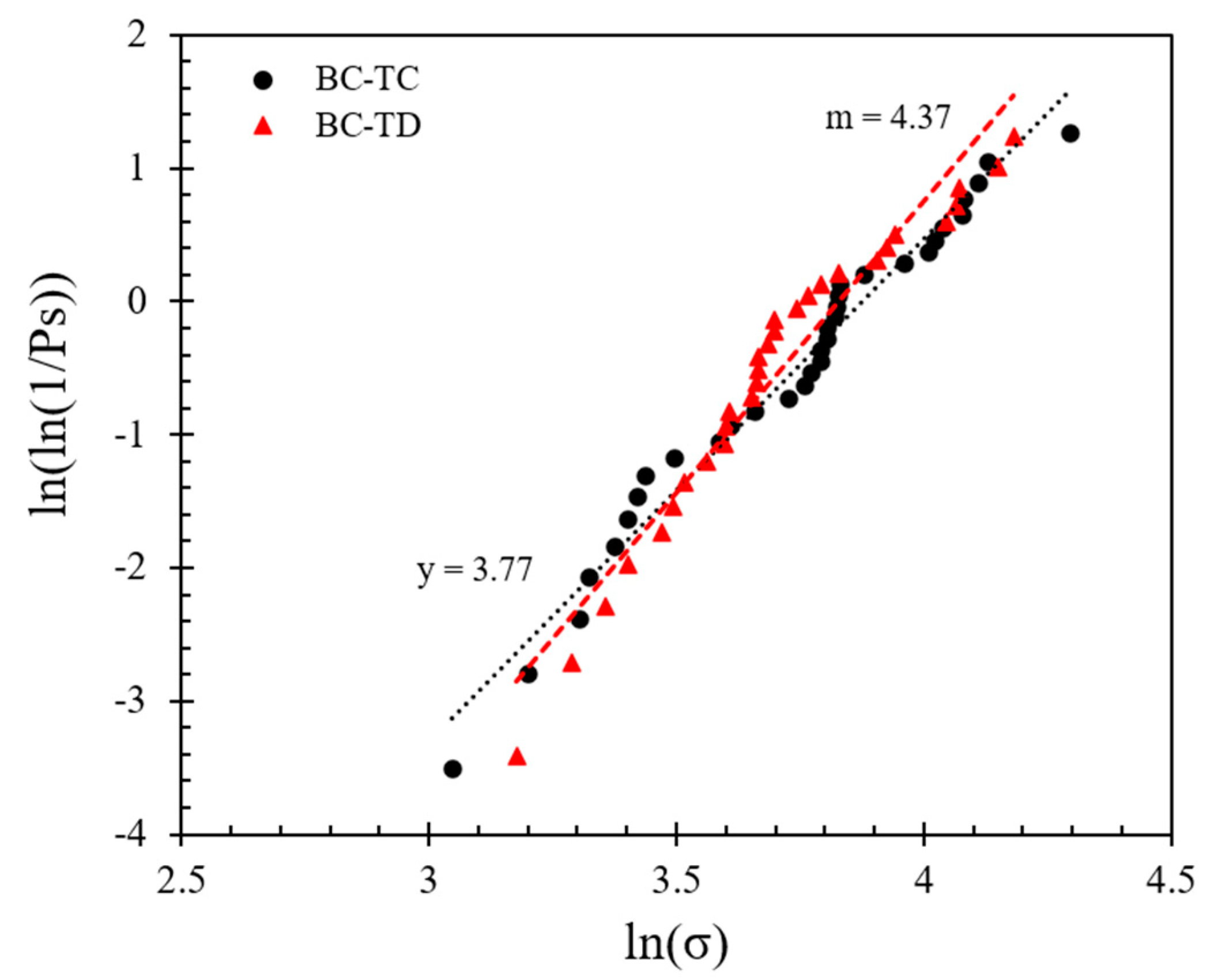
3.2. Contact Strength Based on Weibull Analysis
3.3. Implementation of Hertz Analysis of the Force–Displacement Curves to Derive Contact Young’s Modulus and Failure Stress
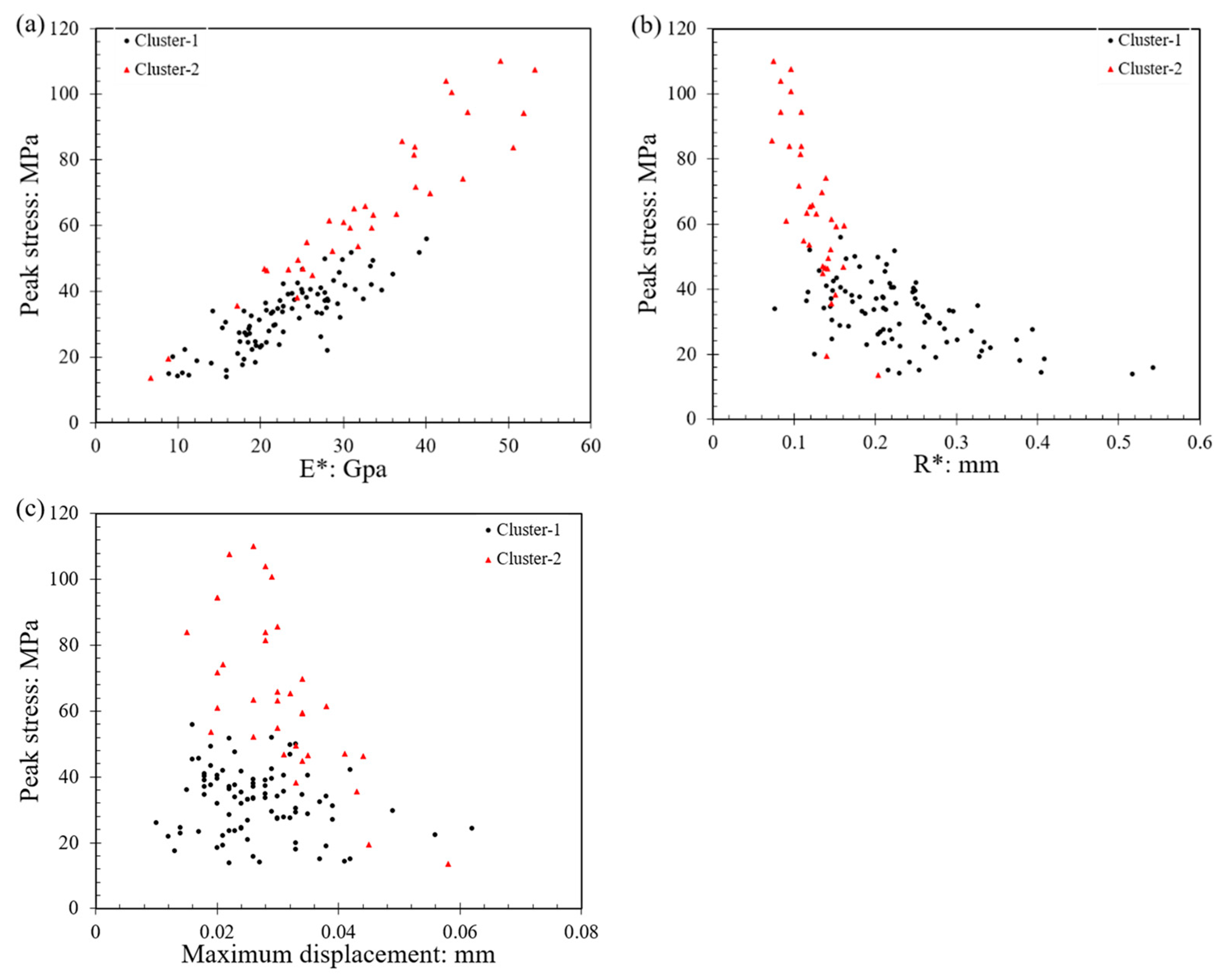
3.4. Clustering Analysis
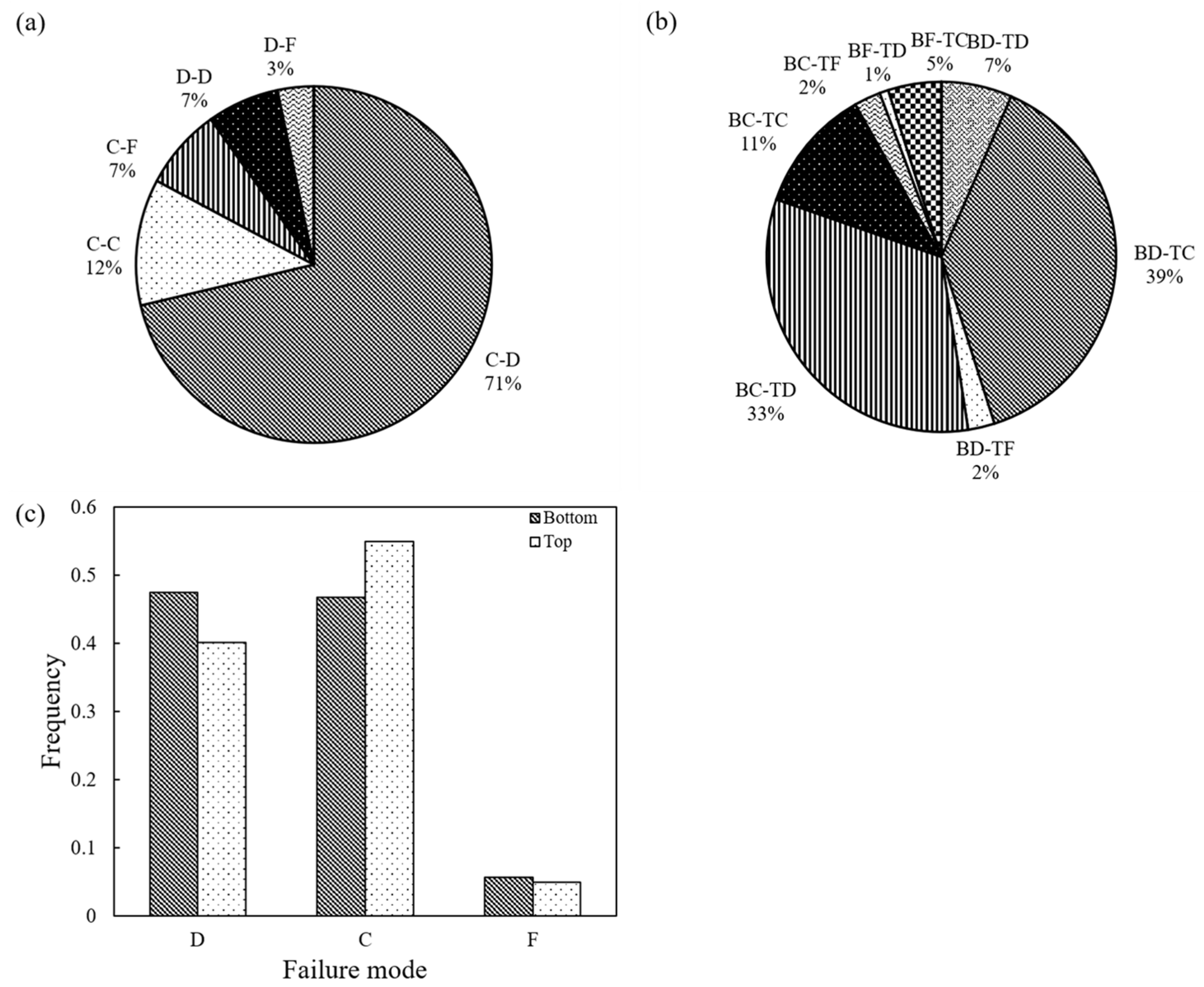
3.5. Failure Modes
3.5.1. General Observations and Classification of Breakage Patterns
3.5.2. Influence of Breakage Patterns on the Load–Displacement Curves
4. Conclusions
- (1)
- The analysis of the data showed that even though the grain-to-grain systems in the present study had a similar range of strength (peak stress) with that of single- and multiple-contact crushing tests as presented in the literature, m-modulus values were, in general, higher in magnitude in the present work. This leads to the conclusion that the restriction of the grains to rotate during their compression leads to a smaller variability of peak stress values, even though it did not influence greatly the absolute values of strength. This may have important implications in integrating laboratory grain-scale tests with discrete-based numerical simulations, as currently the majority of numerical works implement in their calibration results from single-grain crushing tests. However, under in situ conditions, it is not necessary for the particles to be represented by the single-grain crushing test model.
- (2)
- The method used to estimate the contact radius and the equivalent radius, thus the contact area (by applying Hertz expressions), heavily influenced the calculated m-modulus. In general, the image processing using Matlab to compute the local radius in the vicinity of grain’s contacts led to much lower values of m-modulus compared with a manual estimation based on the obtained digital images. Despite that, the computed equivalent radius had a significant influence on the resultant peak stress, though this influence was more pronounced for the data where Matlab analysis was used compared with the manual method. It is noted that the manual method is not conceptually incorrect, in that the user defines, based on a digital image, a circle in the vicinity of the particle peak (where the contact with the neighboring grain is expected to occur), through which the local morphology is assessed. However, the Matlab analysis can capture more precisely the small differences in the morphologies of different grains, and this is very important to be considered in natural materials that display irregular shapes. The manual method homogenizes to some extend the assessed morphological characteristics of natural grains, giving rise to increased m-modulus values that inherently represent the variation of the characteristics within a population. Previous studies examining the breakage of grains have considered more “global” shapes rather than the locality of the particles, which, based on the present study, may lead to inaccurate estimation of the failure stress (as the failure stress is influenced by the estimated contact area).
- (3)
- The application of the Hertz model was implemented in two different steps. First, it was used to estimate the contact area to derive stresses from the measured forces; second, it was used to compute the contact Young’s modulus (E *) of each individual sample. Implementing the Hertz model to compute E * for each individual test had an influence on the resultant peak stress compared with the manual method (eyeball fitting), in which E * was assumed to be the same (30 GPa) for all the pairs of grains. This means that in the analysis of the breakage of particles, assessment of the elastic (and morphological) characteristics of the given sample is desirable.
- (4)
- Despite the significant differences in the estimated peak stress based on the method of analysis used, experiments at two different speeds (0.01 and 1 mm/min) provided similar results in terms of peak stress and m-modulus values. However, the speed of the tests had some influence on the mode of failure of the samples and also on the shape of the force–displacement curves. As the speed in the present study was examined within two folders, it is recommended that in future research works a wider range of velocities could be applied to examine the problem of grain breakage.
- (5)
- In general, the majority of the tests had a conservative-destructive or conservative mode of failure, where conservative implies micro-scale damage and formation of debris in the vicinity of grain contacts, while destructive implies macroscopic grain breakage. In some of the tests, a fragmentary mode of failure was observed, in which case meso-scale breakage and formation of small fragments occurred. A greater portion of fragmentary-type failure was observed at a higher speed. Thus, in the calibration of discrete-based numerical samples, it is important to consider how grains interact with respect to their breakage behavior rather than implementing the modes of failure as single-grain crushing tests would suggest (i.e., at the breakage point, a particle should not be seen as an isolated body, but its interaction with neighboring grains must be taken into account).
- (6)
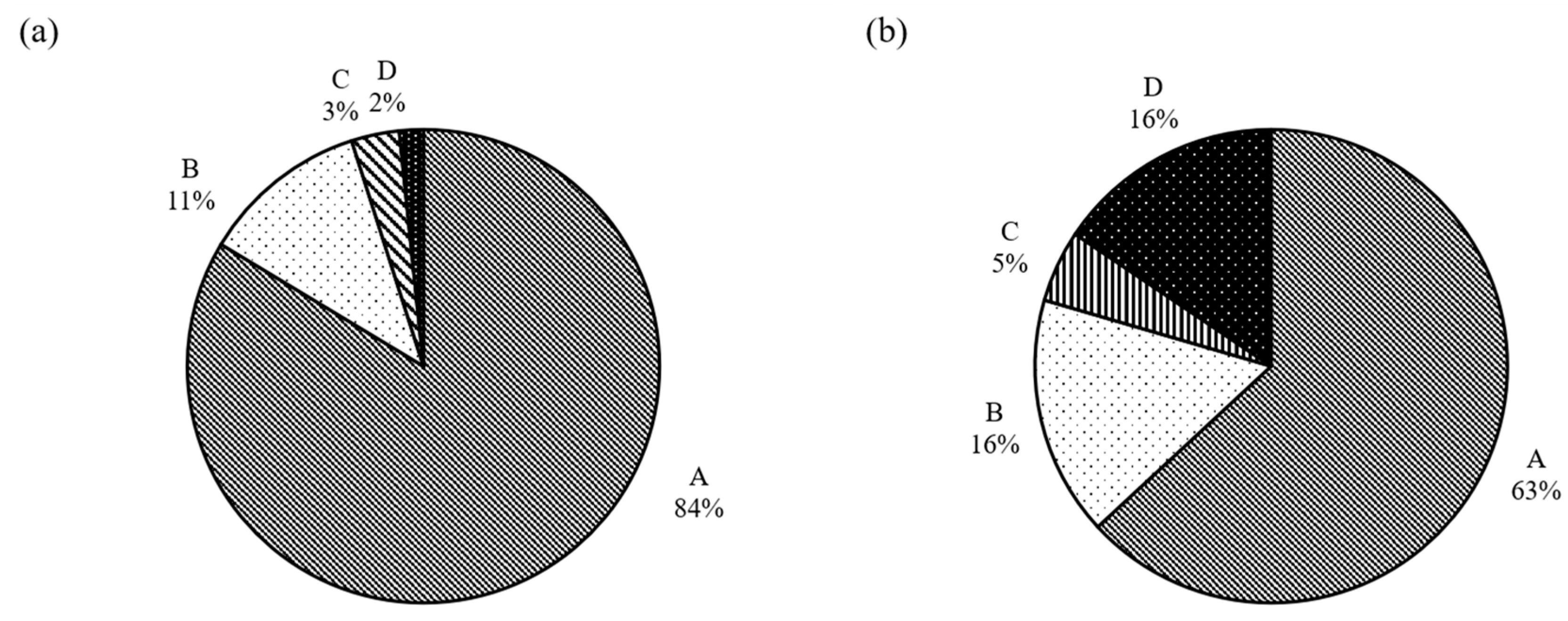
- Four classes of force–displacement curves were distinguished, in which case most of the samples had a brittle failure with clear peak stress (with or without the occurrence of hardening prior to reaching peak stress). In some of the tests, more prominently at the higher speed, multiple peaks were observed with a significant shift of the displacements (corresponding to peak stress) to higher values. This behavior was ascribed to possible creep influences; however, it is recommended that future studies could further explore this behavior to draw firm conclusions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- McDowell, G.; Bolton, M.; Robertson, D. The fractal crushing of granular materials. J. Mech. Phys. Solids 1996, 44, 2079–2101. [Google Scholar] [CrossRef]
- Indraratna, B.; Salim, W. Modelling of particle breakage of coarse aggregates incorporating strength and dilatancy. Geotech. Eng. 2002, 155, 243–252. [Google Scholar] [CrossRef]
- Einav, I. Breakage mechanics—Part II: Modelling granular materials. J. Mech. Phys. Solids 2007, 55, 1298–1320. [Google Scholar] [CrossRef]
- Wang, J.; Yan, H. DEM analysis of energy dissipation in crushable soils. Soils Found. 2012, 52, 644–657. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Yan, H. On the role of particle breakage in the shear failure behavior of granular soils by DEM. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 832–854. [Google Scholar] [CrossRef]
- Sazzad, M.; Suzuki, K. Effect of Interparticle Friction on the Cyclic Behavior of Granular Materials Using 2D DEM. J. Geotech. Geoenviron. Eng. 2011, 137, 545–549. [Google Scholar] [CrossRef]
- Li, W.; Kwok, C.; Sandeep, C.; Senetakis, K. Sand type effect on the behaviour of sand-granulated rubber mixtures: Integrated study from micro- to macro-scales. Powder Technol. 2019, 342, 907–916. [Google Scholar] [CrossRef]
- Bandara, K.M.A.S.; Ranjith, P.G.; Rathnaweera, T.D. Proppant Crushing Mechanisms Under Reservoir Conditions: Insights into Long-Term Integrity of Unconventional Energy Production. Nat. Resour. Res. 2018, 28, 1139–1161. [Google Scholar] [CrossRef]
- Bandara, K.; Ranjith, P.; Rathnaweera, T.; Wanniarachchi, W.; Yang, S. Crushing and embedment of proppant packs under cyclic loading: An insight to enhanced unconventional oil/gas recovery. Geosci. Front. 2020. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, S.; Xiao, H. Tribological properties of sliding quartz sand particle and shale rock contact under water and guar gum aqueous solution in hydraulic fracturing. Tribol. Int. 2019, 129, 416–426. [Google Scholar] [CrossRef]
- He, H.; Senetakis, K. A micromechanical study of shale rock-proppant composite interface. J. Pet. Sci. Eng. 2020, 184, 106542. [Google Scholar] [CrossRef]
- He, H.; Luo, L.; Senetakis, K. Effect of normal load and shearing velocity on the interface friction of organic shale—Proppant simulant. Tribol. Int. 2020, 144, 106119. [Google Scholar] [CrossRef]
- Fonseca, J.; Nadimi, S.; Reyes-Aldasoro, C.; O’Sullivan, C.; Coop, M. Image-based investigation into the primary fabric of stress-transmitting particles in sand. Soils Found. 2016, 56, 818–834. [Google Scholar] [CrossRef]
- Fonseca, J.; O’Sullivan, C.; Coop, M.; Lee, P. Quantifying the evolution of soil fabric during shearing using directional parameters. Géotechnique 2013, 63, 487–499. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Nguyen, N.G.H.; Lambert, S.; Nicot, F.; Prunier, F.; Djeran-Maigre, I. The role of force chains in granular materials: From statics to dynamics. Eur. J. Environ. Civ. Eng. 2016, 21, 874–895. [Google Scholar] [CrossRef]
- Lade, P.V.; Nam, J.; Liggio, C.D., Jr. Effect of particle crushing in stress drop-relaxation experiments on crushed coral sand. J. Geotech. Geoenvironmental Eng. 2010, 136, 500–509. [Google Scholar] [CrossRef]
- Zhang, J.M.; Wang, R.; Shi, X.F. Compression and crushing behavior of calcareous sand under confined compression. Chin. J. Rock Mech. Eng. 2005, 24, 3327–3331. [Google Scholar]
- Zhang, J.M.; Jang, G.S.; Wang, R. Research on influences of particle breakage and dilatancy on shear strength of calcareous sands. Rock Soil Mech. 2009, 30, 2043–2048. [Google Scholar]
- Leung, C.F.; Lee, F.H.; Yet, N.S. The role of particle breakage in pile creep in sand. Can. Geotech. J. 1996, 33, 888–898. [Google Scholar] [CrossRef]
- Sandeep, C.S.; Li, S.; Senetakis, K. Scale and surface morphology effects on the micromechanical contact behavior of granular materials. Tribol. Int. 2021, 159, 106929. [Google Scholar] [CrossRef]
- Wang, W.; Coop, M.R. An investigation of breakage behaviour of single sand particles using a high-speed microscope camera. Géotechnique 2016, 66, 984–998. [Google Scholar] [CrossRef] [Green Version]
- Todisco, M.C.; Wang, W.; Coop, M.R.; Senetakis, K. Multiple contact compression tests on sand particles. Soils Found. 2017, 57, 126–140. [Google Scholar] [CrossRef]
- Sandeep, C.S.; Senetakis, K. Exploring the Micromechanical Sliding Behavior of Typical Quartz Grains and Completely Decomposed Volcanic Granules Subjected to Repeating Shearing. Energies 2017, 10, 370. [Google Scholar] [CrossRef] [Green Version]
- Sandeep, C.S.; Senetakis, K. Effect of Young’s Modulus and Surface Roughness on the Inter-Particle Friction of Granular Materials. Materials 2018, 11, 217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sandeep, C.; Senetakis, K. Grain-scale mechanics of quartz sand under normal and tangential loading. Tribol. Int. 2018, 117, 261–271. [Google Scholar] [CrossRef]
- Nakata, Y.; Hyde, A.F.L.; Hyodo, M.; Murata, H.; McDowell, G.R. A probabilistic approach to sand particle crushing in the triaxial test. Géotechnique 2001, 51, 285–287. [Google Scholar] [CrossRef]
- Kasyap, S.; Senetakis, K. A micromechanical experimental study of kaolinite-coated sand grains. Tribol. Int. 2018, 126, 206–217. [Google Scholar] [CrossRef]
- Nad, A.; Saramak, D. Comparative Analysis of the Strength Distribution for Irregular Particles of Carbonates, Shale, and Sandstone Ore. Minerals 2018, 8, 37. [Google Scholar] [CrossRef] [Green Version]
- Bandini, V.; Coop, M. The Influence of Particle Breakage on the Location of the Critical State Line of Sands. Soils Found. 2011, 51, 591–600. [Google Scholar] [CrossRef] [Green Version]
- Coop, M.R.; Sorensen, K.K.; Bodas Freitas, T.; Georgoutsos, G. Particle breakage during shearing of a carbonate sand. Géotechnique 2004, 54, 157–163. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.-M. Fractal Behavior of Coral Sand During Creep. Front. Earth Sci. 2020, 8, 134. [Google Scholar] [CrossRef]
- Zhu, F.; Zhao, J. A peridynamic investigation on crushing of sand particles. Géotechnique 2019, 69, 526–540. [Google Scholar] [CrossRef] [Green Version]
- Zhou, B.; Wei, D.; Ku, Q.; Wang, J.; Zhang, A. Study on the effect of particle morphology on single particle breakage using a combined finite-discrete element method. Comput. Geotech. 2020, 122, 103532. [Google Scholar] [CrossRef]
- Kasyap, S.S.; Li, S.; Senetakis, K. Influence of natural coating type on the frictional and abrasion behaviour of siliciclastic-coated sedimentary sand grains. Eng. Geol. 2021, 281, 105983. [Google Scholar] [CrossRef]
- Sandeep, C.S.; Senetakis, K. The Tribological Behavior of Two Potential-Landslide Saprolitic Rocks. Pure Appl. Geophys. 2018, 175, 4483–4499. [Google Scholar] [CrossRef]
- Hertz, H. Uber die Beruhrang fester elastischer Korper (on the contact of elastic solids). J. Der. Rennin. Angew. Math. 1882, 92, 156–171. [Google Scholar]
- Kasyap, S.; Senetakis, K. Interface load–displacement behaviour of sand grains coated with clayey powder: Experimental and analytical studies. Soils Found. 2019, 59, 1695–1710. [Google Scholar] [CrossRef]
- Ren, J.; Li, S.; He, H.; Senetakis, K. The tribological behavior of iron tailing sand grain contacts in dry, water and biopolymer immersed states. Granul. Matter 2021, 23, 1–23. [Google Scholar] [CrossRef]
- Kasyap, S.S.; Senetakis, K. Experimental Investigation of the Coupled Influence of Rate of Loading and Contact Time on the Frictional Behavior of Quartz Grain Interfaces under Varying Normal Load. Int. J. Geomech. 2019, 19, 04019112. [Google Scholar] [CrossRef]
- Sandeep, C.; Senetakis, K. An experimental investigation of the microslip displacement of geological materials. Comput. Geotech. 2019, 107, 55–67. [Google Scholar] [CrossRef]
- Sandeep, C.S. Micromechanics of Hong Kong Debris Flow Materials. Ph.D. Thesis, Architecture and Civil Engineering Department, City University of Hong Kong, Hong Kong, China, 2019. [Google Scholar]
- Sandeep, C.; He, H.; Senetakis, K. An experimental micromechanical study of sand grain contacts behavior from different geological environments. Eng. Geol. 2018, 246, 176–186. [Google Scholar] [CrossRef]
- Đuriš, M.; Arsenijevic, Z.; Jaćimovski, D.; Radoicic, T.K. Optimal pixel resolution for sand particles size and shape analysis. Powder Technol. 2016, 302, 177–186. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Lim, W.L.; McDowell, G.R.; Collop, A.C. The application of Weibull statistics to the strength of railway ballast. Granul. Matter 2004, 6, 229–237. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, J.; Wang, H. A new probabilistic approach for predicting particle crushing in one-dimensional compression of granular soil. Soils Found. 2014, 54, 833–844. [Google Scholar] [CrossRef] [Green Version]
- McDowell, G.R. On the Yielding and Plastic Compression of Sand. Soils Found. 2002, 42, 139–145. [Google Scholar] [CrossRef]
- McDowell, G.; Amon, A. The Application of Weibull Statistics to the Fracture of Soil Particles. Soils Found. 2000, 40, 133–141. [Google Scholar] [CrossRef] [Green Version]
- Nakata, Y.; Kato, Y.; Hyodo, M.; Hyde, A.F.; Murata, H. One-Dimensional Compression Behaviour of Uniformly Graded Sand Related to Single Particle Crushing Strength. Soils Found. 2001, 41, 39–51. [Google Scholar] [CrossRef] [Green Version]
- Rabarijoely, S.; Bilski, P.; Falkowski, T. Usage of the graph clustering algorithm to the recognition of geotechnical layers. Ann. Wars. Univ. Life Sci. SGGW Land Reclam. 2007, 38, 57–67. [Google Scholar] [CrossRef]
- Liu, K.; Rassouli, F.S.; Liu, B.; Ostadhassan, M. Creep Behavior of Shale: Nanoindentation vs. Triaxial Creep Tests. Rock Mech. Rock Eng. 2021, 54, 321–335. [Google Scholar] [CrossRef]
- Deirieh, A.; Ortega, J.A.; Ulm, F.-J.; Abousleiman, Y. Nanochemomechanical assessment of shale: A coupled WDS-indentation analysis. Acta Geotech. 2012, 7, 271–295. [Google Scholar] [CrossRef]
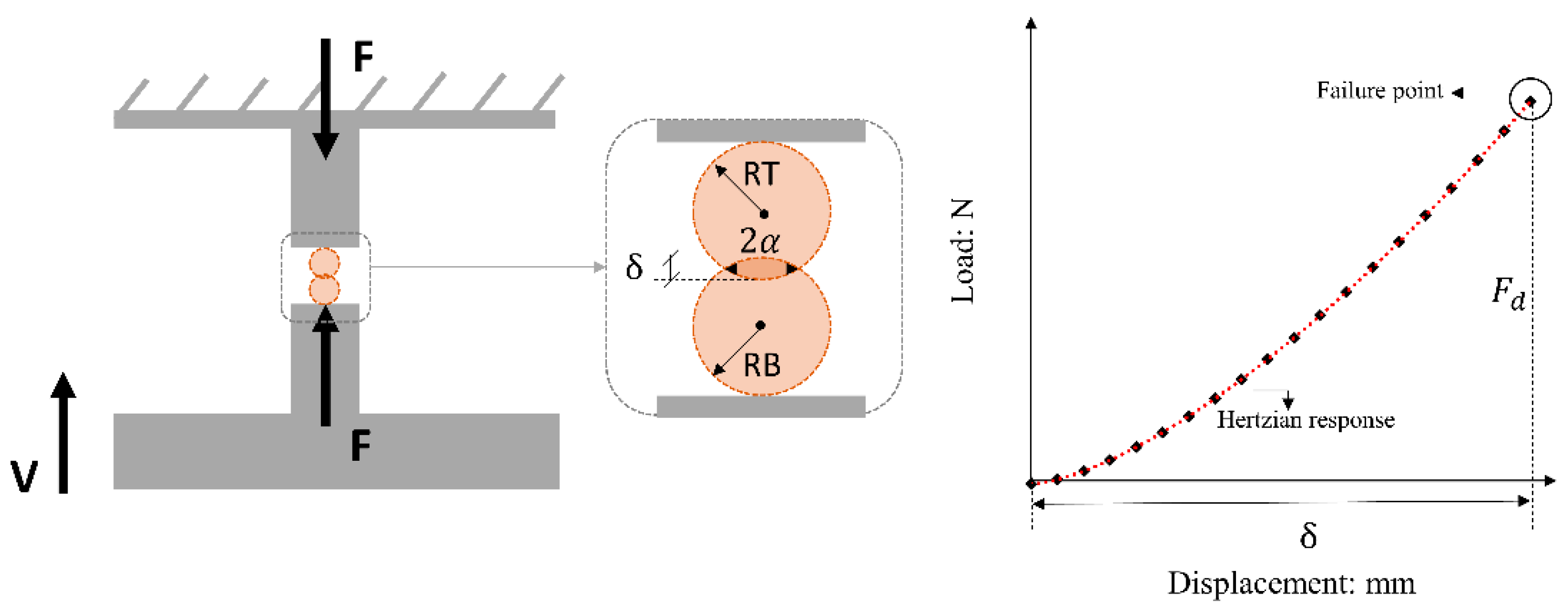













| Materials: Leighton Buzzard Sand (LBS); Size: 1.18–2.36 mm | ||||
|---|---|---|---|---|
| Loading Rate | Number of Tests | Test for Radius | Hertz Fitting | |
| Manual | Matlab | |||
| 0.01 mm/min | 122 | • | • | • |
| 1 mm/min | 122 | • | • | |
| Local Radius (R): mm | Equivalent Radius (R*): mm | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Position | Mean | Stdev | Max | Min | Mean | Stdev | Max | Min | |
| Matlab | Bottom | 0.46 | 0.22 | 1.34 | 0.11 | 0.2 | 0.09 | 0.54 | 0.07 |
| Top | 0.44 | 0.25 | 1.49 | 0.09 | |||||
| Manual | Bottom | 0.42 | 0.12 | 0.94 | 0.16 | 0.2 | 0.04 | 0.33 | 0.11 |
| Top | 0.41 | 0.12 | 0.83 | 0.17 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Kasyap, S.S.; Senetakis, K. A Study on the Failure Behavior of Sand Grain Contacts with Hertz Modeling, Image Processing, and Statistical Analysis. Sensors 2021, 21, 4611. https://doi.org/10.3390/s21134611
Li S, Kasyap SS, Senetakis K. A Study on the Failure Behavior of Sand Grain Contacts with Hertz Modeling, Image Processing, and Statistical Analysis. Sensors. 2021; 21(13):4611. https://doi.org/10.3390/s21134611
Chicago/Turabian StyleLi, Siyue, Sathwik S. Kasyap, and Kostas Senetakis. 2021. "A Study on the Failure Behavior of Sand Grain Contacts with Hertz Modeling, Image Processing, and Statistical Analysis" Sensors 21, no. 13: 4611. https://doi.org/10.3390/s21134611
APA StyleLi, S., Kasyap, S. S., & Senetakis, K. (2021). A Study on the Failure Behavior of Sand Grain Contacts with Hertz Modeling, Image Processing, and Statistical Analysis. Sensors, 21(13), 4611. https://doi.org/10.3390/s21134611







