Pre-Processing Method to Improve Cross-Domain Fault Diagnosis for Bearing
Abstract
:1. Introduction
2. Preliminary Knowledge of the Paper
2.1. Formulation of Cross-Domain Fault Daignosis
2.2. Convolution Neural Network (CNN)
2.3. Signal Processing
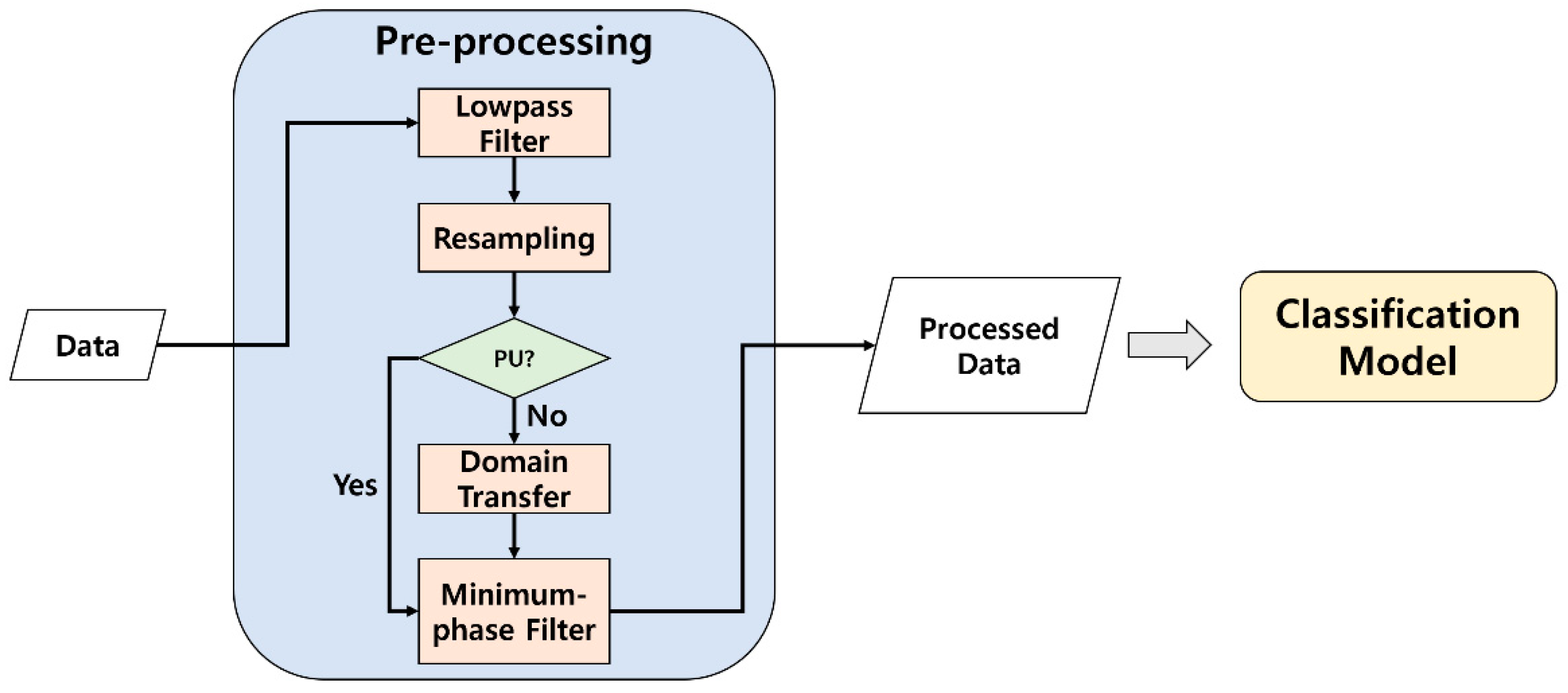
3. Proposed Method
4. Experiments and Results
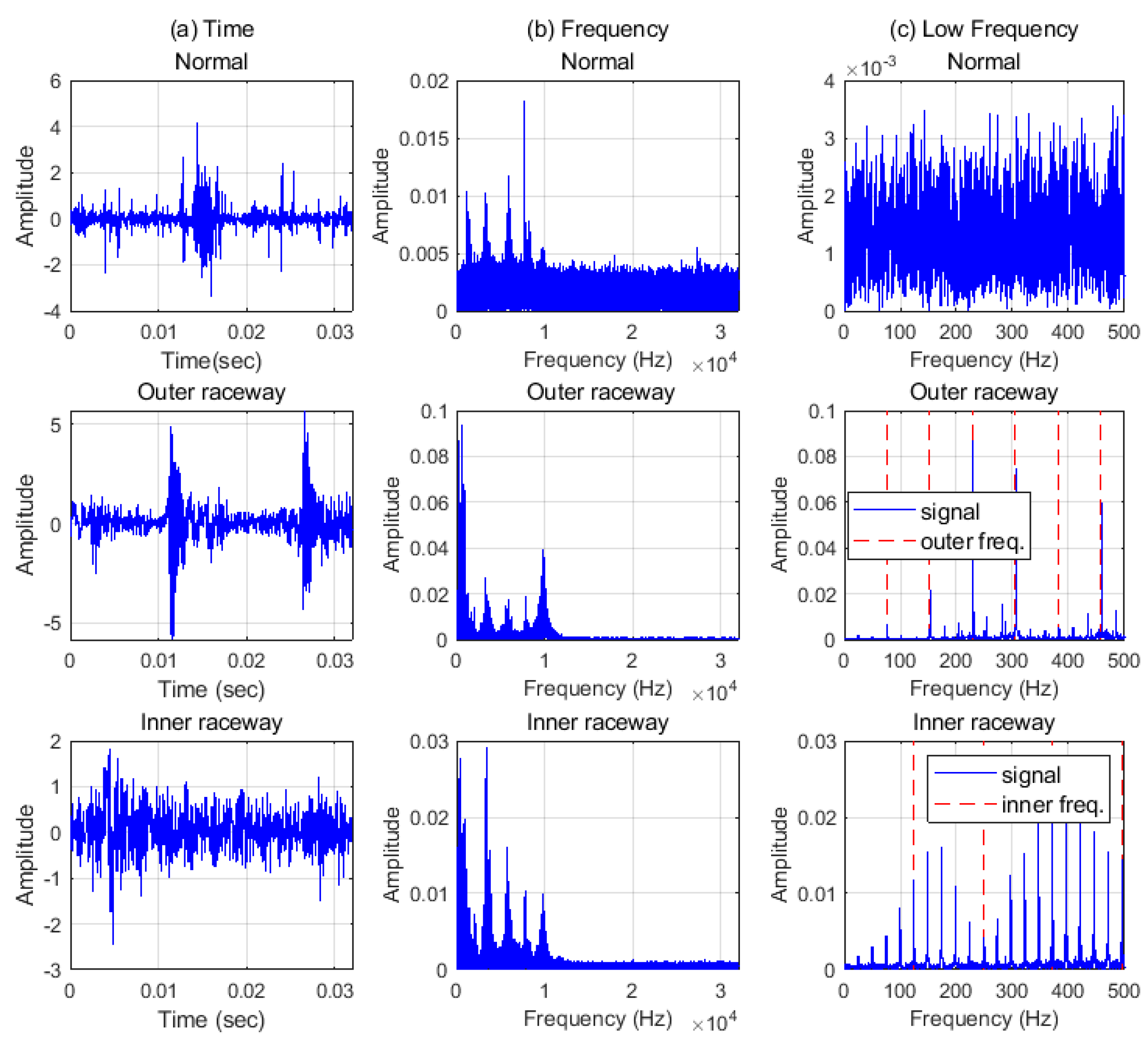
4.1. Datasets and Analyzing of Signals
4.1.1. Case Western Reserve University Data
4.1.2. Paderborn University Data
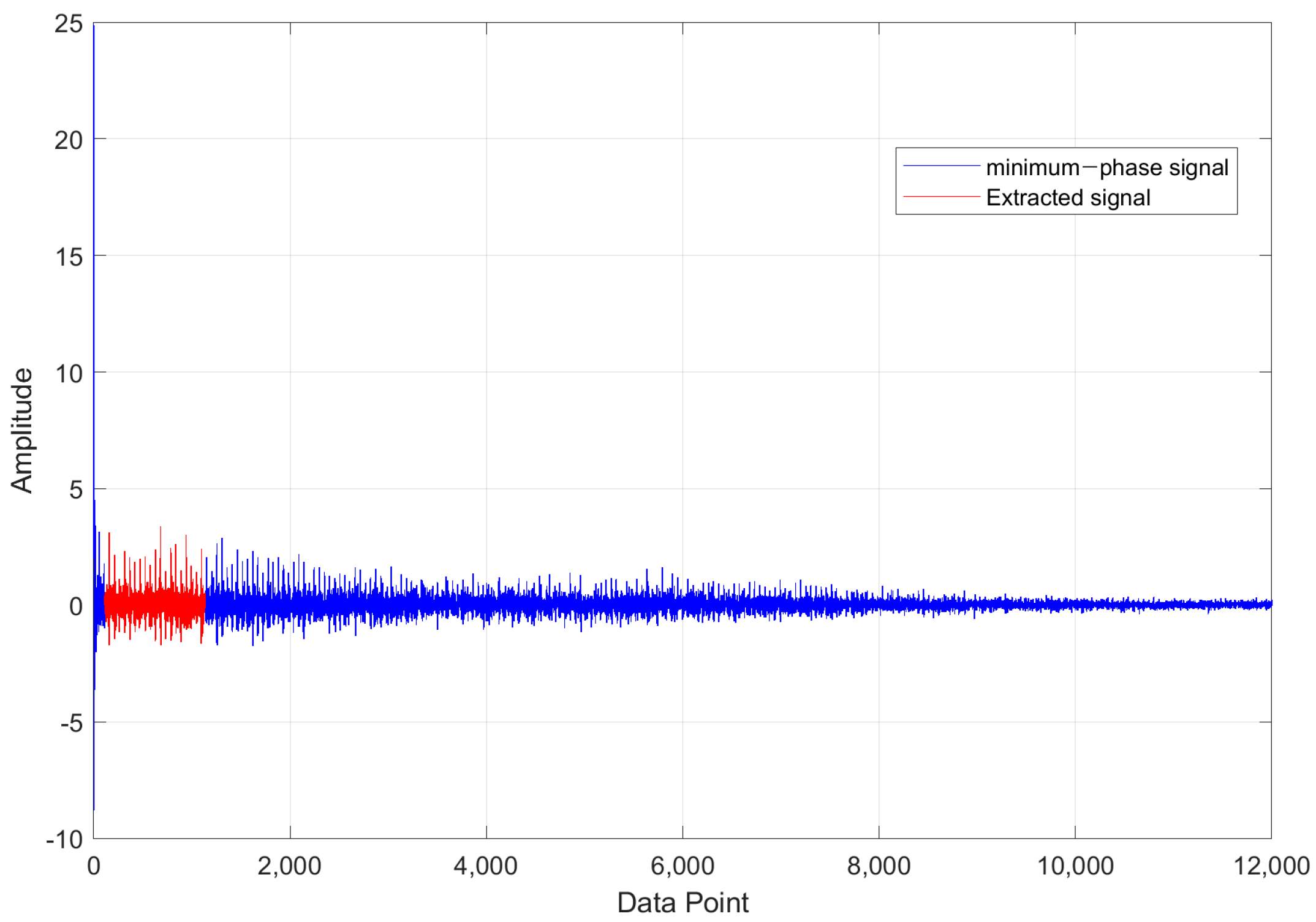
4.2. Results of Pre-Process
4.3. Experimental Results and Discussion
4.3.1. Model Description
- MK-MMD: MMD was proposed by K.M. Borgwardt et al. [51] and widely used in a cross-domain fault diagnosis for bearing diagnosis [23,24,25,26,27]. The features of the source domain and the target domain were embedded in the reproducing kernel Hilbert space (RKHS), and then the mean distance between the two domains was calculated. By training while reducing this distance, the difference between the two domains was reduced. The MK-MMD method [52] is a method of further reducing domain mismatch by using multi kernel MMD [28,29,30].
- Domain adversarial neural network (DANN): This method was first proposed by Ganin et al. [53] and used in several studies [42,43]. In this method, a discriminator is added, and the features of the source domain and the target domain are not known. For this purpose, a discriminator described in Table 3 was designed and used with gradient reversal layer.
4.3.2. Case 1: CNN with Pre-Processing
4.3.3. Case 2: CNN with Domain Adaptation
4.3.4. Case 3: CNN with Pre-Processing and Domain Adaptation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PU | Paderborn University |
| CWRU | Case Western Reserve University |
| CNN | Convolution Neural Network |
| FFT | Fast Fourier Transform |
| IFFT | Inverse Fast Fourier Transform |
| CORAL | CORrelation ALignment |
| MK-MMD | Multi Kernel Maximum Mean Discrepancy |
| DANN | Domain Adversarial Neural Network |
| PCA | Principal Component Analysis |
References
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification. In Proceedings of the European Conference of the Prognostics and Health Management Society, Bilbao, Spain, 5–8 July 2016; pp. 5–8. [Google Scholar]
- Loparo, K. Case Western Reserve University Bearing Data Center Website. Available online: https://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 9 June 2021).
- Smith, W.; Randall, R. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Alshorman, O.; Irfan, M.; Saad, N.; Zhen, D.; Haider, N.; Glowacz, A.; Alshorman, A. A review of artificial intelligence methods for condition monitoring and fault diagnosis of rolling element bearings for induction motor. Shock. Vib. 2020, 2020, 8843759. [Google Scholar] [CrossRef]
- Hoang, D.-T.; Knag, H.-J. A survey on Deep Learning based bearing fault diagnosis. Neurocomputing 2019, 335, 327–335. [Google Scholar] [CrossRef]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Walle, R.; Van Hoecke, S. Convolutional neural network based fault detection for rotating machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Peng, D.; Liu, Z.; Wang, H.; Qin, Y.; Jia, L. A novel deeper one-dimensional CNN with residual learning for fault diagnosis of wheelset bearings in high-speed trains. IEEE Access 2019, 7, 10278–10293. [Google Scholar] [CrossRef]
- Huang, W.; Cheng, J.; Yang, Y.; Guo, G. An improved deep convolutional neural network with multi-scale information for bearing fault diagnosis. Neurocomputing 2019, 359, 77–92. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network-based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2017, 65, 5990–5998. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Yan, R.; Gao, R.X. A new intelligent bearing fault diagnosis method using SDP representation and SE-CNN. IEEE Trans. Instrum. Meas. 2020, 69, 2377–2389. [Google Scholar] [CrossRef]
- Xue, Y.; Dou, D.; Yang, J. Multi-fault diagnosis of rotating machinery based on deep convolution neural network and support vector machine. Measurement 2020, 156, 107571. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, J.; Zhong, Y.; Zhou, Y. Convolutional neural network-based hidden Markov models for rolling element bearing fault identification. Knowl. Based Syst. 2018, 144, 65–76. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y.; Zhou, J.; Zang, Y. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.; Zhou, B. Intelligent fault diagnosis of rolling bearing using hierarchical convolutional network based health state classification. Adv. Eng. Inform. 2017, 32, 139–151. [Google Scholar] [CrossRef]
- Fuan, W.; Hongkai, J.; Haidong, S.; Wenjing, D.; Shuaipeng, W. An adaptive deep convolutional neural network for rolling bearing fault diagnosis. Meas. Sci. Technol. 2017, 28, 095005. [Google Scholar] [CrossRef]
- Li, G.; Deng, C.; Wu, J.; Xu, X.; Shao, X.; Wang, Y. Sensor data-driven bearing fault diagnosis based on deep convolutional neural networks and s-transform. Sensors 2019, 19, 2750. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zheng, L.; Du, W.; Cai, W.; Zhou, J.; Wang, J.; Han, X.; He, G. A novel method for intelligent fault diagnosis of bearing based on capsule neural network. Complexity 2019, 2019, 6943234. [Google Scholar] [CrossRef] [Green Version]
- Zuo, L.; Zhang, L.; Zhang, Z.-H.; Luo, X.-L.; Liu, Y. A spiking neural network-based approach to bearing fault diagnosis. J. Manuf. Syst. 2020. [Google Scholar] [CrossRef]
- Lex, E.; Seifert, C.; Granitzer, M.; Juffinger, A. Cross-Domain Classification: Trade-Off between Complexity and Accuracy. In Proceedings of the 2009 International Conference for Internet Technology and Secured Transactions, (ICITST), London, UK, 9–12 November 2009; pp. 1–6. [Google Scholar]
- Zhu, Y.; Zhuang, F.; Wang, J.; Chen, J.; Shi, Z.; Wu, W.; He, Q. Multi-representation adaptation network for cross-domain image classification. Neural Netw. 2019, 119, 214–221. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Wang, R.; Yang, Y.; Yin, J.; Li, Y.; Li, Y.; Xu, M. Cross-domain fault diagnosis using knowledge transfer strategy: A review. IEEE Access 2019, 7, 129260–129290. [Google Scholar] [CrossRef]
- Lu, W.; Liang, B.; Cheng, Y.; Meng, D.; Yang, J.; Zhang, T. Deep model based domain adaptation for fault diagnosis. IEEE Trans. Ind. Electron. 2017, 64, 2296–2305. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep convolutional transfer learning network: A new method for intelligent fault diagnosis of machines with unlabeled data. IEEE Trans. Ind. Electron. 2019, 66, 7316–7325. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. A robust intelligent fault diagnosis method for rolling element bearings based on deep distance metric learning. Neurocomputing 2018, 310, 77–95. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X. A new deep transfer learning based on sparse auto-encoder for fault diagnosis. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 49, 136–144. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jia, F.; Xing, S. An intelligent fault diagnosis approach based on transfer learning from laboratory bearings to locomotive bearings. Mech. Syst. Signal Process. 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jia, F.; Xing, S. A Transfer Learning Method for Intelligent Fault Diagnosis from Laboratory Machines to Real-Case Machines. In Proceedings of the 2018 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Xi’an, China, 15–17 August 2018; pp. 35–40. [Google Scholar]
- An, Z.; Li, S.; Wang, J.; Xin, Y.; Xu, K. Generalization of deep neural network for bearing fault diagnosis under different working conditions using multiple kernel method. Neurocomputing 2019, 352, 42–53. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J.-Q. Multi-Layer domain adaptation method for rolling bearing fault diagnosis. Signal Process. 2019, 157, 180–197. [Google Scholar] [CrossRef] [Green Version]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. Deep transfer network with joint distribution adaptation: A new intelligent fault diagnosis framework for industry application. ISA Trans. 2020, 97, 269–281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Jiang, H.; Liu, S.; Zhang, J.; Xu, J. A unified framework incorporating predictive generative denoising autoencoder and deep Coral network for rolling bearing fault diagnosis with unbalanced data. Measurement 2021, 178, 109345. [Google Scholar] [CrossRef]
- An, J.; Ai, P.; Liu, D. Deep domain adaptation model for bearing fault diagnosis with domain alignment and discriminative feature learning. Shock. Vib. 2020, 2020, 4676701. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.; Zhou, B.; Ma, G.; Wu, D.; Yuan, Y. Wasserstein distance based deep adversarial transfer learning for intelligent fault diagnosis. Neurocomputing 2020, 409, 35–45. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, D.; Lu, W.; Yang, J.; Li, Z.; Liang, B. A deep transfer model with wasserstein distance guided multi-adversarial networks for bearing fault diagnosis under different working conditions. IEEE Access 2019, 7, 65303–65318. [Google Scholar] [CrossRef]
- Wang, X.; Liu, F. Triplet loss guided adversarial domain adaptation for bearing fault diagnosis. Sensors 2020, 20, 320. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Tao, H.; Wu, L.; Guan, Y. Transfer learning with neural networks for bearing fault diagnosis in changing working conditions. IEEE Access 2017, 5, 14347–14357. [Google Scholar] [CrossRef]
- Chen, D.; Yang, S.; Zhou, F. Incipient Fault Diagnosis Based on DNN with Transfer Learning. In Proceedings of the 2018 International Conference on Control, Automation and Information Sciences (ICCAIS), Hangzhou, China, 24–27 October 2018; pp. 303–308. [Google Scholar]
- Hasan, M.J.; Kim, J.-M. Bearing fault diagnosis under variable rotational speeds using stockwell transform-based vibration imaging and transfer learning. Appl. Sci. 2018, 8, 2357. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.J.; Islam, M.M.M.; Kim, J.-M. Acoustic spectral imaging and transfer learning for reliable bearing fault diagnosis under variable speed conditions. Measurement 2019, 138, 620–631. [Google Scholar] [CrossRef]
- Kim, H.; Youn, B.D. A new parameter repurposing method for parameter transfer with small dataset and its application in fault diagnosis of rolling element bearings. IEEE Access 2019, 7, 46917–46930. [Google Scholar] [CrossRef]
- Wang, X.; Liu, F.; Zhao, D. Cross-Machine fault diagnosis with semi-supervised discriminative adversarial domain adaptation. Sensors 2020, 20, 3753. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. A novel adversarial learning framework in deep convolutional neural network for intelligent diagnosis of mechanical faults. Knowl. Based Syst. 2019, 165, 474–487. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Q.; Sun, C.; Wang, S.; Yan, R.; Chen, X. Unsupervised deep transfer learning for intelligent fault diagnosis: An open source and comparative study. arXiv 2019, arXiv:1912.12528. [Google Scholar]
- Zheng, H.; Yang, Y.; Yin, J.; Li, Y.; Wang, R.; Xu, M. Deep domain generalization combining a priori diagnosis knowledge toward cross-domain fault diagnosis of rolling bearing. IEEE Trans. Instrum. Meas. 2021, 70, 3501311. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 2nd ed.; Prentice Hall: New Jersey, NJ, USA, 1999; pp. 280–291. [Google Scholar]
- Harris, T.A. Rolling Bearing Analysis, 4th ed.; John Wiley & Sons Inc.: New York, NY, USA, 2000. [Google Scholar]
- Sun, B.; Feng, J.; Saenko, K. Return of frustratingly easy domain adaptation. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Sun, B.; Saenko, K. Deep Coral: Correlation Alignment for Deep Domain Adaptation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 443–450. [Google Scholar]
- Borgwardt, K.M.; Gretton, A.; Rasch, M.J.; Kriegel, H.-P.; Schölkopf, B.; Smola, A.J. Integrating structured biological data by Kernel Maximum Mean Discrepancy. Bioinformatics 2006, 22, e49–e57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hinton, G.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov., R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Ganin, Y.; Lempitsky, V. Unsupervised domain adaptation by backpropagation. arXiv 2014, arXiv:1409.7495. [Google Scholar]











| Types of Faults | Normal | Inner Fault | Outer Fault | Normal | Inner Fault | Outer Fault | Normal | Inner Fault | Outer Fault | Normal | Inner Fault | Outer Fault |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diameter of a defect (Inches) | - | 0.007 | 0.007 | - | 0.007 | 0.007 | - | 0.007 | 0.007 | - | 0.007 | 0.007 |
| Load level | 0 hp | 1 hp | 2 hp | 3 hp | ||||||||
| Domain | C1 | C2 | C3 | C4 | ||||||||
| Bearing Code | Data Number | Rotational Speed (rpm) | Load Toque (Nm) | Radial Force (N) | Types of Faults | Domain |
|---|---|---|---|---|---|---|
| K001 | 1 | 1500 | 0.7 | 1000 | Normal | P |
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| KA16 | 1 | 1500 | 0.7 | 1000 | Outer fault | |
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| KI16 | 1 | 1500 | 0.7 | 1000 | Inner fault | |
| 2 | ||||||
| 3 | ||||||
| 4 |
| Role | Layers | Parameters |
|---|---|---|
| - | Input | - |
| Extractor | Convolution 1 | Kernel_size = 20, stride = 1, channel = 32 |
| Batch normalization 1 | - | |
| ReLU 1 | - | |
| Average pooling 1 | Kernel_size = 2, stride = 2 | |
| Convolution 2 | Kernel_size = 5, stride = 1, channel = 64 | |
| Batch normalization 2 | - | |
| ReLU 2 | - | |
| Average pooling 2 | Kernel_size = 2, stride = 2 | |
| Convolution 3 | Kernel_size = 3, stride = 1, channel = 128 | |
| Batch normalization 3 | - | |
| ReLU 3 | - | |
| Adaptive average pooling 1 | Output size = 4 | |
| Fully connected 1 | Out features = 256 | |
| ReLU 4 | - | |
| Classifier | Fully connected | Output = 3 |
| Discriminator (for DANN) | Fully connected 1 | Out features = 512 |
| ReLU 1 | - | |
| Fully connected 2 | Out features = 1024 | |
| ReLU 2 | - | |
| Fully connected3 | Out features = 1 | |
| Sigmoid | - |
| Domain | Label | Results (%) | |
|---|---|---|---|
| Raw Data | Processed Data | ||
| Train: P | Normal: 0 Inner fault: 1 Outer fault: 2 | 0.00 | 45.69 |
| Test: C1–C4 | |||
| Domain | Label | Model and Results (%) | |||||
|---|---|---|---|---|---|---|---|
| CORAL | MK-MMD | DANN | |||||
| Best | Average | Best | Average | Best | Average | ||
| Train: P | Normal: 0 Inner fault: 1 Outer fault: 2 | 33.28 | 31.70 | 0.00 | 0.00 | 33.32 | 21.13 |
| Test: C1–C4 | |||||||
| Domain | Label | Model and Results (%) | |||||
|---|---|---|---|---|---|---|---|
| CORAL | MK-MMD | DANN | |||||
| Best | Average | Best | Average | Best | Average | ||
| Train: P | Normal: 0 Inner fault: 1 Outer fault: 2 | 96.24 | 94.00 | 100.00 | 100.00 | 100.0 | 100.00 |
| Test: C1-C4 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.; Chai, J. Pre-Processing Method to Improve Cross-Domain Fault Diagnosis for Bearing. Sensors 2021, 21, 4970. https://doi.org/10.3390/s21154970
Kim T, Chai J. Pre-Processing Method to Improve Cross-Domain Fault Diagnosis for Bearing. Sensors. 2021; 21(15):4970. https://doi.org/10.3390/s21154970
Chicago/Turabian StyleKim, Taeyun, and Jangbom Chai. 2021. "Pre-Processing Method to Improve Cross-Domain Fault Diagnosis for Bearing" Sensors 21, no. 15: 4970. https://doi.org/10.3390/s21154970
APA StyleKim, T., & Chai, J. (2021). Pre-Processing Method to Improve Cross-Domain Fault Diagnosis for Bearing. Sensors, 21(15), 4970. https://doi.org/10.3390/s21154970





