Performance Analysis in Ski Jumping with a Differential Global Navigation Satellite System and Video-Based Pose Estimation
Abstract
1. Introduction
2. Materials and Methods
2.1. Video Based PosEst Method
2.2. dGNSS Based Method
2.3. Parameter Definition and Calculation
2.4. Part I: Comparison of PosEst and dGNSS Method
2.5. Part II: Case Study
3. Results and Discussion
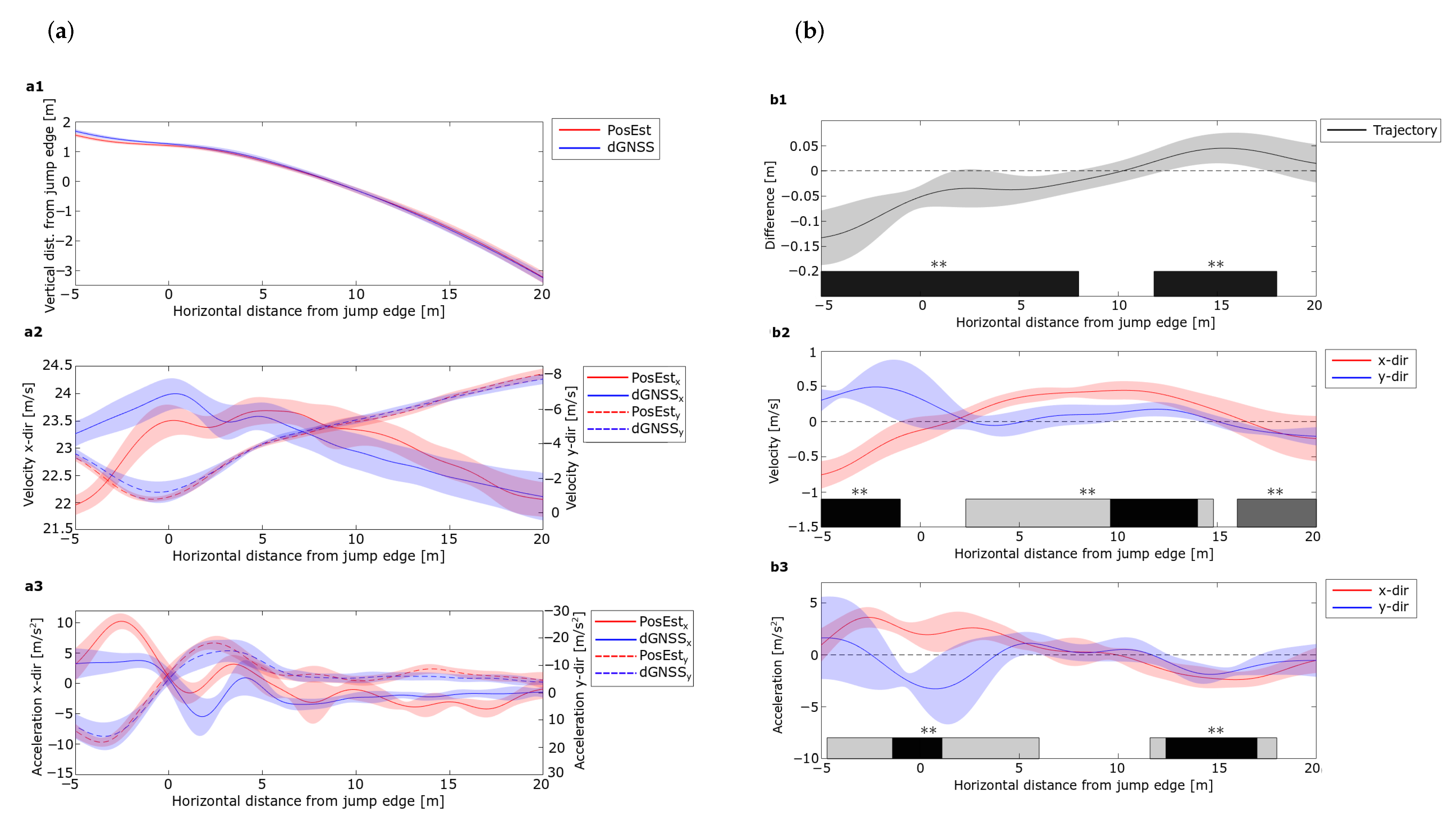
3.1. Part I: Comparison of PosEst and dGNSS Data
3.2. Part II: Case Study
3.2.1. External Data
3.2.2. In-Run
3.2.3. Take-Off and Early Flight Phase
3.2.4. Flight Phase
3.3. Possibilities and Limitations
3.4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CoM | Center of Mass |
| ConvNet | Convolutional Neural Network |
| dGNSS | differential Global Navigation Satellite System |
| Braking force | |
| Drag force | |
| Friction force | |
| Lift force | |
| /-ratio | Lift-to-drag ratio |
| Normal force | |
| Perpendicular force | |
| FIS | International Ski Federation |
| IMU | Inertial Measurement Units |
| MAE | Mean Absolute Error |
| PosEst | Markerless Video-based Pose Estimation |
| SPM | Statistical Parametric Mapping |
Appendix A. Statistical Parametric Mapping Analysis


References
- Schwameder, H. Biomechanics research in ski jumping, 1991–2006. Sport. Biomech. 2008, 7, 114–136. [Google Scholar] [CrossRef]
- Virmavirta, M.; Isolehto, J.; Komi, P.; Schwameder, H.; Pigozzi, F.; Massazza, G. Take-off analysis of the Olympic ski jumping competition (HS-106 m). J. Biomech. 2009, 42, 1095–1101. [Google Scholar] [CrossRef]
- Ettema, G.; Braaten, S.; Danielsen, J.; Fjeld, B.E. Imitation jumps in ski jumping: Technical execution and relationship to performance level. J. Sport. Sci. 2020, 38, 2155–2160. [Google Scholar] [CrossRef] [PubMed]
- Chardonnes, J.; Favre, J.; Le Callennec, B.; Cuendet, F.; Gremion, G.; Aminan, K. Automatic measurement of key ski jumping phases and temporal events with a wearable system. J. Sport Sci. 2012, 30, 53–61. [Google Scholar] [CrossRef]
- Jones, R.L.; Wallace, M. Another bad day at the training ground: Coping with ambiguity in the coaching context. Sport. Educ. Soc. 2005, 10, 119–134. [Google Scholar] [CrossRef]
- Elfmark, O.; Ettema, G. Aerodynamic investigation of the inrun position in Ski jumping. Sports Biomech. 2021, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Müller, W. Determinants of ski-jump performance and implications for health, safety and fairness. Sport. Med. 2009, 39, 85–106. [Google Scholar] [CrossRef] [PubMed]
- Adesida, Y.; Papi, E.; McGregor, A.H. Exploring the role of wearable technology in sport kinematics and kinetics: A systematic review. Sensors 2019, 19, 1597. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, G.; Nevill, A.M. Selected issues in the design and analysis of sport performance research. J. Sport Sci. 2001, 19, 811–827. [Google Scholar] [CrossRef]
- Lorenzetti, S.; Ammann, F.; Windmüller, S.; Häberle, R.; Müller, S.; Gross, M.; Plüss, M.; Plüss, S.; Schödler, B.; Hübner, K. Conditioning exercises in ski jumping: Biomechanical relationship of squat jumps, imitation jumps, and hill jumps. Sport. Biomech. 2019, 18, 63–74. [Google Scholar] [CrossRef]
- Virmavirta, M.; Komi, P.V. Measurement of take-off forces in ski jumping: Part I. Scand. J. Med. Sci. Sport. 1993, 3, 229–236. [Google Scholar] [CrossRef]
- Virmavirta, M.; Komi, R.V. Measurement of take-off forces in ski jumping: Part II. Scand. J. Med. Sci. Sport. 1993, 3, 237–243. [Google Scholar] [CrossRef]
- Bessone, V.; Petrat, J.; Schwirtz, A. Ground reaction forces and kinematics of ski jump landing using wearable sensors. Sensors 2019, 19, 2011. [Google Scholar] [CrossRef] [PubMed]
- Bessone, V.; Petrat, J.; Seiberl, W.; Schwirtz, A. Analysis of landing in ski jumping by means of inertial sensors and force insoles. Proceedings 2018, 2, 311. [Google Scholar] [CrossRef]
- Virmavirta, M.; Komi, P.V. Plantar pressures during ski jumping take-off. J. Appl. Biomech. 2000, 16, 320–326. [Google Scholar] [CrossRef]
- Pauli, C.A.; Keller, M.; Ammann, F.; Hübner, K.; Lindorfer, J.; Taylor, W.R.; Lorenzetti, S. Kinematics and kinetics of squats, drop jumps and imitation jumps of ski jumpers. J. Strength Cond. Res. 2016, 30, 643. [Google Scholar] [CrossRef]
- Arndt, A.; Brüggemann, G.P.; Virmavirta, M.; Komi, P. Techniques used by Olympic ski jumpers in the transition from takeoff to early flight. J. Appl. Biomech. 1995, 11, 224–237. [Google Scholar] [CrossRef]
- Müller, W.; Platzer, D.; Schmölzer, B. Dynamics of human flight on skis: Improvements in safety and fairness in ski jumping. J. Biomech. 1996, 29, 1061–1068. [Google Scholar] [CrossRef]
- Schmölzer, B.; Müller, W. The importance of being light: Aerodynamic forces and weight in ski jumping. J. Biomech. 2002, 35, 1059–1069. [Google Scholar] [CrossRef]
- Schmölzer, B.; Müller, W. Individual flight styles in ski jumping: Results obtained during Olympic Games competitions. J. Biomech. 2005, 38, 1055–1065. [Google Scholar] [CrossRef]
- Schwameder, H.; Müller, E.; Lindenhofer, E.; DeMonte, G.; Potthast, W.; Brüggemann, P.; Virmavirta, M.; Isolehto, J.; Komi, P. Kinematic characteristics of the early flight phase in ski-jumping. In Science and Skiing III; Meyer & Meyer Verlag: Oxford, UK, 2005; pp. 381–391. [Google Scholar]
- Virmavirta, M.; Isolehto, J.; Komi, P.; Brüggemann, G.P.; Müller, E.; Schwameder, H. Characteristics of the early flight phase in the Olympic ski jumping competition. J. Biomech. 2005, 38, 2157–2163. [Google Scholar] [CrossRef] [PubMed]
- Colyer, S.L.; Evans, M.; Cosker, D.P.; Salo, A.I. A review of the evolution of vision-based motion analysis and the integration of advanced computer vision methods towards developing a markerless system. Sport. Med.-Open 2018, 4, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, K.; Einfalt, M.; Lienhart, R. Robust estimation of flight parameters for ski jumpers. In Proceedings of the 2020 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), London, UK, 6–10 July 2020; pp. 1–6. [Google Scholar]
- Katircioglu, I.; Rhodin, H.; Constantin, V.; Spörri, J.; Salzmann, M.; Fua, P. Self-supervised training of proposal-based segmentation via background prediction. arXiv 2019, arXiv:1907.08051. [Google Scholar]
- Chardonnens, J.; Favre, J.; Cuendet, F.; Gremion, G.; Aminian, K. A system to measure the kinematics during the entire ski jump sequence using inertial sensors. J. Biomech. 2013, 46, 56–62. [Google Scholar] [CrossRef] [PubMed]
- Chardonnens, J.; Favre, J.; Cuendet, F.; Gremion, G.; Aminian, K. Measurement of the dynamics in ski jumping using a wearable inertial sensor-based system. J. Sport. Sci. 2014, 32, 591–600. [Google Scholar] [CrossRef] [PubMed]
- Glowinski, S.; Łosiński, K.; Kowiański, P.; Waśkow, M.; Bryndal, A.; Grochulska, A. Inertial sensors as a tool for diagnosing discopathy lumbosacral pathologic gait: A preliminary research. Diagnostics 2020, 10, 342. [Google Scholar] [CrossRef]
- Groh, B.H.; Warschun, F.; Deininger, M.; Kautz, T.; Martindale, C.; Eskofier, B.M. Automated ski velocity and jump length determination in ski jumping based on unobtrusive and wearable sensors. Proc. ACM Interact. Mobile Wearable Ubiquitous Technol. 2017, 1, 1–17. [Google Scholar] [CrossRef]
- Logar, G.; Munih, M. Estimation of joint forces and moments for the inrun and take-off in ski jumping based on measurements with wearable inertial sensors. Sensors 2015, 15, 11258–11276. [Google Scholar] [CrossRef]
- Ohgi, Y.; Hirai, N.; Murakami, M.; Seo, K. Aerodynamic study of ski jumping flight based on inertia sensors (171). In The Engineering of Sport 7; Springer: Paris, France, 2008; pp. 157–164. [Google Scholar]
- Brodie, M.; Walmsley, A.; Page, W. Fusion motion capture: A prototype system using inertial measurement units and GPS for the biomechanical analysis of ski racing. Sport. Technol. 2008, 1, 17–28. [Google Scholar] [CrossRef]
- Blumenbach, T. High precision kinematic GPS positioning of ski jumpers. In Proceedings of the 17th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2004), Long Beach, CA, USA, 21–24 September 2004; pp. 761–765. [Google Scholar]
- Gilgien, M.; Kröll, J.; Spörri, J.; Crivelli, P.; Müller, E. Application of dGNSS in alpine ski racing: Basis for evaluating physical demands and safety. Front. Physiol. 2018, 9, 145. [Google Scholar] [CrossRef]
- Gilgien, M.; Spörri, J.; Chardonnens, J.; Kröll, J.; Müller, E. Determination of external forces in alpine skiing using a differential global navigation satellite system. Sensors 2013, 13, 9821–9835. [Google Scholar] [CrossRef]
- Gilgien, M.; Spörri, J.; Chardonnens, J.; Kröll, J.; Limpach, P.; Müller, E. Determination of the centre of mass kinematics in alpine skiing using differential global navigation satellite systems. J. Sport. Sci. 2015, 33, 960–969. [Google Scholar] [CrossRef]
- Supej, M. D measurements of alpine skiing with an inertial sensor motion capture suit and GNSS RTK system. J. Sport. Sci. 2010, 28, 759–769. [Google Scholar] [CrossRef]
- Supej, M.; Holmberg, H.C. A new time measurement method using a high-end global navigation satellite system to analyze alpine skiing. Res. Q. Exerc. Sport 2011, 82, 400–411. [Google Scholar] [CrossRef]
- Gilgien, M.; Spörri, J.; Limpach, P.; Geiger, A.; Müller, E. The effect of different global navigation satellite system methods on positioning accuracy in elite alpine skiing. Sensors 2014, 14, 18433–18453. [Google Scholar] [CrossRef]
- Virmavirta, M.; Kivekäs, J. The effect of wind on jumping distance in ski jumping–fairness assessed. Sport. Biomech. 2012, 11, 358–369. [Google Scholar] [CrossRef]
- Groos, D.; Ramampiaro, H.; Ihlen, E.A. EfficientPose: Scalable single-person pose estimation. Applied Intell. 2020, 51, 2518–2533. [Google Scholar] [CrossRef]
- De Leva, P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Ettema, G.J.; Bråten, S.; Bobbert, M.F. Dynamics of the inrun in ski jumping: A simulation study. J. Appl. Biomech. 2005, 21, 247–259. [Google Scholar] [CrossRef]
- Barelle, C.; Ruby, A.; Tavernier, M. Experimental model of the aerodynamic drag coefficient in alpine skiing. J. Appl. Biomech. 2004, 20, 167–176. [Google Scholar] [CrossRef]
- Virmavirta, M.; Kivekäs, J.; Komi, P. Ski jumping takeoff in a wind tunnel with skis. J. Appl. Biomech. 2011, 27, 375–379. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gardan, N.; Schneider, A.; Polidori, G.; Trenchard, H.; Seigneur, J.M.; Beaumont, F.; Fourchet, F.; Taiar, R. Numerical investigation of the early flight phase in ski-jumping. J. Biomech. 2017, 59, 29–34. [Google Scholar] [CrossRef]
- Lee, K.D.; Park, M.J.; Kim, K.Y. Optimization of ski jumper’s posture considering lift-to-drag ratio and stability. J. Biomech. 2012, 45, 2125–2132. [Google Scholar] [CrossRef]
- Crenna, F.; Rossi, G.B.; Belotti, V.; Palazzo, A. Filtering signals for movement analysis in biomechanics. In Proceedings of the XXI IMEKO World Congress, Prague, Czech Republic, 30 August–4 September 2015. [Google Scholar]
- Adler, R.J. The Geometry of Random Fields; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Serrien, B.; Ooijen, J.; Goossens, M.; Baeyens, J.P. A motion analysis in the volleyball spike—Part 1: Three dimensional kinematics and performance. Int. J. Hum. Mov. Sport. Sci. 2016, 4, 70–82. [Google Scholar] [CrossRef]
- Virmavirta, M.; Kivekäs, J. Is it still important to be light in ski jumping? Sports Biomech. 2019, 20, 407–418. [Google Scholar] [CrossRef]
- Virmavirta, M. Aerodynamics of ski jumping. In The Engineering Approach to Winter Sports; Springer: New York, NY, USA, 2016; pp. 153–181. [Google Scholar]
- Virmavirta, M.; Kivekäs, J. Aerodynamics of an isolated ski jumping ski. Sport. Eng. 2019, 22, 1–6. [Google Scholar] [CrossRef]
- Ettema, G.; Hooiveld, J.; Braaten, S.; Bobbert, M. How do elite ski jumpers handle the dynamic conditions in imitation jumps? J. Sport. Sci. 2016, 34, 1081–1087. [Google Scholar] [CrossRef] [PubMed]














| Phase | Dist. | Method | Tr. | v | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [] | [] | [m s−1] | [] | [] | [] | [ s−1] | |||||||||||
| in-run | −65–0 | dGNSS | X | X | X | X | X | X | |||||||||
| Take-off | −5–20 | PosEst | X | X | X | X | X | X | X | X | X | X | X | X | X | ||
| Flight | 0–90 | dGNSS | X | X | X | X | X | X | X | ||||||||
| Phase [] | −5–0 | 0–5 | 5–10 | 10–15 | 15–20 |
|---|---|---|---|---|---|
| Tr [] | 0.10 | 0.04 | 0.02 | 0.03 | 0.03 |
| [m s−1] | 0.49 | 0.15 | 0.41 | 0.34 | 0.15 |
| [m s−1] | 0.41 | 0.10 | 0.08 | 0.13 | 0.15 |
| [m s−2] | 2.45 | 2.19 | 0.43 | 1.44 | 1.56 |
| [m s−2] | 1.44 | 1.89 | 0.57 | 0.97 | 0.92 |
| Gate | Distance | Total Wind Score | Wind Measurements at [m s−1] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [#] | [] | Points | [m s−1] | Points | 10 m | 38 m | 57 m | 76 m | 95 m | |
| Jump 1 | 15 | 96 | 62 | 0.40 | −3.2 | 1.63 | 0.80 | 0.71 | 0.52 | 0.29 |
| Jump 2 | 12 | 91 | 52 | 0.46 | −3.7 | 1.44 | 0.94 | 0.50 | 0.78 | 0.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elfmark, O.; Ettema, G.; Groos, D.; Ihlen, E.A.F.; Velta, R.; Haugen, P.; Braaten, S.; Gilgien, M. Performance Analysis in Ski Jumping with a Differential Global Navigation Satellite System and Video-Based Pose Estimation. Sensors 2021, 21, 5318. https://doi.org/10.3390/s21165318
Elfmark O, Ettema G, Groos D, Ihlen EAF, Velta R, Haugen P, Braaten S, Gilgien M. Performance Analysis in Ski Jumping with a Differential Global Navigation Satellite System and Video-Based Pose Estimation. Sensors. 2021; 21(16):5318. https://doi.org/10.3390/s21165318
Chicago/Turabian StyleElfmark, Ola, Gertjan Ettema, Daniel Groos, Espen A. F. Ihlen, Rune Velta, Per Haugen, Steinar Braaten, and Matthias Gilgien. 2021. "Performance Analysis in Ski Jumping with a Differential Global Navigation Satellite System and Video-Based Pose Estimation" Sensors 21, no. 16: 5318. https://doi.org/10.3390/s21165318
APA StyleElfmark, O., Ettema, G., Groos, D., Ihlen, E. A. F., Velta, R., Haugen, P., Braaten, S., & Gilgien, M. (2021). Performance Analysis in Ski Jumping with a Differential Global Navigation Satellite System and Video-Based Pose Estimation. Sensors, 21(16), 5318. https://doi.org/10.3390/s21165318






