Fault-Tolerant Control of Magnetically-Levitated Rotor with Redundant Structures Based on Improved Generalized Linearized EMFs Model
Abstract
:1. Introduction
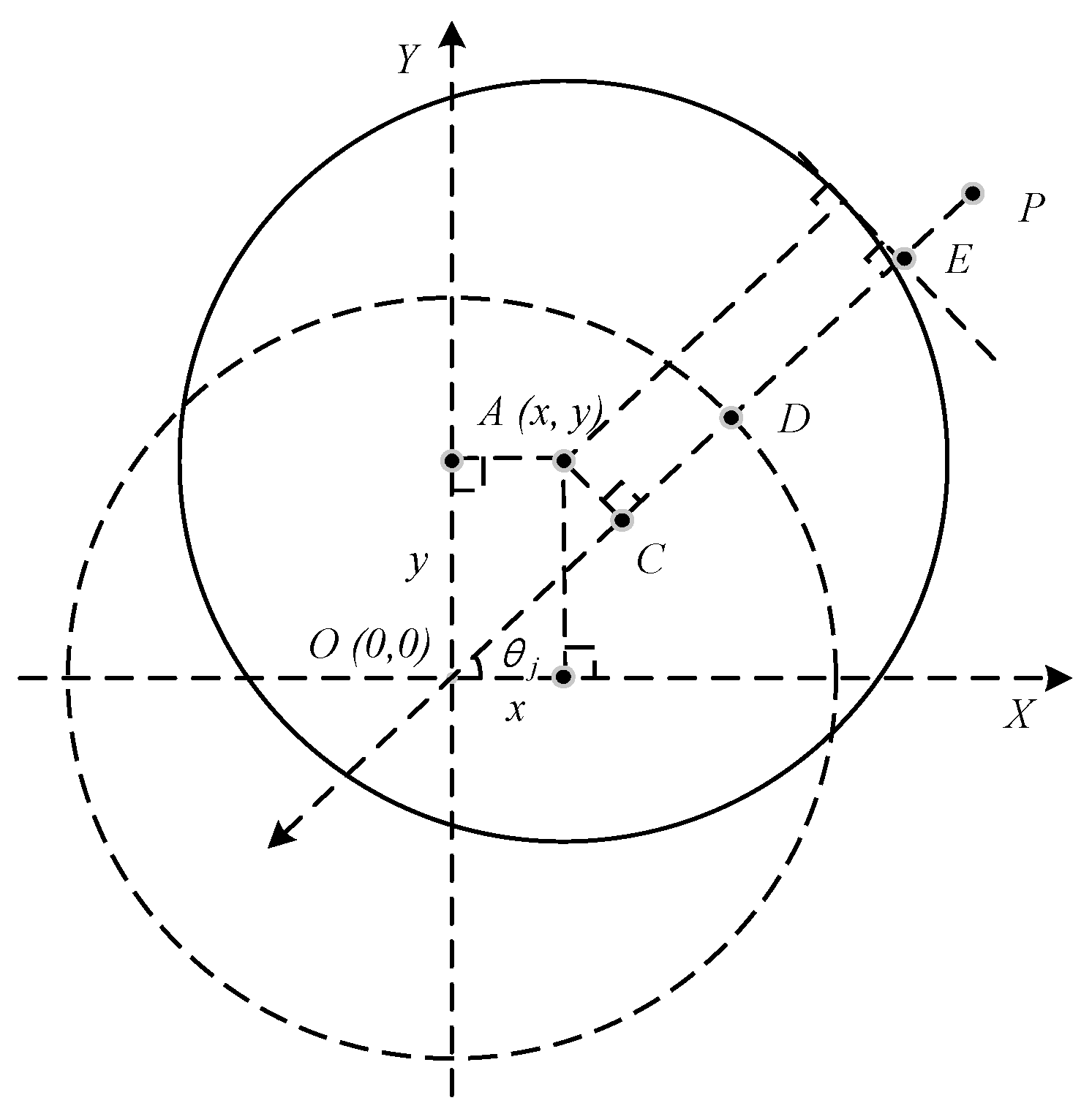
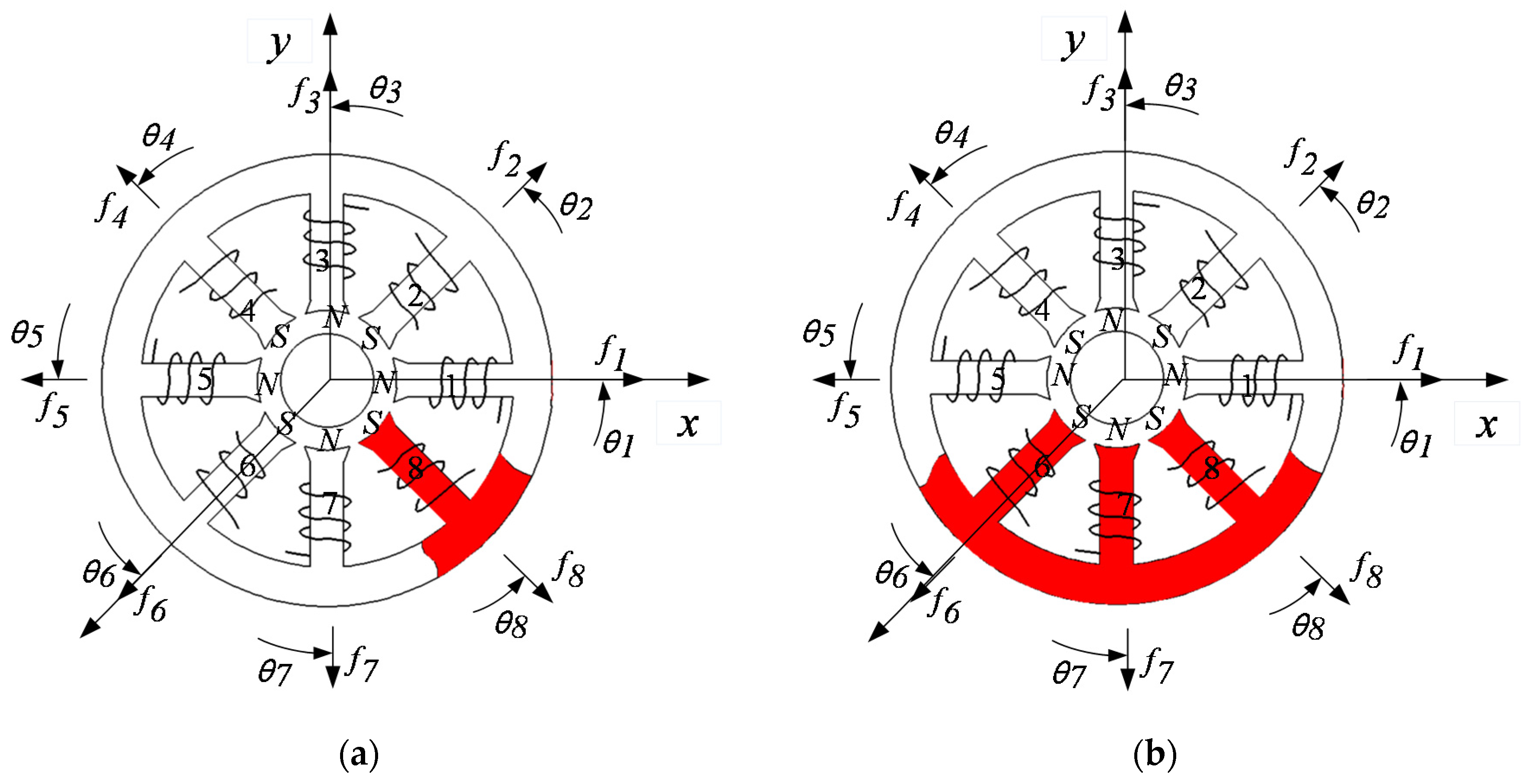
2. Generalized Bias Current Linearization of Magnetic Bearings
3. Fault-Tolerant Control Based Improved EMFs Model
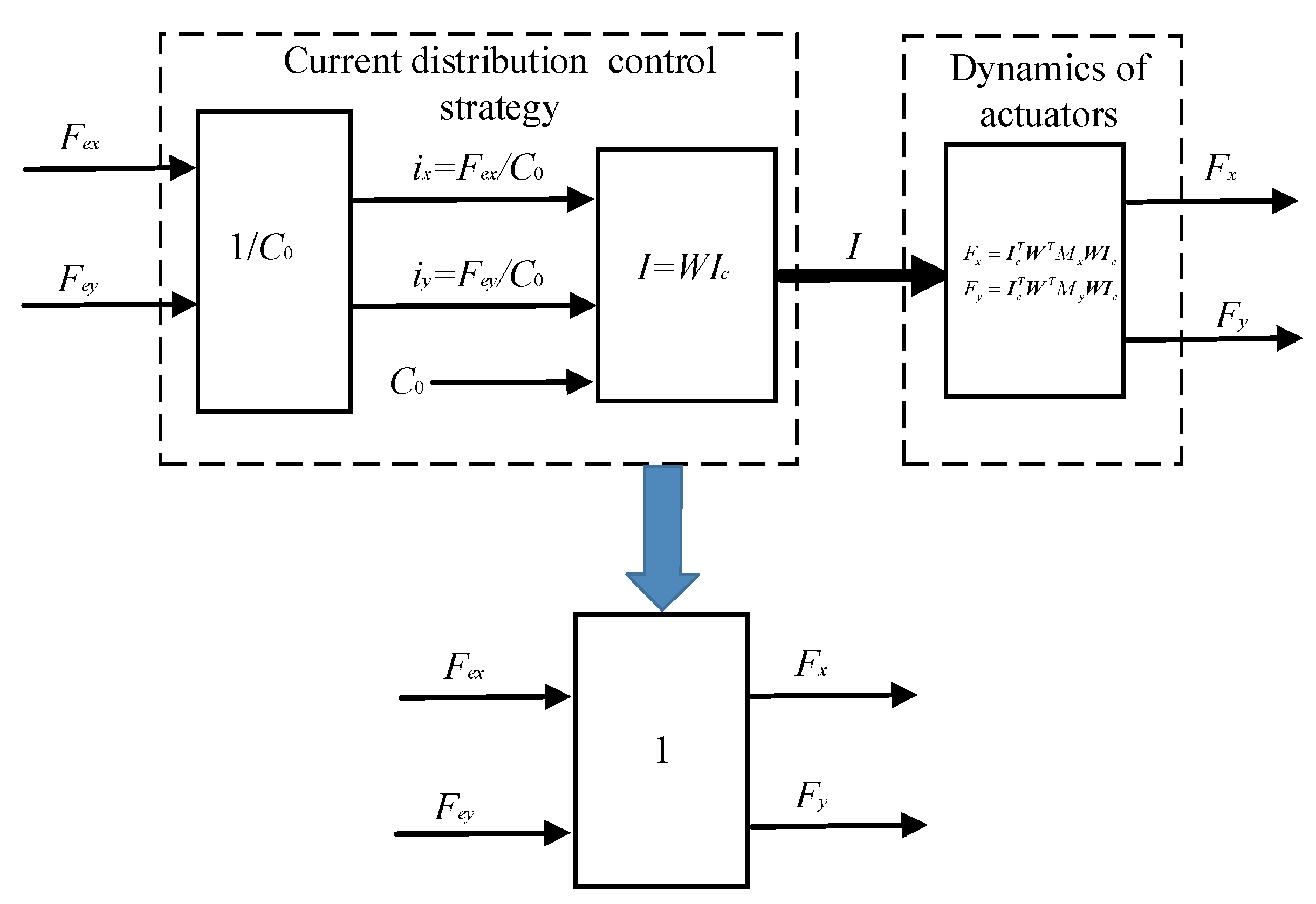
3.1. Improved EMF Model
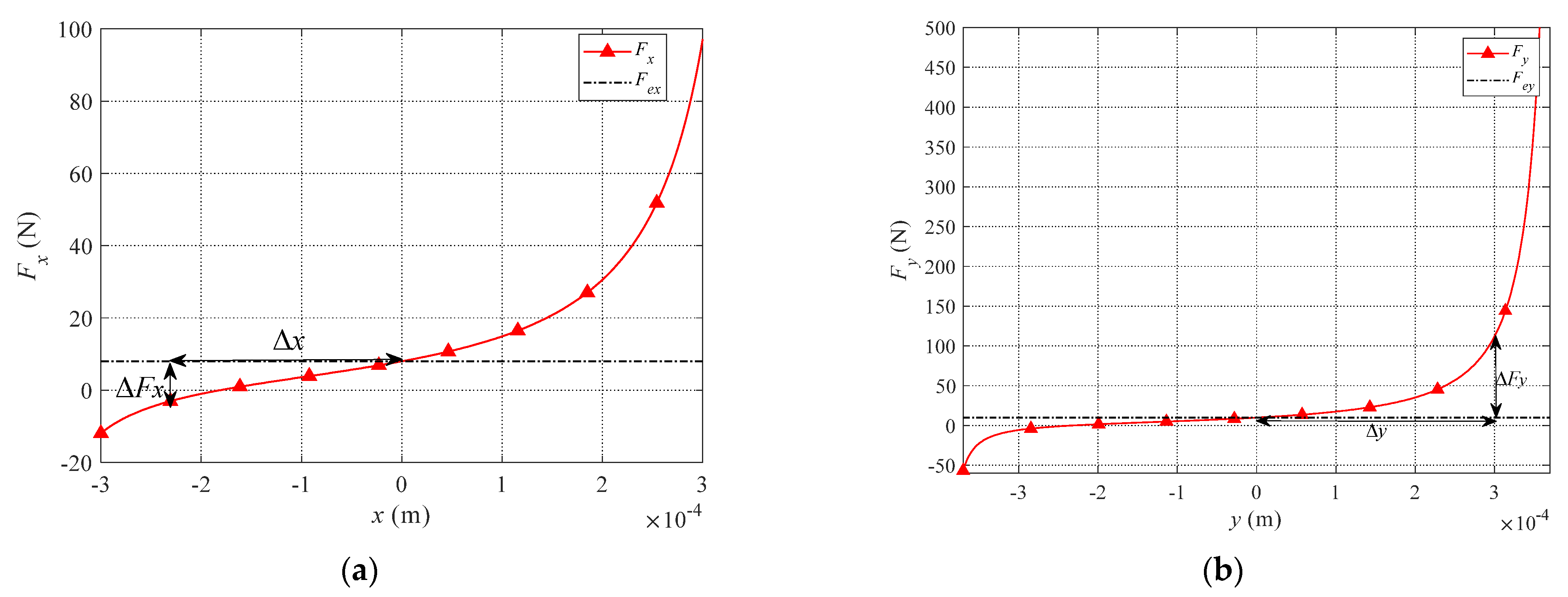
3.2. Numerical Calculation of the Improved EMF Model
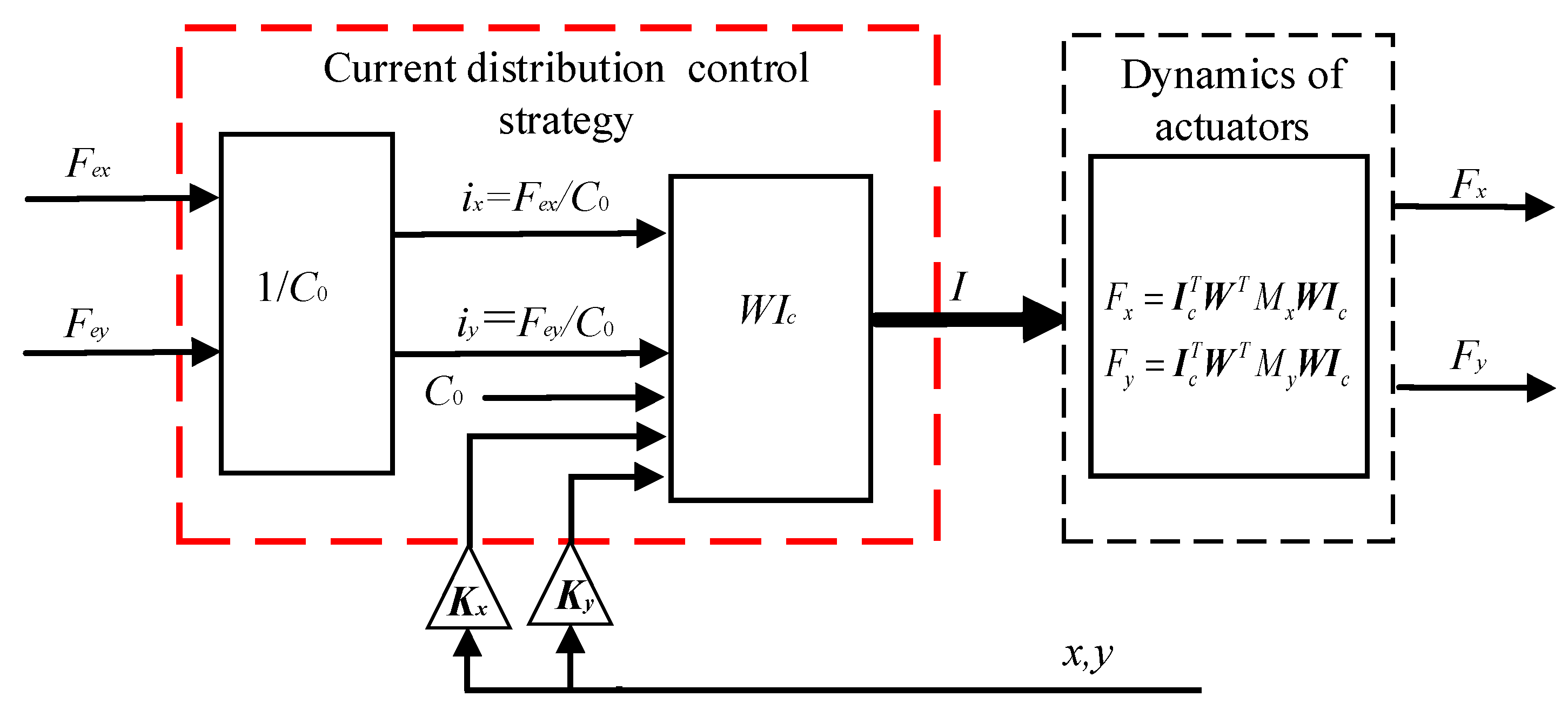
3.3. Design the Fault-Tolerant Controller
4. Simulation of Fault-Tolerant Control in the Magnetically-Levitated Rotor
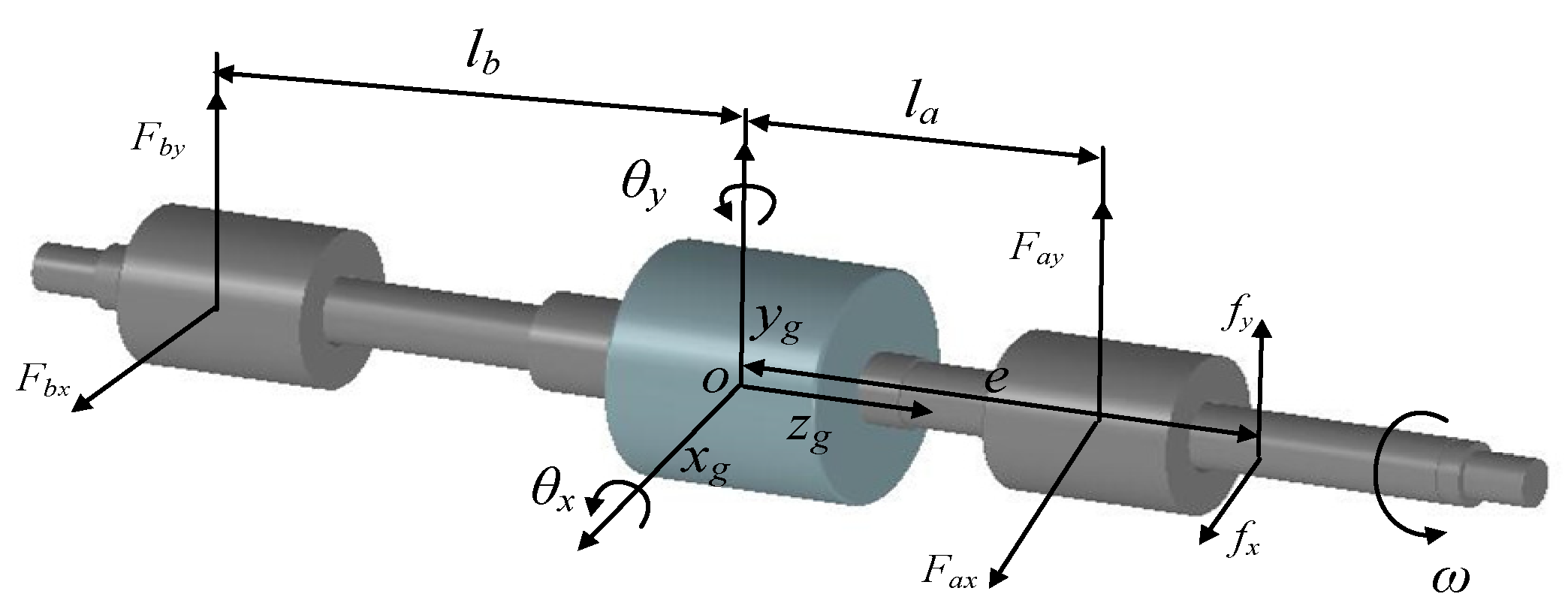
4.1. Magnetically-Levitated Rotor Dynamics
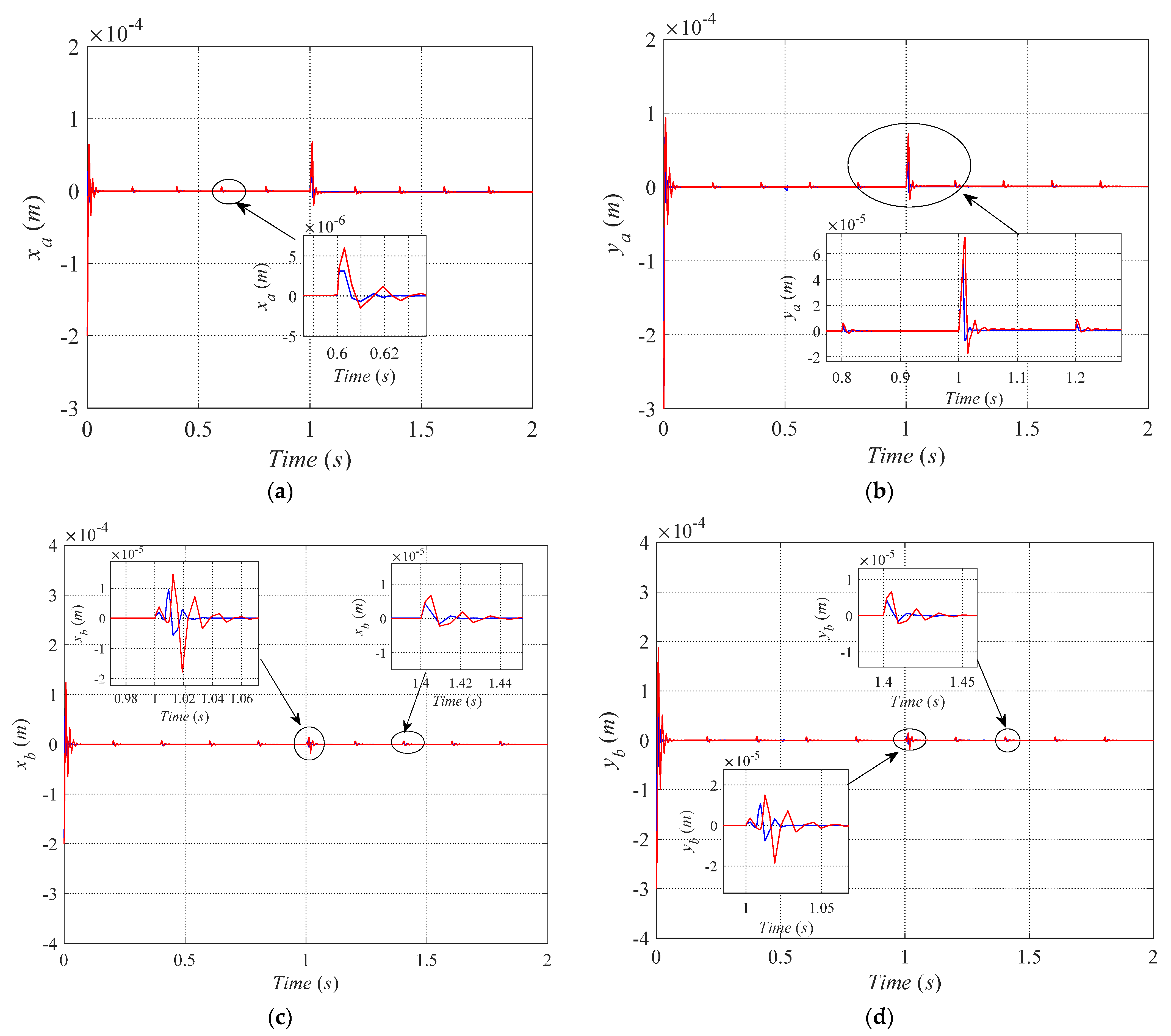
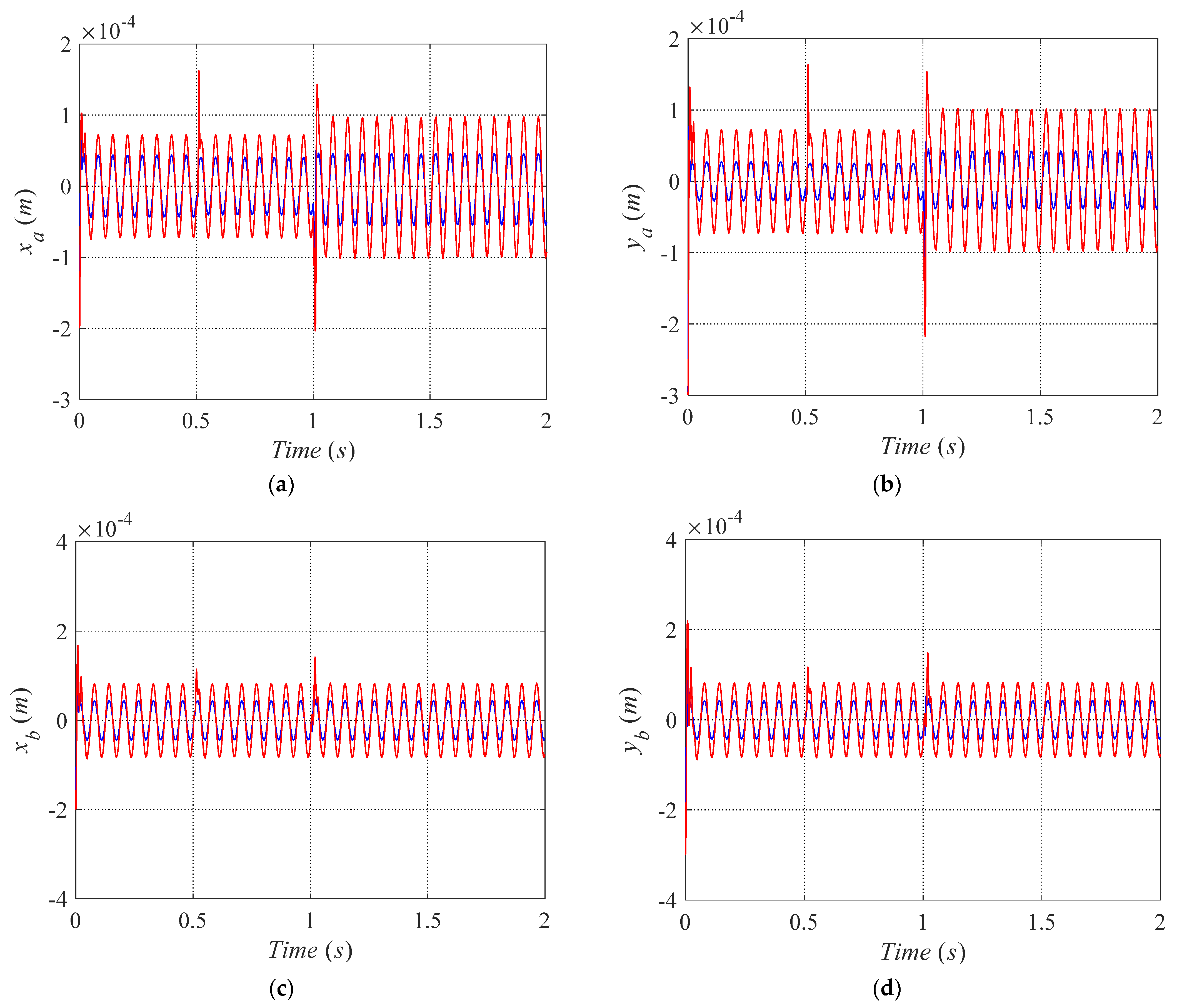
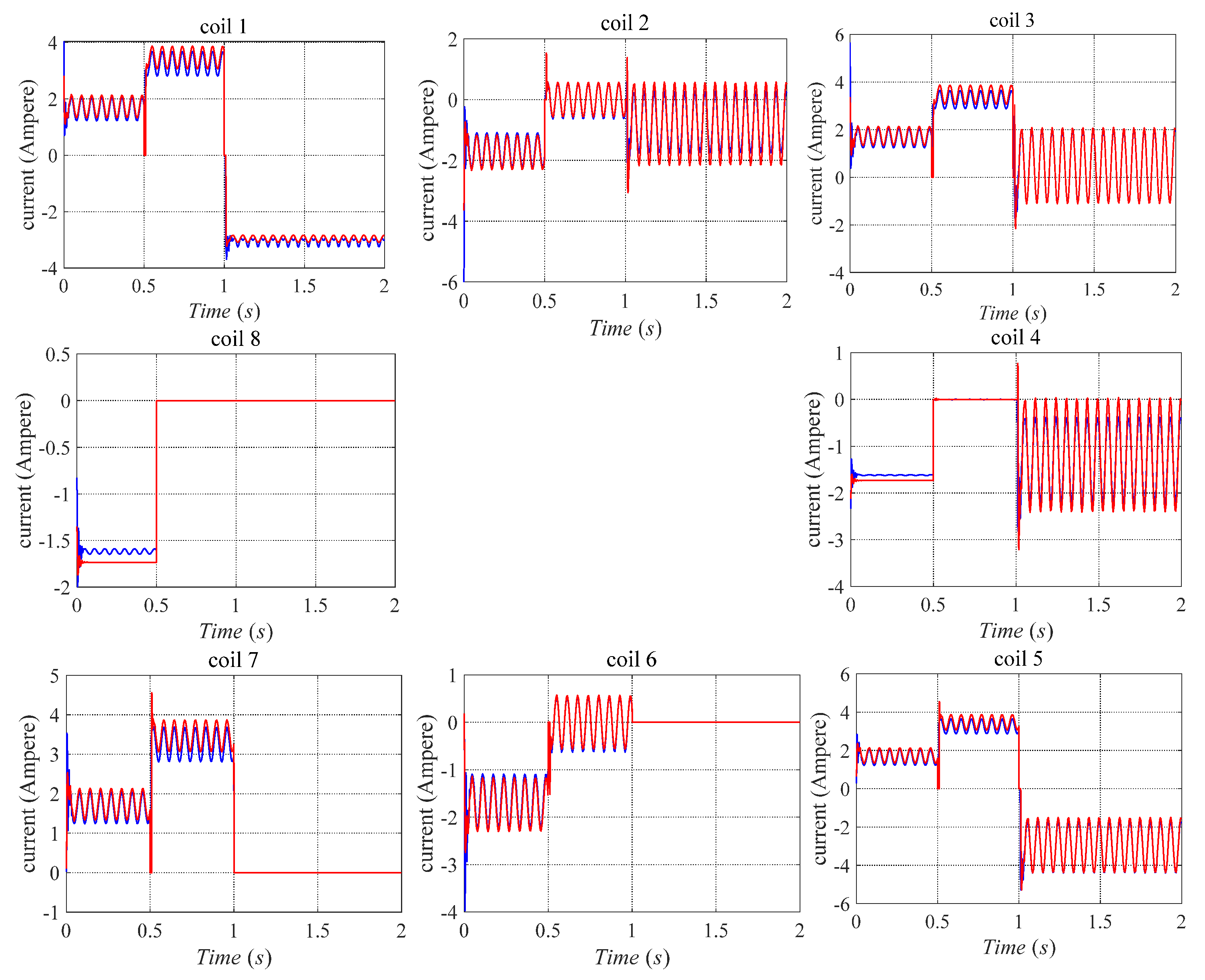
4.2. Simulation Verification
- (1)
- Periodic pulse disturbance test
- (2)
- Sinusoidal disturbance test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allaire, P.E.; Fitto, R.L.; Maslen, E.H.; Wakefield, W.C. Measured force/current relations in solid magnetic thrust bearings. ASME J. Eng. Gas Turbines Power 1997, 119, 137–142. [Google Scholar] [CrossRef]
- Keogh, P.; Cole, M.O.T. Dynamics and Control Issues for Fault Tolerance in Magnetic Bearings; Schweitzer, G., Maslen, E.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 407–433. [Google Scholar] [CrossRef]
- Park, Y. Design and Implementation of an Electromagnetic Levitation System for Active Magnetic Bearing Wheels. IET Control Theory A 2014, 8, 139–148. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Mung, N.X.; Thanh HL, N.N.; Huynh, T.T.; Lam, N.T.; Hong, S.K. Adaptive Sliding Mode Control for Attitude and Altitude System of a Quadcopter UAV via Neural Network. IEEE Access 2021, 9, 40076–40085. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Huynh, T.T.; Do, X.P.; Xuan Mung, N.; Hong, S.K. Robust Fault Estimation Using the Intermediate Observer: Application to the Quadcopter. Sensors 2020, 20, 4917. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.L.; Lin, S.Y.; Toh, C.S. Adaptive Unbalance Compensation for a Three-Pole Active Magnetic Bearing System. IEEE Trans. Ind. Electron. 2020, 67, 2097–2106. [Google Scholar] [CrossRef]
- Ren, Y.; Fang, J. High-Precision and Strong-Robustness Control for an MSCMG Based on Modal Separation and Rotation Motion Decoupling Strategy. IEEE Trans. Ind. Electron. 2014, 61, 1539–1551. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, B.; Chen, Q.; Zhang, L.; Liu, H.; Song, S. A unified design and the current ripple characteristic analysis of digital switching power amplifier in active magnetic-levitated bearings. Int. J. Appl. Electromagn. Mech. 2017, 55, 391–407. [Google Scholar] [CrossRef]
- Maslen, E.H.; Meeker, D.C. Fault tolerance of magnetic bearings by generalized bias current linearization. IEEE Trans. Magn. 1995, 31, 2304–2314. [Google Scholar] [CrossRef] [Green Version]
- Na, U.J.; Palazzolo, A.B. Optimized realization of fault-tolerant heteropolar magnetic bearings. ASME J. Vibr. Acoust. 2000, 122, 209–221. [Google Scholar] [CrossRef] [Green Version]
- Na, U.J.; Palazzolo, A.B.; Provenza, A. Test and theory correlation study for a flexible rotor on fault-tolerant magnetic bearings. ASME J. Vibr. Acoust. 2002, 124, 359–366. [Google Scholar] [CrossRef]
- Noh, M.D.; Cho, S.-R.; Kyung, J.-H.; Ro, S.K.; Park, J.K. Design and implementation of a fault-tolerant magnetic bearing system for Turbo-Molecular Vacuum Pump. IEEE-ASME Trans. Mechatron. 2005, 10, 626–631. [Google Scholar] [CrossRef]
- Meeker, D.C.; Maslen, E.H.; Noh, M.D. An augmented circuit model for magnetic bearings including eddy currents, fringing and leakage. IEEE Trans. Magn. 1996, 32, 3219–3227. [Google Scholar] [CrossRef]
- Na, U.J.; Palazzolo, A.B. Fault tolerance of magnetic bearings with material path reluctances and fringing factors. IEEE Trans. Magn. 2000, 36, 3939–3946. [Google Scholar] [CrossRef] [Green Version]
- Na, U.J. Fault tolerant control of magnetic bearings with force invariance. KSME J. Mech. Sci. Technol. 2005, 19, 731–742. [Google Scholar] [CrossRef]
- Na, U.J. Fault tolerant homopolar magnetic bearings with flux invariant control. KSME J. Mech. Sci. Technol. 2006, 20, 643–651. [Google Scholar] [CrossRef]
- Cheng, X.; Chen, Q.; Zeng, H.; Wang, X.; Zhou, R. ReconFigureuration rules for loosely-coupled redundant supporting structure in radial magnetic bearings. Int. J. Appl. Electromagn. Mech. 2016, 51, 91–106. [Google Scholar] [CrossRef]
- Meeker, D. A generalized unbiased control strategy for radial magnetic beatings. Actuators 2017, 6, 1. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X.; Cheng, B.; Liu, H.; Allen, G.M. An Accurate Linearization of Electromagnetic Force of Heteropolar Magnetic Bearings With Redundant Structures. J. Eng. Gas Turbines Power-Trans. Asme 2020, 142. [Google Scholar] [CrossRef]
- David, M.; Eric, M. A Parametric Solution to the Generalized Bias Linearization Problem. Actuators 2020, 3, 14. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X.; Deng, S.; Cheng, B.; Lu, M.; Zhou, R. Optimization of bias current coefficient in the fault-tolerance of active magnetic bearings based on the redundant structure parameters. Automatika 2020, 61, 602–613. [Google Scholar] [CrossRef]
- Cheng, X.; Deng, S.; Cheng, B.X.; Hu, Y.F.; Wu, H.C.; Zhou, R.G. Design and Implementation of a Fault-Tolerant Magnetic Bearing Control System Combined With a Novel Fault-Diagnosis of Actuators. IEEE Access 2020, 9, 2454–2465. [Google Scholar] [CrossRef]
- Cui, D.; Xu, L. Fault tolerant control of radial active magnetic bearing based on coordinate transformation. Control Decis. 2010, 25, 1420–1430. [Google Scholar]
- Li, M.H.; Palazzolo, A.B.; Kenny, A.; Provenza, A.J.; Beach, R.F.; Kascak, A.F. Fault Tolerant Homopolar Magnetic Bearings. IEEE Trans. Magn. 2004, 40, 3308–3318. [Google Scholar] [CrossRef]
- Wu, B. Coil Fault-tolerant Control for Radial Active Magnetic Bearings. Chin. J. Mech. Eng. 2005, 41, 157–162. [Google Scholar] [CrossRef]
- Zhou, W.; Lu, B.; Habetler, T.G.; Harley, R.G. Incipient bearing fault detection via motor current noise cancellation using wiener filter. IEEE Trans. Ind. Appl. 2009, 45, 1309–1316. [Google Scholar] [CrossRef]
- Cade, I.S.; Keogh, P.S.; Sahinkaya, M.N. Fault identification in rotor/magnetic bearing systems using discrete time wavelet coefficients. IEEE/ASME Trans. Mechatron. 2005, 10, 648–657. [Google Scholar] [CrossRef]
- Tsai, N.C.; King, Y.H.; Lee, R.M. Fault diagnosis for magnetic bearing systems. Mech. Syst. Signal Process. 2009, 23, 1339–1351. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Hong, S.K. Fault diagnosis and fault-tolerant control scheme for quadcopter UAVs with a total loss of actuator. Energies 2019, 12, 1139. [Google Scholar] [CrossRef] [Green Version]
- Florian, L. Detection and correction of actuator and sensor faults in active magnetic bearing system. In Proceedings of the 8th International Symposium on Magnetic Bearing, Mito, Japan, 26–28 August 2002. [Google Scholar]
- Zhao, K.; Li, P.; Zhang, C.; Li, X.; He, J.; Lin, Y. Sliding mode observer-based current sensor fault reconstruction and unknown load disturbance estimation for PMSM driven system. Sensors 2017, 17, 2833. [Google Scholar] [CrossRef] [Green Version]
- Nagel, L.; Galeazzi, R.; Voigt, A.J.; Santos, I.F. Fault diagnosis of active magnetic bearings based on Gaussian GLRT detector. In Proceedings of the 2016 3rd Conference on Control and Fault-Tolerant Systems (SysTol), Barcelona, Spain, 7–9 September 2016; pp. 540–547. [Google Scholar]




| Structure Parameter | Value | Unit |
|---|---|---|
| Pole area, A0 | 5.4 × 10−5 | m2 |
| Turns per coil, N | 56 | / |
| Pole initial gap g0 | 4 × 10−4 | m |
| Pole angle, θj | (j − 1) π/4 | rad |
| Saturation magnetic-flux density, Bsat | 1.2 | T |
| Rotor weight, m | 0.8 | kg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, B.; Cheng, X.; Song, S.; Deng, S.; Zhou, R.; Hu, Y.; Wu, H. Fault-Tolerant Control of Magnetically-Levitated Rotor with Redundant Structures Based on Improved Generalized Linearized EMFs Model. Sensors 2021, 21, 5404. https://doi.org/10.3390/s21165404
Cheng B, Cheng X, Song S, Deng S, Zhou R, Hu Y, Wu H. Fault-Tolerant Control of Magnetically-Levitated Rotor with Redundant Structures Based on Improved Generalized Linearized EMFs Model. Sensors. 2021; 21(16):5404. https://doi.org/10.3390/s21165404
Chicago/Turabian StyleCheng, Baixin, Xin Cheng, Shao Song, Shuai Deng, Rougang Zhou, Yefa Hu, and Huachun Wu. 2021. "Fault-Tolerant Control of Magnetically-Levitated Rotor with Redundant Structures Based on Improved Generalized Linearized EMFs Model" Sensors 21, no. 16: 5404. https://doi.org/10.3390/s21165404






