Microwave Spoof Surface Plasmon Polariton-Based Sensor for Ultrasensitive Detection of Liquid Analyte Dielectric Constant
Abstract
:1. Introduction
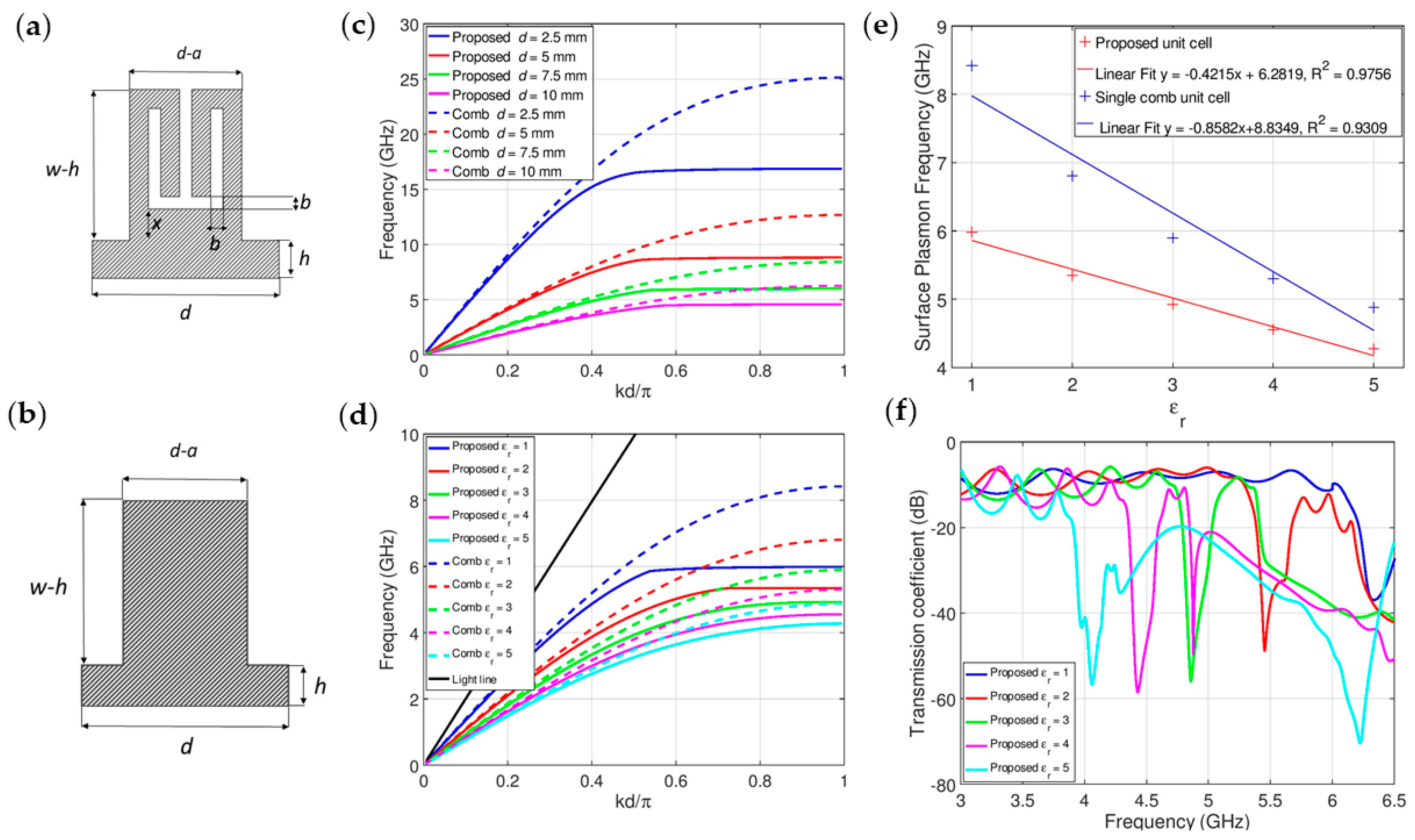
2. Theoretical and Numerical Analysis
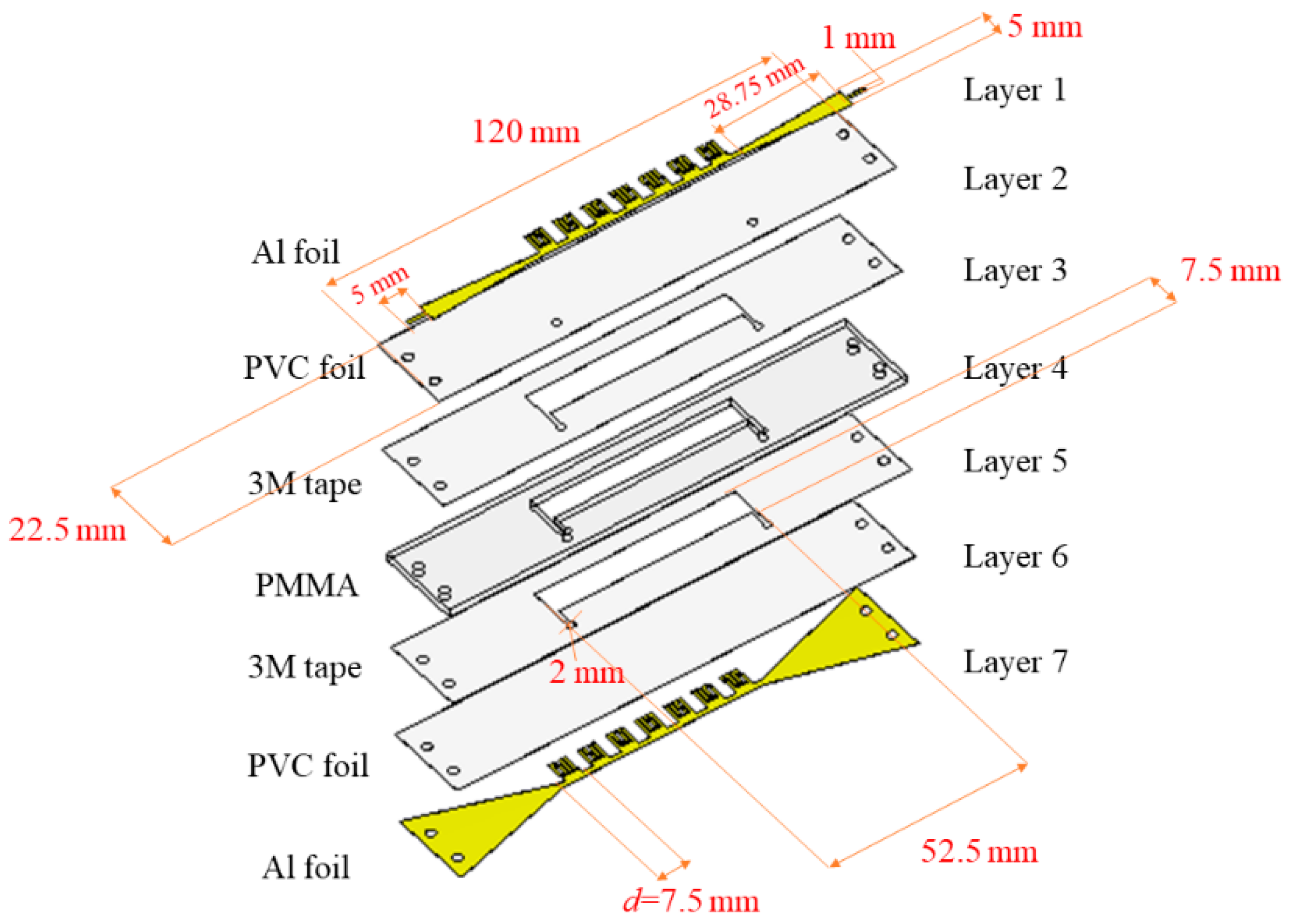
3. Materials and Methods
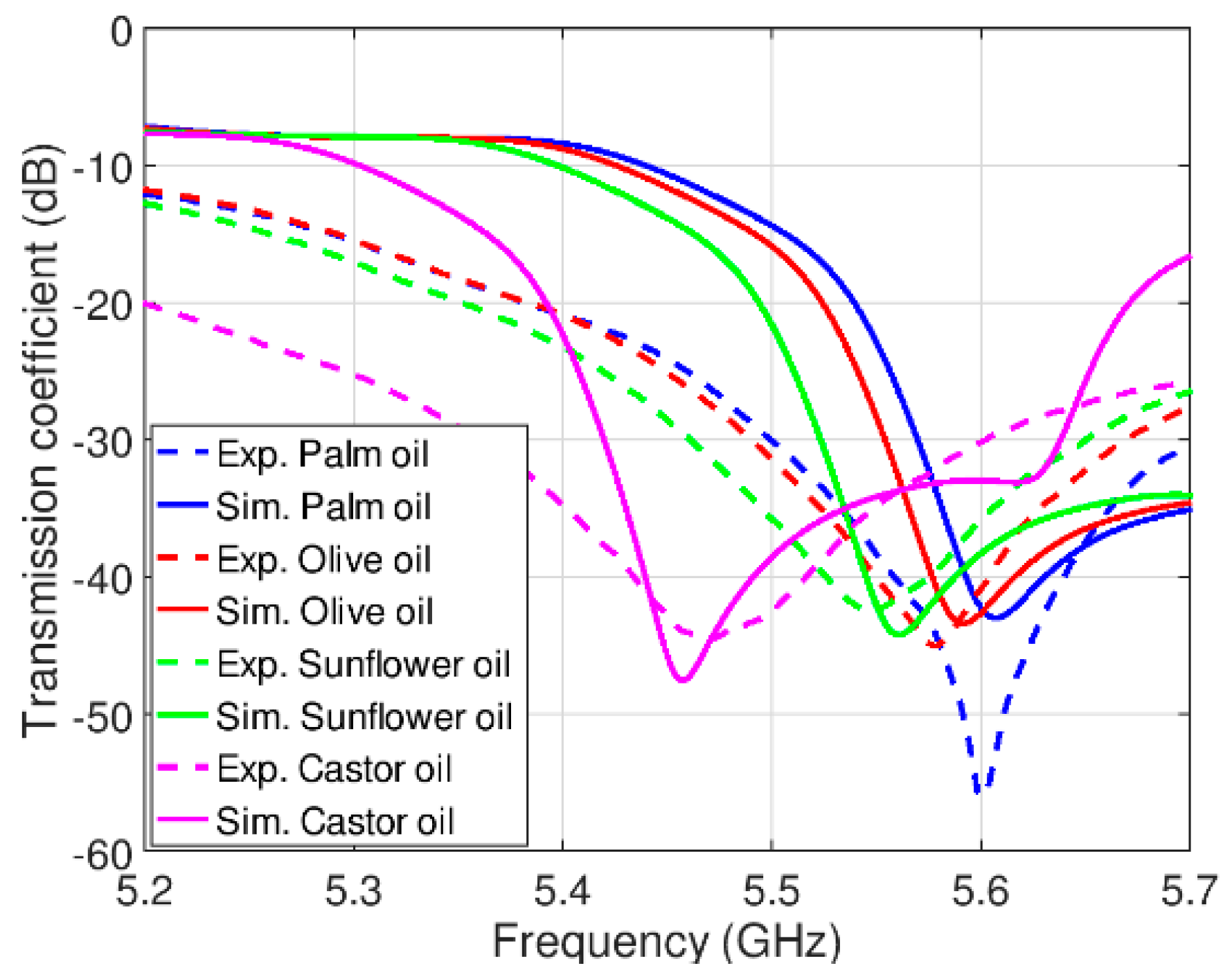
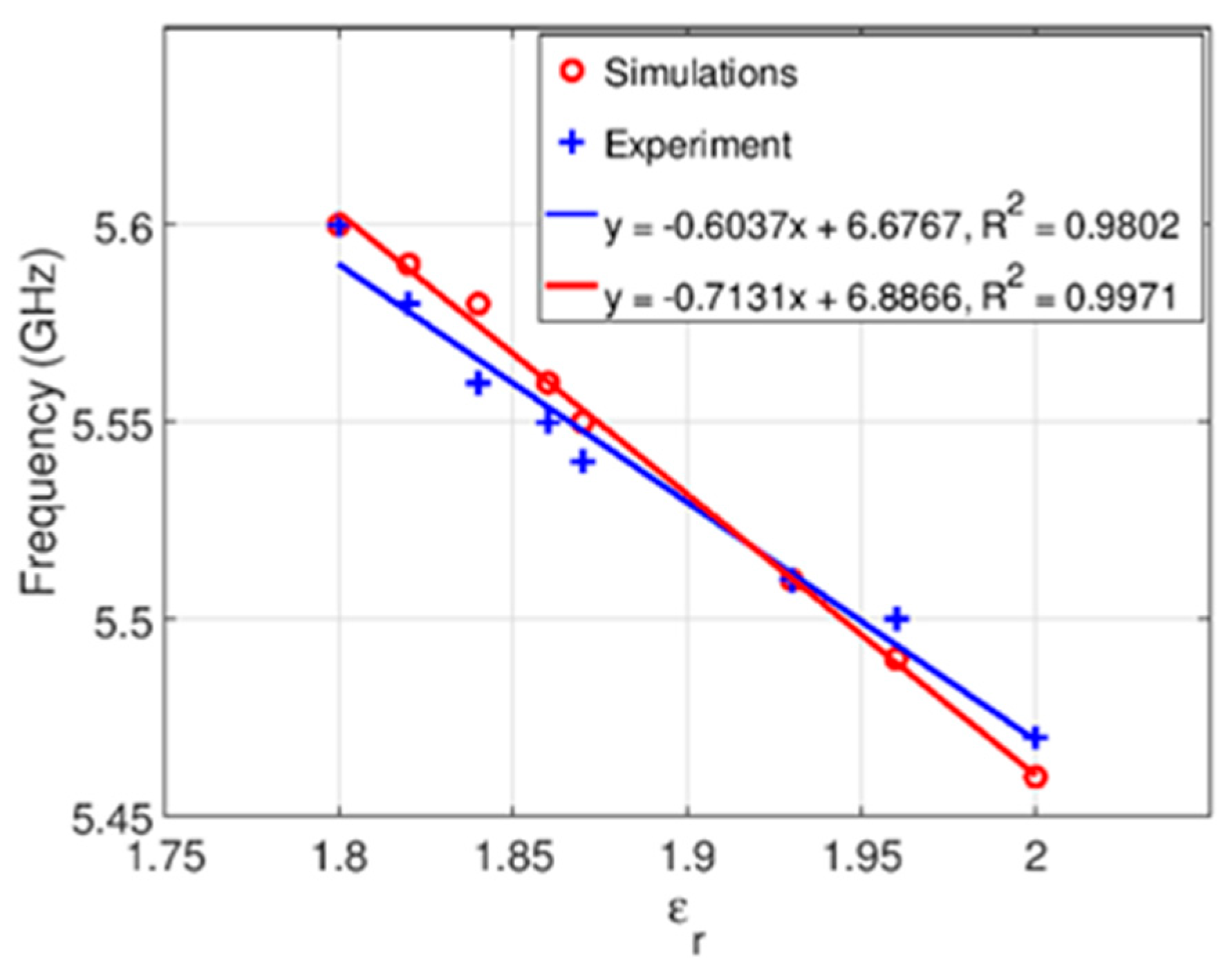
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saadat-Safa, M.; Nayyeri, V.; Ghadimi, A.; Soleimani, M.; Ramahi, O.M. A pixelated microwave near-field sensor for precise characterization of dielectric materials. Sci. Rep. 2019, 9, 13310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muñoz-Enano, J.; Coromina, J.; Vélez, P.; Su, L.; Gil, M.; Casacuberta, P.; Martín, F. Planar phase-variation microwave sensors for material characterization: A review and comparison of various approaches. Sensors 2021, 21, 1542. [Google Scholar] [CrossRef] [PubMed]
- Hao, H.; Wang, D.; Wang, Z.; Yin, B.; Ruan, W. Design of a high sensitivity microwave sensor for liquid dielectric constant measurement. Sensors 2020, 20, 5598. [Google Scholar] [CrossRef] [PubMed]
- Ramzan, R.; Omar, M.; Siddiqui, O.F. Energy-tunneling dielectric sensor based on substrate integrated waveguides. IEEE Sens. J. 2017, 17, 1264–1268. [Google Scholar] [CrossRef]
- Wei, Z.; Huang, J.; Li, J.; Xu, G.; Ju, Z.; Liu, X.; Ni, X. A high-sensitivity microfluidic sensor based on a substrate integrated waveguide re-entrant cavity for complex permittivity measurement of liquids. Sensors 2018, 18, 4005. [Google Scholar] [CrossRef] [Green Version]
- Reyes-Vera, E.; Acevedo-Osorio, G.; Arias-Correa, M.; Senior, D.E. A submersible printed sensor based on a monopole-coupled split ring resonator for permittivity characterization. Sensors 2019, 19, 1936. [Google Scholar] [CrossRef] [Green Version]
- Abdolrazzaghi, M.; Daneshmand, M.; Iyer, A.K. Strongly enhanced sensitivity in planar microwave sensors based on metamaterial coupling. IEEE Trans. Microw. Theory Tech. 2018, 66, 1843–1855. [Google Scholar] [CrossRef] [Green Version]
- Jafari, F.S.; Ahmadi-Shokouh, J. Reconfigurable microwave SIW sensor based on PBG structure for high accuracy permittivity characterization of industrial liquids. Sens. Actuators A Phys. 2018, 283, 386–395. [Google Scholar] [CrossRef]
- Cselyuszka, N.; Sakotic, Z.; Crnojevic-Bengin, V.; Radonic, V.; Jankovic, N. Microwave surface plasmon polariton-like sensor based on half-mode substrate integrated waveguide for highly sensitive dielectric constant detection. IEEE Sens. J. 2018, 18, 9984–9992. [Google Scholar] [CrossRef]
- Tiwari, N.K.; Singh, S.P.; Akhtar, M.J. Novel improved sensitivity planar microwave probe for adulteration detection in edible oils. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 164–166. [Google Scholar] [CrossRef]
- Liu, M.; Qin, X.; Chen, Z.; Tang, L.; Borom, B.; Cao, N.; Barnes, D.; Cheng, K.; Chen, J.; Wang, T.; et al. Frying oil evaluation by a portable sensor based on dielectric constant measurement. Sensors 2019, 19, 5375. [Google Scholar] [CrossRef] [Green Version]
- Khaled, A.Y.; Aziz, S.A.; Rokhani, F.Z. Capacitive sensor probe to assess frying oil degradation. Inf. Process. Agric. 2015, 2, 142–148. [Google Scholar] [CrossRef] [Green Version]
- Cataldo, A.; Piuzzi, E.; Cannazza, G.; de Benedetto, E.; Tarricone, L. Quality and anti-adulteration control of vegetable oils through microwave dielectric spectroscopy. Measurement 2010, 43, 1031–1039. [Google Scholar] [CrossRef]
- Qureshi, S.A.; Abidin, Z.Z.; Ashyap, I.A.Y.; Majid, H.A.; Kamarudin, M.R.; Yue, M.; Zulkipli, M.S.; Nebhen, J. Millimetre-wave metamaterial-based sensor for characterisation of cooking oils. Int. J. Antennas Propag. 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- Erdoğan, M.; Ünal, E.; Özkan Alkurt, F.; Abdulkarim, Y.I.; Deng, L.; Karaaslan, M. Determination of frying sunflower oil usage time for local potato samples by using microwave transmission line based sensors. Measurement 2020, 163, 108040. [Google Scholar] [CrossRef]
- Huang, J.; Li, J.-S.; Xu, G.; Wei, Z. A microfluidic sensor based on meta-surface absorber for rapid and nondestructive identification of edible oil species. Prog. Electromagn. Res. C 2019, 96, 153–163. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ruan, C.; Wang, W.; Cao, Y. Submersible high sensitivity microwave sensor for edible oil detection and quality analysis. IEEE Sens. J. 2021, 21, 13230–13238. [Google Scholar] [CrossRef]
- Yadav, R.; Patel, P.N. Experimental study of adulteration detection in fish oil using novel PDMS cavity bonded EBG inspired patch sensor. IEEE Sens. J. 2016, 16, 4354–4361. [Google Scholar] [CrossRef]
- Galindo-Romera, G.; Herraiz-Martinez, J.F.; Gil, M.; Martinez-Martinez, J.J.; Segovia-Vargas, D. Submersible printed split-ring resonator-based sensor for thin-film detection and permittivity characterization. IEEE Sens. J. 2016, 16, 3587–3596. [Google Scholar] [CrossRef]
- Li, F.; Zheng, Y.; Hua, C.; Jian, J. Gas sensing by microwave transduction: Review of progress and challenges. Front. Mater. 2019, 6, 101. [Google Scholar] [CrossRef]
- Bogner, A.; Steiner, C.; Walter, S.; Kita, J.; Hagen, G.; Moos, R. Planar microstrip ring resonators for microwave-based gas sensing: Design aspects and initial transducers for humidity and ammonia sensing. Sensors 2017, 17, 2422. [Google Scholar] [CrossRef] [PubMed]
- Rossignol, J.; Harrabi, A.; Stuerga, D.; Pribetich, P.; Bailly, G.; Leblois, T. Critical influence of dielectric sensitive material and manufactured process in microwave gas-sensing: Application of ammonia detection with an interdigital sensor. ACS Omega 2020, 5, 11507–11514. [Google Scholar] [CrossRef]
- Li, Z.; Xue, Q.; Wang, Q.; Zhang, H.; Duan, X. Biomolecules detection using microstrip sensor with highly-ordered nanowires array. In 2019 IEEE Sensors; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Jha, A.K.; Havelka, D.; Krivosudsky, O.; Cifra, M. TRL Calibrated Coplanar Microwave Sensor for Characterization of Biomolecules. In Proceedings of the 2017 IEEE MTT-S International Microwave and RF Conference (IMaRC); IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Omer, A.E.; Shaker, G.; Safavi-Naeini, S.; Kokabi, H.; Alquié, G.; Deshours, F.; Shubair, R.M. Low-cost portable microwave sensor for non-invasive monitoring of blood glucose level: Novel design utilizing a four-cell CSRR hexagonal configuration. Sci. Rep. 2020, 10, 15200. [Google Scholar] [CrossRef] [PubMed]
- Zapasnoy, A.S.; Belichenko, V.P.; Yakubov, V.P.; Gorst, A.V.; Mironchev, A.S.; Klokov, A.V.; Zavyalova, K.V. Application of broadband microwave near-field sensors for glucose monitoring in biological media. Appl. Sci. 2021, 11, 1470. [Google Scholar] [CrossRef]
- Gennarelli, G.; Romeo, S.; Scarfi, M.R.; Soldovieri, F. A microwave resonant sensor for concentration measurements of liquid solutions. IEEE Sens. J. 2013, 13, 1857–1864. [Google Scholar] [CrossRef]
- Sethi, W.; Ibrahim, A.; Issa, K.; Albishi, A.; Alshebeili, S. A new approach to determining liquid concentration using multiband annular ring microwave sensor and polarity correlator. Electronics 2020, 9, 1616. [Google Scholar] [CrossRef]
- Foroutan, F.; Nikolova, N.K. Active sensor for microwave tissue imaging with bias-switched arrays. Sensors 2018, 18, 1447. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Islam, M.T.; Ullah, M.A.; Alam, T.; Singh, M.J.; Cho, M. Microwave imaging sensor using low profile modified stacked type planar inverted F antenna. Sensors 2018, 18, 2949. [Google Scholar] [CrossRef] [Green Version]
- Abdolrazzaghi, M.; Daneshmand, M. Multifunctional ultrahigh sensitive microwave planar sensor to monitor mechanical motion: Rotation, displacement and stretch. Sensors 2020, 20, 1184. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C.; Chen, Y.; Zhuang, Y.; Huang, J. Displacement and strain measurement up to 1000 °C using a hollow coaxial cable fabry-perot resonator. Sensors 2018, 18, 1304. [Google Scholar] [CrossRef] [Green Version]
- Jankovic, N.; Radonic, V. A microwave microfluidic sensor based on a dual-mode resonator for dual-sensing applications. Sensors 2017, 17, 2713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gan, H.-Y.; Zhao, W.-S.; Liu, Q.; Wang, D.-W.; Dong, L.; Wang, G.; Yin, W.-Y. Differential microwave microfluidic sensor based on microstrip complementary split-ring resonator (MCSRR) structure. IEEE Sens. J. 2020, 20, 5876–5884. [Google Scholar] [CrossRef]
- Hamzah, H.; Abduljabar, A.A.; Porch, A. High Q microwave microfluidic sensor using a central gap ring resonator. IEEE Trans. Microw. Theory Tech. 2020, 68, 1830–1838. [Google Scholar] [CrossRef]
- Fu, L.; Huang, J.; Xiang, Y.; Chen, Y.; Gu, W.; Wu, Y. A miniaturized differential microwave microfluidic sensor with high decoupling. IEEE Microw. Wirel. Compon. Lett. 2021, 31, 909–912. [Google Scholar] [CrossRef]
- Kiani, S.; Rezaei, P.; Navaei, M. Dual-sensing and dual-frequency microwave SRR sensor for liquid samples permittivity detection. Measurement 2020, 160, 107805. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, Y. One-dimensional plasmonic sensors. Front. Phys. 2020, 8, 312. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Guo, Y.; Zhang, S.; Li, H. Surface plasmon polariton high-sensitivity refractive index sensor based on MMF-MOF-MMF structure. Infrared Phys. Technol. 2021, 114, 103685. [Google Scholar] [CrossRef]
- Joseph, S.; Sarkar, S.; Joseph, J. Grating-coupled surface plasmon-polariton sensing at a flat metal-analyte interface in a hybrid-configuration. ACS Appl. Mater. Interfaces 2020, 12, 46519–46529. [Google Scholar] [CrossRef]
- Gomez-Cardona, N.; Reyes-Vera, E.; Torres, P. High sensitivity refractive index sensor based on the excitation of long-range surface plasmon polaritons in h-shaped optical fiber. Sensors 2020, 20, 2111. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Wang, F.; Gao, Y.; Zhang, D.; Sun, X.; Berini, P. Straight long-range surface plasmon polariton waveguide sensor operating at l0 = 850 nm. Sensors 2020, 20, 2507. [Google Scholar] [CrossRef]
- Heydari, M.; Habibzadeh-Sharif, A.; Jabbarzadeh, F. Design of a compact refractive-index sensor based on surface plasmon polariton slot waveguide. Photonics Nanostruct. Fundam. Appl. 2020, 38, 100755. [Google Scholar] [CrossRef]
- Tang, W.X.; Zhang, H.C.; Ma, H.F.; Jiang, W.X.; Cui, T.J. Concept, theory, design and applications of spoof surface plasmon polaritons at microwave frequencies. Adv. Opt. Mater. 2019, 7, 1800421. [Google Scholar] [CrossRef] [Green Version]
- Pendry, J.B.; Martín-Moreno, L.; Garcia-Vidal, F.J. Mimicking surface plasmons with structured surfaces. Science 2004, 305, 847–848. [Google Scholar] [CrossRef]
- Liu, L.; Li, Z.; Xu, B.; Ning, P.; Chen, C.; Xu, J.; Chen, X.; Gu, C. Dual-band trapping of spoof surface plasmon polaritons and negative group velocity realization through microstrip line with gradient holes. Appl. Phys. Lett. 2015, 107, 201602. [Google Scholar] [CrossRef]
- Zhao, R.; Lu, G.; Yin, H.; Liang, J.; Zeng, D.; Xiao, H. Terahertz sensor study based on spoof surface plasmon polaritons. Int. J. Antennas Propag. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- He, H.P.; Zhang, C.H.; Gao, X.; Niu, Y.L.; Tang, X.W.; Lu, J.; Zhang, P.L.; Cui, J.T. A novel spoof surface plasmon polariton structure to reach ultra-strong field confinements. Opto Electron. Adv. 2019, 2, 19000101–19000107. [Google Scholar]
- Liu, L.; Wang, J.; Yin, X.; Chen, Z. Wide-angle beam scanning leaky-wave antenna using spoof surface plasmon polaritons structure. Electronics 2018, 7, 348. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Chen, L.; Fang, B.; Zhu, Y. Spoof localized surface plasmons excited by plasmonic waveguide chip with corrugated disk resonator. Plasmonics 2017, 12, 947–952. [Google Scholar] [CrossRef]
- Farokhipour, E.; Mehrabi, M.; Komjani, N.; Ding, C. A spoof surface plasmon polaritons (SSPPs) based dual-band-rejection filter with wide rejection bandwidth. Sensors 2020, 20, 7311. [Google Scholar] [CrossRef]
- Jaiswal, R.K.; Pandit, N.; Pathak, N.P. Spoof surface plasmon polariton-based reconfigurable band-pass filter using planar ring resonator. Plasmonics 2018, 14, 631–646. [Google Scholar] [CrossRef]
- Guo, Y.-J.; Xu, K.-D.; Deng, X.; Cheng, X.; Chen, Q. Millimeter-wave on-chip bandpass filter based on spoof surface plasmon polaritons. IEEE Electron Device Lett. 2020, 41, 1165–1168. [Google Scholar] [CrossRef]
- Zhao, H.; Zhou, P.; Xu, Z.; Li, S.; Yang, M.; Liu, L.; Yin, X. Tri-band band-pass filter based on multi-mode spoof surface plasmon polaritons. IEEE Access 2020, 8, 14767–14776. [Google Scholar] [CrossRef]
- Cao, D.; Li, Y.; Wang, J. A millimeter-wave spoof surface plasmon polaritons-fed microstrip patch antenna array. IEEE Trans. Antennas Propag. 2020, 68, 6811–6815. [Google Scholar] [CrossRef]
- Liu, L.; Chen, M.; Yin, X. Single-layer high gain endfire antenna based on spoof surface plasmon polaritons. IEEE Access 2020, 8, 64139–64144. [Google Scholar] [CrossRef]
- Pan, B.C.; Luo, G.Q.; Liao, Z.; Cai, J.L.; Cai, B.G. Wideband miniaturized design of complementary spoof surface plasmon polaritons waveguide based on interdigital structures. Sci. Rep. 2020, 10, 3258. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.L.; Chan, C.H. Compact spoof surface plasmon polaritons waveguide integrated with blind vias and its applications. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3038–3042. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, K.; Wu, Q.; Jiang, T. Efficient propagation of spoof surface plasmon polaritons supported by substrate integrated waveguide with bandpass features. J. Phys. D Appl. Phys. 2020, 53, 425104. [Google Scholar] [CrossRef]
- Chen, X.; Fan, W. Ultrasensitive terahertz metamaterial sensor based on spoof surface plasmon. Sci. Rep. 2017, 7, 2092. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Cheng, D.; Zhang, B.; Shu, G.; Wang, J. A microwave biosensor based on spoof surface plasmon polaritons for in vivo measurement of the water content of human skin tissues. J. Phys. D Appl. Phys. 2019, 52, 205401. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, D. A microwave detector based on spoof surface plasmon polaritons structure. AIP Adv. 2021, 11, 035008. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, J.; Jing, B.; Dong, Y.; Yu, X. New method for the discrimination of adulterated flaxseed oil using dielectric spectroscopy. Food Anal. Methods 2019, 12, 2623–2629. [Google Scholar] [CrossRef]
- Valantina, S.R.; Susan, D.; Bavasri, S.; Priyadarshini, V.; Saraswathi, R.R.; Suriya, M. Experimental investigation of electro-rheological properties of modeled vegetable oils. J. Food Sci. Technol. 2016, 53, 1328–1337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lizhi, H.; Toyoda, K.; Ihara, I. Dielectric properties of edible oils and fatty acids as a function of frequency, temperature, moisture and composition. J. Food Eng. 2008, 88, 151–158. [Google Scholar] [CrossRef]
- Kraszewski, A. Prediction of the dielectric properties of two-phase mixtures. J. Microw. Power 1977, 12, 216–222. [Google Scholar] [CrossRef]
- Sairin, M.A.; Nizar, N.N.A.; Aziz, S.A.; Rokhani, F.Z. Study of Dielectric Permittivity and Fatty Acid Composition for Fats and Oil in Wide Frequency Spectroscopy Measurement at 0.5–50 GHz. In Proceedings of the 2016 10th International Conference on Sensing Technology (ICST), Nanjing, China, 11–13 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Sonkamble, A.A.; Sonsale, R.P.; Kanshette, M.S.; Kabara, K.B.; Wananje, K.H.; Kumbharkhane, A.C.; Sarode, A. Relaxation dynamics and thermophysical properties of vegetable oils using time-domain reflectometry. Eur. Biophys. J. 2016, 46, 283–291. [Google Scholar] [CrossRef]
- Xu, X.-Q.; Tran, V.H.; Palmer, M.; White, K.; Salisbury, P. Chemical and physical analyses and sensory evaluation of six deep-frying oils. J Am. Oil Chem. Soc. 1999, 76, 1091–1099. [Google Scholar] [CrossRef]
- Ibrahim, N.A.; Zaini, M.A.A. Microwave-assisted solvent extraction of castor oil from castor seeds. Chin. J. Chem. Eng. 2018, 26, 2516–2522. [Google Scholar] [CrossRef]



| Sample Number | Diel. Const. | tanδ | Reference |
|---|---|---|---|
| Palm Oil | 1.80 | 0.03 | [67] |
| Olive oil | 1.82 | 0.04 | [68] |
| Sunflower oil | 1.86 | 0.03 | [69] |
| Castor oil | 2 | 0.08 | [70] |
| Mixed samples | Diel. Const. | tanδ | Ratio-Castor: Palm oil |
| Sample 1 | 1.84 | 0.04 | 1:3.5 |
| Sample 2 | 1.87 | 0.04 | 1:2 |
| Sample 3 | 1.93 | 0.06 | 2:1 |
| Sample 4 | 1.96 | 0.07 | 3.5:1 |
| Application | Design | Technology | Technology Complexity | Sample Volume | Sensitivity (MHz/) | Operating Frequency | Ref. |
|---|---|---|---|---|---|---|---|
| Adulteration detection | Double complementary SRR | PCB | Medium | Immersed | 1133 | 11.56 GHz | [10] |
| Characterization of Cooking oils | Metamaterial—SRR | Designed | Medium | Estimated: 0.01 mL | 1120 | 30 GHz | [14] |
| Determination of frying time | Transmission line—sensor 1 | PCB | Medium | Immersed | Estimated 243 | Estimated 5.45 GHz | [15] |
| Determination of frying time | Transmission line—sensor 2 | PCB | Medium | Immersed | Estimated 270 | Estimated 5.45 GHz | [15] |
| Identification of edible oils | Meta-surface absorber | PCB | Medium | Estimated <1 mL | 500 | 9.887 GHz | [16] |
| Adulteration detection | EBG-inspired Patch resonator | PDMS | High | 0.8 mL | 205.1 | 2.592 GHz | [18] |
| Dielectric characterization | Double SRR | PCB | Medium | Immersed | 74.37 | 1.85 GHz | [19] |
| Proposed sensor | SSPP | Hybrid | Simple | 0.8 mL | 850 | 6.32 GHz | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podunavac, I.; Radonic, V.; Bengin, V.; Jankovic, N. Microwave Spoof Surface Plasmon Polariton-Based Sensor for Ultrasensitive Detection of Liquid Analyte Dielectric Constant. Sensors 2021, 21, 5477. https://doi.org/10.3390/s21165477
Podunavac I, Radonic V, Bengin V, Jankovic N. Microwave Spoof Surface Plasmon Polariton-Based Sensor for Ultrasensitive Detection of Liquid Analyte Dielectric Constant. Sensors. 2021; 21(16):5477. https://doi.org/10.3390/s21165477
Chicago/Turabian StylePodunavac, Ivana, Vasa Radonic, Vesna Bengin, and Nikolina Jankovic. 2021. "Microwave Spoof Surface Plasmon Polariton-Based Sensor for Ultrasensitive Detection of Liquid Analyte Dielectric Constant" Sensors 21, no. 16: 5477. https://doi.org/10.3390/s21165477
APA StylePodunavac, I., Radonic, V., Bengin, V., & Jankovic, N. (2021). Microwave Spoof Surface Plasmon Polariton-Based Sensor for Ultrasensitive Detection of Liquid Analyte Dielectric Constant. Sensors, 21(16), 5477. https://doi.org/10.3390/s21165477






