Parallel Potentiometric and Capacitive Response in a Water-Gate Thin Film Transistor Biosensor at High Ionic Strength
Abstract
1. Introduction
2. Materials and Methods
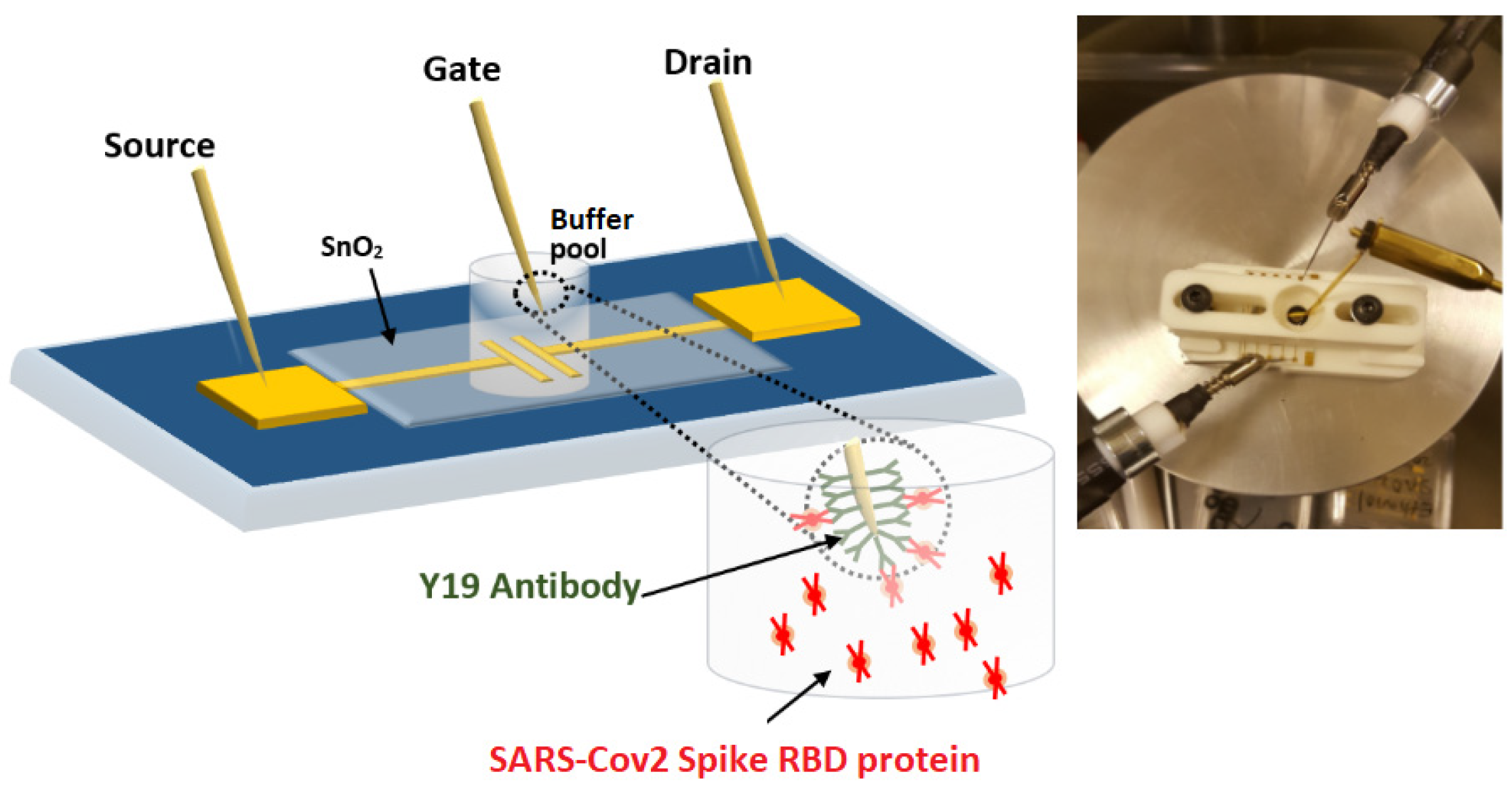
2.1. Preparing WGTFT Substrates
2.2. Sensitising the WGTFT Gate Contact
2.3. Contacting and Characterising the WGTFT Sensor
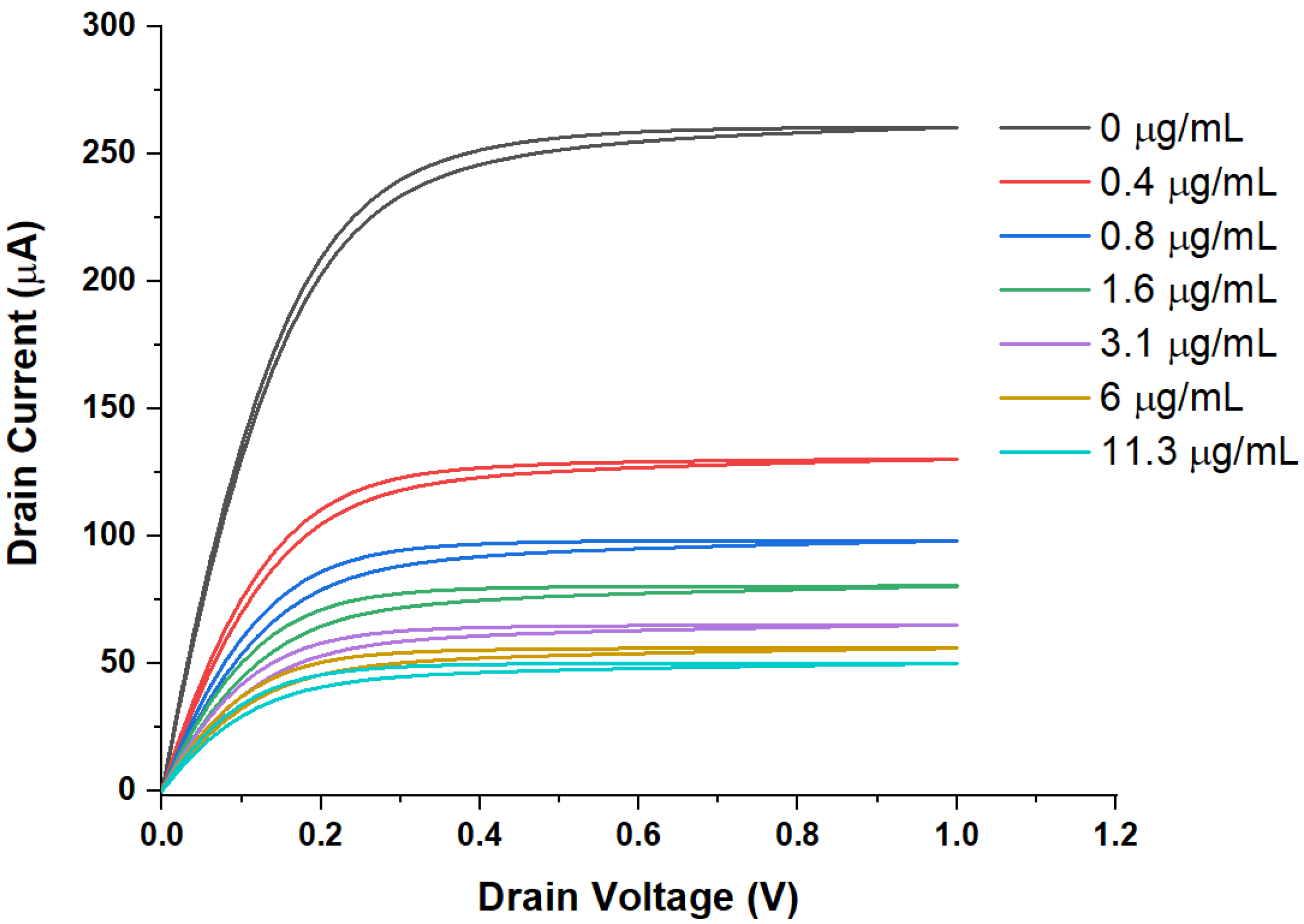
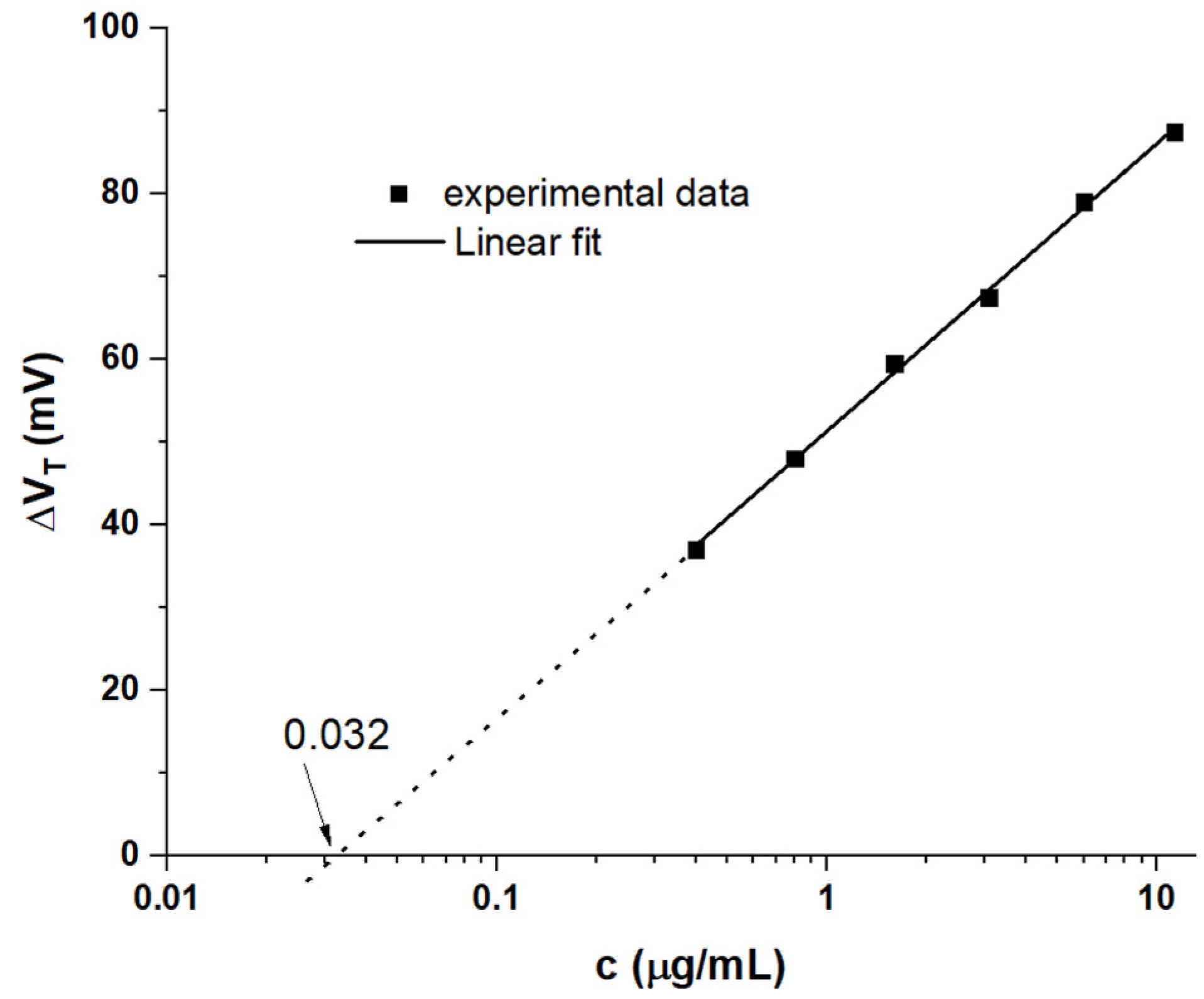
3. Results
WGTFT Characteristics under Spike Protein Exposure
4. Discussion
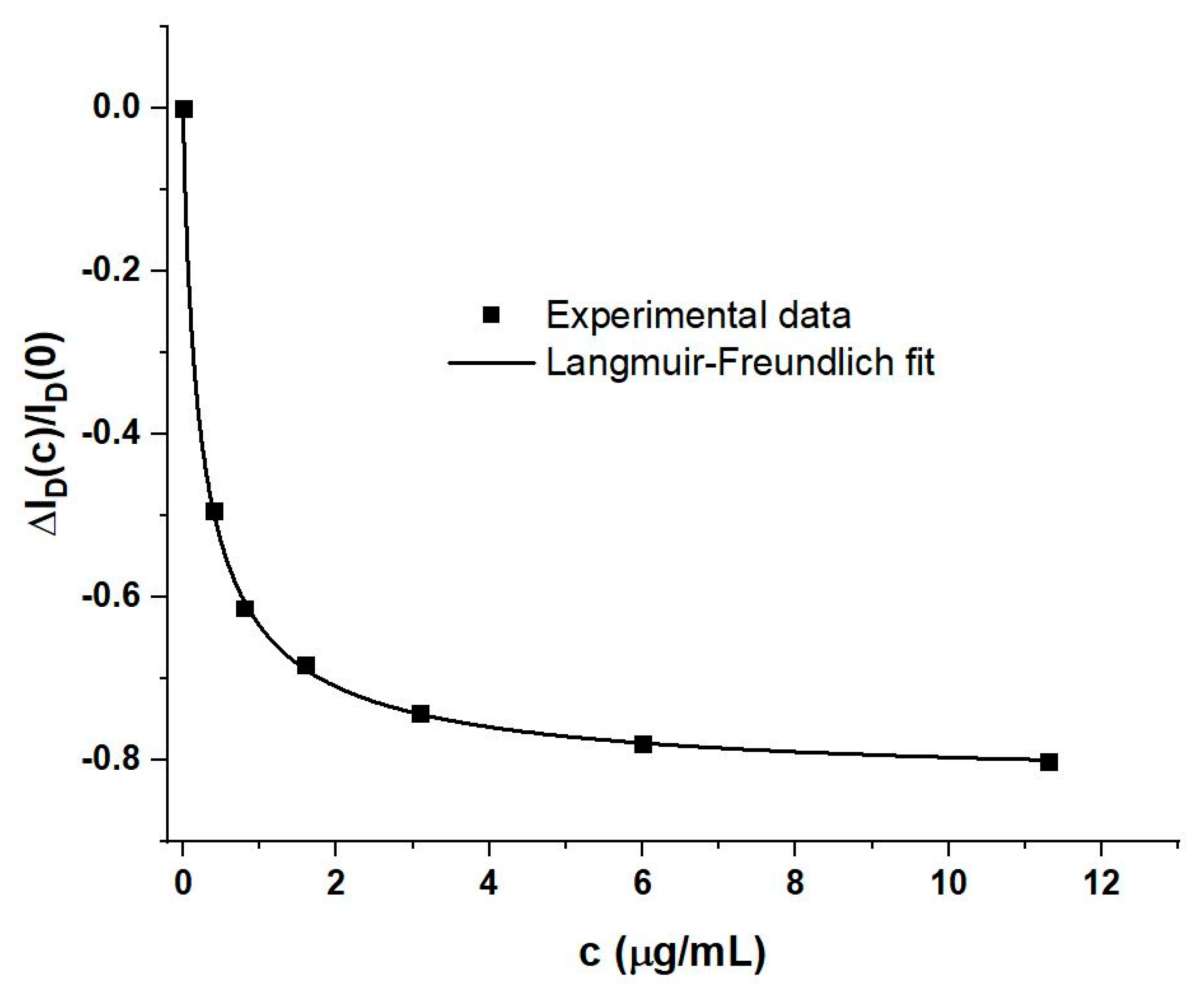
4.1. Generic Evaluation of WGTFT Response to RBD Spike Protein
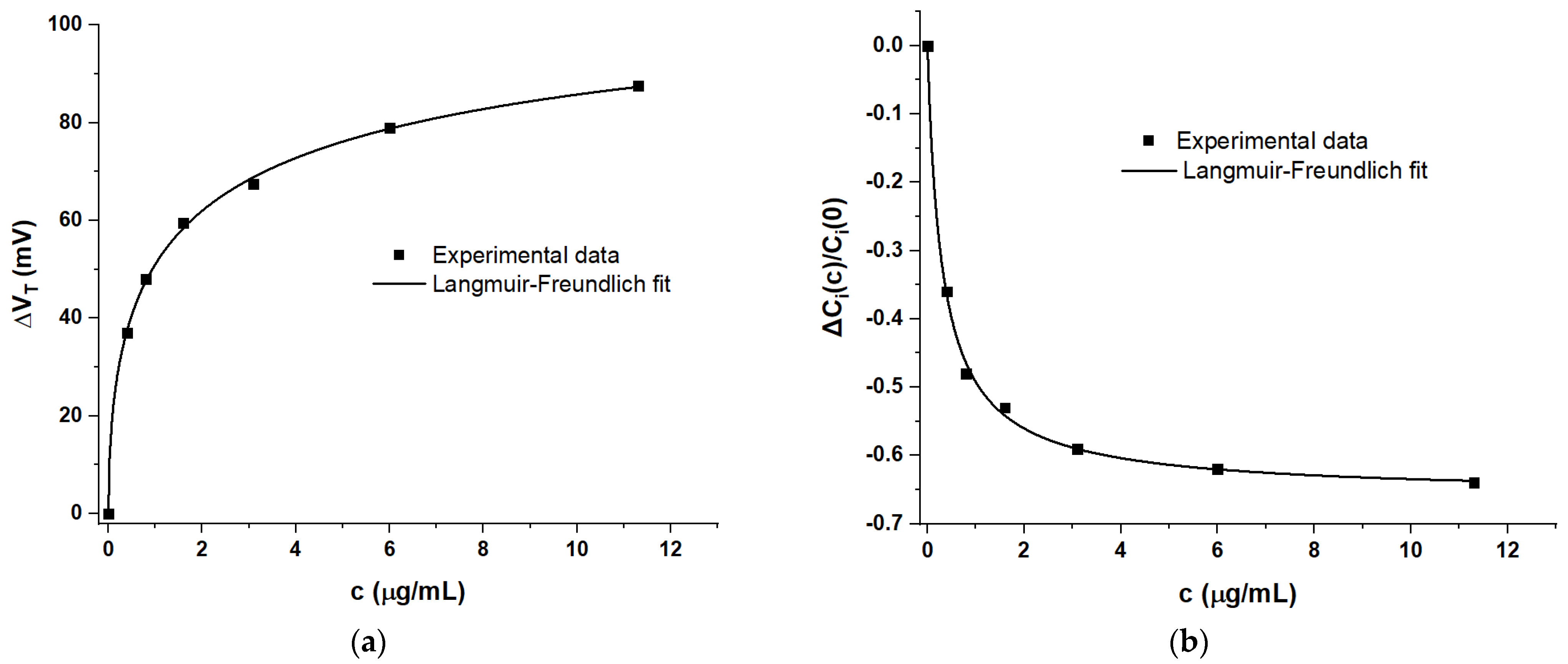
4.2. Delineating Capacitive and Potentiometric WGTFT Response
4.3. Modelling Response Characteristics
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bergveld, P. Development of an Ion-Sensitive Solid-State Device for Neurophysiological Measurements. IEEE Trans. Biomed. Eng. 1970, 17, 70–71. [Google Scholar] [CrossRef]
- Bergveld, P. Thirty years of ISFETOLOGY: What happened in the past 30 years and what may happen in the next 30 years. Sens. Actuators B Chem. 2003, 88, 1–20. [Google Scholar] [CrossRef]
- Poghossian, A.; Jablonski, M.; Molinnus, D.; Wege, C.; Schöning, M.J. Field-Effect Sensors for Virus Detection: From Ebola to SARS-CoV-2 and Plant Viral Enhancers. Front. Plant Sci. 2020, 11, 598103. [Google Scholar] [CrossRef]
- van der spiegel, J.; Lauks, I.; Chan, P.; Babic, D. The extended gate chemically sensitive field effect transistor as multi-species microprobe. Sens. Actuators 1983, 4, 291–298. [Google Scholar] [CrossRef]
- Kergoat, L.; Herlogsson, L.; Braga, D.; Piro, B.; Pham, M.-C.; Crispin, X.; Berggren, M.; Horowitz, G. A Water-Gate Organic Field-Effect Transistor. Adv. Mater. 2010, 22, 2565–2569. [Google Scholar] [CrossRef]
- Casalini, S.; Leonardi, F.; Cramer, T.; Biscarini, F. Organic field-effect transistor for label-free dopamine sensing. Org. Electron. 2013, 14, 156–163. [Google Scholar] [CrossRef]
- Berto, M.; Vecchi, E.; Baiamonte, L.; Condò, C.; Sensi, M.; Di Lauro, M.; Sola, M.; De Stradis, A.; Biscarini, F.; Minafra, A.; et al. Label free detection of plant viruses with organic transistor biosensors. Sens. Actuators B Chem. 2019, 281, 150–156. [Google Scholar] [CrossRef]
- Alghamdi, N.; Alqahtani, Z.; Zhou, C.; Sano, N.; Conte, M.; Grell, M. Sensing aromatic pollutants in water with catalyst-sensitized water-gated transistor. Chem. Pap. 2020, 74, 4169–4180. [Google Scholar] [CrossRef]
- Palazzo, G.; De Tullio, D.; Magliulo, M.; Mallardi, A.; Intranuovo, F.; Mulla, M.Y.; Favia, P.; Vikholm-Lundin, I.; Torsi, L. Detection Beyond Debye’s Length with an Electrolyte-Gated Organic Field-Effect Transistor. Adv. Mater. 2015, 27, 911–916. [Google Scholar] [CrossRef]
- Seo, G.; Lee, G.; Kim, M.J.; Baek, S.-H.; Choi, M.; Ku, K.B.; Lee, C.-S.; Jun, S.; Park, D.; Kim, H.G.; et al. Rapid Detection of COVID-19 Causative Virus (SARS-CoV-2) in Human Nasopharyngeal Swab Specimens Using Field-Effect Transistor-Based Biosensor. ACS Nano 2020, 14, 5135–5142. [Google Scholar] [CrossRef]
- Schmoltner, K.; Kofler, J.; Klug, A.; List-Kratochvil, E.J.W. Electrolyte-Gated Organic Field-Effect Transistor for Selective Reversible Ion Detection. Adv. Mater. 2013, 25, 6895–6899. [Google Scholar] [CrossRef]
- Alghamdi, N.; Alqahtani, Z.; Grell, M. Sub-nanomolar detection of cesium with water-gated transistor. J. Appl. Phys. 2019, 126, 064502. [Google Scholar] [CrossRef]
- Alqahtani, Z.; Alghamdi, N.; Grell, M. Monitoring the lead-and-copper rule with a water-gated field effect transistor. J. Water Health 2020, 18, 159–171. [Google Scholar] [CrossRef]
- Althagafi, T.M.; Al Baroot, A.F.; Algarni, S.A.; Grell, M. A membrane-free cation selective water-gated transistor. Analyst 2016, 141, 5571–5576. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Buth, F.; Kumar, D.; Stutzmann, M.; Garrido, J.A. Electrolyte-gated organic field-effect transistors for sensing applications. Appl. Phys. Lett. 2011, 98, 153302. [Google Scholar] [CrossRef]
- Manoli, K.; Palazzo, G.; Macchia, E.; Tiwari, A.; di Franco, C.; Scamarcio, G.; Favia, P.; Mallardi, A.; Torsi, L. Electrolyte gated TFT biosensors based on the Donnan’s capacitance of anchored biomolecules. In Proceedings of the Organic Sensors and Bioelectronics X, San Diego, CA, USA, 6–7 August 2017; Volume 10364, p. 103640J. [Google Scholar]
- Alqahtani, Z.; Alghamdi, N.; Robshaw, T.J.; Dawson, R.; Ogden, M.D.; Buckely, A.; Grell, M. Water-Gated Transistor Using Ion Exchange Resin for Potentiometric Fluoride Sensing. Micromachines 2020, 11, 923. [Google Scholar] [CrossRef]
- Kergoat, L.; Piro, B.; Berggren, M.; Pham, M.C.; Yassar, A.; Horowitz, G. DNA detection with a water-gated organic field-effect transistor. Org. Electron. 2012, 13, 1–6. [Google Scholar] [CrossRef]
- Horowitz, G. Organic Field-Effect Transistors. Adv. Mater. 1998, 10, 365–377. [Google Scholar] [CrossRef]
- Kumar Singh, V.; Mazhari, B. Measurement of threshold voltage in organic thin film transistors. Appl. Phys. Lett. 2013, 102, 253304. [Google Scholar] [CrossRef]
- Burt, R.; Birkett, G.; Zhao, X.S. A review of molecular modelling of electric double layer capacitors. Phys. Chem. Chem. Phys. 2014, 16, 6519–6538. [Google Scholar] [CrossRef]
- Gold Plated Needles. Available online: https://www.debscrossstitch.co.uk/gold-plated-needles-34-c.asp (accessed on 18 August 2021).
- SARS-CoV-2 Spike RBD Proteins. Available online: https://www.invivogen.com/sars2-spike-proteins (accessed on 18 August 2021).
- Anti-SARS-CoV Spike mAb (Clone CR3022), Human & Mouse Isotypes. Available online: https://www.invivogen.com/sars2-spike-cr3022-mab-isotypes (accessed on 18 August 2021).
- Shihana, F.; Dawson, A.H.; Dissanayake, D.M. Method of stabilizing blood for the determination of methemoglobin. J. Clin. Lab. Anal. 2011, 25, 366–368. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, K.; Sun, H.; Zhao, S.; Chen, X.; Qian, D.; Mao, H.; Zhao, J. Novel graphene biosensor based on the functionalization of multifunctional nano-bovine serum albumin for the highly sensitive detection of cancer biomarkers. Nano Micro Lett. 2019, 11, 20. [Google Scholar] [CrossRef]
- Sze, S.M. Physics of Semiconductor Devices, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 1981. [Google Scholar]
- Hill, A.V. The possible effects of the aggregation of the molecules of hæmoglobin on its dissociation curves. J. Physiol. 1910, 40, iv–vii. [Google Scholar]
- Pawlowski, P.H. Charged amino acids may promote coronavirus SARS-CoV-2 fusion with the host cell. AIMS Biophys. 2021, 8, 111–120. [Google Scholar] [CrossRef]
- Stern, E.; Wagner, R.; Sigworth, F.J.; Breaker, R.; Fahmy, T.M.; Reed, M.A. Importance of the Debye Screening Length on Nanowire Field Effect Transistor Sensors. Nano Lett. 2007, 7, 3405–3409. [Google Scholar] [CrossRef]
- Melzer, K.; Münzer, A.M.; Jaworska, E.; Maksymiuk, K.; Michalska, A.; Scarpa, G. Selective ion-sensing with membrane-functionalized electrolyte-gated carbon nanotube field-effect transistors. Analyst 2014, 139, 4947–4954. [Google Scholar] [CrossRef]
- Guo, D.; Zhuo, M.; Zhang, X.; Xu, C.; Jiang, J.; Gao, F.; Wan, Q.; Li, Q.; Wang, T. Indium-tin-oxide thin film transistor biosensors for label-free detection of avian influenza virus H5N1. Anal. Chim. Acta 2013, 773, 83–88. [Google Scholar] [CrossRef] [PubMed]


| c (μg/mL) | VDX (mV) | (ID/VD)X (mA/V) | VT | W/L μCi(c) (mA/V2) | ΔVT | ΔCi(c)/Ci(0) |
|---|---|---|---|---|---|---|
| (mV) | (mV) | |||||
| 0 | 550 | 1.6 | 25 | 5.8 | 0 | 0 |
| 0.4 | 476 | 0.88 | 62 | 3.7 | 37 | −0.36 |
| 0.8 | 454 | 0.69 | 73 | 3 | 48 | −0.48 |
| 1.6 | 431 | 0.57 | 84.5 | 2.7 | 59.5 | −0.53 |
| 3.1 | 415 | 0.49 | 92.5 | 2.4 | 67.5 | −0.59 |
| 6 | 392 | 0.43 | 104 | 2.2 | 79 | −0.62 |
| 11.3 | 375 | 0.4 | 112.5 | 2.1 | 87.5 | −0.64 |
| Parameter | ΔID(∞)/ID(0) | ΔVT(∞) | ΔCi(∞)/Ci(0) | k | Β | |
|---|---|---|---|---|---|---|
| Metric | (mV) | (mL/μg) | ||||
| Amperometric | −0.83 ± 0.01 | ----- | ----- | 3.97 ± 0.15 | 0.85 ± 0.05 | |
| Potentiometric | ----- | 120 ± 11 | ----- | 0.57 ± 0.21 | 0.53 ± 0.06 | |
| Capacitive | ----- | ----- | −0.659 ± 0.018 | 3.16 ± 0.25 | 0.94 ± 0.13 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlQahtani, H.; Alswieleh, A.; Al-Khurayyif, I.; AlGarni, S.; Grell, M. Parallel Potentiometric and Capacitive Response in a Water-Gate Thin Film Transistor Biosensor at High Ionic Strength. Sensors 2021, 21, 5618. https://doi.org/10.3390/s21165618
AlQahtani H, Alswieleh A, Al-Khurayyif I, AlGarni S, Grell M. Parallel Potentiometric and Capacitive Response in a Water-Gate Thin Film Transistor Biosensor at High Ionic Strength. Sensors. 2021; 21(16):5618. https://doi.org/10.3390/s21165618
Chicago/Turabian StyleAlQahtani, Hadi, Abdullah Alswieleh, Ibrahim Al-Khurayyif, Saad AlGarni, and Martin Grell. 2021. "Parallel Potentiometric and Capacitive Response in a Water-Gate Thin Film Transistor Biosensor at High Ionic Strength" Sensors 21, no. 16: 5618. https://doi.org/10.3390/s21165618
APA StyleAlQahtani, H., Alswieleh, A., Al-Khurayyif, I., AlGarni, S., & Grell, M. (2021). Parallel Potentiometric and Capacitive Response in a Water-Gate Thin Film Transistor Biosensor at High Ionic Strength. Sensors, 21(16), 5618. https://doi.org/10.3390/s21165618






